Заряженная частица движется по окружности радиусом R = 1 см в однородном магнитном поле с индукцией B = 0,1 Тл. Паралле — Спрашивалка
Заряженная частица движется по окружности радиусом R = 1 см в однородном магнитном поле с индукцией B = 0,1 Тл. Паралле — СпрашивалкаЮлия Деревенская
Заряженная частица движется по окружности радиусом R = 1 см в
однородном магнитном поле с индукцией B = 0,1 Тл. Параллельно магнитному
полю возбуждено электрическое поле напряженностью Е = 100 В/м. Вычис-
лить промежуток времени ∆t, в течение которого должно действовать электри-
ческое поле, для того чтобы кинетическая энергия частицы возросла вдвое
- радиус
- окружность
- частица
- индукция
КС
Кумушка Сабирова
Радиус окружности при движении в магнитном поле выражается формулой r = q/m * v/B. Нам сейчас по фигу, чему конкретно равны q, m и v, важно лишь, что формула вот такая, и что скорость всегда направлена перпендикулярно линиям магнитного поля.
Нам сейчас по фигу, чему конкретно равны q, m и v, важно лишь, что формула вот такая, и что скорость всегда направлена перпендикулярно линиям магнитного поля.
Похожие вопросы
электрон движется в однородном магнитном поле с индукцией 10^-2 Тл.
3.3.16. В однородном магнитном поле с индукцией 1,00 Тл находится квадратная рамка со стороной 10,0 см, по которой течёт
Электрон движется в однородном постоянном магнитном поле с индукцией Тл по окружности радиусом см. Определите импульс
Во сколько раз увеличится радиус траектории движения заряженной частицы, движущейся в однородном магнитном поле ?
Электрон влетает в однородное магнитное поле со скоростью 10000 км/с и движется по окружности радиусом 2 см.
Электрон движется в однородном магнитном поле по кругу радиусом 9,1 мкм. Модуль магнитной индукции поля равен 3 Тл. Опред
в однородное магнитное поле влетает отрицательно заряженная частица со скоростью v (см рис 207)
Кольцо радиусом R=10см находится в однородном магнитном поле (В=0,318 Тл).
от каких факторов зависит радиус кривизны траектории заряженной частицы, которая движется по кругу в магнитном поле
протон и альфа частица влетают в однородное магнитное поле перпендикулярно линиям индукции и движутся по окружностям
2.
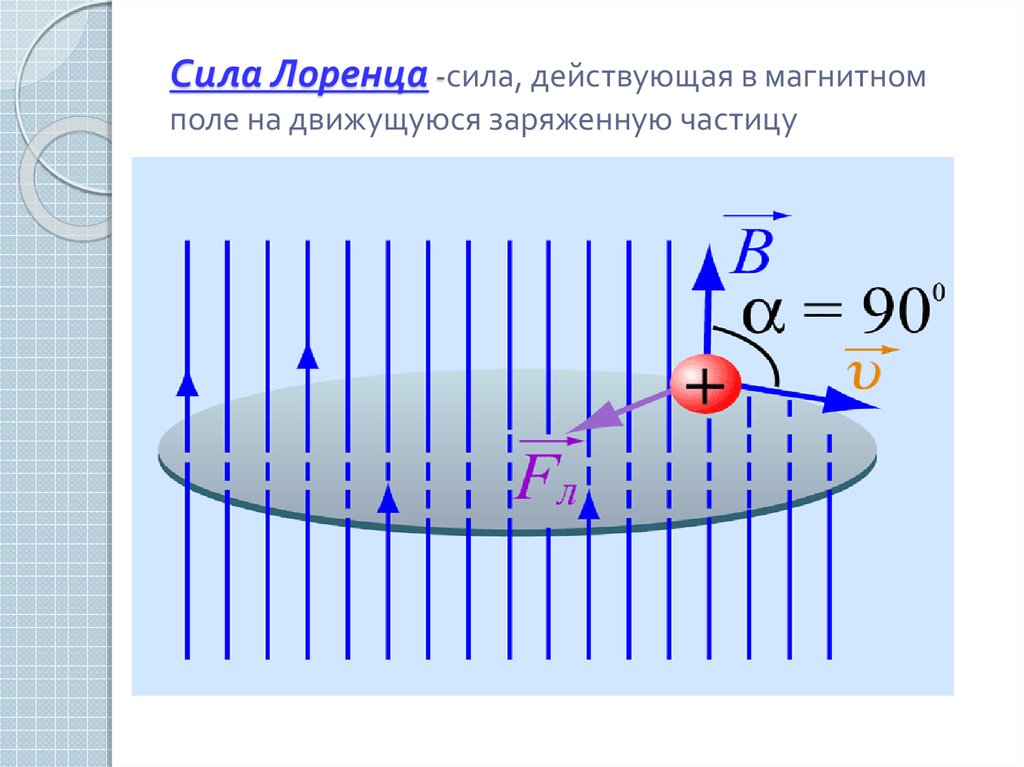
 1. Сила Лоренца. Движение заряженной частицы в однородном постоянном магнитном поле
1. Сила Лоренца. Движение заряженной частицы в однородном постоянном магнитном полеОсновные формулы
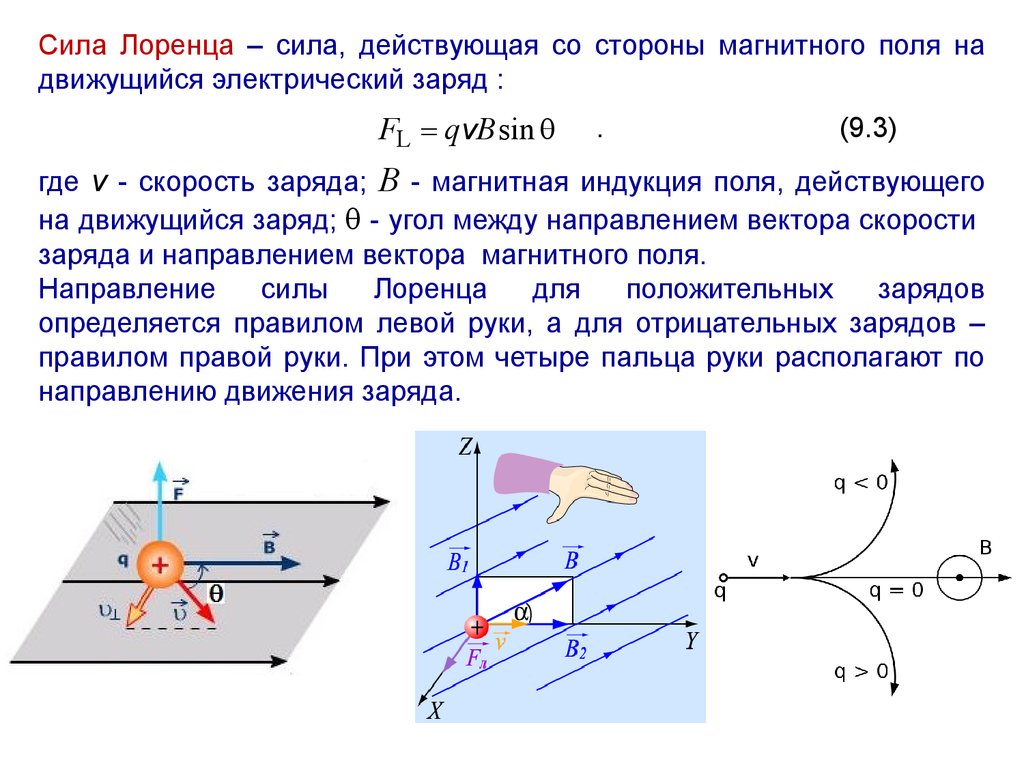
Сила, действующая на электрический заряд , движущийся со скоростью в магнитном поле
, (18)
где – вектор магнитной индукции поля.
Модуль силы, действующей на заряженную частицу, движущуюся в магнитном поле
, (19)
где – модуль заряда частицы; – модуль вектора скорости; – модуль вектора индукции магнитного поля, – угол между векторами и .
Направление силы определяется по правилу левой руки:
если
ладонь левой руки расположить так, чтобы
в нее входил вектор магнитной индукции ,
а четыре вытянутых пальца направить
вдоль скорости движения положительного
заряда (против направления движения
отрицательного заряда), то отогнутый
на 90° большой палец покажет направление
силы, действующей на заряд.
Если заряд движется в области, где существуют одновременно электрическое и магнитное поля, то на него действует полная сила
, (20)
формула (20) называется формулой Лоренца.
Методические рекомендации
1. Полная электромагнитная сила (сила Лоренца), действующая на заряд, определяется формулой (20). Данная формула справедлива как для постоянных, так и для переменных электрических и магнитных полей.
Важная
особенность силы Лоренца – она всегда
перпендикулярна вектору скорости заряда
и поэтому не совершает над зарядом
работы. Следовательно, в постоянном
магнитном поле энергия движущейся
заряженной частицы всегда постоянна.
Разделение полной электромагнитной силы на электрическую и магнитную зависит от выбора системы отсчета, так как магнитная составляющая силы Лоренца меняется при переходе от одной системы отсчета к другой, а значит, меняется и электрическая составляющая.
2. Под действием силы Лоренца заряженные частицы движутся в магнитном поле по криволинейным траекториям. Характер движения частицы в магнитном поле зависит от угла между первоначальным направлением скорости движения частицы и направлением линий индукции магнитного поля.
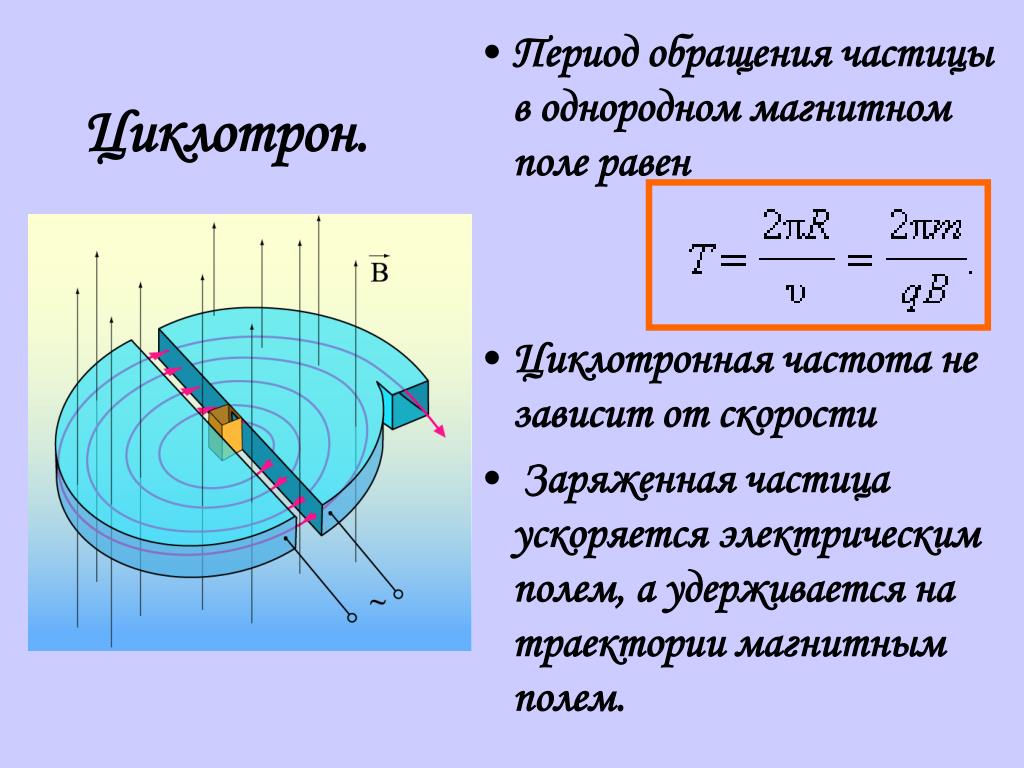
Если скорость частицы перпендикулярна линиям магнитной индуции, то частица движется по круговой траектории (рис. 23).
Радиус окружности траектории
;
Рис. 23
период вращения частицы по окружности:
,
где
–
масса частицы;
–
модуль скорости частицы;
–
модуль вектора индукции магнитного
поля;
–
модуль электрического заряда.
Если заряженная частица движется вдоль линий магнитной индукции, сила Лоренца на нее не действует и характер ее движения не меняется.
Если угол между первоначальным направлением скорости частицы и линиями магнитной индукции не равен ни 0°, ни 90°, ни 180°, траектория движения частицы представляет собой винтовую линию, накручивающуюся на линии магнитной индукции (рис. 24).
Рис. 24
– тангенциальная составляющая скорости ; ;
– нормальная составляющая скорости; ;
– шаг винтовой линии; .
3.
При движении заряженной частицы в
области пространства, занятой одновременно
и электрическим и магнитным полями
характер ее движения зависит от
направления этих полей и величины сил,
действующих с их стороны, а также от
скорости частицы.
► Векторы и взаимно-перпендикулярны и скорость положительно заряженной частицы перпендикулярна силовым линиям этих полей. В этом случае на частицу действуют две силы: электрическая и магнитная , которые могут быть как сонаправлены, так и противоположно направлены. Если силы противоположно направлены и равны по модулю ( ), то частица будет двигаться равномерно и прямолинейно, согласно первому закону Ньютона.
В случае если силы не уравновешивают друг друга, то движение частицы будет сложным: она будет двигаться с ускорением вдоль линии напряженности электрического поля и совершать вращательное движение вокруг линии индукции магнитного поля.
Если силы, действующие на движущуюся заряженную частицу сонаправлены, то движение частицы также будет представлять суперпозицию двух движений: прямолинейного с ускорением вдоль линий вектора и вращательного вокруг линий вектора .
► Частица
влетает в область пространства параллельно
векторам
и
.
Примеры решения задач
Пример 1. Протон влетает в однородное магнитное поле с индукцией 20 мкТл перпендикулярно линиям индукции магнитного поля. Сколько оборотов в секунду будет делать протон в магнитном поле?
Решение
На заряженную частицу в магнитном поле действует сила
, (а)
где – заряд частицы, – индукция магнитного поля, – скорость частицы, – угол между векторами и .
В данной задаче , значит протон будет двигаться в магнитном поле по окружности радиуса с центростремительным (нормальным) ускорением
(б)
По второму закону Ньютона
, (в)
где
–
масса частицы.
Приравнивая правые части выражений (б) и (в), с учетом формулы (а), получаем
, (г)
так как , то после небольшого преобразования получаем
. (д)
С другой стороны,
, (е)
где – угловая скорость.
Получаем
. (ж)
Приравняем правые части уравнений (д) и (л), получим
,
откуда выразим – частоту вращения, т. е. число оборотов в секунду,
. (и)
Размерность: .
Подставляем числовые значения в формулу (и):
.
Вычисления дают .
Пример 2. Электрон, имеющий скорость 8·106 м/с, влетает в однородное магнитное поле с индукцией 31,4 мТл под углом 30° к его направлению. Определите радиус и шаг винтовой линии, по которой будет двигаться электрон (рис. 24).
Решение
Скорость разложим на две составляющие: тангенциальную , параллельную линиям индукции магнитного поля и нормальную , перпендикулярную им,
; (а)
. (б)
На электрон действует магнитная сила (благодаря нормальной составляющей скорости)
. (в)
Под действием этой силы электрон будет двигаться по окружности радиуса , который можно найти из условия:
, (г)
так
как сила Лоренца является центростремительной
силой.
Из формулы (г) получаем
, (д)
где – модуль заряда электрона; – масса электрона; – индукция магнитного поля.
Вдоль силовых линий поля магнитная сила не действует, поэтому частица движется прямолинейно с постоянной скоростью .
В результате суперпозиции двух движений электрон будет двигаться по винтовой линии радиусом и шагом винта :
, (е)
где – период движения по окружности,
. (ж)
С учетом формул (б), (д) и (ж), уравнение (е) принимает вид:
. (и)
Размерность: .
Подставляем числовые данные в выражение (и):
.
Вычисления дают:
.
Пример 3. Перпендикулярно магнитному полю с индукцией 0,1 Тл возбуждено электрическое поле напряженностью 1·105 В/м. Перпендикулярно обоим полям, не отклоняясь от прямолинейной траектории, движется заряженная частица. Найти скорость этой частицы (рис. 25). Решение Согласно условию задачи, частица движется равномерно и прямолинейно ( ). По первому закону Ньютона геометрическая сумма сил, действующих на частицу, равна нулю. В данном случае на частицу действует сила Лоренца , где – электрическая составляющая силы Лоренца, – её магнитная составляющая (рис. 25). |
|
Следовательно, ,
т. е. электрическая и магнитная силы
равны по модулю и противоположно
направлены:
е. электрическая и магнитная силы
равны по модулю и противоположно
направлены:
откуда скорость частицы равна:
Согласно условию ( ), поэтому
.
Размерность:
.
Подставляем числовые данные: .
Получаем при вычислении: .
Пример 4. Электрон влетает со скоростью 600 м/с в область пространства, где имеются сонаправленные однородные электрическое и магнитное поля, под углом 60° к силовым линиям полей. Напряженность электрического поля 0,2 кВ/м, индукция магнитного поля 20 мТл. С каким ускорением станет двигаться электрон в этой области пространства? (рис. 26). Решение Согласно второму закону Ньютона, ускорение электрона имеет вид: , где
–
сила Лоренца, действующая на электрон
со стороны электрического и магнитного
полей;
–
масса электрона. Сила Лоренца определяется по формуле |
|
,
где – электрическая составляющая силы Лоренца; – её магнитная составляющая (рис. 26).
Вектор направлен противоположно вектору , так как заряд электрона отрицательный. Вектор магнитной силы перпендикулярен вектору магнитной индукции. Следовательно, векторы и взаимно-перпендикулярны.
Модуль силы находится по теореме Пифагора:
,
где – модуль заряда электрона (элементарный заряд).
Ускорение
.
Направление совпадает с направлением вектора , определяемом по правилу сложения векторов.
Подставим числовые значения:
=
600 м/с;
=
60°; =
0,2 кВ/м = 200 В/м;
=
20 мТл = 2·10-2 Тл;
=
1,6 ·10-19 Кл;
=
9,11·10-31 кг.
Вычисления дают: = 3,5 ·1013 м/с2.
Пример 5. Шарик массой , заряженный положительным зарядом и подвешенный на нити длиной , движется по окружности в вертикальном однородном магнитном поле с индукцией. Определите кинетическую энергию шарика, если во время движения нить образует угол с вертикалью.
Решение
Выберем систему отсчета x0y, начало которой поместим в ту точку пространства, где находится шарик в начальный момент времени. Предположим, что нить – невесома, нерастяжима и неэлектропроводна. Заряженный шарик примем за материальную точку. Заряд шарика будем считать точечным.
На шарик действуют сила тяжести , сила натяжения нити и сила со стороны магнитного поля (рис. 27).
|
|
По второму закону Ньютона
. (а)
(а)
Направление всех сил указано на рис. 27 в предположении, что вектор магнитной индукции направлен вверх, а шарик движется по часовой стрелке.
Запишем уравнение (а) в проекциях на выбранные оси координат
; (б)
. (в)
После преобразования, получаем
; (г)
. (д)
Разделим (г) на (д), получим
. (и)
Шарик движется с нормальным ускорением , (к)
где – линейная скорость шарика по окружности, – радиус окружности.
Из чертежа следует:
. (л)
(л)
Сила Лоренца определяется выражением
, (м)
где = 90° (по условию задачи),
С учетом выражений (к)–(м) уравнение (и) принимает вид:
,
или
.
Решаем квадратное уравнение относительно переменной :
,
получаем
.
Так как модуль скорости > 0, то из последнего выражения следует:
.
Кинетическая энергия определяется соотношением:
.
Задачи для самостоятельного решения
1.
Пучок
электронов движется в вакууме в магнитном
поле с напряженностью 5,56·103 А/м по окружности радиусом 3 см.
Определите скорость и энергию электронов,
период обращения и момент импульса.
(Ответ: = 36,3·106 м/с; = 33·10-23 Дж; = 5·10-9 с; = 99·10-26 (кг·м2)/с).
2. В однородном магнитном поле с индукцией 0,1 Тл по окружности движется электрон. Найти величину эквивалентного кругового тока, созданного движением электрона.
(Ответ: = 4,5·10-10 А).
3. Однозарядный ион натрия прошел ускоряющую разность потенциалов 1 кВ и влетел в однородное магнитное поле с индукцией 0,5 Тл перпендикулярно силовым линиям поля. Определите относительную массу иона, если он описал окружность радиусом 4,37 см.
(Ответ: 23 а.е.м.).
4.
Протон,
прошедший ускоряющую разность потенциалов
600 В, влетел в однородное магнитное поле
с напряженностью 2,4·104 А/м перпендикулярно линиям магнитной
индукции. Найти радиус описанной протоном
окружности, его импульс и частоту
вращения протона в магнитном поле.
(Ответ: = 0,33 м; = 18·10-21 Н·с; = 3·103с-1).
5. Два иона, имеющие одинаковый заряд и прошедшие одинаковую ускоряющую разность потенциалов, влетели в однородное магнитное поле. Первый ион движется по дуге окружности радиусом 5 см, второй – по дуге окружности радиусом 2,5 см. Определите отношение масс ионов.
(Ответ: ).
6. Электрон влетает в область магнитного поля ширины . Скорость электрона перпендикулярна как индукции поля, так и границам области. Под каким углом к границам области электрон вылетит из магнитного поля?
(Ответ: , если ; рад, если ).
7. Предполагая, что электрон в атоме водорода движется по круговой орбите радиусом 53 пм, определите период обращения электрона вокруг ядра и индукцию магнитного поля, создаваемого движущимся электроном в центре его орбиты.
(Ответ:
=
1,5·10-16 с;
=
12,45 Тл).
8. Частица, имеющая элементарный заряд, влетает в однородное магнитное поле под углом 45° к линиям индукции и движется по винтовой линии с шагом 2 см. Определите импульс частицы, если индукция поля равна 10-2 Тл.
(Ответ: = 7,2·10-24 кг·м/с).
9. Электрон, кинетическая энергия которого 1,5 МэВ, движется по окружности в однородном магнитном поле с индукцией 20 мТл. Определите период обращения электрона.
(Ответ: = 7 нс).
10. Электрон в однородном магнитном поле движется по винтовой линии радиусом 5 см и шагом 20 см. Определить скорость электрона, если индукция магнитного поля 0,1 Тл.
(Ответ: = 1,04 Мм/с).
11.
Протон,
находящийся в магнитном поле с индукцией
20 мТл описывает окружность радиусом 40
см. Найти импульс протона и его кинетическую
энергию.
Найти импульс протона и его кинетическую
энергию.
(Ответ: = 1,3·10-21 кг·м/с; = 5·10-16 Дж).
12. Протон и альфа-частица влетают в однородное магнитное поле перпендикулярно его силовым линиям. Во сколько раз различаются радиусы окружностей, по которым движутся эти частицы, если у них одинаковы: а) скорость; б) кинетическая энергия? Заряд альфа-частицы в два раза больше заряда протона, а масса альфа-частицы в четыре раза больше массы протона.
(Ответ: (а) ; б) ).
13. В масс-спектрографе заряженная частица, пролетев без начальной скорости ускоряющую разность потенциалов , влетает в однородное магнитное поле индукцией перпендикулярно магнитным линиям. Удельный заряд частицы . Определить диаметр окружности , по которой стала двигаться частица.
(Ответ: ).
14. В вертикальном направлении создано однородное магнитное поле индукцией . Шарик массой и зарядом , подвешенный на нити длиной , движется по окружности так, что нить составляет угол с вертикалью. Найти угловую скорость движения шарика.
(Ответ: ).
15. Однозарядные ионы гелия и водорода, ускоренные из состояния покоя в электрическом поле напряжением 2 кВ, влетают вместе в магнитное поле индукцией 100 мТл перпендикулярно магнитным линиям. Описав полуокружность, они попадают на фотопластинку. Найти расстояние между следами этих ионов на фотопластинке.
(Ответ: = 1,3 см).
16. Электрон с кинетической энергией 1 кэВ попал в однородное магнитное поле с индукцией 21 мТл и стал двигаться по окружности. Определить магнитный момент эквивалентного кругового тока.
(Ответ: = 7,6·10-15 А·м2).
17.
Электрон,
ускоренный разностью потенциалов 300 В,
движется параллельно прямолинейному
длинному проводу на расстоянии 4 мм от
него. Какая сила действует на электрон,
если по проводнику пропустить ток силой
5
А?
Какая сила действует на электрон,
если по проводнику пропустить ток силой
5
А?
(Ответ: = 4·10-16 Н).
18. Электрон влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Скорость электрона 4·107 м/с. Индукция магнитного поля 1 мТл. Найти тангенциальное и нормальное ускорения электрона в магнитном поле. (Ответ: = 0; = 7·1015 м/с2). 19.
Пучок
электронов, ускоренных разностью
потенциалов 300 В, влетает в однородное
магнитное поле, направленное от чертежа
«к нам»
(рис. 28). Ширина
поля
=
2,5 см. В отсутствие магнитного поля
пучок электронов дает пятно в точке
А флуоресцирующего экрана, расположенного
на расстоянии
=
5 см от края полюсов магнита. |
|
(Ответ: x = 4,9 см).
20. В
установке для разделения изотопов
U235 и U238 пучок однократно ионизованных
ускоренных ионов с энергией 5 кэВ
попадает от источника через щель S
(рис. 29) в однородное магнитное поле,
перпендикулярное к плоскости рисунка.
В магнитном поле ионы разных масс
движутся по различным окружностям и,
совершив полуоборот, попадают в
приемники. Конструкция последних
должна быть такова, чтобы расстояние
между пучками изотопов на выходе было
не меньше
=
5 мм. (Ответ: 4000 Гс). |
|
21. В конденсаторе, электроды которого составляют часть коаксиальных цилиндрических поверхностей радиусами 5 и 6 см, вдоль оси цилиндров действует однородное магнитное поле с индукцией 0,2 Тл (рис. 30). Через узкую щель в диафрагме АА в конденсатор влетает α-частица с энергией 1 кэВ. Какую разность потенциалов следует создать между электродами конденсатора, чтобы α-частица прошла посередине между электродами? (Внешний электрод имеет отрицательный потенциал).
(Ответ: = 38,5 В).
22.
В
магнетроне анод представляет металлический
цилиндр радиусом
=1
см, а катод – металлическую нить радиусом ,
расположенную по оси цилиндра (рис. 31).
Постепенно увеличивая индукцию магнитного
поля, направленного вдоль оси цилиндра,
добились того, что при анодном напряжении
100 В и индукции 6,7·10-3 Тл анодный ток стал равен нулю. Какое
значение удельного заряда получается
по результатам этого опыта?
Какое
значение удельного заряда получается
по результатам этого опыта?
(Ответ: = 1,76·1011 Кл/кг).
Рис. 30 Рис. 31
23. Магнитное поле напряженностью 8 кА/м и электрическое поле напряженностью 1 кВ/м направлены одинаково. Электрон влетает в электромагнитное поле со скоростью 105 м/с. Найти нормальное, тангенциальное и полное ускорение электрона. Задачу решить для случая, когда скорость электрона направлена параллельно силовым линиям полей.
(Ответ: = 0; = 1,76·1014 м/с2).
24.
Магнитное
поле напряженностью 8 кА/м и электрическое
поле напряженностью 1 кВ/м направлены
одинаково. Электрон влетает в
электромагнитное поле со скоростью 105 м/с. Найти нормальное, тангенциальное
и полное ускорение электрона. Задачу
решить для случая, когда скорость
электрона направлена перпендикулярно
силовым линиям полей.
Электрон влетает в
электромагнитное поле со скоростью 105 м/с. Найти нормальное, тангенциальное
и полное ускорение электрона. Задачу
решить для случая, когда скорость
электрона направлена перпендикулярно
силовым линиям полей.
(Ответ: = 0; = 2,5·1014 м/с2).
25. Магнитное поле с индукцией 0,5 мТл направлено перпендикулярно электрическому полю напряженностью 1 кВ/м. Электрон влетает в электромагнитное поле перпендикулярно к плоскости, в которой лежат векторы и . Найти скорость электронов, если при одновременном действии обоих полей пучок не испытывает отклонения. Каким будет радиус траектории движения электронов при условии включения одного магнитного поля?
(Ответ: = 2·106 м/с; = 2,3 см)
26.
Электрон
влетает в плоский горизонтальный
конденсатор параллельно его пластинам
со скоростью 107 м/с. Длина конденсатора 5 см. Напряженность
электрического поля конденсатора 10
кВ/м. При вылете из конденсатора электрон
попадает в магнитное поле, перпендикулярное
к электрическому. Индукция магнитного
поля 10 мТл. Найти радиус и шаг винтовой
траектории электрона в магнитном
поле.
Длина конденсатора 5 см. Напряженность
электрического поля конденсатора 10
кВ/м. При вылете из конденсатора электрон
попадает в магнитное поле, перпендикулярное
к электрическому. Индукция магнитного
поля 10 мТл. Найти радиус и шаг винтовой
траектории электрона в магнитном
поле.
(Ответ: = 5 мм; = 3,6 см).
27. Протон влетел в скрещенные под углом 120° магнитное и электрическое поля. Определить ускорение протона, если его скорость 4·105 м/с перпендикулярна векторам и , напряженность электрического поля 20 кВ/м, индукция магнитного поля 50 мТл.
(Ответ: = 3,3·1012 м/с2)
28.
Через
сечение алюминиевой
пластинки (
– толщина,
–
высота) пропускается ток
=
5 А. Пластинка помещена в магнитное поле,
перпендикулярное к ребру
и
направлению тока. Найти возникающую
при этом поперечную разность потенциалов.
Индукция магнитного поля
=
0,5 Тл. Толщина пластинки
=
0,1 мм. Концентрацию электронов проводимости
считать равной концентрации атомов.
Концентрацию электронов проводимости
считать равной концентрации атомов.
(Ответ: = 2,7 мкВ).
29. Через сечение медной пластинки ( – толщина, – высота) пропускается ток = 20 А. При помещении пластинки в магнитное поле, перпендикулярное к ребру и направлению тока, возникает поперечная разность потенциалов = 3,1 мкВ. Индукция магнитного поля = 1 Тл. Найти концентрацию электронов проводимости в меди и их скорость при этих условиях.
(Ответ: = 8,1 ·1028 м-3; = 0,31 мм/с).
30.
Заряженная
частица, двигаясь перпендикулярно
скрещенным под прямым углом электрическому
(
= 400 кВ/м) и магнитному (
= 0,25 Тл) полям,
не испытывает отклонений от своей
траектории при определенной скорости.
Определить эту скорость и возможные
отклонения от нее, если значения индукции
магнитного и напряженности электрического
полей могут быть обеспечены с точностью,
не превышающей 0,2 %.
(Ответ: = 1,6·106 м/с; = 6,4 ·103 м/с).
11.3 Движение заряженной частицы в магнитном поле – University Physics Volume 2
Глава 11. Магнитные силы и поля
Цели обучения
К концу этого раздела вы сможете:
- Объяснять, как заряженная частица во внешнем магнитном поле совершает круговое движение
- Объясните, как определить радиус кругового движения заряженной частицы в магнитном поле
Заряженная частица испытывает силу при движении через магнитное поле. Что произойдет, если это поле будет однородным по движению заряженной частицы? По какому пути движется частица? В этом разделе мы обсудим круговое движение заряженной частицы, а также другие движения, возникающие в результате попадания заряженной частицы в магнитное поле.
Простейший случай имеет место, когда заряженная частица движется перпендикулярно однородному B -полю ( рис.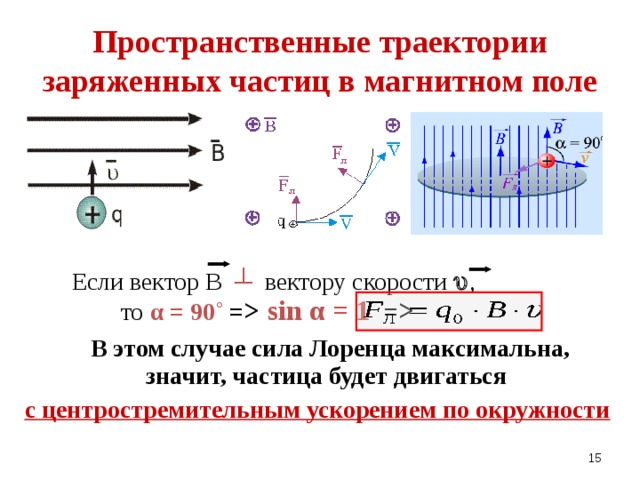 11.7 ). Если поле находится в вакууме, магнитное поле является доминирующим фактором, определяющим движение. Поскольку магнитная сила перпендикулярна направлению движения, заряженная частица движется по криволинейному пути в магнитном поле. Частица продолжает следовать по этому изогнутому пути, пока не образует полный круг. Другой способ взглянуть на это состоит в том, что магнитная сила всегда перпендикулярна скорости, так что она не действует на заряженную частицу. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Направление движения влияет, но не скорость.
11.7 ). Если поле находится в вакууме, магнитное поле является доминирующим фактором, определяющим движение. Поскольку магнитная сила перпендикулярна направлению движения, заряженная частица движется по криволинейному пути в магнитном поле. Частица продолжает следовать по этому изогнутому пути, пока не образует полный круг. Другой способ взглянуть на это состоит в том, что магнитная сила всегда перпендикулярна скорости, так что она не действует на заряженную частицу. Таким образом, кинетическая энергия и скорость частицы остаются постоянными. Направление движения влияет, но не скорость.
 )
9{2}}{r}.[/латекс]
)
9{2}}{r}.[/латекс]Решение для r дает
[латекс]r=\frac{mv}{qB}.[/латекс]
Здесь r — радиус кривизны пути заряженной частицы массой м и зарядом q , движущейся со скоростью v , перпендикулярной магнитному полю напряженностью B . Время прохождения заряженной частицей круговой траектории определяется как период, равный пройденному расстоянию (окружности), деленному на скорость. Основываясь на этом и уравнении 11.4, мы можем получить период движения как
[латекс] T = \ frac {2 \ pi r} {v} = \ frac {2 \ pi } {v} \ phantom {\ rule {0.2em} {0ex}} \ frac {mv} {qB} = \frac{2\pi·m}{qB}.[/latex]
Если скорость не перпендикулярна магнитному полю, то мы можем сравнивать каждую составляющую скорости отдельно с магнитным полем. Составляющая скорости, перпендикулярная магнитному полю, создает магнитную силу, перпендикулярную как этой скорости, так и полю:
[латекс] {v} _ {\ text {perp}} = v \ phantom {\ rule {0. 1em} {0ex}} \ text {sin} \ phantom {\ rule {0.1em} {0ex}} \ theta ,\phantom{\rule{0.5em}{0ex}}{v}_{\text{para}}=v\text{cos}\phantom{\rule{0.1em}{0ex}}\theta .[/ латекс]
1em} {0ex}} \ text {sin} \ phantom {\ rule {0.1em} {0ex}} \ theta ,\phantom{\rule{0.5em}{0ex}}{v}_{\text{para}}=v\text{cos}\phantom{\rule{0.1em}{0ex}}\theta .[/ латекс]
, где [латекс]\тета[/латекс] — угол между и и B . Составляющая, параллельная магнитному полю, создает постоянное движение в том же направлении, что и магнитное поле, что также показано в уравнении 11.7. Параллельное движение определяет шаг p спирали, который представляет собой расстояние между соседними витками. Это расстояние равно параллельной составляющей скорости, умноженной на период:
[латекс] р = {v} _ {\ текст {пара}} Т. [/латекс]
Результатом является спиральное движение , как показано на следующем рисунке.
Рисунок 11.8 Заряженная частица, движущаяся со скоростью, отличной от направления магнитного поля. Составляющая скорости, перпендикулярная магнитному полю, создает круговое движение, тогда как составляющая скорости, параллельная полю, перемещает частицу по прямой линии. Шаг — это горизонтальное расстояние между двумя последовательными кругами. Результирующее движение является спиральным.
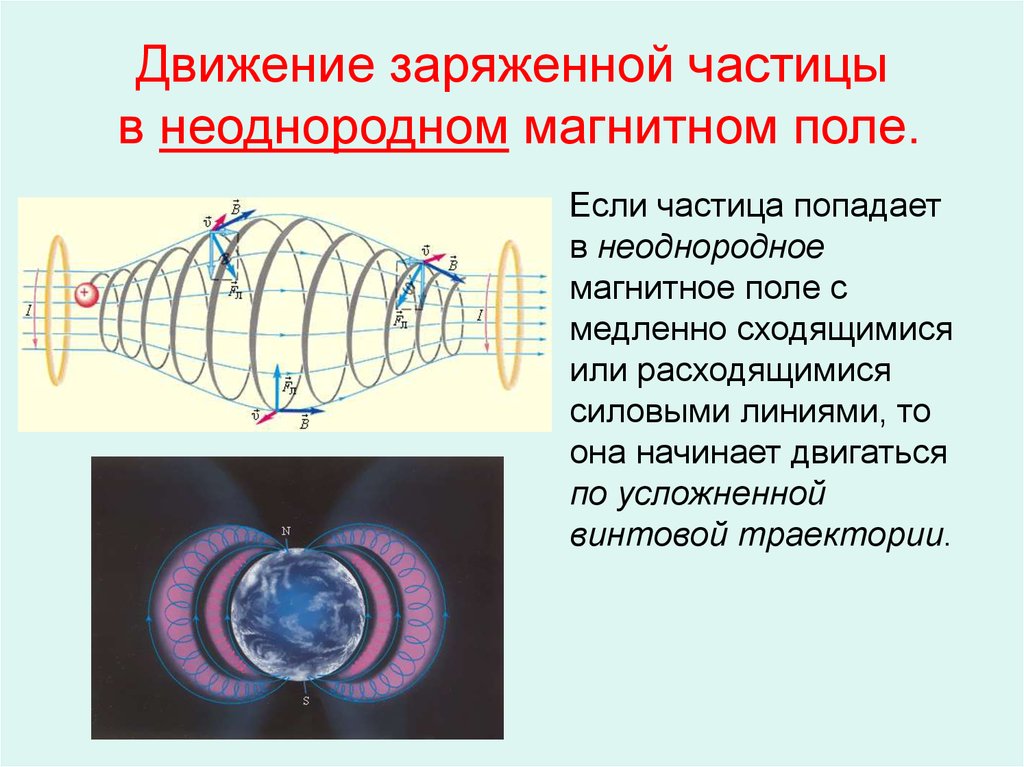
Шаг — это горизонтальное расстояние между двумя последовательными кругами. Результирующее движение является спиральным.Когда заряженная частица движется по винтовой траектории, она может попасть в область, где магнитное поле не является однородным. В частности, предположим, что частица перемещается из области сильного магнитного поля в область более слабого поля, а затем обратно в область более сильного поля. Частица может отразиться назад, прежде чем попасть в область более сильного магнитного поля. Это похоже на волну на струне, идущую от очень легкой тонкой струны к твердой стене и отражающуюся назад. Если отражение происходит с обоих концов, частица попадает в так называемую магнитную бутылку.
Частицы, захваченные магнитными полями, обнаружены в радиационных поясах Ван Аллена вокруг Земли, которые являются частью магнитного поля Земли. Эти пояса были обнаружены Джеймсом Ван Алленом при попытке измерить поток космических лучей на Земле (частиц высокой энергии, приходящих из-за пределов Солнечной системы), чтобы увидеть, был ли он подобен потоку, измеренному на Земле. Ван Аллен обнаружил, что из-за вклада частиц, захваченных магнитным полем Земли, поток на Земле был намного выше, чем в открытом космосе. Полярные сияния, как и знаменитое северное сияние (полярное сияние) в Северном полушарии (рис. 11.9).), представляют собой прекрасные проявления света, излучаемого при рекомбинации ионов с электронами, попадающими в атмосферу, когда они движутся по спирали вдоль силовых линий магнитного поля. (Ионы в основном представляют собой атомы кислорода и азота, которые первоначально ионизируются в результате столкновений с энергичными частицами в атмосфере Земли.) Полярные сияния также наблюдались на других планетах, таких как Юпитер и Сатурн.
Ван Аллен обнаружил, что из-за вклада частиц, захваченных магнитным полем Земли, поток на Земле был намного выше, чем в открытом космосе. Полярные сияния, как и знаменитое северное сияние (полярное сияние) в Северном полушарии (рис. 11.9).), представляют собой прекрасные проявления света, излучаемого при рекомбинации ионов с электронами, попадающими в атмосферу, когда они движутся по спирали вдоль силовых линий магнитного поля. (Ионы в основном представляют собой атомы кислорода и азота, которые первоначально ионизируются в результате столкновений с энергичными частицами в атмосфере Земли.) Полярные сияния также наблюдались на других планетах, таких как Юпитер и Сатурн.
 (кредит b: модификация работы старшего летчика ВВС США Джошуа Странга)
9{-19}\text{C}\right)[/latex] изгибается через 90-градусную область с однородным магнитным полем 0,050 Тл (рис. 11.10). а) В каком направлении должно быть приложено магнитное поле? б) Сколько времени требуется альфа-частицам, чтобы пересечь область однородного магнитного поля? Рисунок 11.10 Вид сверху на установку дефлектора луча.
(кредит b: модификация работы старшего летчика ВВС США Джошуа Странга)
9{-19}\text{C}\right)[/latex] изгибается через 90-градусную область с однородным магнитным полем 0,050 Тл (рис. 11.10). а) В каком направлении должно быть приложено магнитное поле? б) Сколько времени требуется альфа-частицам, чтобы пересечь область однородного магнитного поля? Рисунок 11.10 Вид сверху на установку дефлектора луча.Стратегия
- Направление магнитного поля показывает RHR-1. Ваши пальцы указывают в направлении v , а большой палец должен указывать в направлении силы, влево. Следовательно, поскольку альфа-частицы заряжены положительно, магнитное поле должно быть направлено вниз.
- Период обращения альфа-частицы по окружности равен
[латекс]T=\frac{2\pi m}{qB}.[/latex]
Поскольку частица движется только по четверти окружности, мы можем взять период, умноженный на 0,25, чтобы найти время нужно пройти этот путь.
Решение
Показать Ответ- Начнем с того, что сосредоточимся на альфа-частице, входящей в поле в нижней части изображения. Во-первых, наведите большой палец вверх на страницу. Чтобы ваша ладонь открылась влево, куда указывает центростремительная сила (и, следовательно, магнитная сила), ваши пальцы должны изменить ориентацию, пока они не укажут на страницу. Это направление приложенного магнитного поля. 9{-7}\text{с.}[/латекс]
Значение
Этого времени может быть достаточно, чтобы добраться до материала, который мы хотим бомбардировать, в зависимости от того, насколько короткоживущий радиоактивный изотоп продолжает испускать альфа-частицы. Если бы мы могли увеличить магнитное поле, приложенное к области, это сократило бы время еще больше. Путь, который должны пройти частицы, можно было бы сократить, но это может оказаться неэкономичным с учетом экспериментальной установки.
Проверьте свое понимание
9{5}\phantom{\rule{0. 2em}{0ex}}\text{м/с}\text{.}[/latex] Под каким углом должно быть магнитное поле от скорости, чтобы шаг результирующего винтовое движение равно радиусу спирали?
2em}{0ex}}\text{м/с}\text{.}[/latex] Под каким углом должно быть магнитное поле от скорости, чтобы шаг результирующего винтовое движение равно радиусу спирали?Стратегия
Шаг движения относится к параллельной скорости, умноженной на период кругового движения, тогда как радиус относится к перпендикулярной составляющей скорости. Установив радиус и шаг равными друг другу, найдите угол между магнитным полем и скоростью или [латекс]\тета .[/латекс]
Решение
Показать ОтветШаг определяется уравнением 11.8, период определяется уравнением 11.6, а радиус кругового движения определяется уравнением 11.5. Обратите внимание, что скорость в уравнении радиуса связана только с перпендикулярной скоростью, при которой происходит круговое движение. Поэтому подставляем синусоидальную составляющую общей скорости в уравнение радиуса, чтобы приравнять шаг и радиус:
[латекс]\begin{array}{ccc}\hfill p& =\hfill & r\hfill \\ \hfill {v}_{\parallel}T& =\hfill & \frac{m{v}_{\perp }}{qB}\hfill \\ \hfill v\text{cos}\phantom{\rule{0.
 1em}{0ex}}\theta \frac{2\pi m}{qB}& =\hfill & \frac {mv\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}\theta}{qB}\hfill \\ \hfill 2\pi & = \hfill & \text{tan}\phantom{\rule{0.1em}{0ex}}\theta \hfill \\ \hfill \theta & =\hfill & 81.0\text{°}\text{.}\hfill \ конец{массив}[/латекс]
1em}{0ex}}\theta \frac{2\pi m}{qB}& =\hfill & \frac {mv\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}\theta}{qB}\hfill \\ \hfill 2\pi & = \hfill & \text{tan}\phantom{\rule{0.1em}{0ex}}\theta \hfill \\ \hfill \theta & =\hfill & 81.0\text{°}\text{.}\hfill \ конец{массив}[/латекс]Значение
Если бы этот угол был [латекс]0\текст{°},[/латекс] имела бы место только параллельная скорость, а спираль не образовалась бы, потому что не было бы кругового движения в перпендикулярной плоскости. Если бы этот угол был [латекс]90\текст{°},[/латекс] имело бы место только круговое движение и не было бы движения кругов, перпендикулярных движению. Именно это создает спиральное движение.
Резюме
- Магнитная сила может создавать центростремительную силу и заставлять заряженную частицу двигаться по круговой траектории радиусом [latex]r=\frac{mv}{qB}.[/latex]
- Период кругового движения заряженной частицы, движущейся в магнитном поле перпендикулярно плоскости движения, равен [latex]T=\frac{2\pi m}{qB}.
 [/latex]
[/latex] - Винтовое движение возникает, если скорость заряженной частицы имеет составляющую, параллельную магнитному полю, а также составляющую, перпендикулярную магнитному полю.
Концептуальные вопросы
В данный момент электрон и протон движутся с одинаковой скоростью в постоянном магнитном поле. Сравните магнитные силы, действующие на эти частицы. Сравните их ускорения.
Показать решениеВеличина магнитных сил протона и электрона одинакова, поскольку они имеют одинаковый заряд. Однако направления этих сил противоположны друг другу. Ускорения противоположны по направлению, и электрон имеет большее ускорение, чем протон, из-за его меньшей массы.
Обязательно ли увеличение величины однородного магнитного поля, через которое движется заряд, означает увеличение магнитной силы, действующей на заряд? Обязательно ли изменение направления поля означает изменение силы, действующей на заряд?
Электрон проходит через магнитное поле, не отклоняясь.
Показать решение Какой вывод вы сделали о магнитном поле?
Какой вывод вы сделали о магнитном поле?Магнитное поле должно быть направлено параллельно или антипараллельно скорости.
Если заряженная частица движется прямолинейно, можете ли вы заключить, что магнитное поле отсутствует?
Как определить, какой полюс электромагнита северный, а какой южный?
Показать решениеКомпас указывает на северный полюс электромагнита. 9{-5}\text{T}.[/latex] Каков радиус окружности, по которой движется электрон?
Show Solution4,27 м
(a) Зрители «Звездного пути» слышали о приводе антиматерии на звездолете «Энтерпрайз ». Одна из возможностей такого футуристического источника энергии — хранить заряженные частицы антивещества в вакуумной камере, циркулирующей в магнитном поле, а затем извлекать их по мере необходимости. Антиматерия уничтожает обычную материю, производя чистую энергию. Магнитное поле какой силы необходимо для удержания антипротонов, движущихся со скоростью [латекс]5.
 {7} \text{м/с}[/latex] по круговой траектории радиусом 2,00 м? Антипротоны имеют ту же массу, что и протоны, но противоположный (отрицательный) заряд. (б) Достижима ли эта напряженность поля с помощью сегодняшних технологий или это футуристическая возможность? 9{-5}\text{T}.[/latex] (а) Электрическое поле какой напряженности нужно приложить перпендикулярно полю Земли, чтобы электрон двигался прямолинейно? (b) Если это сделать между пластинами, расстояние между которыми составляет 1,00 см, какое напряжение будет приложено? (Обратите внимание, что телевизоры обычно окружены ферромагнитным материалом, чтобы защитить от внешних магнитных полей и избежать необходимости такой коррекции.)
{7} \text{м/с}[/latex] по круговой траектории радиусом 2,00 м? Антипротоны имеют ту же массу, что и протоны, но противоположный (отрицательный) заряд. (б) Достижима ли эта напряженность поля с помощью сегодняшних технологий или это футуристическая возможность? 9{-5}\text{T}.[/latex] (а) Электрическое поле какой напряженности нужно приложить перпендикулярно полю Земли, чтобы электрон двигался прямолинейно? (b) Если это сделать между пластинами, расстояние между которыми составляет 1,00 см, какое напряжение будет приложено? (Обратите внимание, что телевизоры обычно окружены ферромагнитным материалом, чтобы защитить от внешних магнитных полей и избежать необходимости такой коррекции.)(a) С какой скоростью протон будет двигаться по круговой траектории того же радиуса, что и электрон в предыдущем упражнении? б) Каким был бы радиус пути, если бы скорость протона была такой же, как у электрона? в) Чему был бы равен радиус, если бы протон имел ту же кинетическую энергию, что и электрон? г) один и тот же импульс? 9{6}\text{V}[/латекс]
Частица с зарядом q и массой m ускоряется из состояния покоя через разность потенциалов В , после чего попадает в однородное магнитное поле B .
 Если частица движется в плоскости, перпендикулярной B , каков радиус ее круговой орбиты?
Если частица движется в плоскости, перпендикулярной B , каков радиус ее круговой орбиты?Глоссарий
- космические лучи
- состоит из частиц, происходящих в основном из-за пределов Солнечной системы и достигающих Земли 9.0249
- спиральное движение
- суперпозиция кругового движения с прямолинейным движением, за которым следует заряженная частица, движущаяся в области магнитного поля под углом к полю
Движение заряженной частицы в магнитном поле. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/11-3-motion-of-a-charged-particle-in-a-magnet-field. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу https://openstax.org/books/university-physics-volume-2/pages/1-introduction
Заряженная частица в магнитном поле
Заряженная частица в магнитном поле
Следующий: Эффект Холла Вверх: Магнетизм Предыдущий: Сила Лоренца Предположим, что частица массы движется по круговой орбите радиус с постоянной скоростью. Как известно, ускорение
частица имеет величину , и всегда
направлен к центру орбиты. Отсюда следует, что
ускорение всегда перпендикулярно мгновенному
направление движения.
Как известно, ускорение
частица имеет величину , и всегда
направлен к центру орбиты. Отсюда следует, что
ускорение всегда перпендикулярно мгновенному
направление движения. Мы видели, что сила, действующая на заряженную частицу магнитным поле всегда перпендикулярно его мгновенному направлению движения. Означает ли это, что поле заставляет частицу совершать круговые движения? орбита? Рассмотрим случай, показанный на рис. 24. Предположим, что частица с положительным зарядом и массой движется в плоскости, перпендикулярной к однородному магнитному полю. На рисунке поле указывает на плоскость бумаги. Предположим, что частица движется в против часовой стрелки, с постоянным скорость (помните, что магнитное поле не может совершать работу над частицы, поэтому она не может влиять на ее скорость) по круговой орбите радиусом . Магнитная сила, действующая на частицу, равна величины и, согласно уравнению (158), эта сила всегда направлен к центру орбиты. Таким образом, если
(166)
то мы имеем самосогласованную картину. Это следует из того
Это следует из того (167)
Угловая частота вращения частицы ( т.е. , количество радианы, на которые частица совершает оборот за одну секунду)(168)
Обратите внимание, что эта частота, известная как Ларморовская частота , делает не зависит от скорости частицы. Для отрицательно заряженной частицы картина точно такая же, как описано выше, за исключением того, что частица движется в орбита по часовой стрелке.Рис. 24: Круговое движение заряженной частицы в магнитном поле. Ясно, из уравнения.
 (168), что угловая частота вращения заряженного
частицы в известном магнитном поле можно использовать для определения ее заряда до
массовое отношение. Кроме того, если известна скорость частицы, то
радиус орбиты также можно использовать для определения по формуле (167).
Этот метод используется в физике высоких энергий для идентификации частиц из
фотографии следов, которые они оставляют в намагниченных камерах Вильсона или пузырьках
камеры. Конечно, положительно заряженные частицы легко отличить друг от друга.
от отрицательно заряженных по направлению отклонения
частицы в магнитном поле.
(168), что угловая частота вращения заряженного
частицы в известном магнитном поле можно использовать для определения ее заряда до
массовое отношение. Кроме того, если известна скорость частицы, то
радиус орбиты также можно использовать для определения по формуле (167).
Этот метод используется в физике высоких энергий для идентификации частиц из
фотографии следов, которые они оставляют в намагниченных камерах Вильсона или пузырьках
камеры. Конечно, положительно заряженные частицы легко отличить друг от друга.
от отрицательно заряженных по направлению отклонения
частицы в магнитном поле. Мы видели, что заряженная частица, помещенная в магнитное поле, совершает круговая орбита в плоскости, перпендикулярной направлению поля. Является ли это самым общим движением заряженной частицы в магнитном поле? Не совсем. Мы также можем добавить произвольный дрейф вдоль направления магнитного поля. Это следует из того, что сила действующее на частицу зависит только от составляющей скорости частицы который перпендикулярен направлению магнитного поля (крест произведение двух параллельных векторов всегда равно нулю, потому что угол они составляют ноль).


 При
включении магнитного поля пятно
смещается в точку В. Найти смещение x
= АВ пучка электронов, если известно,
что индукция магнитного поля 14,6 мкТл.
При
включении магнитного поля пятно
смещается в точку В. Найти смещение x
= АВ пучка электронов, если известно,
что индукция магнитного поля 14,6 мкТл.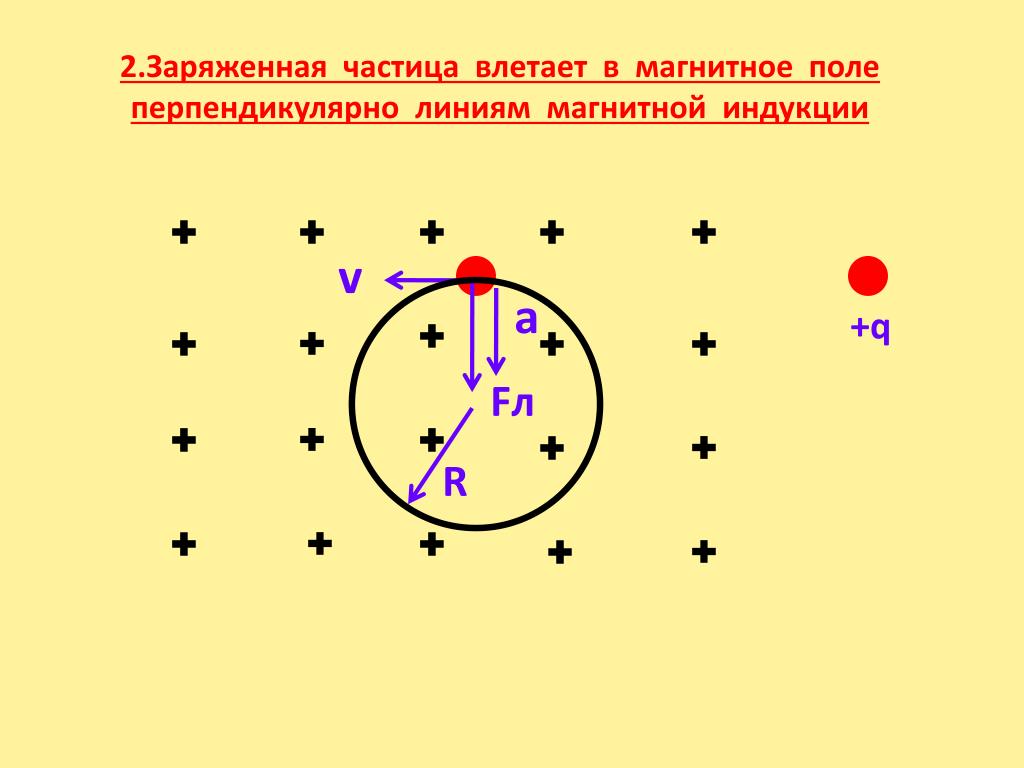 Каково должно быть магнитное
поле, удовлетворяющее этому
условию?
Каково должно быть магнитное
поле, удовлетворяющее этому
условию?  2em}{0ex}}\text{м/с}\text{.}[/latex] Под каким углом должно быть магнитное поле от скорости, чтобы шаг результирующего винтовое движение равно радиусу спирали?
2em}{0ex}}\text{м/с}\text{.}[/latex] Под каким углом должно быть магнитное поле от скорости, чтобы шаг результирующего винтовое движение равно радиусу спирали? 1em}{0ex}}\theta \frac{2\pi m}{qB}& =\hfill & \frac {mv\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}\theta}{qB}\hfill \\ \hfill 2\pi & = \hfill & \text{tan}\phantom{\rule{0.1em}{0ex}}\theta \hfill \\ \hfill \theta & =\hfill & 81.0\text{°}\text{.}\hfill \ конец{массив}[/латекс]
1em}{0ex}}\theta \frac{2\pi m}{qB}& =\hfill & \frac {mv\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}\theta}{qB}\hfill \\ \hfill 2\pi & = \hfill & \text{tan}\phantom{\rule{0.1em}{0ex}}\theta \hfill \\ \hfill \theta & =\hfill & 81.0\text{°}\text{.}\hfill \ конец{массив}[/латекс] [/latex]
[/latex]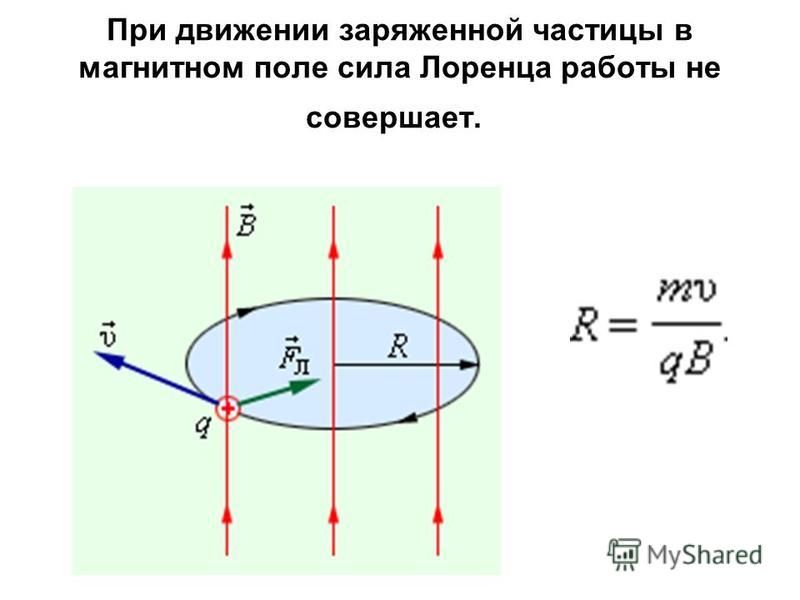 Какой вывод вы сделали о магнитном поле?
Какой вывод вы сделали о магнитном поле?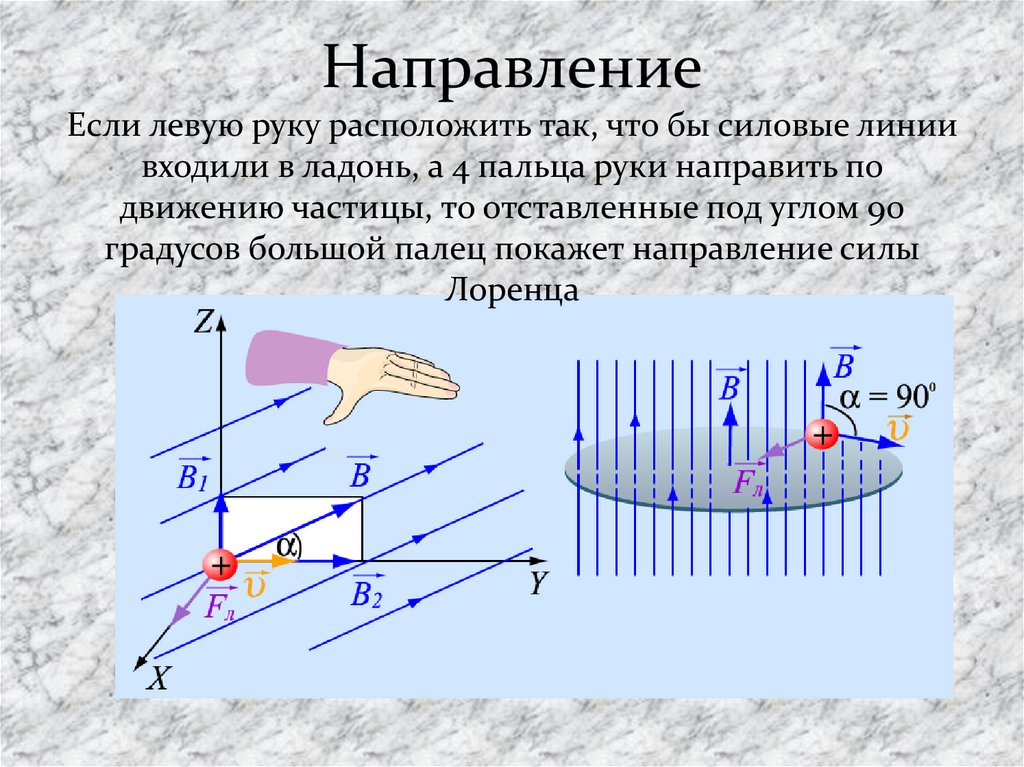 {7} \text{м/с}[/latex] по круговой траектории радиусом 2,00 м? Антипротоны имеют ту же массу, что и протоны, но противоположный (отрицательный) заряд. (б) Достижима ли эта напряженность поля с помощью сегодняшних технологий или это футуристическая возможность? 9{-5}\text{T}.[/latex] (а) Электрическое поле какой напряженности нужно приложить перпендикулярно полю Земли, чтобы электрон двигался прямолинейно? (b) Если это сделать между пластинами, расстояние между которыми составляет 1,00 см, какое напряжение будет приложено? (Обратите внимание, что телевизоры обычно окружены ферромагнитным материалом, чтобы защитить от внешних магнитных полей и избежать необходимости такой коррекции.)
{7} \text{м/с}[/latex] по круговой траектории радиусом 2,00 м? Антипротоны имеют ту же массу, что и протоны, но противоположный (отрицательный) заряд. (б) Достижима ли эта напряженность поля с помощью сегодняшних технологий или это футуристическая возможность? 9{-5}\text{T}.[/latex] (а) Электрическое поле какой напряженности нужно приложить перпендикулярно полю Земли, чтобы электрон двигался прямолинейно? (b) Если это сделать между пластинами, расстояние между которыми составляет 1,00 см, какое напряжение будет приложено? (Обратите внимание, что телевизоры обычно окружены ферромагнитным материалом, чтобы защитить от внешних магнитных полей и избежать необходимости такой коррекции.) Если частица движется в плоскости, перпендикулярной B , каков радиус ее круговой орбиты?
Если частица движется в плоскости, перпендикулярной B , каков радиус ее круговой орбиты?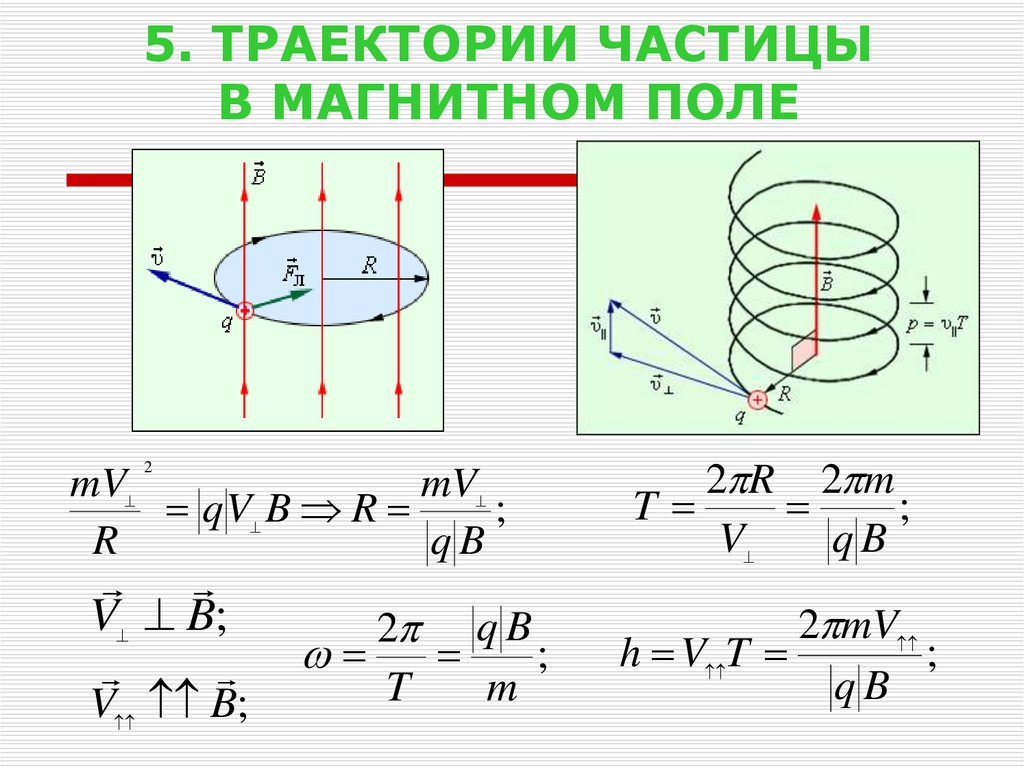 Как известно, ускорение
частица имеет величину , и всегда
направлен к центру орбиты. Отсюда следует, что
ускорение всегда перпендикулярно мгновенному
направление движения.
Как известно, ускорение
частица имеет величину , и всегда
направлен к центру орбиты. Отсюда следует, что
ускорение всегда перпендикулярно мгновенному
направление движения.  Это следует из того
Это следует из того  (168), что угловая частота вращения заряженного
частицы в известном магнитном поле можно использовать для определения ее заряда до
массовое отношение. Кроме того, если известна скорость частицы, то
радиус орбиты также можно использовать для определения по формуле (167).
Этот метод используется в физике высоких энергий для идентификации частиц из
фотографии следов, которые они оставляют в намагниченных камерах Вильсона или пузырьках
камеры. Конечно, положительно заряженные частицы легко отличить друг от друга.
от отрицательно заряженных по направлению отклонения
частицы в магнитном поле.
(168), что угловая частота вращения заряженного
частицы в известном магнитном поле можно использовать для определения ее заряда до
массовое отношение. Кроме того, если известна скорость частицы, то
радиус орбиты также можно использовать для определения по формуле (167).
Этот метод используется в физике высоких энергий для идентификации частиц из
фотографии следов, которые они оставляют в намагниченных камерах Вильсона или пузырьках
камеры. Конечно, положительно заряженные частицы легко отличить друг от друга.
от отрицательно заряженных по направлению отклонения
частицы в магнитном поле.