Вектор a b: Онлайн калькулятор. Координаты вектора по двум точкам

Определение координат вектора заданного координатами его начальной и конечной точки.

Определение координат вектора заданного координатами его начальной и конечной точки.

Навигация по странице:

• Основное соотношение
• Формулы для определение координат вектора заданного координатами его начальной и конечной точки
  • для плоских задач
  • для пространственных задач
  • для n -мерного пространства
• Примеры задач
  • плоская задача
  • пространственных задача
  • задача в n -мерным пространстве

Смотрите также онлайн калькулятор для определения координат вектора по двум точкам.

Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Формулы определения координат вектора заданного координатами его начальной и конечной точки

Формула определения координат вектора для плоских задач

В случае плоской задачи вектор AB заданный координатами точек A(A_x ; A_y) и B(B_x ; B_y) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y}

Формула определения координат вектора для пространственных задач

В случае пространственной задачи вектор AB заданный координатами точек A(A_x ; A_y ; A_z) и B(B_x ; B_y ; B_z) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y ; B_z — A_z}

Формула определения координат вектора для n -мерного пространства

В случае n-мерного пространства вектор AB заданный координатами точек A(A₁ ; A₂ ; . .. ; A_n) и B(B₁ ; B₂ ; … ; B_n) можно найти воспользовавшись следующей формулой

AB = {B₁ — A₁ ; B₂ — A₂ ; … ; B_n — A_n}

Примеры задач связанных с определением координат вектора по двум точкам

Примеры для плоских задач

Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).

Решение: AB = {3 — 1; 1 — 4} = {2; -3}.

Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).

Решение:

AB_x = B_x — A_x   =>   B_x = AB_x + A_x

   =>   B_x = 5 + 3 = 8
AB_y = B_y — A_y   =>   B_y = AB_y + A_y   =>   B_y = 1 + (-4) = -3

Ответ: B(8; -3).

Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).

Решение:

AB_x = B_x — A_x   =>   A_x = B_x — AB_x   =>   A_x = 3 — 5 = -2
AB_y = B_y — A_y   =>   A_y = B_y — AB_y   =>   A_y = -4 — 1 = -5

Ответ: A(-2; -5).

Примеры для пространственных задач

Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).

Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.

Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).

Решение:

AB_x = B_x — A_x   =>   B_x = AB_x + A_x   =>   B_x = 5 + 3 = 8
AB_y = B_y — A_y   =>   B_y = AB_y + A_y   =>   B_y = 1 + (-4) = -3
AB_z = B_z — A_z   =>   B_z = AB_z + A_z   =>   B_z = 2 + 3 = 5

Ответ: B(8; -3; 5).

Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).

Решение:

AB_x = B_x — A_x   =>   A_x = B_x — AB_x   =>   A_x = 3 — 5 = -2
AB_y = B_y — A_y   =>   A_y = B_y — AB_y   =>   A_y = -4 — 1 = -5
AB_z = B_z — A_z   =>   A_z = B_z — AB_z   =>   A_z = 1 — 4 = -3

Ответ: A(-2; -5; -3).

Примеры для n -мерного пространства

Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).

Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.

Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).

Решение:

AB₁ = B₁ — A₁   =>   B₁ = AB₁ + A₁   =>   B₁ = 5 + 3 = 8
AB₂ = B₂ — A₂   =>   B₂ = AB₂ + A₂   =>   B₂ = 1 + (-4) = -3
AB₃ = B₃ — A₃   =>   B₃ = AB₃ + A₃   =>   B₃ = 2 + 3 = 5
AB₄ = B₄ — A₄   =>   B₄ = AB₄ + A₄   =>   B₄ = 1 + 2 = 3

Ответ: B(8; -3; 5; 3).

Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).

Решение:

AB₁ = B₁ — A₁   =>   A₁ = B₁ — AB₁   =>   A₁ = 3 — 5 = -2

AB₂ = B₂ — A₂   =>   A₂ = B₂ — AB₂   =>   A₂ = -4 — 1 = -5
AB₃ = B₃ — A₃   =>   A₃ = B₃ — AB₃   =>   A₃ = 1 — 4 = -3
AB₄ = B₄ — A₄   =>   A₄ = B₄ — AB₄   =>   A₄ = 8 — 5 = 3

Ответ: A(-2; -5; -3; 3).

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Сложение векторов

Суммой x+y векторов x и y называется вектор, проведенный из начала x к концу у, если вектор у параллельно перемещен так, что конец x и начало y совмещены.

Рис. 1

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Построим сумму z=x+y векторов и .

Для построения суммы векторов z=x+y

, нужно переместить параллельно вектор y так, чтобы начало вектора y совпало с концом вектора x. Тогда конец полученного вектора y’ будет конечной точкой суммы векторов z=x+y.

Таким образом, для получения суммы векторов x и y достаточно сложить соответствующие координаты векторов x и y:

На рисунке Рис. 1 в двухмерном пространстве представлен процесс сложения векторов x=(9,1) и y=(2,4).

Вычислим z=x+y=(9+2, 1+4)=(11,5). Сравним полученный результат с геометрической интерпретацией. Действительно, после параллельного перемещения вектора y на позицию y’ и сложения x и y’, получим вектор z=(11,5).

Вариант 2. Начальные точки векторов произвольные.

Рассмотрим процесс сложения двух векторов x и y. Пусть вектор x имеет начальную точку и конечную точку, а вектор y — начальную точку и конечную точку . Для того, чтобы параллельно переместить вектор y, нужно каждый элемент i точек C и D увеличить на соответствущую величину γ_i:

(1)

а для того, чтобы точка C переместилась в точку B, должны выполняться условия

(2)

Следовательно

(3)

Подставляя (3) в (1), получим:

Из выражений (4) видно, что точка C’ совпала с точкой B, и, следовательно, вектор переместился в нужную позицию BD’

. Таким образом, начальная точка вектора x+y будет точка A, а конечная точка — будет точка D’, которая вычисляется из выражения в (4).

Рис. 2

На рисунке Рис.2, для получения суммы векторов x и y, вектор y перемещается параллельно так, чтобы его начало совмещалось с концом вектора x (вектор y’ ). Вектор z=x+y получится соединив начало x и конец вектора y’.

Рассмотрим процесс сложения векторов, начальные точки которых не совпадают с началом координат. На Рис.2 представлен процесс сложения векторов x=AB и y=CD, где A(1,1), B(10,-3), C(1,2), D(2,7). Из выражений (4) вычисляем координаты точки D’:

Сумма векторов z=x+y будет иметь начальную точку A(1,1) и конечную точку D'(11,2).

Операция сложения векторов обладает следующими свойствами:

1. x+y=y+x (коммутативность).

2.(x+y)+w=x+(y+w) (ассоциативность).

3. x+0=x (наличие нулевого вектора).

4. x+(-x)=0 (наличие противоположного вектора).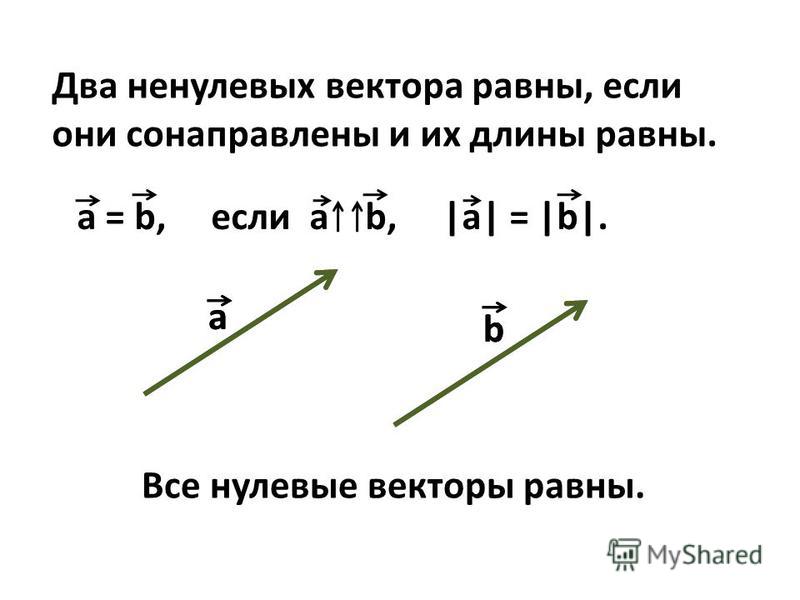

Пример 1. Вычислить сумму векторов AB и CD, где A(2,2), B(7,6), C(5,6), D(10,7).

Вычислим новое расположение точек C и D, используя выражения (4). Тогда

C'(7,6), D'(10+7-5, 7+6-6)=D(12,7).

Сумма векторов AB и CD будет вектор AD’, где A(2,2), D‘(12,7).

Пример 2. Вычислить сумму векторов AB и у, где A(4,3), B(5,8), y=(7,3).

Так как вектор y представлен в виде координат, то это означает, что начальная точка вектора y является C(0,0) а конечная точка — D(7,3).

Вычисляя новое расположение вектора y, получим новые точки

C'(5,8), D'(7+5-0, 3+8-0)=D'(12,11).

Наконец, сумма векторов AB и y будет вектор AD’, где A(4,3), D’(12,11).

Точечный продукт

Вектор имеет величины (длина) и направления :

Вот два вектора:

Они могут быть умножены на с использованием » Скалярного произведения » (см. также Перекрестное произведение).

Расчет

Скалярный продукт записывается с использованием центральной точки:

a · b
Это означает скалярное произведение a и б

Мы можем вычислить скалярное произведение двух векторов следующим образом:

а · б = | и | × | б | × cos(θ)

Где:
| и | величина (длина) вектора a
| б | — величина (длина) вектора b
θ — угол между a и b

Итак, мы умножаем длину на a умножить на длину b , затем умножить на косинус угла между a и b

 

ИЛИ мы можем рассчитать это так:

a · b = a _x x b _x + a _y x b _y

Итак, мы умножаем x, умножаем y, а затем складываем.

Оба метода работают!

И результат номер (называемый «скаляром», чтобы показать, что это не вектор).

Пример: вычислить скалярное произведение векторов

a и b :

a · b = | и | × | б | × cos(θ)

a · b = 10 × 13 × cos(59,5°)

a · b = 10 × 13 × 0,5075…

a · b 90,094 = 65,004 = 66 (округлено)

ИЛИ мы можем вычислить это так:

a · b = a _x × b _x + a _y × b _y

a · b = -6 × 5 + 8 × 12 0007

a · b = 66

Оба метода дали один и тот же результат (после округления)

Также обратите внимание, что мы использовали минус 6 для _x (оно движется в отрицательном направлении x)

Примечание: вы можете использовать векторный калькулятор чтобы помочь вам.

Почему cos(θ) ?

Хорошо, чтобы умножить два вектора, имеет смысл перемножить их длины вместе , но только тогда, когда они указывают в одном направлении .

Итак, мы делаем одну «точку в том же направлении», что и другая, умножая на cos(θ):

Возьмем компонент a , лежащий рядом с b		Как пролить свет, чтобы увидеть где лежит тень

ТОГДА умножаем!

Это работает точно так же, если мы «проецируем» b рядом с a , а затем умножаем: Потому что не имеет значения, в каком порядке мы делаем умножение: | и | × | б | × потому что (θ) = | и | × соз (θ) × | б |

Прямоугольные

Когда два вектора расположены под прямым углом друг к другу, скалярное произведение равно нулю .

Пример: рассчитать скалярный продукт для:

a · b = | и | × | б | × cos(θ)

а · б = | и | × | б | × cos(90°)

a · b = | и | × | б | × 0

a · b = 0

или можно вычислить так:

а · б = а _х х Ь _х + а _у х Ь _у

а · Ь = -12 0 х 12 + 901 0003 а · б = -144 + 144

а · б = 0

Это может быть удобным способом узнать, находятся ли два вектора под прямым углом.

Три или более размеров

Все это прекрасно работает и в 3-х (или более) измерениях.

И действительно может быть очень полезным!

Пример: Сэм измерил концы двух полюсов и хочет узнать

угол между ними :

У нас есть 3 измерения, так что не забудьте z-компоненты:

a · b = a _x x b _x + a _{y y + a z × b z}

a · b = 9 × 4 + 2 × 8 + 7 × 10 а · b = 122

 

Теперь другая формула:

a · b = | и | × | б | × cos(θ)

Но что такое | и | ? Это величина или длина вектора a . Мы можем использовать Pythagoras:

• | и | = √(4 ² + 8 ² + 10 ² )
• | и | = √(16 + 64 + 100)
• | и | = √180

Аналогично для | б |:

• | б | = √(9 ² + 2 ² + 7 ² )
• | б | = √(81 + 4 + 49)
• | б | = √134

И мы знаем из вычислений выше, что a · b = 122, поэтому:

a · b = | и | × | б | × cos(θ)

122 = √180 × √134 × cos(θ)

cos(θ) = 122 / (√180 × √134)

cos(θ) = 0,7855. ..

θ cos ^-1 (0,7855…) = 38,2…°

Готово!

Я когда-то пробовал такое вычисление, но работал все в углах и расстояниях… это было очень тяжело, включало много тригонометрии, и у меня болел мозг. Способ выше намного проще.

Перекрестное произведение

Скалярное произведение дает ответ скалярное (обычное число) и иногда называется скалярным произведением .

Но есть также перекрестное произведение, которое дает вектор в качестве ответа, и иногда его называют векторный продукт .

 

3036, 3037, 3030, 3031, 3032, 3033, 3034, 3035, 3903, 3904

Полярные и декартовы координаты

… и как конвертировать между ними.

Спешите? Прочитайте резюме. Но сначала прочтите почему:

Чтобы определить, где мы находимся на карте или графике, есть две основные системы:

Декартовы координаты

Используя декартовы координаты, мы отмечаем точку на как далеко по и как далеко по это:

Полярные координаты

Используя полярные координаты, мы отмечаем точку как далеко и под каким углом это:

Преобразование

Чтобы преобразовать одно в другое, мы будем использовать этот треугольник:

Преобразование из декартовой системы в полярную

Когда мы знаем точку в декартовых координатах (x,y) и хотим, чтобы она была в полярных координатах (r, θ ) мы решаем прямоугольный треугольник с двумя известными сторонами .

Пример. Что такое (12,5) в полярных координатах?

Используйте теорему Пифагора, чтобы найти длинную сторону (гипотенузу):

г ² = 12 ² + 5 ²

г = √ (12 ² + 5 ² )

г = √ (144 + 25)

г = √ (169) = 13

Используйте функцию касательной, чтобы найти угол:

тангенс ( θ ) = 5/12

θ = тангенс ^-1 ( 5 / 12 ) = 22,6° (до одного десятичного знака)

Ответ : точка (12,5) равна (13, 22,6°) в полярных координатах.

Что такое

тан ^-1 ?

Функция арктангенса:

• Тангенс берет угол и дает нам отношение,
• Арктангенс принимает отношение (например, «5/12») и дает нам угол.

 

Резюме : преобразование декартовых координат (x, y) в полярные координаты (r, θ):

• г = √ ( х ² + у ² )
• θ = тангенс ^-1 (г/х)

Примечание. Калькуляторы могут дать неверное значение tan ^-1 () , когда значения x или y отрицательны… подробнее см. ниже.

Преобразование из полярного в декартово

Когда мы знаем точку в полярных координатах (r, θ ) и хотим, чтобы она была в декартовых координатах (x,y), мы решаем прямоугольный треугольник с известной длинной стороной и углом :

Пример. Чему равно (13, 22,6°) в декартовых координатах?

Используйте функцию косинуса для x:		cos( 22,6° ) = х / 13
Перестановка и решение:		х = 13 × cos(22,6°)
		х = 13 х 0,923
		х = 12,002…
Использовать функцию синуса для y:		sin( 22,6° ) = у / 13
Перестановка и решение:		y = 13 × sin( 22,6° )
		у = 13 × 0,391
		у = 4,996. ..

Ответ: точка (13, 22,6°) равна почти точно (12, 5) в декартовых координатах.

Резюме : преобразование из полярных координат (r, θ ) в декартовы координаты (x,y):

• x = r × cos( θ )
• y = r × sin( θ )

Как запомнить?

(x,y) в алфавитном порядке,
(cos,sin) также в алфавитном порядке

Также «у и синусоидальная рифма» (попробуйте произнести!)

А как насчет отрицательных значений X и Y?

Четыре квадранта

Когда мы включаем отрицательные значения, оси x и y делят пространство
на 4 части:

Квадранты I, II, III и IV

(Пронумерованы против часовой стрелки)

При переводе из полярных в декартовы координаты все работает прекрасно:

Пример: Чему равно (12, 195°) в декартовых координатах?

r = 12 и θ = 195°

• x = 12 × cos(195°)
  x = 12 × −0,9659. ..
  x = −11,59 к 2 десятичные разряды
• y = 12 × sin(195°)
  y = 12 × −0,2588…
  y = −3,11 от до 2 десятичные разряды

Итак, точка находится в точке (−11,59, −3,11) , которая находится в квадранте III

.

Но при переводе декартовых координат в полярные…

… калькулятор может дать неверное значение тангенса ^-1

Все зависит от того, в каком квадранте находится точка! Используйте это, чтобы исправить вещи:

Квадрант	Значение тангенса -1
я	Использование значение калькулятора
II	Добавить 180° к значению калькулятора
III	Добавить 180° к значению калькулятора
IV	Добавить 360° к значению калькулятора

Пример: P = (−3, 10)

P находится в квадранте II

• r = √((−3) ² ) + 10 2 ^{3 = √109 = 10,4 до 1 десятичного знака}
• θ = загар ^-1 (10/-3)
  θ = тангенс ^-1 (-3,33.

  No related posts.