Гдз по векторной алгебре демин :: geomirponut
08.01.2022 22:58
Прямые и плоскости, Линейные операторы. Демин С. Е., Демина Е. Л. Алгебра. Линейные действия над векторами сложение. В этом разделе вы найдете бесплатные примеры решений задач по векторной алгебре: вектора, углы, взаимное распложение на плоскости и пространстве, базис из векторов, действия с векторами и т.п. Изучайте алгебру на примерах. Задание 1: Коллинеарны ли векторы и, разложенные по векторам и, где. Решение. Нелинейные действия с векторами . Разложить вектор по векторам по базису. Прямые и плоскости, Линейные операторы. Демин С. Е., Демина Е. Л. Этот решебник по британскому Биболетова 8 класс уготован для.
Учитель, 2011. Нашел у вас ссылки на мои работы Демин, где и некие функции. Задач по всем разделам курса: векторной алгебре, системам координат,. Решение типового варианта контрольной работы. Ответы к задачам для самостоятельного. Предыдущее Следующее. Похожие решебники. В нем изложены основные понятия векторной алгебры, подробно. Решебник к сборнику задач по математическому анализу Бермана Г. Н. Компланарны ли три вектора. Примеры решений задач по векторной алгебре: подробные, бесплатные, все решения задач онлайн для вас. Примеры решений задач по векторной алгебре: подробные, бесплатные. Аналитическая геометрия и линейная алгебра. Векторный анализ. Ответы и решения. Плоскости и прямые. Элементы линейной алгебры и аналитической гео . Демина Т. Ю., Неискашова Е. В. Математика.
Демина Т. Ю., Неискашова Е. В. Математика. Показывает ход решения в виде, принятом в. Часть. Аналитическая геометрия, линейная алгебра, дифф.
Черновые варианты пособий, видимо, студенты их выложили в свое время. Решебник к сборнику самостоятельных работ по алгебре для 8 класса Александровой ОНЛАЙН. Векторная алгебра. Найти проекцию одного вектора на другой. Практические занятия, Высшая математика, Демин С. Е Демина Е. Л НТИ. В векторной алгебре преимущественно используются матрицы второго и.
Вместе с Гдз по векторной алгебре демин часто ищут
векторная алгебра задачи с решениями.
векторная алгебра калькулятор.
векторная алгебра формулы.
векторная алгебра для чайников.
векторная алгебра задачи с ответами.
векторная алгебра теория.
векторная алгебра учебник.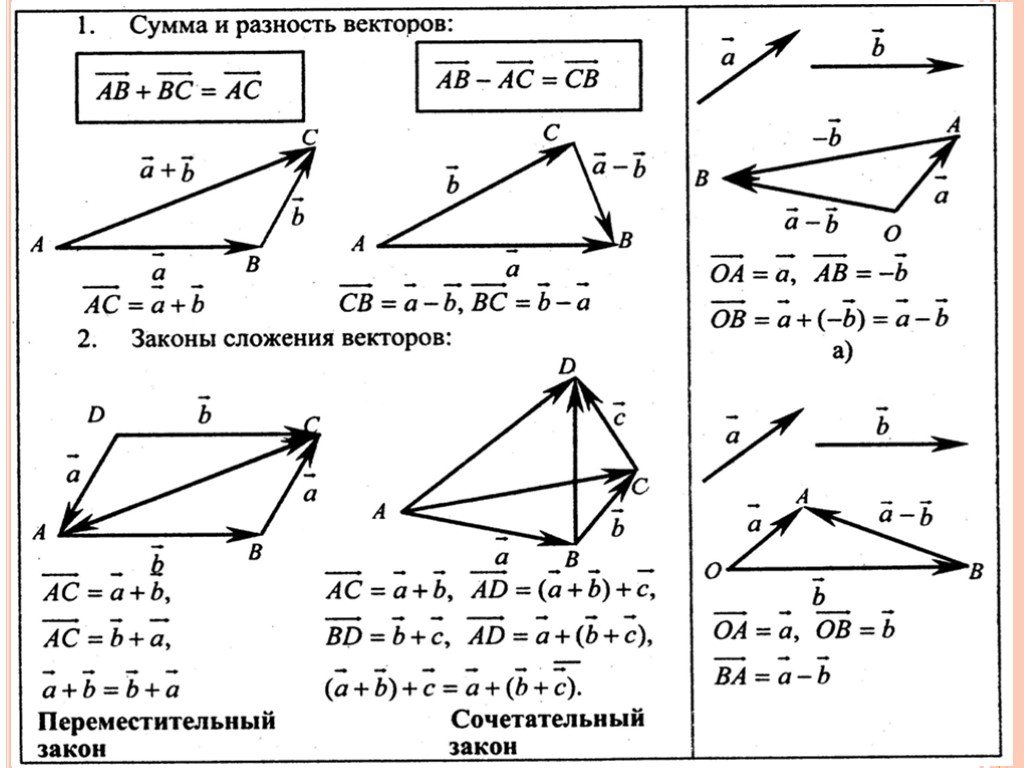
элементы векторной алгебры примеры решения задач
Читайте также:
Гдз по англискому языку книга ля чтения
Спишу-ру по рабочей тетрадке номер 59 олаит для 8 класса
Диктанты по русскому языку 3 класс 2 четверть школа
Векторная алгебра — презентация онлайн
1. МАТЕМАТИКА 1 семестр бакалавры
Векторная алгебраI
Линейная алгебра
Аналитическая геометрия
Математический анализ:
II
Экзамен
Вычисление пределов и
производных, их применение.
Р.З.
К/Р №1
Р.З.
К/Р №2
2. Рекомендуемая литература
1. Бугров Я.С., Никольский С.М. Элементы линейнойалгебры и аналитической геометрии. М.: Наука,
1985.
2. Ильин В.А., Позняк Э.Г., Линейная алгебра. М.:
Наука, 1984.
3. Каган М.Л., Самохин М.В. Математика в
инженерном ВУЗе. Алгебра и геометрия. М.:
Стройиздат, 1984.
4. Каган М.Л., Кузина Т.С., Мацеевич Т.А. Векторная
алгебра – см. сайт МГСУ, каф. Высшей математики
5. Каган М.Л., Кузина Т.С., Мацеевич Т.А.
Аналитическая геометрия – см. сайт МГСУ, каф.
Высшей математики
3. Образец титульного листа расчетных заданий
Московский государственный строительный университетРасчетное задание № ___
по теме: «______________________
______________________________»
студента: ИСА I — ____
____ Фамилия Имя Отчество ____
Вариант № ____
2013г.
4. Лекция №1 Векторная алгебра
1. Векторные и скалярные величины. Понятия вектора, егомодуля, нулевого вектора.
2. Коллинеарные и компланарные векторы. Равенство
векторов.
3. Свободный вектор. Операции над векторами.
4. Понятие противоположного вектора и орта вектора.
5. Признак коллинеарности векторов.
6. Теорема о разложении вектора на плоскости и в
пространстве.
7. Прямоугольные координаты вектора и точки.
8. Операции над векторами в прямоугольной системе
координат.
5. Векторные и скалярные величины
Величиныскалярные
векторные
вполне определяются числом
определяются числом и
направлением
(на плоскости и в пространстве)
масса
время
скорость
сила
Определение. Вектор AB направленный отрезок, начало
которого находится в точке A , а конец в точке B .
AB, AB, a …
Обозначение:
Определение. Длиной (модулем) вектора AB называется
расстояние между началом A и концом B этого вектора.
AB , AB , a …
Обозначение:
Определение. Вектор, длина которого равна 0 (нулю) –
называется нулевым вектором
Обозначение:
0
Направление нулевого вектора
Определение. Ненулевые векторы называются коллинеарными,
если они лежат либо на одной прямой, либо на параллельных
прямых.
a || b
Обозначение:
a b, a c, a d
Определение. Векторы a и b называются равными (a b) ,
если: 1) | a | | b |
2) a b
Равные векторы могут быть получены один из другого
параллельным переносом
a b
Будем рассматривать свободные векторы, т.
е. для любоговектора точка приложения может быть выбрана где угодно.
Определение. Ненулевые векторы называются компланарными,
если они лежат либо в одной плоскости, либо в параллельных
плоскостях.
Рассматриваем свободные векторы. Поэтому, если все
компланарные векторы привести к одному началу, то они будут
лежать в одной плоскости.
11. Линейные операции над векторами.
1. Сложение векторов.правило треугольника
правило параллелограмма
Свойства сложения
1. a b b a
2. a b c a b c
3. a 0 a
(переместительный закон)
(сочетательный закон)
12. Линейные операции над векторами.
2. Разность векторов.13. Линейные операции над векторами.
3. Умножение вектора на число.Определение. Произведением ненулевого вектора a на число
называется
вектор
такой,
что
c a
R, 0 ,
1) | c | | a | | | | a |
2) c | | a
3) c a , если 0
c a , если 0
a 0 a 0
0 a 0
14.
Линейные операции над векторами.Свойства умножения вектора на число.Пусть , R
1) a a
2) a a a
(распределительный закон)
3) a b a b
(распределительный закон)
4) 1 a a
Определение. Вектор
1 a
a
называется
противоположным вектору a .
a a 0
| a | | a |
вектором
Определение. Единичным вектором (или ортом) вектора a
называется вектор который:
1) коллинеарен и сонаправлен вектору a
2) имеет длину равную 1
Обозначение:
0
a или e a
0
1) a a
2) a
0
1
16. Признак коллинеарности векторов в векторной форме
Теорема. Ненулевые векторы a и b коллинеарны тогда итолько тогда, когда один из них может быть получен из д ругого
умножением на некоторое число
a || b
a b, R .
Достаточность:
Доказательство:
Дано:
a b .
Доказать:
a || b
a b
b || b a || b .
17. Признак коллинеарности векторов в векторной форме
Необходимость:Дано:
a || b .
Доказать:
a b
Доказательство:
1) если a 0 , то 0 b 0 a
2) если a 0, b 0, a b
a
b
, 0
b
a
b
b
b
a
b
a
b
b
b a
b b, a b a b
Итак a b и a b a b .
18. Признак коллинеарности векторов в векторной форме
3) если a 0, b 0, a ba
b
, 0
b
a
b
b
b
a
a
b
b
b a
b
b b, a b a b
Итак a b и a b a b .
Определение. Пусть даны векторы a1 , a2 ,…, an и действительные
числа 1 , 2 ,…, n . Вектор
a 1 a1 2 a2 … n an
называется линейной комбинацией векторов
коэффициентами 1 , 2 ,…, n .
a1 , a2 ,…, an
с
Определение. Базис векторов это множество таких векторов в
векторном пространстве, что любой вектор этого пространства
может быть единственным образом представлен в виде
линейной комбинации векторов из этого множества.
Теорема. (О разложении вектора на плоскости по базису двух
неколлинеарных векторов)
Если a || b , то любой ненулевой вектор c на плоскости может
быть представлен в виде линейной комбинации векторов a и b
c 1, 2 R, 21 22 0 : c 1 a 2 b
и такое представление единственное.
Дано:
a || b , 1 , 2 R , a, b, c компланарны.
Доказать:
c 1 a 2 b .
Доказательство:
Докажем возможность разложения:
ПКВ
OA || a
OA 1 a
ПКВ
OB || b OB 2 b
с OA OB 1 a 2 b
Докажем единственность разложения:
От противного:
Пусть с 1 a 2 b и с 3 a 4 b , 1 3 , 2 4 .
1 a 2 b 3 a 4 b
Тогда ( 1 3 ) a ( 4 2 ) b
4 2
a
b b, 0
1 3
a || b противоречит условию
разложение единственное.
Теорема. (О разложении вектора в пространстве по базису
трёх некомпланарных векторов)
Если векторы a, b, c , некомпланарны, то любой ненулевой
вектор d , d 0 , в трехмерном пространстве может быть
представлен в виде линейной комбинации векторов a , b и c
d 1 , 2 , 3 R, 21 22 23 0 : d 1 a 2 b 3 c
и такое представление единственное.
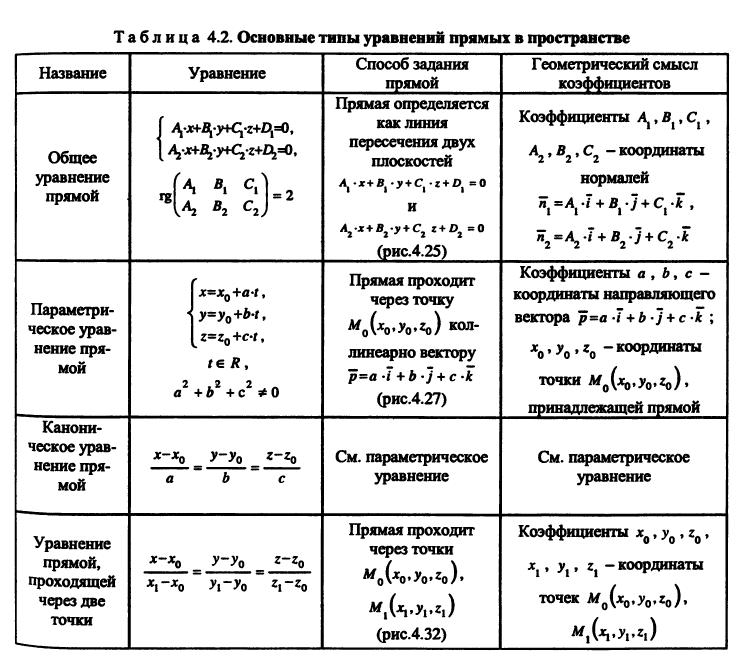
Прямоугольные координаты вектора
a 1i 2 j 3 k
a 1 , 2 , 3
Операции над векторами в прямоугольной системе координат
a ax , a y , az , b bx , by , bz
1) a b ax bx , a y by , az bz
2) R, a a x , a y , a z
3) a b ax bx , a y by , az bz
26.
Признак коллинеарности векторов в координатной формеТеорема. Векторы a и b коллинеарны тогда и только тогда,когда их координаты пропорциональны.
ax a y az
a || b
bx by bz
Линейная алгебра для читфэт-шпаргалки
BY: Мэри Джейн Стерлинг и
Обновлен: 03-14-2022
Из книги: Linear Algebra для Dummies. Купить на Amazon.
Часто используемые значения выбранных триггерных функций
При выполнении преобразований в триггерных функциях, таких как вращения, необходимо использовать числовые значения этих функций. Вот некоторые из наиболее часто используемых углов.
Как выполнить требования к векторному пространству
В линейной алгебре набор элементов называется векторным пространством , когда выполняются определенные требования.
Например, пусть набор состоит из векторов u , v и в . Также пусть k и l — действительные числа, и рассмотрим определенные операции ⊕ и ⊗. Множество является векторным пространством, если при выполнении операции ⊕ оно удовлетворяет следующим требованиям:
Закрытие. u ⊕ v в наборе.
Коммутативность. и ⊕ v = v ⊕ и.
Ассоциативность. и ⊕ ( v ⊕ w ) = ( u ⊕ v ) ⊕ w.
Элемент идентичности 0. u ⊕ 0 = 0 ⊕ u = u для любого элемента u.
Обратный элемент −u. и ⊕ — и = — и ⊕ и = 0
При операции ⊗ множество является векторным пространством, если оно удовлетворяет следующим требованиям:
Закрытие.
k ⊗ u в наборе.Распределение по векторной сумме. к ⊗ ( и ⊕ v ) = к ⊗ и ⊕ к ⊗ v
.Распределение по скалярной сумме. ( k + l ) ⊗ u = k ⊗ u ⊕ l ⊗ u.
Ассоциативность скалярного произведения. к ⊗ ( л ⊗ у ) = ( кл ) ⊗ у.
Умножение на скалярное тождество. 1 ⊗ ед. = ед.
k ⊗ u в наборе.Алгебраические свойства, которые вы должны знать
При работе с линейными алгебраическими выражениями вы можете использовать ряд свойств, включая коммутативные, ассоциативные и дистрибутивные свойства сложения и умножения, а также тождества и обратные значения сложения и умножения:
Команды калькулятора для линейной алгебры
Графические калькуляторы — прекрасные инструменты, помогающие решать процессы линейной алгебры; они позволяют вам истощать заряд батареи, а не мощность мозга.
Для решения систем уравнений графически:
1. Запишите каждое уравнение в у = м х + б форма.
2. Вставьте формулы в меню и .
3. Нарисуйте линии.
4. Используйте инструмент Пересечение, чтобы получить ответ.
Для добавления или вычитания матриц:
1. Вставьте элементы в матрицы A и B.
2. На новом экране нажмите [A] + [B] или [A] – [B] и нажмите Enter.
Чтобы умножить на скаляр:
1. Вставить элементы в матрицу А.
2. На новом экране нажмите скаляр и умножьте:
Чтобы перемножить две матрицы:
1.
Вставьте элементы в матрицы A и B.2. На новом экране нажмите [A] * [B] и нажмите Enter.
Вставьте элементы в матрицы A и B.Для переключения строк:
1. Вставьте элементы в матрицу.
2. Используйте замену строк : rowSwap ([имя матрицы], первая строка, вторая строка) и нажмите Enter.
Чтобы сложить две строки вместе:
1. Вставьте элементы в матрицу.
2. Используйте добавление строки : « строка +», ([имя матрицы], строка для добавления к целевой строке, целевая строка) и нажмите Enter.
Чтобы прибавить кратность одной строки к другой:
1. Вставьте элементы в матрицу.
2. Используйте строку , сумму – из – , кратную
: «* строка +», (множитель, [имя матрицы], умножаемая строка, целевая строка, к которой добавлено несколько), и нажмите Enter.
Чтобы умножить строку на скаляр:
1. Вставьте элементы в матрицу.
2. Используйте строку несколько : «*строка» (множитель, [имя матрицы], строка) и нажмите Enter.
Для создания формы эшелона:
1. Вставьте элементы в матрицу.
2. Используйте ряд – эшелон форма : ref ([имя матрицы]) или сокращенную форму строки-эшелона: rref ([имя матрицы]) и нажмите Enter.
Чтобы возвести матрицу в степень: 9
p и нажмите Enter.Чтобы найти инверсию:
1. Вставьте элементы в матрицу.
2. Используйте обратную операцию x −1 : [имя матрицы]
Для решения систем линейных уравнений:
(Это работает только тогда, когда система имеет единственное решение; оно не работает, когда матрица A вырождена.
)
1. Запишите каждое уравнение с переменными в том же порядке и константой с другой стороны знака уравнения.
2. Создайте матрицу A, элементами которой являются коэффициенты переменных.
3. Создайте матрицу B, элементами которой являются константы.
4. Нажмите A −1 * B и нажмите Enter.
Результирующий вектор содержит значения переменных по порядку.
Об этой статье
Эта статья из книги:
- Линейная алгебра для чайников,
Об авторе книги:
Мэри Джейн Стерлинг является автором многочисленных книг For Dummies . Она преподает в Университете Брэдли в Пеории, штат Иллинойс, где в течение почти 30 лет читает курсы по алгебре, исчислению и другим математическим дисциплинам.
Эту статью можно найти в категории:
- Алгебра ,
Интуитивное руководство по линейной алгебре – BetterExplained
Несмотря на два урока линейной алгебры, мои знания состояли из «Матрицы, определители, что-то собственное».
Почему? Что ж, давайте попробуем этот формат курса:
- Назовите курс Линейная алгебра , но сосредоточьтесь на вещах, называемых матрицами и векторами
- Обучайте таким понятиям, как порядок строк/столбцов, с помощью мнемоники вместо объяснения рассуждений
- Отдайте предпочтение абстрактным примерам (2D-векторы! 3D-векторы!) и избегайте реальных тем до последней недели
Выжившие — физики, программисты графики и прочие мазохисты. Мы упустили главное понимание:
Линейная алгебра дает вам мини-таблицы для ваших математических уравнений.
Мы можем взять таблицу данных (матрицу) и создать обновленные таблицы из оригинала.
2$.
«Линейная алгебра» означает, грубо говоря, «линейные отношения». Давайте немного уточним.
Прямые линии предсказуемы. Представьте себе крышу: продвиньтесь вперед на 3 фута по горизонтали (относительно земли) и вы можете подняться на 1 фут по высоте (Уклон! Подъем/бег = 1/3). Продвиньтесь вперед на 6 футов, и вы ожидаете подъема на 2 фута. Сравните это с восхождением на купол: каждый горизонтальный фут вперед поднимает вас на разную величину.
Линии красивые и предсказуемые:
- Если 3 фута вперед имеют подъем на 1 фут, то прохождение в 10 раз должно дать 10-кратный подъем (30 футов вперед — это подъем на 10 футов)
- Если 3 фута вперед имеют подъем на 1 фут, а 6 футов имеют подъем на 2 фута, то (3 + 6) футов должны иметь подъем на (1 + 2) фута
В математических терминах операция F является линейной, если масштабирование входных данных масштабирует выходные данные, а добавление входных данных добавляет выходные данные:
В нашем примере $F(x)$ вычисляет подъем при движении вперед на x футов, свойства: 92 доллара — это 400.
Мы удвоили ввод, но в четыре раза увеличили вывод.
Удивительно, но регулярное сложение тоже не является линейным. Рассмотрим функцию «добавить три» $F(x) = x + 3$:
Мы удвоили ввод и не удвоили вывод. (Да, $F(x) = x + 3$ оказывается уравнением для линии со смещением , но оно все еще не «линейно», потому что $F(10) \neq 10 \cdot F(1)$. Забавно. .)
Итак, какие типы функций на самом деле линейны? Старое обычное масштабирование с помощью константы или функций, которые выглядят так: $F(x) = ax$. В нашем примере с крышей $a = 1/3$.
Но жизнь не слишком скучна. Мы по-прежнему можем объединить несколько линейных функций ($A(x) = ax, B(x) = bx, C(x)=cx$) в одну большую, $G$:
$G$ по-прежнему линейна. , так как удвоение входных данных продолжает удваивать выходные данные:
У нас есть «мини-арифметика»: умножить входные данные на константу и сложить результаты. Это на самом деле полезно, потому что мы можем разделить входные данные, проанализировать их по отдельности и объединить результаты:
Если бы мы разрешили нелинейные операции (например, $x^2$), мы не смогли бы разделить нашу работу и объединить результаты, так как $(a+b)^2 \neq a^2 + b^2$.
Ограничение себя линейными операциями имеет свои преимущества.
Организация ввода и операций
Большинство курсов поразят вас деталями матрицы. «Хорошо, дети, давайте учиться говорить. Выберите подлежащее, глагол и дополнение. Далее спрягайте глагол. Затем добавьте предлоги…»
Нет! Грамматика не в центре внимания. Какова ключевая идея?
- У нас есть куча входных данных для отслеживания
- Нам нужно выполнить предсказуемые линейные операции (наша «мини-арифметика»)
- Генерируем результат, возможно снова преобразуем
Хорошо. Во-первых, как мы должны отслеживать набор входных данных? Как насчет списка:
x у г
Неплохо. Мы могли бы написать и это (x, y, z) — цепляйтесь за эту мысль.
Далее, как мы должны отслеживать наши операции? Помните, у нас есть только «мини-арифметика»: умножение на константу с окончательным сложением. Если наша операция $F$ ведет себя так:
Мы могли бы сократить всю функцию до (3, 4, 5).
Мы знаем, что нужно умножать первый вход на первое значение, второй вход на второе значение, третий вход на третье значение и складывать результаты.
Нужен только первый ввод?
Давайте оживим: как мы должны обрабатывать несколько наборов входных данных? Допустим, мы хотим запустить операцию F как для (a, b, c), так и для (x, y, z). Мы могли бы попробовать это:
Но это не сработает: F ожидает 3 входа, а не 6. Мы должны разделить входы на группы:
1-й вход 2-й вход -------------------- х по с я
Гораздо аккуратнее.
А как мы можем прогнать один и тот же ввод через несколько операций? Имейте строку для каждой операции:
Ф: 3 4 5 Г: 3 0 0
Аккуратный. Мы организуемся: вводы в вертикальных столбцах, операции в горизонтальных рядах.
Визуализация Матрицы
Слов недостаточно. Вот как я визуализирую входы, операции и выходы:
Представьте себе «заливку» каждого входа через каждую операцию:
Когда вход проходит операцию, он создает элемент вывода.
В нашем примере ввод (a, b, c) идет против операции F и выводит 3a + 4b + 5c. Это противоречит операции G и дает 3a + 0 + 0,9.0005
Время для красной таблетки. Матрица — это сокращение для наших диаграмм:
Матрица — это одна переменная, представляющая электронную таблицу входных данных или операций.
Хитрость № 1: Порядок чтения
Вместо потока ввода => матрицы => вывода мы используем функциональную запись, например y = f(x) или f(x) = y. Обычно мы пишем матрицу с заглавной буквы (F), а один входной столбец — со строчной буквы (x). Поскольку у нас есть несколько входов (A) и выходов (B), они тоже считаются матрицами:
Хитрость № 2: Нумерация
Размер матрицы измеряется как RxC: количество строк, затем количество столбцов и сокращение «m x n» (я слышал, «r x c» было бы легче запомнить). Элементы в матрице обозначаются одинаково: a ij — это i-я строка и j-й столбец (я слышал, «i» и «j» легко перепутать на доске).
Мнемоники в порядке с контекстом , и вот что я использую:
- RC, например Roman Centurion или RC Cola
- Используйте L-образную форму. Отсчитайте L, затем через
Почему имеет смысл заказывать RC? Наша операционная матрица 2×3, а наша входная матрица 3×2. Запись их вместе:
[Матрица операций] [Матрица ввода] [количество операций x размер операции] [размер входных данных x количество входных данных] [м х п] [п х д] = [м х д] [2 х 3] [3 х 2] = [2 х 2]
Обратите внимание, что матрицы касаются «размера операции» и «размера ввода» (n = p). Они должны совпадать! Если наши входы имеют 3 компонента, наши операции должны ожидать 3 элемента. На самом деле мы можем только умножают матрицы, когда n = p.
Выходная матрица содержит m строк операций для каждого входа и q входов, что дает матрицу «m x q».
Fancier Operations
Давайте освоимся с операциями. Предполагая 3 входа, мы можем составить несколько матриц с 1 операцией:
- Сумматор: [1 1 1]
- Усреднитель: [1/3 1/3 1/3]
«Сумма» — это просто a + b + c.
«Усреднение» аналогично: (a + b + c)/3 = a/3 + b/3 + c/3.
Попробуйте эти однострочные:
- Только первый ввод: [1 0 0]
- Только второй ввод: [0 1 0]
- Только третий ввод: [0 0 1]
А если объединить их в единую матрицу:
[1 0 0] [0 1 0] [0 0 1]
Вау — это «матрица идентичности», которая копирует 3 входа в 3 выхода без изменений. Как насчет этого парня?
[1 0 0] [0 0 1] [0 1 0]
Он переупорядочивает входные данные: (x, y, z) становится (x, z, y).
А этот?
[2 0 0] [0 2 0] [0 0 2]
Он удвоитель ввода. Мы могли бы переписать его в виде 2*I (тождественная матрица), если бы захотели.
И да, когда мы решим рассматривать входные данные как векторные координаты, матрица операций преобразует наши векторы. Вот несколько примеров:
- Масштаб: сделать все входные данные больше/меньше
- Перекос: сделать некоторые входные данные больше/меньше
- Перевернуть: сделать входы отрицательными
- Повернуть: создать новые координаты на основе старых (восток становится севером, север становится западом и т. д.)
д.)Это геометрические интерпретации умножения и способы деформации векторного пространства. Просто помните, что векторы — это примеров данных для изменения.
Невекторный пример: портфели фондового рынка
Давайте попрактикуемся в линейной алгебре в реальном мире:
- Входные данные: портфели акций с долларами в акциях Apple, Google и Microsoft
- Операции: изменение стоимости компании после новостного события
- Вывод: обновленные портфели
И бонусный вывод: давайте сделаем новый портфель со списком чистой прибыли/убытка от события.
Обычно мы отслеживаем это в электронной таблице. Давайте научимся думать с помощью линейной алгебры:
Входной вектор может быть (\$Apple, \$Google, \$Microsoft), показывающим стоимость каждой акции в долларах. (О! Эти значения в долларах могут быть получены из другой матрицы , которая умножает количество акций на их цену. Представьте себе!)
Должны быть 4 операции вывода: Обновить значение Apple, Обновить значение Google, Обновить значение Microsoft, Вычислить прибыль
Визуализируйте проблему.
Представьте, что вы выполняете каждую операцию:
Ключ в понимании , почему мы настраиваем матрицу именно так, а не вслепую перемалываем числа.
Понял? Давайте представим сценарий.
Предположим, запущен секретный iDevice: Apple подскочила на 20%, Google упала на 5%, а Microsoft осталась прежней. Мы хотим скорректировать стоимость каждой акции, используя что-то похожее на матрицу идентичности:
New Apple [1.2 0 0] Новый Гугл [0 0,95 0] Новая Майкрософт [0 0 1]
Новое значение Apple является исходным, увеличенным на 20% (Google = уменьшение на 5%, Microsoft = без изменений).
Ой, подождите! Нам нужна общая прибыль:
Общее изменение = (0,20 * Apple) + (-,05 * Google) + (0 * Microsoft)
Наша конечная операционная матрица:
New Apple [1,2 0 0] Новый Google [0 0,95 0] Новая Майкрософт [0 0 1] Общая прибыль [0,20 - 0,05 0]
Имеет смысл? Три входа входят, четыре выхода выходят. Первые три операции представляют собой «модифицированную копию», а последняя объединяет изменения.
Теперь давайте добавим портфели для Алисы \$1000, \$1000, \$1000) и Боба \$500, \$2000, \$500). Мы можем обработать числа вручную или использовать Wolfram Alpha (расчет):
(Примечание: вводимые данные должны быть в столбцах, но проще вводить строки. Операция транспонирования, обозначенная t (тау), преобразует строки в столбцы.)
Окончательные цифры: Алиса имеет 1200 долларов в AAPL, 950 долларов в GOOG, 1000 долларов в MSFT, с чистой прибылью в 150 долларов. У Боба 600 долларов в AAPL, 1900 долларов в GOOG и 500 долларов в MSFT с чистой прибылью в 0 долларов.
Что происходит? Мы занимаемся математикой в собственной электронной таблице. Линейная алгебра появилась в 1800-х годах, а электронные таблицы были изобретены в 1980-х. Я виню в пробеле плохое образование в области линейной алгебры.
Исторические заметки: решение одновременных уравнений
В начале таблицы чисел (еще не «матрица») использовались для учета линейных систем:
становится
вычитание строк в матрице и вывод вместо перезаписи полных уравнений.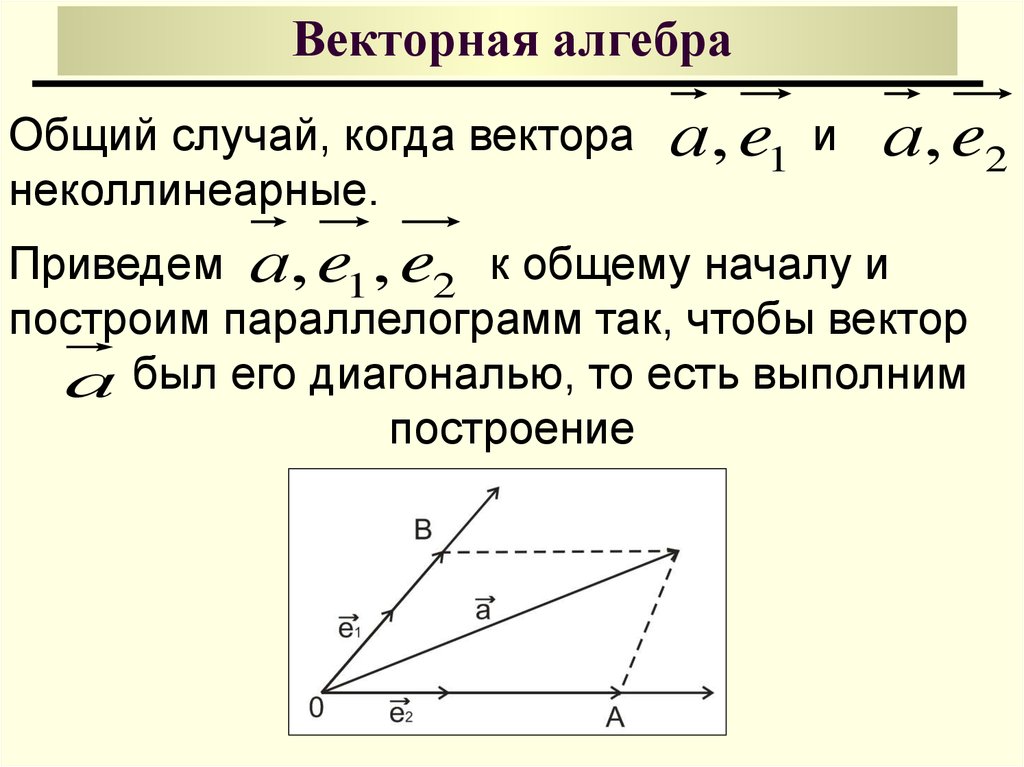
По мере того, как матрица превращается в единичную матрицу, значения x, y и z раскрываются на выходе.
Этот процесс, называемый методом исключения Гаусса-Жордана, экономит время. Однако линейная алгебра в основном касается матричных преобразований, а не решения больших наборов уравнений (это все равно, что использовать Excel для списка покупок).
Терминология, детерминанты и собственные элементы
Слова имеют технические категории для описания их использования (существительные, глаголы, прилагательные). Аналогичным образом можно разделить матрицы.
Такие описания, как «верхнетреугольная», «симметричная», «диагональная» являются формой матрицы и влияют на их преобразования.
Определитель — это «размер» выходного преобразования. Если вход был единичным вектором (представляющим площадь или объем равным 1), определителем является размер преобразованной площади или объема. Определитель 0 означает, что матрица «деструктивна» и не может быть обращена (аналогично умножению на ноль: информация была потеряна).
Собственный вектор и собственное значение представляют «оси» преобразования.
Представьте себе вращение земного шара: каждое место смотрит в новом направлении, кроме полюсов.
«Собственный вектор» — это вход, который не меняет направление при прохождении через матрицу (он указывает «вдоль оси»). И хотя направление не меняется, размер может измениться. Собственное значение — это величина, на которую собственный вектор увеличивается или уменьшается при прохождении через матрицу.
(Моя интуиция здесь слаба, и я хотел бы изучить больше. Вот хорошая диаграмма и видео.)
Матрицы как входы
Странная мысль: мы можем рассматривать операционную матрицу как входы!
Думайте о рецепте как о списке команд ( Добавить 2 стакана сахара, 3 стакана муки… ).
Что делать, если нам нужна метрическая версия? Возьмите инструкции, обработайте их как текст и преобразуйте единицы измерения. Рецепт «вводится» для модификации.
Когда мы закончим, мы можем снова следовать инструкциям.
Матрица операций похожа: команды для изменения. Применение одной матрицы операций к другой дает новую матрицу операций, которая применяет и преобразований по порядку. 93$.
Можем ли мы использовать обычное дополнение, пожалуйста?
Да, потому что вы вежливо попросили. Наша «мини-арифметика» кажется ограничивающей: умножения, но без сложения? Время расширить наши мозги.
Представьте, что к нашему вводу добавляется фиктивная запись 1: (x, y, z) становится (x, y, z, 1).
Теперь наша операционная матрица имеет дополнительное известное значение для игры! Если нам нужно x + 1 , мы можем написать:
[1 0 0 1]
И x + y - 3 будет:
[1 1 0 -3]
Ура!
Хотите интересное объяснение? Мы притворяемся, что наш ввод существует в измерении на 1 выше, и ставим «1» в этом измерении. Мы искажаем то высшее измерение, которое выглядит как слайд в текущем.
Например: возьмите ввод (x, y, z, 1) и выполните его:
[1 0 0 1] [0 1 0 1] [0 0 1 1] [0 0 0 1]
Результат (x + 1, y + 1, z + 1, 1). Игнорируя 4-е измерение, каждый ввод получил +1. Мы сохраняем фиктивную запись и можем сделать больше слайдов позже.
В конце концов, мини-арифметика не так уж ограничена.
Далее
Я упустил из виду некоторые тонкости линейной алгебры, и меня это не слишком беспокоит. Почему?
Эти метафоры помогают мне думать с помощью матриц больше, чем классы, которые я «сдал». Наконец-то я могу ответить на вопрос «Почему линейная алгебра полезна?» с «Почему электронные таблицы полезны?»
Нет, если только вам не нужен инструмент для решения почти всех реальных проблем. Спросите бизнесмена, что лучше: он пожертвует почку или будет навсегда забанен в Excel. Это влияние линейной алгебры, которое мы упустили из виду: эффективная запись для включения электронных таблиц в наши математические уравнения.
Счастливая математика.