Сообщество Экспонента
- вопрос
- 15.11.2022
Системы связи, Математика и статистика, Цифровая обработка сигналов, Радиолокация, Робототехника и беспилотники
Создать с стандартными параметрами и хорошим его рисунком, спектром, автокореляцией! Спасибо за внимание!
Создать с стандартными параметрами и хорошим его рисунком, спектром, автокореляцией! Спасибо за внимание!
1 Ответ
- вопрос
- 05.11.2022
Другое
В системе Win10 установлен MinGW64. Matlab не видит компиляторы из папки C:\mingw64 Добавил в путь матлаба и в переменные среды Windows директорию C:\mingw64\bin\, где лежит gfortran.exe, но не помога…
В системе Win10 установлен MinGW64. Matlab не видит компиляторы из папки C:\mingw64 Добавил в путь матлаба и в переменные среды Windows директорию C:\mingw64\bin\, где лежит gfortran.exe, но не помога…
- вопрос
- 05.
11.2022
11.2022Другое
Добрый день! Сегодня произошло неожиданное событие. При загрузке Матлаб он мне сообщил, что лицензия отсутствует. Я поискал ее в каталоге Матлаб, и обнаружил следующее: license_DESKTOP-NITFQJQ_4101619…
Добрый день! Сегодня произошло неожиданное событие. При загрузке Матлаб он мне сообщил, что лицензия отсутствует. Я поискал ее в каталоге Матлаб, и обнаружил следующее: license_DESKTOP-NITFQJQ_4101619…
- Публикация
- 30.10.2022
Системы связи
Мероприятие призвано собрать на одной площадке всех специалистов данной тематики для обмена знаний, опыта и технологий, чтобы вооруживший последними технологиями дать быстрый старт в развитии отечественного оборудования систем связи 5G. Подробная программа 09:…
Приглашаем разработчиков систем связи на семинар для всестороннего обсуждения вопросов построения отечественного оборудования систем связи 5G
.Пройдет офлайн в Москве 17 ноября в 10:00.
- MATLAB
- Simulink
- САУ
- ЦОС
- ПЛИС
- МОП
- 5G
- Модельно ориентированное проектирование
30.10.2022
- Публикация
- 26.10.2022
Встраиваемые системы
Эта статья написана совместно с нашими партнерами — компанией «РИТМ». Компания занимается разработкой полунатурных стендов и комплексов полунатурного моделирования «РИТМ», которые используются нашими заказчиками. Клиенты в некотор…
Уже много лет мы занимаемся продвижением модельно-ориентированного проектирования в России. Поэтому наш опыт сконцентрирован вокруг инструментов модельно-ориентированного проектирования — то есть различных сред моделирования и симуляции — и применения их в инженерных разработках.
- MATLAB
- Simulink
- САУ
- ЦОС
- ПЛИС
- МОП
- fpga
- экспонента
- Модельно ориентированное проектирование
26.
10.2022
- Публикация
- 26.10.2022
Электропривод и силовая электроника
Основа всех трех сценариев – цифровое моделирование в режиме жесткого реального времени. Наша команда инженеров показала, что КПМ РИТМ способен решать ряд сложных задач, которые стоят перед российской энергетикой. Мы благодарны всем гостям и всегда рады…
13 октября в нашем офисе прошел семинар. Всего за 5 часов мы обсудили, как использовать КПМ РИТМ для:
- Тестирования микропроцессорных реле;
- Построения систем мониторинга переходных режимов;
- Исследования кибер-инцидентов в электроэнергетике.
- экспонента
- микропроцессор
- электроэнергетика
- РИТМ
- энергетика
26.10.2022
- Публикация
- 26.10.2022
Электропривод и силовая электроника
Вас ждут:
Заметки по созданию цифровых двойников;
Полезные статьи и видео;
Анонсы вебинаров и семинаров.
Подписывайтесь: https://t.me/exponenta_energy
Наша команда инженеров электроэнергетики создала канал, где вы найдёте множество материалов про то, как используют машины реального времени в энергетике.
- MATLAB
- HIL
- РИТМ
- Hardware In the Loop
- Model In the Loop
26.10.2022
- Публикация
- 25.10.2022
Глубокое и машинное обучение(ИИ), Математика и статистика
В ходе вебинара будет рассказано о существующих подходах к организации предсказательного обслуживания. Также будет продемонстрирована экспериментальная установка, состоящая из электродвигателя, передаточного механизма, нагрузки и системы датчиков. Установка мо…
Приглашаем на вебинар «Предсказание отказов в промышленности: от теории к практике», который пройдет 8 ноября в 10:00.
Предсказание отказов промышленного оборудования достигается за счёт непрерывного мониторинга и контроля состояния оборудования.
Предсказательное обслуживание призвано существенно снизить затраты на техническое обслуживание оборудование, сократить количество поломок и время просто оборудования.
- MATLAB
- Simulink
- САУ
- ЦОС
- ПЛИС
- МОП
- ИИ
- Модельно ориентированное проектирование
25.10.2022
- вопрос
- 24.10.2022
Системы связи, ПЛИС и СнК, Радиолокация, Робототехника и беспилотники, Встраиваемые системы, Цифровая обработка сигналов
Есть модуль в Симулинк детектор приамбулы. Он считает количество бит от начала на котором находится приамбула. Выдает на выходе число. Хочу это значение использовать в модуле Си но симулинк выдает оши…
Есть модуль в Симулинк детектор приамбулы. Он считает количество бит от начала на котором находится приамбула.
Выдает на выходе число. Хочу это значение использовать в модуле Си но симулинк выдает оши…
3 Ответа
- вопрос
- 19.10.2022
Математика и статистика, Цифровая обработка сигналов, Финансы
u = (y³)/3 + 8xy — 9y — 4x² — 10 Справка
u = (y³)/3 + 8xy — 9y — 4x² — 10 Справка
3 Ответа
Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие.
Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.
Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2.
2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.
2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1.
Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.
3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1).
Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1.
Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.
1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1.
Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themЗадачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1.
Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2.
Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1.
Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1.
Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.
5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1).
Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1.
Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)Вопрос Видео: Вычисление скалярного тройного произведения и векторного тройного произведения трех векторов в трехмерном пространстве компоненты минус один ноль три, а 𝐖 имеет компоненты два ноль минус два.
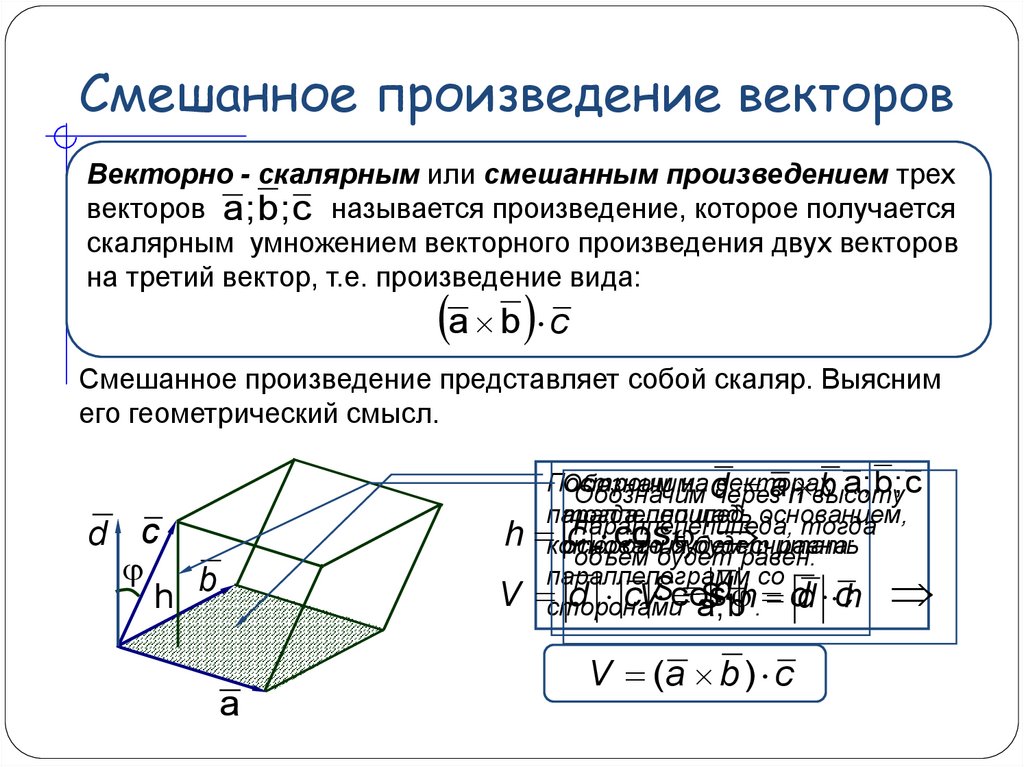Рассчитайте 𝐔 точка 𝐕 крест 𝐖 и 𝐔 крест 𝐕 крест 𝐖.Этот вопрос касается скалярного произведения и векторного произведения векторов. Нам нужно найти скалярное произведение вектора 𝐔 на вектор 𝐕 крест 𝐖 и векторное произведение вектора 𝐔 на вектор 𝐕 крест 𝐖. Общая нить здесь 𝐕 крест 𝐖, перекрестное произведение векторов 𝐕 и 𝐖, который сам является вектором.
Итак, давайте сначала найдем 𝐕 крест 𝐖. Мы можем записать это векторное произведение как определитель матрицы три на три, где первая строка матрицы содержит единичные векторы в 𝑥-, 𝑦- и 𝑧-направления; то есть векторы 𝑖, 𝑗 и 𝑘. Вторая строка содержит компоненты первого вектора в векторном произведении, в в этом случае 𝐕 с отрицательными компонентами один, ноль и три. А третья строка содержит компоненты второго вектора в векторном произведении, в нашем случае 𝐖 с компонентами два, ноль и минус два.
Теперь вычислим этот определитель.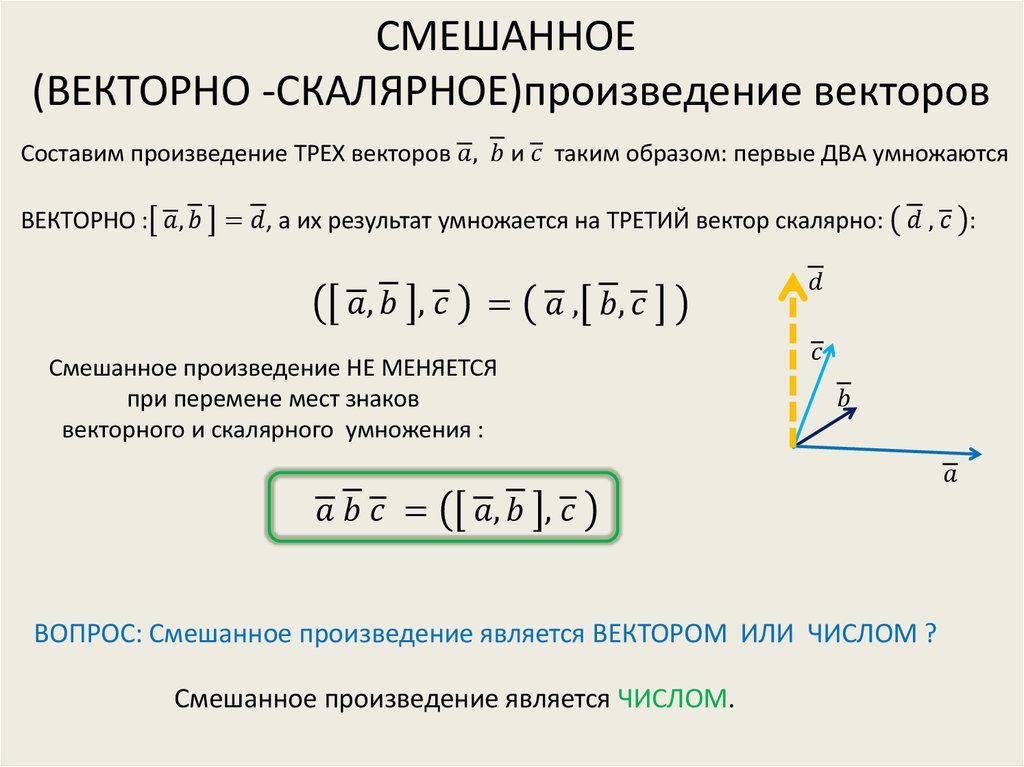
Мы можем разложить этот определитель по верхней строке. Таким образом, мы получаем в 𝑖 раз больше определителя матрицы, которую вы получили, удалив строку и
столбец, содержащий 𝑖 минус 𝑗, умноженный на определитель полученной матрицы
удаление строки и столбца, содержащих 𝑗 плюс 𝑘 умноженное на определитель
матрица, которую вы получите, удалив строку и столбец, содержащие 𝑘.
Мы можем вычислить детерминанты два на два обычным способом. И таким образом упрощая, мы получаем ноль 𝑖 плюс четыре 𝑗 плюс ноль 𝑘, что мы можем записать в компонентная форма как ноль, четыре, ноль. Теперь мы нашли компоненты 𝐕 креста 𝐖. Давайте освободим немного места и используем их, чтобы найти 𝐔 точку 𝐕 крест 𝐖 и 𝐔 крест 𝐕 крест 𝐖.
Итак, что такое 𝐔 точка 𝐕 крестик 𝐖? Ну, нам даны компоненты 𝐔 в вопросе. 𝐔 имеет компоненты один, ноль, два. И, конечно же, мы только что проработали компоненты 𝐕 креста 𝐖. Это ноль, четыре и ноль.
И найти скалярное произведение двух векторов в компонентной форме очень сложно.
простой. Это произведение 𝑥-компонентов плюс произведение 𝑦-компонентов плюс
произведение 𝑧-компонент.
И когда компонент 𝐔 отличен от нуля, соответствующий компонент 𝐕 пересекает 𝐖 равно нулю. Эта сумма очень проста. Это ноль плюс ноль плюс ноль, что равно нулю. Прежде чем мы перейдем к нахождению векторного произведения 𝐔 и 𝐕 на 𝐖, давайте возьмем момент, чтобы рассмотреть геометрическую интерпретацию скалярного произведения 𝐔 и 𝐕 крестик 𝐖 равен нулю.
Скалярное произведение двух векторов 𝐴 и 𝐵 равно нулю, когда 𝐴 и 𝐵
перпендикуляр. Таким образом, 𝐔 точка 𝐕 крестик 𝐖, равный нулю, говорит нам, что 𝐔 и 𝐕 крестик 𝐖 равны
перпендикуляр. Вектор 𝐕 крест 𝐖 перпендикулярен как вектору 𝐕, так и вектору 𝐖. На самом деле, вы могли бы знать, что, по крайней мере, когда 𝐕 крест 𝐖 отличен от нуля, 𝐕 крест 𝐖 является
нормали к плоскости, натянутой на векторы 𝐕 и 𝐖.
Поскольку 𝐔 перпендикулярно нормали к плоскости, натянутой на 𝐕 и 𝐖, 𝐔 должно лежать в этой плоскости. И на самом деле, из вопроса мы можем видеть, что 𝑦-компоненты 𝐔, 𝐕 и 𝐖 все нулевые. И, следовательно, 𝐔, 𝐕 и 𝐖 лежат в 𝑥𝑧-плоскости. Мы могли бы предположить, что 𝐔 точка 𝐕 крест 𝐖 равна нулю, не производя никаких вычислений. просто используя тот факт, что три вектора 𝐔, 𝐕 и 𝐖 лежат в одном и том же самолет.
Мы вернемся к этому моменту в конце видео, но сначала давайте посчитаем 𝐔 крест 𝐕 крест 𝐖. Это просто перекрестное произведение двух векторов. Просто один из векторов является перекрестным произведением двух других. векторы. Если бы это сделало вас счастливее, вы могли бы просто позвонить 𝐕 крест 𝐖 𝐴, и тогда мы бы просто ищем перекрестное произведение 𝐔 и 𝐴.
Мы вычисляем это, используя определители, как и раньше, с единичными векторами 𝑖, 𝑗 и 𝑘 в
первая строка, компоненты 𝐔 во второй строке и компоненты 𝐕
крест 𝐖 или 𝐴 в третьем ряду.
Снова расширяем определитель по первой строке и вычисляем каждую попарно.
определитель в обычном порядке.
Записывая компоненты, мы видим, что векторное произведение 𝐔 и 𝐕 креста 𝐖 имеет компоненты минус восемь, ноль, четыре. Итак, теперь мы нашли как скалярное произведение 𝐔 и 𝐕, так и перекрестное произведение 𝐖 из 𝐔 и 𝐕 пересекаются 𝐖. Ранее я обещал еще несколько геометрических интерпретаций этих вещей. 𝐔 точка 𝐕 крест 𝐖 называется скалярным тройным произведением 𝐔, 𝐕 и 𝐖. А 𝐔 крест 𝐕 крест 𝐖 — это векторное тройное произведение 𝐔, 𝐕 и 𝐖.
Оба они являются тройными произведениями, поскольку включают три вектора 𝐔, 𝐕 и 𝐖. Но 𝐔 точка 𝐕 крестик 𝐖 возвращает скаляр, другими словами число, в нашем случае ноль,
тогда как 𝐔 cross 𝐕 cross 𝐖 возвращает вектор, в нашем случае вектор с
компоненты минус восемь, ноль, четыре. Скалярное тройное произведение имеет красивую геометрическую интерпретацию.
Примерно так же, как величина вектора 𝐕 пересечения 𝐖 является площадью параллелограмма с стороны 𝐕 и 𝐖, абсолютное значение скалярного тройного произведения 𝐔, 𝐕 и 𝐖 — объем трехмерного параллелепипеда с ребрами 𝐔, 𝐕 и 𝐖. И так же, как перекрестное произведение двух векторов, равных нулю или имеющих нулевую величину говорит нам, что эти два вектора параллельны или лежат на одной прямой.
Скалярное тройное произведение трех векторов говорит нам, что эти три вектора лежат в тот же самолет. Векторное тройное произведение немного сложнее интерпретировать геометрически. Но как есть перпендикулярно 𝐕 кресту 𝐖, приложив немного усилий, вы можете убедиться, что это должны лежать в одной плоскости с 𝐕 и 𝐖. И, немного поработав, вы можете явно записать его как линейную комбинацию векторы 𝐕 и 𝐖.
И последнее, что следует здесь отметить, это то, что перекрестное произведение 𝐔 и 𝐕 креста 𝐖 не равно
то же, что перекрестное произведение 𝐔 креста 𝐕 и 𝐖.
Здесь действительно важно, где стоят скобки. Технический термин для описания этого явления состоит в том, что векторное произведение векторов
не является ассоциативным. Это отличает его не только от обычного умножения действительных чисел, но и
из умножения матриц, которое является ассоциативным, хотя и не
коммутативный.
Скалярное тройное произведение
Скалярное тройное произведение , как следует из названия, представляет собой способ умножения трех векторов, который дает в результате скалярное значение . Он фактически объединяет операции скалярного произведения и векторного произведения для получения скалярного значения с использованием трех векторов, которые в целях этого обсуждения мы будем называть векторами a , b и c . Скалярное тройное произведение векторов a , b и c записывается как ( a b c ) и определяется как:
( a b c ) = a · ( b × c )
Иногда вы можете видеть, что круглые скобки опущены, поскольку оператор векторного произведения имеет приоритет над оператором скалярного произведения.
Скалярное тройное произведение векторов a , b и c 9Таким образом, 0040 является скалярным произведением вектора a и вектора, заданного перекрестным произведением векторов b и c . Прежде чем мы продолжим, может быть полезно рассмотреть, чем скалярное тройное произведение трех векторов не является (и почему). Рассмотрим следующие схемы, включающие три вектора и операторы скалярного или векторного произведения:
( а · б ) · с
( а · б ) × с
( а × б 0 ) 4 9 с
Первая схема не будет работать, потому что скалярное произведение векторов a и b будет скалярным значением, и мы не сможем впоследствии найти скалярное произведение скалярного значения и вектора. Второе расположение также не является стартовым, потому что снова скалярное произведение векторов a и b будут скалярным значением, и мы не можем найти перекрестное произведение скалярного значения и вектора.
Третье расположение вполне осуществимо, так как векторное произведение векторов на и b на будет вектором, и мы можем найти векторное произведение двух векторов. Это последнее расположение, однако, отличается от того, что мы рассматриваем на этой странице, и на самом деле производит нечто, называемое векторным тройным произведением (другой вектор, а не скалярное значение).
Скалярное тройное произведение часто используется в геометрии для нахождения объема параллелепипеда , который представляет собой трехмерную фигуру с шестью гранями, каждая из которых является параллелограммом . Три вектора можно рассматривать как три соседних ребра параллелепипеда, исходящие из общей вершины. Значение скалярного тройного произведения, если оно не равно нулю, будет положительным значением, если векторы a , b и c определены с использованием правая система координат , иначе будет отрицательной.
Очевидно, что при использовании для нахождения объема параллелепипеда необходимо использовать абсолютное значение (беззнаковое) независимо от направления системы координат.
Скалярное тройное произведение также является проверкой того, являются ли три вектора линейно независимыми . Если векторы , а не линейно независимы, значение скалярного тройного произведения будет равно ноль . Линейная зависимость означает, что для данного набора векторов по крайней мере один из векторов может быть продублирован некоторой комбинацией одного или нескольких других векторов в наборе (или их кратных). Это означает, что для того, чтобы наши три вектора были линейно независимыми, не более двух векторов могут лежать в одной плоскости, а векторы, из которых составляют , лежат в одной плоскости, должны указывать в разных направлениях. (т.е. они должны быть непараллельными).
Давайте подумаем об этом по-другому.
Мы сказали, что скалярное тройное произведение дает нам объема параллелепипеда. Если скалярное тройное произведение имеет значение ноль , параллелепипеда нет, так как объем трехмерного объекта не может быть равен нулю. Рассмотрим иллюстрацию ниже, на которой изображен параллелепипед. Три смежных ребра параллелепипеда образованы векторами a = (1, 1, 1), b = (4, 2, 0) и с = (0, 2, -1). Оси x , y и z включены, чтобы показать ориентацию используемой системы координат (в данном случае правосторонней системы).
Векторы a , b и c образуют три смежных ребра параллелепипеда
Чтобы найти скалярное тройное произведение векторов a , b и c , нам сначала нужно найти векторное произведение векторов b и c . Если вы читали страницу, озаглавленную «Перекрестное произведение двух векторов», вы знаете, что мы можем найти компоненты x , y и z вектора перекрестного произведения (которое для удобства мы будем называть вектором ).
d ) с использованием компонентов x , y и z векторов b и c следующим образом:
d x = b y c z — b z c y = (2)(-1) — (0)(2) = -2
d y = b z c x — b x c z = (0)(0) — (4)(-1) = 4
d z = b x c y — b y c x = (4)(2 ) — (2)(0) = 8
Теперь нам нужно найти скалярное произведение векторов a и d .
Если вы читали страницу, озаглавленную «Скалярное произведение двух векторов», вы знаете, что найти скалярное произведение несложно, если вы знаете x , y и z компонентов двух векторов, и находится следующим образом:
a · d = a x d x + a y d y + a z d z = ((1)(-2)) + ((1)(4)) + ((1)(8)) = -2 + 4 + 8 = 10
Мы также можем получить скалярное тройное произведение несколько более прямым способом, используя матричную арифметику. Скалярное произведение будет определителем матрицы три на три , каждая строка которой будет состоять из компонентов x , y и z одного из векторов.
Первая строка будет координатами x , y и z вектора a , вторая строка будет x , y и z координаты вектора b , а третья строка будет координатами x , y и z вектора c . Матрица для векторов a , b и c показана ниже.
| a x | a y | a z | ||
| b x | b y | b z | ||
| c x | c y | с г |
Вектор векторного произведения получается путем нахождения определителя этой матрицы.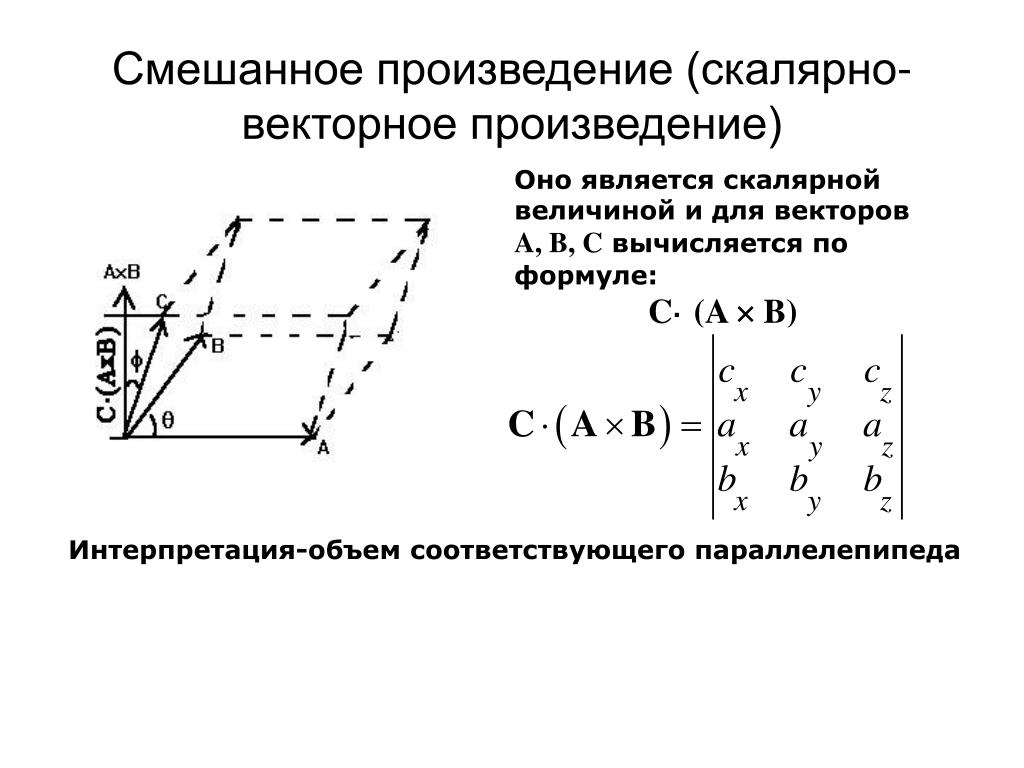
Если вы не знакомы с матрицами, возможно, вы захотите просмотреть страницу о матрицах в Раздел Алгебра , чтобы увидеть, как находится определитель матрицы три на три. Ниже приведен фактический расчет для нахождения определителя вышеуказанной матрицы (т.е. скалярного тройного произведения векторов a , b и c ). Обратите внимание, что определитель матрицы записывается в том же формате, что и исходная матрица, но вместо скобок столбцы заключены в вертикальные черточки.
| ( а б в ) = a · ( b × c ) = | a x | a y | a z | = a x | b y | b z | — a y | b x | b z | + a z | b x | b y | |||||||||
| b x | b y | b z | c y | c z | c x | c z | c x | c z | |||||||||||||
| c x | c y | c z | |||||||||||||||||||
Подставляя фактические значения, получаем:
| ( a b c ) = a · ( b × c ) = | 1 | 1 | 1 | = | 2 | 0 | — | 4 | 0 | + | 4 | 2 | ||||||||
| 4 | 2 | 0 | 2 | -1 | 0 | -1 | 0 | 2 | ||||||||||||
| 0 | 2 | — 1 | ||||||||||||||||||
Тогда расчет становится:
( a b c ) = a · ( b × c ) = ((2)(-1) — (2)(0)) — ((4)(-1) — (0 )(0)) + ((4)(2) — (0)(2))
( a b c ) = a · ( b × c ) = -2 + 4 + 8 = 10
Это дает нам тот же результат, что и раньше, как и должно быть.
Прежде чем мы покинем скалярное тройное произведение, стоит отметить пару вещей о нем. Во-первых, тот же результат можно получить, используя другой порядок векторов, при условии, что циклический порядок, в котором они появляются, остается постоянным. Это дает нам следующие эквивалентности:
( A B C ) = ( B C A ) = ( C A B ) = A · ( B × C ) = B · () = B · () = B · () = B · () = B · () = B · (). в · ( а × б )
Во-вторых, замена двух векторов в перекрестном произведении части выражения скалярного тройного произведения инвертирует значение скалярного тройного произведения (0039 абсолютное значение остается прежним, но меняется знак ).