Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика
Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ Момент силы относительно точки Алгебраический момент силы Основные типы связей и их реакции Упражнения ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ Сходящиеся силы. Приведение сходящихся сил к простейшему виду Вычисление и построение равнодействующей Условия равновесия сходящихся сил Теорема о трех силах Теорема Вариньона Пара сил и ее момент Приведение системы пар сил к простейшему виду или сложение пар сил Упражнения ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ Момент силы относительно оси Аналитический способ вычисления момента Геометрический способ вычисления момента Преобразование пространственной произвольной системы сил Приведение пространственной произвольной системы сил к данному центру.  Главный вектор и главный момент. Основная теорема статики Главный вектор и главный момент. Основная теорема статикиВычисление и построение главного вектора и главного момента Перемена центра приведения ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ Случаи приведения к простейшему виду Условия (уравнения) равновесия пространственной произвольной системы сил Частные случаи системы сил Плоская система сил Система параллельных сил Равновесие системы тел Вопросы для самопроверки ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ Центр параллельных сил Распределенные силы Центр тяжести Интегральные формулы для координат центра тяжести Метод разбиения Вопросы для самопроверки ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ Трение покоя и трение скольжения Трение качения Решение задач статики при учете сил трения Упражнения КИНЕМАТИКА ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ Способы задания движения точки Определение траектории, скорости и ускорения точки при векторном способе задания движения Определение траектории, скорости и ускорения точки при координатном способе задания движения Определение скорости и ускорения точки при естественном способе задания движения Естественные координатные оси и их орты Определение скорости Определение ускорения Вопросы для самопроверки ЛЕКЦИЯ 8. 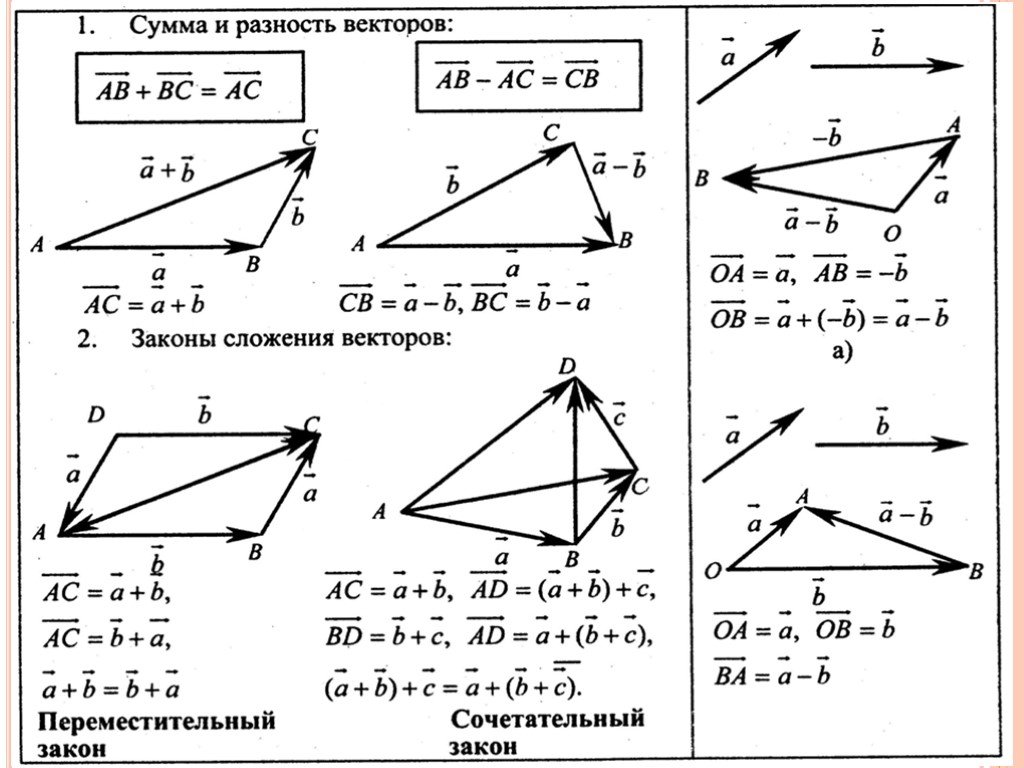 ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛАПоступательное движение Вращательное движение Уравнение вращательного движения. Угловая скорость и угловое ускорение тела Траектории, скорости и ускорения точек тела Векторы угловой скорости и углового ускорения тела Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела Вопросы для самопроверки ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА Уравнения движения Угловая скорость и угловое ускорение тела при плоскопараллельном движении Определение скоростей точек тела. Метод полюса Мгновенный центр скоростей Определение скоростей точек плоской фигуры через мгновенный центр скоростей Различные случаи определения положения мгновенного центра скоростей Определение ускорений точек тела Вопросы для самопроверки ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ Теорема сложения скоростей Теорема сложения ускорений Причины появления ускорения Кориолиса Вычисление и построение ускорения Кориолиса Вопросы для самопроверки ДОБАВЛЕНИЕ. 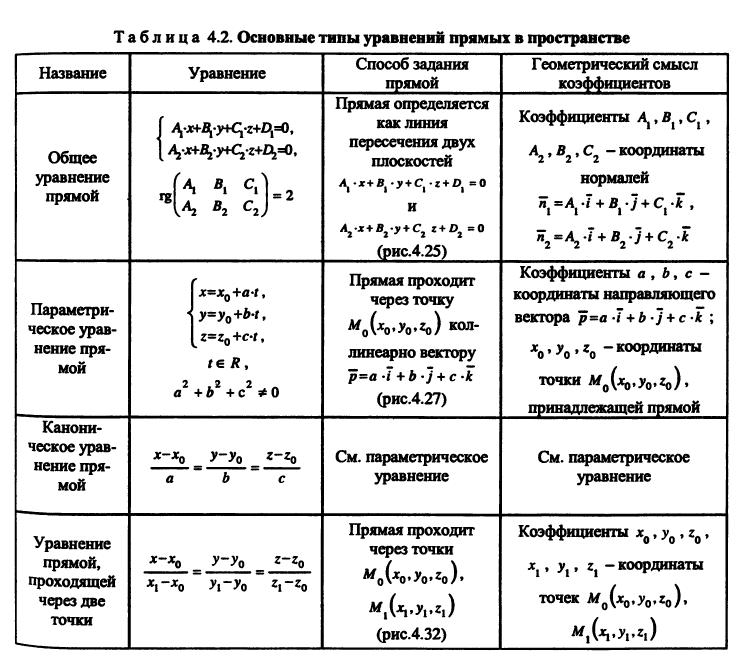 КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫСхема и расчетная модель процесса фугования Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА |
Векторный способ задания движения точки
Связь векторного способа задания движения точки с координатным. Формулы для вычисления скорости точки, ускорения, радиуса кривизны траектории, касательной, нормали и бинормали при векторном способе задания движения точки.
Введение
Положение точки однозначно определяется заданием ее радиус-вектора , который изменяется со временем при движении точки. При векторном способе задания движения считается, что задан закон изменения радиус-вектора от времени . Векторный способ задания движения применяется для описания движения в общем виде, используя векторные формулы.
Например, для точки, движущейся с постоянным ускорением , радиус-вектор определяется одной векторной формулой:
,
где – постоянные векторы, не зависящие от времени. Применяя формулы, мы можем найти кинематические величины в векторном виде, не зависимо от выбранной системы координат.
При координатном способе задания движения, мы выбираем систему координат, и в ней задаем зависимости координат точки от времени . Таким образом, координатный способ привязан к выбранной системе координат, а векторный способ не зависит от системы координат.
Связь векторного способа задания движения с координатным осуществляется по формуле:
,
где – единичные векторы (орты) в направлении осей выбранной системы координат.
Основные формулы при векторном способе задания движения
Скорость точки
Выводы приведенных ниже формул и изложение теории приводится на странице “Кинематика материальной точки”. Здесь мы приводим основные результаты этой теории в векторном виде.
Итак, нам задана зависимость радиус-вектора материальной точки M от времени :
.
Дифференцируя радиус-вектор по времени, мы находим вектор скорости точки:
.
Модуль вектора скорости:
,
где в круглых скобках обозначено скалярное произведение векторов.
Скорость точки направлена по касательной к траектории. Пусть – единичный вектор в направлении касательной. Тогда скорость может быть направленной либо вдоль вектора :
,
либо в противоположную сторону:
.
Чтобы охватить эти два случая, вводят алгебраическую величину скорости :
.
Это скалярная величина, равная по абсолютной величине модулю скорости, но она может принимать как положительные, так и отрицательные значения:
.
При , вектор скорости сонаправлен с . При он направлен в противоположную сторону. Величина является проекцией вектора скорости на направление . Поскольку – это единичный вектор, то
.
Единичный вектор в направлении касательной к траектории:
.
Ускорение точки
Дифференцируя вектор скорости по времени, находим вектор ускорения точки:
.
Модуль вектора ускорения:
.
Разложим вектор ускорения на две взаимно перпендикулярные компоненты: – параллельную касательной к траектории; и – перпендикулярную к ней.
.
Компонента называется касательным, или тангенциальным ускорением, а компонента – нормальным ускорением.
Тангенциальное ускорение
Алгебраическая величина тангенциального ускорения – это скалярная величина, равная проекции полного ускорения на направление единичного вектора , касательного к траектории:
.
Тогда вектор тангенциального ускорения можно записать в следующем виде:
.
Величина может быть как положительной, так и отрицательной. При положительном , вектор касательного ускорения сонаправлен с единичным вектором . При отрицательном – вектор касательного ускорения направлен в противоположную сторону. Модуль равен модулю касательного ускорения:
Модуль равен модулю касательного ускорения:
.
Алгебраическая величина тангенциального ускорения равна производной по времени от алгебраической величины скорости:
.
Производная по времени модуля скорости:
.
Если между векторами скорости и ускорения острый угол, то движение ускоренное. Если между ними тупой угол, то движение замедленное.
Нормальное ускорение
Вектор нормального ускорения:
.
; .
Единичный вектор в направлении главной нормали траектории:
.
Вектор перпендикулярен вектору и направлен к центру кривизны траектории. Нормальное ускорение всегда направлено к центу кривизны траектории. Поэтому, если выразить его через единичный вектор главной нормали:
,
то . Поэтому .
Модуль нормального ускорения равен проекции полного ускорения на направление главной нормали:
.
Имеют место следующие формулы:
.
Радиус кривизны траектории:
.
Центр кривизны траектории:
.
Единичный вектор в направлении бинормали:
.
Исчисление II. Касательные, нормальные и бинормальные векторы
Онлайн-заметки Пола
Главная
/
Исчисление II
/
Трехмерное пространство
/ Касательные, нормальные и бинормальные векторы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 12.8: Касательные, нормальные и бинормальные векторы
В этом разделе мы хотим рассмотреть применение производных для векторных функций. На самом деле есть пара приложений, но все они возвращаются к необходимости первого.
В прошлом мы использовали тот факт, что производной функции был наклон касательной. С векторными функциями мы получаем точно такой же результат, за одним исключением.
Учитывая векторную функцию \(\vec r\left( t \right)\), мы называем \(\vec r’\left( t \right)\) касательным вектором , если он существует и если \(\vec r’\left( t \right) \ne \vec 0\). Касательная линия к \(\vec r\left( t \right)\) в \(P\) — это линия, которая проходит через точку \(P\) и параллельна касательному вектору, \(\vec г’\влево( т \вправо)\). Обратите внимание, что нам действительно нужно требовать \(\vec r’\left( t \right) \ne \vec 0\) для того, чтобы иметь касательный вектор. Если бы у нас было
\[\vec r’\left( t \right) = \vec 0\]у нас был бы вектор, который не имел величины и поэтому не мог бы дать нам направление касательной.
Показать решение
Во-первых, под общей формулой мы подразумеваем, что мы не будем подставлять конкретную \(t\), и поэтому мы найдем формулу, которую мы сможем использовать позже, если мы хотим найти тангенс в точке любую точку на кривой. С учетом сказанного, на данный момент на самом деле не так уж много нужно сделать, кроме как выполнять работу.
Вот касательный вектор к кривой.
\[\vec r’\left( t \right) = 2t\,\vec i + 2\cos t\,\vec j — 2\sin t\,\vec k\] 92}\,\vec i + 2\sin t\,\vec j + 2\cos t\,\vec k\) в \(\displaystyle t = \frac{\pi} {3}\).
Показать решение
Во-первых, нам нужен касательный вектор, и, поскольку это функция, с которой мы работали в предыдущем примере, мы можем просто повторно использовать касательный вектор из этого примера и подставить \(t = \frac{\pi }{3}\ ).
\[\ vec r ‘\ влево ( {\ frac {\ pi} {3}} \ right) = \ frac {{2 \ pi}} {3} \, \ vec i + 2 \ cos \ влево ( {\ frac{\pi} {3}} \right)\,\vec j — 2\sin \left( {\frac{\pi} {3}} \right)\,\vec k = \frac{{2\ pi }}{3}\,\vec i + \vec j — \sqrt 3 \,\vec k\] 92}}}{9},\sqrt 3 ,1} \right\rangle + t\left\langle {\ frac{{2\pi}}}{3},1, — \sqrt 3} \right\rangle \ ]
Прежде чем двигаться дальше, давайте отметим пару вещей о предыдущем примере. Во-первых, мы могли бы использовать единичный касательный вектор, если бы захотели, для параллельного вектора. Однако это привело бы к более сложному уравнению для касательной.
Во-вторых, обратите внимание, что мы использовали \(\vec r\left( t \right)\) для представления касательной линии, несмотря на то, что мы использовали ее и для функции. Не волнуйтесь по этому поводу. \(\vec r\left( t \right)\) здесь очень похоже на \(y\) с нормальными функциями. В случае нормальных функций \(y\) — это общая буква, которую мы использовали для обозначения функций, а \(\vec r\left( t \right)\) имеет тенденцию использоваться таким же образом с векторными функциями.
Далее нам нужно поговорить о единичных нормальных и бинормальных векторах.
Единичный вектор нормали определен как
\[\vec N\left( t \right) = \frac{{\vec T’\left( t \right)}}{{\left\| {\ vec T ‘\ влево ( т \ вправо)} \ вправо \ |}} \]
Единичная нормаль ортогональна (или нормальна, или перпендикулярна) к единичному касательному вектору и, следовательно, к кривой. Мы уже видели векторы нормалей, когда имели дело с уравнениями плоскостей. Они будут появляться с некоторой регулярностью в нескольких темах Calculus III.
Определение единичного вектора нормали всегда кажется немного загадочным, когда вы впервые видите его. Это следует непосредственно из следующего факта.
Факт
Предположим, что вектор \(\vec r\left( t \right)\) такой, что \(\left\| {\vec r\left( t \right)} \right\| = c \) для всех \(t\). Тогда \(\vec r’\left( t \right)\) ортогонален \(\vec r\left( t \right)\).
Доказать этот факт довольно просто. Из утверждения факта и отношения между величиной вектора и скалярным произведением мы имеем следующее. 92}} \справа) = 0\]
Из утверждения факта и отношения между величиной вектора и скалярным произведением мы имеем следующее. 92}} \справа) = 0\]
Также, вспоминая факт из предыдущего раздела о дифференцировании скалярного произведения, мы видим, что
\[\ frac{d}{{dt}}\left( {\vec r\left( t \right)\,\centerdot \,\vec r\left( t \right)} \right) = \vec r ‘\left( t \right)\,\centerdot \,\vec r\left( t \right) + \vec r\left( t \right)\,\centerdot \,\vec r’\left( t \ справа) = 2\vec r’\left( t \right)\,\centerdot \,\vec r\left( t \right)\]
Или, сложив все вместе, получим
\[2\vec r’\left( t \right)\,\centerdot \,\vec r\left( t \right) = 0\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25 in}\hspace{0.25in}\vec r’\left( t \right)\,\centerdot \,\vec r\left( t \right) = 0\]
Следовательно, \(\vec r’\left( t \right)\) ортогонален \(\vec r\left( t \right)\).
Определение единицы нормального затем вытекает непосредственно из этого. Поскольку \(\vec T\left( t \right)\) является единичным вектором, мы знаем, что \(\left\| {\vec T\left( t \right)} \right\| = 1\) для всех \(t\) и, следовательно, по факту \(\vec T’\left( t \right)\) ортогонален \(\vec T\left( t \right)\). Однако, поскольку \(\vec T\left( t \right)\) касается кривой, \(\vec T’\left( t \right)\) также должен быть ортогонален или нормален к кривой. и, таким образом, быть нормальным вектором для кривой. Все, что нам нужно сделать, это разделить на \(\left\| {\vec T’\left( t \right)} \right\|\), чтобы получить единичный вектор нормали.
Далее идет вектор бинормалей. Вектор бинормалей определяется как
\[\vec B\left( t \right) = \vec T\left( t \right) \times \vec N\left( t \right)\]
Поскольку вектор бинормалей определяется как векторное произведение единичного касательного и единичного вектора нормали, мы знаем, что вектор бинормали ортогонален как касательному вектору, так и вектору нормали.
Пример 3 Найдите вектор нормали и бинормали для \(\vec r\left( t \right) = \left\langle {t,3\sin t,3\cos t} \right\rangle \). 92}t} = \sqrt {10} \end{align*}\]
Тогда единичный касательный вектор равен
\[\ vec T \ left( t \ right) = \ left \ langle {\ frac {1} {{\ sqrt {10}}}, \ frac {3} {\ sqrt {10}}} \ cos t , — \frac{3}{{\sqrt {10} }}\sin t} \right\rangle \]
Единичный вектор нормали теперь требует производной единичного тангенса и его модуля.
\[\begin{align*}\vec T’\left( t \right) & = \left\langle {0, — \ frac {3}{{\ sqrt {10}}} \ sin t, — \ frac {3}{{\sqrt {10}}}\cos t} \right\rangle \\ \left\| {\ vec T ‘\ влево ( т \ вправо)} \ вправо \ | & знак равно \ sqrt {\ гидроразрыва {92} t} = \ sqrt {\ frac {9} {{10}}} = \ frac {3} {{\ sqrt {10}}} \ end {align *} \]
Тогда единичный вектор нормали равен
\[\vec N\left( t \right) = \frac{{\sqrt {10}}}}{3}\left\langle {0, — \frac{3}{{\sqrt {10}}}\ sin t, — \frac{3}{{\sqrt {10} }}\cos t} \right\rangle = \left\langle {0, — \sin t, — \cos t} \right\rangle \]
Наконец, вектор бинормалей равен
\[\begin{align*}\vec B\left( t \right) & = \vec T\left( t \right) \times \vec N\left( t \right)\\ & = \left| {\ begin {array} {* {20} {c}} {\ vec i} & {\ vec j} & {\ vec k} \\ {\ frac {1} {{\ sqrt {10}}}} &{\ frac {3} {{\ sqrt {10}}} \ cos t} & { — \ frac {3} {{\ sqrt {10}}} \ sin t} \\ 0 & { — \ sin t} &{ — \cos t}\end{массив}} \right|\,\,\,\,\,\begin{массив}{*{20}{c}}{\vec i}&{\vec j }\\{\frac{1}{{\sqrt {10}}}}&{\frac{3}{{\sqrt {10}}}\cos t}\\0&{ — \sin t}\end {массив}\\ & = — \frac{3}{{\sqrt {10}}}{\cos ^2}t\,\vec i — \frac{1}{{\sqrt {10}}}\ sin t \,\vec k + \frac{1}{{\sqrt {10}}}\cos t\,\,\vec j — \frac{3}{{\sqrt {10}}}}{\sin ^ 2} t \, \ vec i \\ & = — \ frac {3} {{\ sqrt {10} }} \, \ vec i + \ frac {1} {{\ sqrt {10}}} \ cos t \,\,\vec j — \frac{1}{{\sqrt {10}}}\sin t\,\,\vec k\end{align*}\]
Векторные уравнения, векторы, чистая математика
Главная >> ЧИСТАЯ МАТЕМАТИКА, векторы, векторные уравнения
Правила компонентов | Уравнение — одноточечный и параллельный вектор | Уравнение — две точки |
Правила компонентов
Рассмотрим два вектора в трехмерном пространстве.
Где ‘m’ — скалярная величина.
Следовательно, величины a и b определяются как:
В трехмерном пространстве, если точка A имеет вектор положения a и точка B имеет вектор положения b , тогда расстояние AB определяется как:
вернуться к началу
Уравнение прямой линии – заданы одна точка и параллельный вектор
A (x 1 y 1 z 1 ) — фиксированная точка на линии.

