Основные формулы метода координат в пространстве. Урок №1. 11 класс
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Методическая разработка урока геометрии в 11 классе по теме «Основные формулы метода координат в пространстве» Урок №1
(профильный уровень)Автор разработки:
Малинская Елена Геннадьевна
учитель математики
МАОУ гимназии № 40 имени Ю. А. Гагарина
г. Калининград, 2015 г.
2.
 Цели:• Изучить основные формулы метода координат
Цели:• Изучить основные формулы метода координатв пространстве
• Рассмотреть методику использования данных
формул при решении задач
• Применить изученный материал при решении
задач методом координат
19.03.2019
2
3. Повторяем теорию:
• Как находят координаты вектора, если известны координатыего начала и конца?
АВ хВ х А ; уВ у А ; z B z A
• Как находят координаты середины отрезка?
х А хВ
;
2
у А уВ
;
2
• Как находят длину вектора?
а х у z
2
2
z A zB
2
2
• Как находят расстояние между точками?
АВ
х
х А у В у А z B z A
2
В
2
2
4. Повторяем теорию:
• Какие векторы называются перпендикулярными?• Что называется скалярным произведением векторов?
а b a b cos
• Чему равно скалярное произведение
перпендикулярных векторов?
0
• Чему равен скалярный квадрат вектора?
Скалярный квадрат вектора равен квадрату его длины.

5. Введение
• В стереометрии используется два основных метода решения задач.Первый метод основан на аксиомах, теоремах и свойствах фигур. Он
требует логической последовательности практических рассуждений.
Второй метод – это метод координат или координатно-векторный метод,
его можно успешно применять при решении большого числа задач, в том
числе, задач Единого Государственного экзамена (задания С2 или № 17 ).
А так как, эти задания — повышенной сложности, то они приносят
учащимся хорошие баллы при сдаче ЕГЭ.
• Сущность метода координат как метода решения задач состоит в том, что,
задавая фигуры уравнениями и выражая в координатах различные
геометрические соотношения, мы можем решать геометрическую задачу
средствами алгебры.
• В отношении школьного курса геометрии можно сказать, что в некоторых
случаях метод координат дает возможность строить доказательства и
решать многие задачи более рационально, красиво, чем чисто
геометрическими способами.

19.03.2019
5
6. Этапы решения задач методом координат
• 1. Выбор системы координат в пространстве• 2. Нахождение координат необходимых точек и
векторов, или уравнения плоскостей, кривых и
фигур
• 3. Решение примера, используя ключевые задачи
или формулы данного метода
• 4. Переход от аналитических соотношений к
метрическим.
19.03.2019
6
7. Угол между прямыми а и в
19.03.20197
Вектор нормали к плоскости
N
M
P
– вектор нормали плоскости
– это вектор перпендикулярный
этой плоскости
Уравнение плоскости:
где A, B, C – координаты вектора нормали плоскости,
9. Угол между прямой и плоскостью
19.03.20199
10. Угол между плоскостями
19.03.201910
Расстояния в пространстве
• Расстояние между двумя точками А и В
Расстояние от точки А до плоскости
19.03.2019
11
12. Расстояние от точки М до прямой а
19.03.201912
13.
 Расстояние между скрещивающимися прямыми а и в19.03.2019
Расстояние между скрещивающимися прямыми а и в19.03.201913
14. Расстояние между параллельными плоскостями
19.03.201914
15. № 464 (а)
Дано: А 3; 2;4 В 4; 1;2 С 6; 3;2 D 7; 3;1Найти: угол между прямыми АВ и CD.
Ваши предложения…
1. Найдем координаты векторов
АВ 1;1; 2 и CD 1;0; 1
2. Воспользуемся формулой:
cos
x1 x2 y1 y 2 z1 z 2
x y z x y z
2
1
2
1
2
1
2
2
2
2
2
2
φ = 300
№ 466 (а)
Дано: куб АВСDA1B1C1D1 , точка М принадлежит
АА1; АМ : МА1 = 3 : 1; N – середина ВС
Вычислить косинус угла между прям. MN и DD1
z
1. Введем систему координат.
2. Рассмотрим DD1 и МN.
3. Пусть АА1= 4, тогда
D1
1
A1
М 0;4;3 N 4;2;0
4. Найдем координаты векторов М
DD1 и MN.
5. По формуле найдем cosφ.
Ответ:
3
29
C
A
у
B1
D
C
B
N
х
17. Подведение итогов
• Метод координат является необходимой составляющейпри изучении геометрии в школе.
 Этот метод позволяет
Этот метод позволяетупростить процесс и сократить ход решения задачи,
помогает учащимся при сдаче ЕГЭ, а, в дальнейшем, и при
изучении математики в высших учебных заведениях.
• п. 48 № 467 (а)- двумя способами,
19.03.2019
17
English Русский Правила
Векторы.Действия над векторами. — Физика
Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»? А в самом деле, что такое векторы и зачем они? Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей». Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными. Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с2. Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины. Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной: Вот другой пример. Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль. Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов. А вот понятие равенства для векторов есть. Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Здесь в скобках записаны координаты вектора — по x и по y. Если координаты вектора заданы, его длина находится по формуле Сложение векторовДля сложения векторов есть два способа. 1. Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и . Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю. 2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего. Представьте, что вы идете из пункта А в пункт В, из В в С, из С в D, затем в Е и в F. Конечный результат этих действий — перемещение из А в F. При сложении векторов и получаем: Вычитание векторовВектор направлен противоположно вектору . Длины векторов и равны. Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора . Умножение вектора на числоПри умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля. Скалярное произведение векторовВекторы можно умножать не только на числа, но и друг на друга. Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними. Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения: Если векторы перпендикулярны, их скалярное произведение равно нулю. Из формулы для скалярного произведения можно найти угол между векторами: Эта формула особенно удобна в стереометрии. |
Решение задач по теме: «Векторы и координаты» | План-конспект урока по геометрии (11 класс) на тему:
Решение задач по теме: «Векторы и координаты»
Цель: обобщение и систематизация знаний по теме: «Векторы и координаты», совершенствование навыков решения задач методом координат. В ходе урока акцентируется внимание на то, что многие задачи можно решать без чертежа, зная формулы и свойства фигур.
Задачи:
образовательные:
– повторение с учащимися вопросов теории
– формирование навыков решения задач базового и продвинутого уровня
воспитательные:
– формирование информационной компетенции
– формирование коммуникативной компетенции
развивающие:
– интеллектуальное, эмоциональное, личностное развитие ученика
– активизация самостоятельной деятельности ученика
Деятельность учителя:
– осуществление дифференцированного развивающего обучения
– поддержание обратной связи с группами в непрерывном виде
Тип урока: урок практической работы.
Форма организации обучения: индивидуальная, групповая.
Оборудование:
- карточки – задания
- тест
- бланки ответа теста
- карточки-подсказки
До тех пор пока алгебра и геометрия двигались различными путями, их развитие было медленным, а применение ограниченным. Но когда эти науки объединились, они почерпнули друг у друга свежие силы и в результате быстро двинулись вперед к совершенству.
Ж.Л.Лагранж
Ход урока
№этапа | Деятельность преподавателя | Деятельность ученика | Время | ||||||||||||||
1. Организационная часть | Приветствие учащихся. Отметка отсутствующих Проверка готовности учащихся и аудитории к занятиям | 2 | |||||||||||||||
2. | Мотивационный момент. Сообщение темы занятия. Постановка целей. План работы на уроке Тема нашего урока: Решение задач по теме: «Векторы и координаты» Цель: обобщение и систематизация знаний по теме: «Векторы и координаты», совершенствование навыков решения задач методом координат, подготовка к контрольной работе План урока:1)повторение вопросов теории, 2)небольшой экскурс в историю, 3)самостоятельное решение задач с последующей само- и взаимо- проверкой В ходе урока вы и ваши соседи по парте будете заполнять балльные таблицы, для того, чтобы в конце урока дать себе самооценку | Решение задач по теме: «Векторы и координаты» Запись темы в тетради | 3 | ||||||||||||||
3. Актуализация опорных знаний | Выполнение математического диктанта
За каждое верно выполненное задание в оценочный лист 1 балл | выполняют в тетрадях на два варианта Взаимопроверка в парах. №424(а,б), 426(а) | 12 | ||||||||||||||
4.Совершенствование практических навыков решения задач | а) практическая работа: б) Организация проверки в парах
за верно выполненное первое задание 1 балл второе задание 3 балла третье задание 5 баллов | 14 | |||||||||||||||
5. | Решению задач помогут следующие советы:
| 448(а,в),454(план решения),464(а) | 10 | ||||||||||||||
6. Задание на дом | п.42-48, №490,491(б),500. | Запись задания в тетрадь | 2 | ||||||||||||||
7. Заключи-тельная часть | Подведение итогов урока. Выставление оценок Сегодня вам пришлось пройти путь, который был совершен математиками в течение веков. | Мои чувства «Взгляд назад»
| 2 |
Простейшие задачи в координатах
Урок 4.
 Геометрия 11 класс ФГОС
Геометрия 11 класс ФГОСУже известные из планиметрии формулы вычисления координат середины отрезка, вычисления длины вектора по его координатам, а также формула вычисления расстояния между двумя точками не трудно адаптировать для пространства. Это учащиеся и смогут сделать на данном уроке. Все полученные формулы будут использованы при решении различных геометрических задач.
Конспект урока «Простейшие задачи в координатах»
Сегодня вы познакомитесь с формулами вычисления координат середины отрезка, вычисления длины отрезка по его координатам и вычисления расстояния между двумя точками.
Такие же задачи вы уже решали на плоскости. Сейчас же рассмотрим их в пространстве.
Итак, первым рассмотрим правило вычисления координат середины отрезка
.Отметим в прямоугольной координатной плоскости Охуz
точку А с координатами x1,
y1
и z1,
а также точку B с координатами x2,
y2
и z2. Отметим точку C, которая является
серединой отрезка АB.
Отметим точку C, которая является
серединой отрезка АB.
Можно записать, что вектор .
Действительно, ведь с одной стороны по правилу треугольника , а с другой стороны .
Сложим покомпонентно эти равенства. Справа видим сумму противоположных векторов , она равна нулю. Отсюда получаем, что вектор .
Векторы ОА и ОB являются радиус-векторами точек А и B соответственно. Отсюда запишем их координаты.
Равенство, выражающее вектор ОC через векторы ОА и ОB, запишем в координатах.
Получим такие координаты для вектора C. Но так как он является радиус-вектором точки C, то очевидно, что точка С будет иметь такие же координаты.
Можем сделать вывод, что каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Задание:
точка М середина отрезка АВ. Найти координаты точки М по координатам точек А и В.
Решение:
Мы рассмотрели примеры применения формул координат середины отрезка, а теперь перейдём к следующему виду задач: вычисление длины вектора по его координатам.
Длина вектора равна корню квадратному из суммы квадратов его координат.
Докажем это утверждение.
Что и требовалось доказать.
Задание: по координатам точек А и В найти длину вектора АВ.
а) , ;
б) , .
Решение:
Задание: Вычислить длины векторов , , , и .
Решение:
Далее рассмотрим ещё одну простейшую задачу в координатах: определение расстояния между двумя точками.
Отметим две произвольные точки пространства М1
и М2. Пусть координаты точки М1,
а координаты точки М2.
Отрезок М1М2 и является расстоянием между этими точками. А ещё он является длиной вектора М1М2. А длину вектора мы умеем находить по его координатам.
Но для начала выразим координаты вектора через координаты его начала и конца.
Теперь выразим длину вектора М1М2, как корень квадратный из суммы квадратов его координат.
Таким образом, мы выразили длину отрезка М1М2 через координаты его концов и получили формулу вычисления расстояния между двумя точками с известными координатами.
Задание: По координатам точек , и определить вид .
а) , , ; б) , ,
Решение:
Зная координаты вершин треугольника, мы можем вычислить длины всех его сторон.
При выполнении этого задания мы применили формулу
вычисления расстояния между двумя точками.
Задача: Найти расстояние от точки начала координат до середины отрезка , если и .
Решение:
Итоги:
На этом уроке вы познакомились с простейшими задачами в координатах. А именно: определением координат середины отрезка, вычислением длины отрезка по его координатам и расстояния между двумя точками.
Предыдущий урок 3 Связь между координатами векторов и координатами точек
Следующий урок 5 Угол между векторами
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 11 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Векторы 9 класс с ответами
Тесты по геометрии 9 класс.
Правильный вариант ответа отмечен знаком +
1. Отрезок, для которого указано, какой из его концов является началом, а какой – концом, называется:
А. луч –
Б. прямая –
В. вектор +
Г. нет верного варианта ответа –
2. Любая точка пространства может рассматриваться как вектор. Такой вектор называется:
А. коллинеарным –
Б. сонаправленным –
В. нулевым +
Г. ненулевым –
3. Два ненулевых вектора, лежащие на одной прямой или на параллельных прямых, называются:
А. сонаправленными –
Б. коллинеарными +
В. противоположно направленными –
Г. равными –
4. Какие слова пропущены в предложении?
Если два ненулевых вектора коллинеарны, то они могут быть направлены либо одинаково (тогда их называют …), либо противоположно (тогда их называют …).
А. сонаправленные; разнонаправленные –
Б. противоположно направленные: сонаправленные –
В. сонаправленные: противоположно направленные +
Г. нет верного варианта ответа –
5. Длиной ненулевого вектора называется:
А. длина луча –
Б. длина отрезка AB +
В. длина прямой –
Г. нет верного варианта ответа –
6. Выберите верное обозначение сонаправленных векторов.
Г. нет верного варианта ответа –
7. Векторы называются равными, если:
А. они коллинеарны –
Б. их длины равны –
В. они сонаправлены –
Г. они сонаправлены и их длины равны +
9. Выберите верное обозначение длины вектора
тест 10.
А. многоугольника –
многоугольника –
Б. четырехугольника –
В. треугольника +
Г. Пифагора –
11. – это формула:
А. разности вектора –
Б. сочетательного закона –
В. нет верного варианта ответа –
Г. переместительного закона +
12. Выберите верную формулу сочетательного закона.
13. Вектор отложен от точки M. Точка M является:
А. концом вектора –
Б. началом вектора +
В. серединой вектора –
Г. нет верного варианта ответа –
14. Если длины двух ненулевых векторов равны, и они противоположно направлены, то они называются:
А. коллинеарными –
Б. равными –
В. противоположными +
Г. сонаправленными –
15. ABC – прямоугольный треугольник, Найдите длину вектора
А. 25 –
Б. 5 +
5 +
В. 12 –
Г. 7 –
16.
17. Найдите длину вектора
А. 10 +
Б. 100 –
В. 14 –
Г. 2 –
18. Дан правильный треугольник ABC со стороной 2. Найдите длину вектора
А. 4 –
Б. 3 –
В. 2 +
Г. недостаточно данных –
19. Выберите пары противоположно направленных векторов.
тест-20. Выберите пары
21. Выберите пары противоположных векторов.
22. Выберите пары равных векторов.
23. Дан параллелограмм ABCD, AC – диагональ Найдите сумму векторов
Г. нет верного варианта ответа –
24. Выберите верную формулировку правила многоугольника.
А. Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов. +
Б. От любой точки можно отложить вектор, равный данному, и притом только один. –
В. Чтоб сложить два вектора, нужно из произвольной точки отложить один вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало одного с концом второго. –
Г. Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов. –
25. Верны ли следующие суждения?
а. Векторы называются равными, если они коллинеарные и их длины равны.
б. Длиной нулевого вектора является длина отрезка CD.
А. верно только а –
Б. верно только б +
В. оба суждения верны –
Г. оба суждения неверны –
26. Верны ли следующие суждения?
а. Направленный отрезок (вектор), длина которого равна нулю, – это нулевой вектор.
б. От любой точки можно отложить вектор, равным данному, и притом только один.
А. верно только а –
Б. верно только б –
В. оба суждения верны +
Г. оба суждения неверны –
27. Верны ли следующие суждения?
а. Разностью векторов называется такой вектор, сумма которого с вектором равна вектору
б. Два ненулевых вектора называются коллинеарными, если их длины равны и они противоположно направлены.
А. верно только а +
Б. верно только б –
В. оба суждения верны –
Г. оба суждения неверны –
28. Верны ли следующие суждения?
А. верно только а –
Б. верно только б +
В. оба суждения верны –
Г. оба суждения неверны –
29. Верны ли следующие суждения?
а. Вектор называется нулевым, если его начальная и конечная точка совпадает.
б. Модулем вектора называется длина вектора, выраженная числовым выражением.
А. верно только а –
Б. верно только б –
В. оба суждения верны +
Г. оба суждения неверны –
тест_30. Верны ли следующие суждения?
а. Скалярные величины характеризуются числом и направлением, а векторные только числом.
б. К векторным величинам относятся скорость, ускорение, перемещение.
К векторным величинам относятся скорость, ускорение, перемещение.
А. верно только а –
Б. верно только б +
В. оба суждения верны –
Г. оба суждения неверны –
Скалярное произведение векторов определение, основные свойства, формулы и условия вычисления, примеры задач с решениями, онлайн-калькулятор
В старших классах на уроках алгебры, геометрии и физики ученики решают задачи с числами-скалярами. Для нахождения результата используется формула скалярного произведения векторов: (а, а) > 0, для всех а≠0. Полученное значение не зависит от системы координат. Оно характеризует длину сомножителей и угол, образованный между ними. Подобной операции соответствует линейность.
Содержание
- Трактовка понятий
- Описание свойств
- Применение в физике
Трактовка понятий
Под скалярным произведением (СП) в пространстве над полем вещественных чисел подразумевается функция (x, y) для соответствующих элементов, принадлежащих указанному координатному пространству. Из определения вытекает линейность СП по первичному аргументу.
Из определения вытекает линейность СП по первичному аргументу.
Для косинуса и синуса справедливо смешанное сопряжение. СП принимает положительную определённость, если соблюдается условие, что x=0. Для вычислений показателя в алгебре используется следующая форма: а = [a1, a2, …, an] и b = [b1, b2, …, bn].
Пример: нужно найти в трёхмерном пространстве произведение двух скаляров [1, 3, −5] и [4, −2, −1]. Решение: необходимо перемножить градиенты (вектора). [1, 3, −5] х [4, −2, −1] = 1 х 4 + 3 х (-2) + (-5) х (-1) = 3.
Геометрическое определение отличается от физического и алгебраического. Чтобы вычислить СП, используя длину и угол между градиентами, которые введены независимым способом, используется следующее выражение: (а, b) = lal x lbl x cos (a, b). Базисом аксиоматики считается скалярное произведение. После его нахождения определяется длина основного вектора и угла.
В современных теоремах понятие СП находится в основе некоторых производных, включая евклидову норму. Термин «длина» используется по отношению к конечномерным векторам. Если имеет смысл криволинейный путь, тогда применяются векторы ненулевой длины. Чаще они находятся в бесконечномерном пространстве.
Термин «длина» используется по отношению к конечномерным векторам. Если имеет смысл криволинейный путь, тогда применяются векторы ненулевой длины. Чаще они находятся в бесконечномерном пространстве.
Угол между такими величинами отличен от нуля. Его значением является число, косинус которого — отношение их СП к произведению их длин. Если пространство псевдоевклидовое (конечномерное, для которого характерна невырожденная индефинитная метрика), понятие «угол» применяется относительно скаляров без изотропных прямых.
Сам угол является числом. Чтобы дать ему значение, вычисляется гиперболический косинус: отношение модуля СП к произведению длин векторов. При перпендикулярности либо ортогональности на плоскости СП равняется нулю. Это свойство скалярного произведения векторов характерно для любого промежутка с положительно определённым СП.
При соблюдении такого условия пространство называется вещественным либо комплексным. Конечномерный вещественный промежуток с положительным СП называется евклидовым, а комплексный — унитарным (эрмитовым).
Конечномерный вещественный промежуток с положительным СП называется евклидовым, а комплексный — унитарным (эрмитовым).
Если скалярное произведение отрицательное либо не считается знакоопределённым, промежуток называется индефинитной метрикой. Примером такого промежутка является пространство Минковского. СП на таких участках не порождает нормы. Из бесконечномерных выделяются пространства:
- Крейна.
- Понтрягина.
Описание свойств
С помощью специальных математических онлайн сервисов или калькулятора легко находится значение СП через теорему косинусов: a = arccos (a, b)/√(а, а)(b, b). Знак зависит от косинуса угла. В норме значения векторов только положительные. СП больше нуля, если угол острый, и меньше, когда он тупой.
Главные свойства умножения скаляров:

Задача 1: вычислить СП векторов а = {1;2} и b = {4;8}. Решение: а х b = 1 х 4 + 2 х 8 = 20.
Задача 2: найти СП скаляров а и b, если из длины равны 3 и 6, а угол — 60 градусов. Решение: а х b = lal x lbl cos α = 3 х 6 х cos60 = 9. Для лучшего усвоения материала два вектора перемножается с помощью матрицы. Чтобы различать множители, первый оформляется в строку, а второй — в столбец. Если в условиях задачи указываются три величины, тогда последняя оформляется в скобки в форме квадратов. Их скалярное произведение вычисляется путём умножения матриц. Результат — единственное число.
Результат — единственное число.
Задача 3: нужно найти СП пар векторов: а = (1; 5; 1), b = (1; -5; 2) и с = (2; 1; 3/2), d = (0; 0; 1). Решение: вычисления проводятся с помощью матричного представления. Первый вектор записывается в строку, а второй — в столбец. Чтобы найти скалярное произведение векторов, потребуется умножить матрицу-строку на матрицу-столбец. Если вектор а умножить на вектор b, получится -22. Аналогично находится значение второй пары. Результат равен 3/2. Простым обобщением конечномерного СП в тензорной (линейной) алгебре считается свёртка с повторяющимся индексом.
Применение в физике
Впервые скалярное произведение ввёл У. Гамильтон в 1846 году. Одновременно учёные начали использовать в своих работах векторное произведение, сумму скаляров. Понятие получило широкое применение и в физике. На его основе сформулированы главные законы электродинамики и механики.
Скаляр является физической величиной. Чтобы его задать, используется одно число. Примеры скаляров в физике:
- масса тела, равная 4 кг;
- температура воздуха на уровне +10 градусов.
В каждом предложенном варианте величина задаётся с помощью одного числа, поэтому масса тела и температура относятся к скалярам. Но это понятие в физике не считается простым числом. Для него характерна размерность.
Если в условиях задачи известно, что масса тела равна 3, необходимо указывать единицу измерения (килограммы, граммы). В математике можно сложить числа 3 и 10, а в физике суммируются только скаляры с одинаковой размерностью: массы с массой, градусы с градусами.
Если рассматривать векторную физическую величину, она характеризуется следующим образом:
Понятие скаляр — модуль вектора либо абсолютная величина. Если предположить, что транспортное средство двигается со скоростью 60 км/ч, такая информация считается неполной. В физике важно знать направление движения. Кроме модуля скорости как абсолютной величины, потребуется знать направление в пространстве, поэтому скорость считается векторной величиной.
В физике важно знать направление движения. Кроме модуля скорости как абсолютной величины, потребуется знать направление в пространстве, поэтому скорость считается векторной величиной.
Если на земле лежит кирпич массой в 1 кг и на него действует сила в 100 Н (модуль), потребуется найти направление движения объекта. Невозможно выяснить параметр, если нет информации о направлении действия силы. Если она идёт вверх, тогда и кирпич будет двигаться в аналогичном направлении.
Если сила идёт вдоль горизонта, тогда объект поедет горизонтально. При вертикальном воздействии силы вниз кирпич останется на прежнем месте. Он будет вжиматься в землю. Подобные явления указывают на то, что сила является вектором, поэтому для неё характерна размерность, модуль.
Для обозначения вектора в физике используются латинские буквы и стрелка:
- вектор скорости: →v;
- вектор силы: →F.

Стрелка является направленным отрезком. Её начальная точка — начало вектора, а конечная или остриё — конец вектора. В математике величина с начальной точкой А и концом В обозначается →АВ. Если начало и конец направленного отрезка совпадают, тогда получается нулевой вектор. Он обозначается →0.
Такой отрезок считается точкой. У него нет конкретного направления, а длина равняется нулю. К безразмерным скалярам относятся коэффициенты трения и полезного действия, показатель преломления света.
Предыдущая
АлгебраКоординаты вектора как найти длину отрезка по двум точкам, правило и формула нахождения в пространстве, свойства, задачи с решением, онлайн-калькулятор
Следующая
АлгебраДифференциальные уравнения определение, типы ДУ, теория, как решать ДУ первого и второго порядка, методы и примеры подробных решений, онлайн-калькулятор
Введение, формула, свойства, решенные примеры и часто задаваемые вопросы
Vedantu имеет учебные материалы по векторам на своей платформе, которые могут использовать все студенты для изучения.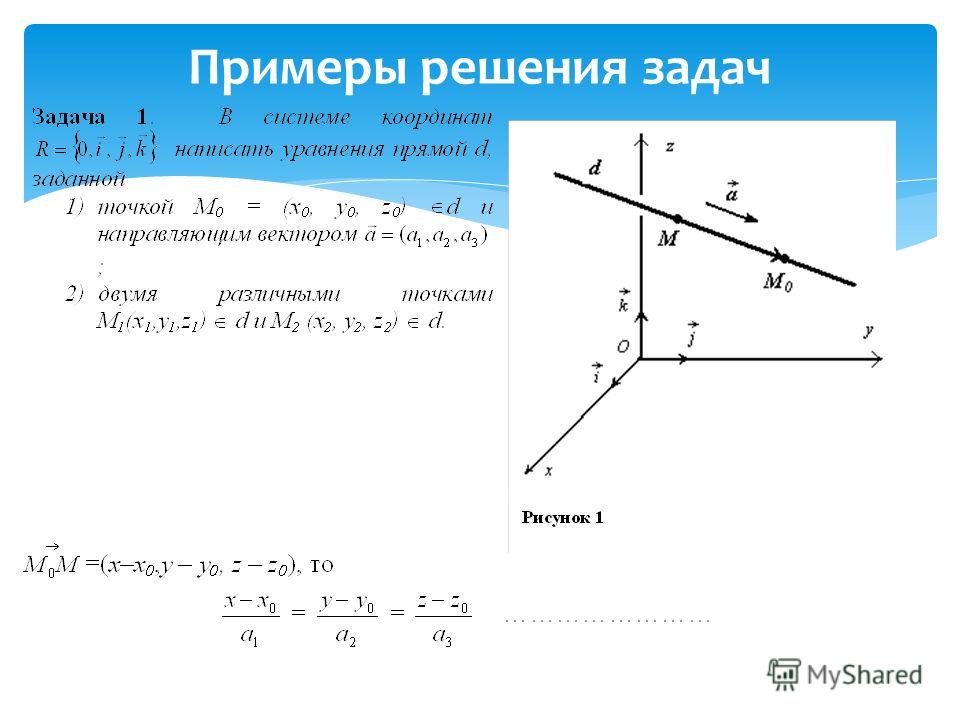 Он имеет определения, словарный запас, математические операции и примеры.
Он имеет определения, словарный запас, математические операции и примеры.
Vedantu сформировала карьеру миллионов студентов и продолжает это делать.
Определение вектора
Математическое представление физических величин, для которых можно определить как величину, так и направление, называется вектором. Вектор любой физической величины изображается прямой линией со стрелкой. В определении вектора длина прямой линии обозначает величину вектора, а стрелка указывает его направление. Любые два вектора можно считать идентичными, если они имеют одинаковую величину и направление. Лучшим примером вектора является сила, приложенная к объекту, поскольку сила и направление приложенной силы влияют на ее действие на объект. Вращение или перемещение вектора вокруг самого себя никогда не изменит его величину.
(Изображение будет загружено в ближайшее время)
Векторная математика
Векторная математика находит широкое применение в различных областях алгебры, геометрии и физики. Как обсуждалось выше, вектор представлен в виде прямой линии со стрелкой. Конечные точки вектора обычно обозначаются буквами английского алфавита в верхнем регистре. Векторы символически представлены конечными точками со стрелкой или строчной буквой со стрелкой.
Как обсуждалось выше, вектор представлен в виде прямой линии со стрелкой. Конечные точки вектора обычно обозначаются буквами английского алфавита в верхнем регистре. Векторы символически представлены конечными точками со стрелкой или строчной буквой со стрелкой.
(Изображение скоро будет загружено)
В приведенном выше векторе область, заключенная в цветочную скобку, указывает величину вектора, а наконечник стрелки указывает направление вектора.
Величина этого вектора задается как |AB| или |а|. Он представляет собой длину вектора и обычно рассчитывается с помощью теоремы Пифагора. Основные математические операции, такие как сложение, вычитание и умножение, могут выполняться над векторами. Однако разделение двух векторов невозможно.
Словарь векторов
Наиболее важными терминами, связанными с векторами, являются:
Нулевой вектор: вектор, величина которого равна нулю.

Единичный вектор : вектор с величиной, равной одной единице.
Вектор положения: Вектор, обозначающий положение точки относительно ее начала.
Co Исходный вектор: два или более вектора с одинаковой начальной точкой.
Подобные и отличные векторы: Векторы с одинаковым направлением называются подобными векторами, а с разными направлениями называются непохожими векторами.
Копланарные векторы: векторы в одной плоскости.
Коллинеарный вектор: векторы, лежащие на одной прямой.
Равные векторы : два или более вектора с одинаковой величиной и направлением.

Вектор смещения : вектор, указывающий смещение объекта из одной точки в другую.
Отрицательное значение вектора: Отрицательное значение любого вектора — это другой вектор с той же величиной, но противоположным направлением.
Математические операции над вектором
Сложение векторов
Сложение векторов выполняется над любыми двумя векторами с использованием закона сложения векторов треугольника. Согласно этому закону два вектора, которые нужно сложить, представляют собой две стороны треугольника с одинаковыми величиной и направлением. Третья сторона дает величину и направление результирующего вектора сложения.
(Изображение скоро будет загружено)
Вычитание векторов
Рассмотрение двух векторов a и b. Если вектор «а» нужно вычесть из вектора «b», необходимо найти отрицательное значение вектора «а» и добавить его к вектору «b» по закону треугольника.
Если вектор «а» нужно вычесть из вектора «b», необходимо найти отрицательное значение вектора «а» и добавить его к вектору «b» по закону треугольника.
B — A = B +( — A) |
Вектор умножение
Умножение. товар’.
а б =|а||б| sin θ n̂ , где |a| является величиной вектора ‘a’ |b| модуль вектора b θ угол разделения двух векторов a и b n̂ единичный вектор, представляющий направление умножения векторов |
а . б =|а||б| cos θ где, |a| является величиной вектора «а» |б| — модуль вектора «b» θ — угол разделения двух векторов «a» и «b» |
Векторная математика Примеры
1 a= (8,13) и вектор b=(12, 15).
Решение: вектор сложения «a» и «b», полученный как 13+15)
с = (20, 27)
2. В одном из векторных вопросов k = (3, 4) и m = (7, 9). Вычтите вектор «k» из вектора «m».
Решение: Чтобы вычесть вектор «k» из вектора «m», нужно найти отрицательный вектор «k».
Отрицательный вектор ‘k’ = — k
= — (3, 4)
= (-3, -4)
Вычитание вектора ‘k’ из вектора ‘m’ задается как:
m — k = m + (-k)
= (7, 9) + (-3, -4)
= (7 — 3), (9 — 4)
= (4, 5)
3. Определить модуль вектора c = (5, 12) 9{o}\]
\[a \cdot b = 63 \times 0\]
\[a \cdot b = 0 \text{единицы}\]
Интересные факты
Произведение векторов — определение, формула , Примеры
Произведение векторов бывает двух типов. Вектор имеет как величину, так и направление, и, исходя из этого, два произведения векторов равны точечному произведению двух векторов и перекрестному произведению двух векторов. Скалярное произведение двух векторов также называется скалярным произведением, поскольку результирующее значение является скалярной величиной. Перекрестное произведение называется векторным произведением, так как в результате получается вектор, перпендикулярный этим двум векторам.
Скалярное произведение двух векторов также называется скалярным произведением, поскольку результирующее значение является скалярной величиной. Перекрестное произведение называется векторным произведением, так как в результате получается вектор, перпендикулярный этим двум векторам.
Давайте узнаем о двух произведениях векторов, рабочих правилах, свойствах, использовании, примерах этих произведений векторов.
| 1. | Что такое произведение векторов? |
| 2. | Рабочее правило для произведения векторов |
| 3. | Свойства произведения векторов |
| 4. | Использование произведения векторов |
| 5. | Примеры произведения векторов |
| 6. | Практические вопросы |
| 7. | Часто задаваемые вопросы о продукте Vectors |
Что такое произведение векторов?
Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на скалярное произведение и перекрестное произведение. Давайте разберемся больше о каждом из произведений векторов.
Мы можем умножать два или более векторов на скалярное произведение и перекрестное произведение. Давайте разберемся больше о каждом из произведений векторов.
Скалярное произведение
Скалярное произведение векторов также называется скалярным произведением векторов. Результат скалярного произведения векторов является скалярным значением. Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом.
Пусть a и b — два ненулевых вектора, а θ — угол между векторами. Тогда скалярное произведение или скалярное произведение обозначается буквой a.b, которая определяется как:
\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ .
Здесь \(|\overrightarrow a|\) — величина \(\overrightarrow a\), \(|\overrightarrow b|\) — величина \(\overrightarrow b\), а θ — величина угол между ними.
Перекрестное произведение
Перекрестное произведение также называется векторным произведением. Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Когда два вектора перемножаются друг с другом и произведение также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.
Мы можем понять это на примере, что если у нас есть два вектора, лежащих в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY. Символ × используется между исходными векторами. Векторное произведение или перекрестное произведение двух векторов отображается как:
\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)
Здесь \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, а \(\overrightarrow{c}\) — результирующий вектор. Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\). Перекрестное произведение двух векторов определяется формулой:
Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\). Перекрестное произведение двух векторов определяется формулой:
\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)
Рабочее правило для произведения векторов
Рабочее правило для произведения двух векторов, скалярного произведения и перекрестного произведения можно понять из приведенных ниже предложений.
Скалярное произведение
Для скалярного произведения двух векторов два вектора выражаются через единичные векторы i, j, k вдоль осей x, y, z, затем скалярное произведение получается следующим образом:
Если \(\overrightarrow a = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow b = a_2 \hat i + b_2 \hat j + c_2\hat k\), то
\(\overrightarrow a. \overrightarrow b\) = \((a_1 \hat i + b_1 \hat j + c_1 \hat k)(a_2 \hat i + b_2 \hat j + c_2 \hat k)\)
= \((a_1a_2) (\hat i. \hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1c_2) (\hat i. \hat k) + \\(b_1a_2) ( \hat j. \hat i) + (b_1b_2)(\hat j. \hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)
\hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1c_2) (\hat i. \hat k) + \\(b_1a_2) ( \hat j. \hat i) + (b_1b_2)(\hat j. \hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)
\(\overrightarrow a. \overrightarrow b\) = \(a_1a_2 + b_1b_2+ c_1c_2\)
Перекрестное произведение
Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\ ) — два вектора, такие, что \(\overrightarrow{a}\)= \(a_1\hat i+b_1 \hat j+c_1 \hat k\) и \(\overrightarrow{b}\) = \(a_2 \ шляпа i+b_2 \ шляпа j+c_2 \ шляпа k\), то с помощью определителей мы могли бы найти перекрестное произведение и записать результат в виде формулы перекрестного произведения, используя следующую матричную запись.
Перекрестное произведение двух векторов также представляется с помощью формулы перекрестного произведения следующим образом: a_2c_1) + \hat k (a_1b_2-a_2b_1)\)
Примечание: \( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, y- ось и ось z соответственно.
Свойства произведения векторов
Скалярное произведение единичного вектора изучается путем взятия единичных векторов \(\hat i\) вдоль оси x, \(\hat j\) вдоль оси y и \(\hat k\) по оси Z соответственно. Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0.
- \(\hat i.\hat i\) = \(\hat j.\hat j\) = \(\hat k.\hat k\)= 1
- \(\шляпа i.\шляпа j\) = \(\шляпа j.\шляпа k\) = \(\шляпа k.\шляпа i\)= 0
Перекрестное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и перекрестное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их векторное произведение равно 0. А угол между двумя перпендикулярными векторами равен 90º, и их векторное произведение дает вектор, который перпендикулярен двум заданным векторам.
- \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)
Перекрестное произведение двух векторов следует циклическому порядку, как показано на изображении ниже. Перекрестное произведение двух векторов в циклической последовательности дает третий вектор в последовательности.
- \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}; \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}; \overrightarrow{k} \times \overrightarrow{i} = \overrightarrow{j}\)
- \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}; \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}; \overrightarrow{i}\times \overrightarrow{k} = \overrightarrow{-j}\)
Свойства произведения векторов помогают получить подробное представление об умножении векторов, а также выполнять многочисленные вычисления с использованием векторов. Здесь перечислены несколько важных свойств произведения векторов.
Здесь перечислены несколько важных свойств произведения векторов.
- Перекрестное произведение двух векторов задается формулой \( \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).
- Скалярное произведение двух векторов определяется формулой \( \overrightarrow{a} . \overrightarrow{b} = |a| |b| \cos(\theta)\).
- Скалярное произведение двух векторов подчиняется свойству коммутативности. \(\vec а. \vec б = \vec б. \vec а \)
- Перекрестное произведение двух векторов не соответствует свойству коммутативности. \( \vec a \times \vec b\neq \vec b \times \vec a \)
- Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
- Распределяющее свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
- Перемножение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
- Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
- Умножить на скалярную величину: \(c(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{ б}\)
- Скалярное произведение двух векторов является скаляром и лежит в плоскости двух векторов.

- Перекрестное произведение двух векторов — это вектор, который перпендикулярен плоскости, содержащей эти два вектора.
Использование произведения векторов
Ниже приведены некоторые важные области применения произведения векторов. Давайте разберемся в каждом из этих применений в следующих параграфах.
- Проекция вектора
- Угол между двумя векторами
- Продукт тройного креста
- Площадь параллелограмма
- Объем параллелепипеда
Проекция вектора
Скалярное произведение полезно для нахождения компонента одного вектора в направлении другого. Проекция вектора одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косеканс угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.
Здесь \(\overrightarrow a\) и \(\overrightarrow b\) — два вектора, а θ — угол между двумя векторами.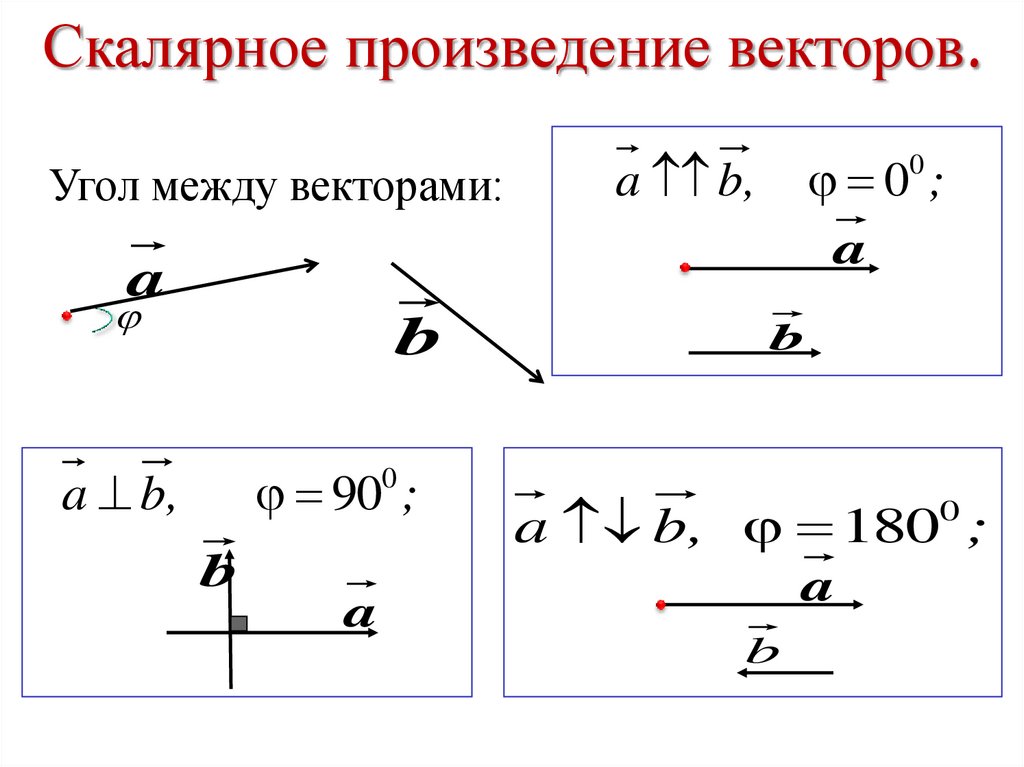 2}}\)
2}}\)
Тройное перекрестное произведение
Перекрестное произведение вектора на произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:
\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)
Площадь параллелограмма
Две смежные стороны параллелограмма могут быть представлены векторами \(\overrightarrow a\) и \(\overrightarrow b\). Площадь параллелограмма равна произведению основания и высоты параллелограмма. Рассмотрим основание параллелограмма как \(|\overrightarrow a|\), а высоту параллелограмма как \(|\overrightarrow b|\)sin θ.
Здесь Основание = \(|\overrightarrow a|\), Высота = \(|\overrightarrow b|\)sin θ, а Площадь параллелограмма = Основание x Высота
Площадь параллелограмма = \(|\overrightarrow a|.|\overrightarrow b|\)sin θ = \(\overrightarrow a \times \overrightarrow b \)
Объем параллелепипеда
Параллелепипед равен шести двусторонняя фигура, каждая из сторон которой является параллелограммом. Здесь параллелограммы противоположных сторон одинаковы. Объем V параллелепипеда можно получить со стороны ребер a, b, c. Объем параллелепипеда можно получить из произведения площади основания на высоту параллелепипеда. Площадь основания параллелепипеда равна |b x c| а высота параллелепипеда равна |a|. Формула расчета объема параллелепипеда выглядит следующим образом.
V = a.(b x c)
Связанные темы
Следующие темы помогают лучше понять произведение векторов.
- Коллинеарные векторы
- Векторы
- Типы векторов
- Добавление векторов
- Перекрестное произведение двух векторов
Часто задаваемые вопросы о продукте векторов
Что такое скалярное произведение векторов?
Скалярное произведение двух векторов имеет два определения. Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением.
Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного произведения векторов является скалярным значением.
Как рассчитать скалярное произведение векторов?
Скалярный продукт можно рассчитать в три простых шага. Сначала найдите величину двух векторов a и b, т.е. |a| и |б|. Во-вторых, найдите косеканс угла θ между двумя векторами. Наконец, возьмите произведение величины двух векторов и косеканса угла между двумя векторами, чтобы получить скалярное произведение двух векторов. (a.b = |a|.|b|.Cosθ. Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.
Почему скалярное произведение называется скалярным произведением векторов?
Скалярное произведение является скалярным, поскольку все отдельные составляющие ответа являются скалярными значениями. В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные величины. Следовательно, скалярное произведение также называют скалярным произведением.
В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные величины. Следовательно, скалярное произведение также называют скалярным произведением.
Почему мы используем косинус в скалярном произведении векторов?
Для нахождения скалярного произведения нам нужно, чтобы два вектора a, b были направлены в одном направлении. Поскольку векторы a и b расположены под углом друг к другу, значение acosθ является компонентом вектора a в направлении вектора b. Следовательно, мы находим cosθ в скалярном произведении двух векторов.
Что такое векторное произведение векторов?
В результате перекрестного произведения двух векторов при умножении третий вектор перпендикулярен двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. a × b = c, где c — векторное произведение двух векторов a и b.
Что такое скалярное произведение и векторное произведение векторов?
Векторы можно перемножать двумя разными способами: точечным произведением и перекрестным произведением. Результаты обоих этих умножений векторов различны. В результате скалярное произведение дает скалярную величину, тогда как векторное произведение дает векторную величину. Скалярное произведение — это скалярное произведение двух векторов, а перекрестное произведение двух векторов — это векторное произведение двух векторов. Скалярное произведение также известно как скалярное произведение, а перекрестное произведение также известно как векторное произведение. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).
Результаты обоих этих умножений векторов различны. В результате скалярное произведение дает скалярную величину, тогда как векторное произведение дает векторную величину. Скалярное произведение — это скалярное произведение двух векторов, а перекрестное произведение двух векторов — это векторное произведение двух векторов. Скалярное произведение также известно как скалярное произведение, а перекрестное произведение также известно как векторное произведение. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).
В чем разница между скалярным произведением и перекрестным произведением векторов?
При умножении векторов скалярное произведение исходных векторов дает скалярную величину, тогда как перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
Что такое правило большого пальца правой руки для перекрестного произведения векторов?
Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора. Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.
Векторы, класс 11, примечания к пересмотру физики — глава 4, формулы, числовые значения
Этот пост охватывает Векторы, класс 11, примечания к пересмотру физики — глава 4 с понятиями, формулами, приложениями, числовыми значениями и вопросами. Эти примечания к пересмотру хороши для CBSE, ISC, UPSC и других экзаменов. Это также относится к программе векторной физики 12 класса некоторых международных советов. Здесь мы рассмотрели основы и типы векторов, законы сложения векторов, точечные и перекрестные произведения, а также относительную скорость дождя относительно движущегося человека (с числовыми значениями).
Это также относится к программе векторной физики 12 класса некоторых международных советов. Здесь мы рассмотрели основы и типы векторов, законы сложения векторов, точечные и перекрестные произведения, а также относительную скорость дождя относительно движущегося человека (с числовыми значениями).
Существуют физические величины, для полного описания которых требуется как величина, так и направление. Простым примером вектора является скорость. Утверждение, что скорость поезда составляет 100 км/ч, не имеет особого смысла, если мы не укажем также направление, в котором движется поезд.
Сила — еще одна такая величина. Мы должны указать не только величину силы, но и направление приложения силы. Такие величины называются векторами. Векторная величина имеет как величину, так и направление. Некоторыми примерами векторных величин в механике являются перемещение, ускорение, импульс, угловой момент, крутящий момент и т. д.
рис. 1 Вектор представлен линией со стрелкой, указывающей его направление. Возьмем вектор AB на рис. 1.
Возьмем вектор AB на рис. 1.
Длина линии представляет его величину в некотором масштабе. Стрелка указывает его направление.
[ Все наши сообщения о Векторе собраны здесь: Уроки по векторной физике . Прочтите их для лучшего понимания ]
Содержание
- Классификация векторов (с диаграммой)
- Равный вектор
- Отрицание вектора
- Нулевой вектор или нулевой вектор
- Блок вектор
- Добавление векторов:
- Liangle Law
- Законодательство Parallogram (Formulas & Angle) 9.9. Закон треугольника
- Умножение векторов – точка и крест, формулы, правила, числа
- Скалярное произведение
- Формула скалярного произведения
- Правила скалярного произведения или скалярного произведения 9
- Правила векторного произведения или векторного произведения – Числа векторной физики | Применение векторного вычитания
- Капли дождя и движущийся человек – относительная скорость (Задача № 1)
- Капли дождя и движущийся человек – относительная скорость (Задача № 2)
- Капля дождя и движущийся человек – относительная скорость (Задача № 3)
- Скалярное произведение
Классификация векторов (с диаграммой) Равный вектор
и они указывают в одном направлении.
Три вектора A, B, и C, показанные на рисунке, равны .
Мы говорим А = В = С .
Но D не равно А .
Вектор (здесь D на рисунке выше), который имеет ту же величину, что и A, но имеет противоположное направление, называется отрицательным из A или – A . Таким образом, D = – A
Нулевой вектор или нулевой векторВектор называется нулевым или нулевым вектором, если величина вектора равна нулю, т. е. начальная точка и конечная точка Вектор тот же.
Единичный вектор Вектор называется единичным, если его величина равна 1 единице и он имеет заданное направление. Единичный вектор — это безразмерный вектор, величина которого точно равна 1. Единичные векторы используются для указания заданного направления и не имеют другого физического значения. Они используются исключительно для удобства описания направления в пространстве.
Они используются исключительно для удобства описания направления в пространстве.
Не имеет ни единиц измерения, ни размеров.
Например, мы можем записать вектор A как A 9шляпы» на символах — это стандартное обозначение единичных векторов, но часто просто жирный шрифт (например, i ) обычно используется без использования шляпы.
Единичные векторы i, j, k образуют набор взаимно перпендикулярных векторов в правой системе координат, как показано на рис. Величина каждого единичного вектора равна 1;
то есть | и | = | и | = | к | = 1.
Единичный вектор вдоль оси x обозначается как i , по оси Y на j и по оси Z на k .
Используя эти обозначения, вектор A , компоненты которого по осям x и y соответственно равны A x и A y , может быть записан как A = A x i + A y 2 j
Добавление векторов:
Можно добавлять только векторы одного типа. Например, можно добавить две силы или две скорости. Но нельзя складывать силу и скорость. Здесь мы обсудим Закон треугольника и Закон параллелограмма для добавления векторов.
Например, можно добавить две силы или две скорости. Но нельзя складывать силу и скорость. Здесь мы обсудим Закон треугольника и Закон параллелограмма для добавления векторов.
обратный порядок. Это называется векторным законом треугольника.
Сумма двух или более векторов называется результирующим вектором. На рис. выше pr является равнодействующей A и B
Закон параллелограмма (формулы и угол)Если можно нарисовать параллелограмм так, что два вектора можно разместить так, чтобы их хвосты были соединены как две смежные стороны параллелограмма с углом θ между ними, то диагональ параллелограмм представляет их результирующий вектор или векторную сумму.
Пусть A и B будут двумя векторами, а θ будет углом между ними, как показано на рисунке выше. Чтобы вычислить векторную сумму, достроим параллелограмм. Здесь сторона PQ представляет вектор A , сторона PS представляет собой B , а диагональ PR представляет результирующий вектор R. Здесь угол α — это угол, который равнодействующая образует с вектором основания, а угол обозначает направление равнодействующей или суммы векторов.
Чтобы вычислить векторную сумму, достроим параллелограмм. Здесь сторона PQ представляет вектор A , сторона PS представляет собой B , а диагональ PR представляет результирующий вектор R. Здесь угол α — это угол, который равнодействующая образует с вектором основания, а угол обозначает направление равнодействующей или суммы векторов.
1)
Вектор Число имеет величину 30 градусов и составляет угол 30 градусов. другой вектор B величины 40. Какова векторная сумма или результат A и B ?
Решение: Пусть R будет векторной суммой A и B .
|Р| = √[30 2 + 40 2 + 2,30,40 cos 30] = 67,66
= 30, B = 40, θ = 30.
tanα = 40 sin 30 / (30 + 40 cos 30) = 20/(30 + 34,64) = 0,31
α = arctg (.31) = 17,22 градуса
Ответ:Результат равен 67,66 на 17,22 градуса от A
2)
две силы, где |A и B равны двум силам = 3 Н и |В| = 4 Н.
Можете ли вы нарисовать векторную сумму этих двух сил, используя закон треугольника?
Также определите его величину и направление, используя подходящую формулу.
Решение: Используя закон треугольника, векторы A и B проведены в хвост к кончику способ нарисовать 2 стороны треугольника. R, сторона треугольника 3 rd (выделена красным) показывает векторную сумму A и B.
Величина векторной суммы может быть рассчитана с использованием теоремы Пифагора в этом случае, и B перпендикулярна A. Таким образом величина векторной суммы: |R| = √(3 2 + 4 2 ) = 5 N
Если он составляет угол α с A, то tanα = 4/3
α = arctg (4/3) = 53,13
Итак, Сумма векторов равна 5 N под углом 53,13 градуса от A
В следующем разделе рассматривается умножение векторов – точка и крест, формулы, правила и числовые задачи.
Умножение векторов – точка и крест, формулы, правила, числа
Скалярное произведение
Скалярное умножение двух векторов дает скалярное произведение. Скалярное умножение также известно как скалярное произведение.
Формула скалярного произведения Скалярное произведение или скалярное произведение двух векторов A и B выражается следующим уравнением:
A.B = AB cos φ, где φ — угол между векторами, A — величина вектора A, а B — величина вектора B. .
1) Скалярное произведение является скаляром, оно коммутативно: A.B = B.A = ABcosθ.
2) Также является распределительным: A.(B + C) = A.B + A.C .
3)
и . Дж = Дж . i = 0
j . к = к .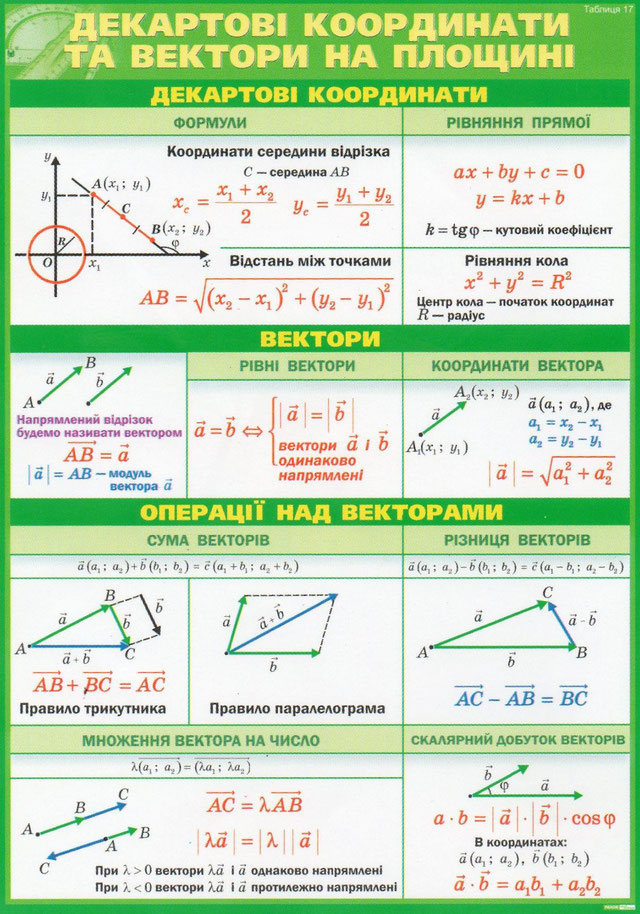 j = 0
j = 0
k . я = я . k = 0
i . i = 1
j . j = 1
k . k = 1
4)
If, A = (A x i + A y j + A z k ) and B = (B x и + В y j + B z k )
Затем найдите A.B
A . B = (A x i + A y j + A z k ) . (B x I + B Y J + B Z K )
= (A x I. = B x I. B x I. B x I. В у у + А x i . B z k )
B x I. В у у + А x i . B z k )
+ (A y j . B x i + A y j . B y j + A y j . B z k )
+ (A z k . B x i + A z k . B y j + A z к. B z k )
= (A x B x i . i + A x B y i . j + A x B z i . k )
+ (A y B x j . i + A y B y j . j + A y B z к. к )
i + A y B y j . j + A y B z к. к )
+ (А з Б х к. i + A z B y k . j + A z B z k . k )
= A x B x + A y B y + A z B z
We define the vector product to be векторную величину с направлением, перпендикулярным этой плоскости (т. е. перпендикулярным обоим A и B ) и величиной, равной AB sinφ.
Формула векторного произведения или векторного произведения если C = AxB , то C = AB sinφ ………………. . (уравнение 1) A, 9059 B [ являются модулями векторов A и B соответственно.
. (уравнение 1) A, 9059 B [ являются модулями векторов A и B соответственно.
C является величиной вектора C .
А, С = (перекрестное) произведение А и B ]
Направление вектора произведения C = A × B определяется правилом правой руки. Если правая рука удерживается так, что загнутые пальцы указывают от А к В через меньший угол между ними, то большой палец, вытянутый под прямым углом к пальцам, будет указывать в направлении С.
Правила векторного произведения Перекрестное произведение1) Направление вектора BxA противоположно направлению вектора AxB . Это означает, что векторное произведение не коммутативно .
2)
i x j = k
j x k =i
k x i =j
j x i = – k
k x j = — I
I x K = — J
I x I = 0
J x J = 0
K x 9. 99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999н. , А = (А х i + A y j + A z k ) and B = (B x i + B y j + B z k )
99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999н. , А = (А х i + A y j + A z k ) and B = (B x i + B y j + B z k )
затем найдите A X B
A x B = (A x I + A Y J + A Y J + A Y J + A Y J + A Y J + A Y J + A Y J + A Y J + A Y . + В у у + В у к )
= (A x i xB x i + A x i x B y j + A x i x B z k )
+ (A y j x B x i + A y j x B y j + A y j x B z k )
+ (A z k x B x i + A z k x B y j + A z k x B z k )
= (A x B x i x i + A x B y i x j + A x B z i x k )
+ (A y B x y x i + A y B y j x j + A y B z j x k )
+ (A z B x k x i + A Z B Y K x J + A Z B Z K x K )
33 = 0 + A 81 B ) = 0 + A 8. 3 = 0 + A 81. B z (- j ) + A y B x (- K ) + 0 + A Y B Z I + A Z B x J + A Z B  K )
K )
= (A Y B Z — A Z B Y ) I + ( Z B x — A x B B B B B B B B B B B B B B B B B B B B B B B ). x B y – A y B x ) k
1) Find out the dot product of vector A and B where A = 4 i + 5 j + 2k , Б = 6 i – 4 j + 3k .
Точечный продукт D = A x B x + A y B y + A z B z = 4,6 + 5(-4) + 2,3 = 24 – 20 + 6 = 10
2) Найдите векторное произведение вектора A и B , где A = 8 9 4 + 5 j + 2k , B = 6 i – 4 j + 3k .
Перекрестное произведение C = (A y B z – A z B y ) i + (A Z B x — A x B Z ) J + ( x B Y — A x B Y — A x B Y — A x B Y — A x B B B B B B B B B B B B B B B B B B ).
=(5,3 – 2(-4)) i + (2,6 – 4,3) j + (4(-4)-5,6) k
= 23 i + 0j -46k = 23i – 46k
В следующем Раздел мы обсудили и решили числовые задачи, связанные с относительной скоростью дождя относительно движущегося человека с помощью Вычитание вектора .
Относительная скорость
Дождя относительно Движущегося Человека – Векторные физические числа | Приложения векторного вычитанияКапля дождя и движущийся человек – относительная скорость (Задача № 1)
Дождь падает вертикально со скоростью 35 м/с. Человек едет на велосипеде со скоростью 12 м/с в направлении с востока на запад. В каком направлении он должен держать свой зонт?
Решение:
Скорость дождя = V r = 35 м/с
Скорость человека = V м = 12 м/с с востока на запад
Относительная скорость дождя относительно человека =V = V r – V м
=> V = V r + (– V м )
На диаграмме мы поменяли направление движения человека на противоположное – V м
Теперь, пусть эта относительная скорость V образует угол θ с вертикалкой.
тангенс θ = V m / V r = 12/35
θ = арктангенс (12/35) = 18,9градусов с вертикалью на запад.
Мужчина должен держать зонтик под углом 18,9 градусов к вертикали.
Капля дождя и движущийся человек – относительная скорость (Задача № 2)Дождь падает вертикально со скоростью x м/с. Человек едет на велосипеде со скоростью 12 м/с в направлении с востока на запад. Каково значение x, если направление, в котором он держит зонтик, составляет 21 градус от вертикали?
Решение:
Скорость дождя = V r = x м/с
Скорость человека = V м = 12 м/с с востока на запад
Относительная скорость дождя по отношению к человеку =V = V r – V м
=> V= x + (– V м )
На диаграмме мы поменяли направление движения человека на противоположное – V м
Если эта относительная скорость V составляет угол θ = 21 градус по вертикали.
тан 21 = V m / V r = 12/x
=> 0,38 =12/x
x=12/0,38=31,57 м/с
Дождь падает вертикально со скоростью 31,57 м/с
Человек – относительная скорость (Задача №3)Дождь падает вертикально со скоростью 40 м/с. Человек едет на велосипеде со скоростью 12 м/с в направлении с востока на запад. Какова будет величина относительной скорости дождя по отношению к человеку? (т. е. какой будет видимая скорость дождя для велосипедиста?)
Решение:
Скорость дождя = V r = 40 м/с
Скорость человека = V м = 12 м/с с востока на запад
Относительная скорость дождя относительно человека =V = V r – V m
=> V= V r + (– V m )
Теперь V = √( V r 2 + V m 2 ) = √( 40 2 + 12 2 ) = 41,76 м/с
Следовательно, кажущаяся скорость дождя для велосипедиста = 41,76 м/с
Примечание: Все наши сообщения о Векторе собраны здесь: Учебники по векторной физике . Прочтите их для лучшего понимания
Прочтите их для лучшего понимания
Движение на плоскости Класс 11 Примечания по физике Глава 4
• Движение на плоскости называется движением в двух измерениях, например, движением снаряда, круговым движением и т. д. Для анализа такого движения мы привязка будет сделана из начала координат и двух координатных осей X и Y.
• Скалярные и векторные величины
Скалярные величины. Физические величины, которые полностью определяются только своей величиной или величиной, называются скалярными величинами.
Примеры. Длина, масса, плотность, скорость, работа и т. д.
Векторные величины. Векторные величины — это те физические величины, которые характеризуются как величиной, так и направлением.
Примеры. Скорость, смещение, ускорение, сила, импульс, крутящий момент и т. д.
• Характеристики векторов
Ниже приведены характеристики векторов:
(i) Они обладают как величиной, так и направлением. ) над количеством.
) над количеством.
• Equal Vectors
• Zero Vector
• Negative of a Vector
• Parallel Vectors
• Coplanar Vectors
Vectors are said to be coplanar if they lie in the same плоскости или параллельны одной плоскости, в противном случае они называются некомпланарными векторами.
• Вектор смещения
Вектор смещения — это вектор, задающий положение точки относительно точки, отличной от начала системы координат.
• Параллелограммный закон сложения векторов
Если два вектора, действующие одновременно в точке, могут быть представлены как по величине, так и по направлению двумя соседними сторонами параллелограмма, проведенного из точки, то равнодействующая представляется полностью как в величина и направление по диагонали параллелограмма, проходящей через эту точку.
• Треугольный закон сложения векторов
Если два вектора представлены как по величине, так и по направлению двумя сторонами треугольника, взятыми в одном порядке, то результирующая этих векторов представлена как по величине, так и по направлению третьей сторону треугольника, взятую в обратном порядке.
• Закон сложения векторов многоугольников
Если несколько векторов представлены как по величине, так и по направлению сторонами многоугольника, взятыми в одном порядке, то результирующий вектор представляется как по величине, так и по направлению замыкающей стороной многоугольника в обратном порядке.
• Свойства сложения векторов
Сложение векторов обладает следующими свойствами:
• Разрешение векторов
Это процесс разделения одного вектора на два или более векторов в разных направлениях, которые вместе производят тот же эффект, что и производится только одним вектором.
Векторы, на которые разбивается данный единичный вектор, называются компонентами векторов. На самом деле разрешение вектора прямо противоположно композиции векторов.
Если компоненты данного вектора перпендикулярны друг другу, то они называются прямоугольными компонентами.
• Вектор положения
• Умножение векторов
(i) Скалярное произведение (Скалярное произведение). Скалярное произведение двух векторов определяется как произведение величины двух векторов на косинус меньшего угла между ними.
Скалярное произведение двух векторов определяется как произведение величины двух векторов на косинус меньшего угла между ними.
• Свойства скалярного произведения
• Свойства перекрестного произведения
• Теорема Лами
Теорема Лами гласит: имеет постоянное отношение к синусу угла между двумя другими силами».
• Движение снаряда
Снаряд — это общее название, данное объекту, которому придана начальная наклонная скорость и который впоследствии следует траектории, определяемой действующей на него гравитационной силой и сопротивлением трения воздуха. Путь, по которому движется снаряд, называется его траекторией.
Уравнение движения снаряда. Общий случай движения снаряда соответствует случаю тела, которому была придана начальная скорость и под некоторым углом 8 выше (или ниже) горизонта. Горизонтальные и вертикальные смещения x и y задаются как
• Угловое смещение
Угловое смещение объекта, движущегося по круговой траектории, определяется как угол, описываемый радиус-вектором в центре круговой траектории в данное время.
θ (угол) = дуга/радиус
θ —> величина углового смещения. Выражается в радианах (rad).
• Угловая скорость
Угловая скорость объекта при круговом движении определяется как скорость изменения во времени его углового смещения.
• Угловое ускорение
Угловое ускорение объекта при круговом движении определяется как скорость изменения его угловой скорости во времени.
• Равномерное круговое движение
Когда тело движется по окружности с постоянной скоростью, то движение тела называется равномерным круговым движением.
Время, за которое объект совершает один оборот по круговой траектории, называется периодом времени. Для кругового движения число оборотов, совершаемых в единицу времени, известно как частота (v). Единица частоты – 1 Герц (1 Гц). Найдено, что
• Центростремительное ускорение
Чтобы поддерживать равномерное круговое движение частицы, необходимо постоянно поддерживать радиальное внутреннее ускорение. Оно известно как центростремительное ускорение.
Оно известно как центростремительное ускорение.
• ВАЖНЫЕ ТАБЛИЦЫ
Примечания по физике для класса 11
Как рассчитать величину силы в физике
Обновлено 08 декабря 2020 г.
. Когда вы работаете в одном измерении, вам не нужно учитывать величину силы. Вычисление величины является более сложной задачей в двух или более измерениях, потому что сила будет иметь «компоненты» вдоль обеих сторон.0512 x- и оси Y и, возможно, ось Z, если это трехмерная сила. Научиться делать это с одной силой и с результирующей силой двух или более отдельных сил — важный навык для любого подающего надежды физика или любого, кто работает над задачами классической физики в школе.
TL;DR (слишком длинный; не читал)
Найдите результирующую силу двух векторов, сначала добавив компоненты x и компоненты y , чтобы найти результирующий вектор, а затем используйте та же формула для его величины.
Основы: что такое вектор?
Первый шаг к пониманию того, что означает вычисление величины силы в физике, — это узнать, что такое вектор. «Скаляр» — это простая величина, которая просто имеет значение, например, температура или скорость. Когда вы читаете температуру 50 градусов по Фаренгейту, это говорит вам все, что вам нужно знать о температуре объекта. Если вы прочитали, что что-то движется со скоростью 10 миль в час, эта скорость говорит вам все, что вам нужно знать о том, как быстро это движется.
«Скаляр» — это простая величина, которая просто имеет значение, например, температура или скорость. Когда вы читаете температуру 50 градусов по Фаренгейту, это говорит вам все, что вам нужно знать о температуре объекта. Если вы прочитали, что что-то движется со скоростью 10 миль в час, эта скорость говорит вам все, что вам нужно знать о том, как быстро это движется.
Вектор отличается тем, что у него есть не только величина, но и направление. Если вы посмотрите отчет о погоде, вы узнаете, насколько быстро дует ветер и в каком направлении. Это вектор, потому что он дает вам дополнительный бит информации. Скорость — это векторный эквивалент скорости, где вы узнаете направление движения, а также скорость его движения. Итак, если что-то движется со скоростью 10 миль в час на северо-восток, скорость (10 миль в час) — это величина, северо-восток — это направление, и обе части вместе составляют вектор скорости.
Во многих случаях векторы разбиваются на «компоненты». Скорость может быть задана как комбинация скорости в северном направлении и скорости в восточном направлении, так что результирующее движение будет на северо-восток, но вам нужны оба бита информации, чтобы определить, как быстро он движется и куда он движется. В задачах по физике восток и север обычно заменяют координатами x и y соответственно.
В задачах по физике восток и север обычно заменяют координатами x и y соответственно.
Величина одиночного вектора силы
Чтобы рассчитать величину векторов силы, вы используете компоненты вместе с теоремой Пифагора. Представьте координату силы x как основание треугольника, компонент y как высоту треугольника, а гипотенузу как результирующую силу обоих компонентов. Удлиняя связь, угол, который образует гипотенуза с основанием, является направлением силы.
Если сила толкает 4 ньютона (Н) в направлении x и 3 Н в направлении y, теорема Пифагора и объяснение треугольника показывают, что вам нужно делать при вычислении величины. Использование 92}
Направление вектора одиночной силы
Направление силы не является предметом этого вопроса, но его легко вычислить на основе треугольника компонентов и результирующей силы из последнего раздела. Вы можете определить направление с помощью тригонометрии. Для большинства задач лучше всего подходит тождество:
Вы можете определить направление с помощью тригонометрии. Для большинства задач лучше всего подходит тождество:
\tan{\theta}=\frac{y}{x}
9{-1}(3/4)=36,9\text{ градусов}
Таким образом, вектор составляет угол примерно 37 градусов с осью x.
Результирующая сила и величина двух или более векторов
Если у вас есть две или более сил, вычислите величину результирующей силы, сначала найдя результирующий вектор, а затем применив тот же подход, что и выше. Единственный дополнительный навык, который вам понадобится, — это найти результирующий вектор, и это довольно просто. Хитрость в том, что вы добавляете соответствующие x и и компоненты вместе. Использование примера должно прояснить это.
Представьте парусник на воде, движущийся вместе с силой ветра и течением воды. Вода придает силу 4 Н в направлении х и 1 Н в направлении у, а ветер добавляет силу 5 Н в направлении х и 3 Н в направлении у. Результирующий вектор представляет собой сложение компонентов x (4 + 5 = 9 Н) и сложение компонентов y (3 + 1 = 4 Н). Таким образом, вы в конечном итоге с 92}\\&=\sqrt{81+16}\\&=\sqrt{97}\\&=9.85\text{ N}\end{aligned}
Результирующий вектор представляет собой сложение компонентов x (4 + 5 = 9 Н) и сложение компонентов y (3 + 1 = 4 Н). Таким образом, вы в конечном итоге с 92}\\&=\sqrt{81+16}\\&=\sqrt{97}\\&=9.85\text{ N}\end{aligned}
Force Is a Vector — манекены
Стивен Хольцнер и
Обновлено: 26 марта 2016 г.
Из книги: Учебник по физике I для чайников с онлайн-практикой
Учебник по физике I для чайников с онлайн-практикой
3 30 Купить на Amazon Сила, как и смещение, скорость и ускорение, является векторной величиной, поэтому второй закон Ньютона записывается как сигма 9.0512 F = м а. Проще говоря, это говорит о том, что векторная сумма сил, действующих на объект, равна его массе (скаляр), умноженной на его ускорение (вектор). Поскольку сила является векторной величиной, вы складываете силы как векторы. Это соответствует второму закону Ньютона.
Это соответствует второму закону Ньютона.
Пример вопроса
Предположим, что у вас есть две силы, как показано: A = 5,0 Н при 40 градусах и B = 7,0 Н при 125 градусах. Какова чистая сила, сигма Ф ?
Правильный ответ: магнитуда 8,9 N, угол 91 градус.
Преобразование силы A в векторную составляющую. Используйте уравнение A x = A cos тета, чтобы найти координату силы x : 5,0 cos 40 градусов = 3,8.
Используйте уравнение A y = A sin theta, чтобы найти y координата силы: 5.0 sin 40 градусов, или 3.2. Это делает вектор A (3.8, 3.2) в координатной форме.
Преобразование вектора B в компоненты. Используйте уравнение B x = B cos theta, чтобы найти координату ускорения x : 7,0 cos 125 градусов = -4,0.

Используйте уравнение B y = B sin тета, чтобы найти y координата второй силы: 7.0 sin 125 градусов или 5.7. Это делает силу B (-4,0, 5,7) в координатной форме.
Выполните сложение векторов, чтобы найти результирующую силу: (3.8, 3.2) + (–4.0, 5.7) = (–0.2, 8.9).
Преобразование вектора (–0,2, 8,9) в форму модуля/угла. Используйте уравнение theta = tan –1 ( y / x ), чтобы найти угол: tan –1 (–44,5) = 91 градус.
Применить уравнение
, чтобы найти величину чистой силы, что дает вам 8,9 Н.
Практические вопросы
Добавьте две силы: A равна 8,0 Н при 53 градусах, а B равна 9,0 Н при 19 градусах.
Добавьте две силы: A равна 16,0 Н при 39 градусах, а B равна 5,0 Н при 125 градусах.

Добавьте две силы: A равна 22,0 Н при 68 градусах, а B равна 6,0 Н при 24 градусах.
Добавьте две силы: A равна 12,0 Н при 129 градусах, а B равна 3,0 Н при 225 градусах.
Ниже приведены ответы на практические вопросы:
Величина: 16 с.ш.; Угол: 35 градусов
Преобразование силы A в векторную составляющую. Используйте уравнение A x = A cos тета, чтобы найти x координату силы A : 8,0 cos 53 градуса = 4,8 Н.
Используйте уравнение A y = A sin theta, чтобы найти y координату силы A : 8,0 sin 53 градуса = 6,4, 909 A 9028, что делает силу равной 9,4,4, 9029 Н. )N в координатной форме.
Преобразование вектора B в компоненты.
 Используйте уравнение B x = B кос-тета, чтобы найти x координата силы B : 9,0 cos 19 градусов = 8,5 Н.
Используйте уравнение B x = B кос-тета, чтобы найти x координата силы B : 9,0 cos 19 градусов = 8,5 Н.Используйте уравнение B y = B sin тета, чтобы найти y координату второй силы: 9,0 sin 19 градусов = 2,9 Н. Это дает силу B 90, (0,8.9) N в координатной форме.
Выполните сложение векторов, чтобы найти результирующую силу: (4.8, 6.4)Н + (8.5, 2.9)Н = (13.3, 9.3)Н.
Преобразование вектора силы (13.3, 9.3) Н в форму величины/угла. Используйте уравнение theta = tan –1 ( y / x ), чтобы найти угол: tan –1 (0,70) = 35 градусов.
Применить уравнение
, чтобы найти величину чистой силы, что даст вам 16 Н.
Величина: 17 с.
 ш.; Угол: 56 градусов
ш.; Угол: 56 градусовПреобразовать усилие A в нотации компонента вектора. Используйте уравнение A x = A cos тета, чтобы найти x координату силы A : 16,0 cos 39 градусов = 12,4 Н.
Use the equation A y = A sin theta to find the y coordinate of force A : 16.0 sin 39 degrees = 10.0 N. That makes force A (12.4, 10.0 )N в координатной форме.
Преобразование силы B в компоненты. Используйте уравнение B x = B cos тета, чтобы найти x координату силы B : 5,0 cos 125 градусов = -2,9 Н.
Используйте уравнение B y = B sin theta , чтобы найти координату y градусов второй силы: 5,0 sin 4,15 N.
 0298 B (–2.9, 4.1)N в координатной форме.
0298 B (–2.9, 4.1)N в координатной форме.Выполните сложение векторов, чтобы найти результирующую силу: (12,4, 10,0)Н + (–2,9, 4,1)Н = (9,5, 14,1)Н.
Преобразование вектора силы (9.5, 14.1) Н в форму величины/угла. Используйте уравнение theta = tan –1 ( y / x ), чтобы найти угол: tan –1 (1,5) = 56 градусов.
Применить уравнение
, чтобы найти величину чистой силы, что даст вам 17 Н.
Величина: 27 с.ш.; Угол: 59 градусов
Преобразование силы A в векторную составляющую. Используйте уравнение A x = A cos тета, чтобы найти x координату силы A : 22,0 cos 68 градусов = 8,24 Н.
Используйте уравнение A y = A sin theta , чтобы найти y координату силы A : 22,0 sin 68 градусов = 20,4 Н.
 Это дает силу A (8,24, 20,4) Н в координатной форме.
Это дает силу A (8,24, 20,4) Н в координатной форме.Преобразование силы B в компоненты. Используйте уравнение B x = B cos theta , чтобы найти x координату силы B : 6,0 cos 24 градуса = 5,5 Н.
Используйте уравнение B y = B sin theta найти координату силы y B : 6,0 sin 24 градуса = 2,9 дюйма (2,4 дюйма) N. Это дает силу 9029. форма координат.
Выполните сложение векторов, чтобы найти результирующую силу: (8.24, 20.3)Н + (5.5, 2.4)Н = (13.7, 22.7)Н.
Преобразование вектора силы (13.7, 22.7)Н в форму величины/угла. Используйте уравнение тета = тангенс –1 ( y / x ), чтобы найти угол: tan –1 (1,66) = 59 градусов.

Применить уравнение
, чтобы найти величину чистой силы, что даст вам 27 Н.
Величина: 12 с.ш.; Угол: 143 градуса
Преобразование силы A в векторную составляющую. Используйте уравнение А x = A cos тета, чтобы найти x координату силы A : 12,0 cos 129 градусов = -7,6.
Используйте уравнение A Y = A SIN THETA , чтобы найти Y Координата FIRCE A : 12,0 y 129.1.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.013. 9013, что 9013, n. , n. 9013, n. 9013, n. , n. 9013, n. , n. . 7.6, 9.3)N в координатной форме.
Преобразование силы B в компоненты. Используйте уравнение B x = B cos тета найти координату силы x B : 3,0 cos 225 градусов = –2,1 Н.



 Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.
Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.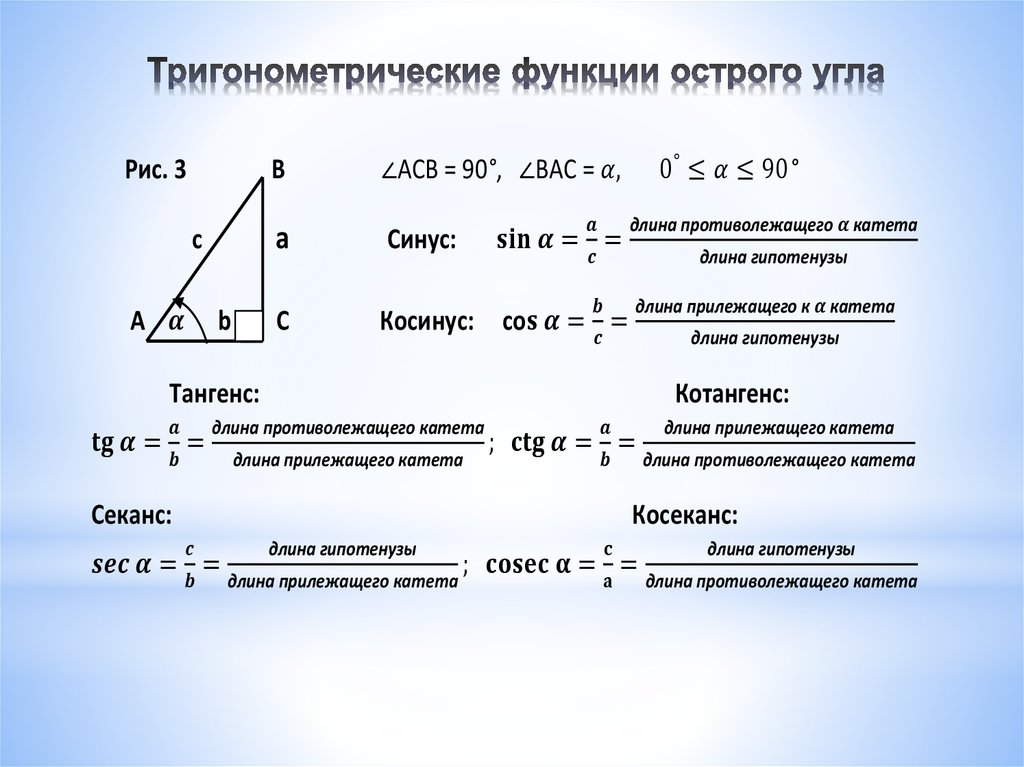 Каждой точке в системе координат соответствуют два числа — ее координаты по x и y, абсцисса и ордината.
Каждой точке в системе координат соответствуют два числа — ее координаты по x и y, абсцисса и ордината.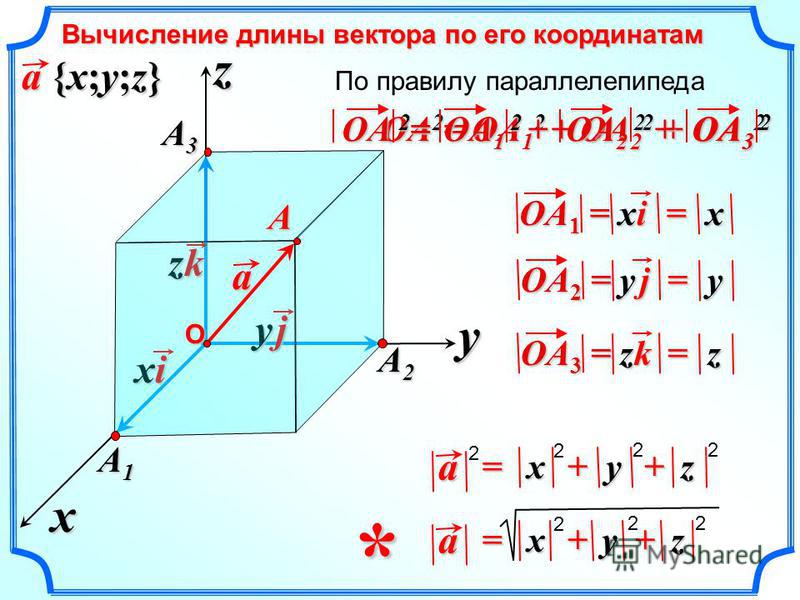 Это и есть сумма векторов и .
Это и есть сумма векторов и .
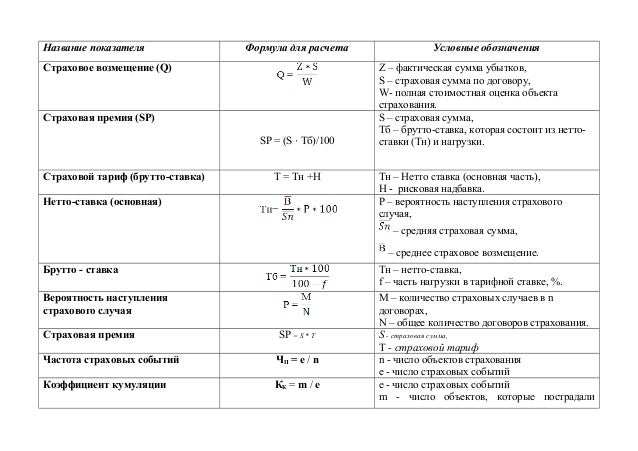 Постановка цели занятия
Постановка цели занятия На какой оси лежит точка А(0,1,0)
На какой оси лежит точка А(0,1,0)
 Закрепление практических навыков
Закрепление практических навыков Решение задач с помощью векторов и координат впервые было предложено Декартом (17 век). Именно поэтому прямоугольная система координат названа его именем. Общие правила своей аналитической геометрии Декарт демонстрировал при решении трудных задач, он решал геометрические задачи алгебраическими методами. Одновременно с Декартом метод координат вводит Пьер Ферма. Три вида задач: плоские, телесные и линейные. Метод координат оказывается эффективным орудием для решения обширного класса задач. Историк математики Г. Цейтен сравнивает реформу математики, связанную с алгебраизацией геометрии, с переходом индустрии от ремесленного к фабричному производству. Математика древняя и юная. Созданные еще в 17 веке основы аналитическо геометрии теперь используются в физике, механике, в аннимации (цветовые системы координат)
Решение задач с помощью векторов и координат впервые было предложено Декартом (17 век). Именно поэтому прямоугольная система координат названа его именем. Общие правила своей аналитической геометрии Декарт демонстрировал при решении трудных задач, он решал геометрические задачи алгебраическими методами. Одновременно с Декартом метод координат вводит Пьер Ферма. Три вида задач: плоские, телесные и линейные. Метод координат оказывается эффективным орудием для решения обширного класса задач. Историк математики Г. Цейтен сравнивает реформу математики, связанную с алгебраизацией геометрии, с переходом индустрии от ремесленного к фабричному производству. Математика древняя и юная. Созданные еще в 17 веке основы аналитическо геометрии теперь используются в физике, механике, в аннимации (цветовые системы координат)