Векторы в пространстве — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Векторы в
пространстве
Цели урока
• Знать: определение вектора в
пространстве и связанные с
ним понятия; равенство
векторов
• Уметь: решать задачи по
данной теме
Физические величины
Скорость v
Ускорение а
Перемещение
Сила F
s
Электрическое поле
Е
+
в
Направление тока
Магнитное поле
Понятие вектора появилось в 19 веке в
Г.
 Грассмана
ГрассманаУ. Гамильтона
Современная символика для обозначения
вектора r была введена в 1853 году
французским математиком О. Коши.
Задание
Повторить все термины по теме «Векторы на
плоскости»
Вектор
Нулевой вектор
Длина вектора
Коллинеарные векторы
Сонаправленные векторы
Противоположно направленные
векторы
Равенство векторов
Определение вектора в пространстве:
вектором называется направленный отрезок
Вектор
имеет начало и конец( А- начало,
В- конец)
В
Обозначение вектора
АВ,
А
с
с
или АВ
Любая точка пространства также
может рассматриваться как вектор. Такой вектор
называется нулевым
0
Т
Обозначение нулевого
вектора
ТТ, 0
Определение
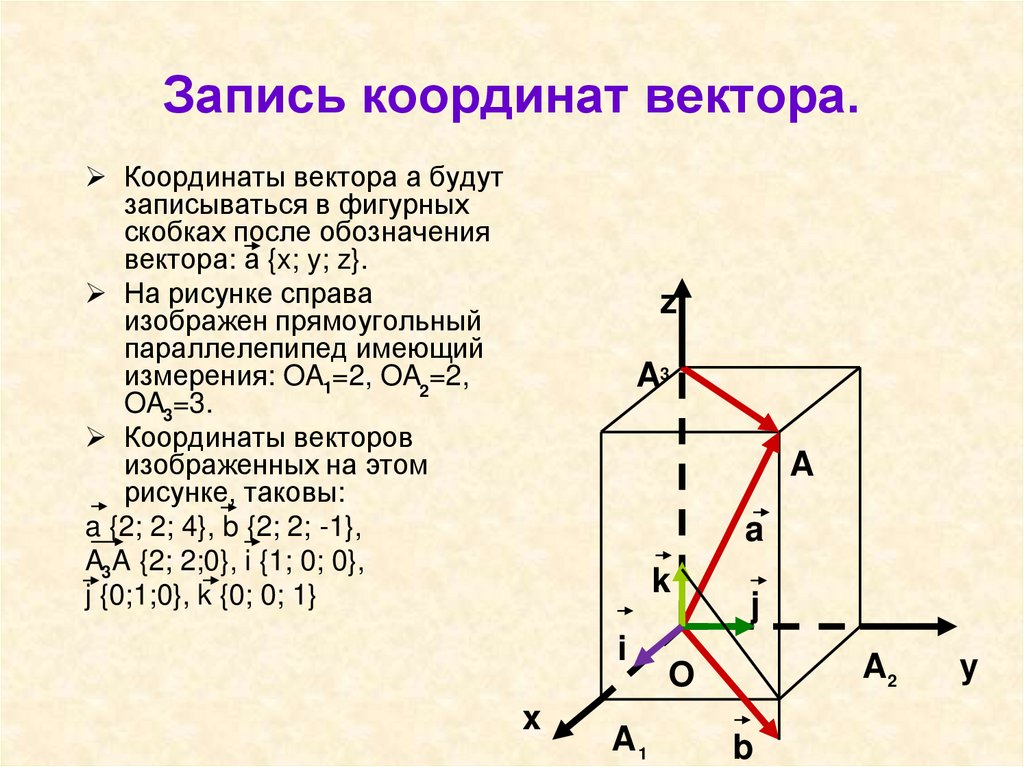
Координатами вектора с началом в точке А1
(х1; у1; z1) и концом в точке
А2 (х2; у2; z2 ) называются числа
х2 — х1, у2 — у1, z2 — z1
Обозначают: А1 А2 ( а1; а2; а3 ) или
а ( а1; а2; а3) или ( а1; а2; а3 ) или
а ( а1; а2; а3)
Решить задачу № 1образец на
следующем слайде)
Даны четыре точки
А(1; 2; 3), С(2; 3; 4),
В(4; 5; 6), Д(7; 8; 9)
• Найти координаты векторов АВ, СД,
ВД, АД, ДС,СВ
Образец решения
А(1; 2; 3),
В(4; 5; 6)
АВ = (4 — 1; 5 — 2; 6 — 3) = (3; 3; 3)
Из координат конечной точки
вычитаем координаты начальной точки
Длина ненулевого вектора
• Длиной вектора АВ с кординатами (а1;а2;а3) или
абсолютной величиной называется длина отрезка
АВ
• Длина вектора АВ (вектора а) обозначается
так:
АВ , а
• Длина нулевого вектора считается равной
нулю:
0 =0
Абсолютная величина
вычисляется по формуле
АВ а1 а2 а3
2
2
2
Решить задачу
• Даны две точки А(1;2;3) и
В(2;3;4).
Далее образец решения
Образец решения:
Сначала найдём координаты вектора:
АВ = (2-1;3-2;4-3) = (1;1;1). Затем по
формуле, найдём модуль
АВ
а1 а2 а3
2
2
2
АВ 12 12 12 3 1,7
Решить
задачу(самостоятельно)
Даны точки С(2;2;3) и
Д(5;3 ;4),М(5;4;7), К(8;3;5) Найти
длину векторов СД и МК
Определение коллинеарности
векторов
• Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых
Коллинеарные векторы
Сонаправленные
векторы
Противоположно
направленные
векторы
Какие векторы на рисунке сонаправленные?
Какие векторы на рисунке противоположно
направленные?
Найти длины векторов АВ; ВС; СС1.
Сонаправленные векторы:
D1 5 см
C1
AA1 BB1, A1D B1C
3 см
AB D1C1
В1
A1
Противоположно-направленные:
9 см
9 см
CD D1C1, CD AB,
C DA BC
D
A
5 см
3 см АВ = 5 см; ВС = 3 см; ВВ1 = 9 см.

B
•Далее не
рассматривать.Дальше будет тема
следующео урока
Равенство векторов
Векторы называются равными, если они
сонаправлены и их длины равны
С
В
АВ=ЕС, так как
АВ ЕС и АВ = ЕС
Е
А
Могут ли быть равными векторы на рисунке?
Ответ обоснуйте
• Рисунок № 1
А
В
Рисунок № 2
О
Н
К
М
С
АВ=СМ, т. к АВ = СМ
А
АН=ОК, т. к АН ОК
• Среди векторов найдите
равные
АВ = (1; 2; 3)
ВС=(2; 2; 3)
СД=(1; 2; 5)
МК=(1; 2; 3)
АВ = МК
Решить задачу
Даны точки: А = (1;2;-3), В=(2;-2;3),
С=(1;-2;5), К=(1;2;3), М=(5;6;7),
Д(0;2;-1)
Найти векторы: АВ, ВС, КМ, ДС и
найти среди них равные
Доказать, что от любой точки
пространства можно отложить вектор,
равный данному, и притом только один
Доказать: в = а, М в, единственный.
Э
М
а
Проведем через вектор а и точку
М плоскость.
В этой плоскости построим
МК = а.
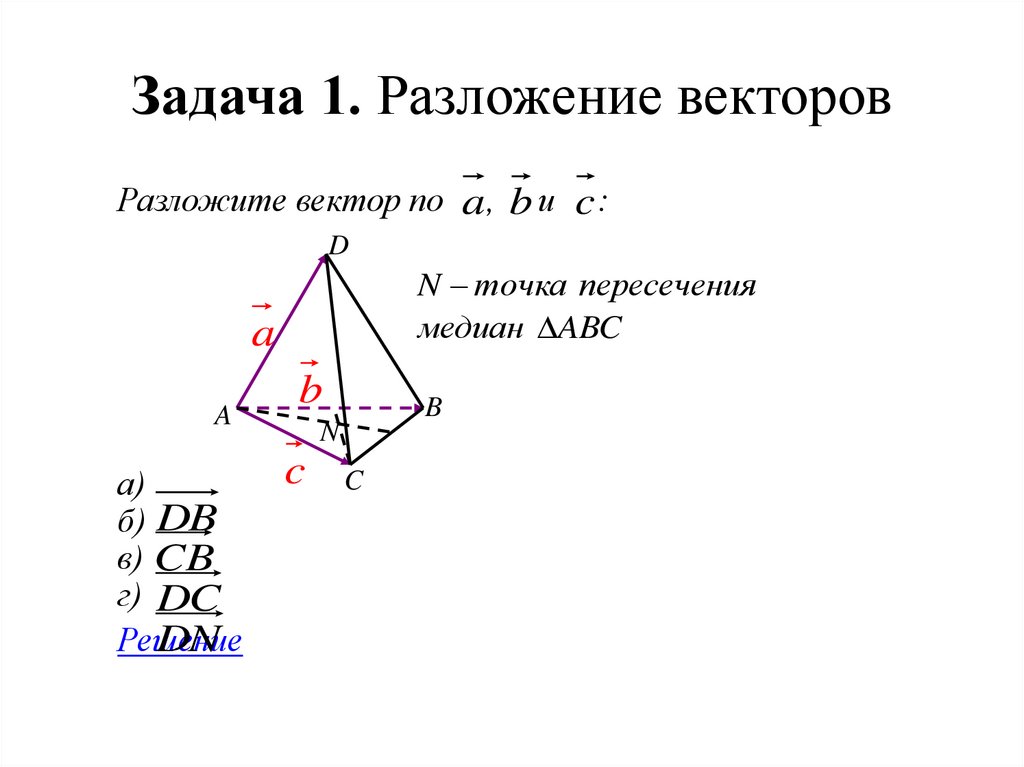
Из теоремы о параллельности
прямых следует МК = а и М МК.
Э
К
Доказательство:
• ДАЛЬШЕ НЕ РАЗБИРАЕМ
Решение задач
№ 322
М
В1
А1
К
С1
Д1
Укажите на этом рисунке
все пары:
а) сонаправленных векторов
ДК и СМ; CВ и С1В1 и Д1А1;
б) противоположно направленных
векторов
СД и АВ; АД и СВ; АА1 и СС1;
С АД и Д1А1; АД и С1В1;
в) равных векторов
А
Д
CВ = С1В1; Д1А1 = С1В1; ДК=СМ
Решение задач
№ 321 (б)
D1
Решение:
C1
A1
DC1 = DC 2 СС12 81 144 15
B1
DB =
D
A
C
B
DB1 =
DА2 АВ 2 81 64 145
DВ 2 BB12 145 144 17
Решение задач
№ 323
N
А
М
Дано: точки М, N, P,Q – середины сторон
D AB, AD, DC, BC; AB=AD= DC=BC=DD=AC;
а) выписать пары равных векторов;
MN = QP; PN = QM; DP = PC;
б) определить вид четырехугольника
Р MNHQ .
Решение: NP-средняя линия треугольника
ADC, NP = 0,5AC, NP\\AC;
MQ-средняя линия тр.
 ABC, MQ = 0,5AC,
ABC, MQ = 0,5AC,С MQ\\AC, NP=MQ, NP\\MQ.
PQ-средняя линия треугольника DВC;
Q PQ = 0,5DB, PQ\\DB;
NM-средняя линяя треугольника ADB,
MN = 0,5DB, MN\\DB, PQ=MN, PQ\\MN.
По условию все ребра тетраэдра равны, то он
правильный и скрещивающиеся ребра в нем
перпендикулярны.
DB перпендикулярно АС .
MNPQNP=MQ=PQ=MN
NP\\MQ
квадрат
MN\\PQ
Решение задач
№ 326 (а, б, в)
М
В1
А1
К
Назовите вектор, который
получится, если отложить:
С1
а) от точки С вектор, равный DD1
D1
CC1 = DD1
б) от точки D вектор, равный СМ
в) от точки А1 вектор, равный АС
С
А
D
А1С1 = АС
Самостоятельная работа
Дан тетраэдр МАВС, угол АСВ прямой. Точки К и Р
середины сторон МВ и МС, АС = 9 см и ВА = 15 см.
Найти КМ .
Решение:
Треугольник АВС, угол АСВ- прямой.
М
М
По теореме Пифагора
К
9
А
15
В
С
ВС АВ2 АС 2 225 81 12
КМ – средняя линия треугольника МВС,
КМ = 0,5ВС = 6 см.

КМ = 6 см.
Кроссворд
2
1
Г А
В Е
К Т
К
4
6
И Н Д У
7
Р А В
М
О
О Л
И
Л
Ь Т О Н
И
Н
Р
Л
О Ш И
5 Д Л И
К Ц И И
Н Ы М И
Е А Р
К
Н А
Н Ы Е
Домашнее задание
Стр. 84 – 85
№ 320, 321(а), 325.
English Русский Правила
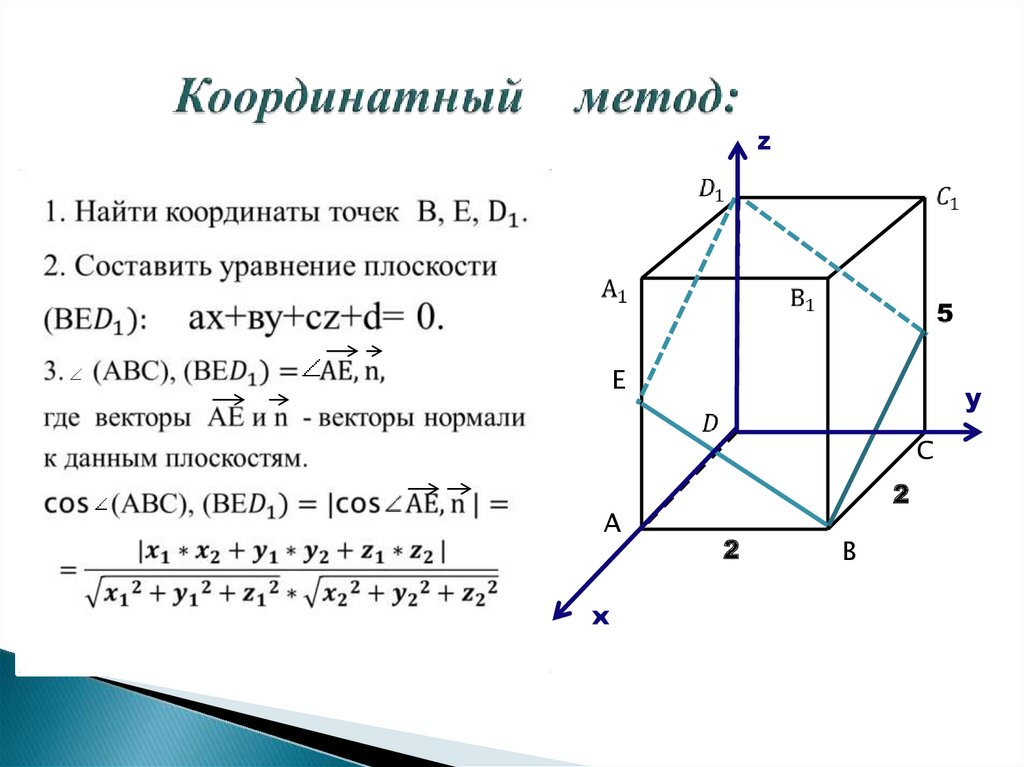
Примеры решения задач по математике
| 1. Даны векторы в некотором базисе. Показать, что система векторов образует базис и найти координаты вектора в этом базисе Решение |
2. Даны координаты вершин пирамиды . Найти: Решение 1) 3) |
3. Составить уравнение высоты треугольника, проведенной через третью вершину . Решение Координаты точки пересечения медиан есть среднее арифметическое соответствующих координат, то есть |
4. Составьте уравнения линии каждая точка которой одинаково удалена от точки и от прямой Решение Пусть — координаты точки этой линии, тогда Данная линия представляет собой параболу |
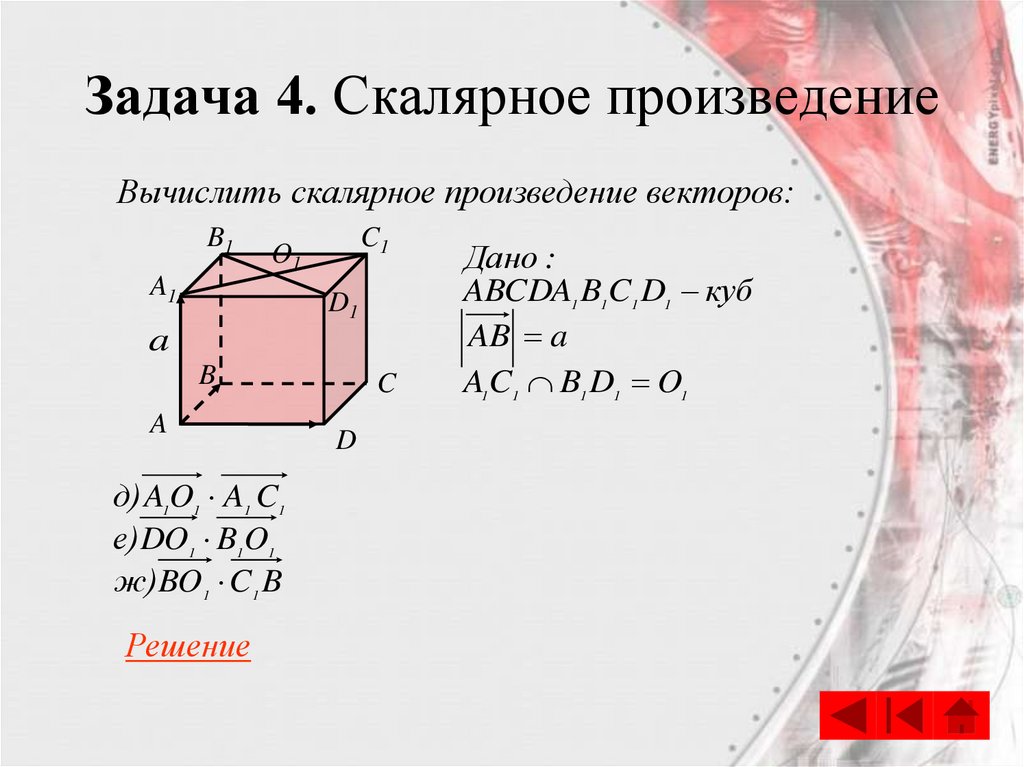
| 5. Дана система линейных уравнений
Решение Решение данной системы уравнений вычисляется по формулам Значит, |
| 6. Даны два линейных преобразования
Решение |
\[
T\left(
\begin{bmatrix}
x \\ y
\end{bmatrix}
\right)
=
\begin{bmatrix}
2x+y \\ 0
\end{bmatrix}
,\;
S\left(
\begin{bmatrix}
x \\ y
\end{bmatrix}
\right)
=
\begin{bmatrix}
x+y \\ xy
\end{bmatrix}
.

\] Определить, являются ли $T$, $S$ и композиция $S\circ T$ линейными преобразованиями.
Прочитать решение
Добавить для решения позже
9{\ транс} А $.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 711
Используя аксиому векторного пространства, докажите следующие свойства.
Пусть $V$ векторное пространство над $\R$. Пусть $u, v, w\in V$.
(a) Если $u+v=u+w$, то $v=w$.
(б) Если $v+u=w+u$, то $v=w$.
(c) Нулевой вектор $\mathbf{0}$ уникален.
(d) Для каждого $v\in V$ аддитивная обратная $-v$ единственна.
(e) $0v=\mathbf{0}$ для каждого $v\in V$, где $0\in\R$ — нулевой скаляр.
(f) $a\mathbf{0}=\mathbf{0}$ для каждого скаляра $a$.
(g) Если $av=\mathbf{0}$, то $a=0$ или $v=\mathbf{0}$.
(h) $(-1)v=-v$.
Первые два свойства называются законом отмены .
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 709
Пусть $S=\{\mathbf{v}_{1},\mathbf{v}_{2},\mathbf{v}_{3},\ mathbf{v}_{4},\mathbf{v}_{5}\}$ где
\[
\mathbf{v}_{1}=
\begin{bmatrix}
1 \\ 2 \\ 2 \\ -1
\end{bmatrix}
,\;\mathbf{v}_{2}=
\begin{bmatrix}
1 \\ 3 \\ 1 \\ 1
\end{bmatrix}
,\ ;\mathbf{v}_{3}=
\begin{bmatrix}
1 \\ 5 \\ -1 \\ 5
\end{bmatrix}
,\;\mathbf{v}_{4}=
\begin{bmatrix}
1 \\ 1 \\ 4 \\ -1
\end{bmatrix}
,\;\mathbf{v}_{5 }=
\begin{bmatrix}
2 \\ 7 \\ 0 \\ 2
\end{bmatrix}
.\]
Найдите базис для пролета $\Span(S)$.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 708
Пусть $A=\begin{bmatrix}
2 & 4 & 6 & 8 \\
1 &3 & 0 & 5 \\
1 & 1 & 6 & 3
\end{bmatrix}$.
(a) Найдите базис для нулевого пространства $A$.
(b) Найдите основу для пространства строк $A$.
(c) Найдите базис для диапазона $A$, состоящего из вектор-столбцов $A$.
(d) Для каждого вектора-столбца, который не является базисным вектором, который вы получили в части (c), выразите его как линейную комбинацию базисных векторов для диапазона $A$.
95$. Если $\mathbf{v}_4$ — другой вектор из $V$, то множество
\[S_2=\{\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3, \ mathbf{v}_4\}\]
все еще остовный набор для $V$? Если да, то докажи. В противном случае приведите контрпример.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 705
Для множества $S$ и векторного пространства $V$ над скалярным полем $\K$ определим множество всех функций от $S$ до $V$
\[ \Fun ( S , V ) = \{ f : S \rightarrow V \} . \]
Для $f, g \in \Fun(S, V)$, $z \in \K$ сложение и скалярное умножение могут быть определены как
\[ (f+g)(s) = f(s) + g(s) \, \mbox{ и } (cf)(s) = c (f(s)) \, \mbox{ для всех } s \in S . \]
(a) Докажите, что $\Fun(S, V)$ — векторное пространство над $\K$. Что такое нулевой элемент?
(б) Пусть $S_1 = \{ s \}$ — множество, состоящее из одного элемента. Найдите изоморфизм между $\Fun(S_1 , V)$ и самим $V$. Докажите, что найденная вами карта на самом деле является линейным изоморфизмом. 9m = \{ (v_1 , v_2 , \cdots , v_m ) \mid v_i \in V \mbox{ для всех } 1 \leq i \leq m \} . \]
\]
(e) Используйте базис $B$ в $V$, чтобы построить базис в $\Fun(S, V)$ для произвольного конечного множества $S$. Какова размерность $\Fun(S, V)$?
(f) Пусть $W \subseteq V$ — подпространство. Докажите, что $\Fun(S, W)$ является подпространством в $\Fun(S, V)$.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 704
Пусть $A=\begin{bmatrix}
2 & 4 & 6 & 8 \\
1 &3 & 0 & 5 \\
1 & 1 & 6 & 3
\end{bmatrix}$ .
(a) Найдите базис для нулевого пространства $A$.
(b) Найдите основу для пространства строк $A$.
(c) Найдите базис для диапазона $A$, состоящего из вектор-столбцов $A$.
(d) Для каждого вектора-столбца, который не является базисным вектором, который вы получили в части (c), выразите его как линейную комбинацию базисных векторов для диапазона $A$.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 703
Используя определение диапазона матрицы, опишите диапазон матрицы
\[A=\begin{bmatrix}
2 & 4 & 1 & -5 \\
1 &2 & 1 & -2 \\
1 & 2 & 0 & -3
\end{bmatrix}.\]
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 692
Пусть $A=\begin{bmatrix}
1 & 0 & 3 & -2 \\
0 &3 & 1 & 1 \\
1 & 3 & 4 & — 1
\end{bmatrix}$. Для каждого из следующих векторов определите, находится ли вектор в нулевом пространстве $\calN(A)$.
(а) $\begin{bmatrix}
-3 \\
0 \\
1 \\
0
\end{bmatrix}$
(б) $\begin{bmatrix} — 90 4\
-1\
2 \\
1
\end{bmatrix}$
(c) $\begin{bmatrix}
0 \\
0 \\
0 \\
0
\end{bmatrix}$
3
3 0 (d) $\begin{bmatrix}
0 \\
0 \\
0
\end{bmatrix}$ Затем опишите нулевое пространство $\calN(A)$ матрицы $A$.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 682
Пусть $V$ обозначает векторное пространство $2 \times 2$ матриц, а $W$ векторное пространство $3 \times 2$ матриц. Определим линейное преобразование $T : V \rightarrow W$ через
\[T \left( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right) = \begin{bmatrix} a+b & 2d \\ 2b – d & -3c \\ 2b – c & -3a \end{bmatrix}.\]
Найдите основу для диапазона $T$.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 664
Пусть $V$ — векторное пространство $k \times k$ матриц. Тогда для фиксированных матриц $R, S \in V$ определим подмножество $W = \{ R A S \mid A \in V \}$. 92$ тогда и только тогда, когда $b = 0$.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 662
Для каких действительных значений $a$ является множество
\[W_a = \{ f \in C(\mathbb{R}) \mid f(0) = a \}\]
подпространство векторного пространства $C(\mathbb{R})$ всех вещественнозначных функций?
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 660
Пусть $V$ векторное пространство матриц $n \times n$, а $M \in V$ фиксированная матрица. Определите
\[W = \{ A \in V \mid AM = MA \}.\]
Множество $W$ здесь называется централизатором множества $M$ в $V$.
Докажите, что $W$ является подпространством в $V$.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 658
Пусть $V$ — векторное пространство $n \times n$ матриц с действительными коэффициентами, и определим
\[ W = \{ \mathbf{v} \in V \mid \mathbf{v} \mathbf{w} = \mathbf{w} \mathbf{v} \mbox{ для всех } \mathbf{w} \ в V \}.\]
Множество $W$ называется центром множества $V$.
Докажите, что $W$ является подпространством в $V$.
Прочитать решение
Добавить для решения позже
Линейная алгебра
Задача 612
Пусть $C[-2\pi, 2\pi]$ — векторное пространство всех вещественнозначных непрерывных функций, определенных на интервале $[-2\pi, 2 \пи]$. 92(x), 1\}$ является базисом для $W$.
Прочитать решение
Добавить для решения позже
линейная алгебра — комбинаторная задача с использованием векторного пространства
$\begingroup$
Позвольте мне сначала изложить проблему. Это упражнение из дискретной математики.
Это упражнение из дискретной математики.
Пусть $k$, $n$ — натуральные числа, где $1 \leq k \leq n$. Пусть $\mathcal{F} = \{A_1,A_2, \cdots, A_m\}$ — множество подмножеств $\{1,2,\cdots,n\}$, таких, что $|A_i \cap A_j | = k$ для всех $i \neq j$. Я хочу показать $m \leq n$. 9n$ имеет базис размера $n$, поэтому $m \leq n$ из-за того, что базис является максимальным линейно независимым подмножеством.
Однако я понятия не имею, как с этим справиться. Как я могу использовать свойство $|A_i \cap A_j| = k$, чтобы доказать их линейную независимость? Это, безусловно, комбинаторная задача, но она предлагает (по-видимому, очень эффективный) подход с использованием векторного пространства.
Спасибо за любую помощь, подсказку или решение.
- линейная алгебра
- комбинаторика
- векторные пробелы
$\endgroup$
2
$\begingroup$
(Должен быть более простой способ сделать это. )
)
Давайте сначала рассмотрим пару немного раздражающих случаев. Во-первых, предположим, что $m = 1$. Тогда, очевидно, $m \le n$, поскольку $n \ge 1$, исходя из нашего предположения (хотя мы могли бы иметь $A_1 = \emptyset$, что испортило бы подсказку).
Менее тривиально, предположим, что $|A_j| = k$ для некоторого $j$. Тогда $A_j$ содержит пересечение друг с другом $A_i$, но оба множества имеют одинаковое количество элементов. Отсюда заключаем, что $A_j = A_j \cap A_i \subseteq A_i$. Итак, $A_j$ — это пересечение $k$ элементов между любыми двумя различными множествами.
В этом случае множества $B_i = A_i \setminus A_j$ образуют множество попарно непересекающихся подмножеств $\{1, 2, \ldots, n\} \setminus A_j$, содержащее $n — k $ баллов. Это означает, что у нас может быть не более $n — k + 1 \le n$ (не забывайте, что $B_j = \emptyset$) различных $B_i$, причем оптимальное решение, включающее каждое $B_i$, является одноэлементным.
Итак, мы предполагаем, что каждый $|A_i|$ не равен $k$. \top B$, что автоматически является положительно-полуопределенной), а вторая положительно определена, поскольку является диагональной матрицей. со строго положительными диагональными элементами. Их сумма положительно определена. В частности, $G$ обратим, поэтому $v_1, \ldots, v_m$ линейно независимы.
\top B$, что автоматически является положительно-полуопределенной), а вторая положительно определена, поскольку является диагональной матрицей. со строго положительными диагональными элементами. Их сумма положительно определена. В частности, $G$ обратим, поэтому $v_1, \ldots, v_m$ линейно независимы.
$\endgroup$
$\begingroup$
Если $m=1$, то сразу $m\le n$, поэтому предположим, что $m > 1$.
Также предположим, что $A_1,…,A_m$ различны.
Обязательно имеем $|A_i|\ge k$ для всех $i$.
Рассмотрим два случая. . .
Случай $(1)$: $\;|A_i|=k$ для некоторого $i$.
Если необходимо изменить маркировку, предположим, что $|A_m|=k$.
Отсюда следует, что $A_m$ является правильным подмножеством $A_i$ для всех $i\in\{1,…,m-1\}$.
92 < 0
\\[4pt]
\конец{выравнивание*}
противоречие, разрешающее случай $(2)$.
Это завершает доказательство.
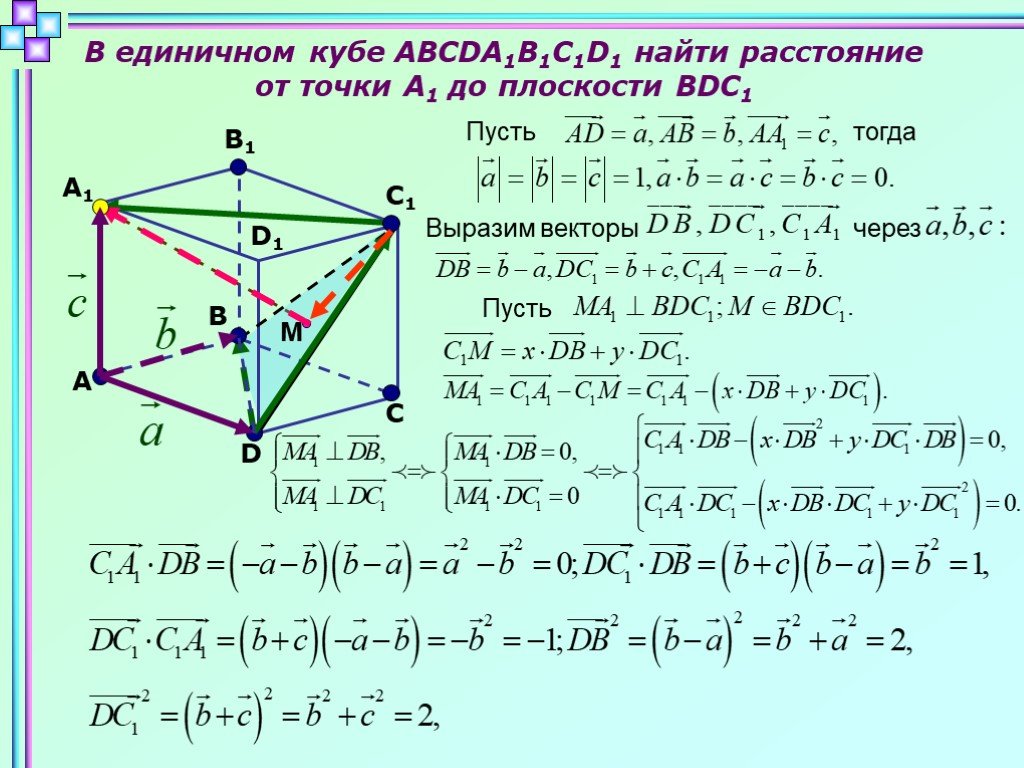
Прочитать решение
\[T \left( \begin{bmatrix} a & b \\ c & d \end{bmatrix} \right) = \begin{bmatrix} a+b & 2d \\ 2b – d & -3c \\ 2b – c & -3a \end{bmatrix}.\]
Прочитать решение

Прочитать решение
\[W_a = \{ f \in C(\mathbb{R}) \mid f(0) = a \}\] подпространство векторного пространства $C(\mathbb{R})$ всех вещественнозначных функций?
Прочитать решение
\[W = \{ A \in V \mid AM = MA \}.\] Множество $W$ здесь называется централизатором множества $M$ в $V$.
Прочитать решение
\[ W = \{ \mathbf{v} \in V \mid \mathbf{v} \mathbf{w} = \mathbf{w} \mathbf{v} \mbox{ для всех } \mathbf{w} \ в V \}.\] Множество $W$ называется центром множества $V$.
Прочитать решение
Прочитать решение
 Это упражнение из дискретной математики.
Это упражнение из дискретной математики.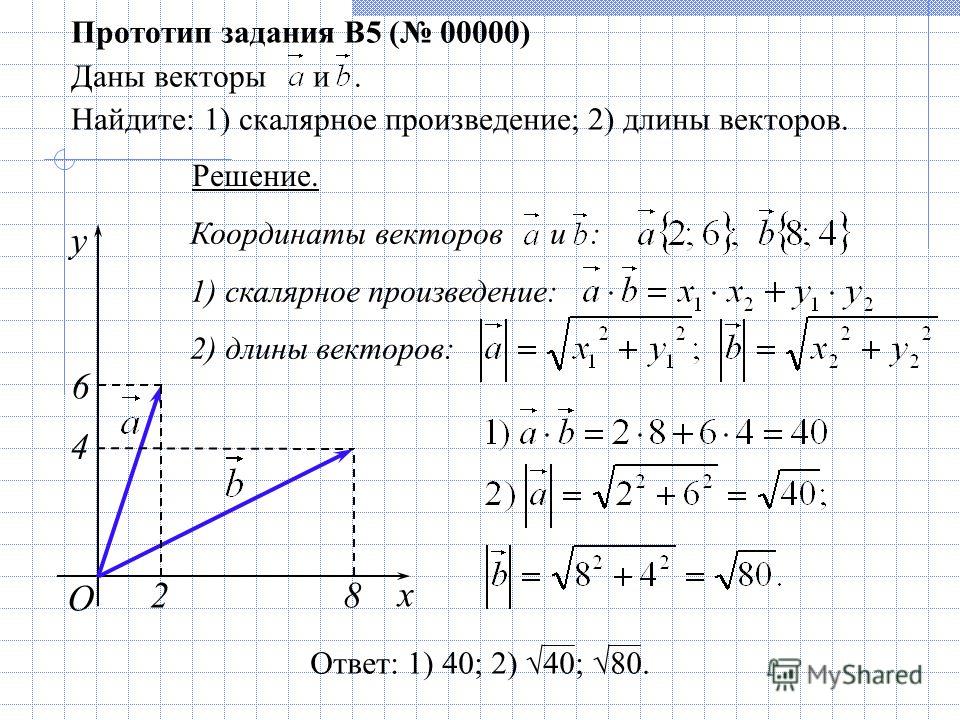 )
) \top B$, что автоматически является положительно-полуопределенной), а вторая положительно определена, поскольку является диагональной матрицей. со строго положительными диагональными элементами. Их сумма положительно определена. В частности, $G$ обратим, поэтому $v_1, \ldots, v_m$ линейно независимы.
\top B$, что автоматически является положительно-полуопределенной), а вторая положительно определена, поскольку является диагональной матрицей. со строго положительными диагональными элементами. Их сумма положительно определена. В частности, $G$ обратим, поэтому $v_1, \ldots, v_m$ линейно независимы.

 Проверим это:
Проверим это: Даны две вершины и и точка пересечения медиан .
Даны две вершины и и точка пересечения медиан .