Ветви параболы: Парабола и квадратные неравенства | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия

2+4=4+4=8
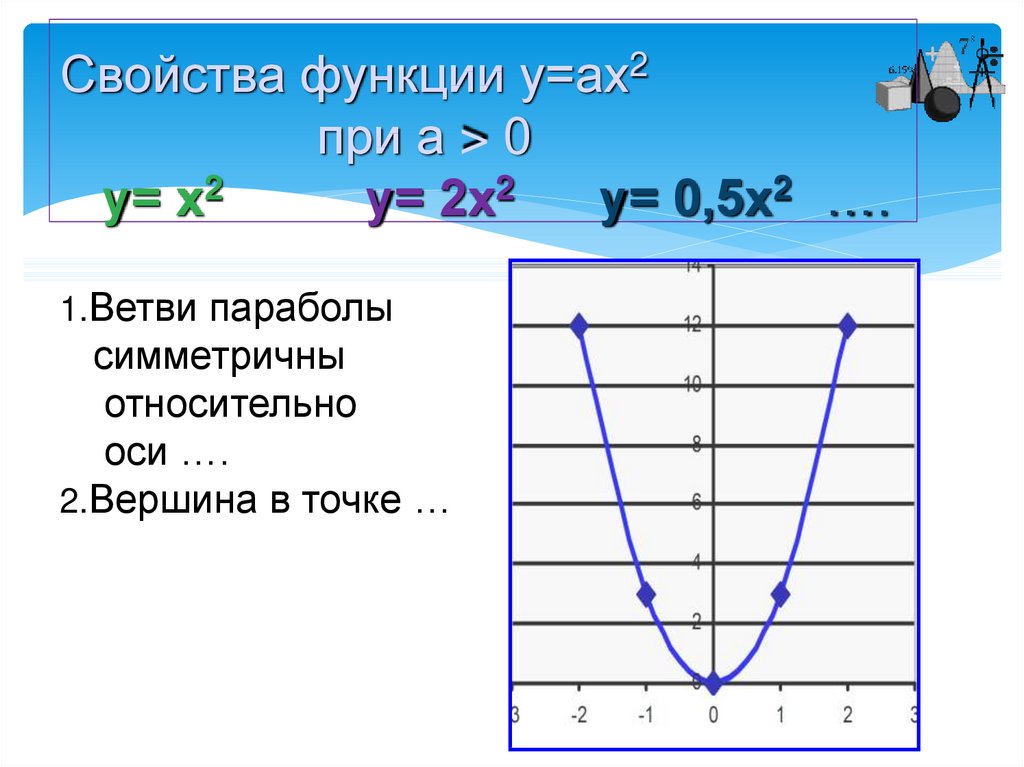
Видно по значениям что значения у симметричны

Подписаться на: Комментарии к сообщению (Atom)

комплексный анализ — Parabolic Branch Cut

спросил 10 лет, 1 месяц назад

Изменено 8 лет назад

Просмотрено 2к раз

$\begingroup$

Ниже приведена задача 19 со страницы 87 книги Саффа и Снайдера «Основы комплексного анализа для математики, науки и техники»,

Как бы вы построили ветвь $\log z$, аналитическую в область D, состоящая из всех точек плоскости, кроме тех, которые лежат на полупарабола $\lbrace x+iy: x \ge 0, y = \sqrt{x}\rbrace$?

Сафф и Снайдер определили, что все логарифмы должны быть приведены к основанию $e$, если не указано иное.

Я понимаю идею ветвления и его назначение в построении однозначной функции из многозначной. Сафф и Снайдер также определили главный логарифм $z$ как 92$ просто имеет два разреза веток. Они лежат на неотрицательной и неположительной мнимых осях соответственно. Я также рассматривал возможность использования разветвления $\log z$, при котором аргумент берется на полуоткрытом интервале $(\pi/4,9\pi/4]$. Это близко к ответу, но срез ветки по-прежнему имеет форму луча, а не полупараболы, не знаю, что еще попробовать…

• комплексный анализ

$\endgroup$

2

$\begingroup$

Чтобы построить эту ветвь журнала $z$, вы просто определяете полупараболу как отсеченную ветвь. Это будет означать, что log $z$ = Log|$z$| + $i\theta$, где $\theta$ равно значению arg $z$ между $\frac{\pi}{2}$ и $2\pi$ для $z$ во втором, третьем или четвертом квадранте, значение arg $z$ между $0$ и $\frac{\pi}{2}$ для $z$ в первом квадранте над полупараболой и значение arg $z$ между $2\pi$ и $ \frac{5\pi}{2}$ для z в первом квадранте под полупараболой.

92}-1}}\bigg)$$

$\endgroup$

$\begingroup$

Просто определите полупараболу как срез ветви, и все готово. Обрезка ветвления не является неотъемлемой частью функции, вы выбираете ее любым способом, который вам нравится, что мешает вам обвести точку ветвления. Например, $\log z$ имеет точки ветвления в $0$ и $\infty$, поэтому любая неограниченная кривая, которая достигает нуля (и не позволяет обвести начало координат), будет разделять ветви этой функции.

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.