Воду при температуре 20 градусов смешали с водой при температуре 100 градусов: 3 л воды, взятой при температуре 20 С, смешали с водой при температуре 100 С….

Содержание

§5. Уравнение теплового баланса.

В задачах этой группы рассматривается теплообмен между телами системы. При этом предполагается, что внешним теплообменом можно пренебречь. Со стороны тел, не входящих в систему, над телами системы работа не совершается. Систему можно считать замкнутой, внутренняя энергия системы не изменяется.

Внутри системы в процессе теплообмена одни тела нагреваются, другие охлаждаются. Однако, суммарное количество теплоты, полученное системой равно нулю:

, (1)

где Q₁; Q₂ … Q_n – количество теплоты, полученное или отданное телами системы в процессе внутреннего теплообмена.

Уравнение (1) называется уравнением теплового баланса и является основным расчетным уравнением для задач этой группы.

Пример решения задачи.

До какой температуры была нагрета стальная фреза массой 0,2 кг, если после погружения ее в алюминиевый калориметр массой 100 г, содержащий 178 г воды при 16, установилась температура 22?

Дано: m₁=0,2 кг, C₁=500, m₂=0,1 кг, C₂=920, m₃=0,178 кг, C₃=4200, 16, 22

Найти:

Анализ:

Так как мы пренебрегаем внешним теплообменом, то можно записать уравнение теплового баланса в виде:

— количество теплоты, которое отдает стальная фреза, остывая от температуры до равновесной температуры .

— количество теплоты, которое получает алюминиевый калориметр, нагреваясь от температуры до равновесной температуры .

— количество теплоты, которое получает вода, нагреваясь от температуры до равновесной температуры .

Отсюда:

Вычисления:

Задачи для самостоятельного решения.

Задача 92. Для аквариума смешали 20 кг воды при 8, 6 кг воды при 50 и 10 кг воды при 40. Определить температуру смеси.

Задача 93. Смешали 39 л воды при 20 и 21 л воды при 60. Определить температуру смеси.

Задача 94. Смешали 6 кг воды при 42, 4 кг воды при 72 и 20 кг воды при 18. Определить температуру смеси.

Задача 95. Сколько литров воды при 95 нужно добавить к 30 л воды при 25, чтобы получить воду с температурой 67?

Задача 96. Смешали 0,4 м³ воды при 20 и 0,1 м³ воды при 70. Какова температура смеси при тепловом равновесии?

Задача 97. В ванну налито 80 л воды при температуре 10. Сколько литров воды при 100 нужно добавить в ванну, чтобы температура смеси была 25?

Задача 98. Чтобы охладить 2 л воды, взятой при 80, до 60, в нее добавляют холодную воду при 10. Какое количество холодной воды требуется добавить?

Задача 99. Для приготовления ванны нужно смешать холодную воду при t₁= 11 с горячей при t₂= 66. Какое количество той и другой воды необходимо взять для получения V = 110 л воды при t₃ = 36?

Задача 100. В каком отношении нужно смешать две массы воды при температурах 50 и 0, чтобы температура смеси была 20?

Задача 101. Необходимо смешать воду при 20 с водой при 100 для получения 300 л воды при 40.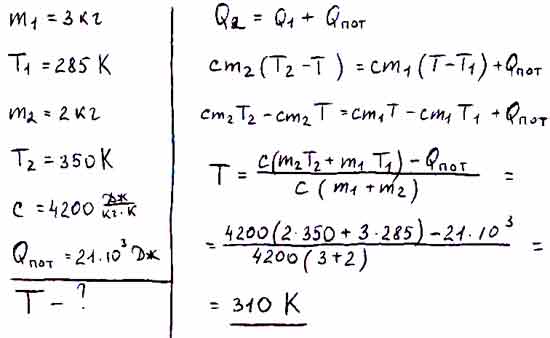 Сколько литров той и другой воды нужно взять?

Задача 102. Паровой котел содержит 40 м³ воды при температуре 225. Какое количество воды при 9 было добавлено, если установилась общая температура 200?

Задача 103. В паровой котел, содержащий 50 m воды при температуре 240, с помощью насоса добавили 3 m воды при температуре 10. Какая установится температура смеси?

Задача 104. Для ванны нужно приготовить 300 кг воды при 36. В водогрейной колонке температура воды 70, а в водопроводе температура воды 10. Сколько той и другой воды нужно взять для приготовления ванны?

Задача 105. В стеклянный стакан массой 0,12 кг при температуре 15 налили 0,2 кг воды при 100. Какая температура воды установилась в стакане?

Задача 106. В стеклянный стакан массой 100 г налито 200 г воды. Температура воды и стакана 75. На сколько понизится температура воды при опускании в нее серебряной ложки массой 80 г при 15?

Задача 107. Стальную деталь машины массой 0,3 кг нагрели до высокой температуры, а затем погрузили для закалки в масло, взятое при 10. Определить начальную температуру стальной детали, если масса масла 3 кг, а конечная температура установилась 30 (удельная теплоемкость масла равна ).

Задача 108. Определить удельную теплоемкость свинца, зная, что 100 г свинца при 100 погрузили в алюминиевый калориметр массой 40 г, содержащий 240 г воды при 15, и температура смеси установилась 16. Проведите подобный опыт.

Задача 109. В латунный калориметр массой 80 г, содержащий 200 г воды при температуре 20, был опущен кусочек алюминия массой 40 г при температуре 100. Температура смеси стала равной 23. Определить удельную теплоемкость алюминия.

Задача 110.

До какой средней температуры нагрелась стальная фреза массой 0,2 кг, если после погружения ее в алюминиевый калориметр массой 100 г, содержащий 178 г воды при температуре 16, установилась температура 22?

Задача 111. Для определения температуры топки котла в нее внесли стальной шарик массой 20 г. Затем перенесли шарик в алюминиевый калориметр массой 60 г, содержащий 200 г воды при температуре 18. Температура смеси установилась 26. Определить температуру топки.

Задача 112. Стальной резец массой 400 г нагрели до 800 и погрузили для закалки в 5 кг воды при 20. До какой температуры охладился резец?

Задача 113. До какой температуры нагрелась во время работы стальная фреза массой 1 кг, если после опускания ее в калориметр температура 1 л воды повысилась от 11,3 до 30? Теплоемкость калориметра не учитывать.

Задача 114. В сосуд, содержащий 2,35 кг воды при 20, опускают кусок олова, нагретого до 230; температура воды в сосуде повысилась на 15. Вычислить массу олова. Испарением воды пренебречь.

Задача 115. Как велика масса стальной детали, нагретой предварительно до 500, если при опускании ее в сосуд, содержащий 18,6 л воды при 13, последняя нагрелась до 35? Испарением воды пренебречь.

Задача 116. Чугунный брусок массой 0,2 кг, предварительно нагретый, опускают в сосуд, содержащий 0,8 кг керосина при 15. Окончательная температура керосина установилась 20. Определить первоначальную температуру бруска.

Задача 117. Для определения удельной теплоемкости вещества проводят следующий опыт: пластинку массой 0,3 кг, предварительно нагретую до 85, опускают в алюминиевый калориметр массой 0,03 кг, содержащий 0,25 кг воды при 22. Общая конечная температура, установившаяся в калориметре, равна 28. Определить удельную теплоемкость вещества пластинки.

Задача 118. В стеклянной колбе, масса которой 50 г, находилось 185 г воды при 20. В колбу вылили некоторое количество ртути при 100, и температура воды в колбе повысилась до 22. Определить массу ртути.

Задача 119. Для определения температуры печи нагретый в ней стальной болт массой 0,3 кг бросили в медный сосуд массой 0,2 кг, содержащий 1,27 кг воды при 15. Температура воды повысилась до 32. Вычислить температуру печи.

Задача 120. В латунный калориметр массой 200 г влили 400 г воды при 17 и опустили тело из серебра массой 600 г при 85. Вода нагрелась до 22. Определить удельную теплоемкость серебра.

Задача 121. После опускания в воду, имеющую температуру 10, тела, нагретого до 100, через некоторое время установилась общая температура 40. Какой станет температура воды, если, не вынимая первого тела, в нее опустить еще одно такое же тело, нагретое до 100.

Задача 122. Для измерения температуры воды, имеющей массу 66 г, в нее погрузили термометр, который показал 32,4. Какова действительная температура воды, если теплоемкость термометра 1,9 Дж/ и перед погружением в воду он показывал температуру помещения 17,8?

Задача 123. В стакане содержится 250 см³ воды. Опущенный в стакан термометр показал 78. Какова действительная температура воды, если теплоемкость термометра 20 Дж/, а до опускания в воду он показывал 20?

Задача 124. В калориметре смешиваются три химически не взаимодействующие жидкости массами 1 кг, 10 кг, 5 кг, имеющие соответственно температуры: 6, — 40, 60. Удельные теплоемкости жидкостей равны соответственно 2 , 4, 2. Определить температуру смеси.

Задача 125. В каком отношении должны быть взяты массы m₁ и m₂ двух жидкостей с удельными теплоемкостями c₁ и c₂, начальными температурами T₁и T₂(T₁>T₂), чтобы общая температура после их смещения получилась равной T₀? Теплоемкость сосуда, в котором находятся жидкости, не учитывать.

Самостоятельная работа 3. Тепловые явления. Количество теплоты. Удельная теплоёмкость. . 8 класс

Категория: Физика.

Самостоятельная работа 3. Тепловые явления. Количество теплоты. Удельная теплоёмкость. . 8 класс

Распечатка самостоятельных работ Кирика Леонида Анатольевича

Начальный уровень

Что потребует большего количества теплоты для нагревания на 1 °С: стакан воды или бидон воды?

2. Что потребует большего количества теплоты для нагревания на 1 °С: 100г воды или 100 г меди?

3. Какое вещество имеет наименьшую удельную теплоемкость?

4. Какое вещество имеет наибольшую удельную теплоемкость?

5. Какое количество теплоты необходимо для нагревании железа массой 1г на 1°С?

6. Чтобы повысить температуру на 1 °С олова массой 1 кг, требуется 230 Дж. Какова удельная теплоемкость олова?

7. Алюминиевая деталь массой 1 кг остывает на 1 °С. Какое количество теплоты выделится при остывании детали?

8. Чугунную деталь массой 1 кг нагрели на 1 °С. На сколько увеличилась при этом внутренняя энергия детали?

Средний уровень

1. Каким количеством теплоты можно нагреть 0,3 кг воды от 12 °С до 20 °С?

2. Какую массу воды можно нагреть на 10 °С 1 кДж теплоты?

3. На сколько градусов остыл кипяток в питьевом баке емкостью 27 л, если он отдал окружающей среде 1500 кДж теплоты?

4. Чтобы нагреть 110 г алюминия на 90 °С, требуется 9,1 кДж. Вычислите удельную теплоемкость алюминия.

5. Какое количество теплоты необходимо для нагревания латунной гири массой 200 г от 20 °С до 28 °С?

6. Какова масса железной детали, если на ее нагревание от 20 °С до 200 °С пошло 20,7 кДж теплоты?

7. На сколько градусов повысилась температура 4 л воды, если она получила количество теплоты, равное 168 кДж?

8. Слиток серебра массой 120 г при остывании от 66 °С до 16 °С передал окружающей среде 1,5 кДж теплоты. Как велика удельная теплоемкость серебра?

Достаточный уровень

1. а) Почему в пустынях днем жарко, а ночью температура падает ниже О °С?

б) Чтобы охладить выточенную из меди деталь, имеющую температуру 100 °С, ее погрузили в 420 г воды с температурой 15 °С. Определите массу детали, если известно, что в процессе теплообмена вода нагрелась до 18 °С.

2. а) По куску свинца и куску стали той же массы ударили молотком одинаковое число раз. Какой кусок нагрелся больше?

б) Стальную деталь массой 300 г нагрели до высокой температуры, а затем погрузили для закалки в 3 кг машинного масла, имеющего температуру 10 °С. Определить начальную температуру детали, если установившаяся температура была 30°С.

3. а) Почему железные печи скорее нагревают комнату, чем кирпичные, но не так долго остаются теплыми?

б) В алюминиевый калориметр массой 140 г налили 250 г воды при температуре 15 °С. После того как брусок из свинца массой 100 г, нагретый до 100 °С, поместили в калориметр с водой, там установилась температура 16 °С. Составить уравнение теплового баланса и определить удельную теплоемкость свинца.

4. а) Почему реки и озера нагреваются солнечными лучами медленнее, чем суша?

б) Мальчик наполнил стакан, емкость которого 200 см³, кипятком на три четверти и дополнил стакан холодной водой. Определите, какая установилась температура воды, если температура холодной воды равна 20 °С.

5. а) Медной и стальной гирькам одинаковой массы передали равные количества теплоты. Температура какой изменится больше?

б) Стальное изделие закалялось нагреванием до температуры 800 °С с последующим опусканием в масло массой 2 кг, взятое при температуре 10 °С. При этом масло нагрелось до температуры 40 °С. Найти массу стального изделия, если при переносе в масло изделие охладилось на 20 °С. Удельная теплоемкость масла 2100 Дж/(кг•°С).

6. а) Что эффективнее использовать в качестве грелки – 2 кг воды или 2 кг песка при той же температуре?

б) Для приготовления ванны вместимостью 200 л смешали холодную воду при температуре 10 °С с горячей при температуре 60 °С. Какие объемы той и другой воды надо взять, чтобы установилась температура 40 °С?

7. а) На что расходуется больше энергии: на нагревание воды или алюминиевой кастрюли, если их массы одинаковы?

б) Вода массой 150 г, налитая в латунный калориметр массой 200 г, имеет температуру 12 °С. Найти температуру, которая установится в калориметре, если в воду опустить железную гирю массой 0,5 кг, нагретую до 100 °С.

8. а) В каком случае горячая вода в стакане охладится больше: если в него опустить серебряную или алюминиевую ложку той же массы? Ответ обосновать.

б) Смешали 39 л воды при 20 °С и 21 л воды при 60 °С. Определить температуру смеси.

Высокий уровень

1. Смешали 6кг воды при 42 °С, 4 кг воды при 72 °С и 20 кг воды при 18 °С. Определить температуру смеси.

2. В алюминиевый сосуд массой 45г налили 150г воды температурой 20°С. В сосуд опустили цилиндр массой 200г, температурой 95°С, при этом температура воды повысилась до 30°С. Определить удельную теплоемкость вещества цилиндра.

3. В 200 г воды при 20 °С помещают 300 г железа при 10 °С и 400 г меди при 25 °С. Найти установившуюся температуру.

4. В латунный калориметр массой 128 г, содержащий 240 г воды при температуре 8,5 °С, опущен цилиндр массой 146 г, нагретый до 100 °С. В результате установилась температура 10 °С. Определить удельную теплоемкость металла цилиндра.

5. Латунный сосуд массой 200 г содержит 400 г анилина при температуре 10 °С. В сосуд долили 400 г анилина, нагретого до температуры 31 °С. Найти удельную теплоемкость анилина, если в сосуде установилась температура 20 °С.

6. В каком отношении надо взять объемы свинца и олова, чтобы их теплоемкости были одинаковы?

7. В железном калориметре массой 100 г находится 500 г воды при температуре 15 °С. В калориметр бросают свинец и алюминий общей массой 150 г и температурой 100 °С. Температура воды поднимается до 17 °С. Определить массы свинца и алюминия.

8. После опускания в воду, имеющую температуру 10 °С, тела, нагретого до 100 °С, через некоторое время установилась общая температура 40 °С. Какой станет температура воды, если, не вынимая первого тела, в нее опустить еще одно такое же тело, нагретое до 100 °С?

А. В. Крушин, МАОУ «СОШ № 7», г. Южноуральск, Челябинская область

Метки: Физика

Теплоемкость воды | Физика Фургон

Категория Выберите категориюО фургоне физикиЭлектричество и магнитыВсе остальноеСвет и звукДвижение вещейНовая и захватывающая физикаСостояния материи и энергииКосмосПод водой и в воздухе

Подкатегория

Поиск

Задайте вопрос

Последний ответ: 22.10.2007

Вопрос:

Сколько энергии требуется, чтобы нагреть 100 миллилитров воды до 100 градусов Цельсия?
— Aimee
Great Lakes College, Australia

Это зависит от начальной температуры. Если вода начинается с 99 градусов Цельсия, для повышения температуры требуется всего 100 калорий. до 100 градусов Цельсия (при условии отсутствия испарения). Количество тепла требуется для изменения температуры одного грамма воды (примерно миллилитр, но вода при нагревании расширяется) на один градус Цельсия составляет одну калорию. Если вы начали с 25 градусов по Цельсию (приличная комната температуры), для выполнения этой работы потребуется 7500 калорий.

НО:

100 градусов Цельсия — особая температура для чистой воды. так как это температура, при которой вода кипит при одной атмосфере давление. Если вы проводите эксперимент чуть ниже одной атмосферы давления (скажем, в Денвере), вы никогда не сможете нагреть воду до 100 градусов Цельсия, потому что температура кипения немного снижена — вся вода выкипит до того, как вы поднимете температуру. Это требуется 540 калорий на грамм дополнительного тепла, чтобы превратить воду в пар.

Кроме того, если вы делаете это, скажем, в открытом горшке, то просто простое испарение отнимет у воды часть ее тепла (а также часть своей воды!).

Если вы начали со льда, то для его растапливания требуется дополнительно 80 калорий на грамм воды.

Том

(опубликовано 22.10.2007)

Дополнение №1: вода испаряется

Вопрос:

Если вода кипит при 100 градусах Цельсия, как она испаряется при комнатной температуре около 20-25 градусов цельсия?
— Чалрин
Мемфис, тн

А:

Молекулы воды всегда улетают с поверхности жидкости в газ и из газа врезаются обратно в жидкость. Скорость выхода жидкости сильно увеличивается по мере нагревания жидкости. Когда достигается точка кипения, с поверхности покидает больше молекул, чем возвращается, даже если газ (при нормальном давлении) состоит только из молекул воды. Тогда даже пузырьки водяного пара в жидкости растут, и жидкость быстро выкипает. Даже намного ниже точки кипения молекулы воды покидают поверхность. Если воздух довольно сухой (низкая влажность) и если есть небольшой ветерок, который смешивает водяной пар с воздухом, скорость испарения будет больше, чем скорость возвращения молекул воды в жидкость. Это то, что обычно происходит при комнатной температуре, 20-25°C.

Mike W.

(опубликовано 22.10.2007)

Дополнение к этому ответу

Связанные вопросы

теплоизоляция
3
063?
ГОРЯЧАЯ ПРЕДУПРЕЖДЕНИЯ Медленно дренируя
Тепловая вместимость при постоянном объеме или давлении
Сохранение холода молока
Избегание термического равновесия
Дифференциальное движение в ячейках
0003
горячая и холодная вода
теплоемкость при постоянном давлении или объеме
вязко-хрупкий переход

Все еще любопытно?

Вопросы и ответы по Expore в смежных категориях

Температура и жара

Конечная температура смесей (закон Рихмана)

Закон смесей Рихмана описывает конечную температуру, приводящую к термодинамическому равновесию при соприкосновении двух тел с разными начальными температурами.

1 Адиабатическое смешивание
2 Вывод формулы для расчета окончательной температуры
3 Численные пример
4 Продюсь до двух тел в термическом контакте
5 Особые случаи Законодательства Рихмана 9003 700377777777777777777 года. смешение
Если два тела с разными начальными температурами привести в соприкосновение друг с другом, температуры будут становиться все более и более равными. В конце концов, будет достигнуто термодинамическое равновесие. Затем температуры полностью выровнялись, и общий была установлена конечная температура , которая также называется температурой смешения .
Такое выравнивание температур можно наблюдать, например, при наливании горячей воды в холодный стакан. Пока стекло нагревается горячей водой, вода остывает на относительно холодном стекле. Через какое-то время разные начальные температуры уравнялись, и стекло стало иметь такую же температуру, как и вода внутри него. Конечная температура находится между этими двумя начальными температурами.
Рисунок: Наливание горячей воды в холодный стакан
В зависимости от того, сколько воды налито в стакан, конечная температура смещается в сторону более высоких или более низких значений. Можно предположить, что при большем количестве воды получаются более высокие конечные температуры, поскольку присутствует больше горячей воды, что вызывает больший нагрев стекла. Выравнивание температур можно объяснить с помощью модели частиц. Это подробно обсуждается в статье Теплота и термодинамическое равновесие.
Далее будет показано, как можно определить конечную температуру, когда два тела находятся в тепловом контакте друг с другом. Предполагается, что тепло передается только между двумя рассматриваемыми телами. Таким образом, теплопередачей в окружающую среду пренебрегают. Такой процесс термического смешения, в котором не учитывается нежелательная теплопередача в окружающую среду, также называется адиабатическое смешение (термин адиабатическая система более подробно объяснен в статье Термодинамические системы).
Вывод формулы для расчета конечной температуры
Основная связь между переданным теплом Q и изменением температуры ΔT тела определяется теплоемкостью C рассматриваемого объекта
\begin{align}
\label{q }
\boxed{Q = C \cdot \Delta T}~\text{,} \\[5px]
\end{align}
где теплоемкость C для однородного тела может быть определена из удельной теплоемкости c вещества и его масса m:
\begin{align}
\label{c}
&\boxed{C = c \cdot m} \\[5px]
\end{align}
Далее мы рассмотрим пример горячей воды и более холодное стекло. Если горячую воду налить в холодный стакан, то теплота перейдет от воды к стакану. Это приводит к тому, что стекло нагревается из-за поглощенного тепла. При этом вода охлаждается за счет выделяемого тепла. Количество теплоты, излучаемой водой (Q _w ), равно количеству теплоты, поглощаемой стеклом (Q _г ):
\begin{align}
\label{e}
Q_\text{g} = Q_\text{w} \\[5px]
\end{align}
Рисунок: Излучаемое тепло вода равна поглощенной теплоте стекла
Обратите внимание, что передачей тепла в окружающую среду пренебрегается, и по соображениям сохранения энергии тепло, излучаемое водой, должно поэтому полностью поглощаться стеклом.
Тепло Q _w, излучаемое водой, вызывает снижение температуры воды на определенную величину ΔT _w согласно уравнению (\ref{q}). Для заданной начальной температуры T _w отдаваемое тепло может быть определено следующим образом, когда общая конечная температура T _f установлена в тепловом равновесии:
\begin{align}
Q_\text{w} = C_\text{w} \cdot \underbrace{\left( T_\text{w}-T_\text{f}\right)}_{\Delta T_\text{w}>0} \\[5px]
\end{align}
Рисунок: Вывод правила Рихмана для смесей (конечная температура)
Аналогично, поглощенное стеклом тепло Q _g можно определить на основе начальной температуры T _g и конечной температуры T _f :
\begin{align}
Q_\text{g} = C_\text{g} \cdot \ underbrace{\left( T_\text{f}-T_\text{g}\right)}_{\Delta T_\text{g}>0} \\[5px]
\end{align}
Обратите внимание, что начальная температура воды больше конечной температуры, а начальная температура стекла ниже конечной температуры (T _w >T _f >T _g ). Поэтому разность температур в двух верхних уравнениях была выбрана так, чтобы в каждом случае давать положительные значения количества тепла. Таким образом, количества теплоты теперь можно приравнять согласно уравнению (\ref{e}) и решить для конечной температуры:
\begin{align}
Q_\text{g} &= Q_\text{w } \\[5px]
C_\text{g} \cdot (T_\text{f} – T_\text{g})&= C_\text{w} \cdot (T_\text{w} – T_\ text{f}) \\[5px]
C_\text{g} \cdot T_\text{f} – C_\text{g} \cdot T_\text{g} &= C_\text{w} \cdot T_\text{w} – C_\text{w} \cdot T_\text{f}\\[5px]
C_\text{g} \cdot T_\text{f} +C_\text{w} \cdot T_\text{f} &= C_\text{w} \cdot T_\text{w} + C_\text {g} \cdot T_\text{g} \\[5px]
T_\text{f} \cdot (C_\text{w} +C_\text{g}) &= C_\text{w} \cdot T_\text{w} + C_\text{g} \cdot T_\text{g} \\[5px]
T_\text{f} &= \frac{C_\text{w} \cdot T_\text{ w} + C_\text{g} \cdot T_\text{g}}{C_\text{w} +C_\text{g}} \\[5px]
\end{align}
\begin{align }
\label{tm}
\boxed{T_\text{f} = \frac{C_\text{w} \cdot T_\text{w} + C_\text{g} \cdot T_\text{g} }{C_\text{w} +C_\text{g}}} \\[5px]
\end{align}
Для однородных веществ уравнение (\ref{c}) можно использовать в уравнении (\ref{tm}) для определения конечной температуры на основе удельных теплоемкостей c и масс m веществ:
\begin{align}
\boxed{T_\text{f} = \frac{c_\text{w} \cdot m_\text{w} \cdot T_\text{w} + c_\ text{g} \cdot m_\text{g} \cdot T_\text{g}}{c_\text{w} \cdot m_\text{w} + c_\text{g} \cdot m_\text{g }}} \\[5px]
\end{align}
Численный пример
В дальнейшем конечная температура определяется на основе конкретных значений. Примем стакан массой m _г = 100 г. Удельную теплоемкость стекла можно принять равной c _г = 0,72 кДж/(кг⋅К). Начальная температура стекла равна комнатной температуре с T _g = 293 K (20 °C). Теперь в стакан наливают 200 мл воды массой m _w = 200 г. Начальная температура воды T _w = 333 K (60 °C). Удельную теплоемкость воды можно принять равной c _w = 4,2 кДж/(кг⋅К).
На самом деле, на данный момент не имеет значения, используются ли температуры в градусах Цельсия или в единицах Кельвина в верхней формуле для расчета конечной температуры. Если температуры используются в градусах Цельсия, конечная температура также выражается в градусах Цельсия. Если, с другой стороны, температуры используются в единицах Кельвина, конечная температура также приводит к единице Кельвина.
Мы используем температуры в градусах Цельсия и получаем таким образом конечную температуру T _f = 56,8 °C:
\begin{align}
\underline{T_\text{f}} = \frac{4,2 \tfrac{\text{кДж}}{\text{кг K}} \cdot 100 \text{ г} \cdot 60 \text{ °C} + 0,72 \tfrac{\text{кДж}}{\text{кг K}} \cdot 200 \text{ г} \cdot 20 \text{ °C }}{4,2 \tfrac{\text{кДж}}{\text{кг K}} \cdot 200 \text{г} + 0,72 \tfrac{\text{кДж}}{\text{кг K}} \cdot 100 \text{ g}} = \underline{56. 8 \text{ °C}}\\[5px]
\end{align}
Очевидно, вода охлаждается всего на 3,2 °C, а стекло нагревается на 36,8 °С. Это связано со значительно большей теплоемкостью воды, что обусловлено, с одной стороны, большей массой, а с другой стороны, значительно большей удельной теплоемкостью. Если бы было добавлено только 20 мл воды, то конечная температура составила бы 41,5 °C. В этом случае теплоемкости воды и стекла примерно равны и температура воды уменьшается на столько же, сколько увеличивается температура стекла (подробнее см. раздел 9).0009 Особые случаи закона смесей Рихмана ).
Распространение на любые два тела, находящихся в тепловом контакте
Формула для расчета конечной температуры была выведена на примере воды и стекла. Однако эту формулу можно перенести на любые два вещества. Неважно, твердое ли это тело и жидкость или два твердых тела, которые находятся в тепловом контакте. Это соотношение применимо и к смесям двух жидкостей!
Рисунок: Конечная температура при смешивании двух жидкостей
Следовательно, в общем случае конечная температура T _f в термодинамическом равновесии для любых двух тел (1) и (2) с разными начальными температурами T ₁ и T ₂ и разными теплоемкостями C ₁ и C ₂ можно рассчитать по следующей формуле:
\begin{align}
\label{rr}
&\boxed{T_\text{f} = \frac{C_{1} \cdot T_{1} + C_{2} \cdot T_{2}}{C_{1} +C_{2}}} \\[5px]
\end{align}
Для тел, состоящих из однородных веществ, теплоемкости можно определить из удельные теплоемкости c и их массы m:
\begin{align}
&\boxed{T_\text{f} = \frac{c_1 \cdot m_1 \cdot T_{1} + c_2 \cdot m_2 \cdot T_{2}}{c_1 \cdot m_1 + c_2 \cdot m_2}} \\[5px]
\end{align}
Эти два уравнения также известны как закон смесей Рихмана ! Для применения этой формулы не имеет значения, какое из двух тел (1 или 2) теплее, а какое холоднее. Также следует еще раз упомянуть, что температуры не обязательно должны использоваться в единицах Кельвина, но также могут использоваться в градусах Цельсия.
Справедливость закона Рихмана должна быть ограничена случаем фазовых переходов, происходящих при выравнивании температур. Например, это происходит, когда в теплый напиток добавляют кубики льда. В этих случаях также необходимо учитывать (скрытые) количества тепла, обусловленные изменением состояния вещества (теплота плавления).
Рисунок: Стакан с кубиком льда
Закон смесей Рихмана описывает результирующую конечную температуру при тепловом контакте двух тел с разными начальными температурами при условии, что не происходит фазового перехода и предполагается, что тепло передается только между этими двумя телами!
Из уравнения (\ref{rr}) видно, что конечная температура получается из взвешенного среднего арифметического начальных температур, где взвешивание производится по теплоемкости! Таким образом, в зависимости от теплоемкости конечная температура смещается в сторону более высоких или более низких значений.
No related posts.