Число
Степень
Показатель степени — это способ представить, сколько раз число, известное как основание, умножается само на себя. Он представлен в виде небольшого числа в правом верхнем углу основания. Например: x²означает, что вы умножаете x на себя два раза, то есть x * x. Аналогично, 4² = 4 * 4 и т. д. Если в данном примере показатель степени равен 3 5³, то результат будет 5 * 5 * 5.
Что такое степень числа?
Это легко с маленькими числами, но для оснований, которые являются большими числами, десятичными знаками или когда они возведены в очень большую или отрицательную степень, используйте наш инструмент. Если вы хотите произвести возведение в степень вручную, сделайте следующее:
- Определите, например, базу и мощность, до которой она поднята
3⁵. - Запишите основание столько же раз, сколько экспонента.
3 3 3 3 3 - Поместите символ умножения между каждым основанием.

3 * 3 * 3 * 3 * 3. - Умножьте!
3 * 3 * 3 * 3 * 3 = 243.
Калькулятор отрицательной степени
Что происходит, когда степень отрицательна? По определению, если оно равно -2, мы умножим само основание на отрицательное значение в два раза. Мы берем величину, обратную основанию, и меняем отрицательный показатель степени на положительный и действуем как обычно. Если вы хотите решить это вручную, сделайте следующее:
- Определите основание и показатель степени.
- Напишите величину, обратную основанию, и измените знак экспоненты на положительный.
- Запишите обратную величину основания столько же раз, сколько экспоненту.
- Поместите между ними символ умножения.
- Умножьте и получите результат.
Вот небольшой пример: 5⁻⁴ = (1/5)⁴ = (1/5) * (1/5) * (1/5) * (1/5) = 1/625 = 0.0016
Законы и правила степени
Формула степени:
а n = а × а × … × а
n раз
База a возводится в степень n, равна n умножению на a.
Например:
2 5 = 2 × 2 × 2 × 2 × 2 = 32
Умножение степени
а н ⋅ а м = а н + м
Пример: 2 3 ⋅ 2 4 = 2 (3 + 4) = 2 7 = 128
a n ⋅ b n = ( a ⋅ b ) n
Пример: 3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 144
Показатели деления
п / м = п — т
Пример: 2 5 /2 3 = 2 (5-3) = 2 2 = 4
а н / б п = ( а / б ) п
Пример: 8 2 /2 2 = (8/2 ) 2 = 4 2 = 16
Степень экспоненты
( a n ) m = a n ⋅ m
Пример: (2 3 ) 4 = 2 (3 ⋅ 4) = 2 12 = 4096
Радикал экспоненты
m √ ( a n ) = a n / m
Пример: 2 √ (2 6 ) = 2 (6/2) = 2 3 = 8
Отрицательная экспонента
a -n = 1 / a n
Пример: 2 -3 = 1/2 3 = 1/8 = 0,125
Нулевой показатель
а 0 = 1
Пример: 4 0 = 1
Некоторые другие решения в следующей таблице.
| 0,1 в степени 3 | 0,00100 |
| 0,5 в степени 3 | 0,12500 |
| 0,5 в степени 4 | 0,06250 |
| 1,2 в степени 4 | 2,07360 |
| 1.02 в 10-й степени | 1,21899 |
| 1.03 в 10-й степени | 1,34392 |
| 1,2 в степени 5 | 2.48832 |
| 1.4 в 10-й степени | 28,92547 |
| 1,05 в степени 5 | 1,27628 |
| 1.05 в 10-й степени | 1,62889 |
| 1.06 в 10-й степени | 1,79085 |
| 2 в 3-й степени | 8 |
| 2 в 3 степени | 8 |
| 2 в степени 4 | 16 |
| 2 в степени 6 | 64 |
| 2 в степени 7 | 128 |
| 2 в 9 степени | 512 |
| 2 в десятой степени | 1024 |
| 2 в 15 степени | 32768 |
| 2 в 10 степени | 1024 |
| 2 в степени 28 | 268435456 |
| 3 в степени 2 | 9 |
| 3 в 3 степени | 27 |
| 3 в 4 степени | 81 год |
| 3 в 8-й степени | 6561 |
| 3 в 9 степени | 19683 |
| 3 в 12 степени | 531441 |
| 3 в какой степени равно 81 | 3 4 |
| 4 в степени 3 | 64 |
| 4 в степени 4 | 256 |
| 4 в степени 7 | 16384 |
| 7 в степени 3 | 343 |
| 12 во 2-й степени | 144 |
| 2,5 в степени 3 | 15,625 |
| 12 в степени 3 | 1728 |
| 10 показатель степени 3 | 1000 |
| 24 во второй степени (24 2 ) | 576 |
| 10 в степени 3 | 1000 |
| 3 в степени 5 | 243 |
| 6 в степени 3 | 216 |
| 9 в степени 3 | 729 |
| 9 в степени 2 | 81 |
| 10 в степени 5 | 100000 |
| 10 в 10 степени | 10 000 000 000 |
Ссылка на калькулятор:
Степень числа и как её найти.
 Как возвести число в степень #
Как возвести число в степень #ГДЗ 1 класс
ГДЗ 10 класс
- Категория: Математика
Уже во втором классе на уроках математики дети сталкиваются с такими величинами, как площадь и объем. Учителя рассказывают, что площадь измеряется в квадратных сантиметрах или метрах и так далее, а объем — в кубических. Дети просто запоминают и пишут см2 или м2 или мм3. Очень немногие в тот момент задумывались, что же означает приписанная в верхнем уголке единицы длины цифра. По-настоящему со степенью мы познакомимся в пятом классе, а если хотите это сделать самостоятельно, можете и раньше :))
Что такое степень числа?
Как вы знаете, с помощью произведения удобно записывать сумму нескольких одинаковых слагаемых. Например 5 + 5 + 5 + 5 + 5 + 5 = 5 * 7
А если это будет не сумма, а произведение одинаковых чисел? Например, множитель 5 взять 7 раз: 5 * 5 * 5 * 5 * 5 * 5 * 5? Для более краткого обозначения такого произведения математики и придумали степень.
5 * 5 * 5 * 5 * 5 * 5 * 5 = 57
Выражение 57 называют «степень», читается как пять в седьмой степени или седьмая степень числа 5. При этом 5 — основание степени, а 7 — показатель степени.
Число 7 показывает, сколько одинаковых множителей содержит произведение.
Как возвести число в степень?
Чтобы найти степень, нужно основание перемножить на себя столько раз, сколько написано в показателе.
25 125 625 3125 15625
57 = 5 * 5 * 5 * 5 * 5 * 5 * 5 = 78125
7 раз
Тут иногда возникает путаница оттого, что дети считают не количество цифр основания, а количество знаков умножения. Считать нужно цифры, а не знаки умножения. 5 * 5 — это уже вторая степень, потому что пятерки две. 5 * 5 * 5 = 5
3, 5 * 5 * 5 * 5 = 54 и так далее.
Рассмотрим еще примеры:
32 = 3 * 3 = 9
23 = 2 * 2 * 2 = 8
а4 = а * а * а * а
(5b)2 = 5b * 5b
Вторую степень числа называют «квадрат числа».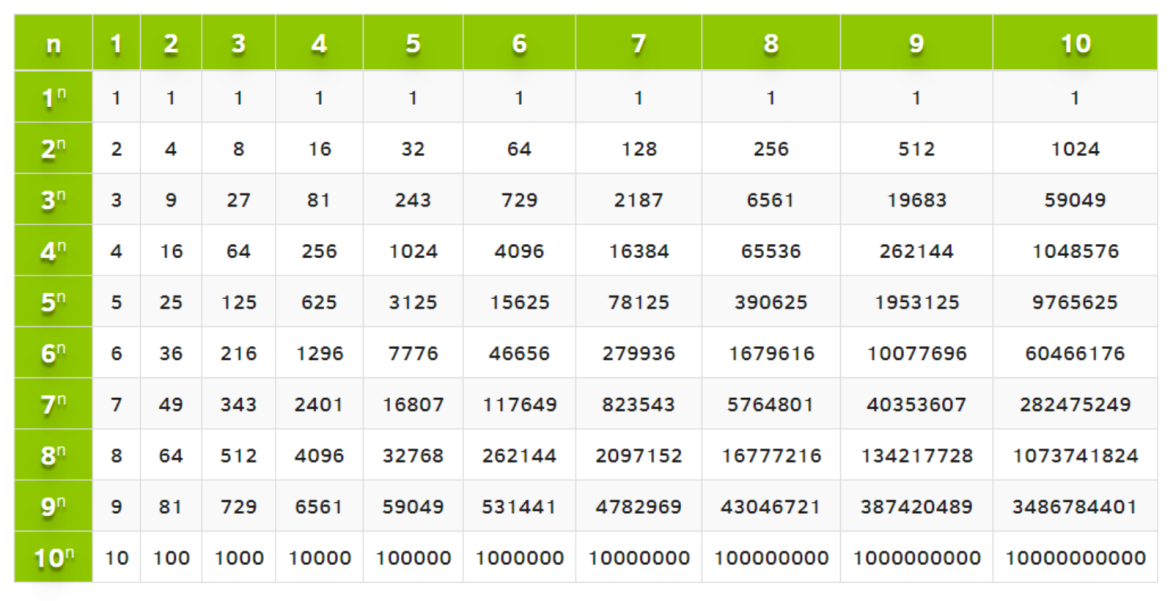 Например, 32 читается как «три в квадрате» или квадрат числа три.
Например, 32 читается как «три в квадрате» или квадрат числа три.
Третью степень числа называют «куб числа». Например 23 читается как «два в кубе» или куб числа два.
Может ли показатель степени быть равным 1? Да, может. Но если любое число взять 1 раз, то получится то же самое число, то есть а1 = а. А поскольку не принято рассматривать произведения, состоящие из одного множителя, то единичку в показателе степени обычно не пишут.
Например 81 = 8, 4561 = 456
Возведение числа в степень — это арифметическое действие
Если в выражение входит степень, то сначала выполняют возведение в степень, а потом — остальные действия в приоритетном порядке.
Например: 5 * 22 = 5 * 4 = 20
5 + 22 = 5 + 4 = 9
А теперь вы поняли, что такое см2? Правильно, это см * см. Именно так мы находим площадь прямоугольника, умножая длину одной стороны в см на длину другой.
А мм3? Это мм * мм * мм. Так мы находим объем.
Чтобы закрепить знания о степени числа, посмотрите видео:
- Назад
- Вперед
умножить наподелить на
- Уроки
- Математика
Простая английская Википедия, бесплатная энциклопедия
Из Простая английская Википедия, бесплатная энциклопедия
В математике возведение в степень ( степень ) — это арифметическая операция над числами. {y} }} и читается как «x {\ displaystyle x} в степени y {\ displaystyle y}» или «x {\ displaystyle x} в степени y {\ displaystyle y}». 9{2}=I\cdot I=I}.
{y} }} и читается как «x {\ displaystyle x} в степени y {\ displaystyle y}» или «x {\ displaystyle x} в степени y {\ displaystyle y}». 9{2}=I\cdot I=I}.
И сложение, и умножение коммутативны. Например, 2+3 равно 3+2, а 2 · 3 равно 3 · 2. Хотя возведение в степень представляет собой повторное умножение, оно не является коммутативным. Например, 2³=8, а 3²=9.
Сложение имеет одну обратную операцию: вычитание. Кроме того, у умножения есть одна обратная операция: деление.
Но возведение в степень имеет две обратные операции: корень и логарифм. Это так, потому что возведение в степень не является коммутативным. Вы можете увидеть это в этом примере:
- Если у вас x+2=3, то вы можете использовать вычитание, чтобы узнать, что x=3−2. То же самое, если у вас 2+x=3: вы также получаете x=3−2. Это потому, что х+2 равно 2+х.
- Если у вас x · 2=3, то вы можете использовать деление, чтобы узнать, что x=32{\textstyle {\frac {3}{2}}}. То же самое, если у вас есть 2 · x = 3: вы также получаете x = 32 {\ textstyle {\ frac {3} {2}}}.
 Это потому, что х · 2 равно 2 · х .
Это потому, что х · 2 равно 2 · х . - Если у вас x²=3, то вы используете (квадратный) корень, чтобы узнать x: вы получаете результат, что x = 32{\textstyle {\sqrt[{2}]{3}}}. Однако, если у вас есть 2
- Экспонента
- Экспоненциальная функция
- Возведение в степень путем возведения в квадрат
- Tetration
- ↑ «Сборник математических символов». Математическое хранилище . 01.03.2020. Проверено 28 августа 2020 г. .
- ↑ Вайсштейн, Эрик В. «Сила». mathworld.wolfram.com . Проверено 28 августа 2020 г. .
- ↑ Нюкамп, Дуэйн. «Основные правила возведения в степень». Знание математики . Проверено 27 августа 2020 г.
{{cite web}}: CS1 maint: url-status (ссылка)
Возведение в степень — свойства, определение, формула, примеры
Возведение в степень — это процесс или операция возведения в степень числа.
| 1. | Что такое возведение в степень? |
| 2. | Формула возведения в степень |
| 3. | Свойства возведения в степень |
| 4. | Двоичное возведение в степень |
| 5. | Часто задаваемые вопросы о возведении в степень |
Что такое возведение в степень?
Возведение в степень — это процесс многократного умножения путем записи данного выражения в виде a b , где a — основание, а b — показатель степени. Предположим, мы умножаем 5 десять раз, поэтому вместо того, чтобы записывать это как факт умножения, мы используем алгоритм возведения в степень, чтобы записать его как 5 
Формула возведения в степень
Существует особый способ записи выражений или чисел в виде возведения в степень. Формула возведения в степень с «a» в качестве основания и «n» в качестве показателя степени приведена ниже:
Используя эту формулу возведения в степень, мы можем легко записать любой повторяющийся факт умножения в экспоненциальной форме.
Свойства возведения в степень
Есть некоторые свойства возведения в степень, которые помогут вам легко упростить выражения со степенями. Они позволяют нам переписывать экспоненты в упрощенном виде, чтобы упростить вычисления. Список свойств возведения в степень или основные правила возведения в степень приведены ниже:
| Свойство возведения в степень | Формула | Пример |
|---|---|---|
| Нулевой показатель | а 0 = 1 | 2 0 = 1 |
| Показатель идентичности | 1 = | 3 1 = 3 |
| Продукт Пауэрса | м × п = а м+п | 2 2 × 2 3 = 2 2+3 = 2 5 |
| Частное свойство | a м /a n = a m-n | 5 5 /5 3 = 5 5-3 = 5 2 |
| Свойство отрицательного экспонента | а -м = 1/а м ; (а/б) -m = (б/а) м | 7 -2 = 1/7 2 |
| Сила силы | (а м ) н = а мн | (2 3 ) 4 = 2 12 |
| Сила продукта | (ab) м = а м б м | (2 × 3) 6 = 2 6 × 3 6 |
| Степень частного | (a/b) м = a м /b м | (2/3) 4 = 2 4 /3 4 |
Мы можем легко решить малые показатели, используя многократное умножение. Например, чтобы найти значение 2 3 , мы можем умножить 2 три раза. Но как решать выражения с большими показателями? Мы можем упростить такие числа или выражения, используя двоичное возведение в степень или возведение в степень путем возведения в квадрат, как описано ниже.
Например, чтобы найти значение 2 3 , мы можем умножить 2 три раза. Но как решать выражения с большими показателями? Мы можем упростить такие числа или выражения, используя двоичное возведение в степень или возведение в степень путем возведения в квадрат, как описано ниже.
Двоичное возведение в степень
Двоичное возведение в степень, также известное как возведение в степень путем возведения в квадрат и алгоритма возведения в квадрат и умножения , используется для вычисления значений больших показателей, скажем, 4 103 . Это трюк, который использует числа с основанием 2 для вычисления значения выражений, включающих большие показатели степени. При возведении в степень путем возведения в квадрат мы используем следующие формулы в зависимости от того, является ли показатель степени четным или нечетным:
Например, если показатель степени — нечетное число, скажем, 4 103 , то мы можем записать его как 4(4 2 ) 51 . Тем не менее, невозможно умножить 4 2 пятьдесят один раз, поэтому снова применим ту же формулу. Теперь мы получаем 4[16(16 2 ) 25 ]. Но тем не менее, новая задача того же типа, мы можем снова применить то же наблюдение. Нам придется применять эту формулу снова и снова, чтобы уменьшить это выражение, что может сделать его более запутанным и сложным. Итак, вот вам трюк. Повторное применение этого алгоритма аналогично разложению показателя степени (от основания 10 до основания 2 или от десятичного до двоичного представления) в последовательность квадратов и произведений. Итак, вместо того, чтобы применять эту формулу снова и снова, мы можем найти двоичный эквивалент показателя степени. Давайте решим 4 10 .
Тем не менее, невозможно умножить 4 2 пятьдесят один раз, поэтому снова применим ту же формулу. Теперь мы получаем 4[16(16 2 ) 25 ]. Но тем не менее, новая задача того же типа, мы можем снова применить то же наблюдение. Нам придется применять эту формулу снова и снова, чтобы уменьшить это выражение, что может сделать его более запутанным и сложным. Итак, вот вам трюк. Повторное применение этого алгоритма аналогично разложению показателя степени (от основания 10 до основания 2 или от десятичного до двоичного представления) в последовательность квадратов и произведений. Итак, вместо того, чтобы применять эту формулу снова и снова, мы можем найти двоичный эквивалент показателя степени. Давайте решим 4 10 .
4 10 (показатель степени с основанием 10) = 4 1010 (показатель степени преобразуется в его двоичный эквивалент)
Дальнейшее расширение показателя степени дает 1010 2 = 1 × 2 2 + 9001 2 2 + 1 × 2 1 + 0 × 2 0 . Его можно упростить как 8 + 0 + 2 + 0.
Его можно упростить как 8 + 0 + 2 + 0.
4 10 = 4 (8+0+2+0)
4 10 = 4 8 × 4
2 2
1 2 Таким образом, мы разбили большой показатель на части. Сейчас 4 8 можно легко решить как 16 4 или 256 2 , а 4 2 равно 16. Вместо того, чтобы умножать 4 в десять раз, теперь нам нужно только умножить 256 × 256 × 16. Это известный как метод двоичного возведения в степень. Этот метод полезен при работе с выражениями с большими показателями.Похожие статьи
Проверьте эти интересные статьи, связанные с возведением в степень в математике.
- Экспоненциальная функция
- Экспоненциальные правила
- Экспоненциальные уравнения
Часто задаваемые вопросы о возведении в степень
Что такое возведение в степень в математике?
Возведение в степень в математике определяется как операция, используемая для представления повторного умножения.


 Это потому, что х · 2 равно 2 · х
Это потому, что х · 2 равно 2 · х