Чтобы возвести рациональную дробь в степень нужно — dj-sensor.ru
Содержание
- Как возвести в степень смешанное число
- Правило возведения алгебраической дроби в степень, его доказательство
- Примеры, решения
Возведение дроби в степень. Наш онлайн-калькулятор позволяет возводить в степень любую дробь. Чтобы задать смешанную дробь заполните поля, соответствующие целой части, числителю и знаменателю. Если дробь не имеет целой части, то тогда оставьте соответствующее поле незаполненным. Если необходимо задать отрицательную дробь – для этого нажмите кнопку [+/-].После нажатия на кнопку «Вычислить» калькулятор выдаст ответ. Ниже под калькулятором будет приведено подробное решение с последовательностью действий, которые необходимо совершить.
При возведении в степень дроби нужно возвести в степень и числитель, и знаменатель.
Данное свойство соответствует другой записи свойства № 5 «Степень частного», расмотренного на предыдущей странице.
Примеры возведения в степень дроби.
- (
3 · b 5c ) 2 =
3 2 · b 2 5 2 · c 2 =
9 · b 2 25 · c 2 =
9b 2 25c 2
Как возвести в степень смешанное число
Чтобы возвести в степень смешанное число, сначала избавляемся от целой части, превращая смешанное число в неправильную дробь. После этого возводим в степень и числитель, и знаменатель.
Формулу возведения в степень дроби применяют как слева направо, так и справа налево, то есть, чтобы разделить друг на друга степени одинаковыми показателями, можно разделить одно основание на другое, а показатель степени оставить неизменным.
- Пример. Найти значение выражения рациональным способом.
На нашем сайте вы также можете проверить свои вычисления и возвести число в степень онлайн.
Тема сводится к тому, что нам необходимо производить умножение одинаковых дробей. Данная статья расскажет, какое необходимо использовать правило, чтобы верно возводить алгебраические дроби в натуральную степень.
Правило возведения алгебраической дроби в степень, его доказательство
Перед тем, как начать возводить в степень, необходимо углубить знания при помощи статьи про степень с натуральным показателем, где имеется произведение одинаковых множителей, которые находятся в основании степени, причем их количество определено показателем. К примеру, число 2 3 = 2 · 2 · 2 = 8 .
При возведении в степень чаще всего используем правило. Для этого в отдельности возводят в степень числитель и отдельно знаменатель. Рассмотрим на примере 2 3 2 = 2 2 3 2 = 4 9 . Правило применимо для возведения дроби в натуральную степень.
При возведении алгебраической дроби в натуральную степень получаем новую, где числитель имеет степень исходной дроби, а знаменатель – степень знаменателя.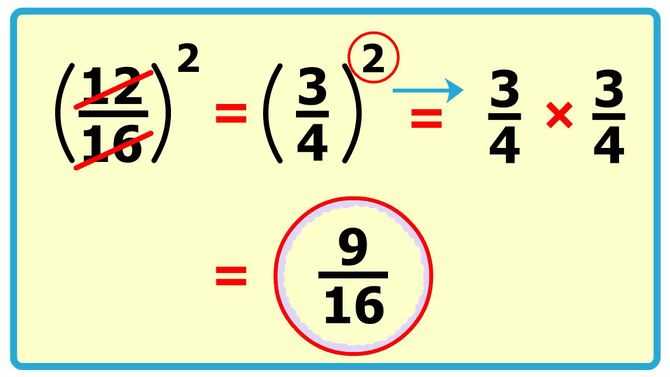 Это все имеет вид a b n = a n b n , где а и b являются произвольными многочленами, b является ненулевым, а n натуральным числом.
Это все имеет вид a b n = a n b n , где а и b являются произвольными многочленами, b является ненулевым, а n натуральным числом.
Доказательство данного правила записывается в виде дроби, которую необходимо возвести в степень, основываясь на самом определении с натуральным показателем. Тогда получаем умножение дробей вида a b n = a b · a b · . . . · a b = a · a · . . . · a b · b · . . . · b = a n b n
Примеры, решения
Правило возведения алгебраической дроби в степень производится последовательно: сначала числитель , потом знаменатель. Когда в числителе и знаменателе имеется многочлен, тогда само задание сведется к возведению заданного многочлена в степень. После чего будет указана новая дробь, которая равна исходной.
Произвести возведение дроби x 2 3 · y · z 3 в квадрат.
Необходимо зафиксировать степень x 2 3 · y · z 3 2 . По правилу возведения алгебраической дроби в степень получаем равенство вида x 2 3 · y · z 3 2 = x 2 2 3 · y · z 3 2 . Теперь необходимо произвести преобразование полученной дроби к виду алгебраической, выполняя возведение в степень. Тогда получим выражение вида
Тогда получим выражение вида
x 2 2 3 · y · z 3 2 = x 2 · 2 3 2 · y 2 · z 3 2 = x 4 9 · y 2 · z 6
Все случаи возведения в степень не предполагают подробного разъяснения, поэтому сам решение имеет краткую запись. То есть, получаем, что
x 2 3 · y · z 3 2 = x 2 2 3 · y · z 3 2 = x 4 9 · y 2 · z 6
Ответ: x 2 3 · y · z 3 2 = x 4 9 · y 2 · z 6 .
Если числитель и знаменатель имеют многочлены, тогда необходимо возводить всю дробь в степень, после чего применять формулы сокращенного умножения для его упрощения.
Возвести дробь 2 · x — 1 x 2 + 3 · x · y — y в квадрат.
Из правила имеем, что
2 · x — 1 x 2 + 3 · x · y — y 2 = 2 · x — 1 2 x 2 + 3 · x · y — y 2
Чтобы преобразовать выражение, необходимо воспользоваться формулой квадрата суммы трех слагаемых в знаменателе, а в числителе – квадратом разности, что позволит упростить выражение. Получим:
2 · x — 1 2 x 2 + 3 · x · y — y 2 = = 2 · x 2 — 2 · 2 · x · 1 + 1 2 x 2 2 + 3 · x · y 2 + — y 2 + 2 · x 2 · 3 · x · y + 2 · x 2 · ( — y ) + 2 · 3 · x · y · — y = = 4 · x 2 — 4 · x + 1 x 4 + 9 · x 2 · y 2 + y 2 + 6 · x 3 · y — 2 · x 2 · y — 6 · x · y 2
Ответ: 2 · x — 1 2 x 2 + 3 · x · y — y 2 = 4 · x 2 — 4 · x + 1 x 4 + 9 · x 2 · y 2 + y 2 + 6 · x 3 · y — 2 · x 2 · y — 6 · x · y 2
Заметим, что при возведении в натуральную степень дробь, которую не можем сократить, получаем также несократимую дробь. Это не упрощает ее для дальнейшего решения. Когда заданная дробь может быть сокращена, тогда при возведении в степень получаем, что необходимо выполнение сокращения алгебраической дроби, во избежание выполнения сокращения после того, как возведем в степень.
Это не упрощает ее для дальнейшего решения. Когда заданная дробь может быть сокращена, тогда при возведении в степень получаем, что необходимо выполнение сокращения алгебраической дроби, во избежание выполнения сокращения после того, как возведем в степень.
- Автор: Мария Сухоруких
- Распечатать
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Здесь будет решение…Данный калькулятор поможет вам возвести в степень онлайн, как целое число, так и десятичную дробь. Наш калькулятор позволяет возводить в степень не только положительные, но и отрицательные числа. Степень, в которую возводится число может быть отрицательной. Инструкции к калькулятору
Вспомнить правила округления десятичных дробей вы можете в соответствующем уроке. Степени небольших чисел (до 20) советуем учить наизусть, скачав для этого «Таблицу степеней» в разделе «Для учёбы». В продолжение разговора про степень числа логично разобраться с нахождением значения степени. Этот процесс получил название возведение в степень. В этой статье мы как раз изучим, как выполняется возведение в степень, при этом затронем все возможные показатели степени – натуральный, целый, рациональный и иррациональный. И по традиции подробно рассмотрим решения примеров возведения чисел в различные степени. Навигация по странице. Что значит «возведение в степень»?Начать следует с объяснения, что называют возведением в степень. Возведение в степень – это нахождение значения степени числа. Таким образом, нахождение значение степени числа a с показателем r и возведение числа a в степень r – это одно и то же. Например, если поставлена задача «вычислите значение степени (0,5) 5 », то ее можно переформулировать так: «Возведите число 0,5 в степень 5 ». Теперь можно переходить непосредственно к правилам, по которым выполняется возведение в степень. Возведение числа в натуральную степеньПо определению степень числа a с натуральным показателем n равна произведению n множителей, каждый из которых равен a , то есть, . Таким образом, чтобы возвести число a в степень n нужно вычислить произведение вида .Отсюда ясно, что возведение в натуральную степень базируется на умении выполнять умножение чисел, а этот материал охвачен в статье умножение действительных чисел. Рассмотрим решения нескольких примеров. Выполните возведение числа −2 в четвертую степень. По определению степени числа с натуральным показателем имеем (−2) 4 =(−2)·(−2)·(−2)·(−2) . Осталось лишь выполнить умножение целых чисел: (−2)·(−2)·(−2)·(−2)=16 . Найдите значение степени .Данная степень равна произведению вида . Вспомнив, как выполняется умножение смешанных чисел, заканчиваем возведение в степень: ..Что касается возведения в натуральную степень иррациональных чисел, то его проводят после предварительного округления основания степени до некоторого разряда, позволяющего получить значение с заданной степенью точности. Например, пусть нам требуется возвести число пи в квадрат. Если округлить число пи до сотых, то получим , а если взять , то возведение в степень даст .Здесь стоит сказать, что во многих задачах нет необходимости возводить в степень иррациональные числа. Обычно ответ записывается либо в виде самой степени, например, , либо по возможности проводится преобразование выражения: .В заключение этого пункта отдельно остановимся на возведении в первую степень. Например, (−9) 1 =−9 , а число в первой степени равно .Возведение в целую степеньВозведение в целую степень удобно рассматривать для трех случаев: для целых положительных показателей, для нулевого показателя, и для целых отрицательных показателей степени. Так как множество целых положительных чисел совпадает со множеством натуральных чисел, то возведение в целую положительную степень есть возведение в натуральную степень. А этот процесс мы рассмотрели в предыдущем пункте. Переходим к возведению в нулевую степень. В статье степень с целым показателем мы выяснили, что нулевая степень числа a определяется для любого отличного от нуля действительного числа a , при этом a 0 =1 . Таким образом, возведение любого отличного от нуля действительного числа в нулевую степень дает единицу. Например, 5 0 =1 , (−2,56) 0 =1 и , а 0 0 не определяется. Чтобы закончить с возведением в целую степень, осталось разобраться со случаями целых отрицательных показателей. Мы знаем, что степень числа a с целым отрицательным показателем −z определяется как дробь вида . В знаменателе этой дроби находится степень с целым положительным показателем, значение которой мы умеем находить. Осталось лишь рассмотреть несколько примеров возведения в целую отрицательную степень.Вычислите значение степени числа 3 с целым отрицательным показателем −2 . По определению степени с целым отрицательным показателем имеем . Значение степени в знаменателе легко находится: 2 3 =2·2·2=8 . Таким образом, ..Найдите значение степени (1,43) −2 . . Значение квадрата в знаменателе равно произведению 1,43·1,43 . Найдем его значение, выполнив умножение десятичных дробей столбиком:Итак, . Запишем полученное число в виде обыкновенной дроби, умножив числитель и знаменатель полученной дроби на 10 000 (при необходимости смотрите преобразование дробей), имеем . На этом возведение в степень завершено. .В заключение этого пункта стоит отдельно остановиться на возведении в степень −1 . Минус первая степень числа a равна числу, обратному числу a . Действительно, . Например, 3 −1 =1/3 , и .Возведение числа в дробную степеньВозведение числа в дробную степень базируется на определении степени с дробным показателем. Известно, что , где a – любое положительное число, m – целое, а n – натуральное число. Так возведение числа a в дробную степень m/n заменяется двумя действиями: возведением в целую степень (о чем мы говорили в предыдущем пункте) и извлечением корня n-ой степени.На практике равенство на основании свойств корней обычно применяется в виде . То есть, при возведении числа a в дробную степень m/n сначала извлекается корень n -ой степени из числа a , после чего полученный результат возводится в целую степень m .Рассмотрим решения примеров возведения в дробную степень. Вычислите значение степени . Покажем два способа решения. Первый способ. По определению степени с дробным показателем . Вычисляем значение степени под знаком корня, после чего извлекаем кубический корень: .Второй способ. По определению степени с дробным показателем и на основании свойств корней справедливы равенства . Теперь извлекаем корень , наконец, возводим в целую степень .Очевидно, что полученные результаты возведения в дробную степень совпадают. .Отметим, что дробный показатель степени может быть записан в виде десятичной дроби или смешанного числа, в этих случаях его следует заменить соответствующей обыкновенной дробью, после чего выполнять возведение в степень. Вычислите (44,89) 2,5 . Запишем показатель степени в виде обыкновенной дроби (при необходимости смотрите статью перевод десятичных дробей в обыкновенные): . Теперь выполняем возведение в дробную степень:(44,89) 2,5 =13 501,25107 . Следует также сказать, что возведение чисел в рациональные степени является достаточно трудоемким процессом (особенно когда в числителе и знаменателе дробного показателя степени находятся достаточно большие числа), который обычно проводится с использованием вычислительной техники. В заключение этого пункта остановимся на возведении числа нуль в дробную степень. Дробной степени нуля вида мы придали следующий смысл: при имеем , а при нуль в степени m/n не определен. Итак, нуль в дробной положительной степени равен нулю, например, . А нуль в дробной отрицательной степени не имеет смысла, к примеру, не имеют смысла выражения и 0 -4,3 .Возведение в иррациональную степеньИногда возникает необходимость узнать значение степени числа с иррациональным показателем. При этом в практических целях обычно достаточно получить значение степени с точностью до некоторого знака. Сразу отметим, что это значение на практике вычисляется с помощью электронной вычислительной техники, так как возведение в иррациональную степень вручную требует большого количества громоздких вычислений. Но все же опишем в общих чертах суть действий. Чтобы получить приближенное значение степени числа a с иррациональным показателем , берется некоторое десятичное приближение показателя степени , и вычисляется значение степени . Это значение и является приближенным значением степени числа a с иррациональным показателем . Чем более точное десятичное приближение числа будет взято изначально, тем более точное значение степени будет получено в итоге. Это значение и является приближенным значением степени числа a с иррациональным показателем . Чем более точное десятичное приближение числа будет взято изначально, тем более точное значение степени будет получено в итоге.В качестве примера вычислим приближенное значение степени 2 1,174367. . Возьмем следующее десятичное приближение иррационального показателя: . Теперь возведем 2 в рациональную степень 1,17 (суть этого процесса мы описали в предыдущем пункте), получаем 2 1,17 ≈2,250116 . Таким образом, 2 1,174367. ≈2 1,17 ≈2,250116 . Если взять более точное десятичное приближение иррационального показателя степени, например, , то получим более точное значение исходной степени: 2 1,174367. ≈2 1,1743 ≈2,256833 .Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Понятие возведения в степеньНачнем с формулирования базовых определений. Возведение в степень — это вычисление значения степени некоторого числа. То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени ( 0 , 5 ) 5 . Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях. Как возвести число в натуральную степеньВспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так: Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Условие: возведите — 2 в степень 4 . Решение Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 . Возьмем пример посложнее. Вычислите значение 3 2 7 2 Решение Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии. Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49 Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример. Выполните возведение в квадрат числа π . Решение Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 . Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой: Это понятно из записи .От основания степени это не зависит. Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 . Как возвести число в целую степеньДля удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число. В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 . 5 0 = 1 , ( — 2 , 56 ) 0 = 1 2 3 0 = 1 0 0 — не определен. У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач. Возведите 2 в степень — 3 . Решение Используя определение выше, запишем: 2 — 3 = 1 2 3 Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 . Тогда ответ таков: 2 — 3 = 1 2 3 = 1 8 Возведите 1 , 43 в степень — 2 . Решение Переформулируем: 1 , 43 — 2 = 1 ( 1 , 43 ) 2 Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом: В итоге у нас вышло ( 1 , 43 ) — 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей). Ответ: ( 1 , 43 ) — 2 = 10000 20449 Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a — 1 = 1 a 1 = 1 a . Пример: 3 − 1 = 1 / 3 9 13 — 1 = 13 9 6 4 — 1 = 1 6 4 . Как возвести число в дробную степеньДля выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n . Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени. У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m . Проиллюстрируем на примере. Вычислите 8 — 2 3 . Решение Способ 1. Согласно основному определению, мы можем представить это в виде: 8 — 2 3 = 8 — 2 3 Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 — 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4 Способ 2. Преобразуем основное равенство: 8 — 2 3 = 8 — 2 3 = 8 3 — 2 После этого извлечем корень 8 3 — 2 = 2 3 3 — 2 = 2 — 2 и результат возведем в квадрат: 2 — 2 = 1 2 2 = 1 4 Видим, что решения идентичны. Можно пользоваться любым понравившимся способом. Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Возведите 44 , 89 в степень 2 , 5 . Решение Преобразуем значение показателя в обыкновенную дробь — 44 , 89 2 , 5 = 49 , 89 5 2 . А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107 Ответ: 13 501 , 25107 . Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника. Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную — значения не имеет: 0 — 4 3 . Как возвести число в иррациональную степеньНеобходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения. Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере: Вычислите приближенное значение 21 , 174367 . Решение Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . |
Конечно, вы не можете записать каждое число в виде дроби, но вы можете хотя бы аппроксимировать каждое число дробью.
$\endgroup$
1
$\begingroup$
Мне очень нравится ваш вопрос. Так много студентов довольны обучением (и так много инструкторов довольны преподаванием) только последовательности клавиш калькулятора, которые дадут правильный ответ. Но чтобы знать математику (и почти все остальное в этом мире), вы должны залезть под капот и «увидеть», что на самом деле происходит. 93)$ операции необходимы для $n$ бит точности. Забавно, что столько работы потребовалось, чтобы получить только 3 десятичных цифры, но я не знаю лучшего способа, который можно было бы легко расширить до произвольной точности.
$\endgroup$
Калькулятор степени дробности | Как упростить рациональные показатели?
Воспользуйтесь удобным инструментом Калькулятор дробных степеней, который мгновенно показывает упрощение заданной степени. Просто введите входную дробную экспоненту в поле ввода и нажмите кнопку расчета, чтобы получить упрощенную экспоненту за доли секунд.
Просто введите входную дробную экспоненту в поле ввода и нажмите кнопку расчета, чтобы получить упрощенную экспоненту за доли секунд.
Калькулятор дробных показателей: Вы боретесь с концепцией дробных показателей? Больше не нужно беспокоиться о концепции, поскольку мы подробно описали ее здесь. Вы можете легко найти корень d-го числа, возведенного в степень n, с помощью этого калькулятора. Познакомьтесь с пошаговым процессом решения дробных показателей или рациональных показателей. Ознакомьтесь с примерами, описанными в последующих модулях, чтобы лучше понять концепцию.
При работе с дробными показателями существует несколько условий. Вы можете увидеть их все и узнать, как решать дробные показатели степени с различными условиями. Они следующие:
- Дробные показатели, имеющие числитель 1
- Дробные показатели, имеющие числитель, отличный от 1 (любые дроби)
Дробные показатели, имеющие числитель 1
. корни в одном обозначении. Давайте рассмотрим несколько примеров, числитель которых равен 1, и узнаем, как они называются.
корни в одном обозначении. Давайте рассмотрим несколько примеров, числитель которых равен 1, и узнаем, как они называются.
36 1/2 = √36
27 3 =∛27
Первый показатель степени 1/2 называется квадратным корнем, а следующий показатель степени 1/3 называется кубическим корнем. . Если мы будем продолжать в том же духе. Показатель 1/k называется k-м корнем.
x 1/k = k √x
Показатель дроби, имеющий числитель, отличный от 1 (любые дроби)
В тех случаях, когда числитель не равен 1(n≠05)
a = x n/dНужно просто возвести число в степень n и вынуть из него корень d-й степени. Вам не нужно беспокоиться о заказе, так как вы можете разделить его на две части.
- Целое число(n)
- Дробная часть(1/d)
x n/d = x( n.1/d )= (x n ) 1/d 9015 (x 1/d ) n
x n/d = d√x n =(d√x) n
Вы можете выбрать любой удобный для вас метод делай свои расчеты.
Пример: вычисление дробной степени 16 3/2 ?
Решение:
Данное фракционное показатель 16 3/2
16 3/2 = 16 (3. 1/2)
= (16 3 )
= (16 3 )
= (16
= (16 3 )
= (16 3 )
=√16 3
= √4096
= 64
Упростите и ускорьте решение математических задач с помощью нашего сайта Onlinecalculator.guru, который предоставляет бесплатные онлайн-калькуляторы для различных математических и статистических концепций.
1. Что понимают под дробными показателями?
Дробные экспоненты — это способ выражения корней и степеней в выражении.
2. Каково другое название дробных показателей?
Дробные показатели также называются рациональными показателями.

 При записи десятичной дроби используйте точку.
При записи десятичной дроби используйте точку. Вот соответствующее определение.
Вот соответствующее определение.
 Здесь достаточно знать, что число a в первой степени – это есть само число a , то есть,
Здесь достаточно знать, что число a в первой степени – это есть само число a , то есть,
 Все определения будут проиллюстрированы примерами.
Все определения будут проиллюстрированы примерами. Приведем примеры.
Приведем примеры.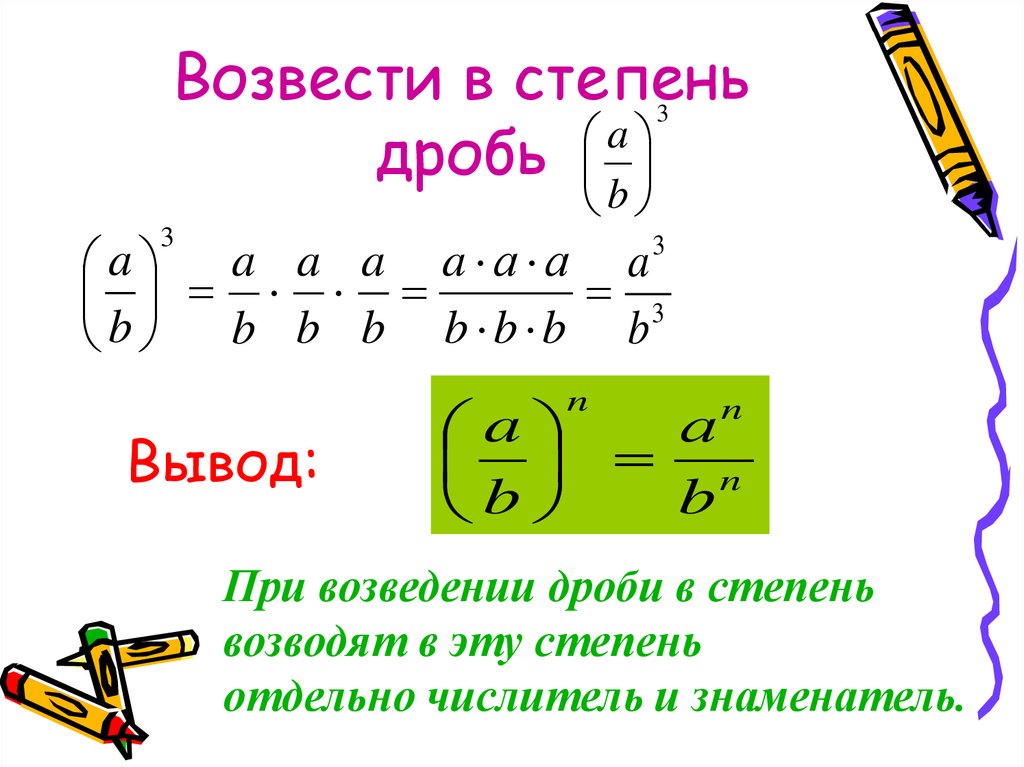 Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .
Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 . О том, как работать с такими степенями, мы уже рассказали выше.
О том, как работать с такими степенями, мы уже рассказали выше.

 Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
