Возведение унимодулярной матрицы в степень. : Высшая алгебра
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| |||
24/04/08 |
| ||
| |||
| Парджеттер |
| |||
07/10/07 |
| |||
| ||||
04.2009, 08:32 | bot |
| |||
21/12/05 |
| |||
| ||||
| Парджеттер |
| |||
07/10/07 |
| |||
| ||||
Математики обычно тоже не в курсе. Поэтому эта информация может быть полезна.
| Профессор Снэйп |
| |||
18/12/07 |
| |||
| ||||
Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…| Padawan |
| |||
13/12/05 |
| |||
| ||||
| Парджеттер |
| |||
07/10/07 |
| |||
| ||||
Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…| BapuK |
| ||
06/03/09 |
| ||
| |||
Хоть возведение в степень, хоть синус-косинус-лонарифм, хоть что ещё…| Padawan |
| |||
13/12/05 |
| |||
| ||||
Поэтому естественно в качестве значения функции при принять значение , где — такой многочлен, что разность делится на характеристический многочлен матрицы. В качестве можно взят интерполяционный многочлен Лагранжа, если корни хар. многочлена простые. Если же корни кратные, то надо еще потребовать, чтобы на корнях совпадали еще и значения производных и до порядка кратности корня. Это называется интерполяционный многочлен Лагранжа-Сильвестра.
| ewert |
| |||
11/05/08 |
| |||
| ||||
Нет просто точки опоры. Нет никакого универсального критерия того, что разумно считать функцией от матрицы.| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: Модераторы Математики, Супермодераторы
Используем быстрое возведение матриц в степень для написания очень быстрого интерпретатора простого языка программирования / Хабр
Недавно на хабре появилась неплохая статья про вычисление N-ного числа фибоначи за O(log N) арифметических операций.
Разумный вопрос, всплывший в комментариях, был: «зачем это может пригодиться на практике». Само по себе вычисление N-ого числа фибоначи может и не очень интересно, однако подход с матрицами, использованный в статье, на практике может применяться для гораздо более широкого круга задач.
В ходе этой статьи мы разберем как написать интерпретатор, который может выполнять простые операции (присвоение, сложение, вычитание и урезанное умножение) над ограниченным количеством переменных с вложенными циклами с произвольным количеством итераций за доли секунды (конечно, если промежуточные значения при вычислениях будут оставаться в разумных пределах). Например, вот такой код, поданный на вход интерпретатору:
loop 1000000000
loop 1000000000
loop 1000000000
a += 1
b += a
end
end
end
end
Незамедлительно выведет a = 1000000000000000000000000000, b = 500000000000000000000000000500000000000000000000000000, несмотря на то, что если бы программа выполнялась наивно, интерпретатору необходимо было бы выполнить октиллион операций.
Я полагаю, что у читателя есть представление о том, что такое матрица, и что такое произведение матриц. В рамках этой статьи мы будем использовать исключетельно квадратные матрицы и полагаться на очень важное свойство умножения квадратных матриц — ассоциативность.
Для простоты ограничим наш интерпретатор четырьмя переменными — A, B, C и D. Для представления состояния интерпретатора в заданный момент будем использовать вектор размера пять, первые четыре элемента которого будут содержать значения четырех переменных соответственно, а последний будет на протяжении всей работы интерпретатора равен единице.
(A, B, C, D, 1)
В начале работы интерпретатора будем полагать значения всех переменных равными нулю.
(0, 0, 0, 0, 1)
Допустим, что первая операция в коде программы содержит строку
A += 5
Эффект этой команды заключается в том, что значение переменной A увеличится на пять, в то время как значения остальных трех переменных не изменятся.
Это можно претставить в виде следующей матрицы:
1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 5 0 0 0 1
Если посмотреть на нее, можно заметить, что она почти идентична единичной матрице (которая, как известно, при умножении любого вектора на нее не меняет его значения), за исключением последнего элемента в первом столбце, который равен пяти. Если вспомнить, как происходит умножение вектора на матрицу, можно понять, что значения всех элементов, кроме первого, не изменятся, в то время как значение первого элемента станет равно
v[0] * 1 + v[4] * 5
Так как v[0] содержит текущее значение в переменной A, а v[4] всегда равен единице, то
v[0] * 1 + v[4] * 5 = A + 5
Если вектор текущего состояния умножить на эту матрицу, полученный вектор будет соответствовать состоянию, в котором A на пять больше, что и требовалось.
Если матрицу поменять немного, убрав единицу в первом элементе первой строки:
0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 5 0 0 0 1
Как и прежде, значения всех элементов кроме первого не изменятся, в то время как первый элемент станет равным v[4] * 5, или просто пяти.
Умножение вектора текущего состояния на такую матрицу эквивалентно выполнению команды
A = 5
Посмотрим на такую матрицу:
1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1
Единственное отличие ее от единичной матрицы — это второй элемент в четвертой строке, который равен единице. Очевидно, что умножение вектора текущего состояния на эту матрицу не изменит значения в первом и последних трех элементах, в то время как значение второго элемента изменится на
v[1] * 1 + v[3] * 1
Так как v[1] содержит текущее значение переменной B, а v[3] содержит текущее значение переменной D, то умножение вектора состояния на такую матрицу эквивалентно выполнению команды B += D
Аналогично рассуждая можно понять, что умножение вектора состояния на следующую матрицу эквивалентно выполнению команды C *= 7
1 0 0 0 0 0 1 0 0 0 0 0 7 0 0 0 0 0 1 0 0 0 0 0 1
Перейдем к комбинированию команд. Пусть вектор v задает текущее состояние, матрица Ma соответствует команде A += 5, а матрица Mm соответствует команде A *= 7.
3
Мы вычисляем матрицу, соответствующую телу цикла, только один раз, после чего возводим ее в степень.
Рассмотренных примеров достаточно, чтобы начать работать над интерпретатором простого языка, поддерживающего присваивание, сложение, вычитание, умножение (только на константу) и циклы. Для этого мы научимся представлять любую такую программу в виде матрицы размера N+1 на N+1, где N — это количество переменных, которыми программа оперирует, после чего будем просто умножать вектор с начальным состоянием на эту матрицу.
Правила представления программы в виде матрицы очень просты:
1. Каждая отдельная команда представляется в виде матрицы, отличающейся от единичной одним элементом (или двумя для операции присваивания). Примеры таких матриц рассмотрены выше в этой статье.
2. Несколько подряд идущих команд представляются в виде матрицы, равной произведению матричного представления каждой отдельной команды.
3. Цикл представляется в виде матрицы, представляющей тело цикла, возведенной в степень количества итераций цикла.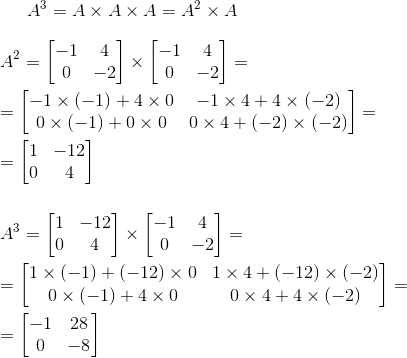
Если у нас есть функция identity, возвращающая единичную матрицу:
def identity():
return [[1 if i == j else 0 for j in range(REGS + 1)] for i in range(REGS + 1)]То фукнция, строящая матрицу для команды r1 += r2 (где r1 и r2 — переменные) может выглядеть так:
def addreg(r1, r2):
ret = identity()
ret[r2][r1] = 1
return retА для команды r += val (r — переменная, val — константа) вот так:
def addval(r, val):
ret = identity()
ret[REGS][r] = val
return retФункции для построения матриц других команд выглядят похоже — получается единичная матрица, в которой заменяется один элемент.
Интерпретатор без циклов теперь пишется очень просто — пусть матрица mat соответствует уже прочитанному коду. В начале она равна единичной матрице, потому что пустая программа не меняет состояния. Затем мы считываем команды по одной, разбиваем их на три элемента (левый операнд, оператор, правый операнд), и в зависимости от оператора домножаем матрицу, соответствующую всей программе, на матрицу, соответствующую текущей команде:
def doit():
mat = identity()
while True:
line = sys.
stdin.readline().lower()
tokens = line.split()
if tokens[0] == 'loop':
# тут будет код для циклов
elif tokens[0] == 'end':
return mat
else:
r1 = reg_names.index(tokens[0])
try:
r2 = reg_names.index(tokens[2])
except:
r2 = -1
if tokens[1] == '+=':
if r2 == -1: cur = addval(r1, long(tokens[2]))
else: cur = addreg(r1, r2)
elif tokens[1] == '-=':
....
mat = matmul(mat, cur)
stdin.readline().lower()
tokens = line.split()
if tokens[0] == 'loop':
# тут будет код для циклов
elif tokens[0] == 'end':
return mat
else:
r1 = reg_names.index(tokens[0])
try:
r2 = reg_names.index(tokens[2])
except:
r2 = -1
if tokens[1] == '+=':
if r2 == -1: cur = addval(r1, long(tokens[2]))
else: cur = addreg(r1, r2)
elif tokens[1] == '-=':
....
mat = matmul(mat, cur)Осталось дело за малым — добавить поддержку циклов. Цикл возводит матрицу тела цикла в степень количества итераций цикла. Возведение в степень, как известно, требует только O(log N) операций, где N — это степень, в которую матрица возводится. Алгоритм возведения в степень очень прост:
1. Если степень равна нулю, вернуть единичную матрицу.
2. Если степень четная, пусть 2N, то можно рекурсивно вычислить M^N, а затем вернуть квадрат получившейся матрицы.
2N, и вернуть полученную матрицу, умноженную на M.
Так как каждые две итерации степень сокращается в двое, сложность такого алгоритма логарифмическая.
def matpow(m, p):
if p == 0: return identity()
elif p % 2 == 0:
tmp = matpow(m, p / 2)
return matmul(tmp, tmp)
else: return matmul(m, matpow(m, p - 1))В интерпретаторе теперь осталось добавить одну строку:
...
if tokens[0] == 'loop':
cur = matpow(doit(), long(tokens[1]))
...И интерпретатор готов.
Пример интерпретатора доступен на гитхабе. Весь код занимает меньше 100 строк.
Для теста скорости можно вернуться к уже упомянутым числам фибоначи. Например, такой код:
A = 1 B = 1 loop 100 C = A C += B A = B B = C end end
Вычислит 101-ое и 102-ое числа фибоначи:
A = 573147844013817084101, B = 927372692193078999176
Замена 100 на 1000000 вычислит миллион первое и миллион второе числа за четыре секунды.
Выполнение такой программы в лоб заняло бы гораздо больше, потому что программе приходится оперировать многотысячезначными числами. Если написать код, которому не приходится оперировать большими числами, например код для вычисления суммы арифметической прогрессии, приведенный в начале статьи, то количество итераций может уходить за рамки разумного, но код будет выполняться за доли секунды
loop 1000000000000000000000000000000000000000000000
loop 1000000000000000000000000000000000000000000000
loop 1000000000000000000000000000000000000000000000
a += 1
b += a
end
end
end
endНа практике этот подход может применяться, например, в оптимизирующих компиляторах, которые могут таким образом сворачивать циклы с большим количеством итераций, оперирующие на небольшом количестве переменных.
N)Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Matrix Power
Инструмент для вычисления матричной экспоненты в алгебре.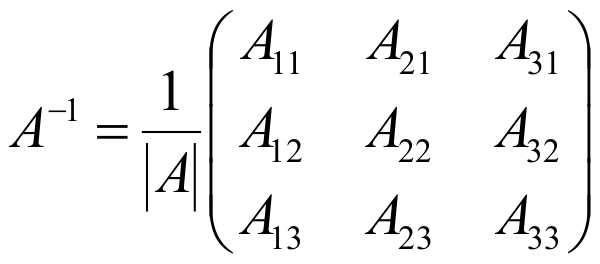
Мощность матрицы заключается в возведении матрицы в степень (умножении на себя).
Результаты
Matrix Power — dCode
Метки: Matrix
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах для решения любых задач. день! 92 = \begin{bmatrix} 1 и 2 \\ 3 и 4 \end{bmatrix} \times \begin{bmatrix} 1 и 2 \\ 3 и 4 \end{bmatrix} = \begin{bmatrix} 7 и 10 \ \ 15 & 22 \end{bmatrix} $$
Размер полученной матрицы идентичен исходной матрице M; т.е. $m$ строк и $m$ столбцов.
Вычисление степени матрицы работает только для квадратных матриц (2×2, 3×3, 4×4, 5×5 и т. д. из-за ограничений с умножением»> матричных произведений) и используется для некоторых матриц, таких как стохастические матрицы. 9к $.
Исходный код
dCode сохраняет право собственности на исходный код Matrix Power. За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Matrix Power», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Matrix Power» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т.
д.) и загрузка всех данных, скрипт, или доступ к API для «Matrix Power» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Matrix Power» или любых ее результатов разрешено, если вы цитируете dCode!
Экспорт результатов в виде файла .csv или .txt можно выполнить бесплатно, нажав значок export . , https://www.dcode.fr/matrix-power
Сводка
- Сила матрицы
- Что такое мощность матрицы? (Определение)
- Как рассчитать мощность матрицы n?
- Зачем диагонализовать матрицу перед вычислением ее мощности?
- Как вычислить отрицательную степень матрицы?
- Как вычислить корень матрицы?
- Как вычислить нецелую степень матрицы?
Аналогичные страницы
- Произведение матриц
- Калькулятор матриц
- Постоянная матрицы
- Сложение матриц
- Тригонализация матрицы
- Транспонирование матрицы
- Ортонормализация Грама-Шмидта
- СПИСОК ИНСТРУМЕНТОВ DCODE
Поддержка
- Paypal 9 8 на Patre 099
Форум/Помощь
Ключевые слова
степень, экспонента ,квадрат,матрица
Звенья
▲
матриц — Как вычислить квадратную матрицу в степени n?
спросил 9n$ используя обычный матричный экспоненциальный трюк, чтобы сделать это быстро?
Редактировать 1 Также есть еще одно свойство матрицы A, заключающееся в том, что ее диагонали всегда состоят из 0 и других элементов либо из 0, либо из 1.
Можем ли мы сделать это, просто используя умножение матриц?
- матрицы
$\endgroup$
18
$\begingroup$
Другой подход называется возведением в степень возведением в квадрат. Это по-прежнему требует, чтобы вы умножали матрицы, как обычно, но вам нужно всего лишь $O(\log n)$ таких умножений. 9{\zeta-1}}{\lambda_+ — \lambda_-} \textbf{I}$$
http://xphysics.wordpress.com/2011/12/03/raising-the-power-of-a -2%c3%972-матрица/
$\endgroup$
1
$\begingroup$
Вы можете использовать теорему Кэли-Гамильтона, которая утверждает, что каждая матрица удовлетворяет своему характеристическому многочлену.
Предположим, у вас есть матрица $A$ размером $k\k$.