Все формулы связанные с дискриминантом
Компьютеры admin 0 комментариев
Содержание
- 1 Решение квадратных уравнений через дискриминант
- 1.1 I случай D > 0 (дискриминант больше нуля)
- 1.2 II случай D = 0 (дискриминант равен нулю)
- 1.3 III случай D (дискриминант меньше нуля)
Дискриминант квадратного уравнения – это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.
| Вид уравнения | Формула корней | Формула дискриминанта |
|---|---|---|
| ax 2 + bx + c = 0 | b 2 — 4ac | |
| ax 2 + 2kx + c = 0 | k 2 — ac | |
| x 2 + px + q = 0 | ||
| p 2 — 4q |
Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:
| Вид уравнения | Формула |
|---|---|
| ax 2 + bx + c = 0 | , где D = b 2 — 4ac |
| ax 2 + 2kx + c = 0 | , где D = k 2 — ac |
| x 2 + px + q = 0 | , где D = |
| , где D = p 2 — 4q |
Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:
- Если дискриминант больше нуля, то уравнение имеет два корня.
- Если дискриминант равен нулю, то уравнение имеет один корень.
- Если дискриминант меньше нуля, то уравнение не имеет корней.
Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:
так как она относится к формуле:
которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.
Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.
Пример 1. Решить уравнение:
Определим, чему равны коэффициенты:
D = b 2 — 4ac = (-4) 2 — 4 · 3 · 2 = 16 — 24 = -8, D 2 — 6x + 9 = 0
Определим, чему равны коэффициенты:
D = b 2 — 4ac = (-6) 2 — 4 · 1 · 9 = 36 — 36 = 0, D = 0
Уравнение имеет всего один корень:
Определим, чему равны коэффициенты:
D = b 2 — 4ac = (-4) 2 — 4 · 1 · (-5) = 16 + 20 = 36,
Решение квадратных уравнений.
Дискриминант. Формула дискриминанта. Теорема Виета.
Квадратным уравнением называется уравнение вида
,
a,b,c — постоянные (числовые) коэффициенты.
В общем случае решение квадратных уравнений сводится к нахождению дискриминанта:
| Формула дискриминанта: | . |
О корнях квадратного уравнения можно судить по знаку дискриминанта (D) :
- D>0 — уравнение имеет 2 различных вещественных корня
- D=0 — уравнение имеет 2 совпадающих вещественных корня
- D 2 .
Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения
.Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
x1;2 =
| −b ± √ D |
| 2a |
, где « D = b 2 − 4ac »
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
D —> , где « D = b 2 − 4ac »
—> —> D = b 2 − 4ac
D = 25 + 56
D = 81
D > 0
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| −5 ± √ 81 |
| 2 · 2 |
x1;2 =
| −5 ± 9 |
| 4 |
| −5 + 9 |
| 4 |
Ответ: x1 = 1; x2 = −3
Вывод: когда « D > 0 » в квадратном уравнении два корня .
II случай
D = 0
(дискриминант равен нулю)
16x 2 − 8x + 1 = 0
D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| 8 ± √ 0 |
| 32 |
x1;2 =
| 8 ± 0 |
| 32 |
x =
x =
Ответ: x =
Вывод: когда « D = 0 » в квадратном уравнении один корень .
III случай
D
(дискриминант меньше нуля)
D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D
x1;2 =
| −b ± √ D |
| 2a |
x1;2 =
| 8 ± √ −36 |
| 32 |
Ответ: нет действительных корней
Вывод: когда « D » в квадратном уравнении нет корней .
Формулы квадратных уравнений, как решать дискриминант, неполные и комплексные уравнения и их решение
В разных практических деятельностях человека вроде физики, инженерии, архитектуры и других точных наук, часто встречаются задачи с математическими моделями, какой являются уравнения, имеющие переменную (x) в иной степени.
Именно они помогают учёным в изучении внешней среды и её использовании.
Содержание
Квадратные уравнения
Квадратным называется равенство вида ax² + bc + c = 0, где x является переменой, a (первый коэффициент), b (второй) и c (свободный) — это действительные числа, которые должны приводить в условии задачи. Нужно помнить при решении, что a ≠ 0. Как уже понятно, оно очень отличается от линейного уравнения, его все изучали в младших классах школы.
Чтобы понять, как решать квадратные уравнения, нужно представить футбольное поле, длина которого на 10 метров больше его ширины, а площадь равна 380 квадратных метров. Нужно найти ширину футбольного поля.
Пусть переменная x — это определённая ширина, тогда её длина будет (х +10) метров. Потом x * (x + 10) = 380, ведь дана площадь 380 квадратных метров в условии задачи, то есть x² + 10x 380 равно нулю. Здесь а = 1, b = 10, а c = -375 Это был один из примеров квадратных равенств.
Различают два вида уравнений:
- Приведённые — это случай, когда в квадратном равенстве a = 1.
- Непривёденные если a ≠ 1.
При этом x² — приведённое, а уже при 5x² оно станет непривёденным.
Понятие дискриминант
Существует определенная система решения таких уравнений. Чтобы найти чётный корень такого равенства, достаточно запомнить приведённую ниже формулу квадратного уравнения.
Буква D — это дискриминант. Звучит сложно, но не стоит пугаться, ведь с латинского языка слово переводится, как разность. Он равен: D = b² 4 ac. Следуя этому, можно записать, что (2ax + b)² = D. Есть определенные правила, как надо решать дискриминант:
- Если D меньше нуля, то действительных корней нет.
- В случае когда D равняется нулю, в решении получается только один действительный корень, но есть редкие случаи с двумя, то есть можно писать при решении в формуле либо +, либо -.
- Если D больше нуля, то в уравнении два действительных корня, то есть и плюс, и минус. Но чтобы укоротить решение достаточно записать ±, вместо двух вариантов решения задачи.
Но чтобы укоротить решение достаточно записать ±, вместо двух вариантов решения задачи.Пример первого способа нахождения через формулу дискриминанта квадратного уравнения и правильным разложением чисел:
- 9х²-6х+1=0,
- D = (-6)² 4 × 9 ×1 = 0,
- D эквивалентен нулю,
- x = -6/2×9 = 1/3.
Как пример можно показать уравнивание: -8x² = 0, у которого b и с равны нулю. Или 2x² 3 = 0, b ничему не равно. В уравнении -7x² + 4x² = 0 c эквивалентно нулю.
Разные квадратные уравнения
Помимо обычных дискриминантов, есть и половинные. Их ищут для равенств, у которых второй коэффициент — это чётное число, по формуле: D1 = 4 k² 4 ac = 4 (k² ac). Чтобы делать меньше ошибок, лучше использовать формулу со скобками. Благодаря этому в ответе получается четверть дискриминанта.
Квадратные равенства с комплексными переменными почти ничем не отличаются от плоскости действительных чисел и тем, которые должны проходить в восьмых классах. И чтобы без проблем их решать, нужно использовать формулу.
Если в квадратном равенстве хотя бы один из общих коэффициентов квадратного трехчлена B или C равен нулю, то такое равенство называют неполным.
Следовательно оно бывает только трёх видов:
- Уравнение вида ax² равно нулю. Поскольку а ≠ 0, имеем случай, когда x² = 0, корнем которого есть число ноль. Как уже понятно, имеется единственный корень х равен нулю.
- ax² + c равно нулю, тогда с не будет равняться нулю. Чтобы это лучше понять, приводится уравнение ах² = -c, x² = -c/a. Поскольку c ≠ 0 тогда и -с/а также не равно нулю. Если -с/а больше нуля, то получается два корня: х1 = корень из -с/а и ещё х2 = корень из с/а. Также можно написать вместо минуса и плюса одно уравнение из знаком: ±. Возможен случай, когда ситуация является обратной (-с/а <, 0), тогда корней совсем нет. Пример: -2х² + 50 равняется нулю. -2х²= -50, х² = 25, х1,2 = ±5.
- ах² + bx = 0, и при этом b нулю не равно. Разложим левую часть уравнения на множители и решим полученное х * (ах + b) = 0. Ответ: x равен нулю или ax + b = 0, но x = -b/a, поскольку a ≠ 0. В итоге должно выйти два корня: х1 = 0 и х2 = -b/a. Один из примеров: 2х² + 5х эквивалентен нулю, х(2х+ 5) = 0, х= 0 или 2х + 5 = 0. На данный момент очевидно, что x2 = -2,5 и х1 эквивалентен нулю.
Возможен случай, когда ситуация является обратной (-с/а <, 0), тогда корней совсем нет. Пример: -2х² + 50 равняется нулю. -2х²= -50, х² = 25, х1,2 = ±5.Из истории математики
Неполные квадратные равенства и некоторые виды неизвестных корней вавилонские математики умели решить и создать ещё 4000 лет тому назад. Такие произведения в Древней Греции решали тем же способом. Люди, обладающие знаниями точных наук, решали некоторые квадратные уравнения геометрическими приёмами.
Это показал древнегреческий учёный Диофант.
Много внимания таким уравнениям также выделял арабский математик Мухаммед Альхорезми. Он нашёл как решать уравнение видов: ах²=bx, ax²=c, ax²+bx=c, ax²+c=bx, bc+c=ax² и получил положительные корни.
Формулы, что связывают между собой корни равенства и его коэффициенты, впервые нашёл французский математик Франсуа Виет в 1591 году. Его заключения в современных обозначениях имеют вид: (а + b)x x² = 0.
После быстрой публикации работы нидерландского математика Жераром, а также француза Декарда и англичанина Ньютона равенство корней квадратного уравнения приобрело современный вид.
| Уравнения | х1 и х2 | х1+х2 | х1×х2 |
| х² -6х + 8 = 0 | 2 и 4 | 6 | 8 |
| x²+x-12=0 | -4 и 3 | -1 | -12 |
| x²-4x-5=0 | -3 и -2 | -5 | 6 |
| x²-4x-5=0 | -1 и 5 | 4 | -5 |
Сейчас речь идёт о теореме Виета, на которую нужно обратить внимание.
Её так называют из-за известного французского математика Франсуа Виета, которым и было открыто это свойство. Сумма корней сведенного квадратного равенства равно другому коэффициенту, взятому с отрицательным знаком, а произведение корней — свободному члену. Часто его записывают в таком виде: х² + px + q эквивалентно нулю.
Теорему можно сформулировать так.
Если х1 и х2 — корни сведенного квадратного равенства х²+px+q эквивалентны нулю, то х1 + х2 = -p, x1 * x2 = q. Поскольку a ≠ 0, поделим две части уравнения на а и получается современная формула: x² b/a * x + c/a равно нулю.
Формула дискриминанта — правила и примеры вычисления корней квадратных уравнений » Kupuk.net
Существует несколько способов решений квадратного уравнения. Один из них — применение формулы дискриминанта.
Помня общее выражение и алгоритм, вычислить корни степенного равенства второй степени не составит труда. Естественно, нужно хорошо знать арифметику, выполнение действий с дробями и сам принцип. При этом дискриминант — это не просто удобный параметр, используя который, можно найти решение. Это ещё и характеристика, имеющая объяснимый геометрический смысл.
Общие сведения
Решение квадратных уравнений — одно из ключевых моментов в математике. Ещё древние вавилоняне и греки пытались найти закономерности при решении таких равенств. Но первым, кто описал методы нахождения дополнением квадрата, был индийский философ Будхаяма. Именно он предложил записывать уравнения в виде: ax 2 = c и ax 2 + bx = c. В дальнейшем способы усовершенствовались. Так, Евклид предложил метод геометрического вычисления ответа.
Но наиболее значимым стало открытие Буля. Изучая формулы различных уравнений, он пришёл к выводу, что выражения почти всегда можно упростить, заменив переменные другим набором, содержащим новые неизвестные.
При этом, найдя их, определить первоначальные уже не составляет труда.
Такой способ был применён и к квадратному уравнению. Благодаря ему стало возможным упростить квадратичную форму с двумя переменными, используя дискриминант. Это понятие тесно связано с многочленом, имеющим следующий вид: d (m) = a 0 *mn + a 1 *mn-1 + a 2 *mn-2 + … + a n-1 *m + a n, где m — искомое неизвестное, a n, a n-1, a n-2, … a 1 и a 0 — числовые постоянные.
Термин «дискриминант» был придуман не математиками, но успешно стал ими использоваться при вычислении квадратичных функций. Произошёл он от латинского слова discriminans, что в дословном переводе означает «разделяющий». Важной величиной стало значение, придуманное Булем и имеющее вид b2 — 4ac. Учёный открыл, что после того как переменные линейно изменятся, дискриминант будет равняться первоначальному, умноженному на член, находимому из функции поведения неизвестных.
При решении равенств, содержащих формулу дискриминанта и его корней, используют формулу для быстрого определения количества возможных решений и их числового нахождения. Математически определение записывают следующим образом: p (x) = m + mx + ⋯ + mx, m ≠ 0, где: D (p) = m∏(m − m). То есть дискриминантом многочлена p (x) является сумма произведений корней на неизвестный коэффициент в основном поле их существования.
Смысл дискриминанта
Дискриминант — одно из эффективных решений квадратных выражений. С его помощью легко можно выявить, сколько корней имеет уравнение или установить, что их нет. Применять его можно как к полным квадратным равенствам, так и неполным. Но всё же во втором случае использовать дискриминант не нужно.
Эта тема изучается в седьмом и восьмом классе средней школы. Лучше понять смысл параметра поможет простой пример. Пусть имеется уравнение вида m2 + 2m — 8 = 0. Не имея понятие о дискриминанте, решение уравнения сводится к приведению его к формуле квадрата суммы m2 + 2m +1 — 1- 8 = 0.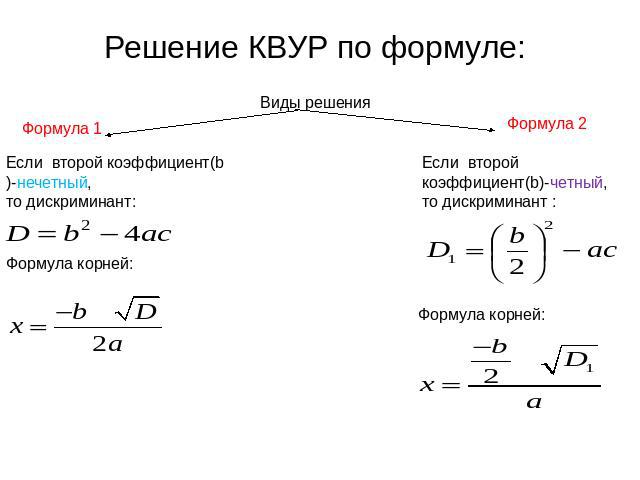
Добавление и вычитание единицы возможно, так как в итоге получается сложение с нулём.
Первые три члена представляют собой квадрат суммы, который можно свернуть по формуле сокращённого умножения до вида a2 +2ab + b2 = (a+b)2. Отсюда, применительно к рассматриваемому примеру, получится: (m + 1)2 — 1 — 8 = 0. После преобразований с переносом неизвестного в одну сторону (а известных — в другую) и раскрытием скобки получится равенство: (m + 1)2 = 9. То есть возможными решениями будут m = 2 для (m + 1) = 3 и m = -4 для (m + 1) = -3.
В общем виде все эти преобразования можно выполнить в следующей последовательности:
Многочлен b2 — 4ac было решено принять за дискриминант. Это выражение по сути и определяет возможность существования решений и количество корней. Выполнив его расчёт, фактически и находится ответ уравнения.
Взаимосвязь параметра
Объяснение дискриминанта имеет и графическое обоснование. Физически задача заключается в комплексном подходе установления взаимосвязи. Фактически это фиксирование нулей параболы уравнения, то есть точек, в которой она пересекает ось абсциссы. Знак при переменной в квадрате будет определять положение веток параболы. Они будут идти вверх при a > 0, и вниз, если a < 0.
Исходя из этого, дискриминант равняется отношению суммы или разности числового коэффициента, стоящего возле неизвестного в первой степени с корнем квадратным из b 2 — 4 ac к удвоенному произведению первого коэффициента в уравнениях x1 = (- b + √ b 2 — 4 ac) / 2a; x2 = (- b — √ b 2 — 4 ac) / 2a. Подкоренное выражение называют формулой сокращённого дискриминанта.
Дискриминант при нахождении корней уравнения может принимать три значения:
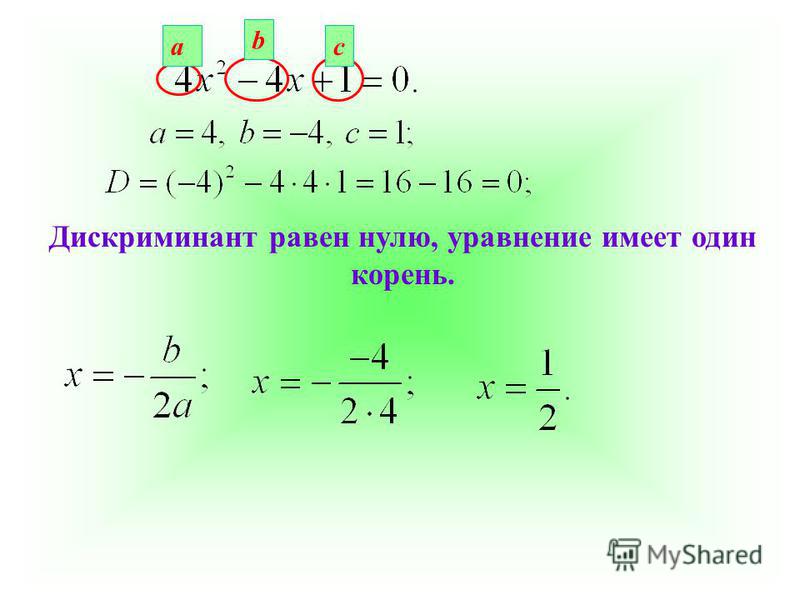Поэтому при таком положении вещей решений или действительных корней у уравнения нет. График уравнения не пересекает ось абсциссы.
Последнее выражение является формулой корней квадратного уравнения. Именно с её помощью могут решаться равенства, в степени которых стоит двойка. Через дискриминант можно вычислять корни и уравнений больших порядков. Для этого используются приёмы понижения степени до квадратного. Но эти операции учащиеся начинают изучать на уроках в выпускном классе, когда проходят решение уравнений n-го порядка.
Типовые примеры
Даже зная правило поиска корней через дискриминант, научиться быстро вычислять корни уравнения не получится, если не практиковаться. Поэтому решение практических задач обязательно входит школьную в программу обучения:
Так: a = 6; b = -13; c = 2. Эти значения нужно подставить в формулу дискриминанта и найти его: D = b2 — 4ac = (-13)2 — 4 * 6 *2 = 149 — 68 = 121. То есть D больше нуля. Значит, согласно правилу, уравнение будет иметь два корня. Теперь их нужно рассчитать: x1 = (13 + √126) / 2 * 6 = 2; x2 = (13 — √126) / 2 * 6 = 1/6. Задание решено.Определить возможность решения уравнения 4m2 — 2m — 3 = 2. Для приведения к удобному виду двойку нужно перенести влево. В итоге получится 4m2 — 2m — 5 =0. Дискриминант равняется: D = 4 — 4 * 4 * (-5) = 4 + 80 = 84. Так как он больше нуля, то корней будет два. Тут сложность заключается в том, что нет целого числа, которое равнялось бы корню из √84. Однако, √84 = √4 * √21 = 2 √21. Используя формулы, получаем что m = (2 ± 2√21) / 2 * 4. Двойку можно вынести в числителе за скобки, получив тем самым удобную запись: m = (2 * (1 ±√21) / 2 * 4 = (1 ± √21) / 4. Это выражение и есть искомое решение.
Решить уравнение: x /3 — x2 / 4 + 1 /6 = 3x / 2 — 4×2 / 3.
Для упрощения равенства нужно правую и левую сторону умножить на двенадцать: 12x / 3 — 12 * x2 / 4 + 12 /6 = (3 * 12x) / 2 — (4 * 12×2) / 3. Получится 4 x — 3 x 2 + 2 = 18 x — 16 x 2. Члены нужно привести к стандарту: 4 x — 3 x 2 + 2 — 18 x + 16 x 2 = 13 x 2 — 14 x + 2 = 0. Считаем дискриминант: D = (-14)2 — 4 * 13 * 2 = 92. Он больше нуля, поэтому есть смысл искать корни: X = (14 ± √ 92) / 2 * 13 = (14 ± 2 √ 23) / 2 * 13 = 2 (7±√23) / 2 *13 = (7± √23) /13.
Таким образом, любое выражение нужно стремиться переписать так, чтобы оно приняло классический вид. Это может быть умножение или деление на какое-либо число, поиск общего знаменателя. А уже после нужно искать дискриминант, по виду которого можно определить, есть ли смысл в дальнейшем нахождении корней уравнения.
Вычисления на онлайн-калькуляторе
Поиск решений уравнения через дискриминант — довольно простая тема.
Необходимо запомнить всего две формулы и свойства, зависящие от значения дискриминанта. Но на практике попадаются примеры содержащие интегралы, логарифмы, экспоненциальные функции. При этом всё это может быть записано в виде сложных дробей.
Решая задания самостоятельно, даже имея большой опыт и знания, есть вероятность допущения ошибки. Поэтому при вычислении сложных примеров стоит использовать онлайн-калькуляторы.
Из сервисов, предлагающих такие услуги, можно отметить:
- Math.semestr;
- Kontrolnaya-rabota;
- Onlinemschool;
- Wpcalc;
- Webmath.
Эти российские сайты. Их интерфейс интуитивно понятен. Для выполнения вычислений не нужно указывать персональные данные или платить за услуги. От пользователя лишь требуется записать в предложенную форму квадратное уравнение или даже матрицу, состоящую из них. Программа автоматически выполнит нужный расчёт и предоставит пошаговое решение. Кроме того, на сайтах решателей уравнений содержится в кратком виде теоретический материал и типовые примеры с подробным решением.
Даже ничего не понимающий в дискриминантах человек, воспользовавшись онлайн-калькулятором несколько раз, сможет восполнить пробелы в знаниях, самостоятельно научиться решать примеры, узнает, как правильно должен писаться дискриминант. Использование онлайн-сайтов для математических решений позволяет сэкономить время и получить точный результат.
Дискриминант квадратного уравнения – mathsathome.com
Видео-урок по дискриминанту
Что такое дискриминант квадратного уравнения?
Дискриминант — это часть квадратной формулы, находящаяся внутри квадратного корня.
Для квадратичного вида a𝑥 2 + b𝑥 + c его дискриминант равен b 2 – 4ac. Квадратное уравнение имеет 2, 1 или 0 решений в зависимости от того, является ли значение дискриминанта положительным, нулевым или отрицательным соответственно.
Дискриминант b 2 – 4ac представлен дельта-символом Δ.
Формула дискриминанта: Δ = b 2 – 4ac, где a – коэффициент при 𝑥 2 , b – коэффициент при 𝑥, а c – постоянный член квадратного числа.
Например, вычислите дискриминант y = 𝑥
2 + 5𝑥 + 2.У нас есть один 𝑥 2 . Коэффициент при 𝑥 2 равен 1. Следовательно, a = 1,
Коэффициент при 𝑥 равен 5. Следовательно, b = 5,
Постоянный член равен 2. Следовательно, c = 2.
Подставляем значения a = 1, b = 5 и c = 2 в формулу для дискриминанта, b 2 – 4ac.
b 2 = 5 2 = 25
и 4ac = 4 × 1 × 2 = 8.
b 2 – 4ac становится 28 – 5 .
важен, потому что он говорит нам, сколько решений имеет любое квадратное уравнение.
- Если дискриминант положительный, то будет 2 решения.
- Если дискриминант равен нулю, будет 1 решение.
- Если дискриминант отрицательный, реальных решений не будет.
Количество решений квадратного уравнения говорит нам о количестве корней квадратного уравнения. Корни квадратного уравнения — это точки пересечения квадратного графика с осью 𝑥. Это точки пересечения оси 𝑥.
В следующей таблице показано количество корней для положительного, отрицательного или нулевого дискриминанта.
| Value of the discriminant | Number of Roots | |
| > 0 | Positive | Two |
| = 0 | Zero | One |
| < 0 | Negative | Ноль |
Как вычислить дискриминант
Для вычисления дискриминанта квадратного уравнения используется формула b 
Подставьте значения a, b и c после считывания их из квадратного уравнения вида а𝑥 2 + b𝑥 + с . Например, для 𝑥 2 – 3𝑥 + 4, a = 1, b = -3 и c = 4. b 2 = 9 и 4ac = 16. Дискриминант – 4ac = – 7.
При вычислении дискриминанта важно учитывать следующие ключевые моменты:
- b 2 всегда положительно. Когда мы возводим в квадрат отрицательное число, это дает нам положительный результат.
- Если 4ac отрицательное, нам нужно выполнить сложение. Когда мы вычитаем отрицательное число, происходит сложение.
Чтобы найти дискриминант:
- Найдите коэффициент 𝑥 2 .
- Найдите b, который является коэффициентом 𝑥.
- Найдите постоянный член c.
- Возведите в квадрат значение b, чтобы найти b 2 .
- Умножьте 4 × a × c, чтобы найти 4ac.
- Используйте эти значения для расчета b 2 – 4ac.
Дискриминантный калькулятор
Чтобы использовать дискриминантный калькулятор:
- Прочтите коэффициент 𝑥 2 , чтобы найти «а».
- Прочтите коэффициент при 𝑥, чтобы найти «b».
- Прочитать постоянный термин, который равен «c».
Положительный дискриминант
Положительный дискриминант означает, что значение b 2 – 4ac больше нуля. Квадратное уравнение с положительным дискриминантом имеет ровно два решения, а это означает, что оно имеет две точки пересечения оси 𝑥. Это означает, что квадратное число имеет 2 корня.
Положительное значение дискриминанта означает, что график квадратного уравнения должен дважды пройти через ось 𝑥.
Если квадратичный коэффициент имеет положительный коэффициент 𝑥 2 (a > 0), график вогнут вверх, а точка минимума будет ниже оси 𝑥, как показано на левом изображении ниже.
Если квадратичный коэффициент имеет отрицательный коэффициент 𝑥 2 (a < 0), график вогнут вниз, а точка минимума будет выше оси 𝑥, как показано на правом изображении ниже.
Положительное значение дискриминанта говорит нам о том, что квадратное уравнение имеет два уникальных решения.
Например, квадратное уравнение 𝑥 2 – 4𝑥 + 3 = 0 имеет два решения: 𝑥 = 3 и 𝑥 = 1.
Это означает, что квадратное уравнение пересекает ось 𝑥 в точках 𝑥 = 1 и 𝑥 = 3
Значение дискриминанта равно 4, что является положительным числом.
Квадратный корень из положительного числа имеет как положительный, так и отрицательный ответ. Следовательно, квадратичная формула дает 2 различных решения.
Если дискриминант представляет собой полный квадрат, то решения квадратного уравнения рациональны. Это означает, что решения будут целыми числами или могут быть записаны в виде дробей. Если дискриминант не является полным квадратом, два решения будут иррациональными.
Это потому, что квадратный корень этого дискриминанта будет surd.
Дискриминант нуля
Дискриминант нуля означает, что значение b 2 – 4ac равно нулю. Квадратное уравнение с нулевым дискриминантом имеет ровно одно решение. Это означает, что график квадратичного уравнения просто касается оси 𝑥 в ее минимальной или максимальной точке.
Дискриминант, равный нулю, означает, что график квадратного уравнения должен коснуться оси 𝑥 один раз. Он не может проходить через ось 𝑥. Вместо этого он просто касается его одним корнем.
Если квадратичный коэффициент имеет положительный коэффициент 𝑥 2 (a > 0), график вогнут вверх и точка минимума будет касаться оси 𝑥, как показано на левом изображении ниже.
Если квадратичный коэффициент имеет отрицательный коэффициент 𝑥 2 (a < 0), график вогнут вниз, и точка максимума будет касаться оси 𝑥, как показано на правом изображении ниже.
Для квадратного уравнения с нулевым дискриминантом будет ровно одно решение.
Это связано с тем, что квадратный корень из дискриминанта берется как часть квадратичной формулы. Квадратный корень из 0 равен 0.
Это означает, что мы прибавляем или вычитаем 0 при вычислении, что делает два ответа одинаковыми.
Решение квадратного уравнения с нулевым дискриминантом называется повторным корнем. Это потому, что одно и то же решение появляется дважды.
Например, квадратичный 𝑥 2 – 4𝑥 + 4 = 0 имеет a = 1, b = -4 и c = 4.
b 2 = 16 и 4ac = 16.
b 2 – 4ac = 0, а один повторяющийся корень квадратного уравнения равен 𝑥 = 2.
Отрицательный дискриминант
Отрицательный дискриминант означает, что значение b 2 – 4ac меньше нуля. При использовании квадратной формулы нельзя найти квадратный корень из отрицательного значения. У квадратного уравнения нет реальных решений. Два решения являются сложными и не могут быть показаны на графике.
Отрицательный дискриминант означает, что график квадратного уравнения не касается оси 𝑥.
Если квадратичный коэффициент имеет положительный коэффициент 𝑥 2 (a > 0), график вогнут вверх и весь график находится над осью 𝑥. Все выходы графика положительны.
Если квадратичный коэффициент имеет отрицательный коэффициент 𝑥 2 (a < 0), график вогнут вниз и весь график находится ниже оси 𝑥. Все выходы графика отрицательные.
Например, в квадратном уравнении 𝑥 2 – 3x + 5 = 0, a = 1, b = -3 и c = 5. дискриминант b 2 – 4ac = -11.
Квадратный корень из отрицательного числа не может быть найден, поэтому не может быть найдено никаких реальных решений, поскольку мы не можем завершить вычисление.
Квадратный корень из -11 должен быть записан в единицах мнимой единицы, т.е.
Поэтому записывается как √11 i. Это комплексное решение можно использовать.
Дискриминант из графика
Количество точек пересечения оси 𝑥 указывает значение дискриминанта:
- График с двумя точками пересечения оси 𝑥 имеет положительный дискриминант.
- График, касающийся оси 𝑥 один раз, имеет нулевой дискриминант.
- График, не касающийся оси 𝑥, имеет отрицательный дискриминант.
Дискриминант кубического уравнения
Дискриминант кубического уравнения a𝑥 3 + B𝑥 2 + C 𝑥 + D IS B 2 C 2 — 4AC 3 — 4B 3 D — 27A 2 D 2 + 18ABCD. Если дискриминант положительный, кубический имеет 3 действительных корня. Если он отрицательный, кубический имеет один действительный корень и два комплексно-сопряженных корня. Если он равен нулю, то по крайней мере два корня равны.
| Значение кубического дискриминанта | Значение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Положительный дискриминант | 3 Real Roots | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дискриминанте с ноль | По крайней мере один повторный корень | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Отрицательный дискриминанте 2 – 3𝑥 + 1, a = 5, b = 2, c = -3 и d = 1. Используя формулу кубического дискриминанта Δ = b 2 c 2 – 4ac 3 – 4b 3 г – 27а 2 г 2 + 18abcd. Δ = -671. Дискриминант кубического числа отрицательный, поэтому у этого кубического числа 1 действительный корень и 2 комплексных корня. Это означает, что его график будет пересекать ось 𝑥 только один раз. Квадратная формула — ChiliMathСуществует несколько методов решения квадратных уравнений. Если квадратное уравнение не может быть легко решено методом факторизации, мы прибегаем к использованию либо дополнения квадрата, либо квадратной формулы . 92+bx+c=0} где a, b и c — действительные числа, но a не равно нулю a \ne 0; а x — неизвестная переменная, мы просто берем значения a, b и c, подставляем их в квадратичную формулу, а затем упрощаем, чтобы найти ответы. Ответы квадратных уравнений называются решениями, нулями или корнями. Но прежде чем мы сможем применить квадратную формулу, мы должны убедиться, что квадратное уравнение имеет стандартную форму. Квадратное уравнение выражается в стандартной форме 92+бх+с=0. Слово «квадратик» произошло от латинского слова « quadratus », что означает «квадрат». В алгебре слово в квадрате означает умножение числа или переменной на себя. Обратите внимание, что старший показатель степени переменной x в квадратном уравнении равен 2 (x возведен во 2-ю степень). Обратите внимание, что в приведенной выше квадратной формуле есть знак плюс или минус \color{red}\large{ \pm}, который подразумевает, что мы собираемся рассмотреть два случая при поиске решений. 92} — 4ac}} } \over {2a}}} Дискриминант квадратичной формулы дает очень полезную информацию о характере решений. Фактически, он может определить количество и тип решений квадратного уравнения. Кроме того, при работе с дискриминантом нам все равно, насколько велико или мало число.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вместо этого нас просто интересует, является ли он положительным, нулевым или отрицательным.
