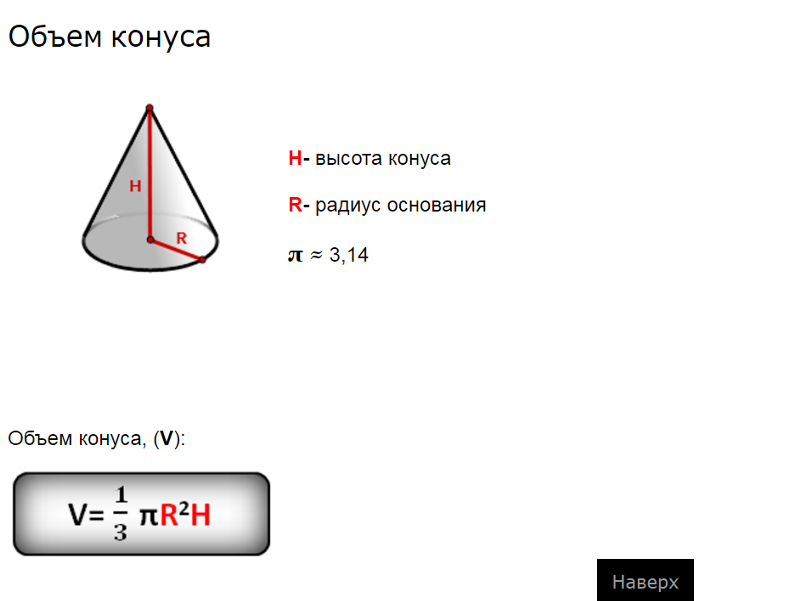
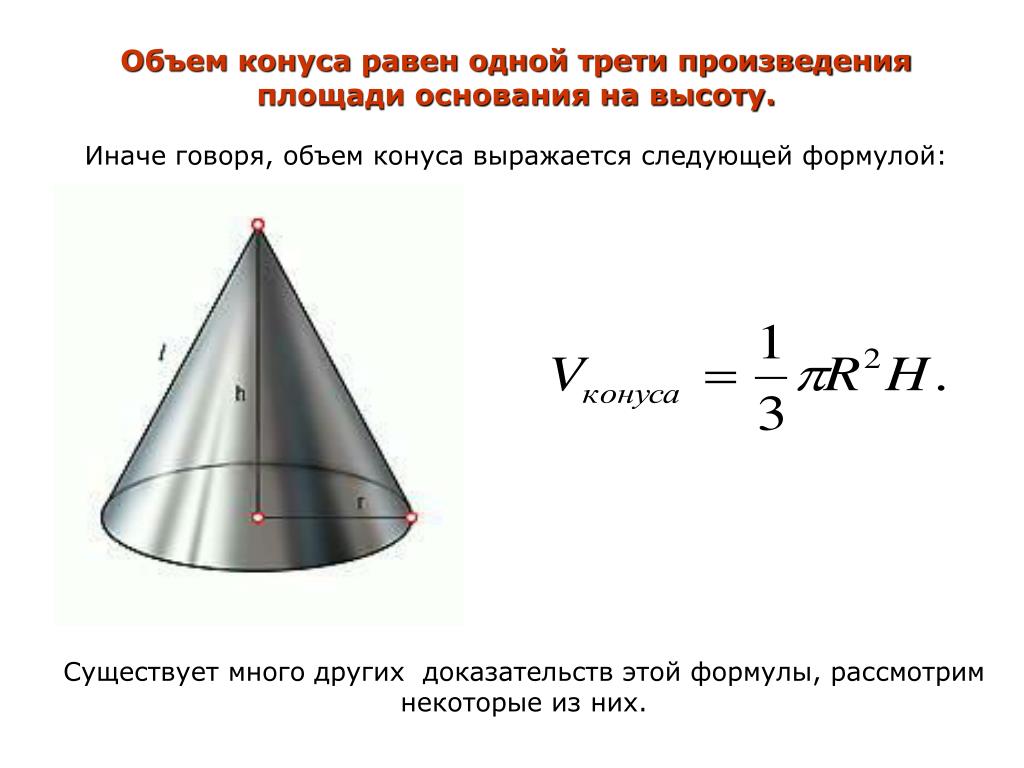
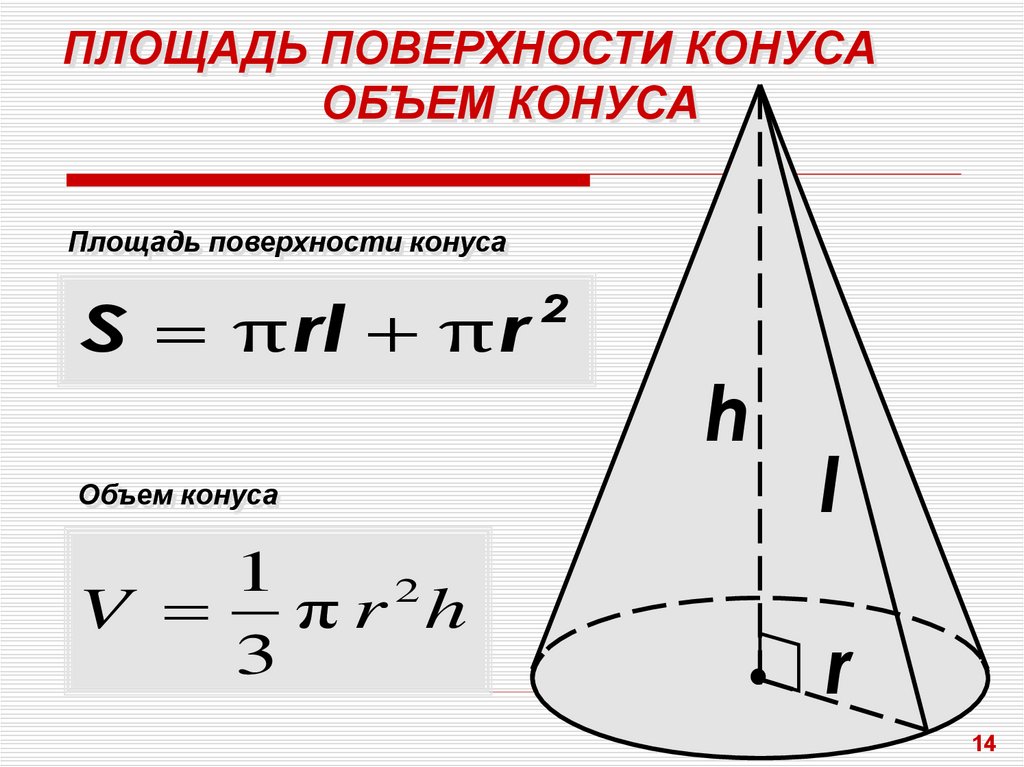
Конус все формулы и свойства. Конус. Основные понятия. Площадь поверхности конуса. Тема урока: Конус и его элементы
Рассмотрим какую-либо линию l (кривую или ломаную), лежащую в некоторой плоскости (рис. 386, а, б), и произвольную точку М, не лежащую в этой плоскости. Всевозможные прямые, соединяющие точку М со всеми точками линии образуют поверхность а; такая поверхность называется конической поверхностью, точка вершиной, линия — направляющей, прямые образующими. На рис. 386 мы не ограничиваем поверхность а ее вершиной, но представляем себе ее простирающейся неограниченно в обе стороны от вершины.
Если коническую поверхность рассечь какой-либо плоскостью, параллельной плоскости направляющей , то в сечении получим линию (кривую или ломаную, в зависимости от того, была ли кривой или ломаной линия ), гомотетичную линии l, с центром гомотетии в вершине конической поверхности. Действительно, отношение любых соответствующих отрезков образующих будет постоянным:
Итак, сечения коническои поверхности плоскостями, параллельными плоскости направляющей, подобны и подобно расположены, с центром подобия в вершине конической поверхности; это же верно для любых параллельных плоскостей, не проходящих через вершину поверхности.
Пусть теперь направляющая — замкнутая выпуклая линия (кривая на рис. 387, а, ломаная на рис. 387, б). Тело, ограниченное с боков конической поверхностью, взятой между ее вершиной и плоскостью направляющей, и плоским основанием в плоскости направляющей, называется конусом (если -кривая линия) или пирамидой (если -ломаная).
Пирамиды классифицируются по числу сторон многоугольника, лежащего в их основании. Говорят о треугольной, четырехугольной и вообще -угольной пирамидах. Заметим, что -угольная пирамида имеет грань: боковых граней и основание. При вершине пирамиды мы имеем -гранный угол с плоскими и двугранными углами.
Они соответственно называются плоскими углами при вершине и двугранными углами при боковых ребрах. При вершинах основания мы имеем трехгранных углов; их плоские углы, образованные боковыми, ребрами и сторонами основания, называются плоскими углами при основании, двугранные углы между боковыми гранями и плоскостью основания — двугранными углами при основании.
Треугольная пирамида иначе называется тетраэдром (т. е. четырехгранником). Любая из ее граней может быть принята за основание.
Пирамида называется правильной при выполнении двух условий: 1) в основании пирамиды лежит правильный многоугольник,
2) высота, опущенная из вершины пирамиды на основание, пересекает его в центре этого многоугольника (иначе говоря, вершина пирамиды проектируется в центр основания).
Заметим, что правильная пирамида не является, вообще говоря, правильным многогранником!
Отметим некоторые свойства правильной -угольной пирамиды. Проведем через вершину такой пирамиды высоту SO (рис. 388).
Повернем всю пирамиду как целое вокруг этой высоты на угол При таком повороте многоугольник основания перейдет сам в себя: каждая из его вершин займет положение соседней. Вершина пирамиды и ее высота (ось вращения!) останутся на месте, и поэтому пирамида как целое совместится сама с собой: каждое боковое ребро перейдет в соседнее, каждая боковая грань совместится с соседней, каждый двугранный угол при боковом ребре также совместится с соседним.
Отсюда вывод: все боковые ребра равны между собой, все боковые грани суть равные равнобедренные треугольники, все двугранные углы при основании равны, все плоские углы при вершине равны, все плоские углы при основании равны.
Из числа конусов в курсе элементарной геометрии мы изучаем прямой круговой конус, т. е. такой конус, основание которого круг, а вершина проектируется в центр этого круга.
Прямой круговой конус показан на рис. 389. Если проведем через вершину конуса высоту SO и повернем конус вокруг этой высоты на произвольный угол, то окружность основания будет скользить сама по себе; высота и вершина останутся на месте, поэтому при повороте на любой угол конус совместится сам с собой. Отсюда видно, в частности, что все образующие конуса равны между собой и одинаково наклонены к плоскости основания. Сечения конуса плоскостями, проходящими через его высоту, будут равнобедренными треугольниками, равными между собой. Весь конус получается от вращения прямоугольного треугольника SOA вокруг его катета (который становится высотой конуса).
Сечения конуса плоскостями, параллельными плоскости его основания, суть круги (хотя бы потому, что они гомотетичны кругу основания).
Задача. Двугранные углы при основании правильной треугольной пирамиды равны а. Найти двугранные углы при боковых ребрах.
Решение. Обозначим временно сторону основания пирамиды через а. Проведем сечение пирамиды плоскостью, содержащей ее высоту SO и медиану основания AM (рис. 390).
На этом уроке мы познакомимся с такой фигурой, как конус. Изучим элементы конуса, виды его сечений. И узнаем, с какой фигурой конус имеет много общих свойств.
Рис.1. Предметы конусовидной формы
В мире огромное количество вещей имеют форму конуса. Зачастую мы их даже не замечаем. Дорожные конусы, предупреждающие о дорожных работах, крыши замков и домов, рожок для мороженого — все эти предметы имеют форму конуса (см. рис. 1).
рис. 1).
Рис. 2. Прямоугольный треугольник
Рассмотрим произвольный прямоугольный треугольник с катетами и (см. рис. 2).
Рис. 3. Прямой круговой конус
Вращая данный треугольник вокруг одного из катетов (не нарушая общности, пусть это будет катет ), гипотенуза опишет поверхность, а катет опишет круг. Таким образом, получится тело, которое называют прямым круговым конусом (см. рис. 3).
Рис. 4. Виды конусов
Раз уж мы говорим о прямом круговом конусе, видимо, существует и непрямой, и не круговой? Если в основании конуса круг, но вершина не проектируется в центр этого круга, то такой конус называют наклонным. Если же основание — не круг, а произвольная фигура, то такое тело также иногда называют конусом, однако, разумеется, не круговым (см. рис. 4).
Таким образом, мы снова приходим к аналогии, уже знакомой нам по работе с цилиндрами. По сути конус — это что-то вроде пирамиды, просто у пирамиды в основании многоугольник, а у конуса (который мы будем рассматривать) — круг (см.
Отрезок оси вращения (в нашем случае это катет ), заключенный внутри конуса, называют осью конуса (см. рис. 6).
Рис. 5. Конус и пирамида
Рис. 6. — ось конуса
Рис. 7. Основание конуса
Круг, образованный вращением второго катета (), называют основанием конуса (см. рис. 7).
А длина этого катета является радиусом основания конуса (или, проще говоря, радиусом конуса) (см. рис. 8).
Рис. 8. — радиус конуса
Рис. 9. — вершина конуса
Вершина острого угла вращающегося треугольника, лежащая на оси вращения, называется вершиной конуса (см. рис. 9).
Рис. 10. — высота конуса
Высота конуса — отрезок, проведенный из вершины конуса перпендикулярно его основанию (см. рис. 10).
Здесь у вас может возникнуть вопрос: чем же тогда отличается отрезок оси вращения от высоты конуса? На самом деле они совпадают только в случае прямого конуса, если же вы будете рассматривать наклонный конус, то заметите, что это два совершенно разных отрезка (см.
Рис. 11. Высота в наклонном конусе
Вернемся к прямому конусу.
Рис. 12. Образующие конуса
Отрезки, соединяющие вершину конуса с точками окружности ее основания, называют образующими конуса. Кстати, все образующие прямого конуса равны между собой (см. рис. 12).
Рис. 13. Природные конусоподобные объекты
В переводе с греческого konos означает «сосновая шишка». В природе достаточно объектов, имеющих форму конуса: ель, гора, муравейник и др. (см. рис. 13).
Но мы-то привыкли, что конус — прямой. У него равные между собой образующие, а высота совпадает с осью. Такой конус мы назвали прямым конусом. В курсе школьной геометрии обычно рассматриваются именно прямые конусы, причем по умолчанию любой конус считается прямым круговым. Но мы уже говорили о том, что бывают не только прямые конусы, но и наклонные.
Рис. 14. Перпендикулярное сечение
Вернемся к прямым конусам. «Разрежем» конус плоскостью, перпендикулярной оси (см.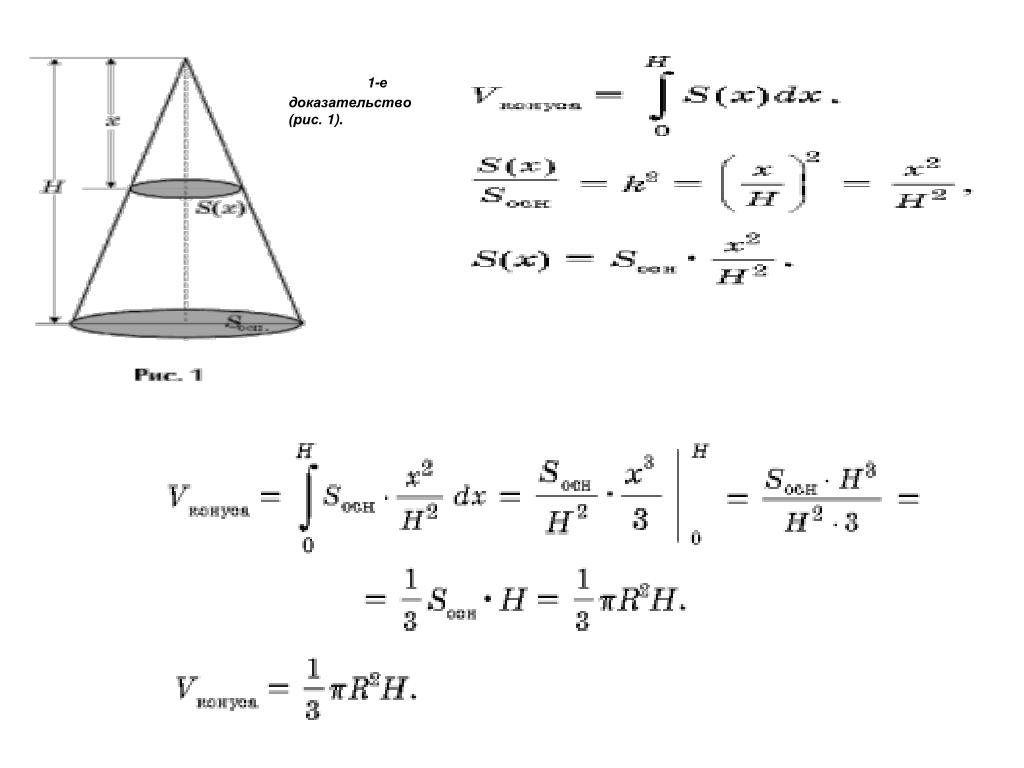 рис. 14).
рис. 14).
Какая же фигура окажется на срезе? Конечно же, круг! Вспомним, что плоскость проходит перпендикулярно оси, а значит, параллельно основанию, которое является кругом.
Рис. 15. Наклонное сечение
А теперь давайте постепенно наклонять плоскость сечения. Тогда наш круг начнет постепенно превращаться во все более вытянутый овал. Но только до тех пор, пока плоскость сечения не столкнется с окружностью основания (см. рис. 15).
Рис. 16. Виды сечений на примере морковки
Любители познавать мир экспериментальным путем могут в этом убедиться с помощью морковки и ножа (попробуйте отрезать от морковки пластинки под разным углом) (см. рис. 16).
Рис. 17. Осевое сечение конуса
Сечение конуса плоскостью, проходящей через его ось, называют осевым сечением конуса (см. рис. 17).
Рис. 18. Равнобедренный треугольник — фигура сечения
Здесь же мы получим совершенно другую фигуру сечения: треугольник. Данный треугольник является равнобедренным (см. рис. 18).
рис. 18).
На этом уроке мы узнали о цилиндрической поверхности, видах цилиндра, элементах цилиндра и сходстве цилиндра с призмой.
Образующая конуса равна 12 см и наклонена к плоскости основания под углом 30 градусов. Найти площадь осевого сечения конуса.
Решение
Рассмотрим искомое осевое сечение. Это равнобедренный треугольник, в котором боковые стороны равны 12, а угол при основании — 30 градусов. Дальше можно действовать по-разному. Либо можно провести высоту, найти ее (половина гипотенузы, 6), потом основание (по теореме Пифагора, ), а затем площадь .
Рис. 19. Иллюстрация к задаче
Либо сразу найти угол при вершине — 120 градусов — и посчитать площадь как полупроизведение сторон на синус угла между ними (ответ будет, тот же).
- Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. — М.: Просвещение, 2009. — 255 с.
- Геометрия 11 класс, А.В. Погорелов, М.: Просвещение, 2002
- Рабочая тетрадь по геометрии 11 класс, В.
 Ф. Бутузов, Ю.А. Глазков
Ф. Бутузов, Ю.А. Глазков
- Yaklass.ru ().
- Uztest.ru ().
- Bitclass.ru ().
Домашнее задание
В машиностроении, наряду с цилиндрическими, широко применяются детали с коническими поверхностями в виде наружных конусов или в виде конических отверстий. Например, центр токарного станка имеет два наружных конуса, из которых один служит для установки и закрепления его в коническом отверстии шпинделя; наружный конус для установки и закрепления имеют также сверло, зенкер, развертка и т. д. Переходная втулка для закрепления сверл с коническим хвостовиком имеет наружный конус и коническое отверстие
1. Понятие о конусе и его элементах
Элементы конуса . Если вращать прямоугольный треугольник АБВ вокруг катета АБ (рис. 202, а), то образуется тело АВГ, называемое полным конусом . Линия АБ называется осью или высотой конуса , линия АВ — образующей конуса . Точка А является вершиной конуса .
При вращении катета БВ вокруг оси АБ образуется поверхность круга, называемая основанием конуса .
Угол ВАГ между боковыми сторонами АВ и АГ называется углом конуса и обозначается 2α. Половина этого угла, образуемая боковой стороной АГ и осью АБ, называется углом уклона конуса и обозначается α. Углы выражаются в градусах, минутах и секундах.
Если от полного конуса отрезать его верхнюю часть плоскостью, параллельной егооснованию (рис. 202, б), то получим тело, называемое усеченным конусом . Оно имеет два основания верхнее и нижнее. Расстояние OO 1 по оси между основаниями называется высотой усеченного конуса . Так как в машиностроении большей частью приходится иметь дело с частями конусов, т. е. усеченными конусами, то обычно их просто называют конусами; дальше будем называть все конические поверхности конусами.
Связь между элементами конуса. На чертеже указывают обычно три основных размера конуса: больший диаметр D, меньший — d и высоту конуса l (рис. 203).
Иногда на чертеже указывается только один из диаметров конуса, например, больший D, высота конуса l и так называемая конусность.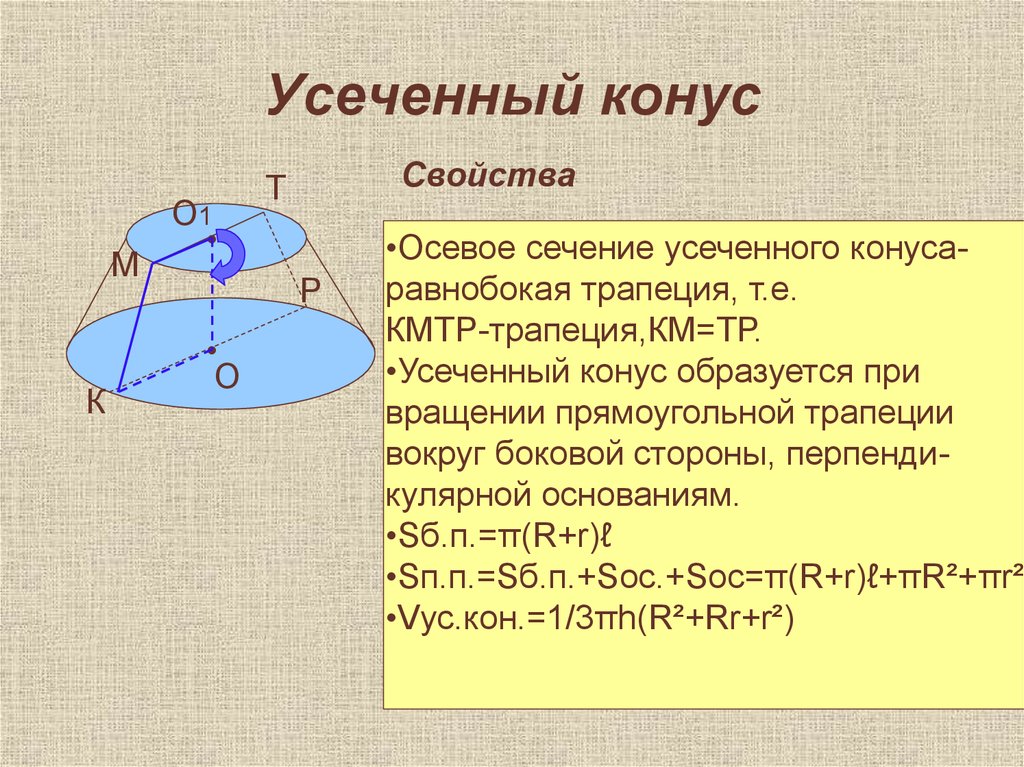 Конусностью называется отношение разности диаметров конуса к его длине. Обозначим конусность буквой K, тогда
Конусностью называется отношение разности диаметров конуса к его длине. Обозначим конусность буквой K, тогда
Если конус имеет размеры: D =80 мм, d = 70 мм и l = 100 мм, то согласно формуле (10):
Это значит, что на длине 10 мм диаметр конуса уменьшается на 1 мм или на каждый миллиметр длины конуса разница между его диаметрами изменяется на
Иногда на чертеже вместо угла конуса указывается уклон конуса . Уклон конуса показывает, в какой мере отклоняется образующая конуса от его оси.
Уклон конуса определяется по формуле
где tg α — уклон конуса;
l — высота конуса в мм.
Пользуясь формулой (11), можно при помощи тригонометрических таблиц определить угол а уклона конуса.
Пример 6. Дано D = 80 мм; d=70мм; l= 100 мм. По формуле (11) имеем По таблице тангенсов находим величину, наиболее близкую к tg α = 0,05, т. е. tg α = 0,049, которому соответствует угол уклона конуса α = 2°50″. Следовательно, угол конуса 2α = 2·2°50″ = 5°40″.
Уклон конуса и конусность обычно выражают простой дробью, например: 1: 10; 1: 50, или десятичной дробью, например, 0,1; 0,05; 0,02 и т.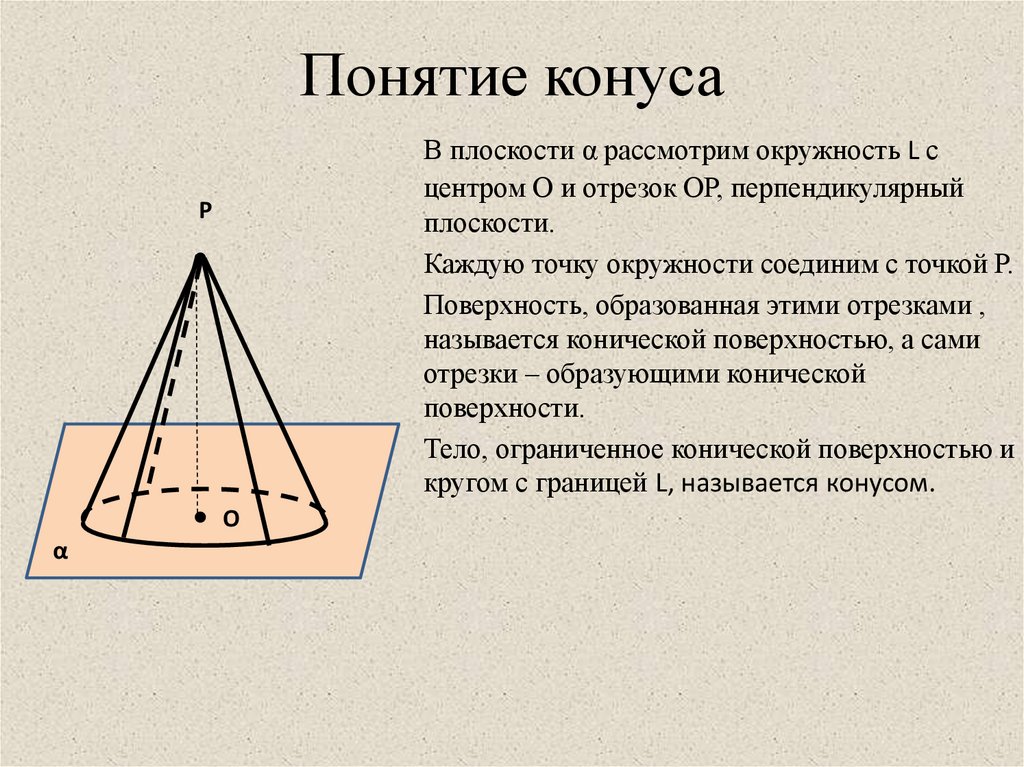 д.
д.
2. Способы получения конических поверхностей на токарном станке
На токарном станке обработка конических поверхностей производится одним из следующих способов:
а) поворотом верхней части суппорта;
б) поперечным смещением корпуса задней бабки;
в) с помощью конусной линейки;
г) с помощью широкого резца.
3. Обработка конических поверхностей поворотом верхней части суппорта
При изготовлении на токарном станке коротких наружных и внутренних конических поверхностей с большим углом уклона нужно повернуть верхнюю часть суппорта относительно оси станка под углом α уклона конуса (см. рис. 204). При таком способе работы подачу можно производить только от руки, вращая рукоятку ходового винта верхней части суппорта, и лишь в наиболее современных токарных станках имеется механическая подача верхней части суппорта.
Для установки верхней части суппорта 1 на требуемый угол можно использовать деления, нанесенные на фланце 2 поворотной части суппорта (рис. 204). Если угол α уклона конуса задан по чертежу, то верхнюю часть суппорта повертывают вместе с его поворотной частью на требуемое число делений, обозначающих градусы. Число делений отсчитывают относительно риски, нанесенной на нижней части суппорта.
204). Если угол α уклона конуса задан по чертежу, то верхнюю часть суппорта повертывают вместе с его поворотной частью на требуемое число делений, обозначающих градусы. Число делений отсчитывают относительно риски, нанесенной на нижней части суппорта.
Если на чертеже угол α не дан, а указаны больший и меньший диаметры конуса и длина его конической части, то величину угла поворота суппорта определяют по формуле (11)
Пример 7. Даны диаметры конуса D = 80 мм, d = 66 мм, длина конуса l = 112 мм. Имеем: По таблице тангенсов находим приближенно: а = 3°35″. Следовательно, верхнюю часть суппорта необходимо повернуть на 3°35″.
Способ обтачивания конических поверхностей поворотом верхней части суппорта имеет следующие недостатки: он допускает обычно применение только ручной подачи, что отражается на производительности труда и чистоте обработанной поверхности; позволяет обтачивать сравнительно короткие конические поверхности, ограниченные длиной хода верхней части суппорта.
4. Обработка конических поверхностей способом поперечного смещения корпуса задней бабки
Для получения конической поверхности на токарном станке необходимо при вращении заготовки вершину резца перемещать не параллельно, а под некоторым углом к оси центров. Этот угол должен равняться углу α уклона конуса. Наиболее простой способ получения угла между осью центров и направлением подачи — сместить линию центров, сдвинув задний центр в поперечном направлении. Путем смещения заднего центра в сторону резца (на себя) в результате обтачивания получают конус, у которого большее основание направлено в сторону передней бабки; при смещении заднего центра в противоположную сторону, т. е. от резца (от себя), большее основание конуса окажется со стороны задней бабки (рис. 205).
Смещение корпуса задней бабки определяют по формуле
где S — смещение корпуса задней бабки от оси шпинделя передней бабки в мм;
D — диаметр большого основания конуса в мм;
d — диаметр малого основания конуса в мм;
L — длина всей детали или расстояние между центрами в мм;
l — длина конической части детали в мм.
Пример 8. Определить смещение центра задней бабки для обтачивания усеченного конуса, если D = 100 мм, d = 80 мм, L = 300 мм и l = 200мм. По формуле (12) находим:
Смещение корпуса задней бабки производят, используя деления 1 (рис 206), нанесенные на торце опорной плиты, и риску 2 на торце корпуса задней бабки.
Если на торце плиты делений нет, то смещают корпус задней бабки, пользуясь измерительной линейкой, как показано на рис. 207.
Преимущество обработки конических поверхностей путем смещения корпуса задней бабки заключается в том, что этим способом можно обтачивать конусы большой длины и вести обтачивание с механической подачей.
Недостатки
этого способа: невозможность растачивать конические отверстия; потеря времени на перестановку задней бабки; возможность обрабатывать лишь пологие конусы; перекос центров в центровых отверстиях, что приводит к быстрому и неравномерному износу центров и центровых отверстий и служит причиной брака при вторичной установке детали в этих же центровых отверстиях.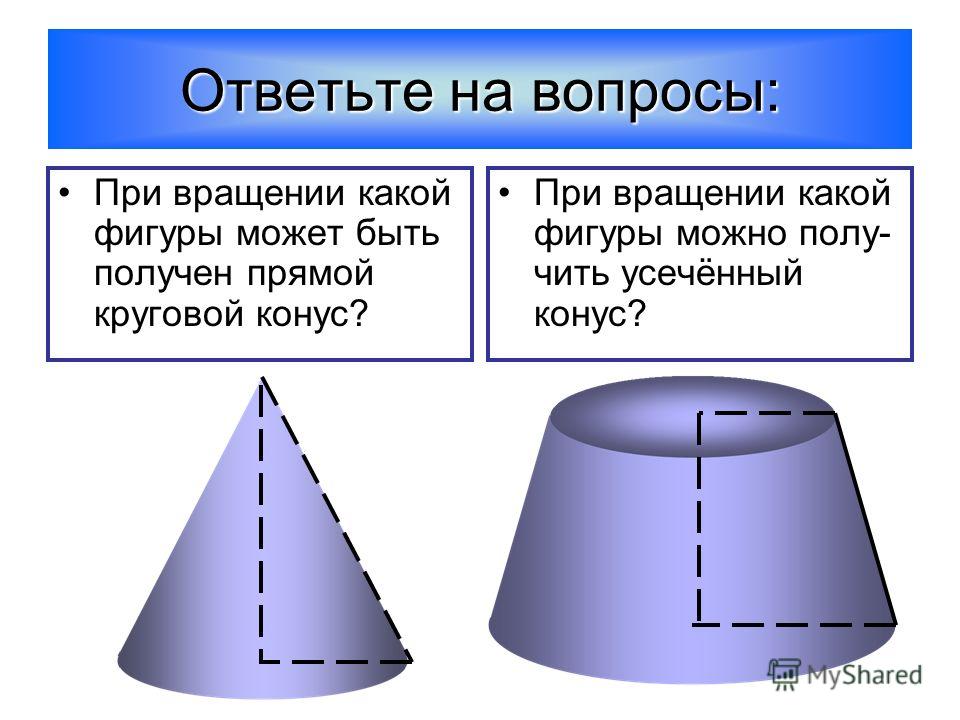
Неравномерного износа центровых отверстий можно избежать, если вместо обычного применять специальный шаровой центр (рис. 208). Такие центры используют преимущественно при обработке точных конусов.
5. Обработка конических поверхностей с применением конусной линейки
Для обработки конических поверхностей с углом уклона а до 10-12° современные токарные станки обычно имеют особое приспособление, называемое конусной линейкой. Схема обработки конуса с применением конусной линейки приводится на рис. 209.
К станине станка прикреплена плита 11, на которой установлена конусная линейка 9. Линейку можно поворачивать вокруг пальца 8 под требуемым углом а к оси обрабатываемой детали. Для закрепления линейки в требуемом положении служат два болта 4 и 10. По линейке свободно скользит ползун 7, соединяющийся с нижней поперечной частью 12 суппорта при помощи тяги 5 и зажима 6. Чтобы эта часть суппорта могла свободно скользить по направляющим, ее отсоединяют от каретки 3, вывинчивая поперечный винт или отсоединяя от суппорта его гайку.
Если сообщить каретке продольную подачу, то ползун 7, захватываемый тягой 5, начнет перемещаться вдоль линейки 9. Так как ползун скреплен с поперечными салазками суппорта, то они вместе с резцом будут перемещаться параллельно линейке 9. Благодаря этому резец будет обрабатывать коническую поверхность с углом уклона, равным углу α поворота конусной линейки.
После каждого прохода резец устанавливают на глубину резания с помощью рукоятки 1 верхней части 2 суппорта. Эта часть суппорта должна быть повернута на 90° относительно нормального положения, т. е. так, как это показано на рис. 209.
Если даны диаметры оснований конуса D и d и его длина l, то угол поворота линейки можно найти по формуле (11).
Подсчитав величину tg α, легко определить значение угла α по таблице тангенсов.
Применение конусной линейки имеет ряд преимуществ:
1) наладка линейки удобна и производится быстро;
2) при переходе к обработке конусов не требуется нарушать нормальную наладку станка, т. е. не нужно смещать корпус задней бабки; центры станка остаются в нормальном положении, т. е. на одной оси, благодаря чему центровые отверстия в детали и центры станка не срабатываются;
е. не нужно смещать корпус задней бабки; центры станка остаются в нормальном положении, т. е. на одной оси, благодаря чему центровые отверстия в детали и центры станка не срабатываются;
3) при помощи конусной линейки можно не только обтачивать наружные конические поверхности, но и растачивать конические отверстия;
4) возможна работа е продольным самоходом, что увеличивает производительность труда и улучшает качество обработки.
Недостатком конусной линейки является необходимость отсоединять салазки суппорта от винта поперечной подачи. Этот недостаток устранен в конструкции некоторых токарных станков, у которых винт не связан жестко со своим маховичком и зубчатыми колесами поперечного самохода.
6. Обработка конических поверхностей широким резцом
Обработку конических поверхностей (наружных и внутренних) с небольшой длиной конуса можно производить широким резцом с углом в плане, соответствующим углу α уклона конуса (рис. 210). Подача резца может быть продольная и поперечная.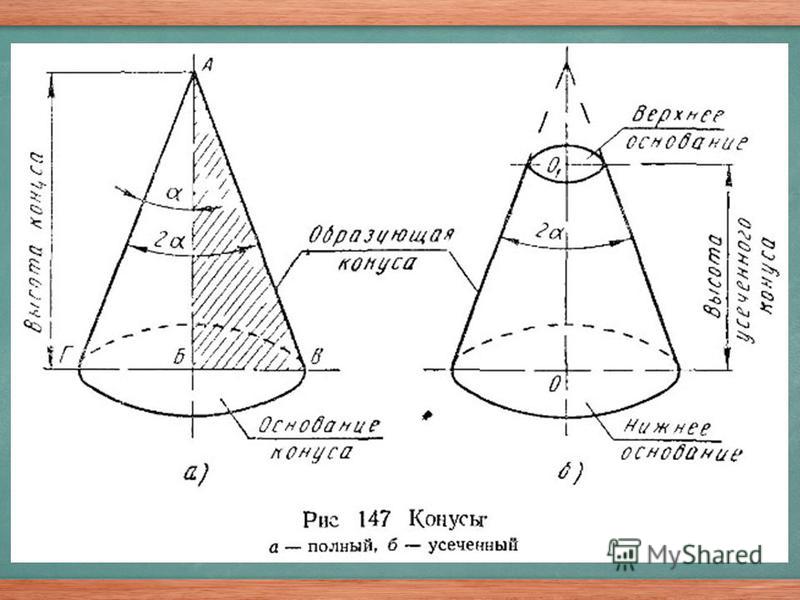
Однако использование широкого резца на обычных станках возможно только при длине конуса, не превышающей примерно 20 мм. Применять более широкие резцы можно лишь на особо жестких станках и деталях, если это не вызывает вибрации резца и обрабатываемой детали.
7. Растачивание и развертывание конических отверстий
Обработка конических отверстий является одной из наиболее трудных токарных работ; она значительно труднее, чем обработка наружных конусов.
Обработку конических отверстий на токарных станках в большинстве случаев производят растачиванием резцом с поворотом верхней части суппорта и реже с помощью конусной линейки. Все подсчеты, связанные с поворотом верхней части суппорта или конусной линейки, выполняются так же, как при обтачивании наружных конических поверхностей.
Если отверстие должно быть в сплошном материале, то сначала сверлят цилиндрическое отверстие, которое затем растачивают резцом на конус или обрабатывают коническими зенкерами и развертками.
Чтобы ускорить растачивание или развертывание, следует предварительно просверлить отверстие сверлом, диаметр d, которого на 1-2 мм меньше диаметра малого основания конуса (рис. 211, а). После этого рассверливают отверстие одним (рис. 211, б) или двумя (рис. 211, в) сверлами для получения ступеней.
После чистового растачивания конуса его развертывают конической разверткой соответствующей конусности. Для конусов с небольшой конусностью выгоднее производить обработку конических отверстий непосредственно после сверления набором специальных разверток, как показано на рис. 212.
8. Режимы резания при обработке отверстий коническими развертками
Конические развертки работают в более тяжелых условиях, чем цилиндрические: в то время как цилиндрические развертки снимают незначительный припуск небольшими режущими кромками, конические развертки режут всей длиной их режущих кромок, расположенных на образующей конуса. Поэтому при работе коническими развертками применяют подачи и скорости резания меньше, чем при работе цилиндрическими развертками.
При обработке отверстий коническими развертками подачу производят вручную, вращая маховичок задней бабки. Необходимо следить за тем, чтобы пиноль задней бабки перемещалась равномерно.
Подачи при развертывании стали 0,1-0,2 мм/об, при развертывании чугуна 0,2-0,4 мм/об.
Скорость резания при развертывании конических отверстий развертками из быстрорежущей стали 6-10 м/мин.
Для облегчения работы конических разверток и получения чистой и гладкой поверхности следует применять охлаждение. При обработке стали и чугуна применяют эмульсию или сульфофрезол.
9. Измерение конических поверхностей
Поверхности конусов проверяют шаблонами и калибрами; измерение и одновременно проверку углов конуса производят угломерами. На рис. 213 показан способ проверки конуса с помощью шаблона.
Наружные и внутренние углы различных деталей можно измерять универсальным угломером (рис. 214). Он состоит из основания 1, На котором на дуге 130 нанесена основная шкала. С основанием 1 жестко скреплена линейка 5. По дуге основания перемещается сектор 4, несущий нониус 3. К сектору 4 посредством державки 7 может быть прикреплен угольник 2, в котором, в свою очередь, закрепляется съемная линейка 5. Угольник 2 и съемная линейка 5 имеют возможность перемещаться по грани сектора 4.
По дуге основания перемещается сектор 4, несущий нониус 3. К сектору 4 посредством державки 7 может быть прикреплен угольник 2, в котором, в свою очередь, закрепляется съемная линейка 5. Угольник 2 и съемная линейка 5 имеют возможность перемещаться по грани сектора 4.
Путем различных комбинаций в установке измерительных деталей угломера можно производить измерение углов от 0 до 320°. Величина отсчета по нониусу 2″. Отсчет, полученный при измерении углов, производится по шкале и нониусу (рис. 215) следующим образом: нулевой штрих нониуса показывает число градусов, а штрих нониуса, совпадающий со штрихом шкалы основания, — число минут. На рис. 215 со штрихом шкалы основания совпадает 11-й штрих нониуса, что означает 2″Х 11 = 22″. Следовательно, угол в данном случае равен 76°22″.
На рис. 216 показаны комбинации измерительных деталей универсального угломера, позволяющие производить измерение различных углов от 0 до 320°.
Для более точной проверки конусов в серийном производстве применяют специальные калибры. На рис. 217, а показан кониче-ский калибр-втулка для проверки наружных конусов, а на рис. 217, б-конический калибр-пробка для проверки конических отверстий.
На рис. 217, а показан кониче-ский калибр-втулка для проверки наружных конусов, а на рис. 217, б-конический калибр-пробка для проверки конических отверстий.
На калибрах делаются уступы 1 и 2 на торцах или наносятся риски 3, служащие для определения точности проверяемых поверхностей.
На. рис. 218 приводится пример проверки конического отверстия калибром-пробкой.
Для проверки отверстия калибр (см. рис. 218), имеющий уступ 1 на определенном расстоянии от торца 2 и две риски 3, вводят с легким нажимом в отверстие и проверяют, нет ли качания калибра в отверстии. Отсутствие качания показывает, что угол конуса правилен. Убедившись, что угол конуса правилен, приступают к проверке его размера. Для этого наблюдают, до какого места калибр войдет в проверяемую деталь. Если конец конуса детали совпадает с левым торцом уступа 1 или с одной из рисок 3 или находится между рисками, то размеры конуса правильны. Но может случиться, что калибр войдет в деталь настолько глубоко, что обе риски 3 войдут в отверстие или оба торца уступа 1 выйдут из него наружу. Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.
Это показывает, что диаметр отверстия больше заданного. Если, наоборот, обе риски окажутся вне отверстия или ни один из торцов уступа не выйдет из него, то диаметр отверстия меньше требуемого.
Для точной проверки конусности применяют следующий способ. На измеряемой поверхности детали или калибра проводят мелом или карандашом две-три линии вдоль образующей конуса, затем вставляют или надевают калибр на деталь и повертывают его на часть оборота. Если линии сотрутся неравномерно, это значит, что конус детали обработан неточно и необходимо его исправить. Стирание линий по концам калибра говорит о неправильной конусности; стирание линий в средней части калибра показывает, что конус имеет небольшую вогнутость, причиной чего обычно является неточное расположение вершины резца по высоте центров. Вместо меловых линий можно нанести на всю коническую поверхность детали или калибра тонкий слой специальной краски (синьки). Такой способ дает большую точность измерения.
10. Брак при обработке конических поверхностей и меры его предупреждения
При обработке конических поверхностей, помимо упомянутых видов брака для цилиндрических поверхностей, дополнительно возможны следующие виды брака:
1) неправильная конусность;
2) отклонения в размерах конуса;
3) отклонения в размерах диаметров оснований при правильной конусности;
4) непрямолинейность образующей конической поверхности.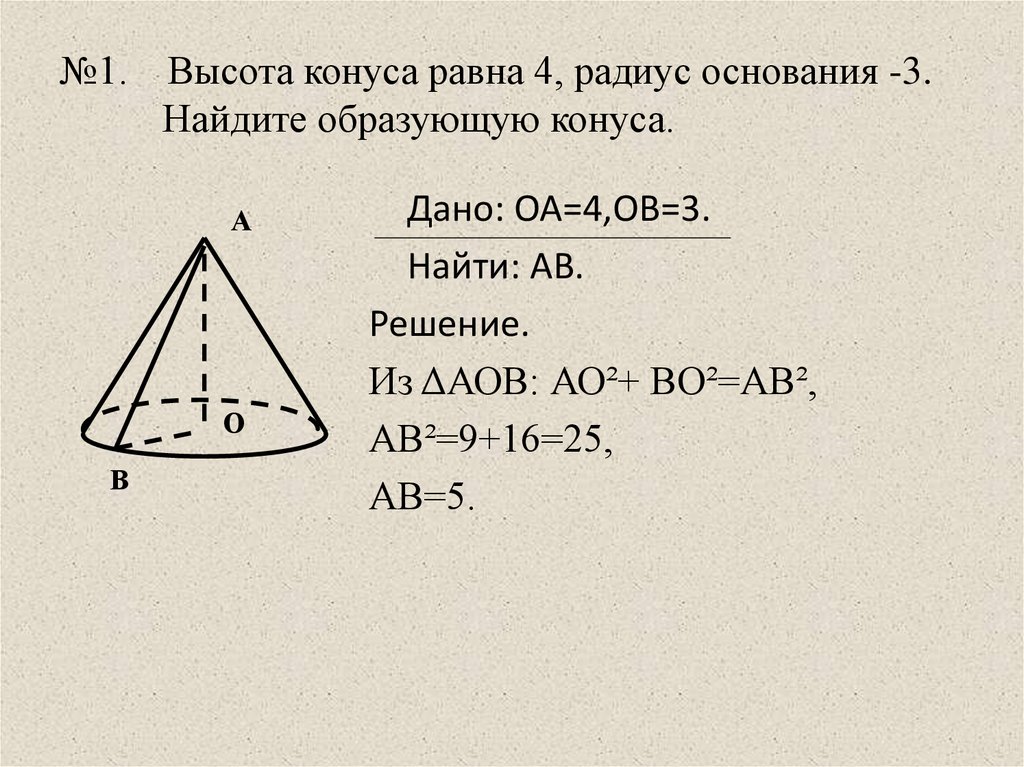
1. Неправильная конусность получается главным образом вследствие неточного смещения корпуса задней бабки, неточного поворота верхней части суппорта, неправильной установки конусной линейки, неправильной заточки или установки широкого резца. Следовательно, точной установкой корпуса задней бабки, верхней части суппорта или конусной линейки перед началом обработки можно брак предупредить. Этот вид брака исправим только в том случае, если ошибка во всей длине конуса направлена в тело детали, т. е. все диаметры у втулки меньше, а у конического стержня больше требуемых.
2. Неправильный размер конуса при правильном угле его, т. е. неправильная величина диаметров по всей длине конуса, получается, если снято недостаточно или слишком много материала. Предупредить брак можно только внимательной установкой глубины резания по лимбу на чистовых проходах. Брак исправим, если снято недостаточно материала.
3. Может получиться, что при правильной конусности и точных размерах одного конца конуса диаметр второго конца неправилен. Единственной причиной является несоблюдение требуемой длины всего конического участка детали. Брак исправим, если деталь излишне длинна. Чтобы избежать этого вида брака, необходимо перед обработкой конуса тщательно проверить его длину.
Единственной причиной является несоблюдение требуемой длины всего конического участка детали. Брак исправим, если деталь излишне длинна. Чтобы избежать этого вида брака, необходимо перед обработкой конуса тщательно проверить его длину.
4. Непрямолинейность образующей обрабатываемого конуса получается при установке резца выше (рис. 219, б) или ниже (рис. 219, в) центра (на этих рисунках для большей наглядности искажения образующей конуса показаны в сильно преувеличенном виде). Таким образом, и этот вид брака является результатом невнимательной работы токаря.
Контрольные вопросы 1. Какими способами можно обработать конические поверхности на токарных станках?
2. В каких случаях рекомендуется делать поворот верхней части суппорта?
3. Как вычисляется угол поворота верхней части суппорта для обтачивания конуса?
4. Как проверяется правильность поворота верхней части суппорта?
5. Как проверить смещение корпуса задней бабки?.Как вычислить величину смещения?
6. Из каких основных элементов состоит конусная линейка? Как настроить конусную линейку на данную деталь?
Из каких основных элементов состоит конусная линейка? Как настроить конусную линейку на данную деталь?
7. Установите на универсальном угломере следующие углы: 50°25″; 45°50″; 75°35″.
8. Какими инструментами измеряют конические поверхности?
9. Для чего на конических калибрах сделаны уступы или риски и как ими пользоваться?
10. Перечислите виды брака при обработке конических поверхностей. Как их избежать?
) — тело в евклидовом пространстве , полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник , такой конус является пирамидой .
Энциклопедичный YouTube
Связанные определения
- Отрезок, соединяющий вершину и границу основания, называется образующей конуса .

- Объединение образующих конуса называется образующей (или боковой ) поверхностью конуса . Образующая поверхность конуса является конической поверхностью .
- Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса .
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
- Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым . При этом прямая, соединяющая вершину и центр основания, называется осью конуса .
- Косой (наклонный ) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
- Круговой конус — конус, основание которого является кругом.
- Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой , содержащей катет (эта прямая представляет собой ось конуса).

- Конус, опирающийся на эллипс , параболу или гиперболу , называют соответственно эллиптическим , параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
- Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом , или коническим слоем .
Свойства
- Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
V = 1 3 S H , {\displaystyle V={1 \over 3}SH,}
где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
- Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
 {2}H.}
{2}H.}- Для усечённого конуса (не обязательно прямого и кругового) объём равен:
V = 1 3 (H S 2 − h S 1) , {\displaystyle V={1 \over 3}(HS_{2}-hS_{1}),}
где S 1 и S 2 — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
- Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом , параболой или гиперболой , в зависимости от положения секущей плоскости).
Уравнение конуса
Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ , вершиной в начале координат и осью, совпадающей с осью Oz :
- В сферической системе координат с координатами (r , φ, θ) :
θ = Θ . {\displaystyle \theta =\Theta .}
- В цилиндрической системе координат с координатами (r , φ, z ) :
z = r ⋅ ctg Θ {\displaystyle z=r\cdot \operatorname {ctg} \Theta } или r = z ⋅ tg Θ .
 {n}f(x,y,z)}
для любого действительного числа α
.
{n}f(x,y,z)}
для любого действительного числа α
.Развёртка
Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.
В создании развёртки конуса могут использоваться всего две величины r и l . Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l , являющаяся радиусом сектора боковой поверхности. Угол сектора φ {\displaystyle \varphi } в развёртке боковой поверхности конуса определяется по формуле:
φ = 360°·(r /l ) .
Тема урока: Конус и его элементы
Цели урока: ввести понятия конуса, образующей, высотой и основания; ввести понятие площади боковой поверхности конуса как площади ее развертки; сформировать навык решения задач на нахождение элементов конуса.

Тип урока: комбинированный.
Оборудование: ПК, мультимедийный проектор, интерактивная доска, модели конусов.
Ход урока:
Проверка домашнего задания у доски.
Самостоятельная работа (Приложение 1.)
Объяснение нового материала.
Понятия конуса, его элементов(вершина, ось, образующие, основание, боковая поверхность). Изображение конуса.
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга,- вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания (рис. 1).
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.
Конус называется прямым , если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
 Сечение конуса разными плоскостями.
Сечение конуса разными плоскостями. Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 3). В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса (рис. 4).
Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность — по окружности с центром на оси конуса.
Доказательство. Пусть — плоскость, параллельная плоскости основания конуса и пересекающая конус (рис.5). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость
Формулы объема геометрических фигур. Формулы объема и площади поверхности. Конус
Содержание
- Онлайн-калькулятор
- Связанные определения для конуса
- Формула образующей конуса
- Объем конуса
- Объем конуса через радиус
- Объем усеченного конуса
- Первый способ вычисления объема усеченного конуса
- Второй способ вычисления объема усеченного конуса
- Элементы конуса
- Формула площади боковой поверхности конуса
- Объемы фигур
- Основные свойства кругового конуса
- Примеры задач
- Введите радиус основания и высоту конуса
- Формула площади основания конуса
- Пример расчета
- Формула площади конуса
Онлайн-калькулятор
Общее определение конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной.
Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
Связанные определения для конуса
Образующая конуса. Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
Образующая поверхность конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Коническая поверхность. Образующая поверхность конуса является конической поверхностью.
Высота конуса (H). Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
Угол раствора конуса. Угол раствора конуса – угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
Прямой конус. Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
Косой (наклонный) конус. Косой (наклонный) конус – конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.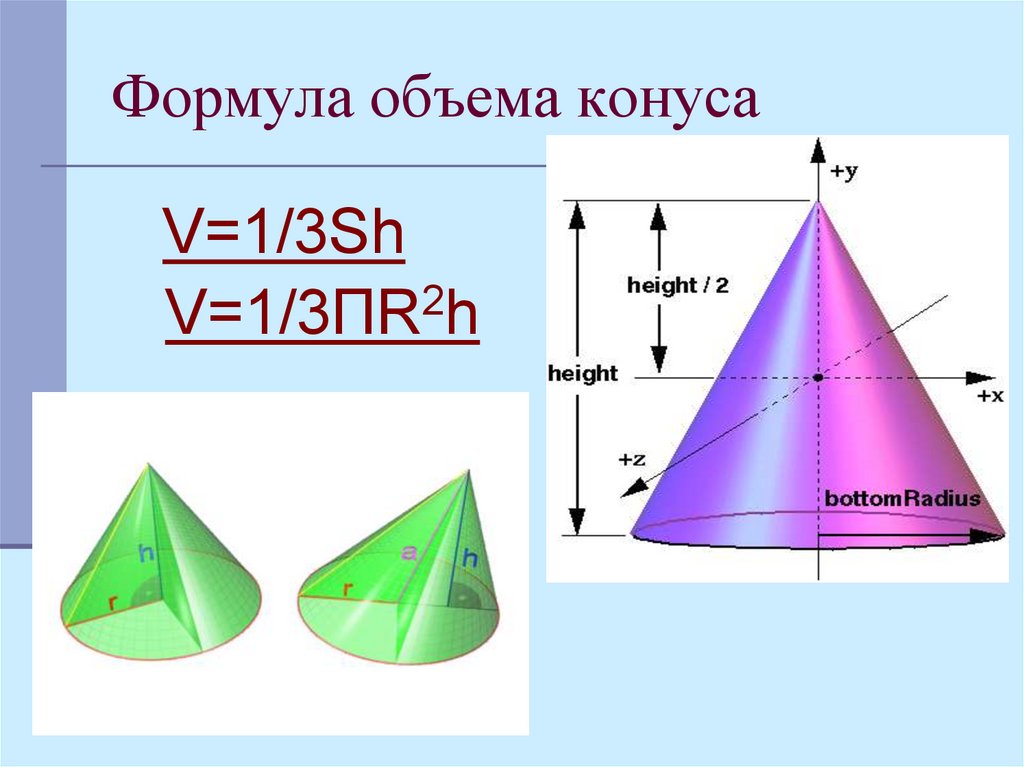
Круговой конус. Круговой конус – конус, основание которого является кругом.
Прямой круговой конус. Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
Эллиптическим конус. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
Усечённый конус. Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Формула образующей конуса
Образующую конуса можно найти, зная ее высоту H и радиус R:
L = √H2 + R2
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
| V = | 1 | π R2 h |
| 3 |
| V = | 1 | So h |
| 3 |
где V – объем конуса,
So – площадь основания конуса,
R – радиус основания конуса,
h – высота конуса,
π = 3.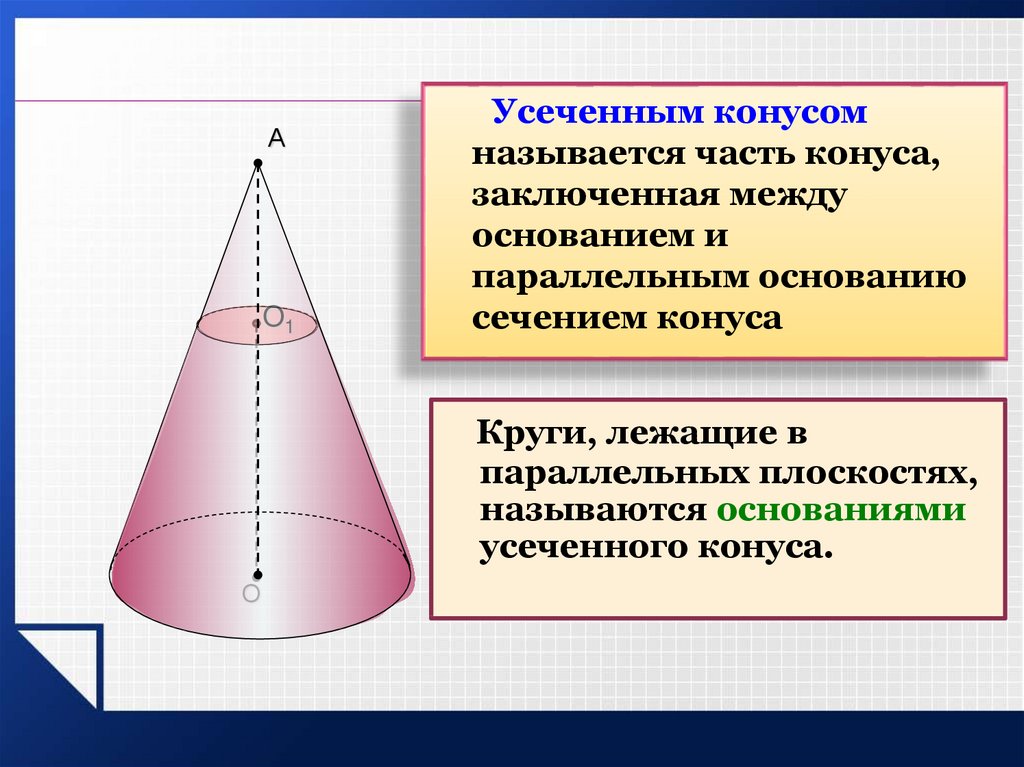 141592.
141592.
Объем конуса через радиус
Данный треугольник для получения конуса должен вращаться вокруг одного из своих катетов, который является не только осью вращения, но и высотой конуса. Второй же катет становится радиусом полученной в результате вращения окружности-основания конуса, а гипотенуза будет апофемой (высотой опущенной под прямым углом к линии окружности, а не центру).
Технически взаимосвязь конуса с цилиндром идентична взаимосвязи пирамиды с кубом (параллелепипедом), единственное, что вывод формулы проходит через отношения интегралов их сферических углов, но тем не менее, он точно также как и пирамида занимает одну треть цилиндра, в который он может быть вписан.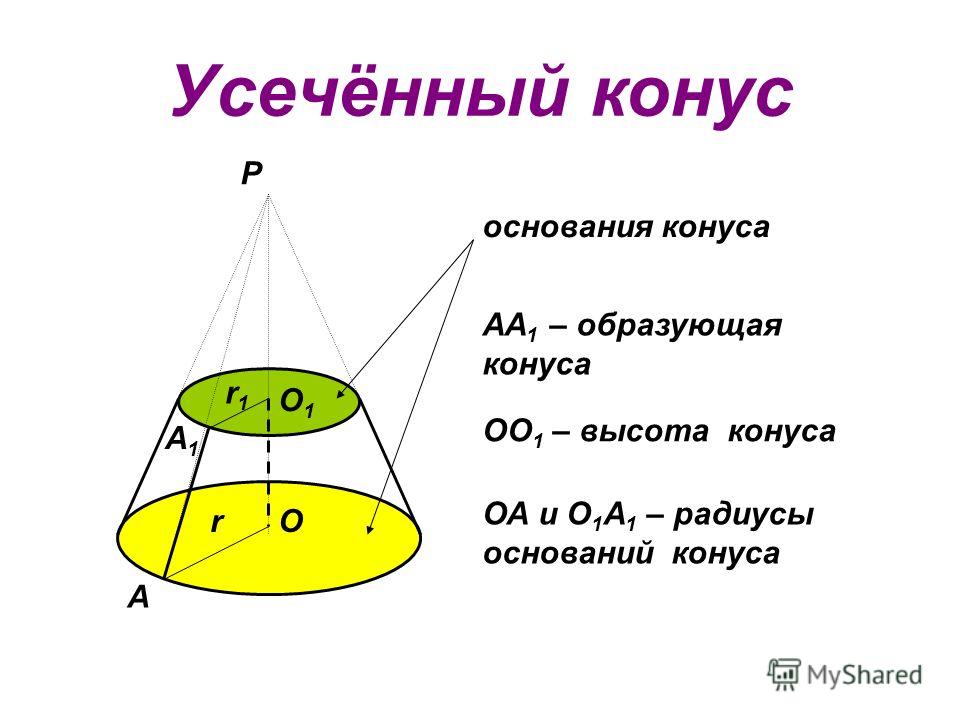
Поэтому его объем равен произведению площади основания на высоту, деленному на три, или произведению числом π на квадрат радиуса и высоту, деленному на три.
Объем усеченного конуса
Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.
Первый способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
[ LARGE V = frac{1}{3} left( Hcdot S_2 + h cdot s_1 right) ]
где:
V – объем конуса
h – расстояния от плоскости верхнего основания до вершины
H – расстояния от плоскости нижнего основания до вершины
S1 – площадь верхнего (ближнего к вершине) основания
S2 – площадь нижнего основания
Второй способ вычисления объема усеченного конуса
Объем усеченного конуса вычисляется по формуле:
[ LARGE V = frac{1}{3} pi h left( R^2 + R cdot r + r^2 right) ]
где:
V – объем конуса
h – высота конуса
R – радиус нижнего основания
r – радиус верхнего основания
Элементы конуса
Определение. Вершина конуса – это точка (K), из которой исходят лучи.
Вершина конуса – это точка (K), из которой исходят лучи.
Определение. Основание конуса – это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):
L2 = R2 + H2
Определение. Направляющая конуса – это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.
Поверхность конуса состоит из боковой поверхности и основания конуса.
Определение. Высота конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С) конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
| C = | D | и C = | D – d |
| H | h |
где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями.
Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:
| α = 2arctg | R |
| H |
где R – радиус основы, а H – высота конуса.
Определение. Осевое сечение конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.
Определение. Касательная плоскость к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
Определение. Прямой конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса:
| V = | 1 | πHR2 |
| 3 |
где R – радиус основы, а H – высота конуса.
Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:
Sb = πRL
Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:
Sp = πRL + πR2
Определение. Косой (наклонный) конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса:
| V = | 1 | SH |
| 3 |
где S – площадь основы, а H – высота конуса.
Определение. Усеченный конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса:
| V = | 1 | (S2H – S1h) |
| 3 |
где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:
Sбок.пов = πRL
Объемы фигур
Основные свойства кругового конуса
1. Все образующие прямого кругового конуса равны между собой.
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис.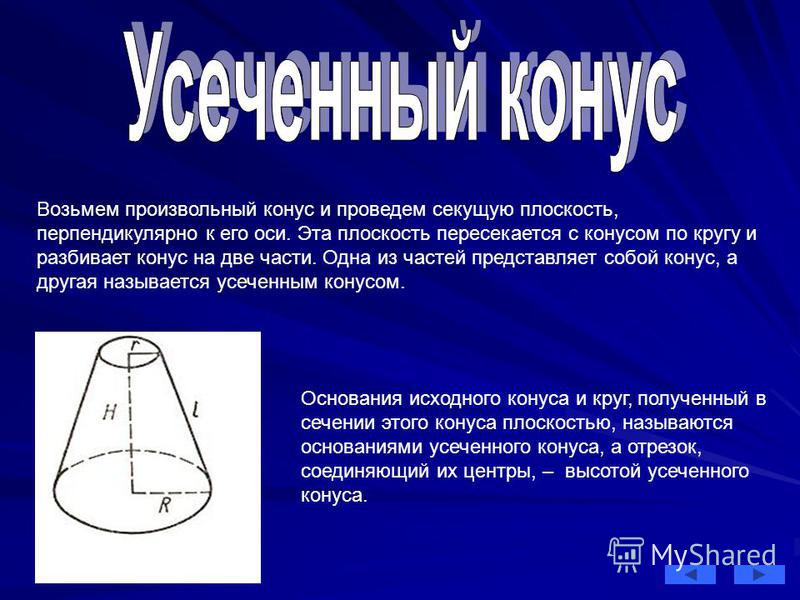 4).
4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.
Примеры задач
Задание 1
Найдите объем конуса, если известна площадь его основания – 50,24 см2, а также, высота – 9 см.
Решение:
Применим первую формулу, подставив в нее заданные значения:
Задание 2
Высота конуса равна 7 см, а его радиус – 4 см. Найдите объем фигуры.
Решение:
Воспользовавшись второй, более расширенной, формулой получаем:
Введите радиус основания и высоту конуса
Конус – геометрическое тело, которое состоит из круга (основание конуса), точки, не лежащей в плоскости этого круга (вершина конуса), и всех точек, соединяющих вершину конуса с точками основания.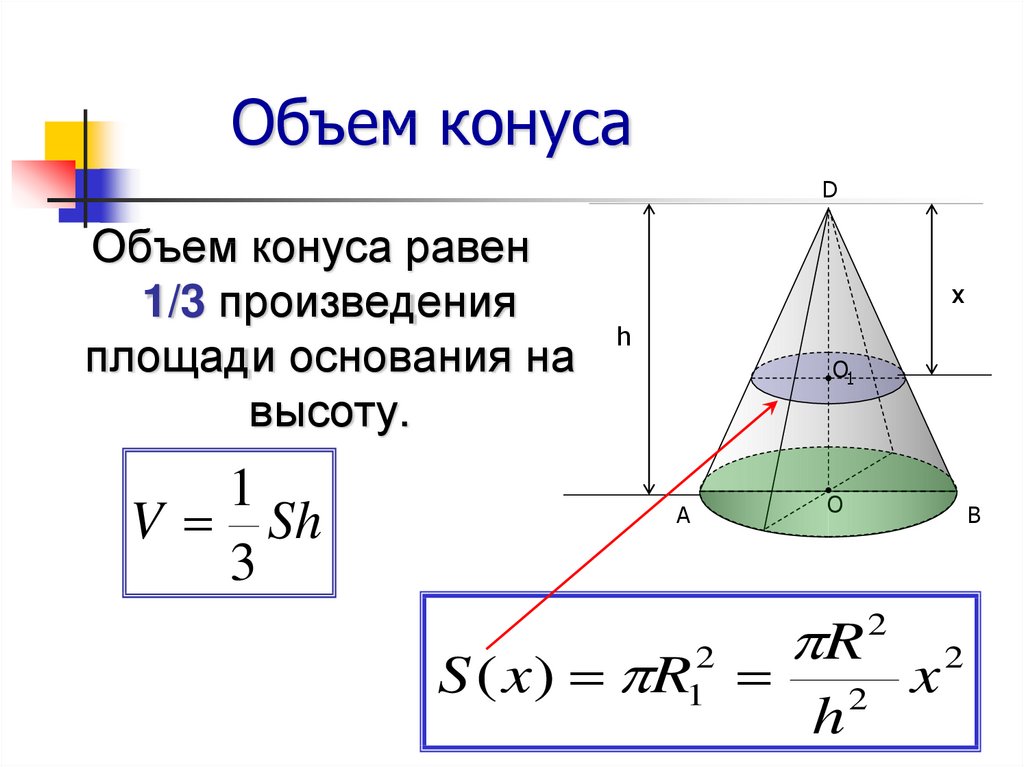 3}
3}
Формула площади конуса
Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:
S = Sбок.пов + Sосн = πRL + πR2
Источники
- https://studwork.org/spravochnik/matematika/obemy-figur/obem-konusa
- https://calcsbox.com/post/formula-obema-konusa.html
- http://worksbase.ru/matematika/formuly/37-konus.html
- https://ru.onlinemschool.com/math/formula/volume/
- https://allcalc.ru/node/36
- https://ru.onlinemschool.com/math/formula/cone/
- https://www.calc.ru/1430.html
- https://MicroExcel.ru/obyom-konusa/
- https://www.calc.ru/obyem-konusa.html
- https://mnogoformul.ru/obem-konusa-formula-i-raschet-onlayn
Конус — свойства, виды и формулы » Kupuk.net
Из огромного перечня математических заданий часто встречаются задачи, связанные с темой «Конус». На уроках геометрии школьники должны усвоить основные понятия и названия всех элементов этой фигуры и понять, как и по каким формулам производится расчет нужных параметров.
О данной геометрической фигуре пойдёт речь в сегодняшней статье.
Определение и элементы конуса
Под конусом понимают тело, состоящее из круга и точки, которая удалена от его поверхности на определённое расстояние.
При этом точка соединяется с основанием посредством проведения лучей, которые называются образующими. Линия, соединяющая центр круга с удалённой точкой, является высотой данной фигуры.
Обратите внимание! Также существует такое понятие, как ось конуса. Это линия, проходящая через его центр и совпадающая с высотой. Образующие строятся относительно оси.
Хотелось бы рассмотреть ещё несколько понятий по этой теме:
1. Под конусностью понимают отношение диаметра основания фигуры и её высоты:
Важно! Конусность отвечает за угол наклона образующих. Чем больше данный параметр, тем острее угол.
2. Осевое сечение предполагает наличие плоскости, которая будет рассекать фигуру, проходя через ось:
3.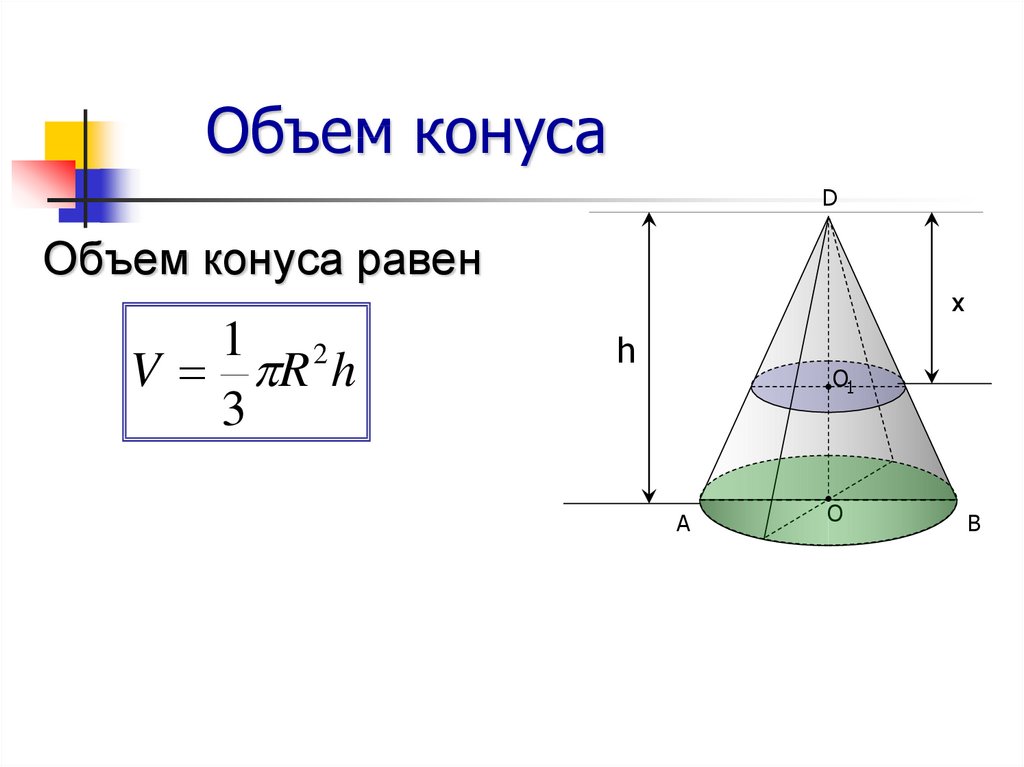 Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.
Касательная— это плоскость, которая соприкасается с образующей конуса. При этом важно, чтобы она была перпендикулярна осевому сечению.
Свойства кругового конуса
Выделяют несколько особенностей, которыми обладает фигура данного типа:
Образующие кругового конуса равны друг другу.
Чтобы найти центр тяжести фигуры, нужно её высоту поделить на четыре части.
Место пересечения плоскости сечения и основы образует параболу. Если через вершину тела провести плоскость сечения, то получится равнобедренный треугольник.
Интересный факт! Если вращать прямоугольный треугольник вокруг одного из катетов, то получится конус. При этом важно, чтобы угол вращения был не менее 360 градусов.
Общая формула объёма фигуры
Чтобы найти объём кругового конуса, необходимо умножить число Пи на его высоту, на радиус в квадрате и всё это произведение поделить на три:
Дополнительная информация! Чтобы узнать объём фигуры, нужно умножить площадь её основы на высоту и поделить на три:
Объём усечённого конуса
Это часть прямого конуса, которая находится в пространстве между основой и плоскостью, параллельной этому основанию. В общем виде выглядит следующим образом:
В общем виде выглядит следующим образом:
Объём данного тела можно вычислить по формуле:
Важно! S и S1 это площади соответствующих основ, которые равняются ПR2 и ПR12 При нахождении этих значений поможет онлайн калькулятор.
Площадь поверхности фигуры
Для вычисления данного параметра потребуется знать площадь боковой поверхности. Она равняется произведению числа π, радиуса и длины образующей.
Чтобы рассчитать площадь всей поверхности, нужно сложить площади его основы и боковой поверхности.
Площадь усечённого конуса
Для нахождения данного параметра нужно воспользоваться формулами:
площади боковой поверхности усечённого конуса Sбок;
полной площади усечённой фигуры Sпол, которая равна сумме площадей двух оснований и площади боковой поверхности:
Здесь l — длина образующей, а R и r — радиусы большего и меньшего оснований соответственно.
Уравнение конуса
Часто требуется при решении математических задач. Записывается в следующем виде:
где x0, y0,z0- координаты по соответствующим осям.
Таким образом, в данной статье были представлены основные сведения, которые могут понадобиться при решении задач на тему «Конус».
Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия
| Справочник по математике | Геометрия (Стереометрия) | Конусы |
| Конусы |
| Усеченные конусы |
| Объем, площади боковой и полной поверхностей конуса и усеченного конуса |
Конусы
Рассмотрим произвольную плоскость α, точку S, не лежащую на плоскости α, и перпендикуляр SO, опущенный из точки S на плоскость α (точка O – основание перпендикуляра).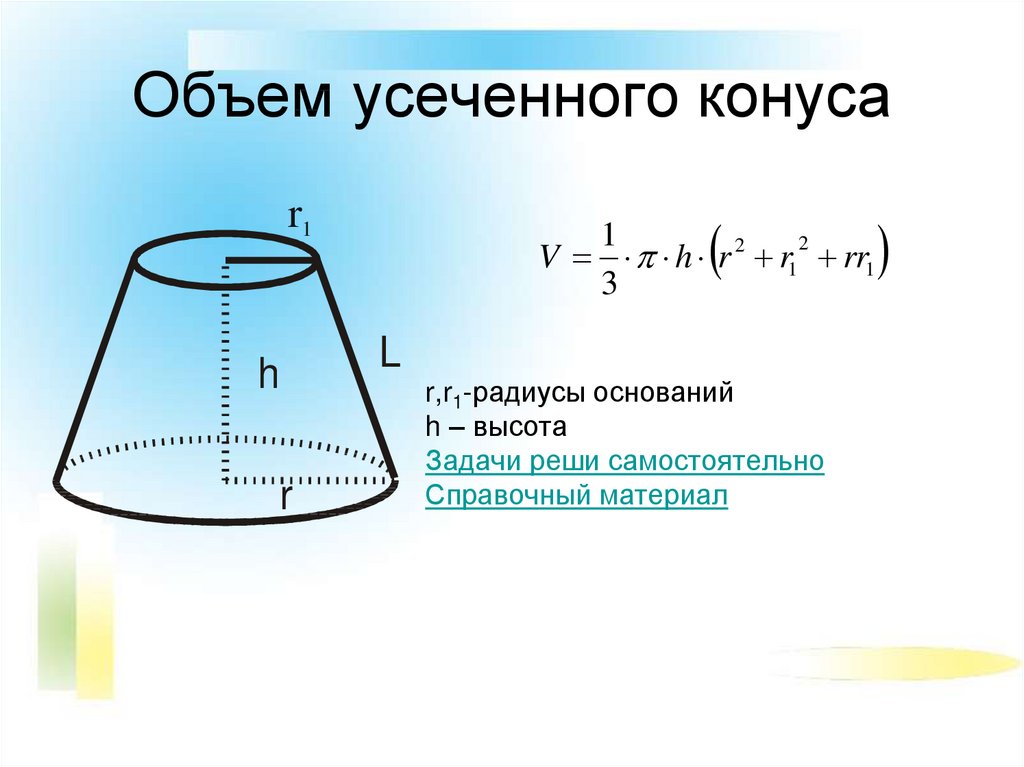 Рассмотрим также произвольный круг с центром в точке O, лежащий на плоскости α.
Рассмотрим также произвольный круг с центром в точке O, лежащий на плоскости α.
Определение 1. Конусом называют фигуру, состоящую из всех отрезков, соединяющих точку S с точками указанного круга с центром в точке O, лежащего на плоскости α (рис. 1).
Рис.1
Определение 2.
Точку S называют вершиной конуса. | |
Отрезок SO называют осью конуса. | |
Расстояние от точки S до плоскостиРасстояние от точки S до плоскости α (длину отрезка SO) называют высотой конуса. | |
Круг с центром в точке O, лежащий на плоскости α, называют основанием конуса, радиус этого круга называют радиусом основания конуса, а саму плоскость α называют плоскостью основания конуса. | |
Отрезки, соединяющие точку S с точками окружности называют образующими конуса. | |
Совокупность всех образующих конуса составляет боковую поверхность конуса (коническую поверхность). | |
Полная поверхность конуса состоит из основания конуса и его боковой поверхности. |
Замечание 1. Отрезок SO часто называют высотой конуса.
Замечание 2. Все образующие конуса имеют одинаковую длину. У конуса с высотой h и радиусом основания r длина образующих равна
Усеченные конусы
Рассмотрим конус с вершиной S, осью SO, радиусом основания r и высотой h. Плоскость β, параллельная параллельная плоскости основания конуса и расположенная на расстоянии h1 от вершины расстоянии h1 от вершины S, пересекает конус по кругу радиуса r1 с центром в точке O1 (рис. 2).
2).
Рис.2
Из подобия прямоугольных треугольников SOA и SO1A1 можно выразить радиус r1 через известные величины r, h и h1:
Таким образом, плоскость β делит конус на две части: конус с осью SO1 и радиусом основания r1, а также вторую часть, называемую усеченным конусом (рис. 3).
Рис.3
Усеченный конус ограничен двумя основаниями: кругом с центром в точке O радиуса r на плоскости α и кругом с центром в точке O1 радиуса r1 на плоскости β, а также боковой поверхностью усеченного конуса, которая представляет собой часть боковой поверхности исходного конуса, заключенную между плоскостями α и β. Полная поверхность усеченного конуса состоит из двух оснований усеченного конуса и его боковой поверхности. Часть каждой образующей исходного конуса, которая заключена между плоскостями α и β, называют образующей усеченного конуса. Например, на рисунке 3 одной из образующих усеченного конуса является отрезок AA1.
Часть каждой образующей исходного конуса, которая заключена между плоскостями α и β, называют образующей усеченного конуса. Например, на рисунке 3 одной из образующих усеченного конуса является отрезок AA1.
Высотой усеченного конуса называют расстояние между плоскостями расстояние между плоскостями оснований усеченного конуса. У усеченного конуса, изображенного на рисунке 2, высота равна h – h1.
Объем, площади боковой и полной поверхностей конуса и усеченного конуса
Введем следующие обозначения
| V | объем конуса (объем усеченного конуса) |
| Sбок | площадь боковой поверхности конуса (площадь боковой поверхности усеченного конуса) |
| Sполн | площадь полной поверхности конуса (площадь полной поверхности усеченного конуса) |
| Sосн | площадь основания конуса |
Sверх. осн осн | площадь верхнего основания усеченного конуса |
| Sнижн.осн | площадь нижнего основания усеченного конуса |
V объем конуса (объем усеченного конуса) |
Sбок площадь боковой поверхности конуса |
Sполн площадь полной поверхности конуса |
Sосн площадь основания конуса |
Sверх.осн площадь верхнего основания усеченного конуса |
Sнижн.осн площадь нижнего основания усеченного конуса |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности конуса, а также формулы для вычисления объема, площади боковой и полной поверхности усеченного конуса.
| Фигура | Рисунок | Формулы для объема, площади боковой и полной поверхности |
| Конус | Sосн = πr2, Sбок= πrl, Sполн = πr2 + πrl, где | |
| Усеченный конус | Sбок= π (r + r1)l , где l – длина образующей усеченного конуса. |
| Конус |
Формулы для объема, площади боковой и полной поверхности: Sосн = πr2, Sбок= πrl, Sполн = πr2 + πrl, где |
| Усеченный конус |
Формулы для объема, площади боковой и полной поверхности: , Sбок= π (r + r1)l , где l – длина образующей усеченного конуса. |
Замечание 3. Формула для вычисления объема конуса
может быть получена из формулы объема правильной n – угольной пирамиды
при помощи предельного перехода, когда число сторон правильной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
Замечание 4. Формула для вычисления объема усеченного конуса
может быть получена из формулы объема правильной усеченной n – угольной пирамиды
при помощи предельного перехода, когда число сторон правильной усеченной пирамиды n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
Однако доказательство этого факта выходит за рамки школьной программы.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Все формулы цилиндра конуса шара. Тела и поверхности вращения. Визуальный гид (2019)
Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.
Планиметрия — раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье — цилиндр.
Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже — коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец — знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.
Определение цилиндра как геометрической фигуры
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».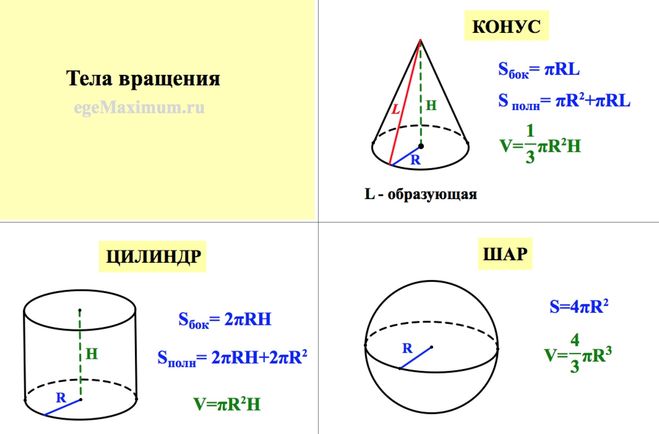
Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами — усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.
Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра — один из элементов данной геометрической фигуры. Другая её важная составляющая — рассмотренные выше круги. Называются они основаниями.
Виды цилиндров
Самый простой и распространённый вид цилиндра — круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр — наклонный.
Что такое поверхность вращения
Прямой круговой цилиндр, без сомнения — самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.
Допустим, имеется некая прямая a , расположенная вертикально. ABCD — прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a . Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения — прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.
В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр.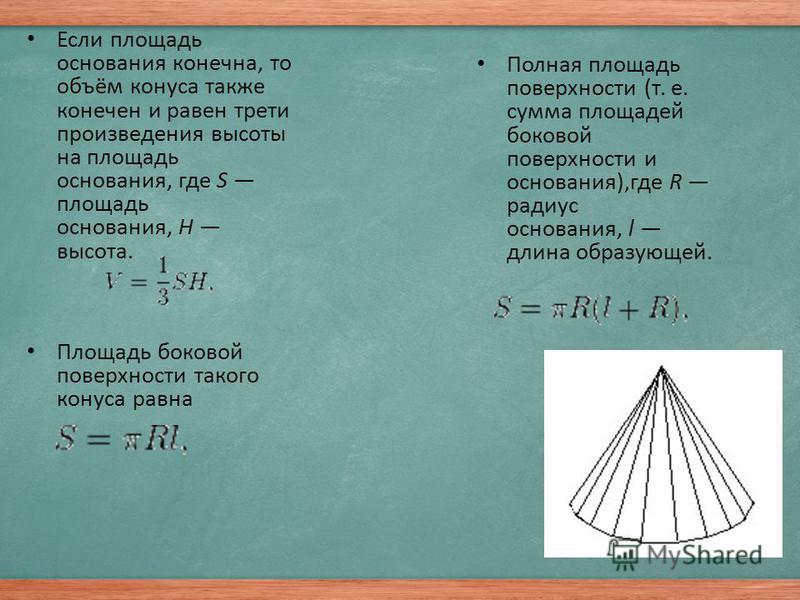 Вращая треугольник, можно получить конус, вращая полукруг — шар и т.д.
Вращая треугольник, можно получить конус, вращая полукруг — шар и т.д.
Площадь поверхности цилиндра
Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.
Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.
Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.
Определение объёма фигуры
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.
Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.
Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.
Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N . Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.
Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.
Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.
Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями — перпендикулярный отрезок, построенный между ними.
Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.
Как построить развёртку цилиндра
В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.
Следует учитывать, что рисунок приведен без учёта швов.
Отличия скошенного цилиндра
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.
На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.
Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.
Геометрические характеристики скошенного цилиндра
Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.
Цели урока:
- Образовательная: формирование знаний о формулах площадей поверхности цилиндра и конуса, умение применять их для решения задач, а также показать применение данных формул в практических ситуациях и на производстве.
- Воспитательная: развивать заинтересованность изучения математики, раскрывая практическую значимость изучаемого материала.
- Развивающая: формирование умений распознавать геометрические модели тел, применять математические знания в практических ситуациях, описанных условием задач.
Тип занятия: сообщение новых знаний.
Методы обучения: устный и практический контроль знаний.
Оборудование: плакаты, карточки для учащихся, карточки для лабораторно-практической работы, компьютер.
1. Организационный момент (1минута).
2. Сообщение целей и темы занятия , мотивация учебной деятельности (3 минуты). Учащиеся с помощью преподавателя формулируют тему и цель занятия. Преподаватель записывает тему на доске, учащиеся в тетрадях.
3. Актуализация знаний проводится по вариантам (1вариант – цилиндр, 2вариант – конус) (7-8 минут)(см. ниже).
4. Сообщение новых знаний (10 минут).
4. 1. Вывод формулы площади поверхности цилиндра.
Плакат 1. – Цилиндр вписан и описан в 4-х-ую призму.
Плакат 2. — Цилиндр вписан и описан в 6-х-ую призму.
Вывод: Если будем увеличивать количество граней призмы, то поверхность цилиндра будет максимально приближаться к граням призмы и на каком–то n – шаге произойдет совпадение поверхности цилиндра с призмой, т.е. совпадут их площади поверхностей.
Площадь поверхности призмы:
Sпов= Sбок+2 Sосн
Sбок= РоснН (слайд2)
Площадь поверхности цилиндра:
Sосн=ПR2 Сдлина окружности=2ПR
Sпов=2ПRН+2ПR2 (слайд3)
Вывод формулы площади поверхности конуса.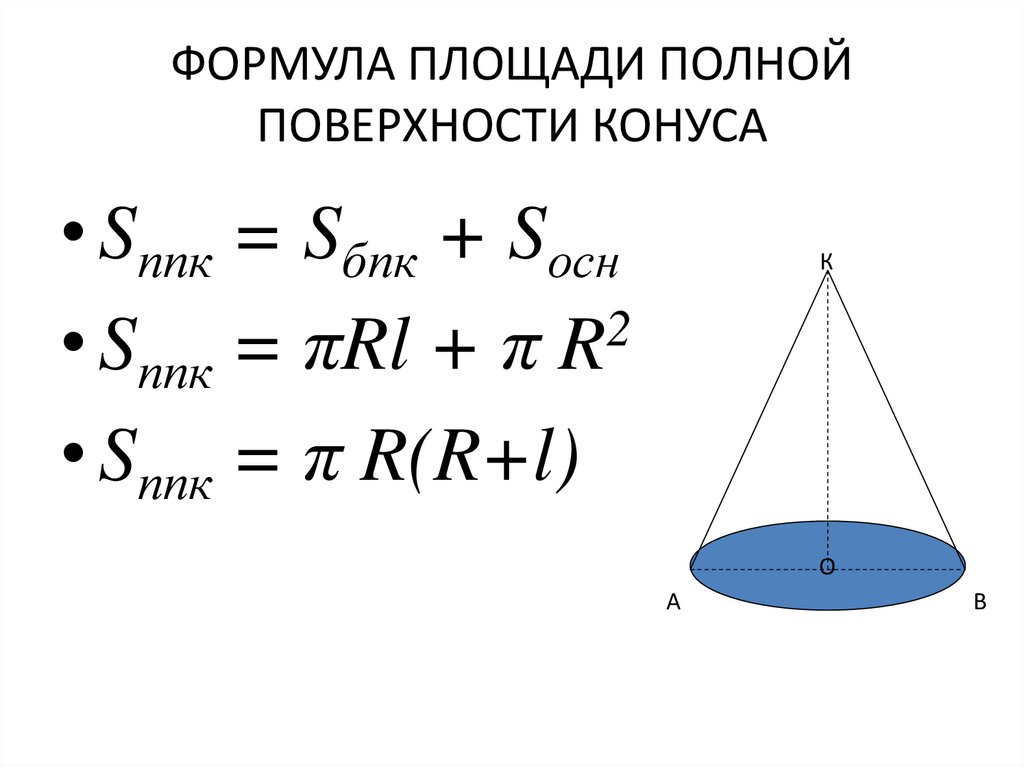
Плакат 3. — Конус вписан и описан в 4-х-ую пирамиду.
Плакат 4. — Конус вписан и описан в 6-х-ую пирамиду.
Вывод: Если будем увеличивать количество граней пирамиды, то поверхность конуса будет максимально приближаться к граням пирамиды и на каком–то n – шаге произойдет совпадение поверхности конуса с пирамидой, т.е. совпадут их площади поверхностей.
Площадь поверхности пирамиды:
Sпов= Sбок+ Sосн
Sбок=1/2РоснL (слайд4)
Площадь поверхности конуса:
Sпов=ПRL+ПR 2 (слайд5)
5. Первичное осмысление и применение изучаемого материала (15 минут).
Задача 1. Пусть S-площадь боковой поверхности цилиндра, D-диаметр основания, Н-высота, заполните пустые ячейки.
| № | S(см 2) | D(см) | Н(см) |
| 1 | 12 | 5 | |
| 2 | 100П | 25 | |
| 3 | 225П | 15 |
Задача 2. Пусть S-площадь боковой поверхности конуса, R-радиус основания, L-образующая конуса, заполните пустые ячейки.
Пусть S-площадь боковой поверхности конуса, R-радиус основания, L-образующая конуса, заполните пустые ячейки.
| № | S(см 2) | R(см) | L(см) |
| 1 | 2√2 | √2 | |
| 2 | 60П | 0,4 | |
| 3 | 30П | √3 |
Задача 3. Тело имеет форму цилиндра с коническим верхом. Радиус его основания 2м, высота 4м, причем цилиндрическая часть имеет высоту 2,5м. Определить полную поверхность тела.
6. Историческая справка (сообщение учащихся) (8 минут).
7. Домашнее задание (1-2 минуты) по сборнику
На «3» В-4(7) стр. 81, В-11(7) стр. 83
На «4» В-16(7) стр 85, В-19(7) стр. 86
86
На «5» 3.72, 3.78 стр. 121
8. Лабораторно-практическая работа (30 минут) (см. Приложение 1 )
9. Итог занятия (1-2 минуты)
Список литературы
- Алёшина Т.Н. Урок математики.- М., «Высшая школа», 1991г.
- Беденко Н.К. Уроки геометрии.- М., «Высшая школа», 1988г.
- Денищева Л.О. и др. Зачеты в системе дифференцированного обучения математике.- М.: Просвещение, 1993 .
- Дорофеев Г.В. Сборник заданий для подготовки и проведения письменного экзамена за курс средней школы. — М.: Дрофа, 2009.
- Дубинчук Е.Е. Обучение геометрии в профессиональных училищах.- М., «Высшая школа», 1989.
- Овсянник Д.П. Практикум по математике в профессиональных училищах металлообрабатывающего профиля. – Ульяновск, 1997.
Литература для учащихся
- Глейзер История математики в школе.- М.: Просвещение,1964.
- Энциклопедия для детей «Математика».- М.: «Аванта», 2002.
\[{\Large{\text{Цилиндр}}}\]
Рассмотрим окружность \(C\)
с центром \(O\)
радиуса \(R\)
на плоскости \(\alpha\)
. Через каждую точку окружности \(C\)
проведем прямую перпендикулярно плоскости \(\alpha\)
. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью .
Через каждую точку окружности \(C\)
проведем прямую перпендикулярно плоскости \(\alpha\)
. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью .
Сами прямые называются образующими данной поверхности.
Проведем теперь через некоторую точку некоторой образующей плоскость \(\beta\parallel \alpha\)
. Множество точек, по которым образующие пересекут плоскость \(\beta\)
, образует окружность \(C»\)
, равную окружности \(C\)
.
Часть пространства, ограниченная двумя кругами \(K\)
и \(K»\)
с границами \(C\)
и \(C»\)
соответственно, а также частью цилиндрической поверхности, заключенной между плоскостями \(\alpha\)
и \(\beta\)
, называется цилиндром .
Круги \(K\)
и \(K»\)
называются основаниями цилиндра; отрезки образующих, заключенных между плоскостями, – образующими цилиндра; часть цилиндрической поверхности, образованная ими, — боковой поверхностью цилиндра. Отрезок, соединяющий центры оснований цилиндра равен образующей цилиндра и равен высоте цилиндра (\(l=h\)
).
Теорема
Площадь боковой поверхности цилиндра равна \
где \(R\) – радиус основания цилиндра, \(h\) – высота (образующая).
Теорема
Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей обоих оснований \
Теорема
Объем цилиндра вычисляется по формуле \
\[{\Large{\text{Конус}}}\]
Рассмотрим плоскость \(\alpha\)
и на ней окружность \(C\)
с центром \(O\)
и радиусом \(R\)
. Через точку \(O\)
проведем прямую, перпендикулярную плоскости \(\alpha\)
. Отметим на этой прямой некоторую точку \(P\)
. Поверхность, образованная всеми прямыми, проходящими через точку \(P\)
и каждую точку окружности \(C\)
, называется конической поверхностью , а эти прямые – образующими конической поверхности. Часть пространства, ограниченная кругом с границей \(C\)
и отрезками образующих, заключенными между точкой \(P\)
и точкой на окружности, называется конусом . Отрезки \(PA\)
, где \(A\in \text{окр. }
C\)
, называются образующими конуса ; точка \(P\)
– вершина конуса; круг с границей \(C\)
– основание конуса; отрезок \(PO\)
– высота конуса.
}
C\)
, называются образующими конуса ; точка \(P\)
– вершина конуса; круг с границей \(C\)
– основание конуса; отрезок \(PO\)
– высота конуса.
Замечание
Заметим, что у конуса высота и образующая не равны друг другу, как было в случае с цилиндром.
Теорема
Площадь боковой поверхности конуса равна \
где \(R\) – радиус основания конуса, \(l\) – образующая.
Теорема
Площадь полной поверхности конуса равна сумме площади боковой поверхности и площадей основания \
Теорема
Объем конуса вычисляется по формуле \
Замечание
Заметим, что цилиндр в каком-то смысле является призмой, только в основании находится не многоугольник (как у призмы), а круг.
Формула объема цилиндра такая же, как и формула объема призмы: произведение площади основания на высоту.
Аналогично конус в каком-то смысле является пирамидой. Поэтому формула объема конуса такая же, как и у пирамиды: треть площади основания на высоту.
\[{\Large{\text{Сфера и шар}}}\]
Рассмотрим множество точек пространства, равноудаленных от некоторой точки \(O\)
на расстояние \(R\)
. Это множество называется сферой с центром в точке \(O\)
радиуса \(R\)
.
Отрезок, соединяющий две точки сферы и проходящий через ее центр называется диаметром сферы.
Сфера вместе со своей внутренностью называется шаром .
Теорема
Площадь сферы вычисляется по формуле \
Теорема
Объем шара вычисляется по формуле \
Определение
Шаровой сегмент – это часть шара, отсекаемая от него некоторой плоскостью.
Пусть плоскость пересекла шар по кругу \(K\)
с центром в точке \(Q\)
. Соединим точки \(O\)
(центр шара) и \(Q\)
и продлим этот отрезок до пересечения со сферой – получим радиус \(OP\)
. Тогда отрезок \(QP\)
называется высотой сегмента.
Теорема
Пусть \(R\) – радиус шара, \(h\) – высота сегмента, то объем шарового сегмента равен \
Определение
Шаровой слой – это часть шара, заключенная между двумя параллельными плоскостями, пересекающими этот шар. Круги, по которым плоскости пересекают шар, называются основаниями шарового слоя, отрезок, соединяющий центры оснований – высотой шарового слоя.
Круги, по которым плоскости пересекают шар, называются основаниями шарового слоя, отрезок, соединяющий центры оснований – высотой шарового слоя.
Две оставшиеся части шара являются в этом случае шаровыми сегментами.
Объем шарового слоя равен разности объема шара и объемов шаровых сегментов с высотами \(AP\) и \(BT\) .
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
1. Объем конуса равен 16.Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Очевидно, что объем меньшего конуса в 8 раз меньше объема большого и равен двум.
Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения.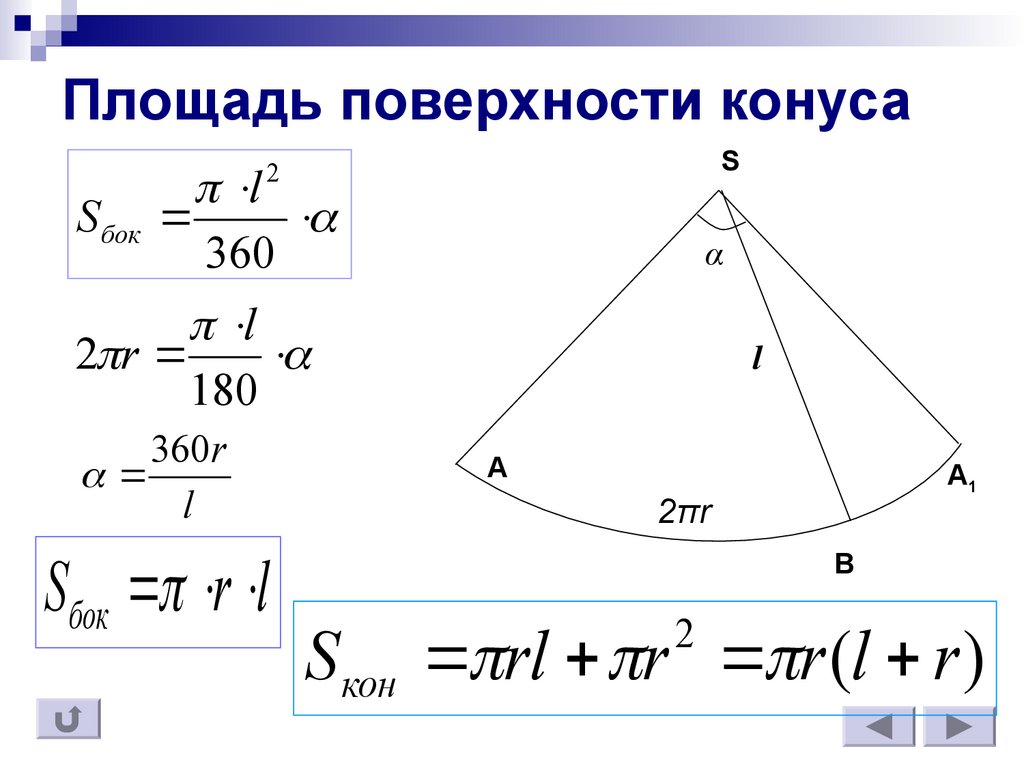 Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в 2 раза больше.
Упражнения для самостоятельной работы.
1.Измерение прямоугольного параллелепипеда 15, 50 и 36 м. Найти ребро равновеликого ему куба.
2.В правильной 4-угольной пирамиде высота 3 см, боковое ребро 5 см. Найти объем пирамиды.
3.Осевое сечение цилиндра – прямоугольник со сторонами 8 дм и 12 дм. Найти объем цилиндра.
Найти объем цилиндра.
4.Образующая конуса наклонена к плоскости основания под углом 30°, радиус основания равен 3 дм. Найти объем конуса.
5.Радиус шара равен 4 м. Найти объем шарового сегмента высотой, равной 3 м.
Список литературы
Геометрия, 10-11: Учеб. для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др.-Москва: Просвещение, 2009 год
2. Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по геометрии для 10 класса.- 4-е издание, испр. и доп.- М.:Илекса, 2007,- 175 с.
3. Геометрия. 10-11 классы: тесты для текущего и обобщающего контроля/авт.сост.Г.И.Ковалёва, Н.И.Мазурова.- Волгоград: Учитель, 2009, 187 стр.
4. Виртуальная школа Кирилла и Мефодия. Репетитор по математике. Москва. 2007 год
5. Учебное электронное издание. Математика 5- 11 класссы. Практикум. Под редакцией Дубровского В.Н., 2004.
ПРАКТИЧЕСКАЯ РАБОТА № 16
«Использование координат и векторов при решении математических задач»
Цель урока:
1) Обобщить теоретические знания по теме: «Использование координат и векторов при решении математических задач».
2) Рассмотреть алгоритмы решений заданий теме «Использование координат и векторов при решении математических задач», решить задачи.
3) Формировать потребность к самопознанию, самоконтролю, достижению поставленных целей.
Теоретический материал
Похожая информация:
- F. Новый максимум цен сопровождается увеличением объема, аналогично точке А. Продолжайте удерживать позицию на повышение
Цели урока:
Образовательные: ввести понятия цилиндра, конуса и шара, познакомить учащихся с формулами нахождения площадей тел вращения, сформировать умения применять формулы (полученные знания) при решении задач на цилиндр, конус и шар;
Воспитательные: воспитание внимательности у учащихся.
Развивающие: развитие пространственного воображения, логического мышления, культуры устной математической речи.
План урока:
- Организационный момент;
- Объяснение нового материала;
- Закрепление нового материала;
- Постановка домашнего задания и подведение
итогов урока.

Оборудование: Компьютер, проектор, экран.
Ход урока
I. Организационный момент.
II. Объяснение нового материала.
Сегодня на уроке мы познакомимся с новыми для вас понятиями: понятием цилиндра, конуса и сферы, площадями боковых поверхностей данных тел и рассмотрим сечения цилиндра и конуса различными плоскостями, а также взаимное расположение сферы и плоскости.
1. Начнем мы с понятия цилиндра .
Рассмотрим две параллельные плоскости и и окружность L с центром в точке O радиуса r, расположенную в плоскости (слайд 2). Через каждую точку окружности L проведем прямую, перпендикулярную к плоскости .
Отрезки этих прямых, заключенные между плоскостям и , образуют цилиндрическую поверхность . Сами отрезки называются образующими цилиндрической поверхности.
Тело, ограниченное цилиндрической
поверхностью и двумя кругами с границами L и L 1 ,
называется цилиндром (слайд 2).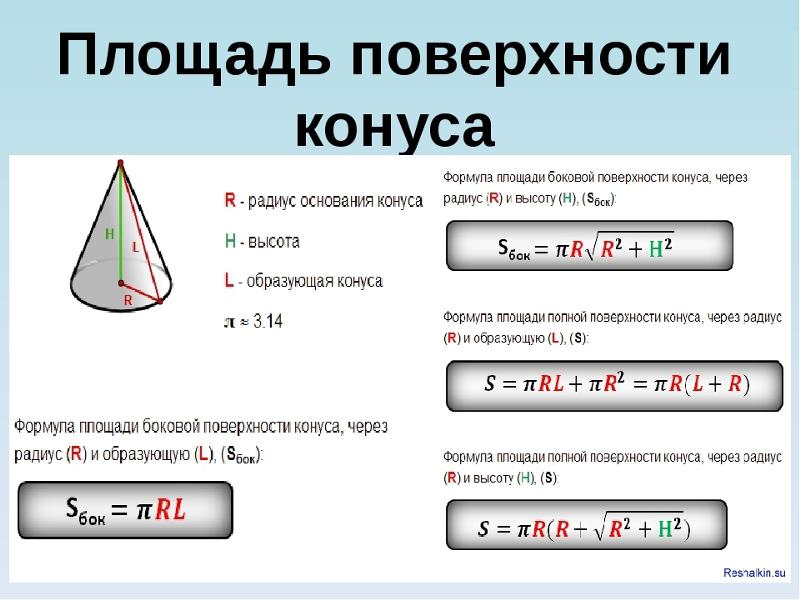
Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра .
Образующие цилиндрической поверхности называются образующими цилиндра , прямая OO 1 – осью цилиндра .
Все образующие цилиндра параллельны и равны друг другу. Почему? (как отрезки параллельных прямых, заключенные между параллельными плоскостями).
Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Ребята, давайте изобразим в своих тетрадях цилиндр и запишем его определение.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон (слайд 2).
Теперь давайте найдем площадь полной
поверхности конуса. Какие будут предложения?
(площадь полной поверхности конуса равна сумме
площадей боковой поверхности и основания) Чему
равна площадь основания конуса? () А площадь боковой
поверхности конуса равна произведению половины
длины окружности основания на образующую, т. е. (пояснить).
Тогда получаем, что .
е. (пояснить).
Тогда получаем, что .
Об усеченном конусе вы прочтете дома (стр.125) и сделаете конспект данного пункта.
3. Понятие сфера и шар .
— Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (слайд 6).
Данная точка называется центром сферы, а данное расстояние – радиусом сферы. Отрезок, соединяющий две точки сферы и проходящей через ее центр, называется диаметром сферы.
Сфера может быть получена вращением полуокружности вокруг ее диаметра (слайд 6).
Тело, ограниченное сферой, называется шаром . Центр, радиус и диаметр сферы называются также центром, радиусом и сферой шара.
А теперь, ребята, давайте выведем уравнение сферы радиуса R с центром в точке C(x 0 , y 0 , z 0) . Изображаем в тетрадях рисунок такой же как у меня (слайд 7).
Расстояние от произвольной точки M (x, y, z) до
точки C вычисляется по формуле .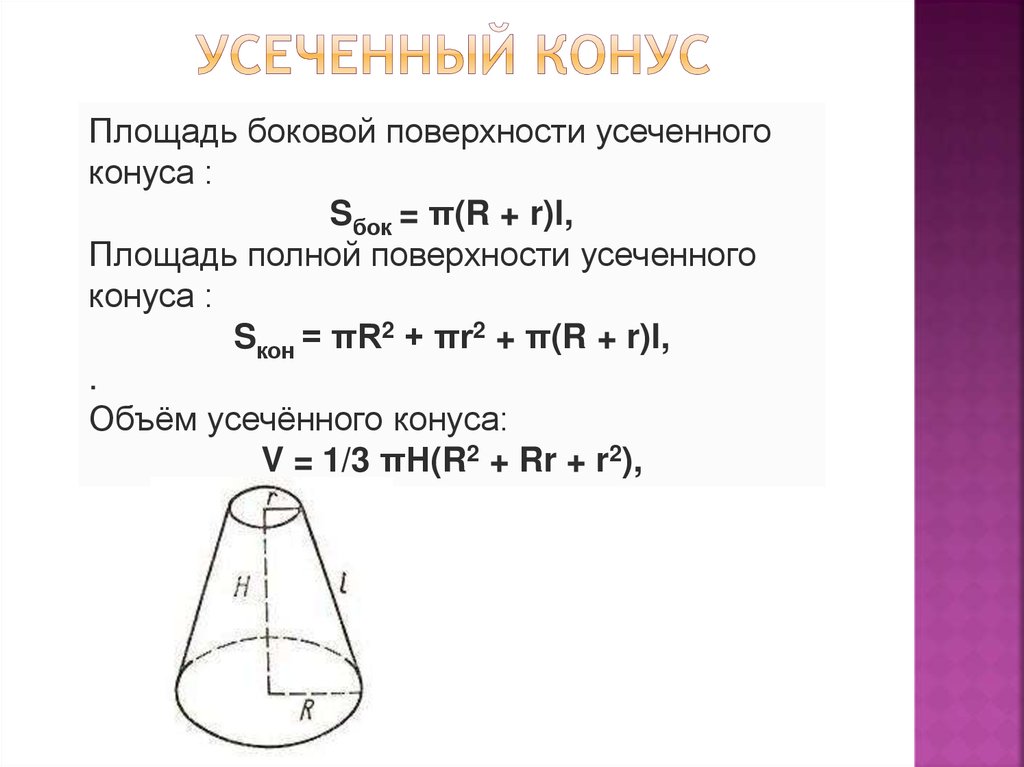 Если точка M лежит на
данной сфере, то или
, т.е. координаты точки M удовлетворяют уравнению .
Если точка M лежит на
данной сфере, то или
, т.е. координаты точки M удовлетворяют уравнению .
Если же точка M (x, y, z) не лежит на данной сфере, то , т.е. координаты точки M не удовлетворяют уравнению. Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром в точке C(x 0 , y 0 , z 0) имеет вид . Запишем это себе в тетрадь. У кого есть вопросы?
Рассмотрим сечения цилиндра различными плоскостями . Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра (слайд 8). Такое сечение называется осевым .
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом (слайд 8). Изображаем у себя в тетрадях.
Рассмотрим сечения конуса различными
плоскостями . Если секущая плоскость проходит
через ось конуса, то сечение представляет собой
равнобедренный треугольник (почему?) ,
основание которого – диаметр основания конуса, а
боковые стороны – образующие конуса. Такое
сечение называется осевым .
Такое
сечение называется осевым .
Если секущая плоскость перпендикулярна к оси конуса, то сечение представляет собой круг, расположенным на оси конуса. Изображаем у себя в тетрадях сечения конуса. Давайте сверим рисунки, посмотрите на экран (слайд 8).
О взаимном расположении сферы и плоскости вы узнаете самостоятельно, сейчас поговорим о касательной плоскости к сфере.
Записываем определение: плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере , а их общая точка называется точкой касания плоскости и сферы (слайд 10).
Касательная плоскость к сфере обладает следующим свойством:
Теорема. Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Доказательство.
Вернемся к нашему рисунку. Докажем, что радиус перпендикулярен к плоскости .
Предположим, что это не так. Тогда радиус является
наклонной к плоскости , и, следовательно, расстояние от центра
сферы до плоскости меньше радиуса сферы. Поэтому сфера и
плоскость пересекаются по окружности. Но это
противоречит тому, что плоскость – касательная, т.е. сфера и
плоскость
имеют только одну общую точку. Полученное
противоречие доказывает, что радиус
перпендикулярен к плоскости . Теорема доказана.
Поэтому сфера и
плоскость пересекаются по окружности. Но это
противоречит тому, что плоскость – касательная, т.е. сфера и
плоскость
имеют только одну общую точку. Полученное
противоречие доказывает, что радиус
перпендикулярен к плоскости . Теорема доказана.
Верна и обратная теорема . Давайте сформулируем ее вместе (если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере)
Формула для вычисления площади сферы: .
III. Закрепление нового материала.
Задача 539. Сколько понадобится краски, чтобы покрасить бак цилиндрической формы с диаметром основания 1,5 м и высотой 3 м, если на один квадратный метр расходуется 200 г краски?
| Вопросы учителя | Ответы учащихся |
| Что нужно найти? | Сколько понадобится краски, чтобы покрасить бак цилиндрической формы с диаметром основания 1,5 м и высотой 3 м, если на один квадратный метр расходуется 200 г краски? |
| Как будем находить? | Давайте сначала найдем площадь
поверхности цилиндра.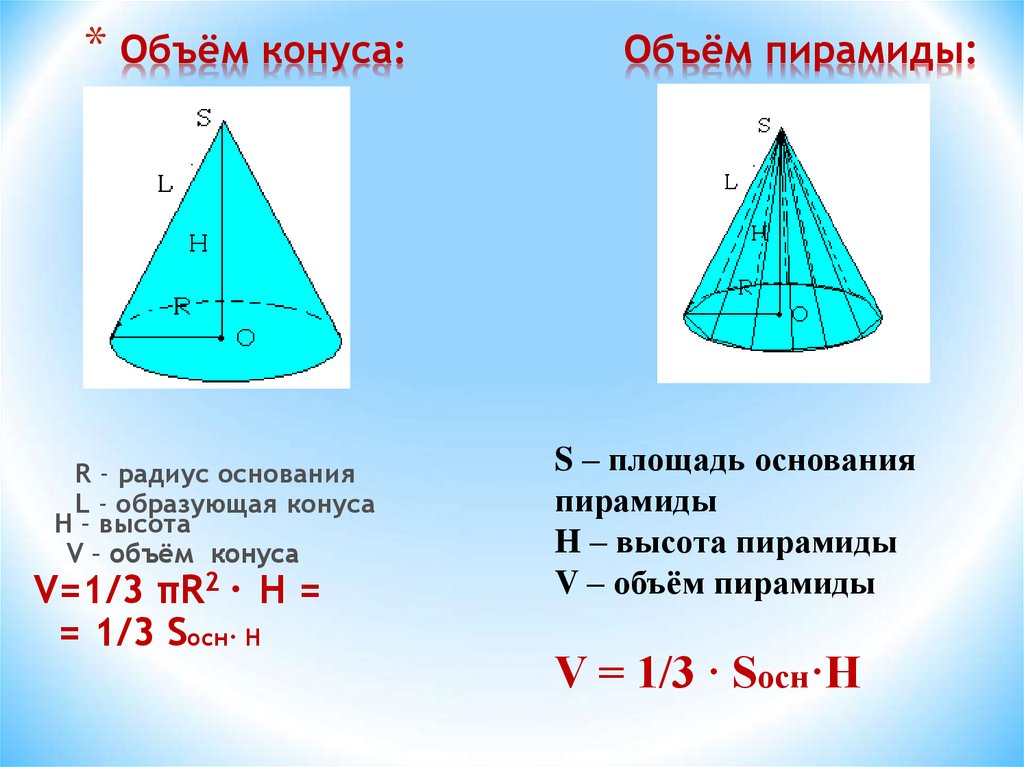 |
| Сразу условимся, что бак будет с крышкой. Тогда будем находить площадь полной поверхности цилиндра или боковой поверхности цилиндра? | Площадь полной поверхности цилиндра. |
| А что потом? | Полученную площадь умножим на 200 г. |
| Запишем ответ |
Сейчас проверим, как вы усвоили материал. (В зависимости от условий проведения урока тест может быть представлен учащимся в электронном варианте или в печатном.)
Решите тест (печатный вариант) . Я вам сейчас выдам таблицу, в первой строке таблицы записаны номера заданий, во второй строке вы пишете номера правильных ответов.
| 1 | 2 | 3 | 4 | 5 |
IV.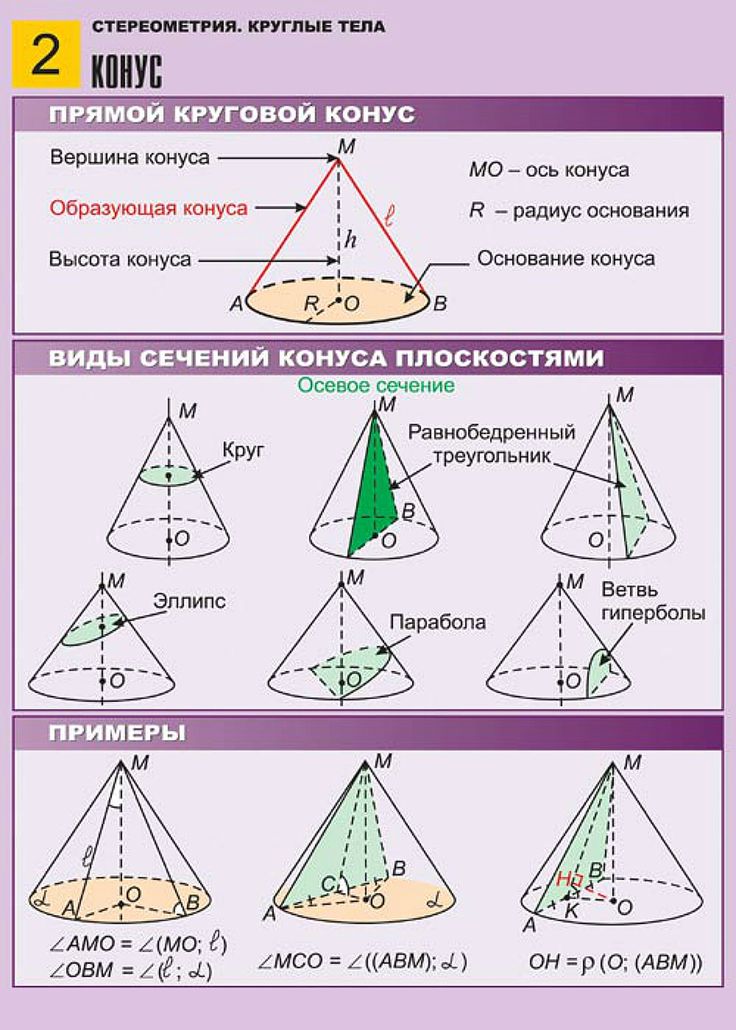 Постановка домашнего задания и
подведение итогов урока.
Постановка домашнего задания и
подведение итогов урока.
Домашнее задание: учебник глава VI (выучить основные определения, теоремы) , задача 541
Итоги: на данном занятии мы познакомились с такими понятиями как цилиндр, конус, шар и сферы (показать
Объем равностороннего конуса формула. Все формулы объемов геометрических тел
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.
Геометрия как наука сформировалась в Древнем Египте и достигла высокого уровня развития. Известный философ Платон основал Академию, где пристальное внимание уделялось систематизации имеющихся знаний. Конус как одна из геометрических фигур впервые упоминается в известном трактате Евклида «Начала». Евклид был знаком с трудами Платона. Сейчас мало кто знает, что слово «конус» в переводе с греческого языка обозначает «сосновая шишка». Греческий математик Евклид, живший в Александрии, по праву считается основоположником геометрической алгебры. Древние греки не только стали преемниками знаний египтян, но и значительно расширили теорию.
Сейчас мало кто знает, что слово «конус» в переводе с греческого языка обозначает «сосновая шишка». Греческий математик Евклид, живший в Александрии, по праву считается основоположником геометрической алгебры. Древние греки не только стали преемниками знаний египтян, но и значительно расширили теорию.
История определения конуса
Геометрия как наука появилась из практических требований строительства и наблюдений за природой. Постепенно опытные знания обобщались, а свойства одних тел доказывались через другие. Древние греки ввели понятие аксиом и доказательств. Аксиомой называется утверждение, полученное практическим путем и не требующее доказательств.
В своей книге Евклид привел определение конуса как фигуры, которая получается вращением прямоугольного треугольника вокруг одного из катетов. Также ему принадлежит основная теорема, определяющая объем конуса. А доказал эту теорему древнегреческий математик Евдокс Книдский.
Другой математик древней Греции, Аполлоний Пергский, который был учеником Евклида, развил и изложил теорию конических поверхностей в своих книгах.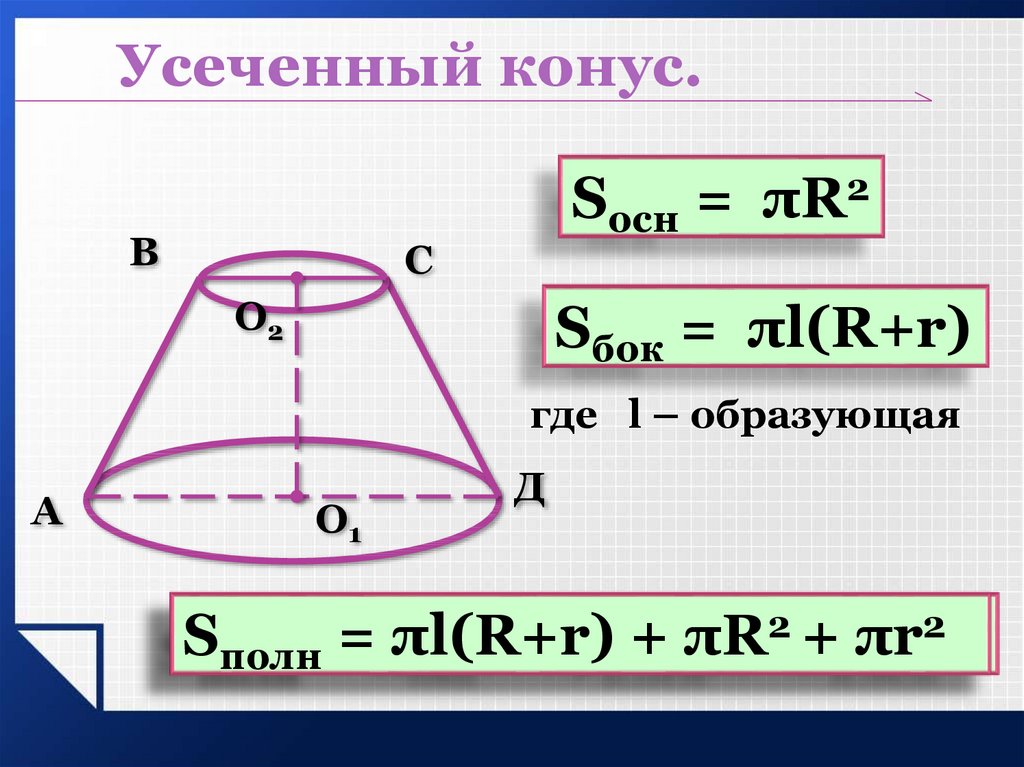 Ему принадлежит определение конической поверхности и секущей к ней. Школьники наших дней изучают Евклидову геометрию, сохранившую основные теоремы и определения с древних времен.
Ему принадлежит определение конической поверхности и секущей к ней. Школьники наших дней изучают Евклидову геометрию, сохранившую основные теоремы и определения с древних времен.
Основные определения
Прямой круговой конус образован вращением прямоугольного треугольника вокруг одного катета. Как видно, понятие конуса не изменилось со времен Евклида.
Гипотенуза AS прямоугольного треугольника AOS при вращении вокруг катета OS образует боковую поверхность конуса, поэтому называется образующей. Катет OS треугольника превращается одновременно в высоту конуса и его ось. Точка S становится вершиной конуса. Катет AO, описав круг (основание), превратился в радиус конуса.
Если сверху провести плоскость через вершину и ось конуса, то можно увидеть, что полученное осевое сечение представляет собой равнобедренный треугольник, в котором ось является высотой треугольника.
где C — длина окружности основания, l — длина образующей конуса, R — радиус основания.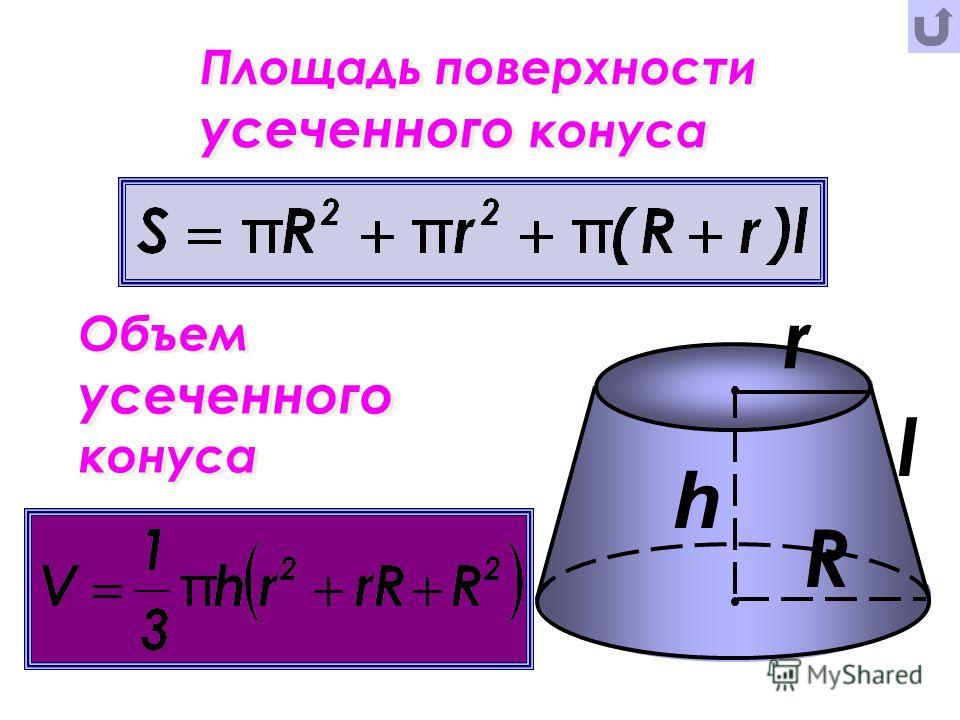
Формула расчета объема конуса
Для расчета объема конуса используется следующая формула:
где S является площадью основания конуса. Так как основание — круг, его площадь рассчитывается так:
Отсюда следует:
где V — объем конуса;
n — число, равное 3,14;
R — радиус основания, соответствующий отрезку AO на рисунке 1;
H — высота, равная отрезку OS.
Усеченный конус, объем
Имеется прямой круговой конус. Если плоскостью, перпендикулярной высоте, отсечь верхнюю часть, то получится усеченный конус. Два его основания имеют форму круга с радиусами R 1 и R 2 .
Если прямой конус образуется вращением прямоугольного треугольника, то усеченный конус — вращением прямоугольной трапеции вокруг прямой стороны.
Объем усеченного конуса рассчитывается по следующей формуле:
V=n*(R 1 2 +R 2 2 +R 1 *R 2)*H/3.
Конус и его сечение плоскостью
Перу древнегреческого математика Аполлония Пергского принадлежит теоретический труд «Конические сечения». Благодаря его работам в геометрии появились определения кривых: параболы, эллипса, гиперболы. Рассмотрим, причем здесь конус.
Благодаря его работам в геометрии появились определения кривых: параболы, эллипса, гиперболы. Рассмотрим, причем здесь конус.
Возьмем прямой круговой конус. Если плоскость пересекает его перпендикулярно оси, то в разрезе образуется круг. Когда секущая пересекает конус под углом к оси, то в разрезе получается эллипс.
Секущая плоскость, перпендикулярная основанию и параллельная оси конуса, образует на поверхности гиперболу. Плоскость, разрезающая конус под углом к основанию и параллельная касательной к конусу, создает на поверхности кривую, которую назвали параболой.
Решение задачи
Даже простая задача о том, как изготовить ведро определенного объема, требует знаний. Например, необходимо рассчитать размеры ведра, чтобы оно имело объем 10 литров.
V=10 л=10 дм 3 ;
Развертка конуса имеет вид, схематически приведенный на рисунке 3.
L — образующая конуса.
Чтобы узнать площадь поверхности ведра, которая вычисляется по следующей формуле:
S=n*(R 1 +R 2)*L,
необходимо вычислить образующую. Ее находим из величины объема V=n*(R 1 2 +R 2 2 +R 1 *R 2)*H/3.
Ее находим из величины объема V=n*(R 1 2 +R 2 2 +R 1 *R 2)*H/3.
Отсюда H=3V/n*(R 1 2 +R 2 2 +R 1 *R 2).
Усеченный конус образуется вращением прямоугольной трапеции, в которой боковая сторона является образующей конуса.
L 2 =(R 2- R 1) 2 +H 2 .
Теперь у нас имеются все данные, чтобы построить чертеж ведра.
Почему пожарные ведра имеют форму конуса?
Кто задумывался, почему пожарные ведра имеют, казалось бы, странную коническую форму? А это не просто так. Оказывается, коническое ведро при тушении пожара имеет много преимуществ перед обычным, имеющим форму усеченного конуса.
Во-первых, как оказывается, пожарное ведро быстрее наполняется водой и при переноске она не расплескивается. Конус, объем которого больше обычного ведра, за один раз позволяет перенести больше воды.
Во-вторых, воду из него можно выплеснуть на большее расстояние, чем из обычного ведра.
В-третьих, если коническое ведро сорвется с рук и упадет в огонь, то вся вода выливается на очаг возгорания.
Все перечисленные факторы позволяют сэкономить время — главный фактор при тушении пожара.
Практическое применение
У школьников часто возникает вопрос о том, зачем учить, как рассчитывать объем разных геометрических тел, в том числе конуса.
А инженеры-конструкторы постоянно сталкиваются с необходимостью рассчитать объем конических частей деталей механизмов. Это наконечники сверл, части токарных и фрезерных станков. Форма конуса позволят сверлам легко входить в материал, не требуя первоначальной наметки специальным инструментом.
Объем конуса имеет куча песка или земли, высыпанная на землю. При необходимости, проведя несложные измерения, можно рассчитать ее объем. У некоторых вызовет затруднение вопрос о том, как узнать радиус и высоту кучи песка. Вооружившись рулеткой, измеряем окружность холмика C. По формуле R=C/2n узнаем радиус. Перекинув веревку (рулетку) через вершину, находим длину образующей. А вычислить высоту по теореме Пифагора и объем не составит труда.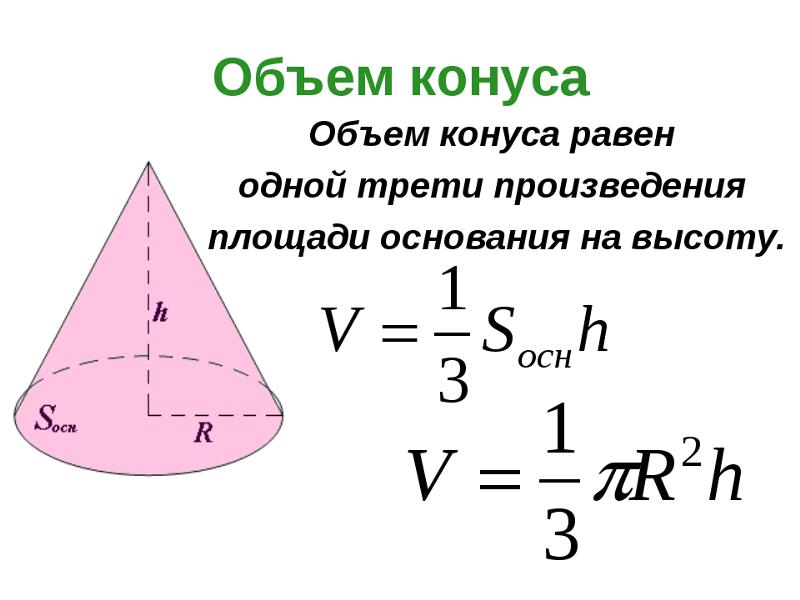 Конечно, такой расчет приблизителен, но позволяет определить, не обманули вас, привезя тонну песка вместо куба.
Конечно, такой расчет приблизителен, но позволяет определить, не обманули вас, привезя тонну песка вместо куба.
Некоторые здания имеют форму усеченного конуса. Например, Останкинская телебашня приближается к форме конуса. Ее можно представить состоящей из двух конусов, поставленных друг на друга. Купола старинных замков и соборов представляют собой конус, объем которого древние зодчие рассчитывали с удивительной точностью.
Если внимательно присмотреться к окружающим предметам, то многие из них являются конусами:
- воронки-лейки для наливания жидкостей;
- рупор-громкоговоритель;
- парковочные конусы;
- абажур для торшера;
- привычная новогодняя елочка;
- духовые музыкальные инструменты.
Как видно из приведенных примеров, умение рассчитать объем конуса, площадь его поверхности необходимо в профессиональной и повседневной жизни. Надеемся, что статья придет вам на помощь.
1. Расчет объема куба
a — сторона куба
Формула объема куба, (V ):
2.
 Найти по формуле, объем прямоугольного параллелепипеда
Найти по формуле, объем прямоугольного параллелепипедаa , b , c — стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V ):
3. Формула для вычисления объема шара, сферы
R — радиус шара
По формуле, если дан радиус, можно найти объема шара, (V ):
4. Как вычислить объем цилиндра?
h — высота цилиндра
r — радиус основания
По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V ):
5. Как найти объем конуса?
R — радиус основания
H — высота конуса
Формула объема конуса, если известны радиус и высота (V ):
7. Формула объема усеченного конуса
r — радиус верхнего основания
R — радиус нижнего основания
h — высота конуса
Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
8.
 Объем правильного тетраэдра
Объем правильного тетраэдраПравильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.
а — ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V ):
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V ):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V ):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h — высота пирамиды
a — сторона основания пирамиды
n — количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V ):
Все формулы объемов геометрических тел
Геометрия, Алгебра, Физика
Объём геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Формула объема куба
1) Объем куба равен кубу его ребра.
V — объем куба
H — высота ребра куба
Формула объема пирамиды
1) Объем пирамиды равен одной трети произведения площади основания S (ABCD) на высоту h (OS).
V — объем пирамиды
S — площадь основания пирамиды
h — высота пирамиды
Формулы объема конуса
1) Объем конуса равен одной трети произведения площади основания на высоту.
2) Объем конуса равен одной трети произведения числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем конуса
S — площадь основания конуса
h — высота конуса
π — число пи (3.1415)
r — радиус конуса
Формулы объема цилиндра
1) Объем цилиндра равен произведению площади основания на высоту.
2) Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
V — объем цилиндра
S — площадь основания цилиндра
h — высота цилиндра
π — число пи (3.1415)
r — радиус цилиндра
Формула объема шара
1) Объем шара вычисляется по приведенной ниже формуле.
V — объем шара
π — число пи (3.1415)
R — радиус шара
Формула объема тетраэдра
1) Объем тетраэдра равен дроби в числителе которой корень квадратный из двух помноженный на куб длины ребра тетраэдра, а в знаменателе двенадцать.
Формулы объема
Формулы объема и онлайн программы для вычисления объема
Формула объема необходима для вычисления параметров и характеристик геометрической фигуры.
Объем фигуры — это количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Параллелепипед .
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
Цилиндр .
Объем цилиндра равен произведению площади основания на высоту.
Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.
Пирамида .
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).
Правильная пирамида — это пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.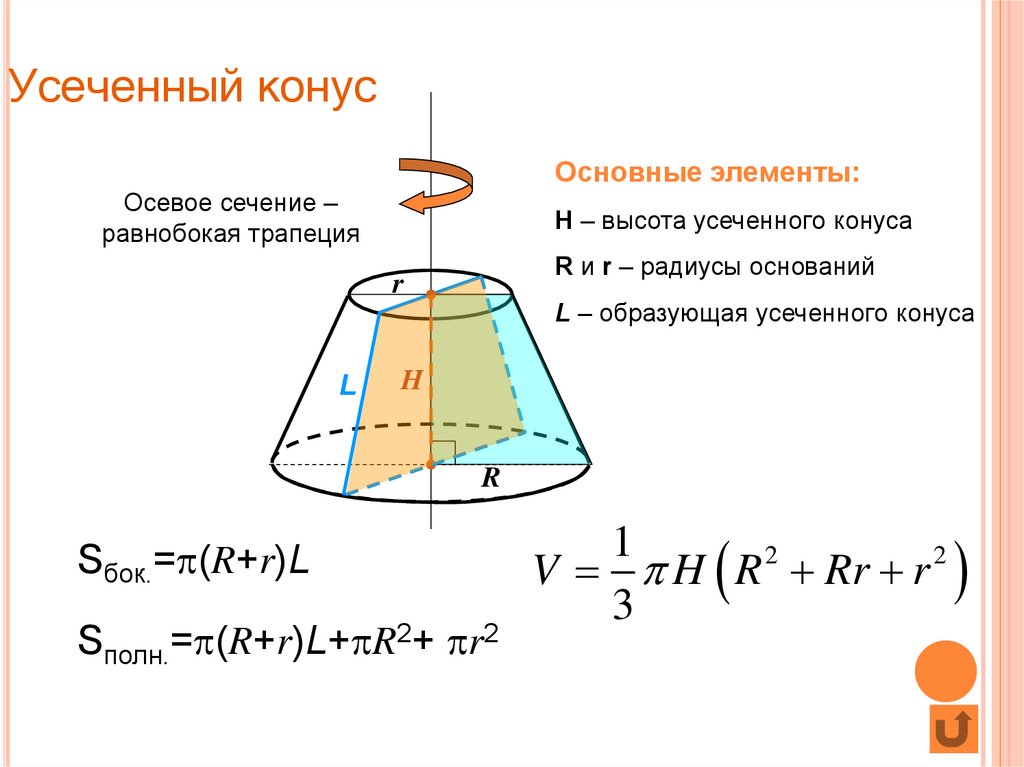
Правильная треугольная пирамида — это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.
Правильная четырехугольная пирамида — это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.
Тетраэдр — это пирамида, у которой все грани — равносторонние треугольники.
Усеченная пирамида .
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S 1 (abcde), нижнего основания усеченной пирамиды S 2 (ABCDE) и средней пропорциональной между ними.
Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 .
Конус — это тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Усеченный конус получится, если в конусе провести сечение, параллельное основанию.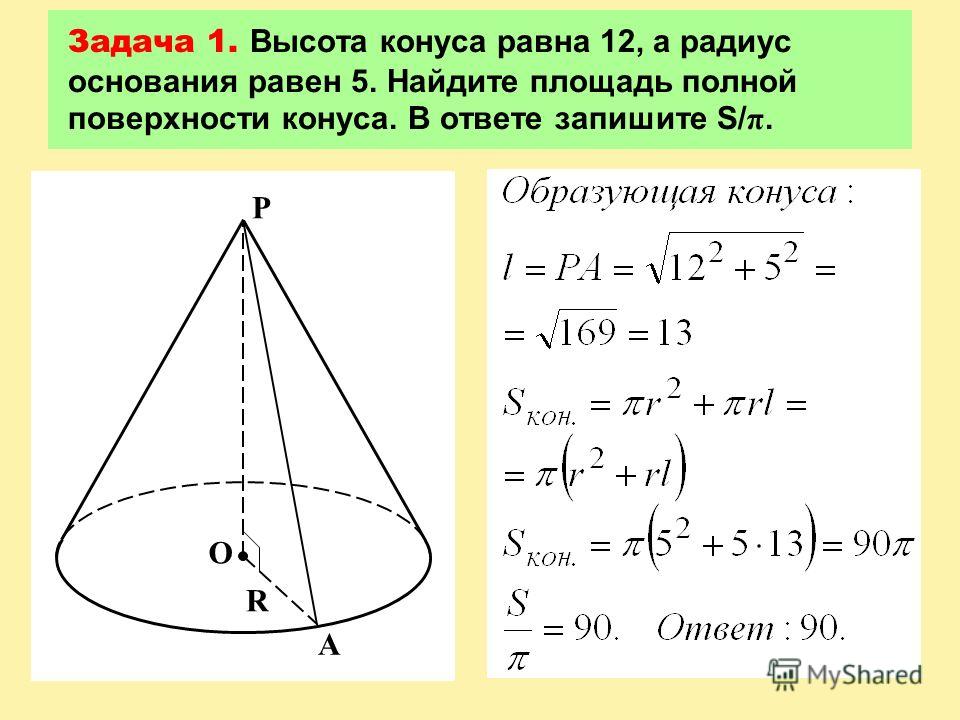
V = 1/3 πh (R 2 + Rr + r 2)
Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.
Призма .
Объем призмы равен произведению площади основания призмы, на высоту.
Сектор шара .
Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара.
Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.
Сегмент шара — это часть шара, осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом
Формула объема
Формула объема куба, шара, пирамиды, параллелограмма, цилиндра, тетраэдра, конуса, призмы и объемы других геометрических фигур.
В курсе стереометрии один из главных вопросов — как рассчитать объем того или иного геометрического тела. Все начинается с простого параллелепипеда и заканчивается шаром.
В жизни тоже часто приходится сталкиваться с подобными задачами.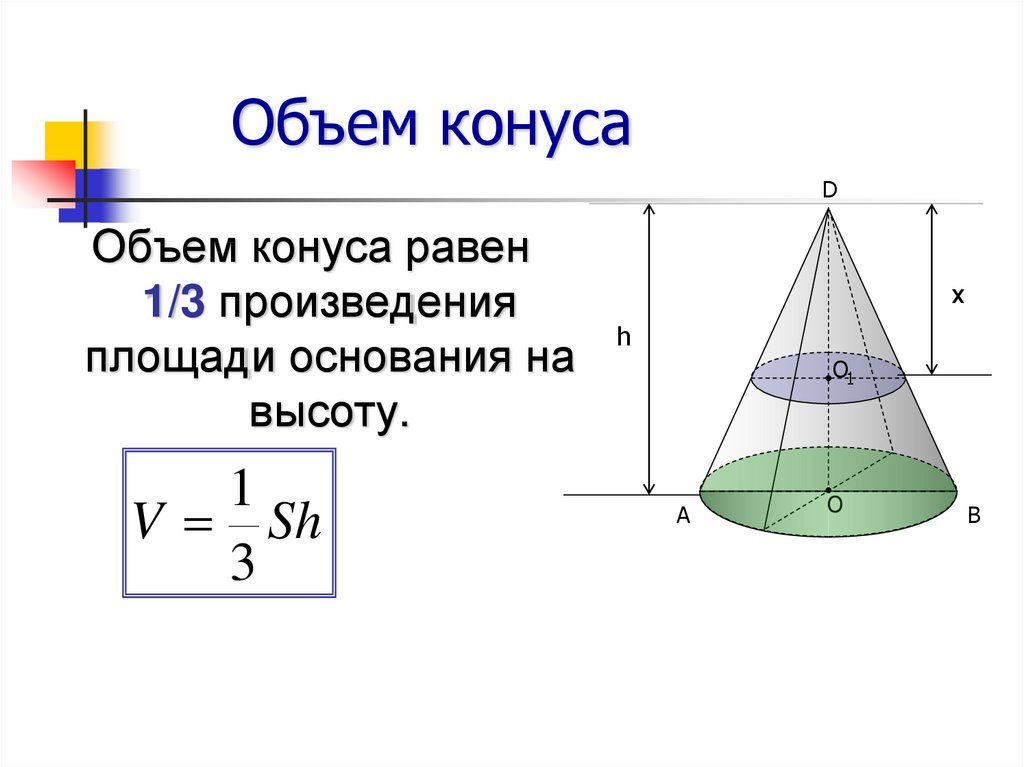 Например, чтобы рассчитать объем воды, которая помещается в ведро или бочку.
Например, чтобы рассчитать объем воды, которая помещается в ведро или бочку.
Свойства, справедливые для объема каждого тела
- Это значение — всегда положительное число.
- Если тело удается разделить на части так, чтобы не было пересечений, то общий объем оказывается равным сумме объемов частей.
- У равных тел одинаковые объемы.
- Если меньшее тело полностью помещается в большем, то объем первого меньше, чем второго.
Общие обозначения для всех тел
В каждом из них есть ребра и основания, в них строятся высоты. Поэтому такие элементы для них одинаково обозначены. Именно так они записаны в формулах. Как рассчитать объем каждого из тел — узнаем дальше и применим на практике новые умения.
В некоторых формулах имеются другие величины. Об их обозначении будет сказано при появлении такой необходимости.
Призма, параллелепипед (прямой и наклонный) и куб
Эти тела объединены, потому что внешне очень похожи, и формулы того, как рассчитать объем, идентичны:
V = S * h.
Различаться будет только S . В случае с параллелепипедом она рассчитывается, как для прямоугольника или квадрата. В призме основанием может оказаться треугольник, параллелограмм, произвольный четырехугольник или другой многоугольник.
Для куба формула существенно упрощается, потому что все его измерения равны:
V = а 3 .
Пирамида, тетраэдр, усеченная пирамида
Для первого из указанных тел существует такая формула, чтобы вычислить объем:
V = 1/3 * S * н.
Тетраэдр является частным случаем треугольной пирамиды. В нем все ребра равны. Поэтому снова получается упрощенная формула:
V = (а 3 * √2) / 12, или V = 1/ 3 S h
Усеченной пирамида становится тогда, когда у нее срезана верхняя часть. Поэтому ее объем равен разности двух пирамид: той, которая была бы целой, и удаленной верхушки. Если есть возможность узнать оба основания такой пирамиды (S 1 — большее и S 2 — меньшее), то удобно пользоваться такой формулой для расчета объема:
Цилиндр, конус и усеченный конус
V =π * r 2 * h.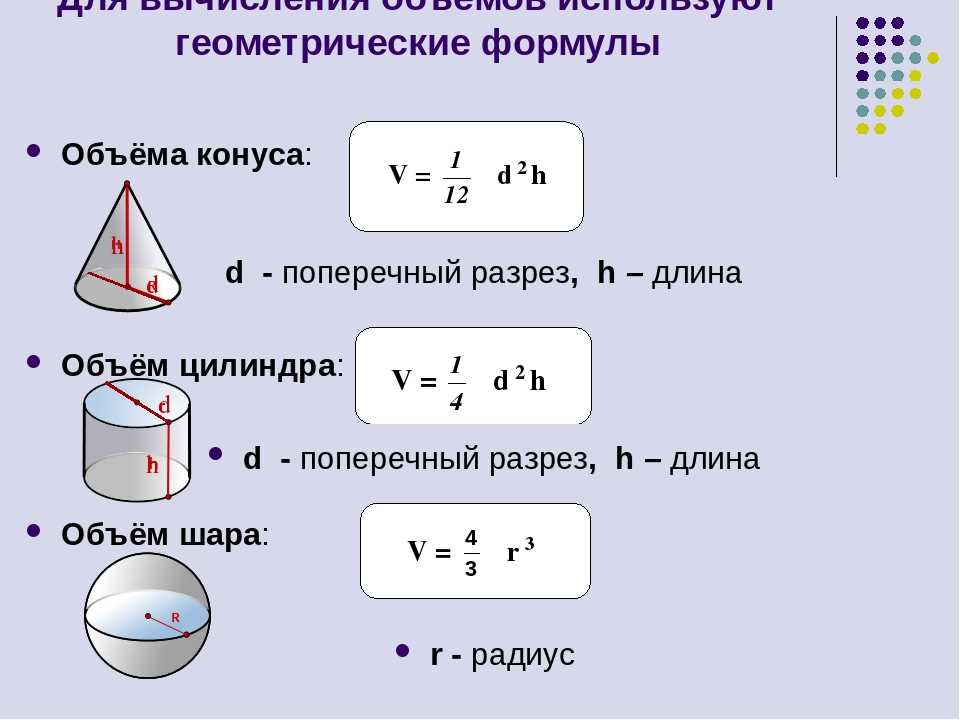
Несколько сложнее обстоит дело с конусом. Для него существует формула:
V = 1/3 π * r 2 * h. Она очень похожа на ту, что указана для цилиндра, только значение уменьшено в три раза.
Так же, как с усеченной пирамидой, дело обстоит непросто с конусом, который имеет два основания. Формула для вычисления объема усеченного конуса выглядит так:
V = 1/3 π * h * (r 1 2 + r 1 r 2 + r 2 2). Здесь r 1 — радиус нижнего основания, r 2 — верхнего (меньшего).
Шар, шаровые сегменты и сектор
Это самые сложные для запоминания формулы. Для объема шара она выглядит так:
V = 4/3 π *r 3 .
В задачах часто есть вопрос о том, как рассчитать объем шарового сегмента — части сферы, которая как бы срезана параллельно диаметру. В этом случае на выручку придет такая формула:
V = π h 2 * (r — h/3). В ней за h взята высота сегмента, то есть та часть, которая идет по радиусу шара.
Сектор делится на две части: конус и шаровой сегмент.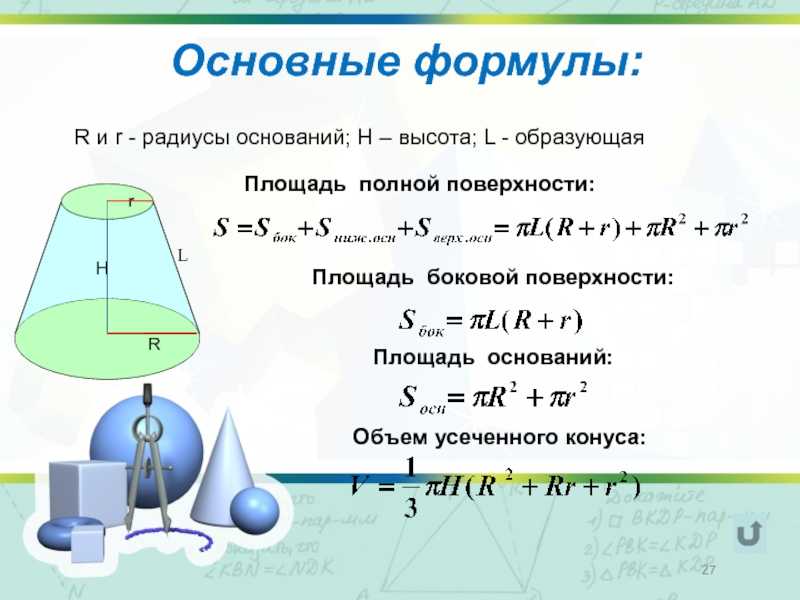 Поэтому его объем определяется как сумма этих тел. Формула после преобразований выглядит так:
Поэтому его объем определяется как сумма этих тел. Формула после преобразований выглядит так:
V = 2/3 πr 2 * h. Здесь h также высота сегмента.
Примеры задач
Про объемы цилиндра, шара и конуса
Условие: диаметр цилиндра (1 тело) равен его высоте, диаметру шара (2 тело) и высоте конуса (3 тело), проверить пропорциональность объемов V 1: V 2: V 3 = 3:2:1
Решение. Сначала потребуется записать три формулы для объемов. Потом учесть, что радиус — это половина диаметра. То есть высота будет равна двум радиусам: h = 2r. Произведя простую замену получается, что формулы для объемов будут иметь такой вид:
V 1 = 2 π r 3 , V 3 = 2/3 π r 3 . Формула для объема шара не изменяется, потому что в ней не фигурирует высота.
Теперь осталось записать отношения объемов и произвести сокращение 2π и r 3 . Получается, что V 1: V 2: V 3 = 1: 2/3: 1/3. Эти числа легко привести к записи 3: 2: 1.
Про объем шара
Условие: имеется два арбуза радиусами 15 и 20 см, как их выгоднее съесть: первый вчетвером или второй ввосьмером?
Решение. Чтобы ответить на этот вопрос, потребуется найти отношение объемов частей, которые достанутся от каждого арбуза. Принимая во внимание, что они — шары, нужно записать две формулы для объемов. Потом учесть, что от первого каждому достанется только четвертая часть, а от второго — восьмая.
Чтобы ответить на этот вопрос, потребуется найти отношение объемов частей, которые достанутся от каждого арбуза. Принимая во внимание, что они — шары, нужно записать две формулы для объемов. Потом учесть, что от первого каждому достанется только четвертая часть, а от второго — восьмая.
Осталось записать отношение объемов частей. Оно будет выглядеть так:
(V 1: 4) / (V 2: 8) = (1/3 π r 1 3) / (1/6 π r 2 3). После преобразования остается только дробь: (2 r 1 3) / r 2 3 . После подстановки значений и вычисления получается дробь 6750/8000. Из нее ясно, что часть от первого арбуза будет меньше, чем от второго.
Ответ. Выгоднее съесть восьмую часть от арбуза с радиусом 20 см.
Про объемы пирамиды и куба
Условие: имеется пирамида из глины с прямоугольным основанием 8Х9 см и высотой 9 см, из этого же куска глины сделали куб, чему равно его ребро?
Решение. Если обозначить стороны прямоугольника буквами в и с, то площадь основания пирамиды вычисляется, как их произведение. Тогда формула для ее объема:
Тогда формула для ее объема:
Формула для объема куба написана в статье выше. Эти два значения равны: V 1 = V 2 . Осталось приравнять правые части формул и сделать необходимые вычисления. Получается, что ребро куба будет равно 6 см.
Про объем параллелепипеда
Условие: требуется сделать ящик вместимостью 0,96 м 3 , известны его ширина и длина — 1,2 и 0,8 метра, какой должна быть его высота?
Решение. Поскольку основание параллелепипеда — прямоугольник, его площадь определяется как произведение длины (а) на ширину (в). Поэтому формула для объема выглядит так:
Из нее легко определить высоту, разделив объем на площадь. Получится, что высота должна быть равна 1 м.
Ответ. Высота ящика равна одному метру.
Как рассчитать объем различных геометрических тел?
В курсе стереометрии одна из главных задач — как рассчитать объем того или иного геометрического тела. Все начинается с простого параллелепипеда и заканчивается шаром.
Объём конуса выражается такой же формулой, что и объём пирамиды: V = 1 / 3 Sh ,
где V — объём конуса, S — площадь основания конуса, h — его высота.
Окончательно V = 1 / 3 πR 2 h , где R — радиус основания конуса.
Получение формулы объёма конуса можно пояснить таким рассуждением:
Пусть дан конус (рис). Впишем в него правильную пирамиду, т. е. построим внутри конуса такую пирамиду, вершина которой совпадает с вершиной конуса, а основанием служит правильный многоугольник, вписанный в основание конуса.
Объём этой пирамиды выразится формулой: V’ = 1 / 3 S’h , где V — объём пирамиды,
S’ — площадь её основания, h — высота пирамиды.
Если при этом за основание пирамиды взять многоугольник с очень большим числом сторон, то площадь основания пирамиды будет весьма мало отличаться от площади круга, а объём пирамиды — весьма мало отличаться от объёма конуса. Если, пренебречь этими различиями в размерах, то объём конуса выразится следующей формулой:
V = 1 / 3 Sh , где V — объём конуса, S — площадь основания конуса, h — высота конуса.
Заменив S через πR 2 , где R — радиус круга, получим формулу: V = 1 / 3 πR 2 h , выражающую объём конуса.
Примечание. В формуле V = 1 / 3 Sh поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы его считать приближённым, но в старших классах средней школы доказывается, что равенство
V = 1 / 3 Sh точное, а не приближённое.
Объем произвольного конуса
Теорема. Объем произвольного конуса равен одной трети произведения площади основания на высоту, т.е.
V = 1 / 3 QH, (1)
где Q — площадь основания, а Н — высота конуса.
Рассмотрим конус с вершиной S и основанием Ф (рис.).
Пусть площадь основания Ф равна Q, а высота конуса равна Н. Тогда существуют последовательности многоугольников Ф n и Ф’ n с площадями Q n и Q’ n таких, что
Ф n ⊂ Ф n ⊂ Ф’ n и \(\lim_{n \rightarrow \infty}\) Q’ n = \(\lim_{n \rightarrow \infty}\) Q n = Q.
Очевидно, что пирамида с вершиной S и основанием Ф’ n будет вписанной в данный конус, а пирамида с вершиной S и основанием Ф n — описанной около конуса.
Объемы этих пирамид соответственно равны
V n = 1 / 3 Q n H , V’ n = 1 / 3 Q’ n H
\(\lim_{n \rightarrow \infty}\) V n = \(\lim_{n \rightarrow \infty}\) V’ n = 1 / 3 QH
то формула (1) доказана.
Следствие. Объем конуса, основанием которого является эллипс с полуосями а и b, вычисляется по формуле
V = 1 / 3 π ab H (2)
В частности, объем конуса, основанием которого является круг радиуса R, вычисляется по формуле
V = 1 / 3 π R 2 H (3)
где Н — высота конуса.
Как известно, площадь эллипса с полуосями а и b равна π ab , и поэтому формула (2) получается из (1) при Q = π ab . Если а = b = R, то получается формула (3).
Объем прямого кругового конуса
Теорема 1. 2 + Rr) $$
2 + Rr) $$
Шар, объем которого равен 8π, вписан в куб. Найдите объем куба.
Решение
Пусть a — это сторона куба. Тогда объем куба равен V = a 3 .
Так как шар вписан в куб, то радиус шара равен половине ребра куба, т.е R = a/2 (см. рис.).
Объем шара равен V ш = (4/3)πR 3 и равен 8π, поэтому
(4/3)πR 3 = 8π,
А объем куба равен V = a 3 = (2R) 3 = 8R 3 = 8*6 = 48.
Задание B9 (Типовые варианты 2015)
Объем конуса равен 32. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Решение
Рассмотрим задачи:
72353. Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Сразу отметим, что исходный и отсечённый конус подобны и если рассматривать отсечённый конус относительно исходного, то можно сказать так: меньший конус подобен большему с коэффициентом равным одной второй или 0,5. Можем записать:
Можем записать:
Можно было записать:
Можно было рассудить так!
Рассмотрим исходный конус относительно отсечённого. Можно сказать – больший конус подобен отсечённому с коэффициентом равным двум, запишем:
Теперь посмотрите решение без использования свойств подобия.
Объём конуса равен одной трети произведения площади его основания и высоты:
Рассмотрим боковую проекцию (вид сбоку) с указанным сечением:
Пусть радиус большего конуса равен R, высота равна Н. Сечение (основание меньшего конуса) проходит через середину высоты, значит его высота будет равна Н/2. А радиус основания равен R/2, это следует из подобия треугольников.
Запишем объём исходного конуса:
Объём отсечённого конуса будет равен:
Столь подробные решения представлены для того, чтобы вы видели как можно выстроить рассуждения. Действуйте любым способом – главное, чтобы вы понимали суть решения. Пусть путь, который вы выбрали будет не рационален, важен результат (верный результат).
Ответ: 1,25
318145. В сосуде, имеющем форму конуса, уровень жидкости достигает половину высоты. Объём жидкости равен 70 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Данная задача схожа с предыдущей. Хоть речь здесь и идёт о жидкости, принцип решения один и тот же.
Имеем два конуса – это сам сосуд и «малый» конус (наполненный жидкостью), они являются подобными. Известно, что объёмы подобных тел соотносятся следующим образом:
Исходный конус (сосуд) подобен конусу наполненному жидкостью с коэффициентом равным 2, так как сказано, что уровень жидкости достигает половину высоты. Можно записать подробнее:
Вычисляем:
Таким образом, долить нужно:
Другие задачи с жидкостями.
74257. Найдите объем V конуса, образующая которого равна 44 и наклонена к плоскости основания под углом 30 0 . В ответе укажите V/Пи.
Объем конуса:
Высоту конуса найдем по свойству прямоугольного треугольника.
Катет лежащий против угла 30° равен половине гипотенузы. Гипотенуза, в данном случае, является образующей конуса. Следовательно высота конуса равна 22.
Квадрат радиуса основания найдем по теореме Пифагора:
*Нам нужен квадрат радиуса, а не сам радиус.
Конус — формула, свойства, типы, примеры
Конус — это трехмерная форма, имеющая круглое основание и сужающаяся к острой точке, называемой вершиной. Один из самых простых примеров из жизни, который можно привести, — это шапка на день рождения в форме конуса. Что касается конуса, у нас есть два типа областей. Один из них — это общая площадь поверхности, а другой — площадь криволинейной поверхности. Полная площадь поверхности конуса определяется как площадь, покрытая его основанием и криволинейной частью конуса, тогда как площадь криволинейной поверхности определяется только как площадь криволинейных поверхностей конуса.
| 1. | Определение конуса |
2. | Свойства конуса |
| 3. | Формула конуса |
| 4. | Типы конусов |
| 5. | Часто задаваемые вопросы о конусе |
Определение конуса
Конус представляет собой трехмерную твердую геометрическую форму, имеющую круглое основание и заостренный край наверху, называемый вершиной. Конус имеет одну грань и вершину. У конуса нет ребер.
Тремя элементами конуса являются его радиус, высота и наклонная высота. Радиус «r» определяется как расстояние между центром круглого основания и любой точкой на окружности основания. Высота «h» конуса определяется как расстояние от вершины конуса до центра круглого основания. Наклонная высота l определяется как расстояние от вершины конуса до любой точки на окружности конуса. На приведенном ниже рисунке показано, как будут выглядеть радиус, высота и высота наклона конуса. Некоторые из реальных примеров конуса включают кепку на день рождения, палатку и разделитель дорог.
Свойства конуса
Конус представляет собой форму с изогнутой поверхностью и круглым основанием. Следующие свойства конуса помогают нам легко его идентифицировать. Они следующие.
- Основание конуса круглое.
- У конуса одна грань, одна вершина и нет ребер.
- Наклонная высота конуса — это длина отрезка, соединяющего вершину конуса с любой точкой окружности основания конуса.
- Конус, вершина которого находится прямо над круглым основанием на перпендикулярном расстоянии, называется прямым круглым конусом.
- Конус, у которого вершина не находится непосредственно над круглым основанием, называется наклонным конусом.
Формула конуса
Есть три важные формулы, связанные с конусом. Это наклонная высота конуса, объем конуса и площадь его поверхности. Наклонная высота конуса получается путем нахождения суммы квадратов радиуса и высоты цилиндра, которая определяется по формуле, приведенной ниже. наклонная высота 92}\)
наклонная высота 92}\)
Площадь криволинейной поверхности конуса
Площадь криволинейной поверхности конуса – это площадь, ограниченная криволинейной частью конуса. Для конуса с радиусом «r», высотой «h» и наклонной высотой «l» площадь криволинейной поверхности будет следующей:
Площадь криволинейной поверхности = πrl квадратных единиц.
Общая площадь поверхности конуса
Общая площадь поверхности представляет собой сумму площади круглого основания и площади изогнутой части конуса. Другими словами, это сумма площади криволинейной поверхности конуса и площади круглого основания, что математически можно записать как:
Общая площадь поверхности (TSA) = площадь основания (окружности) + площадь криволинейной поверхности конуса (CSA).
TSA = (πr 2 + πrl) квадратных единиц.
Общая площадь поверхности иногда упоминается как только площадь поверхности. Итак, всякий раз, когда нас просят вычислить площадь поверхности конуса, это означает, что мы должны найти общую площадь поверхности.
Объем конуса
Объем конуса — это пространство, занимаемое конусом. Формула для нахождения объема конуса, радиус которого равен «r», а высота равна «h», задается следующим образом: Объем = (1/3) πr 2 ч куб.ед. Пусть A = площадь основания конуса и h = высота конуса. Следовательно, объем конуса = (1/3) × A × h. Поскольку основание конуса круглое, мы заменяем площадь на πr 2 . Объем конуса = (1/3) × π × r 2 × h кубических единиц. Кроме того, объем конуса составляет одну треть объема цилиндра.
Объем конуса = (1/3) × объем цилиндра.
Типы конусов
Обычно конусы бывают двух типов. Один из них представляет собой правильный круговой конус, а другой — наклонный конус. В таблице ниже перечислены некоторые отличия этих двух типов конусов.
| Правый круглый конус | Косой конус |
|---|---|
Вершина прямого кругового конуса противоположна круговому основанию. | Наклонный конус не имеет вершины, прямо противоположной круглому основанию. |
| Линия, представляющая высоту конуса, проходит через центр базовой окружности и перпендикулярна радиусу. | Линия, представляющая высоту конуса, не проходит через центр базовой окружности. |
☛Темы, связанные с конусом
Ознакомьтесь с некоторыми интересными статьями, связанными с конусом.
- Формула высоты конуса
- Калькулятор наклонной высоты конуса
- Площадь основания конуса
- Боковая часть конуса
Примеры конусов
Пример 1: Сэм должен найти отношение объема конуса к объему цилиндра. Как вы можете помочь Сэму найти требуемое соотношение?
Решение:
Чтобы найти отношение, Сэм сначала должен найти объемы конуса и цилиндра. Используя формулу конуса и формулу цилиндра, имеем:
Объем конуса = (1/3)πr 2 h
Объем цилиндра = πr 2 h
Отношение объема конуса и объем цилиндра = (1/3)πr 2 h: πr 2 h
Объем конуса: Объем цилиндра = 1/3: 1
= 1:3
Следовательно, отношение объема конуса к объему цилиндра равно 1:3.
Пример 2: Мэри использует толстый лист бумаги и готовит праздничную шапку в форме конуса. Радиус шапки равен 3 единицам, а высота — 4 единицам. Как Мэри может найти наклонную высоту шапочки на день рождения?
Решение:
Дан радиус (r) = 3 единицы и высота (h) = 4 единицы.
Используя формулу высоты наклона конуса, т. е. высота наклона 2 = радиус 2 + высота 2
л 2 = р 2 + ч 2
3 2 + 4 2 = 9 + 16
л 2 = 25
л = √25
л = 5
Следовательно, наклонная высота конуса = 5 ед.Пример 3: Джейн была в походе на выходных. Там она наблюдает коническую палатку и аппроксимирует, что высота палатки в три раза больше радиуса (r) палатки. Вам нужно помочь Джейн, найти примерный объем палатки, исходя из ее радиуса.
Решение:
Учитывая, что высота в три раза больше радиуса. Таким образом, мы можем сказать, что h = 3r. Следовательно, объем конуса равен
Таким образом, мы можем сказать, что h = 3r. Следовательно, объем конуса равенОбъем конуса = (1/3) πr 2 ч. Подставив значение h = 3r, получим
Объем конуса = (1/3) πr 2 × 3r
= (1/3) 3πr 3
= πr 3
Следовательно, объем палатки равен πr 3 кубических единиц.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
Практические вопросы на конусе
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о конусе
Что такое конус?
Конус представляет собой трехмерную фигуру с круглым основанием и криволинейной поверхностью. Заостренный кончик наверху конуса называется «Вершина». Конус имеет одну грань (круглую) без ребер и одну вершину, являющуюся вершиной конуса.
Конус имеет одну грань (круглую) без ребер и одну вершину, являющуюся вершиной конуса.
Сколько граней, ребер и вершин у конуса?
Конус имеет одну грань без ребер и одну вершину. Конус имеет круглое основание и криволинейную поверхность. Поскольку конус имеет только одну вершину, у него нет ребра. Также в конусе есть только одна плоская поверхность, образующая основание.
Что такое наклонная высота конуса?
Расстояние от вершины или вершины конуса до точки на окружности основания называется наклонной высотой. Наклонная высота получается квадратным корнем из суммы квадратов радиуса и высоты конуса.
Какова площадь поверхности конуса?
Площадь поверхности конуса может быть получена путем сложения площади его основания и криволинейной поверхности. Основание конуса круглое. Формула для нахождения площади поверхности конуса: (πr 2 + πrl) квадратных единиц. Здесь «r» — радиус конуса, а «l» — наклонная высота конуса. Здесь πr 2 — площадь его основания, а площадь криволинейной поверхности — πrl.
Каков объем конуса?
Объем конуса — это количество пространства, занимаемого конусом. Конус радиуса r и высоты h имеет объем (1/3)πr 2 ч.
Что такое площадь основания конуса?
Основание конуса — это величина, показывающая площадь, покрытую круглым основанием конуса. Формула площади основания конуса: A = πr 2 , где r — радиус основания конуса.
Какие бывают два типа конуса?
Два типа конусов: прямой круговой конус и наклонный конус. У прямого круглого конуса линия оси проходит через центр круглого основания, тогда как в наклонном конусе линия оси не проходит через центр круглого основания.
Для чего нужен калькулятор конуса?
В геометрии конус определяется как объемная объемная геометрическая фигура, имеющая круглое основание на одном конце и заостренный край на другом конце. Попробуйте онлайн-инструмент Cuemath’s Cone Calculator, который поможет вам за несколько секунд рассчитать такие параметры, как площадь поверхности, объем и наклонная высота конуса.
Скачать БЕСПЛАТНЫЕ учебные материалы
Конусные листы
Что такое конус? Определение, формула, свойства, примеры
Конусы можно найти во многих предметах, которые мы видим каждый день. Рожок для мороженого, дорожный конус и кепка на день рождения — это лишь некоторые распространенные примеры формы конуса.
Несмотря на то, что конусы в изобилии присутствуют в нашей повседневной жизни, мы все еще не можем понять основы конусов в геометрии.
Чтобы помочь вам понять чудо шишек, мы подготовили руководство, которое познакомит вас со всеми основами. Давайте начнем!
Что такое конус в математике?
В математике конус определяется как отличительная трехмерная геометрическая фигура с плоской изогнутой поверхностью, направленной вверх. Термин «конус» происходит от греческого слова «конос», что означает клин или пик. Заостренный конец называется вершиной, а плоская поверхность называется основанием.
Три основных свойства конуса:
- Он имеет одну круглую грань.

- Не имеет ребер.
- Имеет одну вершину (угол).
Что такое элементы конуса?
Тремя основными элементами конуса являются его радиус, высота и наклонная высота.
Радиус конуса
Радиус определяется как расстояние между центром круглого основания и любой точкой на окружности основания.
Высота конуса
Высота представляет собой расстояние от вершины конуса до центра круглого основания.
Наклонная высота конуса
Наклонная высота конуса — это расстояние от вершины конуса до точки на внешнем крае круглого основания. Формула для наклонной высоты получена с использованием теоремы Пифагора.
Здесь l — наклонная высота конуса, r — радиус, h — высота конуса.
Типы конусов
При изучении конусов в геометрии мы обычно рассматриваем правильный круг. Но конус может быть двух категорий, в зависимости от положения вершины на основании:
- Прямой круговой конус — это конус, вершина которого перпендикулярна основанию.
 Здесь ось образует прямой угол.
Здесь ось образует прямой угол. - Если положение вершины находится где-то за пределами центра основания, это наклонный конус. Здесь ось неперпендикулярна.
Несколько интересных фактов о конусах
1. Конус и пирамида связаны между собой. Формулы их площади поверхности также схожи!
2. Наши глаза имеют 6–7 миллионов колбочек, которые помогают им приспосабливаться к цветовой чувствительности.
Конус образован набором линий, которые соединяются с одной точкой, называемой вершиной.
Давайте изучим различные формулы, связанные с конусом, которые помогут вам решить некоторые интересные задачи в будущем.
Изогнутая поверхность конуса
Конус имеет как плоскую, так и изогнутую поверхность. Когда мы говорим о площади криволинейной поверхности конуса, это относится только к площади изогнутой части конуса, а не к круглому основанию.
Площадь криволинейной поверхности конуса определяется по формуле:
Площадь криволинейной поверхности = π ✕ r ✕ l квадратных единиц,
, где r = радиус основания конуса, l = наклонная высота конуса, и π = 3,14
Общая площадь поверхности конуса
Общая площадь поверхности конуса равна сумме площадей его круглого основания и криволинейной поверхности.
Площадь криволинейной поверхности конуса определяется по формуле:
Общая площадь поверхности = площадь криволинейной поверхности + площадь круглого основания
TSA = π ✕ r ✕ l + π ✕ r²
или TSA = π ✕ r ✕ (l + r) квадратных единиц.
Объем конуса
Объем конуса в геометрии — это количество пространства, которое занимает конус. Объем конуса также можно определить как вместимость жидкости, которую может удержать конус, если бы он был полым изнутри. Поскольку конус имеет круглое основание, мы можем легко рассчитать объем конуса, измерив радиус «r» и высоту «h».
V = $\frac{1}{3}$ ✕ (π ✕ r² ✕ h) кубическая единица.
Решенные примеры
Пример 1: Найдите объем конуса, где r = 5 см и h = 7 см.
Решение : Используя формулу объема конуса, получаем:
V = (1/3)πr² h
Здесь r = 5 см, h = 7 см
V= $ \frac{1}{3}$ ✕ 3,14 ✕ 5 ✕ 5 ✕ 7
= $\frac{1}{3}$ ✕ 549,5 = 183,16 см³
Пример 2. Рассчитайте площадь криволинейной поверхности конуса, где радиус основания 8 см, высота наклона 24 см.
Рассчитайте площадь криволинейной поверхности конуса, где радиус основания 8 см, высота наклона 24 см.
Решение . Площадь криволинейной поверхности конуса можно найти по формуле
Площадь криволинейной поверхности данного конуса = 3,14 ✕ 8 ✕ 24 = 602,88 см².
Пример 3. Если высота наклона конуса 25 см, а его радиус 7,5 см, найдите общую площадь поверхности конуса.
Решение :
Общая площадь поверхности конуса равна,
Общая площадь поверхности = π ✕ r ✕ (l + r)
Здесь r = 7,5 см, а l = 25 см.
Следовательно,
Общая площадь поверхности заданного конуса = 3,14 ✕ 7,5 ✕ (7,5 + 25)
= 23,55 ✕ (32,5)
= 765,37 см²
Практические задачи
870,82 см
820,53 см³
Правильный ответ: 870,82 см³
Используя формулу объема конуса, получаем:
V = (1/3) πr² h
Здесь r = 8 см, h = 13 см
V= $\frac {1} {3} $ ✕ 3,14 ✕ 8 ✕ 8 ✕ 13
= $ \ frac {1} {3} $ ✕ 2612. 48 = 870,82 см 9 0003
48 = 870,82 см 9 0003
1298,67 см²
1349.502
43,4444444442929294444444444444444444444444444444444444444444444444444444444444444444444444444a2н 9н02
9000 2
9000 2
92.5044. Правильный ответ: 1243,44 см²
Общая площадь поверхности конуса равна
Общая площадь поверхности = π ✕ r ✕ (l + r)
Здесь r = 12 см, а l = 21 см.
Следовательно,
Общая площадь поверхности заданного конуса = 3,14 ✕ 12 ✕ (12 + 21)
= 37,68 ✕ 33
= 1243,44 см²
659,4 см²
782.4 CM²
689 CM²
69.6 CM2
689 CM²
69.6 CM²
689 CM²
689 CM²
99.6 CM² 689 CM U. : 659,4 см²
Площадь криволинейной поверхности конуса можно найти по формуле
Площадь криволинейной поверхности = π ✕ r ✕ l
Здесь r = 10 см, l = 21 см заданный конус = 3,14 ✕ 10 ✕ 21 = 659,4 см².
Часто задаваемые вопросы
Сколько граней и вершин у конуса?
Конус имеет одну грань с одной вершиной. Заостренная вершина или вершина конуса также называется его вершиной.
Заостренная вершина или вершина конуса также называется его вершиной.
Какие реальные примеры конуса?
Колбочки окружают нас повсюду. Шляпы, которые мы используем на вечеринках, рождественская елка, которую мы видим во время праздничных гуляний, а иногда даже морковь, которую мы едим, являются реальными примерами конуса.
Чем конус отличается от треугольника?
Конус представляет собой трехмерную геометрическую фигуру с круглым основанием и заостренным краем. Треугольник, с другой стороны, представляет собой двумерную фигуру, которая имеет три ребра и вершины.
Конус. Формулы, характеристики и свойства конуса
Навигация по странице: Определение конуса Элементы конуса Объем конуса Площадь поверхности конуса Уравнение конуса Основные свойства конуса
Определение.
Конус представляет собой геометрическое тело, образованное совокупностью лучей, исходящих из точки вершины (вершины) и пересекающих любую плоскую поверхность, а при пересечении образуют основание конуса.
| Рис.1 | Рис.2 | |
| Рис.3 | Рис.4 |
Элементы конуса
Определение. Вершина (вершина) конуса — это точка (К), из которой выходят лучи.
Определение. Основание конуса плоское образуется в результате пересечения плоской поверхности и всего излучения, исходящего от вершины конуса. В конус могут входить такие основания, как окружность, эллипс, парабола и гипербола.
Определение. Боковая высота (L) прямого круглого конуса — это расстояние от любой точки окружности до вершины конуса.
Формула. Боковая высота прямого кругового конуса через радиус R и высоту H (по теореме Пифагора):
Боковая высота прямого кругового конуса через радиус R и высоту H (по теореме Пифагора):
L = √R 2 + H 2
Определение. Направляющая кривая конуса – кривая, описывающая основание конуса контура.
Определение. Боковая сторона конуса есть множество всех образующих конуса. То есть поверхность которой образована движением образующей по направляющей кривой конуса
Определение. Площадь поверхности конуса, состоящая из боковой поверхности конуса и оснований.
Определение. Высота конуса (H) – это отрезок, который исходит из вершины конуса и перпендикулярен его основанию.
Определение. Ось конуса (а) представляет собой линию, проходящую через вершину конуса и центр основания.
Определение. Осевое сечение конуса представляет собой конусообразную плоскость сечения, проходящую через ось конуса. Это сечение образует равнобедренный треугольник, стороны которого образованы образующей, а основание треугольника является диаметром основания конуса.
Определение. Касательная плоскость к конусу представляет собой плоскость, проходящую через образующую конуса и перпендикулярную осевому сечению конуса.
Определение. Конус, основанный на окружности, эллипсе, параболе или гиперболе, соответственно называется круговой, эллиптический, гиперболический или параболический конус (последние два имеют бесконечный объем).
Определение. Прямой конус представляет собой конус, ось которого перпендикулярна основанию. В таком конусе ось совпадает с высотой и все образующие равны.
Формула. Объем круглого конуса :
| В = | 1 | πHR 2 |
| 3 |
Формула. Площадь боковой грани (A l ) прямого конуса по радиусу R и длине образующей L:
A l = πRL
Формула. Суммарная площадь поверхности (A t ) прямой окружности с точки зрения радиуса R и длины образующей L:
Суммарная площадь поверхности (A t ) прямой окружности с точки зрения радиуса R и длины образующей L:
А t = πRL + πR 2
Определение. Наклонный конус — это конус, ось которого не перпендикулярна основанию. В таком конусе ось не совпадает с высотой.
Формула. Объем любого конуса :
| В = | 1 | AH |
| 3 |
Определение. Усеченный конус представляет собой часть конуса, расположенную между конусом основания и плоскостью пересечения конуса.
Формула. Объем усеченного конуса :
| В = | 1 | (A 2 H — A 1 h) |
| 3 |

Уравнение конуса
1. Уравнение прямого кругового конуса с центром в начале координат в декартовой системе координат (x, y, z) :
| x 2 | + | y 2 | — | z 2 | = 0 |
| a 2 | b 2 | c 2 |
2. Уравнение прямого эллиптического конуса с центром в начале координат в декартовой системе координат (x, y, z) :
| x 2 | + | y 2 | = | z 2 |
| a 2 | b 2 | c 2 |
Основные свойства конуса
1. Все образующие непосредственно конуса равны.
2. При вращении прямоугольного треугольника вокруг его катета на 360° образуется правильный круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180° образуется прямоугольный круговой конус.
4. При пересечении плоскостей конуса параллельно основанию конуса образуется окружность. (См. Усеченный конус).
5. Если пересечение плоскостей не параллельно конусу и не перекрывается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения, проходящая через основание, образуется на пересечении параболы (рис. 4).
7. Если плоскость проходит через верхнее сечение, то пересечение образует равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса составляет одну четвертую высоты центра основания.
Формулы геометрии
Площадь. Формулы и свойства квадрата
Прямоугольник. Формулы и свойства прямоугольника
Параллелограмм. Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Круг, диск, сегмент, сектор. Формулы и свойства
Эллипс. Формулы и свойства эллипса
Цилиндр. Формулы и свойства цилиндра
Конус. Формулы, характеристики и свойства конуса
Область. Формулы площади
Периметр. Формулы периметра
Объем. Формулы объема
Формулы площади поверхности
Формулы и свойства ромба
Круг, диск, сегмент, сектор. Формулы и свойства
Эллипс. Формулы и свойства эллипса
Цилиндр. Формулы и свойства цилиндра
Конус. Формулы, характеристики и свойства конуса
Область. Формулы площади
Периметр. Формулы периметра
Объем. Формулы объема
Формулы площади поверхности
Все таблицы и формулы
Определения, формулы Imp, примеры, свойства
- Написано Гурудатом
- Последнее изменение 19-07-2022
- Автор Гурудат
- Последнее изменение 19-07-2022
Конус: Конус – это трехмерный твердотельный геометрический объект, имеющий круглое основание и заостренный край наверху, называемый вершиной или вершиной. Он имеет одну криволинейную поверхность и одно круглое основание, одну вершину и одно ребро.
Элементами конуса являются радиус, высота и наклонная высота. Радиус \(r\) — это расстояние между центром круглого основания и любой точкой на окружности основания. Высота \(h\) конуса — это расстояние от вершины конуса до центра круглого основания. Наклонная высота \(l\) — это расстояние от вершины конуса до любой точки на окружности конуса. В этой статье давайте подробно разберемся с концепцией конуса и его свойствами.
Высота \(h\) конуса — это расстояние от вершины конуса до центра круглого основания. Наклонная высота \(l\) — это расстояние от вершины конуса до любой точки на окружности конуса. В этой статье давайте подробно разберемся с концепцией конуса и его свойствами.
Последнее обновление:
? 18 октября : Центральный совет среднего образования (CBSE) выпустил CBSE 10-й и 12-й лист данных по основным предметам.
? 21 октября : CBSE выпустила 10-й и 12-й листы данных для второстепенных предметов.
Изучение концепций экзамена на Embibe
Здесь, в Embibe, вы можете получить бесплатный пробный тест CBSE Revised MCQ 2021 по всем темам. Тест MCQ, предлагаемый Embibe, курируется на основе пересмотренных учебников CBSE Class Books, бумажных шаблонов и учебного плана на 2021 год. В этой серии пробных тестов представлен широкий выбор соответствующих вопросов и их решений. Кандидаты в совет CBSE могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои экзамены совета.
В этой серии пробных тестов представлен широкий выбор соответствующих вопросов и их решений. Кандидаты в совет CBSE могут пройти эти бесплатные пробные тесты, чтобы попрактиковаться и найти области, в которых им нужно улучшить свои экзамены совета.
Объем конуса: формула, примеры
Содержание- Введение в конусы
- Что такое конус?
- Какой формы конус?
- Что такое формулы конуса?
- Каковы свойства конуса?
- Какие бывают типы конусов?
- Решенные примеры — конус
- Резюме
- Часто задаваемые вопросы (FAQ) — конус
РАЗЪЯСНИТЕ СВОИ КОНЦЕПТУАЛЬНЫЕ СОМНЕНИЯ НА КОНУСЕ
Знакомство с конусами
День рождения был одним из самых радостных событий для нас в детстве. Детям нравится стоять вокруг торта, носить праздничные кепки и улыбаться от всего сердца в камеры. Не так ли? Некоторые дети сами делают шапочки на день рождения из цветной бумаги, бумаги для оригами и т. д. В этот момент они еще не подозревают, что в игру вступают геометрические фигуры. Кепка на день рождения представляет собой трехмерный объект конической формы.
Детям нравится стоять вокруг торта, носить праздничные кепки и улыбаться от всего сердца в камеры. Не так ли? Некоторые дети сами делают шапочки на день рождения из цветной бумаги, бумаги для оригами и т. д. В этот момент они еще не подозревают, что в игру вступают геометрические фигуры. Кепка на день рождения представляет собой трехмерный объект конической формы.
В наших домах, на рабочих местах, в лабораториях и т. д. есть несколько конусообразных предметов и устройств. Примеры: рожки для мороженого, вафельные рожки, дорожные конусы, воронки и т. д.
Что такое конус?
Конус представляет собой типичную трехмерную геометрическую фигуру, которая имеет плоскую поверхность и изогнутую поверхность, направленную вверх. Заостренный конец конуса называется вершиной, а плоская поверхность — основанием.
Какой формы конус?
Конус — это фигура, образованная набором отрезков, соединяющих общую точку, называемую вершиной, со всеми точками круглого основания. Расстояние от вершины конуса до основания есть высота \(h\) конуса. Круговое основание имеет радиус \(r\). Длина конуса от вершины до любой точки окружности основания есть наклонная высота \(l\).
Расстояние от вершины конуса до основания есть высота \(h\) конуса. Круговое основание имеет радиус \(r\). Длина конуса от вершины до любой точки окружности основания есть наклонная высота \(l\).
Практические экзаменационные вопросы
Что такое формулы конуса?
Чтобы вывести формулу площади поверхности и объема конуса, нужно знать наклонную высоту. Формула для наклонной высоты выводится с использованием теоремы Пифагора. 92}h\)
Попытка пробных испытаний
Какие бывают конусы?
Есть два типа конусов.
- Наклонный конус
- Правый круговой конус
Наклонный конус
Конус, поверхность которого образована отрезками прямой, соединяющими фиксированную точку с точками окружности, а неподвижная точка, лежащая на прямой, не перпендикулярна окружности в ее центре, называется наклонным конусом.
То есть, если ось конуса не перпендикулярна плоскости круглого основания, то конус является наклонным конусом.
Правый круглый конус
Прямоугольный конус – это конус с окружностью в основании и отрезком, перпендикулярным основанию, проходящим через его центр и проходящим через вершину или вершину конуса, образованного поворотом прямоугольного треугольника вдоль одной из сторон. называется прямоугольным конусом.
То есть, если ось конуса перпендикулярна плоскости кругового основания, то конус является прямым круговым конусом. 92}.\).
Вопрос 3 : Найдите площадь криволинейной поверхности прямого круглого конуса, высота наклона которого равна \(10\,{\text{см}}\), а радиус основания равен \(7\,{\text{ см}}\)
Рассмотрим \(\pi = \frac{{22}}{7}\)
Ответ: Мы знаем, что площадь криволинейной поверхности конуса \( = \pi rl\)
Дано: \(l = 10\,{\text{см}}\) и \(r = 7\, {\text{см}}\)
Итак, площадь криволинейной поверхности конуса \( = \frac{{22}}{7} \times 7 \times 10\,{\text{c}}{{\ текст{м}}^2}\) 92}\)
Вопрос 4 : Высота конуса равна \(16\,{\text{см}}\), а радиус основания равен \(12\,{\text{см}}\). 2}} \right) } \) 92} = 12 \умножить на 32,028\)
2}} \right) } \) 92} = 12 \умножить на 32,028\)
\( = 384,336\)
Следовательно, стоимость покраски \(50\) конусов равна \( = 384,34.\)
Резюме
Из этой статьи мы узнали, что такое форма конуса, определение конуса, элементы конуса, свойства и различные типы конуса, формулы для нахождения площади криволинейной поверхности, высоты наклона, общей площади поверхности. , и объем конуса. Также мы решили несколько примеров задач на конусы.
Площадь криволинейной поверхности конуса: формула, примеры 92}} \справа)} \)
Вопрос 2 : Как еще называется криволинейная поверхность конуса?
Ответ : Изогнутая сторона конуса также называется боковой поверхностью.
Вопрос 3 : Какой формы конус?
Ответ : Конус — это фигура, образованная набором отрезков, соединяющих общую точку, называемую вершиной, со всеми точками круглого основания.
Вопрос 4 : В чем разница между вершинами и ребрами?
Ответ : Вершина — это угол, в котором сходятся ребра. Точка, где встречаются две грани, называется ребром.
Вопрос 5 : У конуса есть \(1\) или \(2\) грани?
Ответ : Конус имеет \(2\) граней. У него одна изогнутая грань и круглое основание.
Вопрос 6 : Сколько ребер в конусе?
Ответ r : Конус имеет только одно ребро, образованное соединением круглого основания и криволинейной поверхности.
Вопрос 7 : Может ли конус катиться?
Ответ : Конус будет катиться по своей изогнутой поверхности по круговой траектории с вершиной в центре и наклонной высотой в качестве радиуса.
ПРАКТИЧЕСКИЕ ВОПРОСЫ ПО КОНУСУ
Теперь, когда у вас есть вся необходимая информация о конусах, мы надеемся, что эта подробная статья поможет вам как можно скорее. Если у вас есть какие-либо вопросы по этой статье или в целом о Cone, напишите нам через поле для комментариев ниже, и мы свяжемся с вами как можно скорее.
Если у вас есть какие-либо вопросы по этой статье или в целом о Cone, напишите нам через поле для комментариев ниже, и мы свяжемся с вами как можно скорее.
Сокращение глупых ошибок; Пройдите бесплатные пробные тесты, связанные с конусами
Калькулятор объема конуса
Создано Ханной Памула, кандидатом наук
Проверено Богной Шик, Джеком Боуотером и Аденой Бенн
Последнее обновление: 10 сентября 2022 г.
Содержание:- Формула объема конуса
- Как найти объем конуса?
- Объем усеченного конуса (объем усеченного конуса)
- Объем наклонного конуса
- Часто задаваемые вопросы
Этот калькулятор объема конуса может помочь в решении ваших математических задач или может ответить на ваши странные повседневные вопросы. Сколько мороженого помещается в мой рожок? Сколько крема можно положить в кондитерский мешок? Или каков объем моего конического бокала для шампанского? Если это вопросы, на которые вы хотели бы получить ответы, продолжайте читать!
Формула объема конуса
Конус представляет собой твердое тело с круглым основанием и единственной вершиной. Чтобы рассчитать его объем, нужно площадь основания (площадь круга: π * r²) умножить на высоту и на 1/3:
Чтобы рассчитать его объем, нужно площадь основания (площадь круга: π * r²) умножить на высоту и на 1/3:
-
объем = (1/3) * π * r² * h
Конус с многоугольным основанием называется пирамидой.
Как найти объем конуса?
Подсчитаем, сколько воды помещается в коническую часть воронки.
- Определить высоту конуса . Для нашей воронки это 4 в .
- Введите базовый радиус . Он может быть равен 3 в .
- Калькулятор теперь отображает объем конуса — в нашем случае это 37,7 у.е. в .
Помните, что вы можете изменить единицы измерения в соответствии со своими потребностями — нажмите на единицу и выберите ее из списка. Воспользуйтесь нашим инструментом для преобразования объема, если вам нужно простое преобразование единиц измерения объема.
Объем усеченного конуса (объем усеченного конуса)
Усеченный конус – это конус со срезанной вершиной, с срезом, перпендикулярным высоте. Вы можете рассчитать объем усеченного конуса, вычитая меньший объем конуса (вырезанный) из большего объема конуса (основной) или используя формулу:
Вы можете рассчитать объем усеченного конуса, вычитая меньший объем конуса (вырезанный) из большего объема конуса (основной) или используя формулу:
-
объем = (1/3) * π * глубина * (r² + r * R + R²), гдеRрадиус основания конуса, аrрадиус верхней поверхности
Пример расчета объема усеченного конуса можно найти в нашем калькуляторе горшечной почвы, так как стандартный цветочный горшок представляет собой усеченный конус.
Объем косого конуса
Косой конус — это конус, вершина которого не расположена над центром основания. Он « наклоняется » в одну сторону, подобно наклонному цилиндру. Формула объема конуса косого конуса такая же, как и для прямого.
Часто задаваемые вопросы
Как рассчитать объем конуса вручную?
Чтобы рассчитать объем конуса, следуйте этим инструкциям:
- Найдите площадь основания конуса
a. Если неизвестно, определите радиус основания конусаr.
- Найдите высоту конуса
h. - Примените формулу объема конуса :
объем = (1/3) * a * h, если известна площадь основания, илиобъем = (1/3) * π * r² * hв противном случае. - Поздравления , вы успешно вычислили объем вашего конуса!
Какая связь между объемом конуса и цилиндра?
Если конус и цилиндр имеют одинаковую высоту и радиус основания, то объем конуса равен одной трети объема цилиндра. То есть вам понадобится содержимое трех конусов, чтобы заполнить этот цилиндр. То же соотношение справедливо для объема пирамиды и призмы (при условии, что они имеют одинаковую площадь основания и высоту).
Каков объем обычного рожка мороженого?
Размер вафли для мороженого варьируется в широких пределах, но есть несколько типичных размеров:
Радиус | Высота | Том |
|---|---|---|
1 из | 6 в | 6,3 у. |
3 см | 11 см | 34,6 см³ |
2,5 см | 11,5 см | 30,1 см³ |
1 7/8 дюйма | 4 5/8 дюйма | 9,1 у.е. в |
1 3/16 дюйма | 6 в | 7,5 у.е. в |
Каков объем конуса с радиусом один и высотой три?
Напомним, что формула объема конуса гласит:
объем = (1/3) * π * r² * h
Итак, в нашем случае имеем:
объем = (1/3) * π * 1² * 3 ,
Итак, объем нашего конуса точно равен π ! Как мы все знаем, это можно приблизительно представить как объема ≈ 3,14159 .
Ханна Памула, кандидат наук
Прямой / наклонный конус
Высота (h)
Радиус (r)
Объем
Усеченный конус 917
Объем и площадь поверхности прямоугольного конуса (видео и практика)
Привет, ребята! Добро пожаловать в сегодняшнее видео, где мы поговорим об объеме и площади поверхности конуса. Мы знаем, что конус на самом деле очень похож на пирамиду. В то время как у пирамиды есть квадратное основание, которое соединяется с заостренным концом на противоположном конце, основание конуса вместо этого представляет собой круг.
Мы знаем, что конус на самом деле очень похож на пирамиду. В то время как у пирамиды есть квадратное основание, которое соединяется с заостренным концом на противоположном конце, основание конуса вместо этого представляет собой круг.
Прежде чем углубляться в детали, давайте убедимся, что вы знакомы с понятиями объема и площади поверхности. Это две ключевые особенности, которыми обладают все \(3\)-мерные фигуры. Объем — это пространство внутри \(3D\) объекта, а площадь поверхности — это просто так! Это общая площадь поверхности фигуры. Думайте об объеме как о количестве жидкости, которой вы можете заполнить объект, а о площади поверхности — как о том, сколько бумаги вы можете обернуть вокруг этого объекта. Каждый куб, сфера, цилиндр, конус (разумеется) и т. д. имеют объем и площадь поверхности; и формулы, используемые для нахождения этих измерений, различны для каждой формы. 9{2}+\pi rl\)
Где \(r\), \(h\) и \(l\) представляют разные измерения на конусе. {2}+\pi rl\) 9{2}+\pi (3)(5)\)
{2}+\pi rl\) 9{2}+\pi (3)(5)\)
Итак:
\(SA=\pi(9)+\pi (15)\)
Что равно \( 24\пи\). В конце концов, мы бы сказали, что площадь поверхности равна \(24\pi\) (или примерно \(75,4\)) квадратных единиц. Обратите внимание на то, как это измеряется! Поскольку мы говорим о площади, мы используем квадратные единицы.
Довольно просто подставить значения для \(r\), \(h\) и \(l\), верно? А что, если бы мы захотели выяснить, какого размера рожок мороженого нам понадобится, чтобы в него поместилось \(30\) кубических дюймов мягкой порции? 9{2}\)
Тогда все, что нам нужно сделать, это извлечь квадратный корень из обеих частей. Итак, когда мы это делаем, мы получаем:
\(r=\frac{3}{\sqrt{\pi }}\приблизительно 1,7\)
Фактически, поскольку линейные размеры конуса измеряются в дюймах, мы знаем, что \(r\) приблизительно равно \(1,7\text{дюймы}\).
Ладно, круто! Так что, если мы хотим вычислить площадь поверхности того конуса, о котором мы только что говорили? Теперь мы знаем три важных параметра этого конуса: объем, высоту и радиус основания. Помните, что в нашем уравнении площади поверхности нам нужны как радиус, так и наклонная высота конуса, чтобы найти площадь поверхности. Хотите верьте, хотите нет, но мы можем рассчитать наклонную высоту, используя значение \(h\), которое нам дали, и значение \(r\), которое мы только что нашли. Нам просто нужно использовать теорему Пифагора. 9{2}ч\). Но помните, нам дан диаметр круглого основания, а не его радиус. Мы не могли просто подставить \(10\) вместо \(r\) в этом уравнении. Вместо этого мы используем то, что знаем о связи между диаметром и радиусом: радиус круга равен \(\frac{1}{2}\) его диаметра. Таким образом, радиус этого конуса на самом деле составляет \(5\) футов; и теперь найти объем довольно просто.
Итак, если мы подставим известные нам переменные, мы получим:
\(V=\frac{1}{3}\pi (5)^{2}(12)\) 92)}\), где \(r\) представляет радиус круглого основания, а \(h\) представляет высоту или высоту конуса.
Q
В чем разница между высотой и наклонной высотой?
A
«Высота» конуса и «наклонная высота» конуса — это не одно и то же. Высота 90 146 90 147 конуса считается вертикальной высотой или высотой конуса. Это перпендикулярное расстояние от вершины конуса до центра круглого основания. наклонная высота конуса — это расстояние от вершины конуса вниз по стороне конуса до края круглого основания.
Q
Как найти вертикальную высоту конуса, зная радиус и наклонную высоту?
A
Вертикальная высота, радиус и наклонная высота конуса образуют три линии, образующие прямоугольный треугольник. Это означает, что теорему Пифагора можно использовать для определения пропущенного значения, если известны как минимум два значения. Например, можно рассчитать вертикальную высоту, если заданы радиус и наклонная высота. Если конус имеет радиус \(92\), что упрощается до \(r=3\).
Практические вопросы
Вопрос № 1:
Чему равен объем конуса высотой 14 дюймов и радиусом 6 дюймов с точностью до ближайшего целого числа?535 in 3
582 in 3
528 in 3
498 in 3
Show Answer
Answer:
The correct answer is 528 in 3 .
2h\), и подставьте 6 вместо 9.3\)
Скрыть ответ
Вопрос №2:
Чему равен объем пи конуса высотой 12 см и радиусом 9 см?324π CM 3
346π CM 3
445π CM 3
3899. 3
Показ Ответ
9057 9072 3. Начните с формулы объема конуса и подставьте 9 вместо 9.3\)
Скрыть ответ
Вопрос №3:
Найдите объем конуса, имеющего радиус 6 метров и высоту 11 метров. Выразите ответ через число пи.227π M 3
432π M 3
145π M 3
132π M 3
Показать ответ
.
Начните с формулы объема конуса и подставьте 6 вместо 9.3\)
Скрыть ответ
Вопрос № 4:
Найдите объем конуса диаметром 18 м и высотой 30 м. Выразите ответ до ближайшего целого числа.2,676 m 3
2,304 m 3
2,499 m 3
2,545 m 3
Show Answer
Answer:
The correct answer is 2,545 m 3 . Если диаметр 18 метров, то диаметр 93\)
Скрыть ответ
Вопрос №5:
Найдите объем конуса, имеющего радиус 6 м и высоту 10 м. Выразите ответ до ближайшего целого числа.488 YD 3
377 YD 3
366 YD 3
411 YD 3
Показать ответ
.

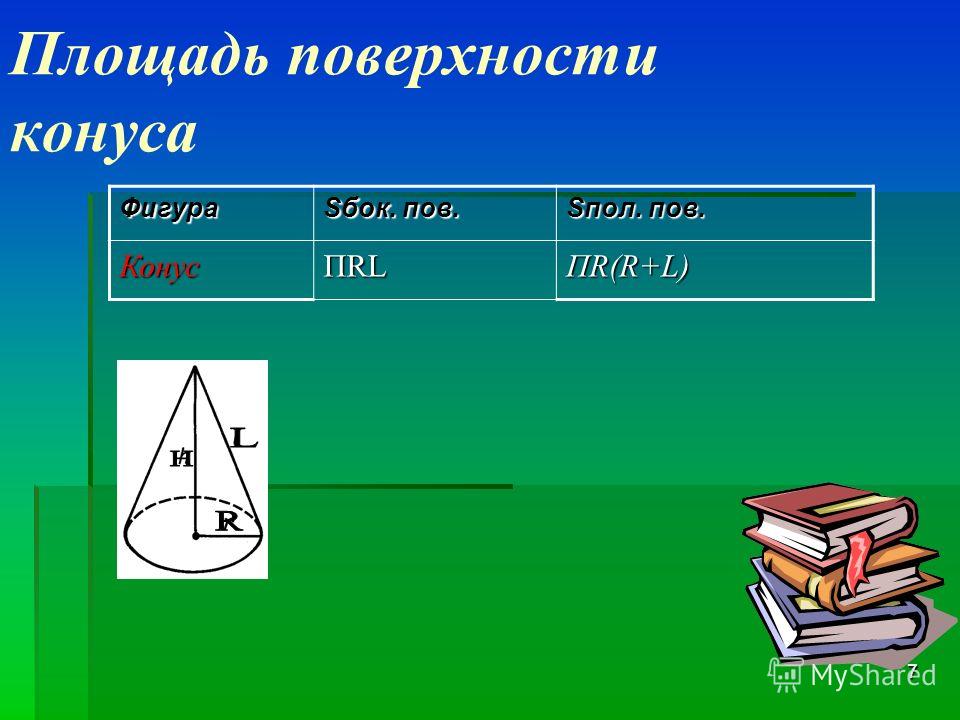 Ф. Бутузов, Ю.А. Глазков
Ф. Бутузов, Ю.А. Глазков

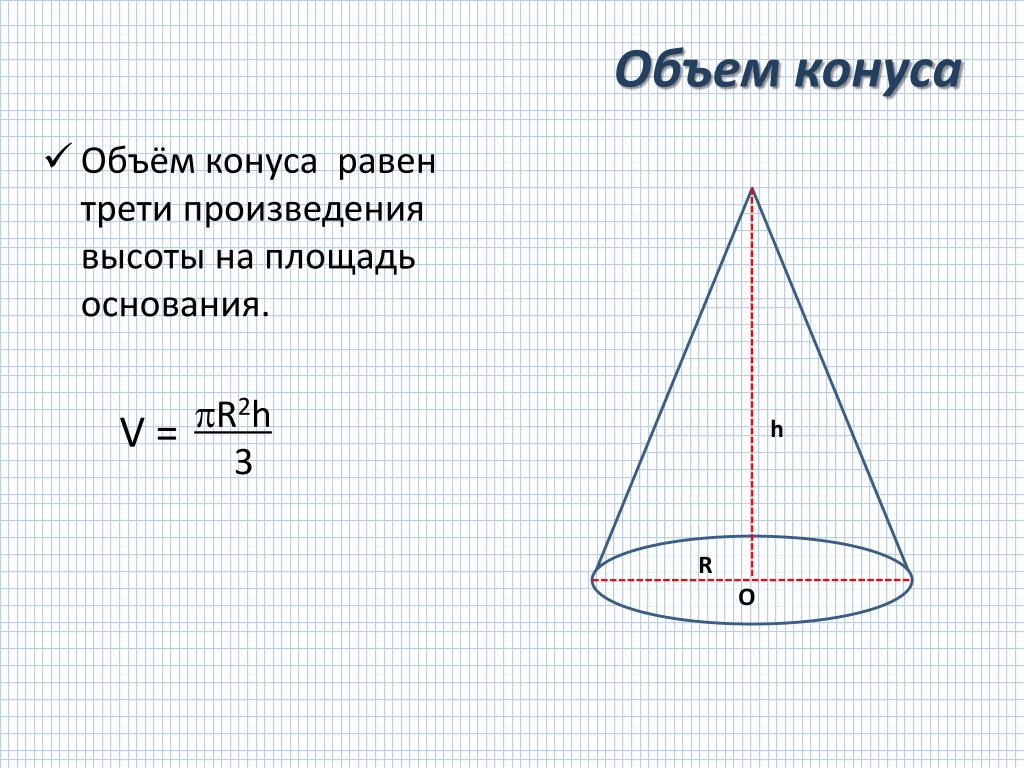 {2}H.}
{2}H.}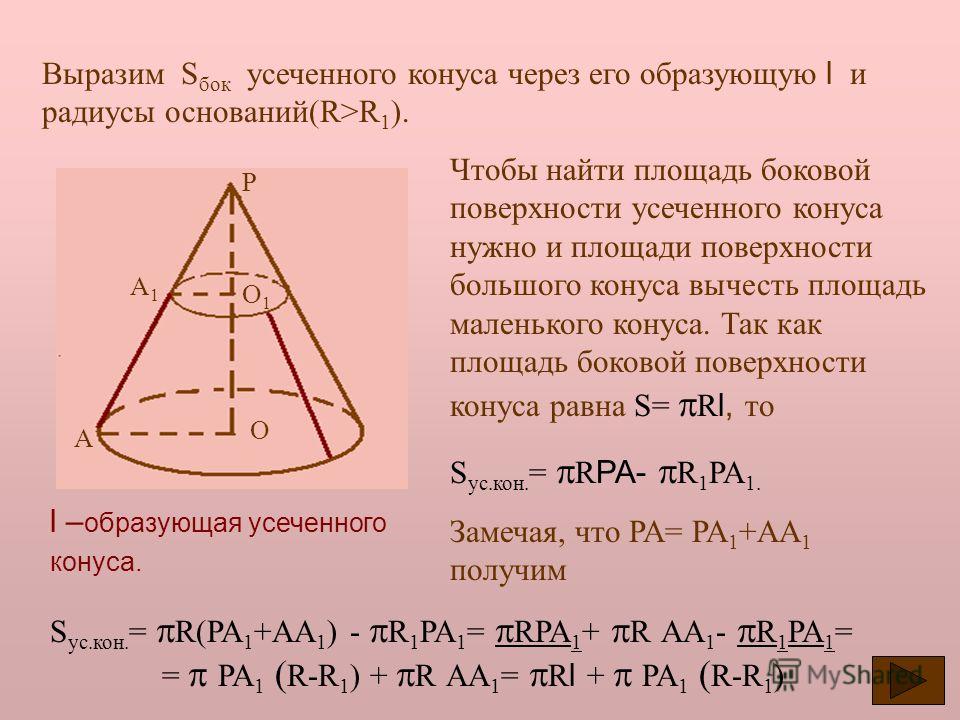 {n}f(x,y,z)}
для любого действительного числа α
.
{n}f(x,y,z)}
для любого действительного числа α
.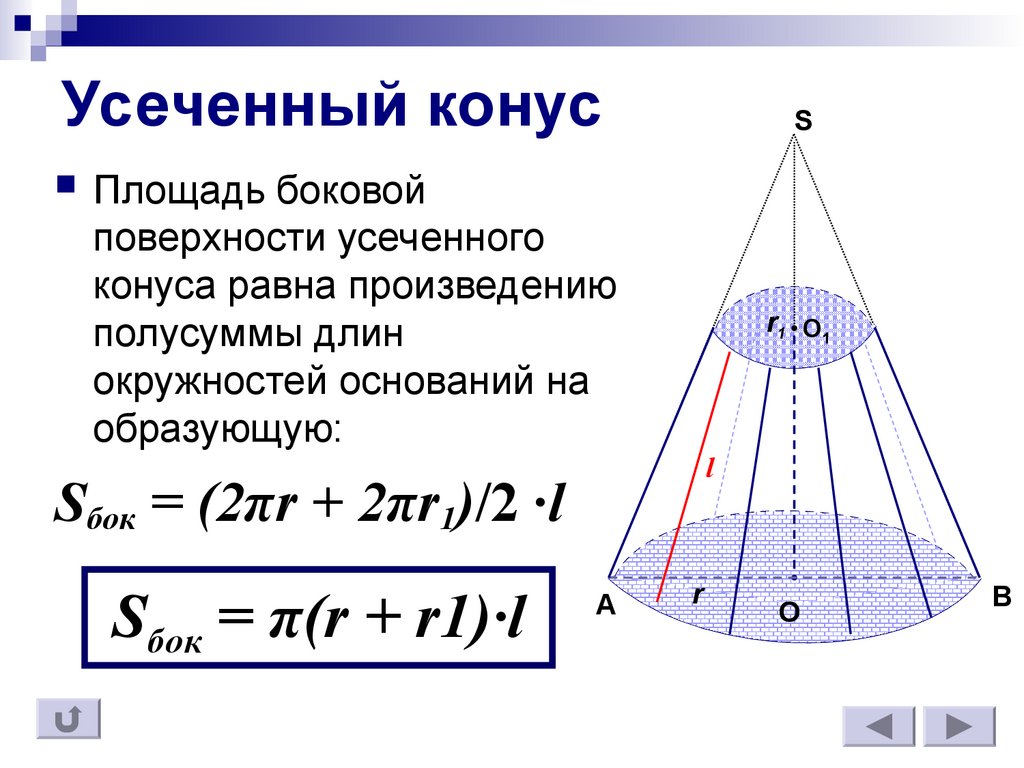
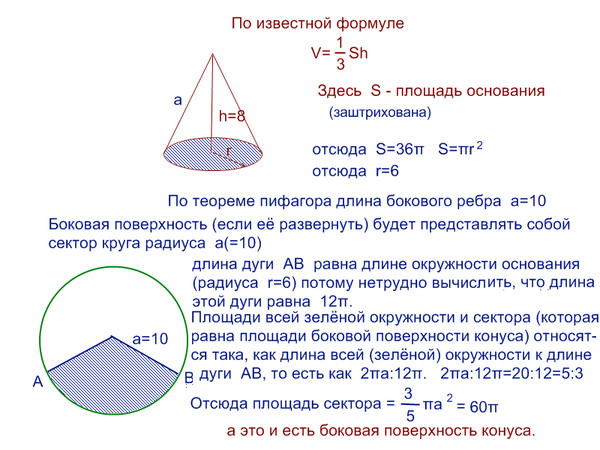 Сечение конуса разными плоскостями.
Сечение конуса разными плоскостями.