Как объяснить ребенку действия с дробями
Дроби – одна из самых непростых, но важных тем в математике. Не подготовленному ученику изучить ее и выполнять различные действия бывает сложно, но при правильном подходе самые трудные разделы точной науки становятся понятными и доступными. Для исследования темы дробей нужно применить фантазию, воображение и доносить материал в игровом формате. Чтобы ученик мог самостоятельно выполнять задания, преподавателю понадобится время и терпение.
Термин «дробь» обозначает деление. В рамках школьной программу к изучению этой темы приступают в средней школе, но педагоги рекомендуют начать ее освоение в дошкольном возрасте. Получение базовых знаний о дробях позволяют тренировать навык счета, концентрацию, логическое и пространственное мышление.
С чего начать изучение дробей детям
Начинать изучение темы следует с понятия «долей». Для этого можно использовать наглядные примеры – разделить блюдо или предмет на равные части, объяснив, что такое половина, треть и четверть.
Хорошим упражнением будет сбор конструктора, где дети могут делить целое на части, запоминать одинаковые кубики и пересчитывать различные элементы. Чем большее количество долей получается при делении, тем меньше они будут. Ребенку следует осознать пользу и востребованность дробей повседневной жизни. Когда он это поймет, то процесс понимания темы будет легче и быстрее.
Дробь не является целым числом. Для записи нужного количества долей применяют понятие обыкновенная дробь. Она состоит из двух показателей: знаменателя и числителя, которые разделены наклонной или горизонтальной чертой. Числитель указывается над дробной чертой, а знаменатель записывается снизу и указывает на количество частей от целого.
Виды дробей: правильные и неправильные дроби
Существуют правильные и неправильные обыкновенные дроби. Правильными называют те дроби, в которых показатель числителя меньше знаменателя (3/4). В неправильных дробях значение числителя больше, чем знаменателя, и в них можно выделить целую часть (6/4).
Числитель делится на знаменатель, вследствие чего формируется целая часть и остаток. К неправильным дробям относятся и те, у которых показатели числителя и знаменателя равны (10/10). Составные части такой дроби превращаются в единицу.
Смешанные числа можно трансформировать в неправильные дроби. Для этого нужно часть целого умножить на знаменатель, а к полученной сумме прибавить числитель. Для упрощения дробей необходимо и сокращать. Если обе части дроби равны, то можно их разделить на единое число. При сложении обыкновенных дробей знаменатель остается без изменений, а числители складывают. Если знаменатели различны, то нужно определить наименьшее общее кратное значение. Аналогичным образом проводится и вычитание дробей. Чтобы умножить обыкновенные дроби, необходимо последовательно перемножить знаменатели и числители между собой. При делении дробей необходимо умножить числитель первой на знаменатель второй и наоборот. При сравнении дробей нужно обратить внимание на числитель: больше будет та, у которой его значение.
При одинаковых числителях будет больше та дробь, знаменатель которой меньше. Если при сравнении одна из дробей является неправильной, то она автоматически становится больше. Эти математические операции часто вызывают затруднения у детей, поэтому разбираться в них нужно на практике.
Если в знаменателе дроби есть числа, кратные десяти, то они, соответственно, называются десятичными. Ученики записывают показатель целого, отделяя запятой десятые части (5,2). В математике существуют также дроби без значения целого. Для этого записывают ноль и после запятой указывают значение числителя (0,05). Десятичные дроби особенно удобны в точных вычислительных операциях. Такая система давно доказала свою практичность, она проста и понятна для учеников.
Когда детям нужно изучать дроби
Для того чтобы изучение темы дробей и их места в математической науке было продуктивным, необходимо тщательно разбирать каждые действия с педагогами, закрепляя полученные знания и умения на практике. Обучение математике онлайн развивает способность анализировать, критически мыслить и делать выводы, воспринимать и обрабатывать информацию, обобщать и систематизировать знания.
Дистанционный формат занятий позволяет приобретать навыки в удобном темпе и комфортных условиях, а результаты будут заметны после первых уроков. Чем раньше дети познакомятся с понятием дробей, тем проще им будет в дальнейшем их записывать и совершать математические действия.
Обучение дробям в школе AMAkids
В Академии развития детского интеллекта AMAkids проводится обучение математике в режиме онлайн для детей от шести лет. В штате образовательной организации работают квалифицированные преподаватели с большим опытом, которые могут найти индивидуальный подход к каждому ребенку. Занятия проводятся на специальной интерактивной платформе с применением электронного пособия и игровых тренажеров. Педагоги доносят материал не в форме стандартных лекций, а в процессе увлекательной игры, руководствуясь авторской методикой.
Математика онлайн от Академии AMAkids состоит из нескольких блоков: арифметика, геометрия, основы программирования и финансовой грамотности. На занятиях по арифметики дети изучают меры величин, знакомятся с понятиями целых чисел и обыкновенных дробей, учатся выполнять простые числовые операции.
На уроках геометрии учащиеся знакомятся с основными геометрическими фигурами и их характерными особенностями, исследуют понятия площади и периметра, симметрии и асимметрии.
Финансовая грамотность включает в себя изучение финансовой безопасности, понятий цены и стоимости, знакомятся с историей валютной системы. Ученики узнают о том, как совершать покупки правильно и с максимальной пользой. На основах программирования дети узнают об алгоритмах и множествах. Дети решают логические задачи и примеры разного уровня сложности, выполняют задания на развитие памяти и произвольного внимания.
Сравнение дробей: правила, примеры, решения
Когда дело доходит до дробей, мы обычно сравниваем две или более. На самом деле, мы сталкиваемся с дробями в нашей повседневной жизни. Простой пример: если вы разрезаете яблоко на две части, оно тоже будет дробью. В принципе, сравнение двух дробей означает определение большей и меньшей части среди них.
Понятие сравнения дробей
Определение
Дробь – это число, представляющее часть целого.
Это целое может быть одним объектом или группой объектов. Дробь записывается как \[\frac{p}{q}\] , где p и q являются целыми числами и q≠0.
Такие числа, как \[\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{1}{17}\] известны как дроби.
Число под линией деления называется знаменателем. Оно описывает нам, на сколько равных частей делится целое. Число над строкой называется числителем. Оно говорит нам, сколько равных частей взято.
Пример: \[\frac{3}{7}, \frac{5}{19}, \frac{3}{116}\] и т.д. являются дробями.
Сравнить две дроби – это значит понять, какая из них больше, а какая меньше. Из двух дробей с равными знаменателями больше будет та, у которой числитель больше, и меньше та, у которой числитель меньше. Примеры сравнения дробей в реальном времени включают различные действия, такие как проверка сниженных цен во время покупок, достижение продаж определенного продукта, медицинские рецепты врача, результаты тестов и экзаменов и т.
д. Опять же, сравнение дробей – это то, что мы испытываем или с чем сталкиваемся в своей повседневной жизни. Если достаточно сосредоточиться, то можно легко получить практическое представление об одном и том же каждый день, выполняя обычные домашние дела и математические вычисления.
Правила сравнения дробей
Есть несколько правил, которым мы должны следовать при сравнении дробей:
- Когда знаменатели дроби одинаковы, дробь с меньшим числителем является меньшей дробью, а дробь с большим числителем считается большей дробью.
- Когда числители равны, дроби считаются эквивалентными.
- Когда дроби имеют один и тот же числитель, чем меньше числитель, тем более значимой считается дробь.
Сравнение дробей с одинаковыми знаменателями
Определение
Подобные дроби — это две или более фракции, имеющие один и тот же знаменатель.
Пример: \[\frac{3}{7}, \frac{5}{7}, \frac{6}{7}\] являются «подобными дробям».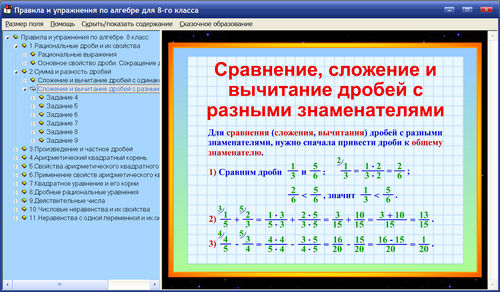
Сравнение подобных дробей
В этом методе необходимо проверить, совпадают ли знаменатели или нет. Если знаменатели одинаковы, то дробь с большим числителем является более значительной дробью. Дробь с меньшим числителем – это меньшая дробь. Если и числители, и знаменатели равны, то дроби также идентичны. Пример: Давайте сравним \[\frac{6}{17}\] и \[\frac{16}{17}\].
- Найдем знаменатели данных дробей: \[\frac{6}{17}\] и \[\frac{16}{17}\]. Здесь знаменатели одинаковы.
- Сравним числители: 16>6.
- Теперь дробь с большим числителем будет больше.
- Следовательно, \[\frac{6}{17}\] и \[\frac{16}{17}\].
Сравнение дробей с разными знаменателями
Определение
Неподобные дроби — это две или более дроби имеющие разные знаменатели.
Пример: \[\frac{5}{17}\] и \[\frac{3}{14}\] являются неподобными дробями.
Сравнение неподобных дробей
Чтобы сравнить дроби с разными знаменателями, следует начать с поиска наименьшего общего знаменателя, чтобы сделать их значения одинаковыми.
Когда знаменатели преобразуются в одни и те же знаменатели, то дробь с большим числителем является более значимой — например, \[\frac{1}{2}\] и \[\frac{2}{5}\].
- Найдите знаменатели данных дробей: \[\frac{1}{2}\] и \[\frac{2}{5}\], здесь знаменатели не совпадают. Возьмем 2 и 5 так, что общий множитель равен 10. Здесь, \[\frac{1}{2}=\frac{1}{2} \times \frac{5}{5} \text{и} \frac{2}{5}=\frac{2}{5} \times \frac{5}{5}\].
- Теперь сравним доли,\[\frac{5}{10}\] и \[\frac{4}{10}\], знаменатели одинаковы.
- Мы сравним числители, 5 > 4.
- Сравнение дроби, \[\frac{5}{10}\] > \[\frac{4}{10}\]. Дробь с большим числителем является большей дробью.
- Таким образом, \[\frac{5}{10}\] > \[\frac{4}{10}\]. Поэтому, \[\frac{1}{2}\] > \[\frac{2}{5}\]
Если знаменатели разные, а числители одинаковые, то можно легко сравнить дроби, посмотрев на их знаменатели. Дробь с меньшим знаменателем имеет большее значение. Дробь с большим знаменателем имеет меньшее значение.
Например, \[\frac{2}{3}\] > \[\frac{2}{6}\]
Десятичный метод сравнения дробей
В этом методе необходимо сравнить десятичные значения дробей. Сначала числитель делится на знаменатель, а затем дробь преобразуется в десятичную дробь. Затем сравниваются десятичные значения.
Пример: \[\frac{4}{5} и \frac{6}{8}\].
- Сначала запишем заданные дроби \[\frac{4}{5} и \frac{6}{8}\] в десятичной форме. \[\frac{4}{5}\]= 0,8 и \[\frac{6}{8}\]= 0,75.
- Теперь сравните десятичные значения, 0,8 > 0,75.
- Здесь дробь с большим десятичным значением является большей дробью.
- Следовательно, \[\frac{4}{5} и \frac{6}{8}\].
Сравнение дробей с помощью перекрестного умножения
В этом методе числитель одной дроби перекрестно умножается на знаменатель другой дроби.
Пример: \[\frac{1}{2} \text { и } \frac{3}{4}\], когда мы перекрестно умножаем, мы получаем 1×4=4 и 2×3=6.
- Теперь цифры 4 и 6 являются числителями, которые мы получаем, если выразим \[\frac{1}{2} \text { и } \frac{3}{4}\] с общим знаменателем 8.
- Далее, новые дроби с одинаковыми знаменателями будут равны \[\frac{4}{8} \text { и } \frac{6}{8}\].
- Итак, число 6 является большим числителем, \[\frac{4}{8} < \frac{6}{8}\].
- Следовательно, \[\frac{1}{2} < \frac{3}{4}\].
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Решение примеров на сравнение дробей
1. Сравните две дроби \[\frac{4}{7}\] и \[\frac{2}{7}\].
Ответ: Мы видим, что знаменатели в данных дробях одинаковы. Здесь мы будем следовать правилу, согласно которому, когда знаменатели дроби одинаковы, дробь с меньшим числителем является меньшей дробью, а дробь с большим числителем считается большей дробью.
Итак, сравните числители 4>2
Следовательно, \[\frac{4}{7}>\frac{2}{7}\]
2. Сравните две заданные дроби: \[\frac{6}{13}\] и \[\frac{6}{20}\].
Ответ: Мы видим, что числители в данных дробях одинаковы. Здесь мы будем следовать правилу, что, когда дроби имеют одинаковый числитель, чем меньше знаменатель, тем больше дробь.
Итак, сравните знаменатели 13>20
Следовательно, \[\frac{6}{13} > \frac{6}{20}\]
3. Сравните данные дроби, используя метод перекрестного умножения: \[\frac{3}{8}\] и \[\frac{5}{10}\].
Ответ: Мы будем использовать метод перекрестного умножения, поэтому это означает, что необходимо умножить 3×10=30 и 5×8=40.
Здесь 30<40
Следовательно, \[\frac{3}{8} < \frac{5}{10}\]
4. Расположите дроби \[\frac{5}{6}, \frac{11}{16}\] и \[\frac{13}{18}\] в порядке возрастания.
Ответ: Сначала мы вычислим общий знаменатель, он равен 144.
Теперь запишем дроби как эквивалентные:
\[\frac{5}{6}=\frac{5 \times 24}{6 \times 24}=\frac{120}{144}\]
\[\frac{11}{16}=\frac{11 \times 9}{16 \times 9}=\frac{99}{144}\]
\[\frac{13}{18}=\frac{13 \times 8}{13 \times 8}=\frac{104}{144}\]
Так, 99 < 104 < 120, следовательно \[\frac{99}{144}<\frac{104}{144}<\frac{120}{144}, \text { итак } \frac{11}{16}<\frac{13}{18}<\frac{5}{6}\]
5.
Что больше: \[\frac{4}{8}\] или \[\frac{6}{12}\]?
Сравним с помощью десятичного метода.
Ответ: Мы можем использовать калькулятор 4÷8 и 6÷12. Теперь получаем, что \[\frac{4}{8}=0,5 \text { и } \frac{6}{12}=0,5\]
Итак, обе доли равны 0,5 = 0,5
Следовательно, \[\frac{4}{8}=\frac{6}{12}\]
дробей — это сложно! | G’Day Math
Дроби — это сложно!
Обзор
Многие ученики — и взрослые! — боятся дробей. И их причины естественны и абсолютно уместны: дроби нюансированы, тонки и тверды.
В ранние годы мы узнаём, что дроби — это «части целого», части круга, точки на числовой прямой между целыми числами и тому подобное. То есть нам дан ряд моделей того, что такое дробь. Но никогда не выясняется, какая из этих моделей говорит окончательную, окончательную истину. Мы идем от одной модели к другой, и нам остается верить, что каким-то образом это покрывает все.
Дело в том, что каждая модель говорит лишь частичную правду.
Ни одна модель не говорит всей правды.
Например, модель частей пирога «объясняет» сложение дробей: чтобы сложить половину пирога и треть пирога, просто физически соедините эти две части пирога и выясните, какая часть всего пирога составляет . Но модель пирога бесполезна для понимания умножения дробей: что такое половина пирога, умноженная на треть пирога? («Одна шестая часть пирога в квадрате»?)
Модель числовой прямой предполагает, что дроби — это числа (вот они: на числовой прямой!), но чтобы объяснить их умножение, мы возвращаемся к поговорке «средств умножения», обращаясь к частям целой модели.
Это миска спагетти идей и оправданий!
Но работа этих младших классов важна и правильна. Это развивает нашу интуицию и понимание того, как должна вести себя система счисления «дробей», какими бы они ни были. Старшеклассники и взрослые готовы к следующему заключительному этапу истории дроби: отступить от истории, представленной в начальных классах, и подумать о том, что все это пытается сказать, и создать всесторонний обзор того, что происходит на самом деле.
в этой миске с макаронами. Я никогда не видел, чтобы это делалось в школьной программе. Итак, давайте сделаем это сейчас!
Эти заметки, Арифметика, глава 5, из нового учебника по арифметике, предназначены для всех тех, кто понимает, что никогда не «знал» дроби, но хочет получить их сейчас.
Наслаждайтесь!
32. Слишком много моделей для интуиции
33. Одна (все еще не идеальная) Модель
Пироги и студенты
Переход назад
Некоторые очевидные свойства фракций
Следует: что -то странное
Более очевидные свойства фракций
Логическое следствие наших четырех свойств
Сравнивая фракции
Zero в качестве знаменателя
Проверка фракций
Смешанные номера
Разделительные фракции
Умножение фракций
A Happy Clactidest: Happy Sticipide: Happy Sticindest: Happy Sticindest: слово «из»
Подразделение и «из»
Добавление фракций
Фракции вычитания
Снова смешанные числа
Умножение и деление на положительные числа больше и меньше одного
34.
Математическая истина о фракциях
35. , Итак… Что такое дробь?
Если вас тоже интересуют десятичные дроби и игра дробей и десятичных дробей, дайте мне знать, и я пришлю вам шестую главу!
Присоединяйтесь к обсуждению в Facebook и Twitter и поделитесь этой страницей, используя кнопки ниже.
Уроки
Ресурсы
Книги
Поднимите свое понимание на новый уровень с помощью простых для понимания книг Джеймса Тантона.
ПРОСМОТРЕТЬ КНИГИ
Умножение и деление дробей с переменными
Чтобы умножить и разделить дроби с переменными:
- Полностью разложить на множители все числители и знаменатели
- Использовать правила умножения и деления дроби:
$$ \cssId{s4}{\frac{A}{B}\cdot\frac{C}{D}} \cssId{s5}{= \frac{AC}{BD}} $$
(Чтобы умножить дроби, умножить «поперек»)
$$ \cssId{s7}{\frac{A}{B}\div\frac{C}{D}} \cssId{s8}{= \frac{A}{B}\cdot\frac{D}{C}} \cssId{s9}{= \frac{AD}{BC}} $$
(Чтобы разделить на дробь, вместо этого умножьте на обратную величину)
- Отмените любые общие факторы; то есть избавиться от любых лишних «факторов $\,1\,$’ 92+4x+3)}} \cssId{s25}{\cdot} \cssId{s26}{\frac{x+1}{x+4}} $
Интересно сопоставить
исходное выражение (до упрощения),
и упрощенное выражение
(после отмены).
Хотя они равны
почти для всех значений $\,x\,$
они немного отличаются,
из-за отмены:
[Следующую таблицу лучше смотреть широко. На маленьких экранах используйте ландшафтный режим.]
| Ценности из $\,х\,$ | 92+20х+15}
\cdot
\фракция{х+1}{х+4}}
$$ В факторизованной форме: $$ \cssId{s49}{\frac{\hphantom{5}(x+1)(x+3)(x-3)}{5(x+1)(x+3)(x+4)}} $$ | Упрощенное выражение: $$ \cssId{s51}{\frac{(x-3)}{5(x+4)}} $$ | Сравнение |
| $х = -4$ | не определено (деление на ноль) | не определено (деление на ноль) | вести себя так же: оба не определены |
| $х = -1$ | не определено (деление на ноль) | $$ \cssId{s60}{\frac{-1-3}{5(-1+4)} = -\frac{4}{15}} $$ | Наличие
$\,\фракция{х+1}{х+1}\,$
вызывает
точка прокола в
$\,х = -1\,$;
см. первый график ниже |
| $х = -3$ | не определено (деление на ноль) | $$ \frac{-3-3}{5(-3+4)} = -\frac{6}{5} $$ | Наличие $\,\фракция{х+3}{х+3}\,$ вызывает точка прокола в $\,х = -3\,$; см. первый график ниже |
| все остальные ценности $\,х\,$ | оба определены; значения равны | вести себя так же: значения равны | |
График
$\displaystyle
\ cssId {s72} {\ frac {\ hphantom {5} (x + 1) (x + 3) (x-3)} {5 (x + 1) (x + 3) (x + 4)}}
$
График:
$\displaystyle
\cssId{s74}{\frac{(x-3)}{5(x+4)}}
$
Концептуальная практика
Для более продвинутых учащихся доступен график.