Основные правила математики с примерами. 7 класс Алгебра.
Основные правила математики с примерами. 7 класс Алгебра.
Содержание
- Уравнения. Равносильные уравнения. Свойства
- Линейное уравнение
- Одночлены и многочлены
- Формулы сокращенного умножения
- Степень. Свойства степени с целым показателем
- Функция. Область определения и область значений функции
- Линейная функция, её график и свойства
- Системы линейных уравнений с двумя переменными
- Графический метод решения системы двух линейных уравнений с двумя переменными
- Решение системы двух линейных уравнений с двумя переменными методом подстановки
- Решение систем линейных уравнений методом сложения
Уравнения. Равносильные уравнения. Свойства
Корень уравнения
- Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство.
- Решить уравнение означает найти все его корни или убедиться, что их вообще нет.
 Также можно сказать, что решить уравнение — это значит найти множество его корней.
Также можно сказать, что решить уравнение — это значит найти множество его корней.
2 x + 6 =36x = 15 —корень уравнения, поскольку2 · 15 + 6 =3636 = 36 —верное равенство.5x — 5x = 100 —не имеет корней, посколькуx(5 — 5)∥0 = 100 0 = 100 — неверно.
Равносильные уравнения
Два уравнения называют равносильными, если они имеют одно и тоже множество корней.
2x — 5 = 5 ≡равносильно 4x — 10 =10,поскольку x = 5 корень и для 1—го, и для 2—го уравнения.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
2x — 5 = 7 +52x — 5 + 5 = 7 + 52x = 12x = 12 : 2x = 6
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
2x — 5 =+5→ 72x = 7 + 52x =12x = 12 : 2x =6
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному
12x = 24 : 1212x :12 = 24 : 12x = 2. x5 = 3 · 5×5 · 5 = 3 · 5x = 15
x5 = 3 · 5×5 · 5 = 3 · 5x = 15
Линейное уравнение
Уравнение вида , где — переменная, и некоторые числа, называют линейным уравнением с одной переменной.
| Значения и | |||
|---|---|---|---|
| Корни уравнения | -любое число | корней нет |
2x = 0, 5y —3 = 12 — линейные уравненияx2 —4 = 0, 5x = 8 —нелинейные уравнения
Одночлены и многочлены
Одночлены
- Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
2x, 356x2y, 0,2a20, b, 15 — одночлены.
- Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
2x, 356x2y, 0,2a20 — одночлены стандартного вида.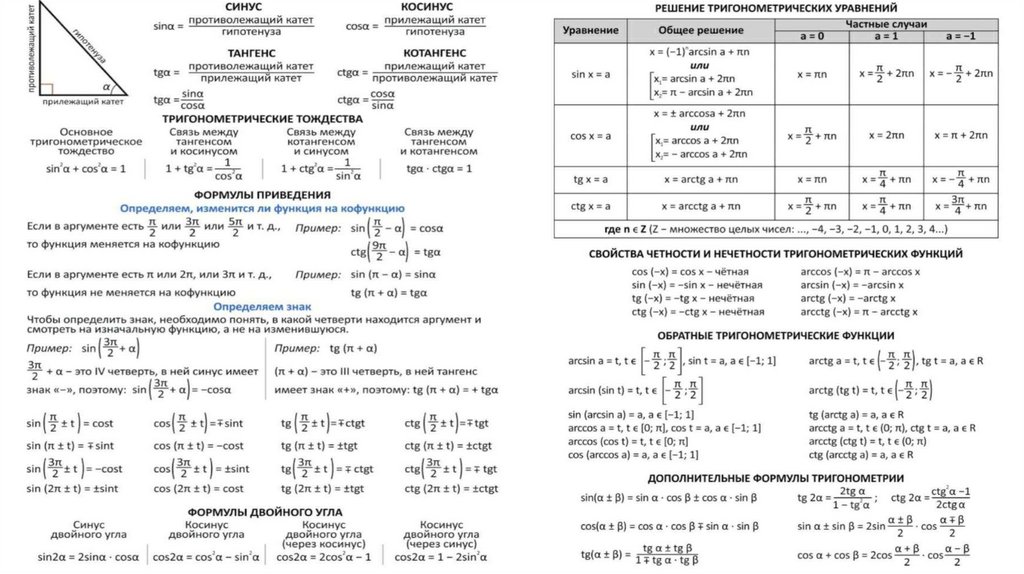
- Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
2x, 356x2y, 0,2a20.2, 356, 0,2 —коэффициенты.
- Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
2x2y3z , —15x2y3z, 0,5x2y3z —подобные.2x2y3z и 2x2y3 — не подобные.
- Нуль-одночлен степени не имеет.
Многочлены
- Выражение, являющееся суммой нескольких одночленов, называют многочленом.
2x + 3x2y
- Одночлены, из которых состоит многочлен, называют членами многочлена.
2x + 3x2y —многочлен;2x и 3x2y — его одночлены
- Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.
Умножение одночлена на многочлен
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.
Умножение многочлена на многочлен
Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
Формулы сокращенного умножения
Разность квадратов двух выражений
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:
Произведение разности и суммы двух выражений
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:
Квадрат суммы и квадрат разности двух выражений
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражении:
Преобразование многочлена в квадрат суммы или разности двух выражений
Формулы
позволяют «свернуть» трёхчлен в квадрат двучлена.
Трёхчлен, который можно представить в виде квадрата двучлена, называют полным квадратом.
Сумма и разность кубов двух выражений
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:
Многочлен называют неполным квадратом суммы.
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:
Многочлен называют неполным квадратом разности.
Степень. Свойства степени с целым показателем
Свойства степени с целым показателем
Для любого и любых целых выполняются равенства:
Для любых , и любого целого выполняются равенства:
Функция. Область определения и область значений функции
Функция
Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной пeременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Способы задания функции
Описательный, табличный, с помощью формулы, графический.
График функции
Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Линейная функция, её график и свойства
- Функцию, которую можно задать формулой вида , где и — некоторые числа, — независимая переменная, называют линейной.
- Графиком линейной функции является прямая.
- Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными
Уравнение с двумя переменными
Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.
Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.
Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.
Если некоторая фигура является графиком уравнения, то выполняются два условия:
- все решения уравнения являются координатами точек, принадлежащих графику;
- координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.
Графический метод решения системы двух линейных уравнений с двумя переменными
Графический метод решения системы уравнений заключается в следующем:
- построить в одной координатной плоскости графики уравнений, входящих в систему;
- найти координаты всех точек пересечения построенных графиков;
- полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:
- если прямые пересекаются, то система имеет единственное решение.
- если прямые совпадают, то система имеет бесконечно много решении.
- если прямые параллельны, то система решений не имеет.
Решение системы двух линейных уравнений с двумя переменными методом подстановки
Чтобы решить систему линейных уравнений методом подстановки, следует:
- выразить из любого уравнения системы одну переменную через другую;
- подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
- решить уравнение с одной переменной, полученное на втором шаге;
- подставить найденное значение переменной в выражение, полученное на первом шаге;
- вычислить значение второй переменной;
- записать ответ.
Решение систем линейных уравнений методом сложения
Чтобы решить систему линейных уравнений методом сложения, следует:
- подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
- сложить почленно левые и правые части уравнений, полученных на первом шаге
- решить уравнение с одной переменной, полученной на втором шаге
- подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
- вычислить значение второй переменной;
- записать ответ.

Данная информация взята из УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир
Все формулы по алгебре за 10 11 класс
Все формулы по алгебре за 10 11 класс
Ежедневно с 10:00 до 21:00
Оставьте заявку и мы перезвоним Вам
Ваш город: Ростов-на-Дону
Ваш город —
Ростов-на-Дону?Выберите Ваш город
Введите название вашего города
- Кострома
Формулы по математике для ЕГЭ
Как выучить все формулы по математике к ЕГЭ
Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.
Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.
Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.
И целого учебного года вполне достаточно, чтобы все выучить.
Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.
Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.
Математические формулы школьного курса алгебры
Степени и корни
Формулы сокращенного умножения
Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители
Логарифмические формулы
Формулы тригонометрии
Основные формулы тригонометрии
Тригонометрические уравнения
Значения тригонометрических функций
Формулы приведения
Сумма и разность углов
Формулы двойного и тройного аргумента
Формулы половинного аргумента
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Формулы дифференциального исчисления
Формулы векторной алгебры из школьного курса математики
Формулы арифметической и геометрической прогрессии
Геометрические формулы школьного курса математики для ЕГЭ
Планиметрия
Стереометрия
Выучить формулы по математике – это еще не все, что надо для успешной сдачи ЕГЭ. Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.
Опыт решения задач, знания правил оформления заданий на экзамене не менее важны. Приглашаем всех школьников 11-х классов на курсы подготовки к ЕГЭ ПАРАГРАФ. С нами Вы подготовитесь к ЕГЭ наиболее продуктивно.
Учите формулы по математике и сдавайте ЕГЭ на максимальные баллы!
Группы разного уровня подготовки
Группы для обучения подбираются согласно текущему уровню подготовки к ЕГЭ Вашего ребенка Это позволяет сделать обучение максимально эффективным для каждого
Полный контроль за процессом обучения
Вам предоставляется доступ в облачный личный кабинет с полной информацией о посещаемости и успеваемости ученика, а также домашними заданиями и тестами
Уникальный преподавательский коллектив
К работе с Вашими детьми допускаются только опытные и харизматичные профессиональные репетиторы и преподаватели ВУЗов, способные зажечь искру любви к предмету
Авторские методики обучения и мотивации
Система тестов, уникальная аттестация, целеполагание и тьюторская поддержка учеников позволяют увеличить эффективность обучения и мотивировать Вашего ребенка на успех
Остались вопросы?
Свяжитесь с нами и мы ответим на все вопросы
- ООО «АКАДЕМИЯ» ОГРН 1056165000924 / ИНН 6165119640 Ростов-на-Дону, Пушкинская, 135/33 8 (863) 311-28-28 info@ege-paragraf.
 ru
ruМы в соцсетях:
Данный сайт не является публичной офертой. Текущую цену в рублях Вы можете уточнить позвонив по телефону: +7 (863) 311-28-28
Ежедневно с 10:00 до 21:00
Оставьте заявку и мы перезвоним Вам
Ваш город: Ростов-на-Дону
Ваш город —
Ростов-на-Дону?Выберите Ваш город
Введите название вашего города
- Кострома
Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.
Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.
Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.
Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.
Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.
Ваш город —Ростов-на-Дону?
Произведение тригонометрических функций.
Ege-paragraf. ru
26.04.2019 17:58:10
2019-04-26 17:58:10
Источники:
Https://ege-paragraf. ru/o-czentre/poleznaya-informacziya/matematicheskie-formulyi-po-algebre-i-geometrii-dlya-ege. html
Математика формулы 10 класс – Основные формулы тригонометрии. Алгебра 10-11 класс Мордкович. – Рамблер/класс — Таловская средняя школа » /> » /> .keyword { color: red; }
Все формулы по алгебре за 10 11 класс
Формулы приведения предназначены для того, чтобы привести тригонометрическую функцию произвольного угла к тригонометрической функции наименьшего из углов.
Рассмотрим конкретный пример. Рассмотрим дуги в и, соответственно, (рис. 1).
Как прямоугольные по гипотенузе и острому углу
Из равенства треугольников следует равенство соответствующих сторон.
Функции большего угла приведены к функциям меньшего угла. В этом суть формул приведения.
Для применения формул приведения тригонометрическую функцию любого угла нужно привести к одному из видов: .
Формул приведения много, но все они подчиняются двум правилам:
Для аргументов функция меняется на кофункцию, т. е. синус на косинус и наоборот, тангенс на котангенс и наоборот.
Для аргументов функция не меняется.
Примеры на первое правило:
Знак пока не учитываем, он определяется вторым правилом, пока важно понять, в каких случаях функция меняется на кофункцию, а в каких не меняется.
Для аргументов вида наименование функции следует изменить на кофункцию.
Для аргументов вида наименование функции не меняется.
Второе правило (для знака приведенной функции, функции угла ).
1) Считаем угол острым,
2) Определяем четверть и знак в ней приводимой функции (функции слева).
3) Ставим этот знак перед приведенной к углу функцией (функцией справа).
Примечание: Угол может быть любым, острым мы его считаем условно, для применения правила.
Примеры на второе правило:
Угол находится во второй четверти. Во второй четверти, ставим знак плюс.
Угол находится в третьей четверти. В третьей четверти ставим знак минус.
Угол находится во второй четверти. Во второй четверти ставим знак минус.
Угол находится в четвёртой четверти. В четвёртой четверти ставим знак минус.
Угол находится в третьей четверти. В третьей четверти ставим знак минус.
Угол находится во второй четверти, во второй четверти ставим знак минус.
Угол находится во второй четверти. Во второй четверти ставим знак минус.
Угол находится в четвёртой четверти. В четвёртой четверти ставим знак минус.
Итак, мы рассмотрели различные примеры применения первого и второго правил формул приведения.
Рассмотрим приемы, облегчающие запоминание формул приведения.
1. «Правило лошади». Глядя на числовую окружность легко ответить на вопрос, меняется ли функция на кофункцию.
Для аргументов, т. е. аргументов, отложенных от вертикальной оси, на вопрос, меняется ли функция на кофункцию, лошадь, глядя на точки, будет утвердительно кивать – функция меняется на кофункцию (рис. 10) .
Для аргументов, т. е. аргументов, отложенных от горизонтальной оси, лошадь, глядя на точки будет отрицательно мотать головой – функция не меняется (рис. 10) .
2. Используем периодичность и четность.
Вспомним, что наименьший положительный период у тангенса и котангенса равен Это значит, что
У синуса и косинуса наименьший положительный период равен
Рассмотрим примеры на использование формул приведения.
1) Вычислить значения всех тригонометрических функций для
Угол находится во второй четверти, синус в этой четверти положителен, косинус, тангенс и котангенс отрицательны.
2) Вычислить значения всех тригонометрических функций угла
Угол находится в третьей четверти, в третьей четверти синус и косинус отрицательны, тангенс и котангенс положительны.
Мы рассмотрели формулы приведения и пояснили их на конкретных примерах. В дальнейшем мы будем активно использовать формулы приведения для преобразования тригонометрических выражений.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 10 класса (учебн
Конспект урока по математике 10 класс Учебник: Мордкович А. Г. «Алгебра и начала анализа» 10-11 класс; Мордкович А.
 Г. «Задачник10-11 класс» Тема: «Формулы приведения»
Г. «Задачник10-11 класс» Тема: «Формулы приведения»Если под знаком преобразуемой тригонометрической функции содержится аргумент вида
Перед полученной функцией от аргумента t (в правой части равенства) надо поставить тот знак, который имела бы преобразуемая функция при условии, что 0 t.
Давайте прочитаем правило в учебнике. (Чтение правила по учебнику)
Попробуем применить это правило к уже перечисленным формулам приведения:
Sin ( + t) = — sin t
Преобразуемая функция аргумента t или полученная функция
Аргумент ( + t), а в третьей четверти преобразуемая функция синус имеет знак отрицательный.
Cos ( + t) = — sin t
Аргумент + t из второй четверти, а в ней преобразуемая функция косинус имеет знак минус, поэтому перед полученной функцией ставим знак «минус».
А теперь с помощью изученного правила получите новую формулу приведения:
Tg ( – t) = ctg t (Работа в парах)
Это правило используется и в случаях, когда аргументы заданы в градусах
Соs (360 + α) = cos α. (Работа в парах)
(Работа в парах)
Выступление ребят.
Кто же из математиков и когда получил формулы приведения. Послушаем сообщение о Леонардо Эйлере.
1. Решаем номер 151 (бв) (один обучающийся у доски, остальные в тетрадях):
Б) cos ( — t) = cos t
В) cos + α) = sin α
А) cos (90 — α) = sin α
Г) cos (180 + α) = — cos α
№ 154 (а, г) (Самостоятельно)
А) tg (90 — α) = ctg α
Г) ctg (360 + α) = ctg α
Подводим итог выполненной работы:
Для чего мы применяли в данных упражнениях формулы приведения? (Для упрощения выражения).
2. А сейчас будем их применять для вычисления.
№ 155 (аб) – разбор учителем с помощью учащихся зданий на доске
А) sin 240 = sin (180 + 60) = — sin 60 = —
Б) tg 300 = tg (36060) = — tg 60 = — 3
3. Работа в группах № 155 (г): какая группа найдет больше различных способов вычисления:
Г) сtg 315 = ctg (360 — 45= — ctg 45 = -1
Сtg 315 = ctg (270 + 45= — tg 45 = -1
№ 158 (а) Упрощаем более сложное упражнение
Sin (90 — α) + cos (180 + α) + tg (270 + α) + ctg (360 + α) = cos α — cos α – ctg α + ctg α = 0
Самостоятельная работа по вариантам с последующей проверкой:
I Вариант № 159 (б):
II Вариант № 159 (г)
165 (А):
2 cos (2 + t) + sin ( + t) = 3
2 cos t + cos t = 3
Б) sin ( + t) + 2 cos ( + t) = 3
— sin t – 2 sin t = 3
Рефлексия по розданным печатным карточкам.
Задачи на следующий урок: чем будем заниматься? (Применять формулы приведения при доказательстве тождеств, решений уравнений).
Домашнее задание: параграф 8; №№ 152 (аб), 153 (бв), 154 (бв), 156 (аб), 161 (а)
Приложение 1
Приложение 2
№ 160 (б) упростите:
Математика.10 класс. Формулы сложения. docx — План урока по математике на …
Раздел 10.4.A. Тригонометрия
Тема: Формулы сложения
Дата: 27.031.04.2017
Date:
Класс: 10 g
Урок № 12
Ожидаемые
Результаты данного
Урока
Learning objectives that
This
Is
Contributing to
Критерии успеха
Языковые цели
Language objectives
Привитие ценностей
Межпредметные связи
Навыки использования
ИКТ
Первоначальные
Знания
Школа: НИШ ХБН г. Атырау
Имя учителя: Адилгалиева Ж. С
Количество
Присутствующих:
Количество
Отсутствующих:
АТ 10.5.выводить и применять формулы приведения, формулы сложения,
Формулы двойного/половинного аргумента, формулы преобразования
Суммы и разности тригонометрических функций в произведение, формулы
Преобразования произведения тригонометрических функций в сумму при
Решении задач
Отработать навыки использования тригонометрических формул сложения,
Двойного аргумента и преобразования суммы в произведение;
Рассмотреть построение графиков функций, полученные путем сжатия,
Растяжения и перемещения исходных графиков тригонометрических функций;
Сформировать умение применять формулы сложения и их свойства, а так же
Свойства функций при решение заданий различной степени сложности;
Учащиеся достиг цели, если
Выводит и применяет формулы приведения, формулы сложения, формулы
Двойного/половинного аргумента, формулы преобразования суммы и разности
Тригонометрических функций в произведение, формулы преобразования
Произведения тригонометрических функций в сумму при решении задач
Учащиеся понимают и объясняют, как использовать графические калькуляторы
Предметная лексика и терминология.
Sin, cos, tan (синус, косинус, тангенс)
Угол возвышения/понижения
Инверсия, горизонтальная, ось (оси), область определения.
Арксинус, арккосинус, арктангенс
Формула приведения/сложения
Преобразование в точке пересечения, преобразование функции
Серия полезных фраз для диалога/письма
Давать четкие, точно выраженные указания по использованию калькулятора,
Например:
Ввести функцию.
Перейти в в 3 ряду.
Выбрать НАСТРОЙКА/УВЕЛИЧЕНИЕ.
Установить расстояние (интервал).
Настроить yMax/yMin.
Нажать на кнопку
Использовать стрелкууказатель
Уважение, сотрудничество, открытость
Привитие ценностей осуществляется посредством/через парную и групповую виды
Работ.
Power point
Имеет представления о тригонометрических функциях
Ход урока
Этапы урока
Planned timings
Первый урок
First lesson
1 мин
Актуализация
Опорных знаний
Запланированная деятельность на уроке
Planned activities
Приветствие учащихся, проверка готовности к уроку,
Мотивация учащихся, объявляет план урока
Включение в деловой ритм, подготовка класса к работе
Активировать знания, необходимые для изучения новой темы
Организация учащихся на постановку темы и целей урока
Актуализация познавательного интереса к изучаемой теме
Ресурсы
Resources
Учебно-методический материал по алгебре (10 класс) по теме: Основные формулы по тригонометрии
По теме: методические разработки, презентации и конспекты
Контроль знаний основных формул по алгебре и началам анализа учащихся 10 класса при подготовке к ЕГЭ.
Материал служит для контроля знаний тригонометрических формул при подготовке к ЕГЭ….
Основные формулы тригонометрии
Основные формулы тригонометрии, которые необходимы при подготовке к ЕГЭ по математике…
ФОРМУЛЫ ПО ТРИГОНОМЕТРИИ ИСПОЛЬЗУЕМЫЕ НА ЕГЭ
Каждый год выпускаю классы и имею подборку тригонометрических формул используемых в обеих частях ЕГЭ, которыми хочу поделиться с Вами….
Основные формулы по геометрии
Формулы по геометрии…
Индивидуальные карточки по алгебре для 10 класса на тему: «Основные формулы тригонометрии»
Цель: сформировать целостное представление об основных понятиях тригонометрии. Задачи:обобщить и систематизировать материал о тригонометрических функциях;изучить методы и способы нахождения значений тр…
Урок по алгебре в 10-м классе по теме «Основные формулы sinа и cosа»
Урок в 10-м классе по алгебре на тему: «Основные формулы sinа и cosа». УМК: . Алгебра и начала анализа. 10 класс: Учебник для общеобразовательных учреждений/С. М. Никольский, М. К. Потапов, Н….
УМК: . Алгебра и начала анализа. 10 класс: Учебник для общеобразовательных учреждений/С. М. Никольский, М. К. Потапов, Н….
Основные формулы по физике
Основные формулы по физике…
Материалы школьной программы по математике за 10 класс
В 10 классе начинается изучение Основ математического анализа. Перво-наперво изучается одно из основных понятий математического анализа – числовая функция. Изучаются свойства различных числовых функций и приводится примерный план для исследования функций.
2 Вычислить значения всех тригонометрических функций угла.
Xn—-8sbanwvcjzh9e. xn--p1ai
25.12.2017 7:24:11
2017-12-25 07:24:11
Источники:
Https://xn—-8sbanwvcjzh9e. xn--p1ai/raznoe-2/matematika-formuly-10-klass-osnovnye-formuly-trigonometrii-algebra-10-11-klass-mordkovich-rambler-klass. html
Основные формулы тригонометрии. Алгебра 10-11 класс Мордкович. – Рамблер/класс » /> » /> .keyword { color: red; }
Все формулы по алгебре за 10 11 класс
ОСНОВНЫЕ ФОРМУЛЫ ТРИГОНОМЕТРИИ
1. Формулы, связывающие тригонометрические функции одного и того же аргумента:
Формулы, связывающие тригонометрические функции одного и того же аргумента:
2. Формулы, связывающие функции аргументов, из которых один вдвое больше другого:
1) sin 2х = 2 sin х cos х;
2) cos 2х = cos 2 х — sin 2 х;
3. Формулы сложения аргументов:
1) sin (х + у) = sin х cos у + cos х sin у;
2) sin (х — у) = sin х cos у — cos х sin у;
3) cos (х + у) = cos х cos у — sin х sin у;
4) cos (х — у) = cos х cos у + sin х sin у;
4. Преобразование сумм тригонометрических функций в произведения:
Преобразование произведений тригонометрических функций в суммы:
3. Формулы сложения аргументов:
1) sin (х + у) = sin х cos у + cos х sin у;
2) sin (х — у) = sin х cos у — cos х sin у;
3) cos (х + у) = cos х cos у — sin х sin у;
4) cos (х — у) = cos х cos у + sin х sin у;
ОСНОВНЫЕ ФОРМУЛЫ ТРИГОНОМЕТРИИ
1. Формулы, связывающие тригонометрические функции одного и того же аргумента:
2. Формулы, связывающие функции аргументов, из которых один вдвое больше другого:
1) sin 2х = 2 sin х cos х;
2) cos 2х = cos 2 х — sin 2 х;
Формулы, связывающие тригонометрические функции одного и того же аргумента 2.
Class. rambler. ru
07.03.2019 11:18:44
2019-03-07 11:18:44
Источники:
Https://class. rambler. ru/temy-gdz/osnovnye-formuly-trigonometrii-algebra-10-11-klass-mordkovich-43172.htm
таблица, примеры использования с ответами по алгебре для 7 класса
В статье мы рассмотрим формулы сокращенного умножения, вспомним основные правила и решим несколько примеров
Наталия Юмагулова
Учитель математики
В математике есть формулы, которые просто необходимо держать всегда в памяти, так как большинство заданий ЕГЭ не могут обойтись без их применения. Это формулы сокращенного умножения. Изучать ФСУ начинают в 7-м классе. Тема считается непростой, но знание их поможет избежать утомительных вычислений и снизить вероятность ошибки.
Что такое формула сокращенного умножения
Из названия следует, что эти формулы позволяют проводить умножение, возведение в степень чисел и многочленов сокращенно, то есть быстрее при более компактной записи решения. Эти тождества служат для разложения многочленов на множители, упрощения выражений и приведения многочленов к стандартному виду.
Эти тождества служат для разложения многочленов на множители, упрощения выражений и приведения многочленов к стандартному виду.
Для удобства мы собрали все формулы сокращенного умножения в одну таблицу. Ее можно использовать при выполнении домашних заданий по алгебре. При решении задач вы можете заменить буквы a и b числами, переменными или даже целыми выражениями.
Формулы сокращенного умножения следует выучить. Без первой тройки формул о «тройке» и мечтать нельзя, без остальных — о «четверке» и «пятерке».
Как запомнить все эти, на первый взгляд, сложные формулы? Можно использовать метод аналогии. Присмотритесь к ФСУ внимательнее и вы увидите, что формула квадрата суммы очень похожа на формулу квадрата разности: здесь нужно запомнить только одно отличие — «плюс» меняется на «минус».
В ТЕМУ
Также легко запомнить куб суммы и куб разности: их формулы практически одинаковы, снова поменялись только знаки. Сумма кубов и разность кубов тоже похожи, к тому же они напоминают первые две формулы.
Сумма кубов и разность кубов тоже похожи, к тому же они напоминают первые две формулы.
И еще: научитесь правильно проговаривать формулы сокращенного умножения. Очень частая ошибка учеников — говорить «формула суммы квадратов». Такой формулы не существует!
Не будем ограничиваться курсом 7-го класса по алгебре и добавим еще несколько формул.
Формула возведения в квадрат суммы трех, четырех и большего количества слагаемых:
(a1+a2+…+an)2=a12+a22+…+an−12+an2+2·a1·a2+2·a1·a3+2·a1·a4+…+2·a1·an−1+2·a1·an+ +2·a2·a3+2·a2·a4+…+2·a2·an−1+2·a2·an+…+2·an−1·an.
Квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых. Для примера возведем в квадрат с использованием этой формулы сумму трех слагаемых x, y и z. Имеем: (x+y+z)2=x2+y2+z2+2·x·y+2·x·z+2·y·z. В частном случае при n=2 эта формула становится уже известной нам формулой квадрата суммы двух слагаемых.
Формула возведения в квадрат суммы трех, четырех и большего количества слагаемых:
an−bn=(a−b)·(an−1+an−2·b+an−3·b2+…+a2·bn−3+a·bn−2+bn−1)
Частными случаями этой формулы являются: разность квадратов (при n=2), разность кубов (при n=3) и сумма кубов (при n=3 и если b заменить на −b).
Важно!
При выполнении заданий важны некоторые свойства формул:
(a – b)2n = (b – a)2n, где n ∈ N
(a – b)2n+1 = –(b – a)2n+1, где n ∈ N
N – множество натуральных чисел
Примеры использования формул сокращенного умножения
Лучше всего формулы запоминаются на практике. Решайте как можно больше примеров, и все формулы запомнятся сами собой, а вы избавитесь от скучной и малоэффективной зубрежки. Итак, рассмотрим примеры и их решения с помощью формул сокращенного умножения.
Решайте как можно больше примеров, и все формулы запомнятся сами собой, а вы избавитесь от скучной и малоэффективной зубрежки. Итак, рассмотрим примеры и их решения с помощью формул сокращенного умножения.
Пример №1
Упростим выражение:
Применим формулу разности квадратов и получим:
Пример №2
Найдем значение выражения:
Применим формулы квадрата разности и квадрата суммы, раскроем скобки, приведем подобные слагаемые, сократим дробь и получим:
Популярные вопросы и ответы
Почему формулы сокращенного умножения изучают на алгебре в 7 классе?
Формулы сокращенного умножения изучаются в 7 классе, так как именно на этом этапе ребята знакомятся с понятием многочлена и действиям с ними.
Как появились формулы сокращенного умножения?
О существовании этих формул люди узнали около 4-х тысяч лет назад. Еще жители древнего Вавилона и Египта пользовались ими. Впервые математическую закономерность квадрата суммы доказал древнегреческий ученый Евклид, живший в в III веке до н.э.
Еще жители древнего Вавилона и Египта пользовались ими. Впервые математическую закономерность квадрата суммы доказал древнегреческий ученый Евклид, живший в в III веке до н.э.
Он использовал геометрический способ вывода формулы, так как ученые древней Эллады не использовали буквы для обозначения чисел: не «a2», а «квадрат на отрезке a», не «ab», а «прямоугольник, заключенный между отрезками a и b». На общепринятом языке математические формулы обосновал Исаак Ньютон.
Сколько всего формул сокращенного умножения?
В школьной практике используются 7 формул сокращенного умножения.
Где используются формулы сокращенного умножения?
Центральное применение формул сокращенного умножения было найдено в выполнении тождественных преобразований:
- упрощении выражений;
- решении уравнений;
- умножении многочленов;
- сокращении дробей;
- выделении квадрата двучлена, в основе которого лежит формула сокращенного умножения — квадрат суммы.

В 10-м и 11-м классах можно применять ФСУ для преобразования выражений всех других видов (например, дробных, иррациональных, логарифмических, тригонометрических), а также при решении интегралов.
Фото на обложке: SHVETS production, pixals.com
Комментарии для сайта Cackle
правила по математике с 5 по 9 класс(математика, алгебра)
Главная / Старшие классы / Алгебра
Скачать
792.17 КБ, 513797.docx Автор: Пачина Вероника Владимировна, 21 Мар 2015
Все основные правила по математике за курс основной школы.
Автор: Пачина Вероника Владимировна
Похожие материалы
| Тип | Название материала | Автор | Опубликован | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| документ | правила по математике с 5 по 9 класс(математика, алгебра) | Пачина Вероника Владимировна | 5 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | правила по математике с 5 по 9 класс(математика, алгебра) | Пачина Вероника Владимировна | 21 Мар 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| разное | Рабочая программа по математике в соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования на основании примерной программы по математики 5-9 классы. Математика 5 класс: И.И.Зубарева, А. Математика 5 класс: И.И.Зубарева, А. | Боровикова Екатерина Ивановна | 6 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| разное | Календарно-тематическое планирование по математике 9 класс | Степанова Ольга Алексеевна | 5 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| разное | Рабочая программа по математике 5 класс (ФГОС) | Фетисова Дарья Анатольевна | 9 Авг 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 5-9 классы + математика 5 класс и 6 класс | Горева Ирина Ивановна | 18 Окт 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Правила по математике 2 класс | Сотникова Наталья Викторовна | 5 Ноя 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | рабочая программа по математике 5-9 класс. | Михайловская Ирина Алексеевна | 5 Мая 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | 5-9 класс. Рабочая программа по математике (ФГОС) | Роговая Татьяна Яковлевна | 21 Мар 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 5-9 класс. | Сметанина Зоя Александровна | 21 Мар 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| разное | Рабочая программа по математике 5-9 класс | Котлярова Ольга Валерьевна | 1 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 5-9 класс | Головченко Наталья Евгеньевна | 1 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| презентация | Задачи по математике на тему здоровья 5-9 класс | Трунина Валентина Ивановна | 1 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Олимпиадные задания по математике 5-9 класс | Заборовская Ольга Юрьевна | 4 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | рабочая программа по математике 9 класс (5 ч) | Сайфетдинова Резеда Равидовна | 1 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | РАБОЧАЯ ПРОГРАММА ПО МАТЕМАТИКЕ 5-9 КЛАСС | Мулярчук Светлана Михайловна | 16 Мая 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 5-9 класс (Учебник Никольского) | Гайдук Лада Вячеславовна | 16 Авг 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 5-9 класс | Коновалова Ольга Владимировна | 20 Сен 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 5-9 класс | Караваева Ирина Витальевна | 16 Дек 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 5-9 класс Мордкович, Атанасян | Савина Наталия Васильевна | 30 Мар 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Тематическое планирование по математике 5- 11 класс автор Мордкович, по физике 7-9 класс Громова, физике 10-11 класс Мякишева, факультативные курсы 9-11 классы по математике | Аленина Наталья Юрьевна | 21 Мар 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| разное | Рабочая программа по математике 5 класс ( учебник «Математика» С. А. Козлова) А. Козлова) | Комарова Елена Игоревна | 9 Июл 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике.9 класс. | Аксенова Надежда Васильевна | 5 Ноя 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Программа элективного курса по математике 9 класс | Попова Татьяна Николаевна | 5 Ноя 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 9 класс | Дмитриева Елена Матвеевна | 5 Сен 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 9 класс | Ушаева Светлана Степановна | 5 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 9 класс | Сенаторова Ляна Георгиевна | 5 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 5 класс Е. А. Бунимович ФГОС А. Бунимович ФГОС | Дубенко Андрей Владимирович | 9 Июл 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | учебная программа по математике 5 класс | Климова Людмила Васильевна | 9 Июл 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | РАБОЧАЯ ПРОГРАММА ПО МАТЕМАТИКЕ 5 класс Н.Я. Виленкин | Горькова Наталия Викторовна | 9 Авг 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Домашнее обучение. Тематическое планирование по математике 5 класс. | Жирнова Алеся Григорьевна | 9 Авг 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике 5-6 класс | Зайнулина Елена Геннадьевна | 9 Авг 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| разное | Самостоятельные и контрольные работы по математике 5-6 класс | Губанова Елена Владимировна | 9 Авг 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Входная контрольная работа по математике (5 класс) | Харченко Наталья Ивановна | 9 Мар 2016 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике , 5 класс, Мерзляк А. Г. Г. | Наумова Наталья Сергеевна | 9 Мар 2016 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Рабочая программа по математике (алгебре) 5-9 классы и рабочая программа по геометрии 7-9 класс | Калинина Ольга Николаевна | 21 Мар 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Технологическая карта с конспектом урока по математике 5 класс | Уварова Юлия Владимировна | 5 Сен 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| разное | Рабочая программа по математике 5 класс | Аникеева Валентина Ивановна МОУ-СОШ с. Калининское | 5 Апр 2015 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Итоговая диагностика по математике 5 класс | Анискина Ирина Сергеевна | 9 Мар 2016 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| документ | Детские книги глазами математика. {n}}\) {n}}\)
abx=(ab)x 0!=1 Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас! Запишитесь на бесплатное тестирование знаний! Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности Наши преподаватели Павел Николаевич Коренев Репетитор по математике Стаж (лет) Образование: Курский государственный медицинский университет Проведенных занятий: Форма обучения: Дистанционно (Скайп)
Репетитор по химии 5-11 классов. Ангелина Витальевна Брусенкова Репетитор по математике Стаж (лет) Образование: Гродненский государственный университет имени Янки Купалы Проведенных занятий: Форма обучения: Дистанционно (Скайп)
Репетитор по русскому языку для 1-8 классов. Анастасия Михайловна Щеглова Репетитор по математике Стаж (лет) Образование: Федеральное государственное бюджетное образовательное учреждение высшего образования Проведенных занятий: Форма обучения: Дистанционно (Скайп)
Добрый день, будущие ученики! Репетитор по русскому языку 5-8 кл, ВПР/ОГЭ. Похожие статьи
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности Как быстро и легко выучить алгебру: советы для школьниковВ статье мы расскажем о платных и бесплатных способах быстро выучить алгебру. Если у вас нет больших пробелов в знании школьной программы, то можно заниматься алгеброй самостоятельно. В интернете вы можете бесплатно скачать разные учебные материалы: электронные учебники, рабочие тетради, схемы, задачники, онлайн-тесты и пр. Самообучение – это самый доступный способ подготовки, так как не нужно оплачивать услуги репетитора, согласовывать время, подстраиваться под расписание преподавателя и т. д. Но выучить алгебру с нуля самому будет сложно, особенно если вы учитесь в 8-9 классе, когда большая часть материала уже пройдена. Минусы самостоятельного обучения:
Самый удобный, эффективный и легкий способ выучить алгебру – это дистанционное обучение в онлайн-школе: на индивидуальных уроках с репетитором или на курсах. Расскажем подробнее про оба варианта. Заниматься с репетитором можно не только лично, но и онлайн. Стоимость часа в этом случае будет ниже, а качество учебного процесса останется высоким. Уроки проходят по видеосвязи: учитель объясняет новую тему, показывает примеры, отвечает на вопросы, проверяет задания, указывает на ошибки и т. д. Для письменных работ есть интерактивная доска: на ней могут писать и ученик, и преподаватель. На нашем сайте есть разные сервисы для онлайн-уроков с репетитором. Еще один способ учиться дистанционно – это онлайн-курсы с готовой программой:
В детском разделе нашего сайта собраны лучшие курсы по алгебре от проверенных онлайн-школ. Вы можете выбрать программу по стоимости, сроку, формату (онлайн или видеокурс), уровню подготовки (базовый, углубленный) и другим параметрам , а также почитать отзывы учеников и их родителей. Для вашего удобства мы разбили курсы по классам:
Подборка курсов Онлайн-курсы по математике (алгебре и геометрии) 7 класса в 2022 году Посмотреть подборку Наши рекомендации для тех, кто хочет выучить все темы по алгебре:
Ниже расскажем подробнее о том, как выучить алгебру за короткий срок. За летоЕсли хотите подтянуть алгебру за лето, то занимайтесь на онлайн-курсах. Не придется подстраиваться под жесткий график, но вы сможете выделить 1-2 часа в неделю для видеоуроков. С помощью курсов вы повторите все темы прошедшего учебного года или изучите новый материал. Подходящие программы есть, к примеру, в онлайн-школе «Фоксфорд»:
За месяцЗа 4-5 недель вы не успеете подготовиться к экзамену, но сможете повторить пройденный материал, чтобы сдать годовую контрольную. А также этого времени хватит, чтобы закрыть пробелы в знаниях. 3 совета, как выучить алгебру за месяц:
За неделюЗа неделю вы успеете повторить все темы, которые изучали в течение четверти или полугодия. Рекомендации от преподавателей — что можно сделать за 5-7 дней:
Реально ли подтянуть знания в более короткие срокиЕсли вы хотите подтянуть знания по алгебре, чтобы написать контрольную или сдать ЕГЭ, то начинайте подготовку заранее. Накануне ответственного события вы можете выделить 2-3 часа на то, чтобы повторить пройденный материал. Но изучить новые темы за 1 день вы не успеете. Поэтому не стоит проводить всю ночь над книгами. Лучше как следует выспаться и морально подготовиться. За 5-10 минут до урока можно полистать конспекты по предыдущей теме, а вот перед сдачей экзамена желательно ничего не читать. Переводите всю новую информацию в наглядную форму – составляйте таблицы, схемы и графики. Важно, чтобы термины, уравнения и функции были собраны в одном месте. Во-первых, так вы лучше их запомните. Во-вторых, вы сможете периодически повторять материал по лекциям. Чтобы выучить все правила по алгебре, разбирайте их смысл. Не стоит заучивать формулу наизусть – вам нужно понять, что означает каждый элемент, какие задачи можно решать с ее помощью. Для тренировки можно пользоваться двухсторонними карточками. Сделайте с одной стороны описание теоремы, с другой – доказательство. Чтобы подтянуть оценки по алгебре:
Что рекомендуют психологи родителям, которые хотят помочь ребенку подтянуть знания по алгебре:
Основы алгебры — правила, операции и формулы Алгебра — это область математики, которая занимается представлением ситуации с использованием математических символов, переменных и арифметических операций, таких как сложение, вычитание, умножение и деление, ведущих к формированию соответствующих математических выражений.
Основы алгебры Нам необходимо знать основную терминологию, относящуюся к алгебре, чтобы понимать ее основы. Выражение, состоящее из 4 основных частей, переменных, операторов, показателей степени, коэффициентов и констант вместе с символом равенства, известно как алгебраическое уравнение. Возьмем уравнение: ax 2 + bx + c = d. В алгебре в начале записывается член с наибольшим показателем, а далее члены записываются в уменьшающих степенях. На изображении выше ax 2 + bx + c = d 4 условия. Алгебраическое уравнение может иметь разные члены, похожие или разные. Подобные члены в уравнении — это те, которые составляют одни и те же переменные и показатели. С другой стороны, разные члены в уравнении представляют собой разные переменные и показатели. Правила алгебрыСуществует пять основных правил алгебры. Это:
Коммутативное правило сложенияВ алгебре коммутативное правило сложения гласит, что при добавлении двух членов порядок добавления не имеет значения. Уравнение для того же записывается как (a + b) = (b + a). Например, (х 3 + 2х) = (2х + х 3 ) Коммутативное правило умножения Коммутативное правило умножения гласит, что при умножении двух членов порядок умножения не имеет значения. Ассоциативное правило сложенияВ алгебре ассоциативное правило сложения гласит, что при добавлении трех или более терминов порядок добавления не имеет значения. Уравнение для того же записывается как a + (b + c) = (a + b) + c. Например, x 5 + (3x 2 + 2) = (x 5 + 3x 2 ) + 2 Ассоциативное правило умножения Аналогично, ассоциативное правило умножения умножается больше терминов, порядок умножения не имеет значения. Уравнение для того же записывается как a × (b × c) = (a × b) × c. Например, х 3 × (2x 4 × x) = (x 3 × 2x 4 ) × x. Распределительное правило умноженияРаспределительное правило умножения гласит, что когда мы умножаем число на сложение двух чисел, результат получается таким же, как сумма их произведений на число по отдельности. Это распределение умножения над сложением. Уравнение для того же записывается как a × (b + c) = (a × b) + (a × c). Например, х 2 × (2x + 1) = (x 2 × 2x) + (x 2 × 1). Алгебраические операцииЧетыре основных алгебраических операции:
В каждой из выполняемых алгебраических операций мы всегда классифицируем члены в наших алгебраических уравнениях как похожие и разные члены. Сложение Когда два или более термина в алгебраическом уравнении разделены знаком плюс «+», алгебраической операцией является сложение. Мы всегда добавляем похожие термины и неодинаковые термины отдельно, так как они рассматриваются как две разные величины.
Как видно из примеров, одинаковые термины при добавлении дают один и тот же термин, а непохожие термины не могут быть добавлены дальше. ВычитаниеКогда два или более членов в любом алгебраическом уравнении разделены знаком минус «-«, алгебраической операцией является вычитание. Как и в случае сложения, термины дифференцируются как похожие или неодинаковые термины, а затем вычитаются дальше.
Умножение Когда два или более члена в алгебраическом уравнении разделены знаком умножения «×», выполняется алгебраическая операция умножения. При умножении одинаковых или разных терминов мы используем законы экспоненты.
ДелениеКогда два или более термина в любом алгебраическом уравнении разделены знаком деления «/», выполняется алгебраическая операция деления. При разделении подобных терминов подобные термины могут быть упрощены, в то время как в случае разнородных терминов термины не могут быть легко упрощены далее.
Алгебраические формулыАлгебраические формулы, которые используются чаще и должны быть сохранены в памяти: Часто задаваемые вопросы по основам алгебрыКаковы основные правила алгебры?Основные правила алгебры:
Что такое золотое правило алгебры? Золотое правило алгебры — уравновешивать обе части уравнения, т. Что такое четыре алгебраических операции?
Как добавлять и вычитать лайки?При добавлении или вычитании одинаковых членов коэффициенты добавляются или вычитаются и записываются перед одинаковыми членами. Можем ли мы сложить или вычесть два непохожих термина?Нет, мы не можем складывать или вычитать два непохожих термина. Самые полезные правила базовой алгебры1 а(b+c)=ab+aca(b+c) = ab+ac а(б+с)=аб+ас Умножение можно распределить на сложение.Если вы умножаете что-то на сумму двух или более других значений, вы можете распределить умножение на каждое из значений, а затем просуммировать результат. «3(4+5) = 3*4 + 3*5 = 27«` 2 a(bc)=abca \left( {b \over c} \right) = { ab \over c }a(cb)=cab Умножение числителя аналогично умножению дроби. Умножение или деление числителя дроби влияет на дробь в целом (и наоборот). Если вам нужно умножить дробь, умножьте числитель. «`6\влево({1 \более 3}\право) = {(6*1) \более 3} = 2«` 3 (ac)b=abc{\left({a \over c}\right) \over b} = {a \over bc}b(ca)=bca Деление числителя равно умножению знаменателя.Если вы разделите числитель на определенное число, это окажет такое же влияние на общее значение дроби, как если бы вы умножили знаменатель на то же число. Деление вверху равняется умножению внизу. «`{ \left({1 \over 5}\right) \over 2} = {1 \over 10} = {1 \over (2*5)}«` 4 «` {a \ над \ влево ({b \ над c} \ справа)} = {ac \ над b} «` Деление знаменателя равно умножению числителя. Аналогично приведенному выше правилу, деление знаменателя дроби дает тот же эффект, что и умножение числителя. «`{1 \over \left({6 \over 2}\right)} = {(1*2) \over 6} = {1 \over 3}«` 5 «` \left({a \over b}\right)+\left({c \over d}\right) = {(ad+bc) \over bd} «` Дроби можно суммировать, умножая между числителями и знаменателями и умножая знаменатели на общий знаменатель.Если верхнюю и нижнюю часть дроби умножить на одно и то же число, дробь останется неизменной. Итак, мы можем сложить две дроби, сначала умножив числитель и знаменатель каждой дроби на знаменатель другой дроби. Затем, поскольку обе дроби теперь имеют один и тот же знаменатель (произведение двух знаменателей), мы можем объединить их в одну дробь с суммой в числителе. «`{3 \более 5}+{1 \более 3} = {(3*3) \более (5*3)} + {(1*5) \более (3*5)} = { (1*5)+(3*3) \более (3*5)} = {14 \более 15}«` 6 «` \left({a \over b}\right)-\left({c \over d}\right) = {(ad-bc) \over bd} «` Как превратить вычитание двух дробей в одну дробь.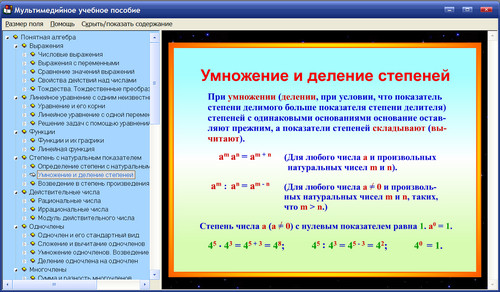 Это другая версия правила 5, но для вычитание из двух дробей, а не сложение. «`{3 \более 5}-{1 \более 3} = {(3*3) \более (5*3)} — {(1*5) \более (3*5)} = { (3*3)-(1*5) \над (3*5)} = {9-5 \более 15} = {4 \более 15}«` 7 «` {(a-b) \over (c-d)} = {(b-a) \over (d-c)} «` Обратное вычитание как в числителе, так и в знаменателе дроби оставляет значение дроби без изменений.Обратное вычитание дает обратный результат: «5-3 = 2; 3-5 = -2«. В дроби, если и числитель, и знаменатель перевернуты, значение дроби останется прежним. Итак, если мы реверсируем вычитание как в числителе, так и в знаменателе, значение дроби не изменится. «`{3-5 \более 2-1} = {-2 \более 1} = {5-3 \более 1-2} = {2 \более -1} = -2«` или ` «{-3 \более -4} = 0,75 = {3 \более 4}«` 8 «` {(a+b) \over c} = {a \over c} + {b \over c} «` Дроби с общими знаменателями можно объединять. Можно сложить две дроби с общими знаменателями, сложив числители и оставив знаменатель без изменений. Идя в другую сторону, мы также можем разбить дробь с прибавлением в числителе на две дроби (каждая с общим знаменателем). «`{(1+2) \более 4} = {3 \более 4} = {1 \более 4} + {2 \более 4}«` 9 «` {ac+bc \over c} = a+b «` Умножение и деление (на одно и то же число) компенсируют друг друга.Деление является обратным умножению: если «{a \over b} = c«, то «b*c = a«. Это означает, что дробь «{ac \ over c}« равна «a«, так как мы умножаем «a« на «c«, а затем сразу делим на «c« снова, что возвращает нас туда, откуда мы начали. Поскольку мы знаем, что «{ac+bc \over c} = {ac \over c} + {bc \over c}« (см. правило 8), и на основании вышеизложенного мы можем видеть, что «{ac \ over c} = a« и «{bc \over c} = b«, у нас есть результат: «a+b«. «`{(4*5)+(2*5) \более 5} = {4*5 \более 5}+{2*5 \более 5} = 4+2«` 10 «` {\ left ({a \ over c} \ right) \ over \ left ({b \ over d} \ right)} = {ad \ over bc} «` Если числитель и знаменатель дроби являются дробями, их можно преобразовать в дробь двух умножений. Объединив правила 3 и 4, мы можем умножить знаменатель нижней дроби на числитель верхней дроби, что даст объединенный числитель и отменит знаменатель нижней дроби; затем мы можем умножить знаменатель верхней дроби на числитель нижней дроби, чтобы получить объединенный знаменатель и сократить знаменатель верхней дроби. 9п} «` Дробь с показателем степени равна такой же дроби с показателем степени в числителе и знаменателе.Сначала это выглядит странно, но причины этого довольно просты. Если бы мы обратили внимание, когда кто-то сказал нам, как умножать дроби (это сомнительно, но мы все равно продолжим), мы бы вспомнили, что для умножения двух дробей вы просто перемножаете числители друг с другом и перемножаете знаменатели друг с другом, чтобы получить полученная дробь. Это правило следует из этого факта. 92} = x*y = \sqrt{a}*\sqrt{b}« «`\sqrt{4*9} = \sqrt{36} = 6 = 2*3 = \sqrt{4} *\sqrt{9}«` 21 «` \sqrt[m]{\sqrt[n]{a}} = \sqrt[nm]{a} «` Преобразование корня корня в один корень.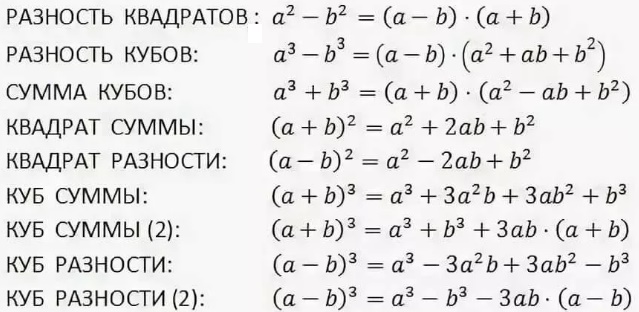 2} = \sqrt{93} = \sqrt[3]{-3*-3*-3} = \sqrt[3]{-27} = -3«` 2} = \sqrt{93} = \sqrt[3]{-3*-3*-3} = \sqrt[3]{-27} = -3«`Краткое изложение алгебры — Темы предварительного исчисленияТемы в ПРЕДВАРИТЕЛЬНАЯ РАБОТА Содержание | Дом 1 Студент, прошедший курс алгебры, найдет здесь полный обзор. Студент, который сейчас проходит такой курс, увидит, что в магазине. АЛГЕБРА – это метод письменных вычислений. А что такое расчет, как не замена одного набора символов другим? В арифметике мы заменяем «2 + 2» на «4». В алгебре мы можем заменить ‘ a + (- b )’ с ‘ a — b .’ a + (− b ) = a − b . Мы называем это формальным правилом. Он показывает, как выражение, написанное в одной форме, может быть заменено другой формой. Знак = означает, что «может быть переписано как» или «может быть заменено на». Если p и q являются утверждениями (уравнениями), то правило Если p , то q , или эквивалент p подразумевает q , означает: Мы можем заменить — в смысле следования — утверждение p заявлением q . x + a = b подразумевает x = b — a . Это означает, что мы можем следовать утверждению ‘ x + a = b ‘ с утверждением » x = b — a .’ Ибо мы решаем уравнения логической последовательностью утверждений. Алгебра зависит от того, как все выглядит. Таким образом, мы можем сказать, что алгебра — это система формальных — грамматических — правил. Далее следует то, что нам разрешено писать. (См. полный курс «Навыки алгебры») 11. Аксиомы равенства
Невозможно дать явное определение слова «равно» или его символа = . Однако эти правила являются неявным определением. Значение «равно» подразумевает эти три правила. О том, как правило симметрии проявляется на практике, см. в Уроке 6 Алгебры. Правило симметрии применяется ко всем приведенным ниже правилам. 12. Коммутативные правила сложения и умножения
13. Тождественные элементы сложения и умножения: 3. 0 и 1 + 0 = 0 + = а · 1 = 1 · а = а Таким образом, если мы «действуем» над числом с элементом идентичности, 14. Аддитивная инверсия a : − a a + (− a ) = — a + a = 0 «Обратное» число отменяет то, что делает число.
Два числа называются обратными друг другу, если их произведение равно 1.
16. Алгебраическое определение вычитания а − б = а + (− б ) Вычитание в алгебре определяется как сложение обратного. 17. Алгебраическое определение деления
Деление в алгебре определяется как умножение по взаимному согласию. 18. Обратное к обратному − (− a ) = a 19. Отношение b − a к a − b б — а = -( а — б ) Сейчас, б + а равно к a + b . 10. Правило знаков для умножения, деления и a (− b ) = − a b . (− a ) b = − a b . (− a )(− b ) = аб.
«Похожие знаки дают положительное число, в отличие от знаков — отрицательное число». 11. Правила для 0 a · 0 = 0 · a = 0, Если a 0, то
Деление на 0 является исключенной операцией. (Навык алгебры, урок 5.) 12. Умножение/факторинг
13. Одинаковая операция с обеими частями уравнения
Мы можем прибавить одно и то же число к обеим частям уравнения; 14. Смена знака в обеих частях уравнения
Мы можем изменить любой знак в обеих частях уравнения. 15. Смена знака в обеих частях неравенства:
Когда мы меняем знаки в обеих частях неравенства, мы должны изменить смысл неравенства. 16. Четыре формы уравнений, соответствующие
См. «Навыки алгебры», урок 9.. 17. Изменение смысла при решении неравенства
18. Абсолютное значение Если | х | = b , тогда x = b или x = — b . Если | х | < b тогда − b < x < б . Если | х | > b (и b > 0), затем x > b или x < − b . 19. Принцип эквивалентных дробей
Мы можем умножать и числитель, и знаменатель на один и тот же коэффициент; мы можем разделить оба на общий множитель. 20. Умножение дробей
21. Деление дробей (сложные дроби) Деление — это умножение на обратное. 22. Сложение дробей
Общий знаменатель – НОК знаменателей. 23. Правила показателей
24.
25. Определение показателя степени 0 а 0 = 1 26. Определение корня квадратного корня Из квадратного корня в квадрате получается подкоренное число. 27. Уравнения вида a 2 = b
28. Умножение/факторизация радикалов
29. 30. Определение рационального показателя Умелее сначала взять рут. 31. Законы логарифмов log xy = log x + log y .
log x n = n log x .
32. Определение сложной единицы i i 2 = −1 Следующая тема: Рациональные и иррациональные числа Содержание | Дом Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн. Copyright © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: [email protected] Анализ правил и выражений алгебры
Упомянутая выше цитата Джона Б. С. Холдейна как нельзя более точна. Тема алгебры может резко разделить мнения: некоторые любят анализировать алгебру, в то время как другие не могут ненавидеть ее больше. В сегодняшней статье мы проанализируем некоторые основные правила алгебры, уравнения, примеры и определения, чтобы сделать алгебраическую информацию более интересной для всех типов учащихся. Лучшие репетиторы по математике Поехали Основные правила алгебрыЗдесь вы найдете различных онлайн-репетиторов по математике. От спорта до алгебры, для всего есть правила. (Источник: pixabay) Без правил и ограничений общество не может эффективно существовать; нам нужно сказать, что делать, чтобы узнать наши ограничения. Необходимо отметить, что на все в жизни есть правила. От расчета расхода топлива до определения количества поездок, совершаемых официантом в час, постоянно используется алгебра. Поэтому, не откладывая, мы рассмотрим некоторые правила алгебры для арифметики, показателей степени и радикалов. Правила алгебры, связанные с арифметикойРаспределительное свойство умноженияРаспределительное свойство умножения основано на том факте, что вы умножаете что-то на сумму двух или более других членов. Ваше умножение может быть распределено по каждому из различных членов, связанных с уравнением. Пример распределительного свойства повторения следующий:
После выработки необходимого порядка действий ответ или проблема найдены. Правила сложения, вычитания, деления и умножения дробейЗаконы алгебры для арифметики немного меняются при работе с уравнениями, в которых есть дроби. Например, если вы хотите умножить дробь, числитель дроби применяется к дроби как к полной цифре. Поэтому, если вам нужно умножить дробь, умножить числитель и цель будет достигнута. Следующий пример поможет тем, кто более нагляден при попытке умножить дроби:
Деление части очень тесно связано с ранее упомянутым правилом умножения. . Деление знаменателя дроби будет иметь тот же эффект, что и умножение числителя. Ниже приведен пример для лучшего понимания: Прекрасный пример правил деления дроби в алгебре. (Источник: Algebrarules.com) Правила сложения и вычитания дробей одинаковы: знаменатели должны совпадать; как и в арифметике. Числители должны быть присоединены, а их суммы должны быть помещены над общим знаменателем. Существует множество других алгебраических правил, связанных с арифметикой, которые можно проанализировать; ранее упомянутые лишь немногие, которые следует освоить с самого начала. Правила алгебры для показателей степениЕсли вы читаете эту статью и забыли, что такое показатели степени, мы освежим вашу память. Показатель степени — это величина, представляющая степень, в которую должно быть возведено число или выражение, обычно выражаемая в виде выпуклого символа рядом с именем или фразой в алгебре. Так же, как и для всего остального в алгебре, существуют правила для показателей степени:
Найдите репетитора по математике рядом со мной здесь. Отличительные правила алгебры для радикаловВ полном мире алгебры радикальные выражения необходимы и могут рассматриваться как полярная противоположность экспоненциальных выражений, поскольку они дают корни. Одно типичное правило, связанное с радикалами в алгебре, можно рассматривать следующим образом: Хотя радикалы и экспоненты совершенно различны, их практика чем-то соответствует. В этом выражении корень числа совпадает с числом, возведенным в единицу над n. (Источник: Algebrarules. com) com)Алгебраическое выражение, изображенное выше, соответствует правилу критического показателя m ∙ a n = a m + n. Есть много других определений, словарных слов и правил, которые можно усвоить о радикалах, ранее упомянутое — это всего лишь небольшая проба, которая позволяет всем понять, насколько логична и хорошо структурирована математика, особенно алгебра. Найдите онлайн-репетитора по математике сегодня на Superprof. Простые алгебраические уравненияПрежде чем выделить некоторые простые уравнения по алгебре, которые можно найти в учебниках или на экзаменах, важно дать определение слову уравнение. Согласно многим источникам, под сравнением можно понимать два выражения по обе стороны от знака, указывающего на их родство. Отношения в уравнении могут быть равны, меньше, больше или в какой-либо форме того и другого. Когда большинство людей упоминают уравнения, они имеют в виду алгебраические уравнения; это уравнения, которые включают буквы и цифры.
Алгебраические уравнения решаются путем определения того, какие числа представляют буквы. Ниже приведен тривиальный пример того, как простые уравнения 1 + 1 = 2 и 2 + 5 > 2 + 4 можно превратить в алгебраические, заменив одно из чисел на x: 1 + 1 = х и х + 5 > х + 4 Следовательно, заменив часть чисел на х, мы можем однозначно определить, что значение х равно 2. Буква х может использоваться для создания алгебраических выражений любым способом; y также используется для представления неизвестных элементов уравнений. В любом уравнении есть термины и компоненты, представляющие разные вещи. Например, если термин включает буквы и цифры, сообщения называются переменными, а числа — коэффициентами. Кроме того, еще одно правило уравнений состоит в том, что если слова имеют в точности одну и ту же переменную, они становятся известными как похожие термины, и их можно складывать, вычитать, делить и умножать, как если бы они были простыми числами. В некоторых ситуациях для эффективного решения алгебраического уравнения необходимо изменить выражение и выделить x. Необходимо следовать простому набору правил, чтобы изменить уравнения, прежде чем их можно будет начать решать и работать над ними. Зная ранее упомянутую информацию об уравнениях, учащиеся готовятся к успеху, избегают путаницы и правильно понимают основы алгебры с самого начала. Откройте для себя другого репетитора по математике на Superprof. Основные примеры алгебры для всех типов учащихсяПоскольку алгебра является академической дисциплиной, которая вызывает у многих людей душевную боль, существует множество доступных онлайн-ресурсов, предлагающих пошаговые объяснения, примеры, видеоуроки, игры и подкасты о различных аспектах. Чтобы найти новые примеры, которые можно изучать после уроков, мы настоятельно рекомендуем посетить такие сайты, как Study.com, посмотреть 5–10-минутные видеоролики (идеально подходит для визуалов!), пройти тесты и усвоить основные понятия. Кроме того, Mathplanet прекрасно организован с алгебраическими примерами, которые касаются реальных событий. Действительно, существует огромное количество информации, предназначенной для того, чтобы помочь учащимся, испытывающим затруднения, добиться успеха, если вы знаете, где искать. Найти репетитора по алгебре — отличная идея, чтобы понять основные понятия алгебры. Определения алгебрыНаличие всех необходимых инструментов для урока математики ничего не стоит, если у вас нет теории и навыков, чтобы их подкрепить. (Источник: pixabay)Если при чтении этой статьи вы не поняли каких-то выражений, терминов или конкретных словарных слов, вы не одиноки. Мы не все математики, и, честно говоря, прежде чем я написал эту статью, мне нужно было изучить некоторые выражения, чтобы освежить мою внешкольную память. Ниже приведены некоторые специальные алгебраические термины вместе с их определениями:
Другие слова на основе алгебры, такие как переменные, можно найти в статьях Superprof. Узнать больше о правилах, уравнениях и конкретных примерах алгебры можно сделать еще до того, как ее начнут изучать в средней школе, на учебной сессии для студентов университетов, желающих улучшить свои знания по математике, или в качестве переподготовки для взрослых которые просто забыли ранее усвоенные понятия. Найдите репетитора по математике на Superprof UK. Рабочие листы по алгебреДобро пожаловать на страницу с рабочими листами по алгебре на сайте Math-Drills.com, где неизвестные являются обычным явлением, а переменные являются нормой. На этой странице вы найдете рабочие листы по алгебре, предназначенные в основном для учащихся средних школ по таким темам алгебры, как алгебраические выражения, уравнения и графические функции. Эта страница начинается с некоторых рабочих листов с пропущенными числами для младших школьников. Затем мы переходим непосредственно к алгебре, помогая учащимся распознавать и понимать основной язык, связанный с алгеброй. Остальная часть страницы посвящена некоторым основным темам, с которыми вы столкнетесь на уроках алгебры. Помните, что, обучая студентов алгебре, вы помогаете создавать будущих финансовых гениев, инженеров и ученых, которые решат все проблемы нашего мира. Алгебра намного интереснее, когда вещи более реальны. Решать линейные уравнения намного веселее, когда есть весы с двумя чашами, несколько загадочных мешочков и куча мармеладок. Самые популярные рабочие листы по алгебре на этой неделеКомбинирование одинаковых терминов и решение простых линейных уравнений ( 931 просмотр на этой неделе )Использование свойства распределения (ответы не включают показатели степени) ( 836 просмотров на этой неделе )Решение квадратных уравнений с положительным коэффициентом а, равным 1 ( 782 просмотров на этой неделе )Перевод алгебраических фраз (простая версия) ( 602 просмотров на этой неделе )Правила смешанной экспоненты (все положительные) ( 437 просмотров на этой неделе )Свойства и законы чисел Рабочие листыКоммутативный закон Коммутативный закон или коммутативное свойство гласит, что вы можете изменить порядок чисел в арифметической задаче и получить тот же результат. Коммутативный закон сложения (только числа) Коммутативный закон сложения (некоторые переменные) Коммутативный закон умножения (только числа) Коммутативный закон умножения (некоторые переменные) Ассоциативный закон Ассоциативный закон или ассоциативное свойство позволяют изменять группировку операций в арифметической задаче с двумя и более шагами без изменения результата. Ассоциативный закон сложения (только целые числа) Ассоциативный закон умножения (только целые числа) Обратные отношения содин пробелРабочие листы с обратными отношениями охватывают предварительные алгебраические навыки, призванные помочь учащимся понять взаимосвязь между умножением и делением, а также связь между сложением и вычитанием. Сложение и вычитание легко Сложение и вычитание сложнее Все факты умножения и деления от 1 до 18 в цвете (без пробелов) Диапазон умножения и деления от 1 до 9Диапазон умножения и деления от 5 до 12 Умножение и деление Все обратные отношения Диапазон от 2 до 9 Умножение и деление Все обратные отношения Диапазон от 5 до 12 Умножение и деление Все обратные отношения Диапазон от 10 до 25 Обратные отношения сдвумя пробеламиСложение и вычитание (суммы 1-18) Сложение и вычитание, обратные отношения с 1 Сложение и вычитание, обратные отношения с 2 Сложение и вычитание, обратные отношения с 3 Сложение и вычитание, обратные отношения с 4 Сложение и вычитание, обратные отношения с 5 Сложение и вычитание, обратные отношения с 6 Сложение и вычитание, обратные отношения с 7 Сложение и вычитание, обратные отношения с 8 Сложение и вычитание, обратные отношения с 9Сложение и вычитание, обратные отношения с 10 Сложение и вычитание, обратные отношения с 11 Сложение и вычитание, обратные отношения с 12 Сложение и вычитание, обратные отношения с 13 Сложение и вычитание, обратные отношения с 14 Сложение и вычитание, обратные отношения с 15 Сложение и вычитание, обратные отношения с 16 Сложение и вычитание, обратные отношения с 17 Сложение и вычитание, обратные отношения с 18 Пропущенные числа или неизвестные в рабочих листах уравнений Пропущенные числа в рабочих листах уравнений трех типов: пробелы для неизвестных, символы для неизвестных и переменные для неизвестных. Рабочие листы с пропущенными числами ипробелами в качестве неизвестныхВ этих таблицах неизвестное ограничивается вопросительной стороной уравнения, которая может быть слева или справа от знака равенства. Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Пробелы Никогда в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Пробелы никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Только дополнение ; Диапазон от 1 до 9 ; Пробелы никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Добавление только ; Диапазон от 1 до 9 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Добавление только ; Диапазон от 1 до 20 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Пробелы Никогда в позиции ответа ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 20 ; Пробелы в любой позиции ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Пробелы никогда не используются в позиции ответа ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Пробелы в любом положении ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 20 ; Пробелы в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Пробелы никогда в позиции ответа ) Пропущенные числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Пробелы в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 20 ; Пробелы в любой позиции ) Рабочие листы с пропущенными числами исимволами в качестве неизвестныхОтсутствующие числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Символы никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; символов в любой позиции ) Отсутствующие числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Символы никогда не используются в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Символы в любой позиции ) Отсутствующие числа в уравнениях ( Только дополнение ; Диапазон от 1 до 9 ; Символы никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Дополнение Только ; Диапазон от 1 до 9 ; символов в любой позиции ) Пропущенные числа в уравнениях ( Добавление только ; Диапазон от 1 до 20 ; Символы в любой позиции ) Отсутствующие числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Символы никогда не используются в позиции ответа ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Символы в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 20 ; Символы в любой позиции ) Отсутствующие числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Символы никогда не используются в позиции ответа ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Символы в любой позиции ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 20 ; символов в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Символы никогда не в позиции ответа ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Символы в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 20 ; Символы в любой позиции ) Равенства с добавлениемв обе стороны уравнения и символов в качестве неизвестныхРавенства со сложением (от 0 до 9) Символ Неизвестный Равенства со сложением (от 1 до 12) Символ Неизвестные Равенства со сложением (от 1 до 15) Символ Неизвестные Равенства со сложением (от 1 до 25) Символ Неизвестные Равенства со сложением (от 1 до 99) Символ Неизвестный Рабочие листы с отсутствующими числами спеременными как неизвестнымиОтсутствующие числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Переменные, которые никогда не находятся в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Отсутствующие числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Переменные, которые никогда не находятся в позиции ответа ) Пропущенные числа в уравнениях ( Все операции ; Диапазон от 1 до 20 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только дополнение ; Диапазон от 1 до 9 ; Переменные, которые никогда не находятся в позиции ответа ) Отсутствующие числа в уравнениях ( Добавление только ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только добавление ; Диапазон от 1 до 20 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Переменные, которые никогда не находятся в позиции ответа ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только вычитание ; Диапазон от 1 до 20 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Переменные никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Пропущенные числа в уравнениях ( Только умножение ; Диапазон от 1 до 20 ; Переменные в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 9 ; Переменные никогда не в позиции ответа ) Пропущенные числа в уравнениях ( Отдел Только ; Диапазон от 1 до 9 ; Переменные в любой позиции ) Отсутствующие числа в уравнениях ( Только раздел ; Диапазон от 1 до 20 ; Переменные в любой позиции ) Решение простых линейных уравненийРешение простых линейных уравнений со значениями от от -9 до 9 (неизвестно слева) Решение простых линейных уравнений со значениями от от -99 до 99 (неизвестно слева) Решение простых линейных уравнений со значениями от от -9 до 9 (неизвестно справа или слева) Решение простых линейных уравнений со значениями от от -99 до 99 (неизвестно справа или слева) Рабочие листы по алгебраическим выражениямИспользование свойства дистрибутива Свойство дистрибутивности — важный навык в алгебре. Распределительное свойство (ответы не включают показатели степени) Распределительное свойство (некоторые ответы включают показатели степени) Распределительное свойство (все ответы включают показатели степени) Вычисление алгебраических выраженийВычисление выражений с одной переменной, одним шагом и без экспонент Вычисление выражений с одной переменной и одним шагом Вычисление выражений с одной переменной и двумя шагами Вычисление выражений с двумя переменными и двумя шагами Вычисление выражений с двумя переменными и тремя шагами Вычисление выражений с тремя переменными и четырьмя шагами Вычисление выражений с тремя переменными и пятью шагами Правила экспоненты и свойстваПрактика сосновными правилами экспоненты Как следует из названия, эти рабочие листы содержат только основные вопросы по правилам экспоненты. Правила смешанной экспоненты (все положительные) Правила смешанной экспоненты (с отрицаниями) Умножение показателей (все положительные) Умножение показателей степени (с отрицательными числами) Умножение одной и той же степени с разными основаниями (все положительные) Умножение одной и той же степени с разными основаниями (с отрицательными числами) Деление показателей с большим показателем в дивиденде (все положительные) Деление показателей с большим показателем в дивиденде (с отрицательными числами) Деление показателей с большим показателем в делителе (все положительные) Деление показателей с большим показателем в делителе (с отрицаниями) Полномочия экспонентов (все положительные) Полномочия экспонент (с отрицаниями) Линейные выражения и уравнения Рабочие листы по линейным уравнениям, включая упрощение, построение графиков, оценку и решение систем линейных уравнений. Знание языка алгебры может помочь извлечь смысл из текстовых задач и ситуаций вне школы. В этих рабочих листах учащимся предлагается преобразовать фразы в алгебраические выражения. Преобразование алгебраических фраз в выражения (простая версия) Перевод алгебраических фраз в выражения (сложная версия) Упрощение линейных выражений (объединение одинаковых членов)Объединение одинаковых терминов часто происходит в алгебре. Студенты могут быть введены в тему и немного попрактиковаться с этими рабочими листами. Планка поднимается с добавлением и вычитанием версий, которые вводят круглые скобки в выражения. Для учащихся, которые хорошо разбираются в дробях, упрощение рабочих листов с простыми алгебраическими дробями представляет собой некоторую проблему по сравнению с другими рабочими листами в этом разделе. Упрощение линейных выражений с 3 терминами Упрощение линейных выражений с 4 терминами Упрощение линейных выражений с 5 терминами Упрощение линейных выражений с от 6 до 10 терминов Добавление и упрощение линейных выражений Сложение и упрощение линейных выражений с множителями Сложение и упрощение линейных выражений с некоторыми множителями . Перепишите линейные уравнения в стандартной форме Преобразование линейных уравнений из 9Стандарт 2489 на форму пересечения с уклоном Преобразование линейных уравнений из Slope-Intercept в стандартную форму Преобразование линейных уравнений между стандартной формой и формой пересечения наклона Переписывание формул (сложение и вычитание; примерно один шаг) Переписывание формул (сложение и вычитание; около двух шагов) Переписывание формул ( умножение и деление ; примерно один шаг) Определение линейных уравнений из наклонов, отрезков у и точек Определите линейное уравнение по наклону и точке пересечения с осью Y Определите линейное уравнение по наклону и точке . Линейное уравнениеГрафикиПостроение линейных уравнений и чтение существующих графиков дает учащимся визуальное представление, которое очень полезно для понимания концепций наклона и точки пересечения по оси Y. График Уравнения пересечения наклона Определите уравнение из графика Определите уклон по графику Определите y-пересечение из графика Определите x-перехват из графика Определите наклон и точку пересечения с осью Y по графику Определите наклон и пересечения с графика Определите наклон , точки пересечения и уравнение из графика Решение линейных уравнений с помощью мармеладок — увлекательное занятие, которое стоит попробовать учащимся, впервые изучающим алгебраические понятия. Вероятно, лучше всего это проиллюстрировать на примере. Давайте использовать 3 x + 2 = 14. Вы можете распознать x как неизвестное, которое на самом деле является количеством мармеладок, которые мы кладем в каждый непрозрачный пакет. 3 в 3 x означает, что нам нужно три мешка. Лучше всего заполнить мешки необходимым количеством мармеладок так, чтобы ученики не видели их, чтобы им действительно пришлось решать уравнение. С одной стороны двухчашечных весов поместите три мешка с драже размером x по одному и по два драже в каждом, чтобы представить +2 часть уравнения. На другой стороне весов поместите 14 мармеладных бобов и три пустых мешка, которые, как вы заметите, необходимы для правильного «баланса» уравнения. Последний шаг — разделить рассыпные мармеладки в одной части уравнения на столько же групп, сколько пакетов. Это, вероятно, даст вам хорошее представление о том, сколько желейных бобов находится в каждом пакете. Если нет, съешьте немного и попробуйте еще раз. Теперь мы понимаем, что это не будет работать для каждого линейного уравнения, так как трудно иметь отрицательные мармеладки, но это еще одна стратегия обучения, которую вы можете использовать для алгебры. Решение линейных уравнений Вопреки всему, уравнения вида a/ x не являются линейными. Объединение одинаковых терминов и решение простых линейных уравнений Решение x = c Линейные уравнения Решение a x = c линейных уравнений, включая отрицательные Решение x /a = c линейных уравнений Решение x /a = c линейных уравнений, включая отрицательные Решение a/ x = c линейных уравнений Решение a/ x = c линейных уравнений, включая отрицательные Решение a x + b = c линейных уравнений Решение a x + b = c линейных уравнений, включая отрицательные Решение x — b = c Линейные уравнения Решение a x — b = c линейных уравнений, включая отрицательные Решение a x ± b = c линейных уравнений Решение a x ± b = c линейных уравнений, включая отрицательные Решение x /a ± b = c линейных уравнений Решение x /a ± b = c линейных уравнений, включая отрицательные Решение a/ x ± b = c линейных уравнений Решение a/ x ± b = c линейных уравнений, включая отрицательные Решение различных а/ x ± b = c и x /a ± b = c Линейные уравнения Решение различных a/ x ± b = c и x /a ± b = c линейных уравнений, включая отрицательные Решение линейных уравнений всех типов Решение линейных уравнений всех типов, включая отрицательные Линейные системыРешение систем линейных уравненийПростые линейные системы с двумя переменными Простые линейные системы с двумя переменными, включая отрицательные значения Линейные системы с двумя переменными Линейные системы с двумя переменными, включая отрицательные значения Простые линейные системы с тремя переменными; Легкий Простые линейные системы с тремя переменными, включая отрицательные значения Линейные системы с тремя переменными Линейные системы с тремя переменными, включая отрицательные значения Решение систем линейных уравнений графическим способомРешение линейных систем с помощью графика (только решения в первом квадранте) Решите стандартные линейные системы графически Решите линейные системы пересечения наклона с помощью графика Решите различные линейные системы с помощью графика Определите зависимую линейную систему по графику Идентифицируйте несовместимую линейную систему с помощью графика Квадратные выражения и уравнения Рабочие листы с квадратными выражениями и уравнениями, включая умножение коэффициентов, разложение на множители и решение квадратных уравнений. Упрощение квадратных выражений с 5 членами Упрощение квадратных выражений с 6 членами Упрощение квадратных выражений с 7 членами Упрощение квадратных выражений с 8 членами Упрощение квадратных выражений с помощью 9условия Упрощение квадратных выражений с 10 членами Упрощение квадратных выражений с 5-10 членами Сложение/вычитание и упрощение квадратных выражений Сложение и упрощение квадратных выражений.
Сложение и упрощение квадратных выражений с помощью множителей.
Добавление и упрощение квадратных выражений с некоторыми множителями.
Вычитание и упрощение квадратных выражений.
Вычитание и упрощение квадратных выражений с помощью множителей.
Вычитание и упрощение квадратных выражений с некоторыми множителями.
Смешанное сложение и вычитание и упрощение квадратных выражений.
Смешанное сложение и вычитание и упрощение квадратных выражений с множителями. Коэффициенты умножения квадратичных чисел с коэффициентами 1 Умножение коэффициентов квадратичных чисел с коэффициентами 1 или -1 Умножение коэффициентов квадратичных чисел с коэффициентами 1 или 2 Умножение коэффициентов квадратичных чисел с коэффициентами 1, -1, 2 или -2 Коэффициенты умножения квадратичных чисел с коэффициентами до 9 Умножение коэффициентов квадратичных чисел с коэффициентами от -9и 9 Разложение квадратных выражений на множители Рабочие листы по факторингу квадратичных выражений в этом разделе содержат много практических вопросов для студентов, чтобы отточить свои стратегии факторинга. Если вы предпочитаете рабочие листы с квадратными уравнениями, см. следующий раздел. Эти рабочие листы бывают разных уровней, самые простые находятся в начале. Факторинг квадратных выражений с положительными коэффициентами «а» 1 Разложение на множители квадратных выражений с положительными или отрицательными коэффициентами ‘a’ числа 1 Факторинг квадратичных выражений с положительным или отрицательным числом ‘a’ коэффициенты 1 с шагом общего множителя Разложение квадратных выражений с положительными коэффициентами «а» до 4 Разложение квадратичных выражений с положительными или отрицательными ‘a’ коэффициентами до 4 Факторинг квадратичных выражений с положительными или отрицательными ‘a’ коэффициентами до 4 с шагом общего множителя Факторинг квадратных выражений с положительными коэффициентами «а» до 5 Факторинг квадратичных выражений с положительными или отрицательными ‘a’ коэффициентами до 5 Факторинг квадратичных выражений с положительными или отрицательными ‘a’ коэффициентами до 5 с шагом общего множителя Разложение квадратных выражений с положительными коэффициентами «а» до 9 Разложение квадратичных выражений с положительными или отрицательными ‘a’ коэффициентами до 9 Факторинг квадратных выражений с положительным или Отрицательные ‘a’ коэффициенты до 9 с шагом общего множителя Разложение квадратных выражений с положительными коэффициентами «а» до 81 Факторизация квадратичных выражений с положительными или отрицательными ‘a’ коэффициентами до 81 Факторизация квадратичных выражений с положительными или отрицательными ‘a’ коэффициентами до 81 с шагом общего множителя Вычисление суммы и произведения (диапазон операндов от 0 до 9 ) Вычисление суммы и произведения (диапазон операндов от 1 до 9 ) Вычисление суммы и произведения (диапазон операндов от 0 до 9, включая отрицательные значения ) Вычисление суммы и произведения (диапазон операндов от 1 до 9, включая отрицательные числа ) Вычисление суммы и произведения (диапазон операндов -20 до 20 ) Вычисление суммы и произведения (диапазон операндов от -99 до 99 ) Определение операндов из пар суммы и произведения (диапазон операндов от 0 до 9 ) Определение операндов из пар суммы и произведения (диапазон операндов от 1 до 9 ) Определение операндов из пар суммы и произведения (диапазон операндов от 0 до 12 ) Определение операндов из пар суммы и произведения (диапазон операндов от 1 до 12 ) Определение операндов из пар суммы и произведения (диапазон операндов от 0 до 9, включая отрицательные числа ) Определение операндов из пар суммы и произведения (диапазон операндов от 1 до 9, включая отрицательные значения ) Определение операндов из пар суммы и произведения (диапазон операндов от -20 до 20 ) Определение операндов из пар суммы и произведения (диапазон операндов от -99 до 99 ) Применяете ли вы метод проб и ошибок, вычисляете квадрат или вычисляете общую квадратичную формулу, эти рабочие листы содержат множество практических вопросов с ответами. Решение квадратных уравнений с положительными коэффициентами «а» числа 1 Решение квадратных уравнений с положительными или отрицательными коэффициентами «а» числа 1 Решение квадратных уравнений с положительными или отрицательными ‘a’ коэффициентами 1 с шагом общего множителя Решение квадратных уравнений с положительными коэффициентами «а» до 4 Решение квадратных уравнений с положительными или отрицательными ‘a’ коэффициентами до 4 Решение квадратных уравнений с положительными или отрицательными ‘a’ коэффициентами до 4 с шагом общего множителя Решение квадратных уравнений с положительными коэффициентами «а» до 5 Решение квадратных уравнений с положительными или отрицательными ‘a’ коэффициентами до 5 Решение квадратных уравнений с положительным или Отрицательные ‘a’ коэффициенты до 5 с шагом общего множителя Решение квадратных уравнений с положительными коэффициентами «а» до 9 Решение квадратных уравнений с положительными или отрицательными ‘a’ коэффициентами до 9 Решение квадратных уравнений с положительными или отрицательными ‘a’ коэффициентами до 9 с шагом общего множителя Решение квадратных уравнений с положительными коэффициентами «а» до 81 Решение квадратных уравнений с положительными или отрицательными ‘a’ коэффициентами до 81 Решение квадратных уравнений с положительными или отрицательными ‘a’ коэффициентами до 81 с шагом общего множителя Решение квадратных уравнений , что равно целому числу (например, ax² + bx + c = d)Решение квадратных уравнений относительно x (коэффициенты «a» равны 1) Решение квадратных уравнений относительно x (коэффициенты «a» равны 1 или -1) Решение квадратных уравнений относительно x (коэффициенты «а» до 4) Решение квадратных уравнений относительно x (коэффициенты «а» между -4 и 4) Решение квадратных уравнений относительно x (коэффициенты «а» до 81) Решение квадратных уравнений относительно x (коэффициенты «а» между -81 и 81) Другие полиномиальные и мономиальные выражения и уравнения Разложение на множители неквадратичных выражений с различными уровнями сложности. Сложение и вычитание; 1 переменная; 3 триместра Сложение и вычитание; 1 переменная; 4 срока Сложение и вычитание; 2 переменные; 4 срока Сложение и вычитание; 2 переменные; 5 терминов Сложение и вычитание; 2 переменные; 6 терминов Упрощающие многочлены , включающие умножение и делениеУмножение и деление; 1 переменная; 3 триместра Умножение и деление; 1 переменная; 4 срока Умножение и деление; 2 переменные; 4 срока Умножение и деление; 2 переменные; 5 терминов Упрощающие многочлены , которые включают сложение, вычитание, умножение и делениеВсе операции; 1 переменная; 3 триместра Все операции; 1 переменная; 4 срока Все операции; 2 переменные; 4 срока Все операции; 2 переменные; 5 терминов Все операции (вызов) Факторные выражения, которыене включают квадратную переменнуюРазложение на множители неквадратичных выражений без квадратов, простых коэффициентов и положительных множителей Разложение на множители неквадратичных выражений без квадратов, простых коэффициентов и отрицательных и положительных множителей Разложение на множители неквадратичных выражений без квадратов, составных коэффициентов и положительных множителей Разложение на множители неквадратичных выражений без квадратов, составных коэффициентов и отрицательных и положительных множителей Факторные выражения, которые всегда включают переменную в квадратеФакторинг неквадратичных выражений со всеми квадратами, простыми коэффициентами и положительными множителями Факторинг неквадратичных выражений со всеми квадратами, простыми коэффициентами и отрицательными и положительными множителями Факторинг неквадратичных выражений со всеми квадратами, составными коэффициентами и положительными множителями Факторинг неквадратичных выражений со всеми квадратами, составными коэффициентами и отрицательными и положительными множителями Факторные выражения, которые иногда включают квадраты переменныхФакторинг неквадратичных выражений с некоторыми квадратами, простыми коэффициентами и положительными множителями Разложение неквадратичных выражений с некоторыми квадратами, простыми коэффициентами и отрицательными и положительными множителями Факторинг неквадратичных выражений с некоторыми квадратами, составными коэффициентами и положительными множителями Факторинг неквадратичных выражений с некоторыми квадратами, составными коэффициентами и отрицательными и положительными множителями Умножение многочленов с двумя множителямиУмножение одночлена на двучлен Умножение двух двучленов Умножение одночлена на трехчлен Умножение двучлена на трехчлен Умножение двух трехчленов Умножение двух случайных мон/полиномов Умножение многочленов с тремя множителямиУмножение одночлена на два двучлена Умножение трех двучленов Умножение двух двучленов на трехчлен Умножение двучлена на два трехчлена Умножение трех трехчленов Умножение трех случайных мон/полиномов Неравенства, включая графики Рабочие листы по неравенствам, включая запись неравенства, соответствующего графику, и построение неравенства на числовой прямой. Написание неравенств для графиков Графические неравенства на числовых прямыхГрафические неравенства (базовые) Решение линейных неравенствРешение неравенств, включающих третий член Решение неравенств, включающих третий член и умножение Решение неравенств, включающих третий член, умножение и деление Основные математические правилаПравила сложенияПравило 1: Положительный + Положительный = Сложение Результат будет положительным Пример: 2 + 1 = 3 9 Правило 30003 Отрицательное + Отрицательное = Добавить Результат будет отрицательным Пример: -3 + (-5) = -8 числа с наибольшим абсолютным значением Пример: -3 + 5 = 2 Правило 2: Положительный + отрицательный = вычесть Взять знак числа с наибольшим абсолютным значением Пример: 0002 3 + (-5) = -2Правила умноженияПравило 1: Положительный x Положительный = положительный Пример: 3 x 5 = 15 Правило 2: Отрицательный x Отрицательный Пример: (-3) x (-5) = 15 Правило 2: Положительный x отрицательный = отрицательный Пример: 3 x (-5) = -15 Правило. Отрицательный x Положительный = Отрицательный Пример: -3 x 5 = -15 Правила деленияПравило 1: Положительный ÷ положительный = положительный Пример: 20 ÷ 4 = 5 Правило 2:Отрицательный ÷ отрицательный Отрицательный = Положительный Пример: (-20) ÷ (-4) = 5 Правило 2: Положительный ÷ Отрицательный = Отрицательный Пример: Правило 2 : Отрицательный ÷ Положительный = Отрицательный Пример: -20 ÷ 4 = -5 Правила показанияПравило 1: x M ⋅ x N = X M+N Пример: 3 4 40055 4 40055 4 40055 4 40055 4 40055 4 40055 4 40055 4. ⋅ 3 5 = 3 4+5 3 4 ⋅ 3 5 = 3 9 Rule 2 : x m ÷ x n = x m-n Пример: 3 7 ÷ 3 5 = 3 7-5 3 7 ÷ 3 5 = 3 2 Правило 3: (x M ) N = x MN 9003 Пример. (3 2 ) 4 = 3 8 Правило 4: (xy) M = X M: (xy) M = X M: (xy) M = x M: (xy) M = X M: (xy) M = X . ⋅ y м Пример: (3 ⋅ 5) 2 = 3 2 ⋅ 5 2 (3 ⋅ 5) 2 = 9 ⋅ 25 (3 ⋅ 5) 2 = 225. Правило 5: (x/y) M = x M 9 (x/y) M = x M (x/y) M = x M (x/y) /Y M Пример: (3/5) 2 = 3 2 /5 2 (3/5) 2 = 9/25 Правило 6: . x -m = 1/x m Пример: 3 -2 = 1/3 2 3 -2 = 1/9 Правило 7: x 0 = 1 Пример: 3 0 = 1 Правило 8: x 1 = x Пример: 3 3 3 3 3 3 30055.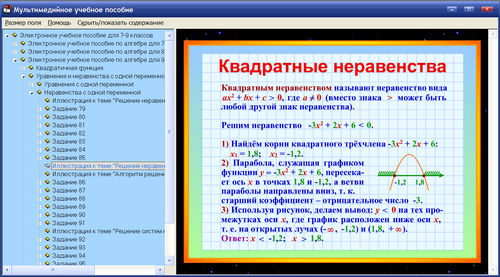 1 = 3 1 = 3Правило 9: x M/N = y —-> x = y N/M Пример: x 1/2 = 3 x = 3 2/1 x = 3 2 x = 9 Правило 10 : (x/y) -m = (y/x) m Пример: (5/3) -2 = (3/5) 2 | 7 9 3) -2 = 3 2 /5 2 (5/3) -2 = 9/25 Правило 11: A x = A Y — —> x = y Пример: 3 m = 3 5 —-> m = 5 0055 a —-> x = y Пример: k 3 = 5 3 —-> k = 5 Можно использовать этот порядок операций2 9005 легко упростить или вычислить сложные числовые выражения с более чем одной бинарной операцией.Очень простой способ запомнить правило PEMDAS: P —-> Скобка E ——> Экспоненты M ——> Умножение D ——> Деление A —-> Сложение S —-> Вычитание Важные примечания: слева направо. 2. Умножение не всегда предшествует делению. Мы должны сделать один за другим в порядке слева направо. 3. В особом упрощении, если у вас есть и сложение, и вычитание, выполняйте операции одну за другой в порядке слева направо. Примеры: 15 ÷ 3 x 2 = 5 x 2 = 10 24 — 8 + 5 = 16 + 5 = 21 В приведенном выше упрощении мы имеем как деление, так и умножение. Слева направо у нас сначала деление, а потом умножение. Итак, сначала мы делаем деление, а потом умножение. Нажмите здесь. Изменение может быть увеличением или уменьшением. Здесь исходная сумма — это значение до увеличения или уменьшения. Для получения дополнительных примеров по процентному увеличению/уменьшению, нажмите здесь Разрядное значениеРазрядное значение цифры в числе – это цифра, умноженная на тысячу или сотню, или в любом другом месте, где она расположена. Пример: В 2 5 486 разряд 5 равен = 5 ⋅ 1000 = 5000 Здесь, чтобы получить значение разряда 5, мы умножаем 5 на 1000. Потому что 5 стоит на разряде тысяч. Номинальная стоимостьНоминальная стоимость цифры в числе — это сама цифра. Точнее, номинал цифры всегда остается одним и тем же, независимо от позиции, в которой она находится. Пример: В 2 5 486 номинал 5 равен 5. Разница между номиналом и номиналом Разница между разрядным значением и номиналом показана на рисунке ниже. УглыОстрый угол: менее 90 ° Тугующий угол: более 90 ° ПРАВИЛЬНЫЙ Угол: 90 ° Прямой угол: 180 ° Комплементарные углы: Два рака. Сумма, измерения которых измерения, измерения которых измерения, измерения которых измерения, измерения которых измерения, измерения которых измерения, измерения которых измерения, измерения которых измерения. составляет 90 градусов. Дополнительные углы: Два угла, сумма мер которых равна 180 градусам. ТреугольникиТреугольники : 1. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Также можно сказать, что решить уравнение — это значит найти множество его корней.
Также можно сказать, что решить уравнение — это значит найти множество его корней.



 Подготовка к ОГЭ, ЕГЭ.
Научу любить и понимать предмет, а не заучить формулы.
Большой успешный опыт преподавания. Подготовка к олимпиадам (многие ученики становились победителями и призерами региональных этапов олимпиады по химии). ЕГЭ более 95 баллов.
Подготовка к ОГЭ, ЕГЭ.
Научу любить и понимать предмет, а не заучить формулы.
Большой успешный опыт преподавания. Подготовка к олимпиадам (многие ученики становились победителями и призерами региональных этапов олимпиады по химии). ЕГЭ более 95 баллов. Самое большое чудо, что создал человек – это язык. Без языка невозможна жизнь на Земле, невозможно развитие человека, его культуры, искусства, науки и техники. На уроках мы будем изучать русский язык при помощи увлекательных заданий. Также обучаю белорусскому языку.
Самое большое чудо, что создал человек – это язык. Без языка невозможна жизнь на Земле, невозможно развитие человека, его культуры, искусства, науки и техники. На уроках мы будем изучать русский язык при помощи увлекательных заданий. Также обучаю белорусскому языку. Считаю, что дистанционные уроки – это эффективно и менее затратно, если правильно подобрать методику преподавания, материал и электронные ресурсы.
Считаю, что дистанционные уроки – это эффективно и менее затратно, если правильно подобрать методику преподавания, материал и электронные ресурсы.
 Разберемся, как запомнить правила, теоремы и функции, какие темы можно освоить за лето, месяц или неделю и как получать хорошие оценки на уроках.
Разберемся, как запомнить правила, теоремы и функции, какие темы можно освоить за лето, месяц или неделю и как получать хорошие оценки на уроках. Придется искать ответы в интернете, тратить время на поиски, читать форумы, проверять достоверность информации и т. д.
Придется искать ответы в интернете, тратить время на поиски, читать форумы, проверять достоверность информации и т. д. Вы сможете выбрать программу по цене, сравнить условия и почитать отзывы.
Вы сможете выбрать программу по цене, сравнить условия и почитать отзывы.




 Желательно делать это разными способами: с помощью онлайн-тестов, расчетных задач и пр.
Желательно делать это разными способами: с помощью онлайн-тестов, расчетных задач и пр. Если у вас растет гуманитарий, то без помощи наставника ему будет тяжело освоить точные науки.
Если у вас растет гуманитарий, то без помощи наставника ему будет тяжело освоить точные науки. В этом уроке мы рассмотрим все правила алгебры, операции и формулы.
В этом уроке мы рассмотрим все правила алгебры, операции и формулы.
 Уравнение для того же записывается как (a × b) = (b × a). Например, (x 4 — 2x) × 3x = 3x × (x 4 — 2x).
Уравнение для того же записывается как (a × b) = (b × a). Например, (x 4 — 2x) × 3x = 3x × (x 4 — 2x). 
 Математически две разные величины не могут быть сложены вместе.
Математически две разные величины не могут быть сложены вместе.
 е. какая бы операция ни использовалась в одной части уравнения, то же самое будет использоваться и в другой части.
е. какая бы операция ни использовалась в одной части уравнения, то же самое будет использоваться и в другой части. Дробь ниже равна умножению выше.
Дробь ниже равна умножению выше. Например,
Например,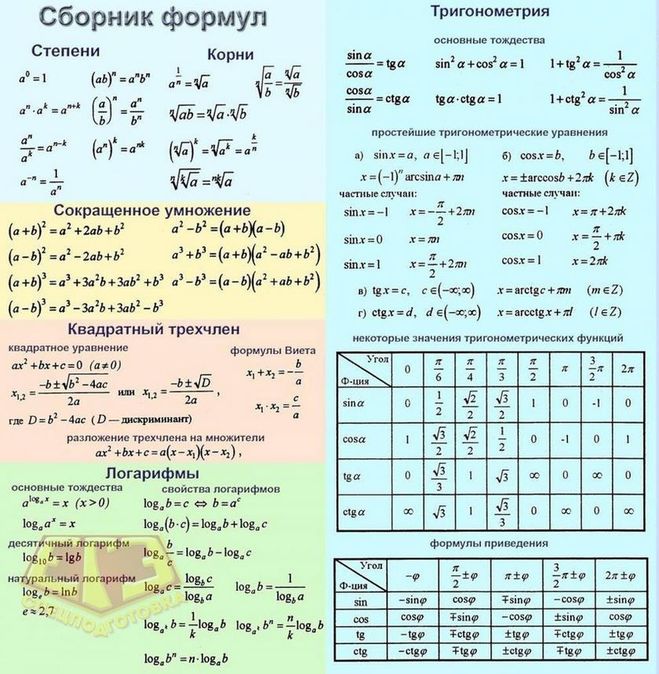


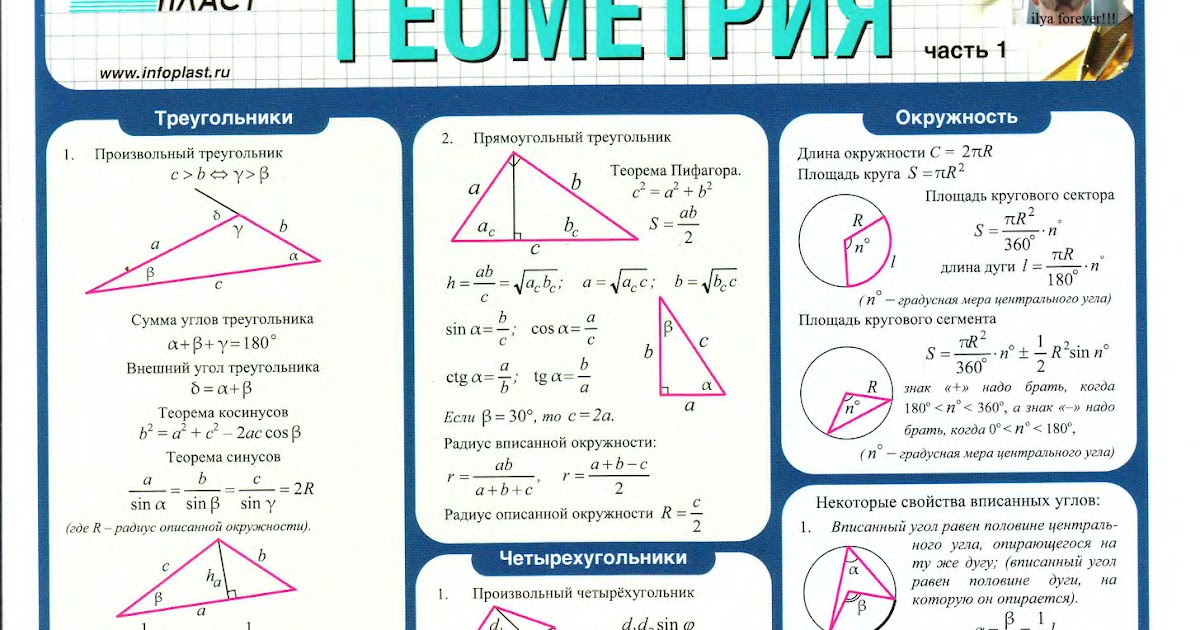 Но b − a — это минус числа a − b .
Но b − a — это минус числа a − b .





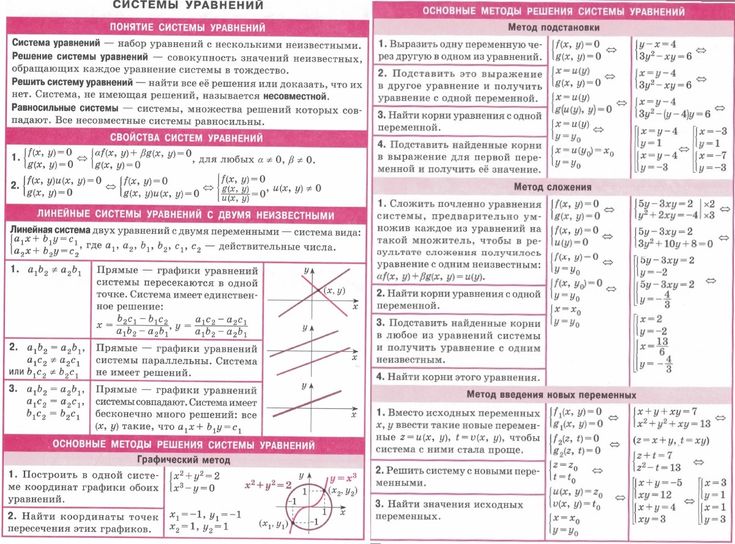
 э.
э.  Определение отрицательного показателя
Определение отрицательного показателя Определение n -го корня
Определение n -го корня
 Следовательно, концепции и дисциплины, которые обычно используются в современном обществе, должны иметь правила, чтобы они могли правильно функционировать и быть понятными людям.
Следовательно, концепции и дисциплины, которые обычно используются в современном обществе, должны иметь правила, чтобы они могли правильно функционировать и быть понятными людям.
 Ниже приведен отличный пример для понимания основ сложения и вычитания дробей в алгебре:
Ниже приведен отличный пример для понимания основ сложения и вычитания дробей в алгебре: Другие второстепенные правила, связанные с «полномочиями к полномочиям», включают правило отношения к мощности.
Другие второстепенные правила, связанные с «полномочиями к полномочиям», включают правило отношения к мощности.




 Плитки алгебры используются многими учителями, чтобы помочь учащимся понять различные темы алгебры. И нет ничего лучше набора координатных осей для решения систем линейных уравнений.
Плитки алгебры используются многими учителями, чтобы помочь учащимся понять различные темы алгебры. И нет ничего лучше набора координатных осей для решения систем линейных уравнений. В контексте арифметики он работает только с операциями сложения или умножения , но не смешанного сложения и умножения. Например, 3 + 5 = 5 + 3 и 9 × 5 = 5 × 9. Забавным занятием, которое вы можете использовать в классе, является мозговой штурм нечисловых вещей из повседневной жизни, которые являются коммутативными и некоммутативными. Например, надевание носков является коммутативным, потому что вы можете надеть правый носок, а затем левый, или вы можете надеть левый носок, а затем правый, и вы получите тот же результат. Однако надевать нижнее белье и брюки некоммутативно.
В контексте арифметики он работает только с операциями сложения или умножения , но не смешанного сложения и умножения. Например, 3 + 5 = 5 + 3 и 9 × 5 = 5 × 9. Забавным занятием, которое вы можете использовать в классе, является мозговой штурм нечисловых вещей из повседневной жизни, которые являются коммутативными и некоммутативными. Например, надевание носков является коммутативным, потому что вы можете надеть правый носок, а затем левый, или вы можете надеть левый носок, а затем правый, и вы получите тот же результат. Однако надевать нижнее белье и брюки некоммутативно. Порядок чисел остается прежним в ассоциативном законе. Как и в случае переместительного закона, он применяется к задачам только на сложение или только на умножение. Лучше всего об этом думать в контексте порядка операций, так как он требует, чтобы сначала были обработаны круглые скобки. Пример ассоциативного закона: (9 + 5) + 6 = 9 + (5 + 6). В этом случае неважно, добавите ли вы сначала 9 + 5 или 5 + 6, вы получите тот же результат. Студенты могут вспомнить несколько примеров из своего опыта, например, класть продукты на поднос во время обеда. Они могли сначала положить на свой поднос молоко и овощи, а затем бутерброд, или они могли начать с овощей и бутерброда, а затем положить молоко. Если их поднос оба раза выглядит одинаково, значит, они смоделировали ассоциативный закон. Чтение книги можно рассматривать как ассоциативное или неассоциативное, поскольку потенциально можно сначала прочитать последние главы и по-прежнему понимать книгу так же, как и тот, кто читает книгу обычным способом.
Порядок чисел остается прежним в ассоциативном законе. Как и в случае переместительного закона, он применяется к задачам только на сложение или только на умножение. Лучше всего об этом думать в контексте порядка операций, так как он требует, чтобы сначала были обработаны круглые скобки. Пример ассоциативного закона: (9 + 5) + 6 = 9 + (5 + 6). В этом случае неважно, добавите ли вы сначала 9 + 5 или 5 + 6, вы получите тот же результат. Студенты могут вспомнить несколько примеров из своего опыта, например, класть продукты на поднос во время обеда. Они могли сначала положить на свой поднос молоко и овощи, а затем бутерброд, или они могли начать с овощей и бутерброда, а затем положить молоко. Если их поднос оба раза выглядит одинаково, значит, они смоделировали ассоциативный закон. Чтение книги можно рассматривать как ассоциативное или неассоциативное, поскольку потенциально можно сначала прочитать последние главы и по-прежнему понимать книгу так же, как и тот, кто читает книгу обычным способом.

 Проще говоря, это означает, что вы можете разделить один из множителей умножения на слагаемые, умножить каждое слагаемое отдельно, сложить результаты, и вы получите тот же ответ. Это также полезно в ментальной арифметике, и пример этого должен помочь проиллюстрировать определение. Рассмотрим вопрос 35 × 12. Разделение 12 на 10 + 2 дает нам возможность мысленно решить вопрос, используя распределительное свойство. Сначала умножьте 35 × 10, чтобы получить 350. Во-вторых, умножьте 35 × 2, чтобы получить 70. Наконец, добавьте 350 + 70, чтобы получить 420. В алгебре свойство распределения становится полезным в тех случаях, когда нельзя легко добавить другой множитель перед умножением. Например, в выражении 3(x + 5) нельзя добавить x + 5, не зная значения x. Вместо этого свойство дистрибутивности можно использовать для умножения 3 × x и 3 × 5, чтобы получить 3x + 15,9.0003
Проще говоря, это означает, что вы можете разделить один из множителей умножения на слагаемые, умножить каждое слагаемое отдельно, сложить результаты, и вы получите тот же ответ. Это также полезно в ментальной арифметике, и пример этого должен помочь проиллюстрировать определение. Рассмотрим вопрос 35 × 12. Разделение 12 на 10 + 2 дает нам возможность мысленно решить вопрос, используя распределительное свойство. Сначала умножьте 35 × 10, чтобы получить 350. Во-вторых, умножьте 35 × 2, чтобы получить 70. Наконец, добавьте 350 + 70, чтобы получить 420. В алгебре свойство распределения становится полезным в тех случаях, когда нельзя легко добавить другой множитель перед умножением. Например, в выражении 3(x + 5) нельзя добавить x + 5, не зная значения x. Вместо этого свойство дистрибутивности можно использовать для умножения 3 × x и 3 × 5, чтобы получить 3x + 15,9.0003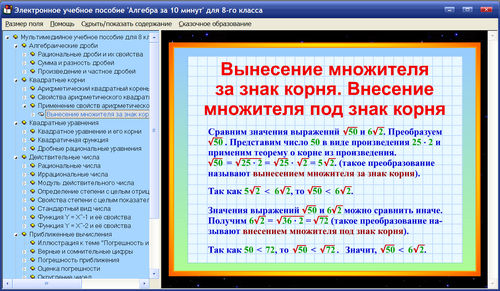 В каждом вопросе нужно иметь дело только с двумя показателями; сложные перепутанные термины и вещи, с которыми мог бы разобраться более продвинутый студент, остаются в покое. Например, 4 2 равно (2 2 ) 2 = 2 4 , но эти рабочие листы просто оставляют это как 4 2 , поэтому учащиеся могут сосредоточиться на изучении того, как умножать и делить степени более или менее изолированно.
В каждом вопросе нужно иметь дело только с двумя показателями; сложные перепутанные термины и вещи, с которыми мог бы разобраться более продвинутый студент, остаются в покое. Например, 4 2 равно (2 2 ) 2 = 2 4 , но эти рабочие листы просто оставляют это как 4 2 , поэтому учащиеся могут сосредоточиться на изучении того, как умножать и делить степени более или менее изолированно.
 Вычитание и упрощение линейных выражений Вычитание и упрощение линейных выражений с множителями Вычитание и упрощение линейных выражений с некоторыми множителями Смешанное сложение, вычитание и упрощение линейных выражений Смешанные сложение, вычитание и упрощение линейных выражений с множителями Смешанные сложение, вычитание и упрощение линейных выражений с некоторыми множителями Упростить простые алгебраические дроби (проще) Упростить простые алгебраические дроби (сложнее)
Вычитание и упрощение линейных выражений Вычитание и упрощение линейных выражений с множителями Вычитание и упрощение линейных выражений с некоторыми множителями Смешанное сложение, вычитание и упрощение линейных выражений Смешанные сложение, вычитание и упрощение линейных выражений с множителями Смешанные сложение, вычитание и упрощение линейных выражений с некоторыми множителями Упростить простые алгебраические дроби (проще) Упростить простые алгебраические дроби (сложнее) Определить линейное уравнение по двум точкам Определение линейного уравнения по двум точкам с помощью графика
Определить линейное уравнение по двум точкам Определение линейного уравнения по двум точкам с помощью графика  В идеале вам понадобятся непрозрачные пакеты без массы, но, поскольку это не совсем возможно (часть без массы), здесь есть небольшое условие, которое на самом деле поможет учащимся лучше понять уравнения. Любые сумки, которые вы используете, должны быть сбалансированы с другой стороны уравнения с пустыми.
В идеале вам понадобятся непрозрачные пакеты без массы, но, поскольку это не совсем возможно (часть без массы), здесь есть небольшое условие, которое на самом деле поможет учащимся лучше понять уравнения. Любые сумки, которые вы используете, должны быть сбалансированы с другой стороны уравнения с пустыми. Теперь самое интересное… если учащиеся удалят две мармеладки с одной стороны уравнения, баланс станет несбалансированным, поэтому им нужно убрать две мармеладки с другой стороны баланса, чтобы сохранить равновесие. Есть желейные бобы необязательно. Цель состоит в том, чтобы изолировать мешки на одной стороне баланса без каких-либо незакрепленных мармеладных бобов, сохраняя баланс уравнения.
Теперь самое интересное… если учащиеся удалят две мармеладки с одной стороны уравнения, баланс станет несбалансированным, поэтому им нужно убрать две мармеладки с другой стороны баланса, чтобы сохранить равновесие. Есть желейные бобы необязательно. Цель состоит в том, чтобы изолировать мешки на одной стороне баланса без каких-либо незакрепленных мармеладных бобов, сохраняя баланс уравнения. Вместо этого они принадлежат другому виду уравнений. Они хороши для их объединения с линейными уравнениями, так как вводят понятие правильных и неправильных ответов для уравнения (то, что позже будет называться областью определения функции). В этом случае неверными ответами для уравнений вида a/ x являются те, у которых знаменатель становится равным 0.
Вместо этого они принадлежат другому виду уравнений. Они хороши для их объединения с линейными уравнениями, так как вводят понятие правильных и неправильных ответов для уравнения (то, что позже будет называться областью определения функции). В этом случае неверными ответами для уравнений вида a/ x являются те, у которых знаменатель становится равным 0.
 Смешанное сложение и вычитание и упрощение квадратных выражений с некоторыми множителями.
Смешанное сложение и вычитание и упрощение квадратных выражений с некоторыми множителями. Упомянутые ниже коэффициенты «а» являются коэффициентами x 2 член как в общем квадратном выражении: ax 2 + bx + c. В этом разделе также есть рабочие листы для вычисления суммы и произведения и для определения операндов для пар суммы и произведения.
Упомянутые ниже коэффициенты «а» являются коэффициентами x 2 член как в общем квадратном выражении: ax 2 + bx + c. В этом разделе также есть рабочие листы для вычисления суммы и произведения и для определения операндов для пар суммы и произведения. В первом разделе рабочие листы включают вопросы, в которых квадратные выражения равны 0. Это делает процесс похожим на разложение квадратных выражений на множители с дополнительным шагом поиска значений x, когда выражение равно 0. Во втором разделе выражения обычно равны чему-то другому, кроме x, поэтому в начале есть дополнительный шаг, чтобы сделать квадратное выражение равным нулю.
В первом разделе рабочие листы включают вопросы, в которых квадратные выражения равны 0. Это делает процесс похожим на разложение квадратных выражений на множители с дополнительным шагом поиска значений x, когда выражение равно 0. Во втором разделе выражения обычно равны чему-то другому, кроме x, поэтому в начале есть дополнительный шаг, чтобы сделать квадратное выражение равным нулю.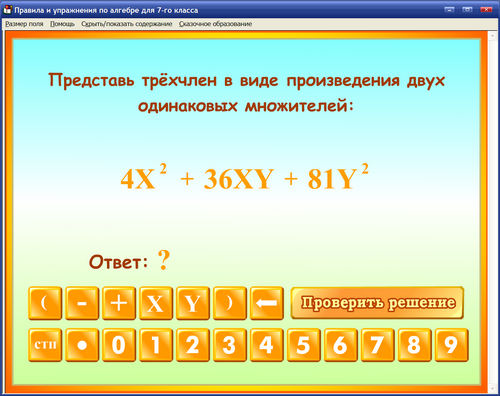

 2 :
2 : Пример. 2 ) 4 = 3 (2) (4)
Пример. 2 ) 4 = 3 (2) (4) 

