Ранняя тригонометрия . Укрощение бесконечности. История математики от первых чисел до теории хаоса
Ранние концепции тригонометрии появляются в трудах индийских математиков и астрономов: «Панча-сиддхантика» («Трактат, включающий пять сиддхант» Варахамихиры, 575 г.), «Брахма-спхута-сиддханта» («Усовершенствованное учение Брахмы» Брахмагупты, 628 г.) и более подробный «Сиддханта-широмани» («Венец учения») Бхаскары, 1150 г.
Индийские математики обычно использовали полухорду, или «арха-джива», по сути современный синус. Варахамихира вычислил эту функцию для 24 целочисленных кратных, с 3°45? до 90°. Примерно в 600 г. в книге Маха-Бхаскария привел полезную приблизительную формулу для синуса острого угла, изобретение которой он приписал Арьябхате. Этим ученым принадлежит авторство многих базовых тригонометрических формул.
Движение Марса, наблюдаемое с Земли
Арабский математик Насир-Ад-Дин Туси в «Трактате о полном четырехстороннике» комбинировал плоскостную и сферическую геометрию в единую унифицированную систему и привел несколько базовых формул для сферических треугольников.
Благодаря тесной привязке к астрономии почти вся тригонометрия оставалась сферической вплоть до 1450 г. В частности, геодезия – нынешняя главная «потребительница» тригонометрии – по сути представляет собой эмпирически разработанные методы, приведенные в систему еще римлянами. Но в середине XV в. плоскостная тригонометрия стала выделяться в отдельную отрасль знаний, и началось это в Северогерманском Ганзейском союзе. Союз контролировал практически всю торговлю, поэтому был богатой и влиятельной организацией. И ему нужны были усовершенствованные методики навигации, наряду с точным измерением времени и практической прикладной астрономией.
Ключевой фигурой того времени был Иоганн Мюллер, более известный как Региомонтан. Он был учеником Георга Пурбаха, начавшего работу над новой редакцией «Альмагеста». В 1471 г. на деньги своего патрона Бернхарда Вальтера он работает над составлением новой таблицы синусов и таблицей тангенсов.
Другие талантливые математики XV–XVI вв. сумели создать собственные тригонометрические таблицы, зачастую поражающие своей точностью. Георг Иоахим Ретик вычислил синусы для окружности с радиусом 1015, причем очень точно, вплоть до 15-го знака после запятой, но умножал все числа на 1015, чтобы получить целые значения – для всех кратных с шагом в одну секунду дуги. Он открыл закон для сферических треугольников:
а также закон для косинусов
cos a = cos b · cos c + sin b · sin c · cos A
в своем «Трактате о сферических треугольниках», написанном в 1562–1563 гг., но опубликованном только в 1596 г. Здесь буквы A, B и C
Виет создал много трудов по тригонометрии, из которых первым был «Математический канон», изданный в 1579 г. Он обобщил и систематизировал разные методы решения треугольников, а именно определение длины всех его сторон и величины углов исходя из другой информации о нем.
Он открыл новые тригонометрические тождества, в том числе несколько интересных выражений для синусов и косинусов углов, кратных ?, представленных через синус и косинус угла ?.
Тригонометрия в таблицах
Тригонометрия в таблицах- Павлова Марина Константиновна, преподаватель цикла СД и ФП
Разделы: Математика
Таблицы по тригонометрии
| a | 0 | ||||||||||||||||
| sin a | 1/2 | 1 | 1/2 | 0 | -1/2 | — | — | -1 | — | — | -1/2 | 0 | |||||
| cos a | 1 | 1/2 | 0 | -1/2 | — | — | -1 | — | — | -1/2 | 0 | 1/2 | 1 | ||||
| tg a | 0 | 1 | — | — | -1 | — | 0 | 1 | — | — | -1 | — | 0 | ||||
| ctg a | — | 1 | 0 | -1 | — | — | 1 | 0 | — | -1 | — | — |
Основные тригонометрические тождества:
Тригонометрические функции суммы и разности двух аргументов:
Представление суммы одноименных тригонометрических функций в виде произведения:
Преобразование произведения тригонометрических функций в сумму:
Формулы двойных аргументов:
Выражение тригонометрических функций через тангенс половинного аргумента:
Формулы приведения («формулы лошади»): a - острый угол!!!
| u | sin u | cos u | tg u | ctg u |
| cos a | — sin a | — ctg a | — tg a | |
| — sin a | — cos a | tg a | ctg a | |
| — cos a | sin a | — ctg a | — tg a | |
| — sin a | cos a | — tg a | — ctg a | |
| cos a | sin a | ctg a | tg a | |
| sin a | — cos a | — tg a | — ctg a | |
| — cos a | — sin a | ctg a | tg a |
Вопросы лошадке:
1) функция меняется?
2) какой был знак и какой поставить в ответ?
Решение тригонометрических уравнений:
| sin x=a <=> |
|
| cos x=a <=> | |
| tg x=a <=> | arcsin(-a)=-arcsina arccos(-a)=p -arccosa |
| ctg x=a <=> | аrctg(-a)=-arctga arcctg(-a)=p -arcctga |
| Частные случаи этих формул: | |
| sin x=1 <=> | |
| sin x=0 <=> | |
| sin x= — 1 <=> |
cos x=1 <=>
cos x=0 <=>
cos x= — 1 <=>
Формулы тройных аргументов:
Кроме того, необходимо знать:
Соотношения между тригонометрическими функциями одного и того же аргумента:
| sin a | cos a | tg a | ctg a | |
| а=sin a | a | |||
| а=соs a | a | |||
| а=tg a | a | |||
| а=ctg a | a |
Найти все углы в заданном диапазоне
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
Помощь по тригонометрии » Углы » Найти все углы в диапазоне заданных выходных данных
Найти все углы между и когда .
Возможные ответы:
и
и
и
Правильный ответ:
и
Объяснение:
Эта задача зависит от понимания опорных углов и котерминальных углов. Базовый угол для угла в стандартном положении – это положительный острый угол между осью x и конечной стороной угла . Таблица опорных углов для каждого квадранта приведена ниже.
Поскольку отрицательно, решения для будут находиться в квадрантах II и III, потому что это квадранты, в которых косинус отрицательный.
Используйте арккосинус и калькулятор, чтобы найти :
В квадранте II у нас есть , итак .
В квадранте III, , так .
Следовательно и .
Сообщить об ошибке
Найти все углы между и когда .
Возможные ответы:
и
и
и
Правильный ответ:
и
Объяснение:
Эта задача зависит от понимания опорных углов и котерминальных углов. Базовый угол для угла в стандартном положении – это положительный острый угол между осью x и конечной стороной угла . Таблица опорных углов для каждого квадранта приведена ниже.
Так как отрицательно, решения для будут находиться в квадрантах II и IV, поскольку это квадранты, в которых тангенс отрицателен. Используйте арктангенс и калькулятор, чтобы найти :
В квадранте II у нас есть , так .
В квадранте IV, , так .
Следовательно и .
Сообщить об ошибке
Найти все углы когда .
Возможные ответы:
и
и
и
и
Правильный ответ: 9090 10 0
Объяснение:Для решения этой задачи мы можем использовать опорные углы, обратную триггерную схему и калькулятор. Ниже приведена таблица опорных углов.
У нас так. Затем подумайте о том, где синус отрицательный, или обратитесь к столбцу «Признаки функции» в приведенной выше таблице. Синус отрицателен в квадрантах III и IV.
В квадранте III, .
В квадранте IV, .
Если бы в этой задаче запрашивались значения между и , наша работа была бы выполнена, но эта задача не ограничивает диапазон, поэтому нам нужно дать все возможных значений , обобщая наши ответы. Для этого мы должны понимать, что все углы, которые сотерминальны и , также будут решениями.
Котерминальные углы складывают или вычитают кратные . Чтобы написать это в общем, мы пишем:
и .
Сообщить об ошибке
Найти все углы когда .
Возможные ответы:
и
и
и
и
Правильный ответ: 9090 10 0
Объяснение:Для решения этой задачи мы можем использовать опорные углы, обратную триггерную схему и калькулятор. Ниже приведена таблица опорных углов.
У нас есть , так . Затем подумайте о том, где тангенс положителен, или обратитесь к столбцу «Признаки функции» в приведенной выше таблице. Тангенс положителен в квадрантах I и III.
В квадранте I, .
В квадранте III, .
Если бы в этой задаче запрашивались значения между и , наша работа была бы выполнена, но эта задача не ограничивает диапазон, поэтому нам нужно дать все возможных значений , обобщая наши ответы.
Для этого мы должны понимать, что все углы, которые сотерминальны и , также будут решениями. Котерминальные углы складывают или вычитают кратные . Чтобы написать это в общем случае, мы пишем:
и
Сообщить об ошибке
Найти все положительные значения меньше для которых .
Возможные ответы:
и
и
Правильный ответ:
и
Пояснение:
На первый взгляд может показаться, что эта задача имеет бесконечное число ответов, поскольку существует бесконечно много отрицательных котерминальных углов, удовлетворяющих этому; однако обратите внимание, что вопрос требует только 9 0199 положительных значений . Другими словами, этот вопрос просто требует значений между и , которые удовлетворяют этому уравнению.
Во-первых, давайте подумаем, где функция косинуса отрицательна.
Согласно диаграмме ниже, это будет в квадрантах II и III.
Косинус исходного угла для каждого углового решения будет равен и равен . См. таблицу опорных углов ниже для квадрантов II и III:
QII:
QIII:
Сообщить об ошибке
Найти все углы между и когда .
Возможные ответы:
и
и
Правильный ответ:
и
Объяснение:
Эта задача зависит от понимания опорных углов и котерминальных углов. Базовый угол для угла в стандартном положении – это положительный острый угол между осью x и конечной стороной угла . Таблица опорных углов для каждого квадранта приведена ниже.
Так как положительное значение, решения для будут находиться в квадрантах I и IV, поскольку в этих квадрантах косинус положителен.
Используйте арккосинус и калькулятор, чтобы найти:
В квадранте I у нас есть , поэтому .
В квадранте IV, , так .
Следовательно и .
Сообщить об ошибке
Найти все углы между и когда .
Возможные ответы:
и
и
и
и
и
Правильный ответ:
и
Объяснение:
Эта задача зависит от понимания опорных углов и котерминальных углов. Базовый угол для угла в стандартном положении – это положительный острый угол между осью x и конечной стороной угла . Таблица опорных углов для каждого квадранта приведена ниже.
Так как положительно, решения для будут находиться в квадрантах I и II, поскольку это квадранты, где синус положителен. Используйте арксинус и калькулятор, чтобы найти :
В квадранте I у нас есть , так что .
В квадранте II, , так .
Следовательно и .
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
Тригонометрическая формула | Тригонометрия Список всех формул
Тригонометрия, раздел математики, связанный с особыми возможностями углов и их программным обеспечением для вычислений. В тригонометрии обычно используются шесть функций отношения. Их названия и сокращения: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических возможностей для прямоугольного треугольника отображаются внутри определения. Например, треугольник включает в себя положение А, и отношение стороны, противоположной А, и стороны, противоположной правому расположению (гипотенуза), известно как синус А или грех А; альтернативные признаки тригонометрии определяются далее.
Эти функции являются домом перспективы. Независимый от размера треугольника, и расчетные значения были сведены в таблицы для множества углов до того, как компьютерные системы сделали тригонометрические таблицы устаревшими. Тригонометрические признаки используются для получения неизвестных углов и расстояний от признанных или измеренных углов в геометрических фигурах.
Тригонометрия возникла из-за необходимости вычислять углы и расстояния в таких областях, как астрономия, картографирование, геодезия и поиск артиллерийских орудий. вопросы, касающиеся углов и расстояний в одной плоскости, защищены в авиационной тригонометрии. в сферической тригонометрии рассматриваются пакеты с сравнимыми проблемами в нескольких самолетах трехмерной области.
Тригонометрия имеет латинское происхождение и происходит от слова triganon, что означает треугольник, и метрон. Сам смысл тригонометрии заключается в измерении треугольников. Этот тип математической функции применяется не только для теоретического решения задач.
Первоначально тригонометрия была важнейшим компонентом навигации в океанах, где не было ориентиров. Это должно показать, насколько сложна эта текущая тема, но также может продемонстрировать, насколько полезными и мощными могут быть функции тригонометрии. Функции тригонометрии используются и для изучения природных явлений, а не только как единица измерения. Но Веданту придумал лучшее решение, чтобы упростить эту сложную концепцию. Эксперт-предметник Vedantu объяснил каждую формулу с примерами таким образом, что ученику понравится читать ее и полностью понимать концепции. Каждый студент очень хорошо знает, насколько важна тригонометрия как с точки зрения экзамена, так и с точки зрения поступления.
Различные тригонометрические формулы
Синус равен стороне, противоположной заданному углу прямоугольного треугольника и гипотенузе.
Косинус равен отношению стороны, прилежащей к острому углу прямоугольного треугольника, к гипотенузе.
Косеканс – это отношение гипотенузы прямоугольного треугольника к стороне, противолежащей острому углу.
Секанс – это отношение гипотенузы к меньшей стороне, примыкающей к острому углу прямоугольного треугольника.
Котангенс — это отношение стороны, отличной от гипотенузы, примыкающей к особо острому углу, к стороне, противоположной углу в прямоугольном треугольнике.
Периодическое тождество тригонометрических углов
\[ sin (\frac{ \pi }{2} – A) = cos A \] & \[cos (\frac{ \pi }{2} – A) = sin A\]
\[ sin (\frac{\pi}{2} + A) = cos A \] & \[ cos (\frac{\pi}{2} + A) = — sin A \]
\[ sin ({3\pi}){2} – A) = – cos A \] & \[ cos (\frac{3\pi}{2} – A) = – sin A \]
\[ sin (\frac{3\pi}{2}+ A) = – cos A \] & \[ cos (\frac{3\pi}{2} + A) = sin A \]
\[ sin (π – A) = sin A \] & \[ cos (π – A) = – cos A \]
\[ sin (π + A) = – sin A \] & \[ cos (π + A) = – cos A \]
\[ sin (2π – A) = – sin A \] & \[ cos (2π – A) = cos A\]
\[ sin (2π + A) = sinA cos (2π + A) = cos A \]
Кофункция Тождество 9{0}− x) = sec x\]
Тригонометрическая формула суммы и разности
\[sin(x + y) = sin(x)cos(y) + cos(x)sin(y)\]
\[cos(x + y) = cos(x)cos(y) – sin(x)sin(y)\]
\[tan(x + y) = \frac{(tan x + tan y)}{(1 − tan x • tan y)} \]
\[sin(x – y) = sin(x)cos(y) – cos(x)sin(y)\ ]
\[cos(x – y) = cos(x)cos(y) + sin(x)sin(y)\]
\[tan(x − y) = \frac{( тангенс x – тангенс y)}{(1 + тангенс x • тангенс y)}\] 9{-1} x \]
Если мы разделим плоскость на четыре квадранта, то все тригонометрические функции положительны в первом квадранте.
В третьем квадранте tan и cot положительны. В 4-м квадранте cos и sec положительны. Все тригонометрические тождества цикличны и повторяются. После константы периодичности повторяются тригонометрические тождества. Эта константа периодичности варьируется от одного тригонометрического тождества к другому.
Формулировка первичного тригонометрического признака
Для нахождения факторов в тригонометрии используется по существу 6 соотношений. их можно назвать тригонометрическими признаками. Шесть тригонометрических возможностей: синус, косинус, секанс, косеканс, тангенс и котангенс.
с помощью прямоугольного треугольника в качестве эталона получены тригонометрические возможности и тождества:
\[cos θ = \frac{\text{примыкающая сторона}}{гипотенуза}\]
\[tan θ = \frac{\text{противоположная грань}}{\text{прилегающая грань}}\]
\[sec θ = \frac{Гипотенуза}{\text{прилегающая грань} }\]
\[cosec θ = \frac{Гипотенуза}{\text{противоположная сторона}}\]
\[cot θ = \frac{\text{соседняя грань}}{\text{ противоположная грань}} \]
Взаимные тождества
Взаимные тождества задаются как:
\[ cosec θ = \frac{1}{sin θ} \]
\[ sec θ = \frac{1}{cos θ} \]
\[ cot θ = \frac{1}{tan θ} \]
\[ sin θ = \ frac{1}{cosec θ} \]
\[ cos θ = \ frac{1}{sec θ} \]
\[ tan θ = \ frac{1}{cot θ} \]
Большинство из них взяты из прямоугольного треугольника.
Когда вершина и сторона основания правильного треугольника признаны, мы узнаем значения синуса, косинуса, тангенса, секанса, косеканса и котангенса при использовании тригонометрических формул. Взаимные тригонометрические тождества также выводятся посредством использования тригонометрических признаков. 9{\circ} \]
\[\frac{\pi}{6}\]
\[\frac{\pi}{4}\]
\[\frac{\ pi}{3}\]
\[\frac{\pi}{2}\]
\[\pi\]
\[\frac{3 \pi}{2} \]
2 \ [\ pi \]
1
9
0
0 0005
0 0005
0 0005
9
9.
\[ \frac{1}{\sqrt{2}}\]
\[ \frac{\sqrt{3}}{2}\]
1
0
-1
0
2
cosθ
1
\[ \frac{\sqrt{3}}{2}\]
\[ \frac{1}{\sqrt{2}0}\]
\[ \frac{1}{2}\]
0
-1
0
1
3
tanθ
0
\[ \frac{1}{\sqrt{3}}\]
1
\[\sqrt{3}\]
\[\infty\]
0
\[\infty\]
0
4
детская кроваткаθ
\[\infty\]
\[\sqrt{3}\]
1
\[\frac{1}{\sqrt{3}} \]
0
\[\ infty\]
0
\[\infty\]
5
csecθ
\[\infty\]
2
\ [\sqrt{2}\]
\[\frac{2}{\sqrt{3}} \]
1
\[\infty\]
-1
\[\infty\]
6
secθ
1
\[\frac{2}{\sqrt{3}} \]
\[\sqrt{2}\]
2
\[\infty\]
17196
\[\infty\]
1
Тождества периодичности (в радианах)
Эти формулы используются для сдвига углов посредством π/2, π, 2π и т.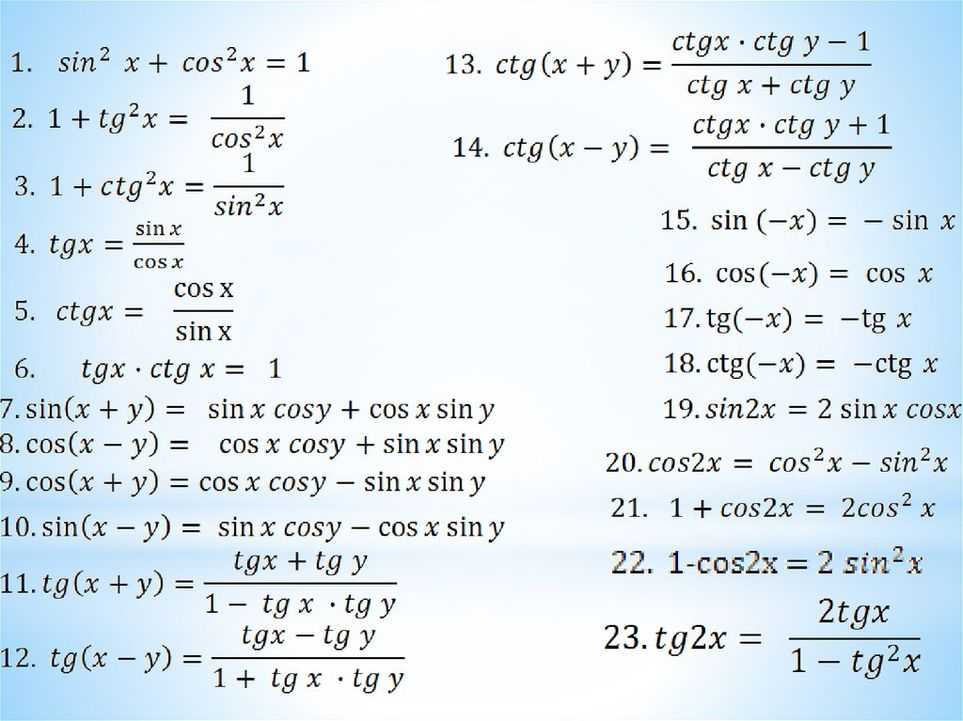
д. их также называют кофункциональными тождествами.
\[ sin (\frac{\pi}{2} – A) = cos A \] & \[ cos (\frac{\pi}{2} – A) = sin A \]
\[sin (\frac{\pi}{2} + A) = cos A \] & \[cos (\frac{\pi}{2} + A) = — sin A \]
\ [sin (\frac{3\pi}{2} – A) = – cos A\] & \[cos ((3π)/2 – A) = – sin A \]
\[sin (\frac{3pi}{2} + A) = – cos A \]& \[cos (\frac{3\pi}{2} + A) = sin A \]
\[sin (π – A) = sin A \]& \[cos (π – A) = – cos A \]
\[sin (π + A) = – sin A \]& \ [cos (π + A) = – cos A \]
\[sin (2π – A) = – sin A\] & \[cos (2π – A) = cos A \]
\ [sin (2π + A) = sin A \]& \[cos (2π + A) = cos A \]
Все тригонометрические тождества имеют циклическую природу.
Они повторяются после этой периодичности. Эта периодичность является единственной в своем роде для уникальных тригонометрических тождеств. загар сорок пять0 = загар 2250, однако это верно для cos сорок пять0 и cos 2250. Сопоставьте с приведенными выше тригонометрическими соотношениями, чтобы подтвердить значения. 9{0}−x) = sec x \]
Идентичности суммы и разности
\[ sin(x+y) = sin(x)cos(y)+cos(x)sin(y) \ ]
\[ cos(x+y) = cos(x)cos(y)–sin(x)sin(y) \]
\[ tan(x+y) = \frac{( tan x + tan y)} {(1−tan x •tan y)} \]
\[ sin(x–y) = sin(x)cos(y)–cos(x)sin(y) \]
\[ cos(x–y) = cos(x)cos(y) + sin(x)sin(y) \]
\[ tan(x−y) = \frac{ (tan x–tan y)} {(1+tan x • tan y)} \]
Тождества двойной перспективы
\[ sin(2x) = 2sin(x) • cos(x) = \frac{2tan x}{(1+tan2 x)} \]
\[ cos(2x) = cos2(x)–sin2(x) = \frac{(1-tan2 x)}{(1+tan2 x)} \]
\[ cos(2x) = 2cos2(x) −1 = 1–2sin2(x) \]
\[ tan(2x) = \frac{(2tan(x))} {(1−tan2(x))} \]
\[ sec (2x) = \frac{sec2 x}{(2-sec2 x)} \]
\[ csc (2x) = \frac{(sec x.
csc x)}{2} \] 9{-1} x \]
csc x)}{2} \] 9{-1} x \]Что такое формула Sin 3x?
Sin 3x — это синус трех случаев отношения в прямоугольном треугольнике, который выражается как:
\[ Sin 3x = 3 sin x – 4sin3x \]
Все тригонометрические формулы делятся на основные системы:
Тригонометрические тождества
Тригонометрические соотношения
Тригонометрические тождества — это формулировки, включающие тригонометрические функции. эти тождества действительны для всех значений переменных. Тригонометрическое соотношение известно связью между измерением углов и длиной ребер прямоугольного треугольника.
Здесь мы предлагаем список всех формул тригонометрии для учащихся. Эти формулы полезны для ученых при решении задач, в первую очередь основанных на этих формулах или любых тригонометрических утилитах.