Определение координаты движущегося тела (9 класс)
Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.
Механическое движение
При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.
Равномерное движение
При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо
Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:
Рис. 1. Формула координаты тела при прямолинейном равномерном движенииГде:
- Xо – начальная координата тела;
- X – координата в момент времени t;
- Vx – проекция скорости на ось X.
Неравномерное движение
Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.
Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)
Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.
Рис. 2. Формула ускоренияСледовательно, скорость в любой момент времени можно найти следующим образом:
V=Vо+at
Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.
Как найти путь при равноускоренном движении?
Рис. 3. Прямолинейное равноускоренное движениеПройденный путь численно равен площади под графиком.
Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2
Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или
X=Xo+Voxt+axt2/2
Движение тела по вертикали
Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.с.
При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.
Координату же можно рассчитать по формуле: Y=Yo+Voyt+gt2/2
Движение тела по окружности
При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.
Что мы узнали?
Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.
Оценка доклада
А какая ваша оценка?
Свободное падение тел. Движение с ускорением свободного падения презентация, доклад
Подготовила:
Климкова Татьяна Юрьевна
СВОБОДНОЕ ПАДЕНИЕ ТЕЛ.
ДВИЖЕНИЕ
С УСКОРЕНИЕМ СВОБОДНОГО ПАДЕНИЯ
v0x=v0cosa
ВСПОМНИМ ИЗУЧЕННОЕ
v0x=v0cosa
vx=v0x+axt
vy=v0y+ayt
sy=v0yt+ayt2/2
x=x0+v0xt+axt2/2
y=y0+v0yt+ayt2/2
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
Какое движение называется
равноускоренным ?
Определение ускорения.
Физический смысл ускорения.
Формула проекции скорости при
равноускоренном движении
Формула проекции перемещения
при равноускоренном движении
v0x=v0cosa
Формула координаты
при равноускоренном движении
v0x=v0cosa
Определите характер движения, пользуясь рисунком
и запишите формулы для расчета v и s
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
v0
v0
v0
v0
а
а
а
а
х
х
х
х
0
0
0
0
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
v0x=v0cosa
равноускоренное
равноускоренное
равнозамедленное
равнозамедленное
v= v0 + at
-v = -v0 — at
-v = -v0+at
v =v0 — at
s=v0t+at2/2
-s= -v0t+at2/2
-s = -v0t- at2/2
s= v0t -at2/2
у
h
g
v0=0
1.
Свободное падение тел
Равноускоренное
движение
Свободное
падение
vx=v0x+axt
vy=v0y+ayt
sy=v0yt+ayt2/2
sx=v0xt+axt2/2
x=x0+v0xt+axt2/2
y=y0+v0yt+ayt2/2
Анализируем рисунок
v0=0,
a=g ,
gy=-g,
y0 =h
Работаем с формулами
vy=v0y+gyt
sy=v0yt+gyt2/2
v
-v = 0 — gt
-h =-gyt2/2
y=y0+v0yt+gyt2/2
y=y0-gt2/2
v =gt
h =gt2/2
y=h-gt2/2
s =h ,
0
y0
vу =-v
График vу(t)
(ось ОУ направлена)
вниз
вверх
0
-30
-20
-10
30
20
10
2
1
3
4
5
vу
vу>0
vу м/с
t, с
График ау(t)
(ось ОУ направлена)
вниз
вверх
0
-30
-20
-10
30
20
10
2
1
3
4
5
ау
ау>0
ау м/с2
t, с
Графическое представление
свободного падения
у
g
v=0
v0
h
2.
Движение тела, брошенного
вертикально
Равноускоренное
движение
vx=v0x+axt
vy=v0y+ayt
sy=v0yt+ayt2/2
sx=v0xt+axt2/2
x=x0+v0xt+axt2/2
Тело брошено вертикально вверх
v0y=v0 ,
a=g ,
gy= -g ,
y=h
s =h ,
Анализируем рисунок
y0=0 ,
Работаем с формулами
0
vy=v0y+gyt
v =v0 -gt
Важно помнить: в верхней точке v=0, и
0 = v0 — gt
v0 =gt
y=y0+v0yt+gyt2/2
y =v0t-gt2/2
h =v0t-gt2/2
y=y0+v0yt+ayt2/2
вниз
вверх
0
vу
vу >0
vу м/с
t, с
v0 /g
График vу(t)
0
t, с
v0 /g
у, м
v02 /2g
Графическое представление
движения тела, брошенного вертикально вверх
График у(t)
(ось ОУ направлена)
3.
Движение тела, брошенного
под углом к горизонту
у
х
a
v0x
v0y
v0
v
vy= 0
l
h
g
По горизонтали:
т.е. вдоль оси ОХ тело
движется равномерно
(т.к. нет ускорения)
с постоянной скоростью,
равной
проекции начальной
Т.о. при рассмотрении движения вдоль оси ОХ нужно пользоваться формулами, полученными для равномерного движения
l=vxt= v0cosa t
x= x0 + v0cosa t
l – дальность полета
v0x=v0cosa
v0x=v0cosa=const
h max
y
x
v0x=v0cosa
Вдоль оси ОХ тело движется равномерно
с постоянной скоростью, равной
проекции начальной скорости на ось ОХ
v0х
v0
v=v0х
v0y
v0х
v0y
v
v
v0x=v0cosa
v=v0х
a
v0x=v0cosa
у
х
a
v0x
v0y
v0
v
vy=0
l
h
g
По вертикали:
Вдоль оси ОУ тело
движется равнозамедленно,
со скоростью, равной проекции начальной скорости на ось ОУ
h — максимальная высота
v0у=v0sina
Таким образом, применимы формулы, которые мы использовали ранее для равноускоренного движения по вертикали
gy= -g ,
v0у=v0sina
=v0sina — gt
vy= v0y+gyt
y=y0+v0yt+gyt2/2 = v0sinat- gt2/2
=v0sina — gt
h max
y
x
a
v
v
v=v0y
v0y
v0y
v0x
v0x
vy =0
v0
v0x=v0cosa
Вдоль оси ОУ тело движется равнозамедленно,
подобно телу, брошенному вертикально вверх со скоростью, равной проекции начальной скорости
на ось ОУ
v0x=v0cosa
v=v0y
h max
y
x
v0у
v0х
v0у
vу
v0х
v
v0
a
v=v0у
v
v=v0x
Некоторые зависимости между величинами
при движении под углом к горизонту
(баллистическом движении)
Время полета в 2 раза
больше времени
подъема тела на
максимальную высоту
t= 2tmax = 2v0sina/g
Дальность полета при одной и той же начальной скорости зависит от угла
l = x max= v02sin2a /g
v =
+ v0у2
v0x2
l = x max
150
750
450
300
600
y
x
v0x=v0cosa
Зависимость дальности полета
от угла, под которым тело
брошено к горизонту
l = x max
l = x max= v02sin2a /g
a
v0x=v0cosa
Дальность полета максимальна, когда максимален sin2a.
Максимальное значение синуса равно единице при угле 2a=900,
откуда a = 450
Для углов, дополняющих друг друга до 900 дальность полета одинакова
4. Движение тела, брошенного
горизонтально
v0у=0,
a=g ,
gy= -g ,
y0 =h
s =h ,
Анализируем рисунок:
По горизонтали:
тело движется равномерно
с постоянной скоростью, равной проекции начальной скорости на ось ОХ
v0x= v0
l=vxt= v0cosa t
l=v0xt= v0 t
По вертикали:
Тело свободно падает с высоты h .
Именно поэтому, применимы формулы для свободного падения:
v =gt
h =gt2/2
y=y0-gt2/2
v0
g
h
l
v0y=0
v0x
у
х
Подумайте и дайте ответ
С каким ускорением движется тело, брошенное вертикально вверх?
С каким ускорением движется тело, брошенное
горизонтально?
Что общего в движении тел, брошенных вертикально и под углом к горизонту?
Три тела брошены так: первое – вниз без начальной
скорости, второе – вниз с начальной скоростью,
третье – вверх.
Что можно сказать об ускорениях этих тел?
Тяжелый предмет подвешен на веревке к воздушному шару, равномерно поднимающемуся с некоторой скоростью.
Каково будет движение предмета, если веревку перерезать?
http://class fizika.narod.ru/9_class/13/66.gif — слайд №1
http://class-fizika.narod.ru/index/119s.jpg — слайд № 16
http://class-fizika.narod.ru/index/131a.jpg — слайд №15
http://class-fizika.narod.ru/index/101a.jpg — слайд №2
Литература и интернет-ресурсы
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский «Физика 10»
Л.А.Кирик и др. «Задачи по физике для профильной школы»
Илекса, Москва, 2008 г.
Скачать презентацию
Сводка по физике
Давайте посмотрим, как можно использовать второй закон Ньютона. чтобы выяснить, как быстро будет лететь ваша ракета. Сначала нам нужно понять
- Скорость
- Ускорение
- Сила
, тогда мы сложим их вместе, чтобы найти скорость вашей ракеты.
Вы могли заметить, что здесь мы делаем все наши измерения, используя метрическая система. Это потому, что метрическая система предназначена для всех уравнения для работы без каких-либо коэффициентов преобразования, просто чтобы исправить смешное единицы. Если мы измеряем в английских единицах, футах, дюймах и фунтах, то Повсюду есть факторы выдумки … очень запутанные.
Это мера вашей скорости, определяемая как расстояние охватывают каждую секунду, или каждую минуту, или каждый час. В уравнении форма, то вы можете найти расстояние, которое вы преодолели, умножение скорости, с которой вы путешествуете, на время ты едешь с такой скоростью:
Расстояние = скорость x время
или сокращенно
с = v х т
Пример:
| Игрушечная машинка катится со скоростью 2 метра в секунду — | |
|---|---|
| После | машина уехала |
| 1 секунда | 2 метра |
| 2 секунды | 4 метра |
| 3 секунды | 6 метров |
| 4 секунды | 8 метров |
Но что, если ваша скорость меняется, например когда у тебя горит двигатель ракеты и ракета быстро ускоряется? Как вы измеряете, как вы ускорение?
Термин для этого ускорение, и мера
чтобы понять, насколько быстрее вы будете двигаться после каждого
секунду (или после каждой минуты или часа).
Если это возьмет мою машину
10 секунд, чтобы разогнаться с 0 до 60 миль в час, затем мой
ускорение составляет 6 миль в час каждую секунду — мы бы сказали
6 миль в час за секунд.
Если я измеряю скорость в метрах в секунду вместо миль в час, тогда ускорение в метрах в секунду в секунду. Звучит смешно, но ты так говоришь.
Теперь, если я знаю свое ускорение и как долго я ускоряюсь, Я могу найти свою скорость (скорость), умножив ускорение умножить на время, или в виде уравнения,
Скорость = ускорение x время
или сокращенно
v = ах т
Пример:
| Автомобиль ускоряется на 5 метров в секунду в секунду — | |
|---|---|
| После | машина едет |
| 1 секунда | 5 метров в секунду |
| 2 секунды | 10 метров в секунду |
| 3 секунды | 15 метров в секунду |
| 4 секунды | 20 метров в секунду |
Примечание: 1 метр в секунду (м/с) равен
2,237 мили в час.
Второй закон Ньютона:
Сила = масса x ускорение или
F = m x a (иногда пишется F = ma)
Вы обычно думаете о силе в фунтах — в метрической системе сила равна измеряется в «ньютонах», да, назван в честь сэра Исаака. Ньютон это не много силы — один фунт равен 4,45 ньютона.
Пример:
| Толкание 0,25-килограммовой ракеты — | |
|---|---|
| Тяга двигателя | ускорение ракеты |
| 1 ньютон | 4 метра/сек/сек |
| 2 ньютона | 8 метров/сек/сек |
| 3 ньютона | 12 метров/сек/сек |
| 4 ньютона | 16 метров/сек/сек |
Так что теперь вы можете найти скорость вашей ракеты пойдет:
Если я знаю силу, приложенную к ракете, и массу
ракеты, я могу использовать второй закон Ньютона, чтобы найти ускорение.
Как только я узнаю свое ускорение и как долго я ускоряюсь, я могу найти скорость (v = a x t).
Сила, конечно же, представляет собой тягу ракеты, создаваемую двигателем. спец. Находим время горения, разделив импульс на тягу, как описано на ракете НАР Веб-страница кодирования двигателей.
Пример:
Моя ракета весит 3,5 унции = 0,1 кг.
Примечание: 1 килограмм равен 35,27 унции
Если мы используем двигатель «C5», он будет иметь тягу 5 ньютонов для 2 секунды, согласно его спецификациям.
Это все, что нам нужно знать! Собрав все вместе, мы имеем:
F = 5 ньютонов
м = 0,1 кг
т = 2 секунды
F = m x a, поэтому 5 = 0,1 x a, поэтому a = 50 м/сек/сек
v = a x t = 50 x 2 = 100 метров в секунду = 223,7 мили в час!
…и билета не получишь! Некоторые из более быстрых моделей ракет получат
до 300 миль в час и даже больше, так что эта скорость на самом деле довольно типична.
Вернуться к Домашняя страница космических исследований
Вопросы
Приветствуются ваши вопросы и комментарии относительно этой страницы.
Вы можете отправить запрос по электронной почте Рэнди Калпу,
предложения, новые идеи или просто поболтать.
Обновлено 8 сентября 2008 г.
Калькулятор скорости, расстояния и времени
Используйте этот калькулятор скорости, чтобы легко рассчитать среднюю скорость, пройденное расстояние и продолжительность поездки транспортного средства: автомобиля, автобуса, поезда, велосипеда, мотоцикла, самолета и т. д. Работает с милями, футами, километрами , метры и т. д.
Быстрая навигация:
- Расчет скорости, расстояния и времени
- Формула средней скорости
- Формула расстояния
- Продолжительность (Время) формула
- Как рассчитать среднюю скорость автомобиля?
Для того, чтобы использовать приведенный выше калькулятор скорости, расстояния и времени или выполнять такие расчеты самостоятельно, вам необходимо знать две из трех метрик: скорость, расстояние, время.
Вам нужно будет преобразовать метрики в те же единицы времени и расстояния, например. мили, километры, метры, ярды, футы и часы, минуты или секунды. Например, если у вас есть скорость в милях в час (мили в час), время также должно быть в часах. Если у вас расстояние в километрах, то и скорость должна быть в км/ч (километры в час).
Единица измерения результата будет зависеть от введенных вами единиц, но наш калькулятор скорости будет удобно отображать дополнительные единицы, где это необходимо.
Формула средней скоростиФормула для средней скорости, также называемая средней скоростью в физике и технике:
v = d / t
это время, поэтому вы можете прочитать его как Скорость = Расстояние / Время . Как отмечалось выше, сначала убедитесь, что вы правильно конвертируете единицы измерения, или воспользуйтесь нашим калькулятором скорости, который делает это автоматически. Полученная единица измерения будет зависеть от единиц времени и расстояния, поэтому, если вы вводили данные в милях и часах, скорость будет в милях в час.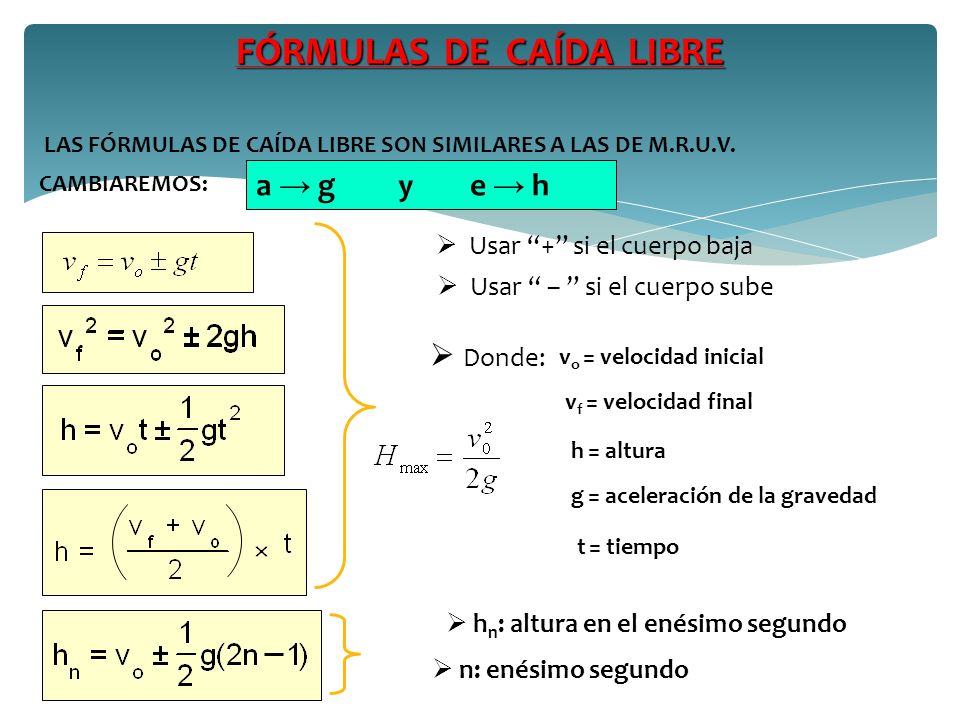
Если это было в метрах и секундах, это будет в м/с (метры в секунду).
Пример: Если вы летели на самолете из Нью-Йорка в Лос-Анджелес и время полета составляло 5 часов, какова была скорость самолета, учитывая, что траектория полета составляла 2450 миль? Ответ: 2450/5 = 490 миль в час (миль в час) средней скорости. Если вам нужен результат в км/ч, вы можете преобразовать мили в км, чтобы получить 788,58 км/ч.
Формула расстоянияФормула расстояния, если известны время (длительность) и средняя скорость:
d = v x t
, где v — скорость (средняя скорость), t — время, а d — расстояние, поэтому вы можете прочитать это как Distance = Speed x Time . Результат будет зависеть от единицы измерения скорости, например, если скорость указана в милях в час, результат будет в милях, если она указана в км/ч, результат будет в километрах. Как обычно, убедитесь, что единица измерения скорости совпадает с единицей времени продолжительности поездки.
Для вашего удобства наш калькулятор расстояний иногда выводит расстояние более чем в одной единице.
Пример: Если грузовик ехал со средней скоростью 80 км/ч в течение 4 часов, сколько миль он проехал за это время? Чтобы найти пройденные мили, сначала рассчитайте 80 * 4 = 320 км, а затем преобразуйте км в мили, разделив на 1,6093 или воспользовавшись нашим конвертером км в мили, чтобы получить ответ: 198,84 мили.
Duration (Time) формула
Время, а точнее продолжительность поездки, можно рассчитать, зная расстояние и среднюю скорость по формуле:
t = d / v
где d — пройденное расстояние, v — скорость (скорость) и t — время, поэтому вы можете прочитать это как Time = Distance / Speed . Убедитесь, что вы конвертируете единицы так, чтобы их компоненты расстояния и времени совпадали, или используйте наш калькулятор продолжительности поездки выше, который автоматически обработает преобразования.
Например, если у вас есть расстояние в милях и скорость в км/ч, вам нужно будет преобразовать скорость в мили в час или расстояние в километры. Единица времени результата будет соответствовать единице времени измерения скорости, поэтому, если она измеряется в чем-то в час, результат будет в часах. Если измерять в какой-то единице в секунду, результат будет в секундах.
Пример: Если поезд может проехать 500 миль со средней скоростью 50 миль в час, сколько времени потребуется, чтобы пройти 500-мильный маршрут? Чтобы найти ответ, используйте формулу и подставьте значения, в результате чего 500/50 = 10 часов.
Как рассчитать среднюю скорость автомобиля? Допустим, вы проехали определенное расстояние на автомобиле или другом транспортном средстве и хотите рассчитать его среднюю скорость. Проще всего это сделать с помощью калькулятора выше, но при желании вы также можете посчитать самостоятельно. В любом случае вам необходимо знать расстояние до удовлетворительного приближения, для чего вы можете использовать карту (например, Google Maps) для измерения расстояния от точки до точки.