Вычисление длины дуги с помощью определенного интеграла: Как найти длину дуги кривой с помощью интеграла

Вычисление длины дуги плоской кривой

20)

Пусть известна функция  и требуется найти длину дуги, заданной функцией  , где  .

Для определения длины дуги необходимо вычислитьопределенный интеграл:

Рассмотрим случай параметрического задания кривой:

где  . В этом случае для определения длина дуги  вычисляется определенный интеграл:

Рассмотрим случай, когда кривая задается в полярных координатах где. Тогда для определения длины дугивычисляется следующийопределенный интеграл:

21)

Как вычислить объем тела вращения с помощью определенного интеграла?

Помимо нахождения площади плоской фигуры с помощью определенного интегралаважнейшим приложением темы является вычисление объема тела вращения. Материал простой, но читатель должен быть подготовленным: необходимо уметь решатьнеопределенные интегралы средней сложности и применять формулу Ньютона-Лейбница в определенном интеграле

. Как и для задачи нахождения площади, нужны уверенные навыки построения чертежей – это чуть ли не самое важное (поскольку интегралы сами по себе чаще будут лёгкими). Освоить грамотную и быструю технику построения графиков можно с помощью методических материалов Графики и свойства Элементарных функций и Геометрические преобразования графиков. Но, собственно, о важности чертежей я уже неоднократно говорил на уроке Определенный интеграл. Как вычислить площадь фигуры.

Вообще в интегральном исчислении очень много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения,длину дуги, площадь поверхности вращения и многое другое. Поэтому будет весело, пожалуйста, настройтесь на оптимистичный лад!

Представьте некоторую плоскую фигуру на координатной плоскости. Представили? … Интересно, кто что представил… =))) Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами:

– вокруг оси абсцисс ; – вокруг оси ординат .

В данной статье будут разобраны оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс. В качестве бонуса я вернусь к задаче нахождения площади фигуры, и расскажу вам, как находить площадь вторым способом – по оси . Даже не столько бонус, сколько материал удачно вписывается в тему.

Начнем с наиболее популярной разновидности вращения.

Вычисление объема тела, образованного вращением плоской фигуры вокруг оси

Пример 1

Вычислить объем тела, полученного вращением фигуры, ограниченной линиями ,вокруг оси.

Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости необходимо построить фигуру, ограниченную линиями,, при этом не забываем, что уравнениезадаёт ось. Как рациональнее и быстрее выполнить чертёж, можно узнать на страницахГрафики и свойства Элементарных функций и Определенный интеграл. Как вычислить площадь фигуры. Это китайское напоминание, и на данном моменте я больше не останавливаюсь.

Чертёж здесь довольно прост:

Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси. На самом деле у тела есть математическое название, но по справочнику что-то лень уточнять, поэтому едем дальше.

Дифференциальное и интегральное исчисления для втузов, т.1

Пискунов Н. С. Дифференциальное и интегральное исчисления для втузов, т.1: Учебное пособие для втузов.— 13-е изд.— М.: Наука. Главная редакция физико-математической литературы, 1985. — 432 с. Хорошо известное учебное пособие по математике для втузов с достаточно широкой математической подготовкой. Первый том включает разделы: введение в анализ, дифференциальное исчисление (функций одной и нескольких переменных), неопределенный и определенный интегралы. Настоящее издание не отличается от предыдущего (1978 г.). Для студентов высших технических учебных заведений. Оглавление ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ § 1. Действительные числа. § 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. n при n целом и положительном § 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23. x, sin x, cos x Упражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6. Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента § 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2. Геометрическое изображение функции двух переменных § 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19. Получение функции на основании экспериментальных данных по методу наименьших квадратов § 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6. Интегрирование по частям § 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9. Формула Чебышева § 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII

Урок Видео: Длина дуги за счет интеграции

Стенограмма видео

используйте интегрирование, чтобы найти длину кривой. К этому моменту вы, возможно, осознаете некоторых ключевых приложений интеграции, областей, объемов и среднего ценности.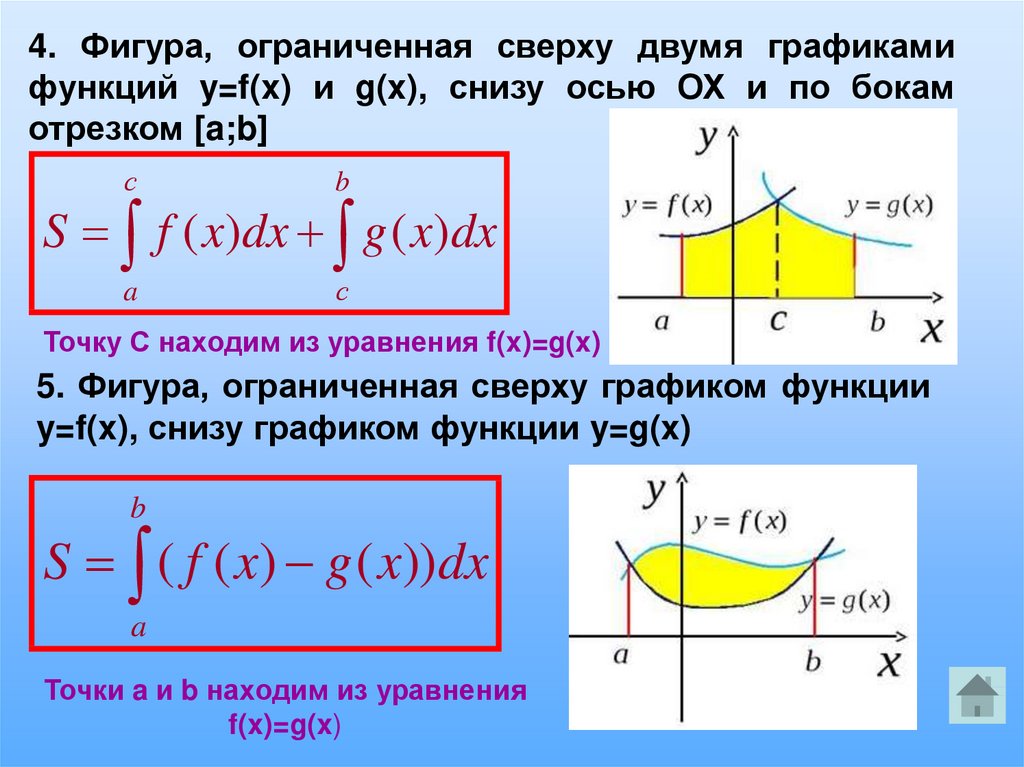 Но знаете ли вы, что интеграция можно также использовать для нахождения длины кривой? В этом видео мы выведем формула для длины дуги с использованием интегрирования, а затем посмотрите на некоторые ключевые применения этой формулы.

Предположим, что кривая 𝑐 определена уравнением 𝑦 равно 𝑓 от 𝑥, где 𝑓 — непрерывная функция на близком интервал от 𝑎 до 𝑏.

Это может выглядеть кое-что так. Тогда мы можем найти оценку для длину 𝑐, разделив наш интервал на подинтервалы, а затем вычислив длина прямой линии, которая соединяет функцию на этих интервалах, как показано. А теперь представьте количество подинтервалы 𝑛 становятся все больше. Что будет с нашим приближение? По количеству подынтервалов увеличивается, каждая прямая становится меньше, и наше приближение становится все ближе и ближе. ближе к точному значению длины 𝑐. Итак, мы собираемся определить длину кривой 𝐿 с уравнением 𝑦 равно 𝑓 кривой 𝑥 как предел длины эти вписанные многоугольники, предполагая, что предел существует.

Проблема в том, что это не очень полезная формула для нас. Но это позволяет нам вывести интегральная формула для 𝐿 при условии, что 𝑓 непрерывна и дифференцируема над этим замкнутый интервал от 𝑎 до 𝑏. Но что мы можем сделать, так это решить длина отрезков с помощью формулы расстояния или теоремы Пифагора определяя индекс Δ𝑦 𝑖 как разницу между индексом 𝑦 𝑖 и 𝑦 индекс 𝑖 минус единица, что, разумеется, равно разнице между 𝑓 𝑥 нижний индекс 𝑖 минус 𝑓 из 𝑥 нижний индекс 𝑖 минус один. Можно сказать, что длина отрезки задаются квадратным корнем из 𝑥 𝑖 минус 𝑥 𝑖 минус один в квадрате плюс 𝑦 𝑖 минус 𝑦 𝑖 минус один квадрат. И мы можем переопределить это как квадрат к Δ𝑥 𝑖 в квадрате плюс Δ𝑦 𝑖 в квадрате.

Затем, применяя среднее значение теоремы к нашей функции 𝑓 на близком интервале 𝑥 𝑖 минус один 𝑥 𝑖, находим, что есть число 𝑥 𝑖 звезда между 𝑥 𝑖 минус один и 𝑥 𝑖 такое, что 𝑓 из 𝑥 𝑖 минус 𝑓 из 𝑥 𝑖 минус единица равна производной оцениваемой функции в этом числе 𝑥 звезда 𝑖 раз 𝑥 𝑖 минус 𝑥 𝑖 минус один. И затем мы переопределяем это, используя обозначения от ранее. Мы находим, что Δ𝑦 𝑖 равно 𝑓 штрих 𝑥 звезды 𝑖 ​​умножить на Δ𝑥. Мы заменили Δ𝑦 𝑖 в нашем выражение для длины отрезков. И затем мы факторим по квадрату корень из Δ𝑥 в квадрате. И мы находим, что длина нашего отрезки равны Δ𝑥 умноженному на квадратный корень из единицы плюс 𝑓 штрих из 𝑥 звезды 𝑖 в квадрате.

Подставляем это в наш исходный лимит. И мы находим, что 𝐿 равно предел, поскольку 𝑥 стремится к бесконечности суммы между 𝑖 равно единице и 𝑛 в Δ𝑥 раз квадратный корень из единицы плюс 𝑓 простое число из 𝑥 звезды 𝑖 ​​в квадрате. По определению можно сказать, что это равен интегралу между 𝑎 и 𝑏 квадратного корня из одного из 𝑓 простых чисел 𝑥 в квадрате относительно 𝑥. И мы получили окончательный формула.

Это говорит о том, что если 𝑓 простое число равно непрерывно на близком интервале от 𝑎 до 𝑏. Тогда длина заданной кривой на 𝑦 равно 𝑓 из 𝑥, учитывая, что 𝑥 больше или равно нулю и меньше или равно 𝑏, равно 𝐿 определенному интегралу, вычисляемому между 𝑎 и 𝑏 квадратный корень из одного плюс 𝑓 простого числа 𝑥 в квадрате относительно 𝑥. Используя обозначения Либени, мы можем запишите это как интеграл между 𝑎 и 𝑏 квадратного корня из единицы плюс d𝑦 на d𝑥 в квадрате оценивается относительно 𝑥. Мы сейчас собираемся посмотреть на применение этой формулы.

Рассчитать длину дуги кривая 𝑦 равна квадратному корню из четырех минус 𝑥 в квадрате между 𝑥 равно нулю а 𝑥 равно двум, что дает ответ с точностью до пяти знаков после запятой.

Используя обозначения Либени, формула длины дуги кривой дается определенным интегралом, вычисляемым между 𝑎 и 𝑏 квадратного корня из единицы плюс d𝑦 на d𝑥 в квадрате относительно 𝑥. Мы знаем, что 𝑦 равно квадратный корень из четырех минус 𝑥 в квадрате, поэтому мы начнем с вычисления d𝑦 через d𝑥. Если мы запишем 𝑦 как четыре минус 𝑥 в квадрате в степени половины, то мы можем использовать общее правило мощности, чтобы найти производная этой функции по 𝑥. Это полтора раза четыре минус 𝑥 возведенный в степень отрицательной половины, умноженный на производную функции который находится внутри скобок. Это минус два 𝑥.

Деление на два и переписывая d𝑦 через d𝑥, мы получаем отрицательное 𝑥 над квадратным корнем из четырех минус 𝑥 в квадрате. Пусть 𝑎 равно нулю, а 𝑏 быть равным двум. А это означает длину интересующая нас кривая равна определенному интегралу между нулем и два квадратного корня из одного плюс минус 𝑥 на квадрат из четырех минус 𝑥 в квадрате по отношению к 𝑥.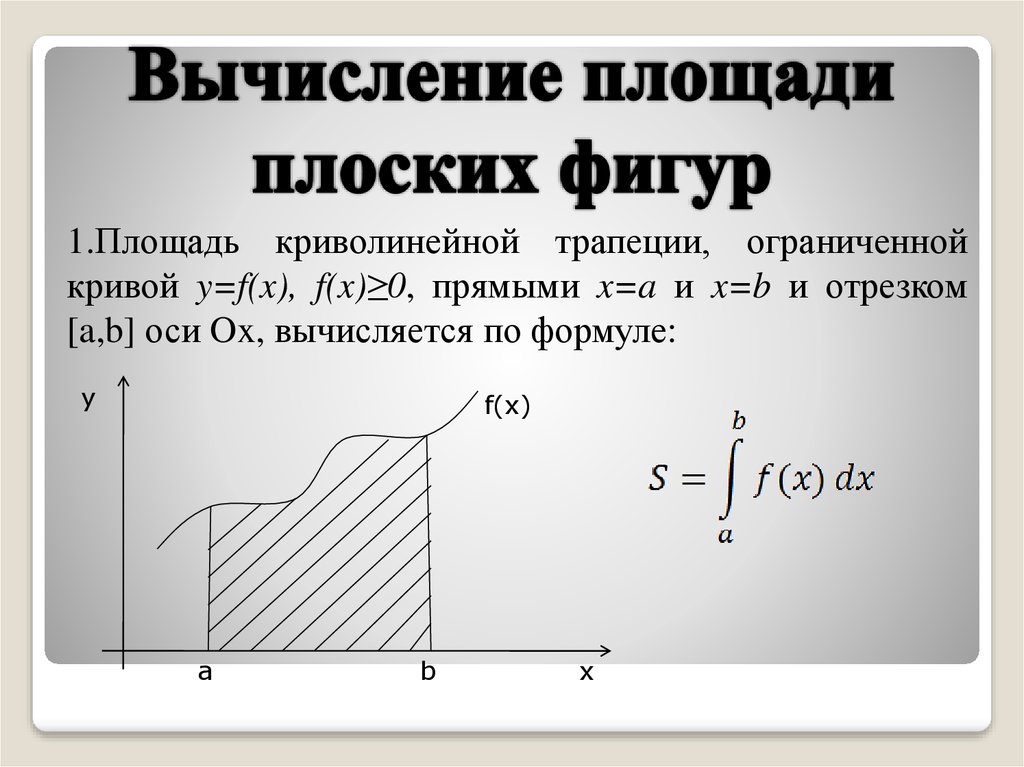 И это довольно упрощает мило. Подынтегральная функция становится квадратом корень из единицы плюс 𝑥 в квадрате из четырех минус 𝑥 в квадрате. Мы можем упростить выражение внутри квадратного корня путем умножения числителя и знаменателя число один на четыре минус 𝑥 в квадрате. И когда мы добавляем это, мы получаем четыре минус 𝑥 в квадрате плюс 𝑥 в квадрате на четыре минус 𝑥 в квадрате. Минус 𝑥 в квадрате плюс 𝑥 в квадрате равен нулю. Таким образом, наша подынтегральная функция становится квадратный корень из четырех на четыре минус 𝑥 в квадрате.

Можно упростить даже дальше. Если мы уберем наш множитель четыре, мы видим, что подынтегральная функция может быть записана как квадратный корень из четырех, умноженных на единицу. квадрат четырех минус 𝑥 в квадрате. Квадрат четыре равен двум. И нам разрешено состояние константы факторы вне интеграла. Итак, мы имеем, что 𝐿 равно двум умножить на определенный интеграл, вычисленный между нулем и двумя единицами по квадрату четыре минус 𝑥 в квадрате. Теперь это может выглядеть действительно противный. Но мы можем вычислить этот интеграл с помощью замены. Напомним, что производная от арксинус 𝑥 равен единице, превышающей квадратный корень из одного минус 𝑥 в квадрате. Итак, мы перепишем наше подынтегральное выражение медленно.

На этот раз мы убираем наш фактор четыре в знаменателе. И мы видим, что два раза один над квадрат четырех отменяется. Мы также можем написать 𝑥 в квадрате четыре как 𝑥 на два в квадрате. Мы выбираем 𝑢 тогда для нашего подстановка равна 𝑥 больше двух. Тогда d𝑢 на d𝑥 равно одна половина. И мы можем сказать, что это эквивалентно тому, что два d𝑢 равны d𝑥. нам тоже нужно менять пределы нашего интеграла. Когда 𝑥 равно двум, 𝑢 равно равно двум разделить на два, что равно единице. А когда 𝑥 равно нулю, 𝑢 равно ноль разделить на два, что равно нулю.

Теперь мы видим, что 𝐿 равно определенный интеграл между нулем и единицей из единицы на квадратный корень из единицы минус 𝑢 в квадрате умножить на два d𝑢. Еще раз, мы вытащим наш общий множитель двух. И теперь мы можем оценить интеграл от единицы на квадратный корень из единицы минус 𝑢 в квадрате. Это просто дуговой грех 𝑢. И мы хотим оценить два умножить на арксинус 𝑢 между единицей и нулем. Это в два раза меньше дуги одного минус арксинус нуля, что равно просто 𝜋. И мы видим, что правильно до пяти десятичных разрядов длина дуги кривой 𝐿 равна 3,14159.

Сейчас мы рассмотрим, как найдите длину дуги кривой, определяемой как 𝑥 с точки зрения 𝑦. Для кривой с уравнением 𝑥 равно 𝑔 из 𝑦, где 𝑔 из 𝑦 непрерывна и имеет непрерывную производную на близких интервал от 𝑐 до 𝑑, длина кривой между 𝑦 равна 𝑐 и 𝑦 равна 𝑑 определяется определенным интегралом, вычисленным между 𝑐 и 𝑑 квадратного корня из одного плюс d𝑥 на d𝑦 в квадрате d𝑦. Применение этой формулы точно так же, как применение предыдущей формулы, которую мы использовали. Посмотрим, как это может выглядеть нравиться.

Найдите длину длины дуга кривой 𝑦 в квадрате равна 𝑥 между 𝑦 равна нулю и 𝑦 равна четыре.

Помните, что для кривой с уравнением 𝑥 равно 𝑔 от 𝑦, где 𝑔 от 𝑦 непрерывно и имеет непрерывную производную на близкий интервал 𝑐 к 𝑑, длина дуги кривой между 𝑦 равна 𝑐 и 𝑦 равно 𝑑 задается определенным интегралом между 𝑐 и 𝑑 квадратный корень из одного плюс d𝑥 на d𝑦 в квадрате d𝑦. Сравним эту формулу с нашей вопрос.

Наша функция 𝑥 через 𝑦 равна 𝑥 равно 𝑦 в квадрате. Итак, мы видим, что нам понадобится дифференцировать 𝑥 по 𝑦. Производная от 𝑥 по до 𝑦 два 𝑦. Нам также говорят, что мы должны найдите длину дуги между 𝑦 равной нулю и 𝑦 равной четырем. Итак, мы собираемся сказать, что 𝑐 равно нулю, а 𝑑 равно четырем. Замена всего, что мы знаем в эту формулу, и мы получаем, что 𝐿 равно определенному интегралу между нулем и четыре из квадратного корня из одного плюс два 𝑦 в квадрате, оцененные по отношению к 𝑦. Ну, два 𝑦 в квадрате — это то же, что четыре 𝑦 в квадрате. Итак, чтобы найти длину дуги нас интересует, нам нужно вычислить определенный интеграл квадратного корня из один плюс четыре 𝑦 в квадрате между нулем и четырьмя. Мы собираемся использовать наш графический калькулятор для этого. И когда мы это делаем, мы получаем, что длина дуги равна 16,81863, что равно 16,8 единицы с точностью до трех значимые фигуры.

Мы видели, что процессы в два примера, которые мы рассмотрели, почти идентичны. Таким образом, мы можем переопределить и формализовать.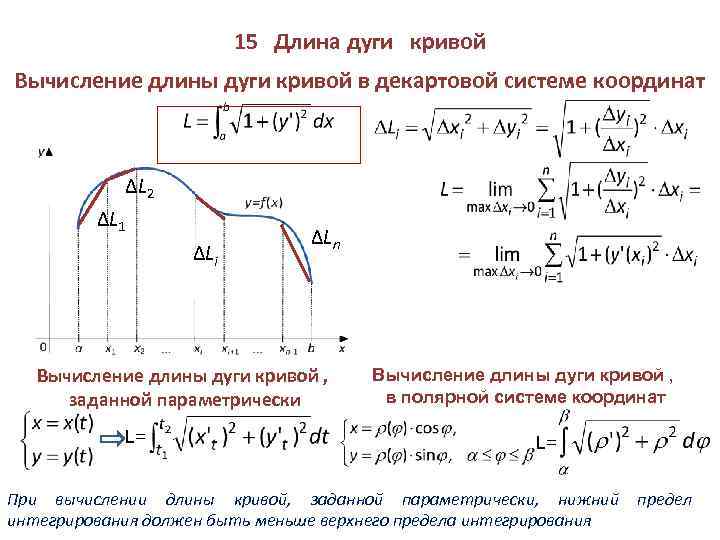 Итак, у нас есть единая формула. Длина дуги определяется как 𝐿 равно интеграл d𝑠, где d𝑠 равен квадратному корню из единицы плюс d𝑦 на d𝑥 в квадрате d𝑥, если 𝑦 равно 𝑓 из 𝑥 на некотором замкнутом интервале от 𝑎 до 𝑏. А d𝑠 равно квадратному корню из один плюс d𝑥 на d𝑦 в квадрате d𝑦, если 𝑥 равно 𝑔 числа 𝑦 для некоторого замкнутого интервала 𝑐 к 𝑑. В нашем последнем примере мы собираемся посмотреть, как определить функцию длины дуги 𝑠 из 𝑥 из заданной точки.

Найдите функцию длины дуги для кривая 𝑦 равна четырем 𝑥 в степени три над двумя, взяв точку с координаты один, четыре в качестве отправной точки.

Помните, формула длины дуги для функции 𝑦 равно 𝑓 от 𝑥 задается как 𝐿 равно интегралу d𝑠, где d𝑠 равно квадратному корню из единицы плюс d𝑦 на d𝑥 в квадрате d𝑥. В нашем случае 𝑦 равно четырем 𝑥 в степени три над двумя. Итак, мы начнем с простой работы узнать, что такое d𝑦 by d𝑥. Не забудьте дифференцировать функции такого рода, мы умножаем на мощность, а затем уменьшаем эту мощность на один. Таким образом, d𝑦 на d𝑥 равно трем более двух раз по четыре 𝑥 в половинной степени. Четыре разделить на два равно два. Итак, мы видим, что d𝑦 на d𝑥 равно до шести 𝑥 в половинной степени. А это значит, что мы можем заменить то, что мы знаем до сих пор в нашей формуле для d𝑠. Получаем квадратный корень из одного плюса шесть 𝑥 в степени половины квадрата d𝑥.

Ну, это очень упрощает; мы получаем квадратный корень из одного плюс 36𝑥. А это значит, что 𝐿 собирается быть равным интегралу квадратного корня из одного плюс 36𝑥, вычисленного относительно к 𝑥. Но каковы наши пределы? Ну, мы работаем в плане 𝑥. И мы знаем, что у нас есть начало точка в 𝑥 равна единице. Так это нижняя граница. Мы ищем генерала функция, поэтому верхний предел будет просто 𝑥. И мы видим, что аргумент функция будет задана интегралом между единицей и 𝑥 квадрата корень из единицы плюс 36𝑥d𝑥. Итак, как мы оцениваем это Интеграл? Мы не можем полагаться на калькулятор, и, на самом деле, нам нужно будет использовать замену.

У нас есть составная функция. Мы собираемся позволить 𝑢 быть равным функция внутри квадратного корня; это один плюс 36𝑥. Можно сказать, что производная от 𝑢 относительно 𝑥 равно 36. И мы также можем эквивалентно сказать тот, что больше 36 d𝑢, равен d𝑥. Прежде чем мы сможем сделать любую замену однако нам нужно будет изменить ограничения. Мы используем нашу замену, чтобы сделать так. А верхний предел равен 𝑥, поэтому, когда 𝑥 равно 𝑥, 𝑢 — это всего лишь один плюс 36𝑥. А нижний предел равен единице, поэтому, когда 𝑥 равно единице, 𝑢 равно единице плюс 36, умноженной на единицу, что равно 37. Теперь мы заменим единицу плюс 36 на 𝑢. Я изменил квадратный корень на сила половины. И заменяем d𝑥 на 36 d𝑢. Так что осталось только оценить этот интеграл между заданными пределами.

Интеграл от 𝑢 в степени половина равна 𝑢 степени трех над двумя, деленной на три над двумя. Таким образом, это означает, что интеграл от 𝑢 в степени половины 36 равно 𝑢 в степени троечки над двойкой более 36 разделить на три на два. И, конечно же, деление на три больше двух равносильно умножению на две трети. Мы можем немного упростить это. И мы видим, что наша длина дуги функция теперь равна единице на 54, умноженной на 𝑢 в степени три на два. Оценка между 37 и одним плюсом 36𝑥. Это один больше, чем 54, умноженный на один плюс 36𝑥 в степени три больше двух минус один больше 54 умножить на 37 в степени три больше двух. И мы закончили.

Мы нашли функцию длины дуги для кривой 𝑦 равно четырем 𝑥 в степени три над двумя, принимая точку с координатами один, четыре в качестве отправной точки. Полезно знать, что сейчас мы имеют эту функцию длины дуги. Мы можем найти длину кривой между точкой 𝑥 равно единице и любой другой точке путем подстановки этого значения 𝑥 в эту формулу.

В этом видео мы увидели, что мы может использовать интегрирование, чтобы помочь нам найти длину дуги кривых, заданных в форме 𝑦 равно 𝑓 из 𝑥 и 𝑥 равно 𝑔 из 𝑦. Мы видели, что формула длины дуги определяется выражением 𝐿 равно интегралу d𝑠, где d𝑠 равно квадратному корню одного плюс d𝑦 на d𝑥 в квадрате d𝑥, если 𝑦 — функция из 𝑥 над некоторым близким интервал от 𝑎 до 𝑏. И это равно квадратному корню одного плюс d𝑥 d𝑦 в квадрате d𝑦, если 𝑥 — функция из 𝑦 на некотором отрезке 𝑐 к 𝑑. Мы также увидели, что мы можем использовать это формула для нахождения общего уравнения длины дуги для функции из заданного отправную точку, изменив верхний предел нашего интеграла на 𝑥 или 𝑦, в зависимости от контекст.

Длина дуги кривой: формула и примеры

Предположим, вы отправляетесь на экскурсию по лесу и вдруг обнаруживаете обрыв. К счастью, есть висячий мост, соединяющий оба конца. Если бы вы пересекли скалу по жесткому мосту, у вас была бы прямая линия, соединяющая оба конца скалы, и в этом случае вы можете без труда найти расстояние между двумя конечными точками. Однако, поскольку мост висячий, он должен быть длиннее, чем расстояние между двумя конечными точками утеса. Так как же найти длину моста?

Висячий мост посреди леса

Исчисление имеет широкий спектр приложений, одним из которых является нахождение свойств кривых. Нахождение длины кривой — яркий пример совместного использования производных и интегралов.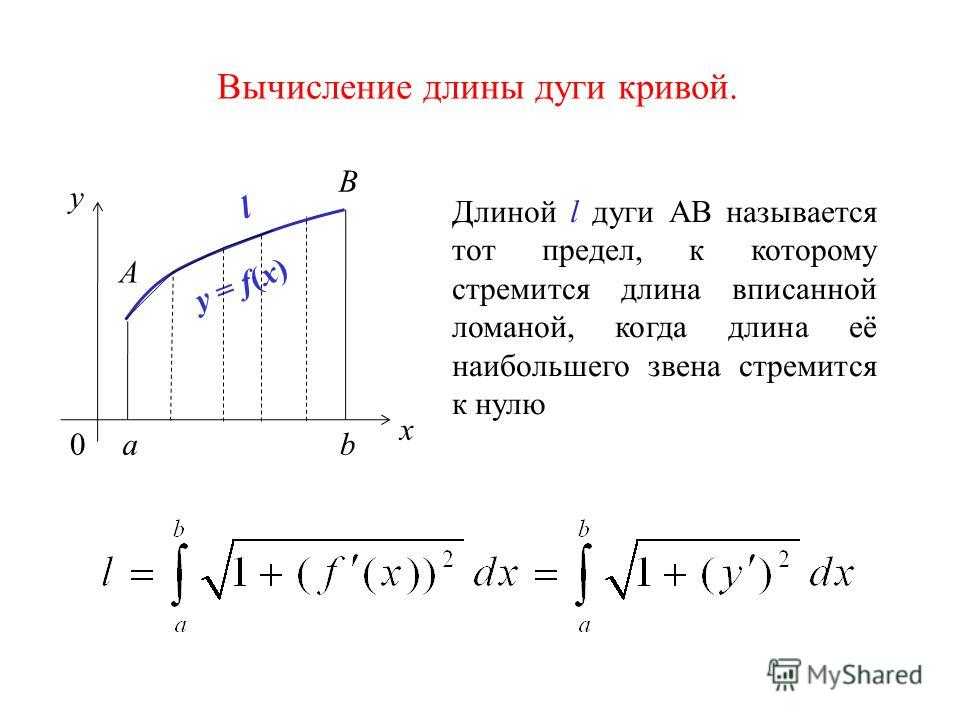 Давайте посмотрим, как производные и интегралы соединяются вместе, чтобы найти длину кривой!

Определение длины дуги кривой

Давайте на мгновение задумаемся о длине кривой. Если бы у вас была прямая линия, а не кривая, вы могли бы легко найти ее длину в заданном интервале, используя теорему Пифагора.

Рис. 1. Теорему Пифагора можно использовать для нахождения длины прямого отрезка.

Точно так же, как вы можете аппроксимировать площадь под кривой, используя прямоугольники, вы можете аппроксимировать длину кривой, используя прямые сегментов. Давайте посмотрим на иллюстрацию того, как это делается.

Рис. 2. Аппроксимация длины параболы с помощью 4 отрезков.

Если вы используете больше сегментов, вы получите лучшее приближение.

Рис. 3. Аппроксимация длины параболы с помощью 8 отрезков.

Знакомо? Как и в случае с суммами Римана, вы начинаете с разделения интервала, а затем оцениваете функцию при каждом значении раздела. На этот раз вам не нужно иметь дело с правыми или левыми конечными точками, поскольку оба значения используются для поиска сегментов. Длину каждого отдельного отрезка можно найти с помощью теоремы Пифагора.

Рис. 4. Теорему Пифагора можно использовать для нахождения длины каждого сегмента.

Наконец, все сегменты складываются, находя приближение длины кривой. Но что, если нам нужно точное значение длины кривой? Затем вам нужно интегрировать .

Формула для длины дуги кривой

Предположим, вам нужно найти аппроксимацию длины кривой в интервале \([a,b]\). Вы можете выполнить следующие шаги:

1. Разделите интервал, используя \(N\) точек.

2. Найдите длину каждого отрезка, соединяющего пару соседних точек разбиения. 93 \sqrt{1+\frac{9}{4}x}\,\mathrm{d}x. \end{align}$$

   Вы можете найти первообразную, используя Интегрирование с заменой. Начните с того, что пусть

   $$u=1+\frac{9}{4}x,$$

   используют Степенное правило для нахождения производной

   $$\frac{\mathrm{d}u}{\mathrm {d}x}=\frac{9}{4},$$

   и используйте его, чтобы найти \( \mathrm{d}x \)$$\mathrm{d}x=\frac{4}{9 }\mathrm{d}u. $$

   Таким образом, вы можете записать интеграл через \(u\) и \(\mathrm{d}u\)

   $$\int\sqrt{1+\ гидроразрыв{9{\frac{3}{2}}.$$

   Приведенное выше выражение можно вычислить с помощью калькулятора. Здесь мы округлим до 2 знаков после запятой в иллюстративных целях, поэтому

   $$\text{Длина дуги}\приблизительно 6,1$$

   Если вы не уверены, является ли функция непрерывной, ознакомьтесь со статьей Continuity Over Интервал.

   Большинство интегралов, которые нам нужно вычислить, чтобы найти длину дуги кривой, сделать сложно. Мы можем использовать систему компьютерной алгебры для вычисления полученных определенных интегралов! 92}\,\mathrm{d}x,$$

   , что можно сделать с помощью тригонометрической замены. К сожалению, это довольно сложно, поэтому вместо вычисления определенного интеграла можно использовать систему компьютерной алгебры:

   $$\text{Длина дуги}\приблизительно 1.8101.$$

   Длина дуги кривой, описываемой уравнением

   До сих пор вы изучали длину дуги кривых, которые можно описать с помощью функций. Однако также можно найти длину дуги кривых, которые описываются с помощью уравнений, таких как уравнение окружности 92.$$

   Приведенное выше уравнение, несмотря на то, что оно не является функцией, также может быть отображено в системе координат. Вы также можете найти его длину дуги! Подход очень похож, но вам нужно учитывать разные факторы. Взгляните на нашу статью «Длина дуги в полярных координатах», чтобы получить обзор на эту тему!

   Длина дуги плоской кривой

   Плоская кривая — это кривая, которую можно нарисовать на плоскости. Все приведенные выше примеры являются кривыми на плоскости .

   Важно подчеркнуть это, потому что также возможно иметь кривых в трехмерном пространстве, , что, к сожалению, выходит за рамки этой статьи.

   Длина дуги параметрической кривой

   Изучая длину дуги кривой, вы можете столкнуться с длиной дуги параметрической кривой. Это относится к другой теме и выходит за рамки данной статьи.

   No related posts.