Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Оснащения врачебно-сестринской бригады. Интересное: Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция | ⇐ ПредыдущаяСтр 2 из 8Следующая ⇒
Минором Мij элемента аij матрицы А, называется определитель матрицы (n-1)-ого порядка, полученной из матрицы А путем вычеркивания i-й строки и j-го столбца. Алгебраическим дополнением называется минор, вычисляемый по формуле: .
Второй способ вычисления определителя
Определитель матрицы любого порядка равен сумме произведений элементов любой строки (или любого столбца) на их алгебраические дополнения: по i-й строке i =1, 2, …, n по j-му столбцу j =1, 2, …, n
Пример: Дана матрица . Надо вычислить Δ. По строке: или или
По столбцу: или или Обычно для вычисления Δ по 2-му способу выбирается строка или столбец, которые содержат больше нулевых элементов, чтобы уменьшить число слагаемых произведений. Согласно схеме вычислений определителя матрицы n-го порядка по 2-му способу необходимо найти определители для матрицы (n-1)-го порядка. Очевидно, что для их нахождения в свою очередь можно использовать ту же схему вычислений и перейти к нахождению определителей матрицы (n-2)-го порядка.
Третий способ вычисления определителя
Самый лучший способ вычисления определителя для матриц большой размерности и если элементы являются нецелыми числами, заключается в преобразовании данной квадратной матрицы к треугольному виду, т.е. к такому виду, когда у полученной после преобразования матрицы все элементы сверху или снизу главной диагонали являются нулевыми
.
Определитель искомой квадратной матрицы А равен произведению диагональных элементов полученной треугольной матрицы . Преобразование квадратной матрицы к треугольному виду рассмотрим позднее («прямой ход» методом Гаусса).
Действия с матрицами
1. Сумма и разность матриц. Могут складываться и вычитаться матрицы только одинакового типа.
Из сложения матриц вытекают следующие свойства:
1) А+(В+С)=(А+В)+С; 2) А+В=В+А; 3) А+0=А.
2. Умножение матрицы на скаляр. Отсюда: 1) 1А=А; 2) 0А=0; 3) α (β А) = (αβ) А; 4) αА + βА = (α+β) А; 5) α (А+В) = αА + αА;
3. Умножение матриц А * В = С.
Перемножать матрицы можно только в том случае, если число столбцов первой матрицы равно числу строк второй матрицы, т.е. g=p, а число строк первой матрицы и число столбцов второй матрицы могут быть любые, т.е. m≠n. Результатом будет матрица С размерностью
Для вычисления элемента, стоящего в i-й строке и j-м столбце произведения двух матриц, нужно элементы i-ой строки первой матрицы умножить на соответствующие элементы j-го столбца второй матрицы и полученные произведения сложить. Свойства: 1) А(ВС)=(АВ)С; 2) α(АВ)=(αА)В; 3) (А+В)=АС+АВ. 4) Запомнить, что в общем случае 4) АВ≠ВА. Пример: В тех частных случаях, когда АВ=ВА, матрицы А и В называются перестановочными. АЕ=ЕА=А. Единичная матрица Е играет роль единицы при умножении.
Транспонированная матрица Если в матрице строки и столбцы поменять местами, то получим транспонированную матрицу. Свойства: 1) дважды транспонированная матрица равна исходной А = (А ) = А; 2) (А+В) =А + В ; 3) (АВ) =В А , т.е. (АВ) ≠ А В ; 4) Если А =А, то матрица А — симметричная (аij = aji)
Обратная матрица
Обратной матрицей по отношению к данной квадратной, называется матрица, которая, будучи умноженной как справа, так и слева на данную матрицу, дает единичную матрицу. Обозначим для матрица А обратную ей матрицу через А-1. АА-1=А-1А=Е. Нахождение обратной матрицы для данной называется обращением данной матрицы. Квадратная матрица называется неособенной, если ее определитель не равен нулю, в противном случае матрица называется особенной или сингулярной. Обратная матрица имеет только у неособенной матрицы. Пусть имеем матричное равенство АС=В. Умножим правую и левую часть равенства на обратную матрицу А-1 А-1АС= А-1В. Поскольку известно, что А-1А=Е, то ЕС= А-1В. И поскольку известно, что ЕС=С, то С= А-1В. То есть, мы равенство АС=В преобразовали в равенство С= А-1В, выразив матрицу С. Если бы у нас были простые алгебраические числа а, b и с, то аналогичные преобразования были бы следующие: . Сравнив преобразования для алгебраических чисел и матриц видим, что обращение матрицы соответствует действию деления. Поэтому понятна необходимость в обратной матрице, в ее вычислениях.
⇐ Предыдущая12345678Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
Линейная алгебра
Линейная алгебраЛинейная алгебра |
назад | оглавление | вперёд |
Рассмотрим систему линейных уравнений.
Задача: определить:
- Совместна или нет данная система
- Если совместна, то сколько имеет решений а)единственное
- Элементарные преобразования получаются с помощью конечного числа преобразований 1 и 2 типа и по уже доказанному на каждом из шагов ранг матрицы не меняется. Следовательно, он не изменится и за конечное число шагов. Ранг матрицы не меняется, если произведено конечное число элементарных преобразований.
б)беск.множество
Понятие ранга матрицы
А=() i= j=
Возьмем в матрице К строк и К столбцов, тогда элементы матрицы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка К. Определитель этой квадратной матрицы называется минором порядка К для матрицы А.
Опр.1. Наибольший порядок минора матрицы,отличный от нуля называется рангом матрицы.
Опр.2. Число
r(A)=k называется рангом
матрицы А, если среди миноров порядка k
есть по крайней мере один,
отличный от нуля, а все миноры большего порядка
равны нулю.
М==0 М==-20 М==0 М==3 Ранг равен 3.
Совершенно очевидно, что нулевой ранг имеет только
нулевая матрица.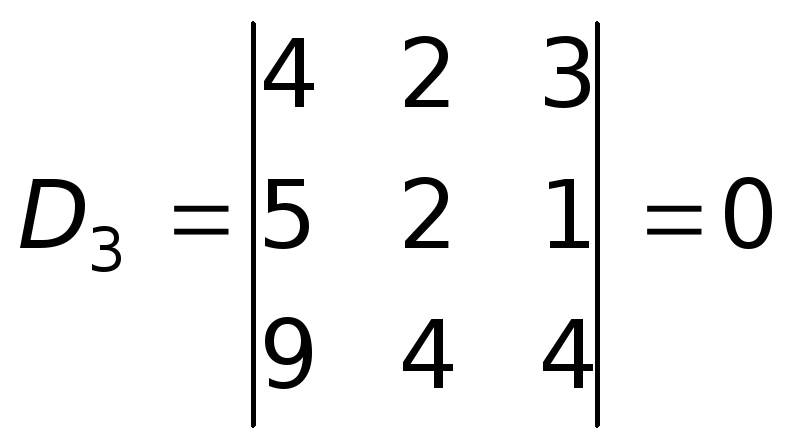 Если матрица не нулевая то её ранг1.
С другой стороны если матрица имеет порядок MxN,
то r(A)min(M,N).
Если матрица не нулевая то её ранг1.
С другой стороны если матрица имеет порядок MxN,
то r(A)min(M,N).
Теоремы о ранге матриц
Т.1. Если матрица А эквивалентна матрице B, то ранг матрицы А равен рангу матрицы B (элементарные преобразования не изменяют ранга матрицы).
Доказательство. Для докозательства достаточно доказать, что каждое из преобразований не может изменить ранга матрицы.
1) А~B B получена умножением строки(столбца) на отличное от нуля число.
А= B=
Если i-я строка не входит в выделенный минор то миноры матриц А и B совпадают. Если i-я строка входит в выделенный минор В=А(по св-ву определителей). Если минор А был отличен от нуля, то В будет отличен от нуля. Таким образом умножение на отличное от нуля число не изменяет ранг матрицы.
2) A~B B получена прибавлением строк
А= В=
Если выбранные строки не содержат i-й
строки, то соответствующие миноры матриц А и В полностью совпадают. Если
минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А0,
то и минор матрицы В0.
Если
минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А0,
то и минор матрицы В0.
Если выбранные миноры содержат i-ю и j-ю строки, тогда М(А)=А=
В=
минор В получен из А путем прибавления строки.
Т.2. Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Вычисление ранга матрицы
Используя утверждение доказанной теоремы, легко вычислить ранг матрицы
- с помощью элементарных преобразований матрица приводится к ступенчатому виду.
- Считается число ненулевых строк ступенчатой матрицы
Ясно, что если матрица является квадратной и невырожденной, то её ранг равен порядку этой матрицы.
ПРИМЕР
~ ~
Ответ: r(A)=2
Исследование систем линейных уравнений. Теорема Кронекера-Капелли.
Рассмотрим систему линейных уравнений
(*)
А=() H=
Т. Кронекера-Капелли.
Система ур-ний (*) совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы r(A)=r(H)
Если система совместна, то она имеет единственное решение, если r(A)=r(H)=n и его можно найти методами Крамера или Гаусса.
Если r(A)=r(H)=k<n, то система имеет бесконечно много решений. В этом случае n-k неизвестных обьявляются свободными неизвестными (принимают любые значения), оставшиеся k неизвестных выражаются через эти свободные неизвестные.
Однородные системы линейных уравнений
Если в системе (*) все свободные
члены
равны нулю, то такая система является однородной.
Однородные системы всегда совместны т.к. ====0 всегда является решением. Такое решение называется тривиальным.
1) то
2) Если ранг матрицы А меньше числа неизвестных,то система имеет бесконечно много решений
Свойства решений линейной однородной системы уравнений.
1) Если является решением системы, то также является решением.
Доказательство.
2) Если является решением системы
также является решением той же самой системы, то и
также является решением системы
Доказательство.
+
откуда получим
3) Если и два различных решения системы, то их линейная комбинация, равная
также является решением системы.
Доказательство.
+
откуда получим
Каждое из решений системы можно записать в виде строки
матрицы,
тогда на основании свойств можно утверждать, что матрицы есть
решения, то также
являются решением. Минимальная возможная система решений через которую
выражаются все остальные решения называется фундаментальной системой решений.
Минимальная возможная система решений через которую
выражаются все остальные решения называется фундаментальной системой решений.
Пример.
~~
{ {
{{
назад | оглавление | вперёд
Калькулятор матрицы кофакторов
— MathCracker.com
Инструкции: Используйте этот калькулятор, чтобы вычислить матрицу кофакторов, связанную с предоставленной вами матрицей. Сначала нажмите на одну из кнопок ниже, чтобы указать размерность матрицы.
Затем нажмите на первую ячейку и введите значение, и перемещайтесь по матрице, нажимая «TAB» или щелкая соответствующие ячейки, чтобы определить ВСЕ значения матрицы.
Кофакторы тесно связаны с обратной матрицей, и они являются ступенями сопряженного метода, используемого для
вычислить обратную матрицу (если она существует).
Вероятно, сами того не зная, вы имели дело с кофакторами при вычислении определителя матрицы размером 3х3 или больше. Итак, как вы подозреваете, кофакторы связаны с определителями, полученными при удалении одной строки и одного столбца.
Как найти кофактор матрицы?
Прежде всего нужно вычислить матрицу миноров. Итак, для данной матрицы размера n x n \(A\) элемент в i-й строке и j-м столбце матрицы матрица миноров равна определителю подматрицы, образованной удалением i-й строки и j-го столбца заданной матрица \(А\).
Итак, если мы называем \(A[i,j]\) подматрицу, полученную удалением i-й строки и j-го столбца \(A\), формально мы определите матрицу миноров \(M\) как:
\[ M_{ij} = \det A[i,j]\]
Обратите внимание, что если \(A\) является матрицей размера n x n, то \(M\) также имеет размер n x n.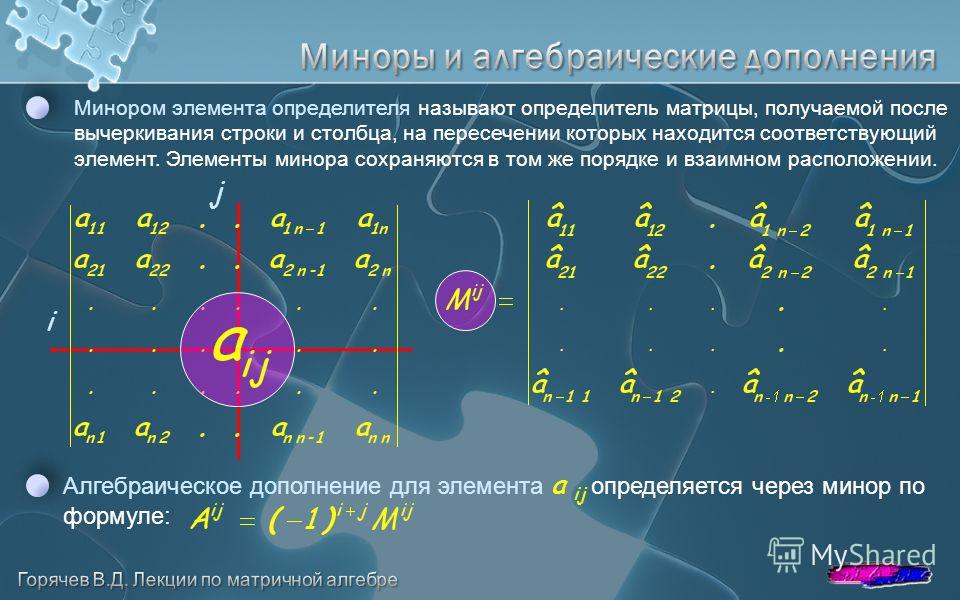
Итак, что такое кофакторная матрица?
Почти готово. Таким образом, миноры — это матрица, содержащая все эти определители соответствующих подматриц, полученные с помощью удаление одной строки и одного столбца. Кофактор почти такой же, за исключением того, что вы добавляете знак (положительный или отрицательный), в зависимости от я и j.
Действительно, матрица кофакторов \(C\) определяется как: 9{я+j} \det A[i,j]\]
Это очень похоже на то, что вы используете при вычислении определителей, да? Итак, чтобы вычислить матрицу кофакторов, вам нужно вычислить кучу определителей.
Как использовать этот калькулятор матрицы кофактора с шагами
Чтобы использовать этот калькулятор кофактора, все, что вам нужно сделать, это предоставить матрицу \(A\). Калькулятор поможет вам в этом процессе
вычисления миноров и знаков для получения кофакторов.
Калькулятор поможет вам в этом процессе
вычисления миноров и знаков для получения кофакторов.
Пример расчета матрицы кофактора
Вопрос: Предположим, у вас есть следующая матрица
\[ \begin{bmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 1\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 2 \end{bmatrix} \] 9{ 3 3} = \begin{vmatrix} \displaystyle 1&\displaystyle 2\\[0.6em]\displaystyle 2&\displaystyle 3 \end{vmatrix} = 1 \cdot \left( 3 \right) — 2 \cdot \left(2 \right) = -1\]
Подводя итоги, матрица миноров:
\[M = \begin{bmatrix}
\displaystyle 5&\displaystyle 3&\displaystyle -1\\[0. 6em]\displaystyle 3&\displaystyle 1&\displaystyle -1\\[0.6em]\displaystyle -1&\displaystyle -1&\displaystyle -1
\end{bmatrix}
\] 9{ 6} \влево(-1\вправо) = 1\]
6em]\displaystyle 3&\displaystyle 1&\displaystyle -1\\[0.6em]\displaystyle -1&\displaystyle -1&\displaystyle -1
\end{bmatrix}
\] 9{ 6} \влево(-1\вправо) = 1\]
Подводя итог, матрица кофакторов:
\[C = \begin{bmatrix} \displaystyle 5&\displaystyle -3&\displaystyle -1\\[0.6em]\displaystyle -3&\displaystyle -1&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{bmatrix} \]
, что завершает расчет.
Примеры алгебры | Матрицы | Нахождение матрицы кофакторов
Шаг 1
Рассмотрим соответствующую таблицу знаков.
Шаг 2
Используйте таблицу знаков и данную матрицу, чтобы найти кофактор каждого элемента.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.1
Вычислить минор для элемента .
Нажмите, чтобы увидеть больше шагов…
Шаг 2.1.1
Минор для — это определитель с удаленными строкой и столбцом.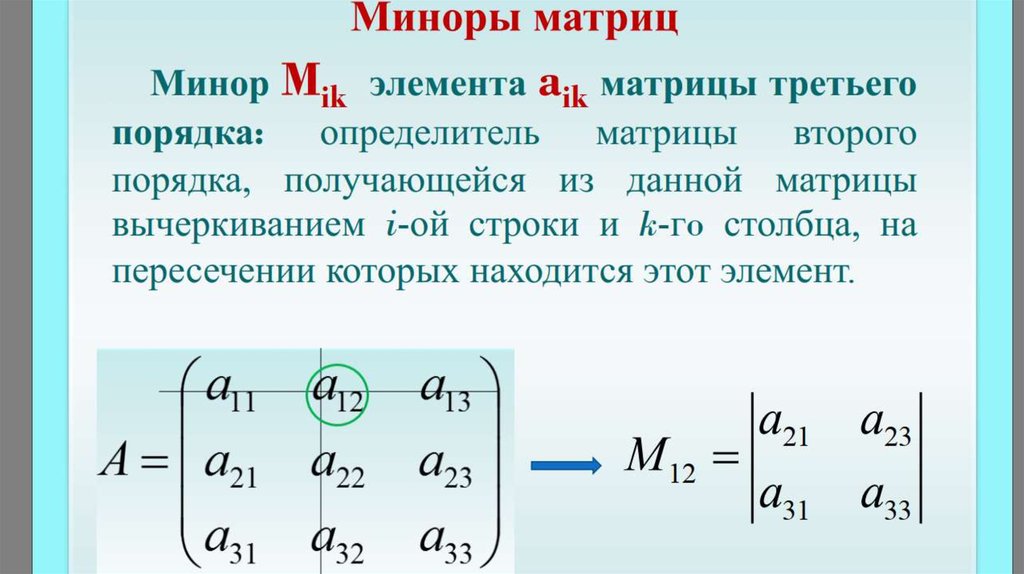
Шаг 2.1.2
Вычислите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.1.2.1
Определитель матрицы можно найти по формуле .
Шаг 2.1.2.2
Упростите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.1.2.2.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.1.2.2.1.1
Умножить на .
Шаг 2.1.2.2.1.2
Умножить на .
Шаг 2.1.2.2.2
Вычесть из .
Шаг 2.2
Вычислить минор для элемента .
Нажмите, чтобы увидеть больше шагов…
Шаг 2.2.1
Минор для — это определитель с удаленными строкой и столбцом.
Шаг 2.2.2
Вычислите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.2.2.1
Определитель матрицы можно найти по формуле .
Шаг 2.2.2.2
Упростите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.2.2.2.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.2.2.2.1.1
Умножить на .
Шаг 2.2.2.2.1.2
Умножить на .
Шаг 2.2.2.2.2
Вычесть из .
Шаг 2.3
Вычислить минор для элемента .
Нажмите, чтобы увидеть больше шагов…
Шаг 2.3.1
Минор для — это определитель с удаленными строкой и столбцом.
Шаг 2.3.2
Вычислите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.3.2.1
Определитель матрицы можно найти по формуле .
Шаг 2.3.2.2
Упростите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.3.2.2.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.3.2.2.1.1
Умножить на .
Шаг 2.3.2.2.1.2
Умножить на .
Шаг 2.3.2.2.2
Вычесть из .
Шаг 2.4
Вычислить минор для элемента .
Нажмите, чтобы увидеть больше шагов…
Шаг 2.4.1
Минор для — это определитель с удаленными строкой и столбцом.
Шаг 2.4.2
Вычислите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.4.2.1
Определитель матрицы можно найти по формуле .
Шаг 2.4.2.2
Упростите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.4.2.2.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.4.2.2.1.1
Умножить на .
Шаг 2.4.2.2.1.2
Умножить на .
Шаг 2.4.2.2.2
Вычесть из .
Шаг 2.5
Вычислить минор для элемента .
Нажмите, чтобы увидеть больше шагов…
Шаг 2.5.1
Минор для — это определитель с удаленными строкой и столбцом.
Шаг 2.5.2
Вычислите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.5.2.1
Определитель матрицы можно найти по формуле .
Шаг 2.5.2.2
Упростите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.5.2.2.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.5.2.2.1.1
Умножить на .
Шаг 2.5.2.2.1.2
Умножить на .
Шаг 2.5.2.2.2
Вычесть из .
Шаг 2.6
Вычислить минор для элемента .
Нажмите, чтобы увидеть больше шагов. ..
..
Шаг 2.6.1
Минор для — это определитель с удаленными строкой и столбцом.
Шаг 2.6.2
Вычислите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.6.2.1
Определитель матрицы можно найти по формуле .
Шаг 2.6.2.2
Упростите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.6.2.2.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.6.2.2.1.1
Умножить на .
Шаг 2.6.2.2.1.2
Умножить на .
Шаг 2.6.2.2.2
Вычесть из .
Шаг 2.7
Вычислить минор для элемента .
Нажмите, чтобы увидеть больше шагов…
Шаг 2.7.1
Минор для — это определитель с удаленными строкой и столбцом.
Шаг 2.7.2
Вычислите определитель.
Нажмите, чтобы увидеть больше шагов. ..
..
Шаг 2.7.2.1
Определитель матрицы можно найти по формуле .
Шаг 2.7.2.2
Упростите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.7.2.2.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.7.2.2.1.1
Умножить на .
Шаг 2.7.2.2.1.2
Умножить на .
Шаг 2.7.2.2.2
Вычесть из .
Шаг 2.8
Вычислить минор для элемента .
Нажмите, чтобы увидеть больше шагов…
Шаг 2.8.1
Минор для — это определитель с удаленными строкой и столбцом.
Шаг 2.8.2
Вычислите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.8.2.1
Определитель матрицы можно найти по формуле .
Шаг 2.8.2.2
Упростите определитель.
Нажмите, чтобы увидеть больше шагов. ..
..
Шаг 2.8.2.2.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.8.2.2.1.1
Умножить на .
Шаг 2.8.2.2.1.2
Умножить на .
Шаг 2.8.2.2.2
Вычесть из .
Шаг 2.9
Вычислить минор для элемента .
Нажмите, чтобы увидеть больше шагов…
Шаг 2.9.1
Минор для — это определитель с удаленными строкой и столбцом.
Шаг 2.9.2
Вычислите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.9.2.1
Определитель матрицы можно найти по формуле .
Шаг 2.9.2.2
Упростите определитель.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.9.2.2.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…
Шаг 2.9.2.




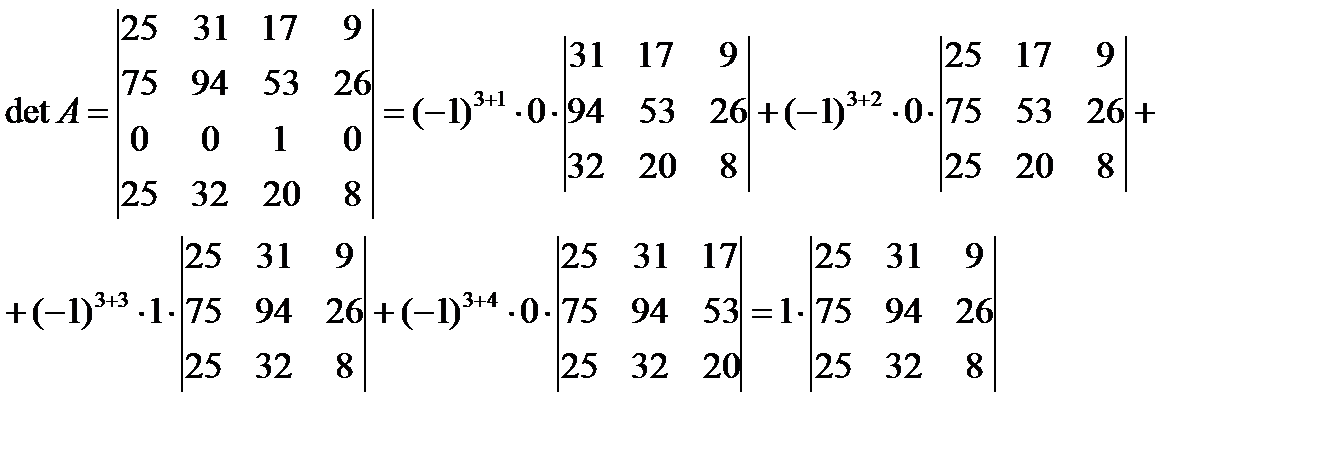
 Например, единичная матрица Е перестановочна с любой матрицей А того же порядка.
Например, единичная матрица Е перестановочна с любой матрицей А того же порядка.
