Организационный этап Задачи: обеспечить нормальную внешнюю обстановку на уроке, психологически подготовить детей к общению | Содержание этапа | ||||||||
1.Приветствие 2. 3.Организация внимания школьников 4.Раскрытие плана проведения урока | |||||||||
Этап проверки домашнего задания. Задачи: установить правильность, полноту и осознанность выполнения всеми учащимися домашнего задания | 1. Выявление степени усвоения заданного учебного материала 2.Определение типичных недостатков в знаниях | ||||||||
Этап актуализации субъектного опыта учащихся. Задачи: обеспечить включение школьников в совместную деятельность по определению целей учебного занятия | 1. Сообщение темы урока 2.Формулирование цели совместно с учениками 3.Показ значимости изучаемого материала 4. Постановка проблемы 5.Актуализация субъектного опыта учащимися | ||||||||
Этап изучения нового материала. Задачи: обеспечить восприятие, осмысление и первичное запоминание изучаемого материала, осознание своих способов проработки учебной информации | 1. 2.Сообщение основного признака изучаемого материала 3.Обеспечить осмысление учащимися методов исследования изучаемых знаний Матрицей размера называется прямоугольная таблица чисел, где– номер строки,– номер столбца, таких, на пересечении которых расположены числа, . Матрица первого порядка содержит единственный элемент, и этот элемент является определителем матрицы. Рассмотрим квадратную матрицу второго порядка,
Для вычисления определителя матрицы A нужно рассмотреть все возможные перестановки индексов, нумерующих ее столбцы. В рассматриваемом случае перечень возможных перестановок множества {1, 2} исчерпывается двумя вариантами: Перестановка {1, 2} не содержит инверсий и поэтому является четной, тогда как перестановка {2, 1} является нечетной, ибо содержит одну инверсию. алгебраическая сумма которых представляет собой определитель матрицы второго порядка:
В случае матрицы третьего порядка существует уже шесть различных перестановок множества {1, 2, 3}: {1, 2, 3}, {2, 3, 1}, {3, 1, 2}, Первые три перестановки являются четными, поскольку каждая из них содержит четное число инверсий. Оставшиеся три перестановки являются нечетными, так как каждая из них содержит нечетное число инверсий (см Примеры). Таким образом,
| ||||||||
Этап первичной проверки новых знаний и способов деятельности. Задачи: установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления | Определитель n-го порядка Определителем или детерминантом n-го порядка называется число записываемое в виде
и вычисляемым по данным числам (действительным или комплексным) — элементам определителя | ||||||||
Этап закрепления новых знаний и способов деятельности. Задачи: обеспечить повышение уровня осмысления учащимися изученного материала, глубины его усвоения | Дать карточки Вычислить определитель третьего порядка: Решение. | ||||||||
Этап подведения итогов урока: Задачи: дать качественную работу класса и всего коллектива | |||||||||
Этап рефлексии Задачи: инициировать рефлексию учащихся по поводу своего эмоционального состояния | Мобилизация учащихся на рефлексию |
Проверка подготовленности к уроку
Организация внимания
Эти перестановки порождают произведения
Вычисление определителей матриц второго и третьего порядка
Самостоятельная работа №1:
Вычисление определителей матриц второго и третьего порядка
Цель работы: овладение методами вычисления определителей второго и третьего порядков.
Студент должен:
Знать:
форму записи определителя и используемую символику
свойства определителей
Теорему Лапласа (о разложении определителя квадратной матрицы с помощью алгебраических дополнений по элементам строки или столбца)
правило Сарусса
Уметь:
вычислять определители первого, второго и третьего порядка
строить миноры и вычислять алгебраические дополнения
Форма выполнения задания: решение задач (письменно)
Время выполнения 20 минут
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1 В чем различие между матрицей и определителем?
2 В чем суть метода разложения определителя по строке или столбцу?
Формирование компетенций:.
Рекомендации по выполнению.
1.Разобрать решение примеров.
2.Выполнить задания тренажера, используя указания.
3.Оформить решение задач тренажера в тетради.
Основной теоретический материал
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно).
Определитель матрицыА обозначается как: det(A), |А| или Δ(A
Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
Определители второго и третьего порядка.
Пусть — квадратная матрица 2-го порядка.
Схема расчета определителя матрицы 2×2.
Определителем 2-го порядка (матрицы а) называется число
D(А) =.
Решение типовых примеров
Пример. Вычислить определитель матрицы
.
РЕШЕНИЕ. D(А) = .
Пусть — матрица 3-го порядка.
Определителем 3-го порядка (матрицы А) называется число
D(А) =
Правило Саррюса (треугольника)
Схемавычисления определителя третьего порядна
Первые два столбца матрицы записываются справа возле матрицы. Произведения элементов, стоящих на линях со знаком «плюс», складываются, затем вычитаются произведения элементов, находящихся на линях со знаком «минус»
Пример. Вычислить определить
Минором элемента aik называется определитель Мik, составленный из элементов, оставшихся после вычеркивания из матрицы А i-ой строки и k-го столбца.
Алгебраическим дополнением элемента aik называется число .
Определителем 3-го порядка (матрицы А) называется сумма произведений элементов первой строки матрицы на их алгебраические допоплнения:
D(А) =
Данную формулу называют разложением определителя по первой строке.
Решение типовых примеров
Пример. Вычислить определитель матрицы третьего порядка
.
Решение. Находим миноры и алгебраические дополнения элементов 1-ой строки матрицы:
Вычисляем искомый определитель:
D(А) = 3.7 + (-2).(-35) + 4.(-7) = 63
.
Далее индуктивно вводится понятие определителей более высоких порядков.
Для матрицы определитель задаётся рекурсивно:
, где — дополнительный минор к элементу . Эта формула называется разложением по строке.
Решение типовых примеров
Пример 1
det A = |
| 4 | -2 | 4 |
| = |
10 | 2 | 12 | ||||
1 | 2 | 2 |
= 4 * 2 * 2 + ( -2) * 12 * 1 + 4 * 10 * 2 — 4 * 2 * 1 — ( -2) * 10 * 2 — 4 * 12 * 2 = 8 Пример 2 |
Самостоятельная работа
Вычислить определитель второго порядка всем | Вычислить определитель второго порядка всем |
1 вариант Вычислить определитель по первой строке | 2 вариант Вычислить определитель по первой строке |
Вычислить определитель по правилу треугольника | Вычислить определитель по правилу треугольника |
3 вариант Вычислить определитель по третьему столбцу | 4 вариант Вычислить определитель по третьему столбцу |
Вычислить определитель по правилу треугольника | Вычислить определитель по правилу треугольника |
5вариант Вычислить определитель по правилу треугольника | 6 вариант Вычислить определитель по правилу треугольника |
Вычислить определитель по второй строке | Вычислить определитель по второму столбцу |
7вариант Вычислить определитель по второй строке | 8 вариант Вычислить определитель по второму столбцу |
Вычислить определитель по правилу треугольника | Вычислить определитель по правилу треугольника |
Оформить отчет.
Требования к оформлению самостоятельной работы
Расчетные задания должны быть выполнены в рабочей тетради.
По результатам решения тренажера выставляется оценка, которая учитывается при приеме дифференцированного зачета.
Шкала оценки образовательных достижений
Процент результативности (правильных ответов) | Оценка уровня подготовки | |
Балл (оценка) | Вербальный аналог | |
90-100 | 5 | отлично |
80-89 | 4 | хорошо |
70-79 | 3 | удовлетворительно |
менее 70 | 2 | неудовлетворительно |
Литература:
Григорьев С.Г., Задулина С.В. Под редакцией В.А. Гусева Математика. – М.:Образовательно-издательский центр «Академия», 2012
Пехлецкий И.
Д. Математика. – М.:Образовательно-издательский центр «Академия», 2012.
Дополнительная литература:
Н.В. Богомолов. Практические занятия по математике. — М., ВШ,2006.
Н.В. Богомолов, П.И. Самойленко. Математика.-М., Дрофа,2008.
Интернет ресурсы:
www/mathematics.ru
http://www.tutoronline.ru/
http://www.exponenta.ru
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/76493-metodicheskie-rekomendacii-k-vneurochnoj-samo
Определитель формулы матрицы 3×3
- Математические сомнения
- Матрицы
- Детерминанты
- Матрица 3 × 3
${\begin{vmatrix} e_{11} & e_{12} & e_{13} \\ e_{21} & e_{22} & e_{23} \\ e_{31} & e_{32} & e_{33} \\ \end{vmatrix}}$ $\,=\,$ $e_{11} \times {\begin{vmatrix} e_{22} & e_{23} \\ e_{32} & e_{33} \\ \end{vmatrix}}$ $\,-\,$ $e_{12} \times {\begin{vmatrix} e_{21} & e_{23} \\ e_{31} & e_ {33} \\ \end{vmatrix}}$ $\,+\,$ $e_{13} \times {\begin{vmatrix} e_{21} & e_{22} \\ e_{31} & e_{ 23} \\ \end{vmatrix}}$
Согласно определению определителя матрицы, формула определителя матрицы 3 на 3 может быть получена в алгебраической форме, выполнив четыре основных шага.
{1+3}$. 9{4} \times {\begin{vmatrix} e_{21} & e_{22} \\ e_{31} & e_{32} \\ \end{vmatrix}}$
$=\,\,\, $ $e_{11} \times 1 \times {\begin{vmatrix} e_{22} & e_{23} \\ e_{32} & e_{33} \\ \end{vmatrix}}$ $\,+ \,$ $e_{12} \times (-1) \times {\begin{vmatrix} e_{21} & e_{23} \\ e_{31} & e_{33} \\ \end{vmatrix}} $ $\,+\,$ $e_{13} \times 1 \times {\begin{vmatrix} e_{21} & e_{22} \\ e_{31} & e_{32} \\ \end{vmatrix }}$
$\следовательно\,\,\,$ ${\begin{vmatrix} e_{11} & e_{12} & e_{13} \\ e_{21} & e_{22} & e_{ 23} \\ e_{31} & e_{32} & e_{33} \\ \end{vmatrix}}$ $\,=\,$ $e_{11} \times {\begin{vmatrix} e_{22 } & e_{23} \\ e_{32} & e_{33} \\ \end{vmatrix}}$ $\,-\,$ $e_{12} \times {\begin{vmatrix} e_{21} & e_{23} \\ e_{31} & e_{33} \\ \end{vmatrix}}$ $\,+\,$ $e_{13} \times {\begin{vmatrix} e_{21} & e_{22} \\ e_{31} & e_{32} \\ \end{vmatrix}}$
Может использоваться как формула для вычисления определителя квадратной матрицы третьего порядка. Его также можно упростить с помощью определителя матрицы второго порядка.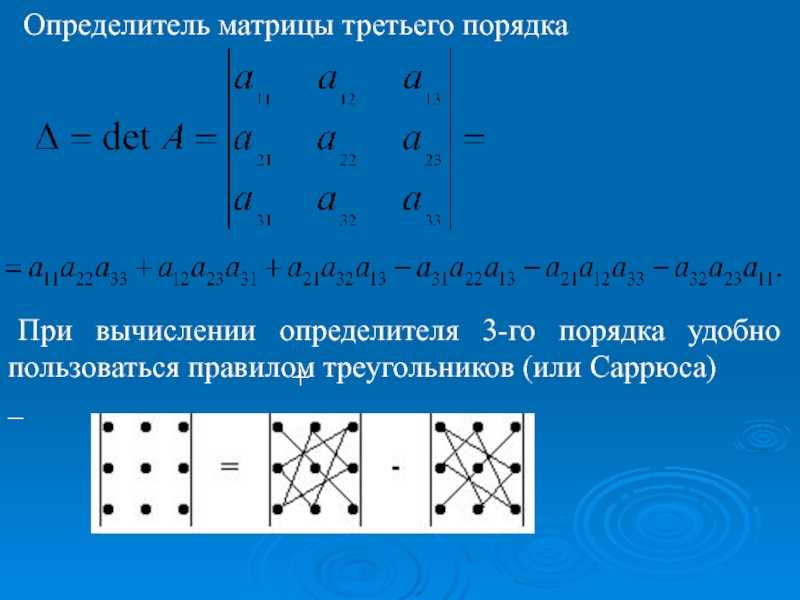
$=\,\,\,$ $e_{11} \times \Big(e_{22} \times e_{33}-e_{23} \times e_{32}\Big)$ $\,- \,$ $e_{12} \times \Big(e_{21} \times e_{33}-e_{23} \times e_{31}\Big)$ $\,+\,$ $e_{13} \times \Big(e_{21} \times e_{32}-e_{22} \times e_{31}\Big)$
$=\,\,\,$ $e_{11} \times \Big (e_{22}e_{33}-e_{23}e_{32}\Big)$ $\,-\,$ $e_{12} \times \Big(e_{21}e_{33}-e_{ 23}e_{31}\Big)$ $\,+\,$ $e_{13} \times \Big(e_{21}e_{32}-e_{22}e_{31}\Big)$
Каждый коэффициент умножения может быть распределен на разность членов выражения с помощью распределительного свойства умножения над вычитанием.
$=\,\,\,$ $e_{11} \times e_{22}e_{33}$ $\,-\,$ $e_{11} \times e_{23}e_{32}$ $\,-\,$ $e_{12} \times e_{21}e_{33}$ $\,+\,$ $e_{12} \times e_{23}e_{31}$ $\,+ \,$ $e_{13} \times e_{21}e_{32}$ $\,-\,$ $e_{13} \times e_{22}e_{31}$
$=\,\, \,$ $e_{11}e_{22}e_{33}$ $\,-\,$ $e_{11}e_{23}e_{32}$ $\,-\,$ $e_{12} e_{21}e_{33}$ $\,+\,$ $e_{12}e_{23}e_{31}$ $\,+\,$ $e_{13}e_{21}e_{32} $ $\,-\,$ $e_{13}e_{22}e_{31}$
$\следовательно\,\,\,$ ${\begin{vmatrix} e_{11} & e_{12} & e_{13} \\ e_{21} & e_{22} & e_{23} \ \ e_{31} & e_{32} & e_{33} \\ \end{vmatrix}}$ $\,=\,$ $e_{11}e_{22}e_{33}$ $\,+\ ,$ $e_{12}e_{23}e_{31}$ $\,+\,$ $e_{13}e_{21}e_{32}$ $\,-\,$ $e_{11}e_ {23}e_{32}$ $\,-\,$ $e_{12}e_{21}e_{33}$ $\,-\,$ $e_{13}e_{22}e_{31}$
Вычисление определителей матриц 2-го и 3-го порядка – MyRank
Определение: Каждая квадратная матрица может быть связана с выражением или числом, известным как ее определитель.
Если А = [а ij ] является квадратной матрицей порядка n, то определитель A обозначается через или |A| или \(\left| \begin{matrix}{{a}_{11}} & {{a}_{12}} & {{a}_{13}} & . & {{a}_{ij }} & . & {{a}_{1n}} \\{{a}_{21}} & {{a}_{22}} & {{a}_{23}} & . & {{ a}_{2j}} & . & {{a}_{2n}} \\. & . & . & . & . & . & . \\{{a}_{i1}} & {{a} _{i2}} & {{a}_{i3}} & . & {{a}_{ij}} & . & {{a}_{in}} \\. & . & . & . & . & . & . \\{{a}_{n1}} & {{a}_{n2}} & {{a}_{n3}} & . & {{a}_{nj}} & . & {{a}_{nm}} \\\end{matrix} \right|\).
Определитель квадратной матрицы порядка 1: Если A = [a 11 ] является квадратной матрицей порядка 1, то определитель матрицы A определяется как |A| = a 11 или |a 11 |= a 11.
Определитель квадратной матрицы второго порядка: Если \(A=\left[\begin{matrix}{{a}_{ 11}}&{{a}_{12}} \\{{a}_{21}}&{{a}_{22}} \\\end{matrix}\right]\) является матрицей порядок 2, то выражение а 11 а 22 – а 12 a 21 определяется как определитель A, т.
е. \(\left| A\right|=\left|\begin{matrix}{{a}_{11}}&{{a}_{12} }\\{{a}_{21}}&{{a}_{22}}\\\end{matrix}\right|\)= a₁₁ a₂₂ – a₁₂ a₂₁.
Определитель квадратной матрицы второго порядка равен произведению диагональных элементов минус произведение диагональных элементов.
Определитель квадратной матрицы третьего порядка: Если \(A=\left[ \begin{matrix}{{a}_{11}} & {{a}_{12}} & {{a}_ {13}} \\{{a}_{21}} & {{a}_{22}} & {{a}_{23}} \\{{a}_{31}} & {{a }_{23}} & {{a}_{33}} \\\end{matrix} \right]\) — квадратная матрица третьего порядка, то выражение a₂₃ a₃₂ – a₂₂ a₁₃ a₃₁ – a₁₂ a₂₁ a₃₃ определяется как определитель A.
\(\left| A \right|=\left| \begin{matrix}{{a}_{11}} & {{a}_{12}} & {{a}_{13}} \ \{{a}_{21}} & {{a}_{22}} & {{a}_{23}} \\{{a}_{31}} & {{a}_{32} } & {{a}_{33}} \\\end{matrix}\right|={{a}_{11}}\left| \begin{matrix}{{a}_{22}} & { {a}_{23}} \\{{a}_{32}} & {{a}_{33}} \\\end{matrix} \right|-{{a}_{12}}\ слева| \begin{matrix}{{a}_{21}} & {{a}_{23}} \\{{a}_{31}} & {{a}_{33}} \\\ end{matrix} \right|+{{a}_{13}}\left| \begin{matrix}{{a}_{21}} & {{a}_{22}} \\{{a} _{31}} & {{a}_{32}} \\\end{matrix} \right|\).
Пример: Вычислить определитель \(A=\left[ \begin{matrix}3 & -2 & 4 \\1 & 2 & 1 \\0 & 1 & -1 \\\end{matrix} \ верно]\).
Решение: \(\left| A \right|=\left| \begin{matrix}3 & -2 & 4 \\1 & 2 & 1 \\0 & 1 & -1 \\\end{ матрица} \справа|\).
= \(3\left| \begin{matrix}2 & 1 \\1 & -1 \\\end{matrix} \right|-\left(-2 \right)\left| \begin{matrix} 1 & 1 \\0 & -1 \\\end{matrix} \right|+4\left| \begin{matrix} 1 & 2 \\ 0 & 1 \\\end{matrix} \right|\).
= 3 (-2 -1) + 2 (-1 -0) + 4 (1 – 0)
= -9 – 2 + 4
= – 7
Только квадратные матрицы имеют определители. Матрицы, которые не являются квадратными, не имеют определителя.
Определитель квадратной матрицы третьего порядка можно разложить по любой строке или столбцу.
Если строка или столбец определителя состоит из всех нулей, то значение определителя равно нулю.
Определитель кососимметричной матрицы нечетного порядка равен нулю.