Вычисления отрицательных и положительных чисел: Сложение Чисел с Разными Знаками

Вычитание отрицательного числа, правило, примеры, как вычесть два отрицательных числа, как из отрицательного числа вычесть положительное

Данная статья посвящена разбору такой темы, как выполнение вычитания отрицательных чисел. Материал представляет собой полезную информацию о правиле вычитания отрицательных чисел и других определениях. Для закрепления сути параграфа мы детально разберем примеры типичных упражнений и задач.

Правило вычитания отрицательных чисел

Для того, чтобы разобраться в данной теме, следует узнать основные определения и понятия.

Определение 1

Правило вычитания отрицательных чисел формулируется так: чтобы из числа a вычесть число b со знаком минус, необходимо к уменьшаемому a прибавить число −b, которое является противоположным вычитаемому b.

Если представить данное правило вычитания отрицательного числа b из произвольного числа a в буквенном виде, то оно будет выглядеть так: a−b=a+(−b).

Для того, чтобы использовать данное правило, необходимо доказать его справедливость.

Возьмем числа a и b. Чтобы вычесть из числа a число b, необходимо найти такое число с, которое в сумме с числом b будет равняться числу a. Другими словами, если найдено такое число c, что c+b=a, то разность a−b равна c.

Для того, чтобы доказать правило вычитания, необходимо показать, что сложение суммы

a+(−b) с числом b – это есть число a. Необходимо вспомнить о свойствах действий с действительными числами. Так как в этом случае работает сочетательное свойство сложения, то равенство (a+(−b)) +b=a+((−b) +b) будет верным.

Так, как сумма чисел с противоположными знаками равняется нулю, то a+((−b) +b) =a+0, а сумма a+0= а (если к числу прибавить нуль, то оно не изменится). Равенство a−b=a+(−b)считается доказанным, значит, доказана и справедливость приведенного правила вычитания чисел со знаком минус.

Мы рассмотрели, как работает данное правило для действительных чисел a и b. Но оно также считается справедливым для любых рациональных и целых чисел a и b. Действия с рациональными и целыми числами также обладают свойствами, использованными при доказательстве. Следует добавить, что с помощью разобранного правила можно выполнять действия числа со знаком минус как из положительного числа, так и из отрицательного или нуля.

Рассмотрим разобранное правило на типичных примерах.

Примеры использования правила вычитания

Рассмотрим примеры с вычитанием чисел. Для начала рассмотрим простой пример, который поможет легко разобраться со всеми тонкостями процесса.

Пример 1

Необходимо отнять от числа −13 число −7.

Возьмем число, противоположное вычитаемому −7. Это число 7. Тогда по правилу вычитания отрицательных чисел имеем (−13) −(−7) =(−13) +7. Выполняем сложение. Теперь получаем: (−13) +7=−(13−7) =−6.

Вот все решение: (−13) −(−7) =(−13) +7=−(13−7) =−6. (−13)−(−7)=−6. Вычитание дробных отрицательных чисел также можно выполнять. Необходимо перейти к обыкновенным дробям, смешанным числам или десятичным дробям. Выбор числа зависит от того, с каким вариантом вам удобнее работать.

Пример 2

Необходимо выполнить вычитание из числа 3,4 числа -2323.

Применяем описанное выше правило вычитания, получаем 3,4—2323=3,4+2323. Заменяем дробь на десятичное число: 3,4=3410=175=325 (как переводить дроби, можно посмотреть в материале по теме), получаем 3,4+2323=325+2323. Выполняем сложение. На этом вычитание отрицательного числа -2323 из числа 3,4 завершено.

Приведем краткую запись решения: 3,4—2323=27115.

Пример 3

Необходимо выполнить вычитание числа −0,(326) от нуля.

По правилу вычитания, которое мы изучили выше, 0−(−0,(326))=0+0,(326)=0,(326).

Последний переход верен, так как здесь работает свойство сложения числа с нулем: 0−(−0,(326))=0,(326).

Из рассмотренных примеров видно, что при вычитании отрицательного числа может получиться как положительное, так и отрицательное число. Вычитание отрицательного числа может в результате дать и число

0, это происходит, когда уменьшаемое равно вычитаемому.

Пример 4

Необходимо вычислить разность отрицательных чисел -5—5.

По правилу вычитания мы получаем -5—5=-5+5.

Мы пришли к сумме противоположных чисел, которая всегда равна нулю: -5—5=-5+5=0 

Итак,-5—5=0.

В некоторых случаях результат вычитания необходимо записать в виде числового выражения. Это справедливо в тех случаях, когда уменьшаемое или вычитаемое является иррациональным числом. К примеру, вычитание из отрицательного числа −2 отрицательного числа –π проводится так: (−2)−(−π)=(−2)+π=π−2. Значение полученного выражения может быть вычислено максимально точно только в том случае, если это необходимо. Для подробной информации можно изучить другие разделы, связанные с данной темой.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Вычитание отрицательных чисел 6 класс онлайн-подготовка на Ростелеком Лицей

Вычитание

В 7 веке индийский математик и астроном Брахмагупта известной касты брахманов (просвещенных), которая сохранилась и до наших времен, изложил правила сложения и вычитания чисел с разными знаками. Он назвал положительные числа «доход», а отрицательные – «расход».

Брахмагупта излагал свои правила так:

1. Сумма двух имуществ есть имущество;
2. Сумма двух долгов есть долг;
3. Сумма имущества и долга равна их разности.

Если говорить современным математическим языком, то первое правило можно прочесть так: имущество – это положительное число, поэтому сумма двух положительных чисел есть число положительное.

Например, 5+3 = 8.

Долг — это отрицательное число. Поэтому второе правило можно сформулировать так: «Сумма двух отрицательных чисел есть число отрицательное».

Например, (-2)+(-3) = -5.

И сформулируем третье правило: «Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший, и перед полученной разностью поставить знак числа, модуль которого больше».

Например, 5+(-7) = (7-5) = -2; 5+(-3) = 5-3 = 2.

Правило можно дополнить, указав, что же получается: имущество или долг. Если имущество больше долга, то получится имущество. Если имущество меньше долга, то получится долг.

Сумма положительного и отрицательного чисел равна их разности: 3 + (-5) = 3 — 5.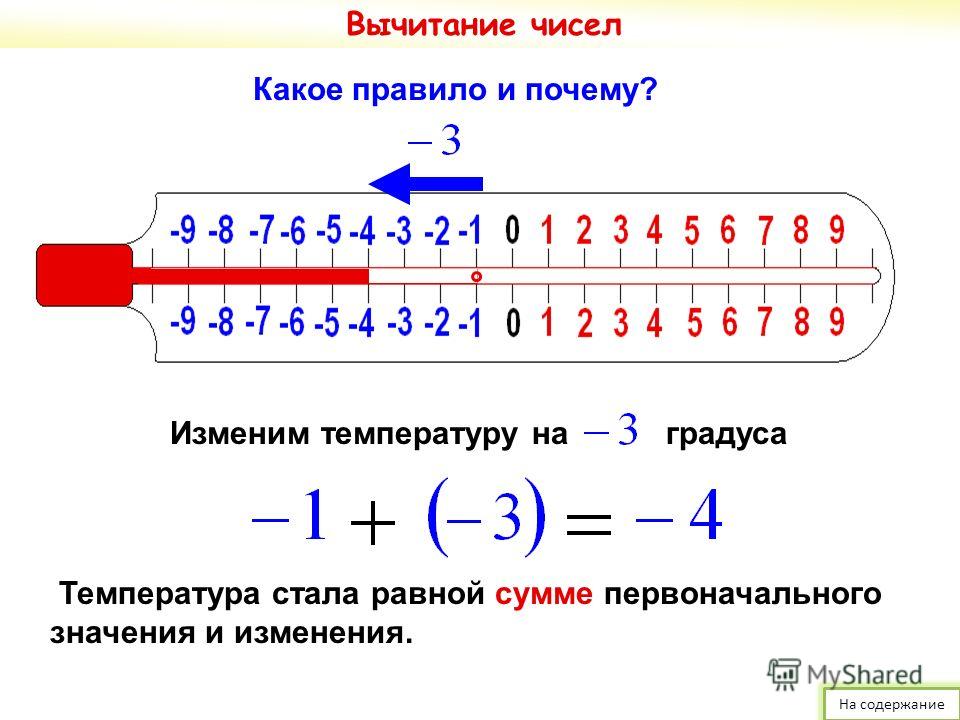 Рассмотрим правую часть и заменим разность суммой: 3 — 5 = 3 + (-5). Уменьшаемое оставим без изменения, а вычитаемое напишем с противоположным знаком.

Таким образом, вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел: по заданной сумме и одному из слагаемых находят другое слагаемое. Чтобы найти искомое слагаемое, можно прибавить к сумме число, противоположное известному слагаемому.

Например, 8-3 = 11 и потому 11-8 = 3, а также 11+(-8) = 3.

Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.

a-b = a+(-b)        a—b = a+b

Например, 4+(-7) = -(7-4) = -3;

13+(-7) = 13-7 = 6;

-13+14 = -13-14 = -412-312 = -112.

Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.

Например, -18-4 = -18+(-4) = -22;

-8+6-с = -8+6+(-с).

Разность двух чисел положительна, если уменьшаемое больше вычитаемого, и отрицательна, если уменьшаемое меньше вычитаемого. Если уменьшаемое и вычитаемое равны, то их разность равна нулю.

Пример 1. Чему равна длина отрезка АВ, если А(-5) и В(6)?

Длина отрезка АВ показывает, на сколько единичных отрезков надо переместить вправо точку А, чтобы она перешла в точку В, т.е. сколько надо прибавить к числу -5, чтобы получилось число 6. Поэтому, если обозначить длину отрезка АВ буквой х, то

-5+х = 6

х = 6-(-5) = 11.

Значит, длина отрезка АВ равна 11 единичным отрезкам.

Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

Пример 2. Найдем длину отрезка АВ, если А(1), В(4).

АВ = 4-1 = 3.

Пример 3. Найдем длину отрезка АС, если А(-2) и С(4).

АС = 4-(-2) = 4+2 = 6.

Калькулятор сложения и вычитания целых чисел

Базовый калькулятор

Сложение и вычитание целых чисел

Введите уравнение для решения:
используйте цифры и + — ( ) Введите уравнение

= ?

Ответ:

-25

---

Показ работы:

= (-12)-16+-22-(33-58)

= (-12)-16-22-(33-58)

= -12-16-22—25

= -12-16-22+25

= -25

Чтобы также использовать умножение и деление, используйте
Math Equation Solver.

Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.

Получить виджет для этого калькулятора

© Calculator Soup

Поделитесь этим калькулятором и страницей

Калькулятор Используйте

Используйте этот калькулятор для сложения и вычитания целых чисел. Положительные и отрицательные целые числа являются целыми числами. Калькулятор показывает работу по математике и показывает, когда менять знак для вычитания отрицательных чисел.

Сложение и вычитание положительных и отрицательных целых чисел, целых чисел или десятичных чисел. Используйте цифры + и -. Вы также можете включить числа со сложением и вычитанием в круглые скобки, и калькулятор решит уравнение.

Примеры ввода

Без скобок

-10 — -22 + 33

45

Со скобками

(-10) — (-22) + 33

3

45 0003

-10 — (- 22 + 33)

-21

Сложение и вычитание положительных и отрицательных чисел

Этот калькулятор сложения и вычитания целых чисел решает уравнения с положительными и отрицательными числами, используя сложение и вычитание. Калькулятор использует стандартные математические правила для решения уравнений.

Для более сложных математических уравнений, требующих правил порядка операций или PEMDAS, используйте Решатель математических уравнений.

Правила сложения целых чисел

Если знаки совпадают, сохраняйте знаки и добавляйте числа.

-21 + -9 = — 30

(+7) + (+13) = (+20)

Если знаки разные, вычесть меньшее число из большего и сохранить знак большего числа.

(-13) + (+5) = (-8)

(-7) + (+9) = (+2)

Правила вычитания целых чисел

Сохраняйте знак первого числа. Замените операции вычитания операциями сложения. Измените знак следующих чисел на противоположный, т. е. положительное станет отрицательным, а отрицательное станет положительным. Затем следуйте правилам сложения задач.

(-15) — (-7) =

(-5) — (+6) =

(+4) — (-3) =

(-15) + (+7) = (- 8)

(-5) + (-6) = (-11)

(+4) + (+3) = (+7)

 

Подписаться на CalculatorSoup:

Целочисленный калькулятор и калькулятор отрицательных чисел

Создано Maciej Kowalski, кандидатом наук

Рецензировано Стивеном Вудингом

Последнее обновление: 02 февраля 2023 г.

Содержание:

• Что такое целое число в математике? – Определение целых чисел
• Строка отрицательных и положительных чисел
• Сложение и вычитание целых чисел
• Умножение целых чисел и целочисленное деление
• Экспоненты, корни и логарифмы
• Использование калькулятора целых чисел
• 0017 целочисленный калькулятор , где мы узнаем все о четырех основных арифметических операциях: сложение и вычитание целых чисел , умножение целых чисел и целочисленное деление . Затем мы перейдем к более сложным операциям, таким как показателей степени , корней и логарифмов . Помните, что целочисленное определение допускает не только положительные целые числа, поэтому этот инструмент также служит калькулятором отрицательных чисел .

  Что такое целое число в математике? Что такое отрицательное число в квадрате или логарифм отрицательного числа?

  Ответ на это и многое другое: прямо под !

  🙋 Хотите научиться решать сложные математические задачи, включающие более одной арифметической операции? Проверьте наш калькулятор распределительной собственности.

  Что такое целое число в математике? – Определение целого числа

  В просторечии целое число – это целое число . Другими словами, они не включают дроби (простые или десятичные: если вы не уверены, что означает любой из этих терминов, быстро перейдите к нашему калькулятору преобразования десятичных дробей в дроби) или иррациональные числа, такие как π из расчетов окружности. Ниже приведены все примеры целых чисел:

  2 , 2021 , 13 , -17 , -173 029 , 0,

  67 ,000 .

  Обратите внимание, что:

  • Все положительные целые числа, какими бы длинными они ни были, являются целыми числами: мы иногда называем их натуральными числами ;
  • Ноль также является целым числом ; и
  • Целые числа включают отрицательных чисел , если они не содержат дробей.

  Формальное определение целого числа выглядит следующим образом:

  💡 Целое число — это любое действительное число, которое мы можем записать без дробной части.

  Подчеркнем слово « can » в приведенном выше целочисленном определении. Обратите внимание, что простая дробь 4/2 равна 2 , так что это целое число путем упрощения дроби, хотя на первый взгляд это не так.

  Прежде чем мы перейдем к операциям, давайте выделим отдельный раздел для различий между положительными целыми числами и отрицательными .

  Отрицательная и положительная числовая линия

  Целые числа (и все другие действительные числа) появляются на бесконечной оси, называемой числовой линией .

  По сути, линия говорит нам, где находится одно число по отношению к другим : оно больше (справа) или меньше (левее) чего-то другого? Когда нас знакомят с математикой, мы считаем на пальцах до десяти, поэтому знаем, что, например, 2 идет после 1 , но перед 3 .

  Отрицательные числа являются зеркальным отражением положительных с зеркалом, установленным на 0 . Другими словами, если мы начнем с нуля и пойдем направо, мы посетим 1 , затем 2 , 3 и так далее. С другой стороны, если идти налево, то встречаются те же числа, но с минусами: -1 , затем -2 , -3 и так далее. Таким образом, число и его противоположность равны 9.0017 на том же расстоянии от 0 , но в противоположные стороны (это расстояние называется абсолютным значением числа).

  Арифметические и алгебраические свойства применяются ко всем значениям в отрицательной и положительной числовой строке. В частности, мы можем складывать, вычитать, умножать, делить, возводить в степень, извлекать корень, вычислять логарифм и т. д., используя эти числа. Различия в правилах отрицательных и положительных чисел невелики, и мы указываем на них в каждом разделе ниже.

  Для данного положительного целого числа мы также можем найти сумму цифр, чтобы определить делимость числа.

  Сложение и вычитание целых чисел

  При сложении и вычитании целых чисел рекомендуется помнить о строке с отрицательными и положительными числами из приведенного выше раздела.

  Предположим, что у нас есть целые числа a и b , и давайте объясним , как мы можем найти a + b и a - b .

  1. Найдите a на отрицательной и положительной числовой строке.
  2. Чтобы найти a + b , переместите b позиций из a :
     • На справа , если b положительный; или
     • К осталось , если b отрицательно.
  3. Чтобы найти a - b , переместите b позиций из a :
     • На осталось , если b положительный; или
     • На вправо , если b отрицательно.

  См. несколько примеров сложения и вычитания целых чисел ниже:

  • 3 + 4 = 7

  • -5 + 9 = 4

  • 10 + (-12) = 10 - 12 = -2

  • -3 + (-7) = -3 - 7 = -10

  • 4 - 5 = -1

  • 3 - (-2) = 3 + 2 = 5

  • -10 - (-4) = -10 + 4 = -6

  Обратите внимание: всякий раз, когда у нас есть два знака рядом друг с другом, , мы должны помещать отрицательное число в скобки . Кроме того, в таком случае можно свести два к одному по следующим правилам:

  • + и + дает + 9.0167 ;
  • + и - дает - ;
  • - и + дают - ; и
  • - и - дают + .

  Первого здесь не бывает, но он пригодится в следующем разделе.

  Умножение целых чисел и целочисленное деление

  По сути, правила отрицательных и положительных чисел для умножения целых чисел и целочисленного деления почти такие же . Единственное, что мы должны помнить, это знак . Чтобы быть точным, знак результата зависит от знаков множителей или делимого и делителя для умножения и деления соответственно.

  С другой стороны, само значение результата, будь то положительное или отрицательное, не слишком заботится о знаках . Таким образом, мы можем начать наши вычисления, как если бы оба целых числа были положительными, вычислить, каким был бы результат в этом случае, и только после этого закрепите соответствующим образом знак . А под « соответственно » мы подразумеваем те же самые отрицательные и положительные числа из предыдущего раздела.

  Ниже мы приводим несколько примеров умножения целых чисел с последующим целочисленным делением.

  • 6 * 8 = 48

  • -4 * 5 = -20

  • 10 * (-2) = -20

  • (-1) * (-8) = 8

  • 12/4 = 3

  • 24 / (-8) = -3

  • -7 / (-2) = 3,5

  На этом завершаются четыре основные операции , охватываемые целочисленным калькулятором Omni (или калькулятором отрицательных чисел, если хотите). Теперь перейдем к более сложным (но все же простым!) алгебраическим выражениям.

  Показатель степени, корни и логарифмы

  • Экспоненты

    Для положительных целых показателей правила для отрицательных и положительных чисел одинаковы: результатом является просто число, умноженное несколько раз на . И мы уже видели, как работает умножение целых чисел в предыдущем разделе, так что давайте просто упомянем несколько примеров:

    Обратите внимание, как для отрицательных оснований экспоненты знак результата зависит от четности степени . Это прямое следствие правил отрицательных и положительных чисел из раздела сложения и вычитания целых чисел. В частности, отрицательное число в квадрате всегда дает положительное значение.

    Теперь, если показатель степени отрицательный, мы сначала избавимся от его знака минус , изменив основание на его мультипликативную обратную величину: a -b = (1/a) b

    Отсюда повторяем обычное дело при этом помня правила умножения дробей. Например:

    4 -3 = (¼) 3 = ¼ * ¼ * ¼ = 1 / 64

    (-3) -4 = (-⅓) 4 = (-⅓) * (-⅓) * (-⅓) * (-⅓) = 1 / 81

    (-2) -5 = (-½) 5 = (-½) * (-½) * (-½) * (-½) * (-½) = - 1 / 32

  • Корни

    Извлечение корня (также называемого радикалом) — это операция, противоположная возведению в степень . Таким образом, некоторые правила применяются к обоим. Самое главное, обратите внимание, что для показателей степени четные степени всегда дают положительный результат , независимо от знака основания. Если мы переведем это свойство в корни, то получим, что радикалов четного порядка существуют только для положительных чисел . В частности, вы не можете иметь квадратный корень из отрицательного числа. На самом деле такие вещи существуют, но это уже не действительные числа, а комплексные числа.

    Давайте посмотрим на пару примеров целых корней:

    • ∜256 = 4

    • ∛(-125) = -5

  • Логарифмы

    Здесь все очень просто: логарифмы определены только для положительных чисел . Другими словами, не существует такой вещи, как логарифм отрицательного числа . Опять же аналогично корням, на самом деле есть, но это выходит за рамки реальных цифр, и история получается достаточно сложной. Если вам интересно, воспользуйтесь нашим калькулятором комплексных чисел

    .

    Закончим эту часть раздела цифрой 9.0017 пара примеров журнала с положительными целыми числами:

    • журнал ₁₀ 1000 = 3

    • журнал ₉ 6561 = 4

    • журнал ₂ 128 = 7

  Для полноты картины давайте завершим краткой инструкцией по использованию калькулятора целых чисел (или калькулятора отрицательных чисел, если хотите).

  Использование целочисленного калькулятора

  Чтобы облегчить вам жизнь, мы подготовили красивую пошаговую инструкцию о том, как использовать целочисленный калькулятор Omni.

  1. В верхней части нашего инструмента выберите операцию , которую вы хотите выполнить. Есть семь вариантов:

     • Дополнение ;
     • Вычитание ;
     • Умножение ;
     • Подразделение ;
     • Экспонента ;
     • Корень ; и
     • Логарифм .

  2. После того, как вы выберете операцию, появится символическая формула внизу с a и b в качестве переменных.

  3. Следуя формуле введите значения из a и b в соответствующие поля.

  4. Считайте результат снизу.

  5. Для четырех арифметических операций: Если вы хотите увидеть расчеты, описанные шаг за шагом, посетите соответствующий инструмент Omni из списка под результатом.

  Вы могли бы назвать это " Инструкции по целочисленному калькулятору ", но мы называем это " Пять простых шагов к счастью и быстрым вычислениям ". Каким бы ни было название, мы надеемся, что этот инструмент сэкономит вам время и поможет с ежедневными домашними заданиями.

  Часто задаваемые вопросы

  Является ли 0 целым числом?

  Да. По определению целые числа состоят из всех положительных целых чисел (т. е. 1, 2, 3 и т. д.), их противоположностей (т. е. -1, -2, -3 и т. д.) и нуля. Первая группа — это положительные целые числа, вторая — отрицательные, а 0 не является ни положительным, ни отрицательным. 9/==1== , что наверняка удовлетворяет условию.

  Очевидно, по-другому не получится: не все рациональные числа являются целыми , например, ½.

  Можно ли извлечь квадратный корень из отрицательного числа?

  Нет , если только вы не работаете с комплексными числами. Как положительное, так и отрицательное число в квадрате дают положительные значения, поэтому невозможно получить квадратный корень из отрицательного числа (или любой другой корень четного порядка, если уж на то пошло).

  Может ли отрицательное число быть целым числом?

  Да. По определению целые числа состоят из всех положительных целых чисел (т. е. 1, 2, 3 и т. д.), их противоположностей (т. е. -1, -2, -3 и т. д.) и нуля. Вторая группа явно включает в себя отрицательные числа.

  Может ли дробь быть целым числом?

  Да. По определению, целое число — это число, которое мы можем выразить без дробных выражений. Например, число 2 явно является целым числом, но мы также можем записать его как 9./==2== , дробь, но приводимая.

  Как складывать целые числа?

  К добавьте целые числа a и b , вам нужно:

  1. Найдите вместо a в отрицательной и положительной числовой строке.
  2. Перемещение b позиций из в :
     • На справа , если b положительный; или
     • К осталось , если b отрицательно.
  3. Точка, в которой вы окажетесь, это сумма .
  4. Наслаждайтесь результатом сложения целых чисел.

  Как вычитать целые числа?

  Чтобы из вычесть целые числа a и b , вам необходимо:

  1. Найдите a в отрицательной и положительной числовой строке.
  2. Перемещение b позиций из в :
     • К слева , если b положительный; или
     • На вправо , если b отрицательно.
  3. Точка, в которой вы окажетесь, это разница .
  4. Наслаждайтесь результатом вычитания целых чисел.

  Все ли целые числа натуральные?

  № По определению целые числа состоят из всех положительных целых чисел (т. е. 1, 2, 3 и т. д.), их противоположностей (т. е. -1, -2, -3 и т. д.) и нуль. Из них натуральные числа являются только первым набором. Некоторые люди также включают ноль в число натуральных чисел, хотя не все ученые с этим согласны.

  Как умножать целые числа?

  Чтобы умножить целые числа a и b , вам необходимо:

  1. Умножить a и b так, как будто они не имеют знаков .
  2. Исправьте знак результата в соответствии со следующими правилами:
     • Если оба фактора были положительными или оба отрицательными, результатом будет положительный ; и
     • Если один фактор был положительным, а один отрицательным, результат равен минус .
  3. Наслаждайтесь результатом умножения целых чисел.

  Как делить целые числа?

  Для целочисленного деления на a и b вам необходимо:

  1. Разделить a и b так, как будто они не имеют знаков .

     No related posts.