Вычислить косинус угла образованного векторами: Как найти косинус угла между векторами: формула, примеры

alexxlab / / Разное

Вариант № 10

Задача 1 Разложить вектор По векторам и .

Пусть , т. е. ;

След., вектор .

Задача 2 Дано: Найти

Вычислим

.

Задача 3 Вычислить проекцию вектора на ось вектора , Если

Вект. ; рассм. ;

Вычислим ; ; .

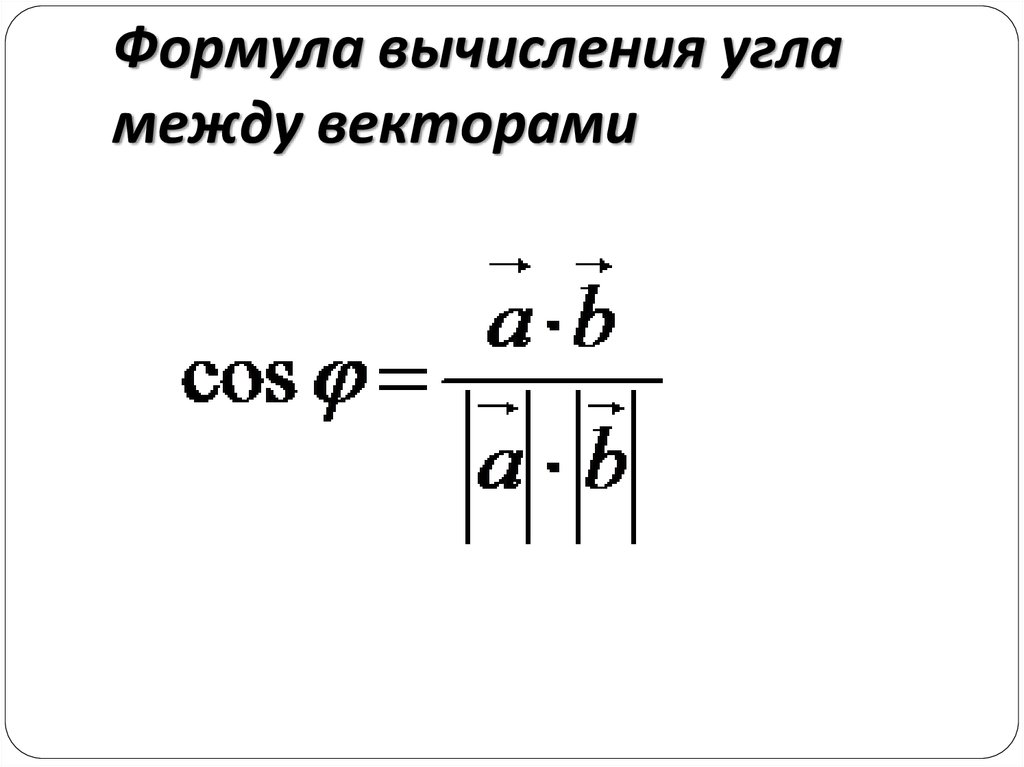
Задача 4 Вычислить косинус угла, образованного векторами и .

Косинус угла между векторами Определим из равенства: ;

Вычислим ; ; .

Задача 5 Найти момент силы, приложенной в точке относительно точки, а также модуль и направляющие косинусы вектора силы

1) , где ; ;

;

2) ;

Направл. косинусы вектора : ; ;

.

Задача 6 Вычислить , если

Рассм.

; по условию задачи угол — острый, след. ;

Вычислим искомое скал. произв-е .

Задача 7 Лежат ли точки в одной плоскости?

Рассмотрим векторы и рассмотрим смешанное

Произведение , след. векторы Компланарны

И, след., точки лежат в одной плоскости.

Задача 8 Найти точку , симметричную точке Относительно прямой .

Рассмотрим один из нормальных векторов прямой ; его можно взять в качестве направляющего вектора прямой и записать уравнение прямой в виде:

или определим координаты точки пересечения прямых

И: ;

Определим теперь координаты искомой точки из условия, что т. есть середина отрезка :

.

Задача 9 Найти координаты вершин и уравнения диагоналей квадрата , если известны уравнение одной стороны

и координаты точки пересечения диагоналей .

1) составим ур-я диагоналей квадрата как ур-я прямых на пл-ти , проходящих через т. и

Составляющих угол со стороной ( ),

Т. е. прямых, для которых вып-ся след. соотношения:

А) рассм. случай

Б) рассм. случай

2) определим координаты вершин квадрата:

Т.- точка пересечения прямых : ;

Т.- точка пересечения прямых : ;

Координаты точки определим из условия, что т.Есть середина отрезка :

;

Координаты точки определим из условия, что т.Есть середина отрезка :

.

Задача 10 Составить уравнение плоскости, проходящей через точку

параллельно векторам

Пусть — искомая плоскость;

Рассм. норм. вектор ;

Рассм. произв. т и рассм. вектор ; ;

, т. е. ; .

Задача 11 Составить канонические и параметрические уравнения прямой , заданной как пересечение двух плоскостей: .

Рассм. норм. векторы ; рассм. направл. вектор прямой : ; рассм. ;

Определим какую-либо точку ; рассм.

Положим , тогда ;

Запишем канонические ур-я прямой Как ур-я прямой, проходящей через т. параллельно вектору : ; параметрические ур-я прямой :

Задача 12 Найти основание перпендикуляра, опущенного из точки на плоскость .

Пусть т. — искомое основание перпендикуляра и — искомый перпендикуляр к плоскости ;

В качестве направл. вектора прямой возьмём нормальный вектор плоскости : и запишем канонические ур-я прямой

Как ур-я прямой, проходящей через т. А параллельно вектору : ; параметрические ур-я прямой :

Определим координаты т. как точки пересечения прямой с плоскостью :

;

Задача 13 Вычислить определитель третьего порядка, пользуясь определением; результат проверить разложением

Определителя по первой строке.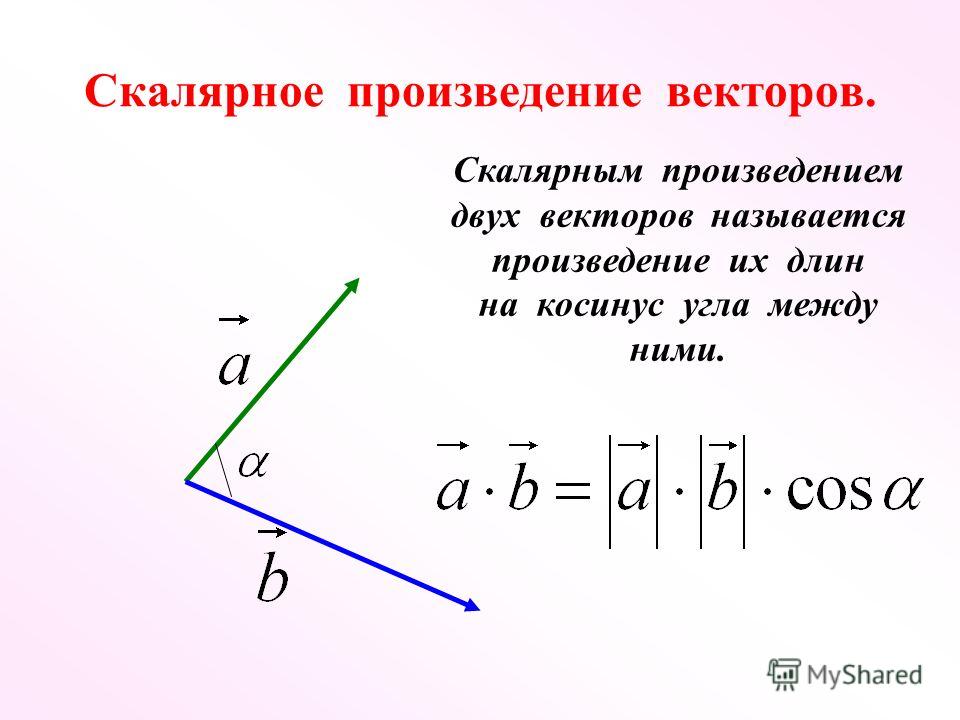

1) Непосредственное вычисление:

2) Разложение по 1-й строке:

.

Задача 14 Решить систему линейных уравнений по правилу Крамера и с помощью обратной матрицы.

Запишем данную систему уравнений в матричной форме: , (1) , где

Рассм. опред-ль матрицы : ,

след., матр. — невырожденная и можно примен. формулы Крамера и вычислять обратную матр.

;

1) решим с – му ур – й (1) по правилу Крамера, т. е. с помощью формул: , , , где ;

реш–е с–мы ур–й (1) в коорд. форме: вектор–решение с-мы (1): ;

2) получим реш–е с–мы ур–й (1) с помощью обратной матр. :

, след., матр.- невырожденная и существует обратная матр. ;

Умножим рав-во (1) слева на матрицу : Вычислим обратную матр. :

Находим алгебр. дополнения для всех эл-тов матрицы и составим из них м-цу :

;

Транспонируем м-цу и получим «присоединённую» м-цу ;

Разделим все эл-ты присоедин. м-цы на опр-ль и получим обратную матр. :

Находим теперь вектор-решение

Задача 15

Установить, являются ли векторы линейно зависимыми.

Вычислим ранг системы векторов методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:

Ранг матрицы , след. данная система векторов линейно зависима.

Задача 16 Исследовать систему линейных уравнений на совместность и в случае совместности найти её решение методом Гаусса:

Выпишем расширенную матрицу данной системы ур-й и приведём её к ступенчатому виду:

Имеем ; так как , то по теореме Кронекера — Капелли данная система уравнений совместна, а так как , то система имеет бесконечное множество решений;

Объявим свободной переменной и выпишем общее решение системы в координатной форме:

;

общее решение данной системы ур-й:

Задача 17 Найти матрицу преобразования, выражающего Через , если

Запишем данные преобразования в матричной форме: , где матрицы и

Вектор — столбцы имеют вид: ;

Рассм. ;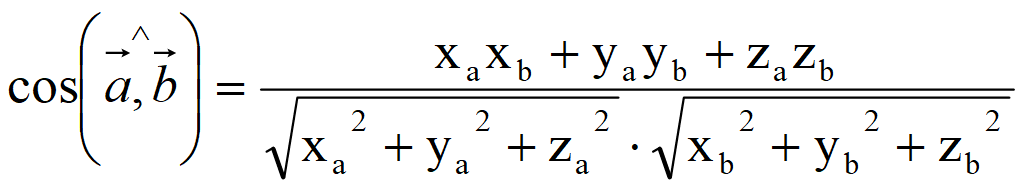

Вычислим матрицу .

Задача 18 Найти собственные числа и собственные векторы линейного преобразования, заданного матрицей

.

1) Находим собств. значения линейного преобразования , т. е. корни характеристического уравнения :

Рассм.

; — собств. значения (действ. и различные ) лин. преобр-я ;

2) находим собств. векторы линейного преобразования , соотв. собств. значениям :

А) рассм. ;

Рассм. Пусть , тогда вектор ;

Б) рассм. ;

пусть , тогда вектор ;

В) рассм. ;

рассм.

Пусть , тогда , вектор ;

След. собств. векторы линейного преобразования суть:

< Предыдущая   Следующая >

Контрольная работа.

Если известны координаты точек и , то координаты вектора — Студопедия

«Векторная алгебра»

Если известны координаты точек и , то координаты вектора

Разложение этого вектора по ортам :

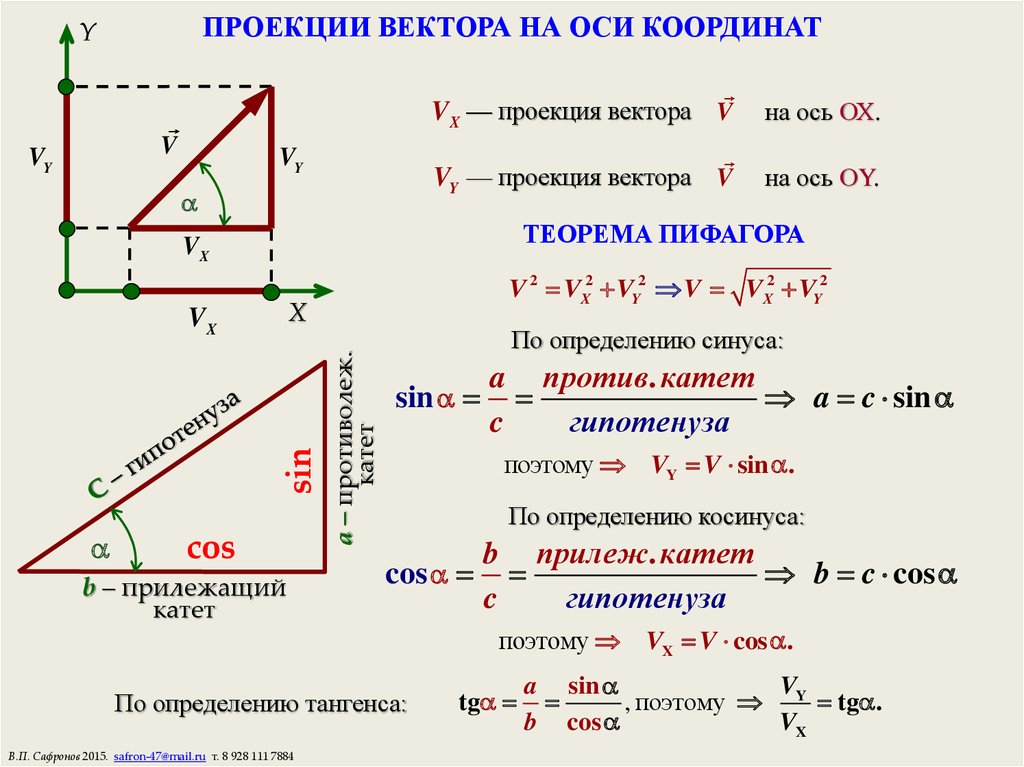
Длина вектора находится по формуле а направляющие косинусы равны Орт вектора

Пример 8.Даны точки

Разложить вектор по ортам и найти его длину, направляющие косинусы, орт вектора . Найдем координаты векторов:

и

Вектор

Контрольные варианты к задаче 8.Даны точки А, В и С. Разложить вектор по ортам Найти длину, направляющие косинусы и орт вектора .

1. 2.  
3. . 4.  
5. 6.  
7. 8.
9. 10.  
11. 12.
13. 14.  
15. 16.  
17. 18.  
19. 20.  
21. 22.  
23. 24.  
25. 26.  
27.   28.  
29. 30.  

Задача 9.Если даны векторы то .

Тогда ; проекция вектора на направление вектора , условие перпендикулярности ненулевых векторов выглядит следующим образом:

Условие коллинеарности векторов: .

Пример 9. Даны вершины треугольника Найти угол при вершине А и проекцию вектора на сторону АС. С

Внутренний угол при вершине А образован векторами ,

А В

Тогда

Проекция на направление вектора :

Контрольные варианты к задаче 9

1. Даны векторы и Найти

2. Найти косинус угла, образованного вектором и осью OZ.

3. Даны векторы и . Найти косинус угла между диагоналями параллелограмма, построенного на векторах .

4. Даны векторы и . Вычислить

5. Найти косинус угла, образованного вектором и осью ОУ.

6. Даны векторы и . Найти косинус угла, образованного вектором и осью ОХ.

7. Даны векторы и . Найти

8. Вычислить проекцию вектора на ось вектора .

9. Определить угол между диагоналями параллелограмма, построенного на векторах и .

10. Определить, при каком значении m векторы и перпендикулярны.

11. Определить, при каком значении векторы и взаимно перпендикулярны.

12. Даны вершины треугольника: . Определить внутренний угол при вершине В.

13. Даны вершины треугольника: . Определить внутренний угол при вершине А.

14. Найти вектор , коллинеарный вектору и удовлетворяющий условию

15. Даны две точки и Вычислить проекцию вектора на ось вектора

16. Даны векторы: и . Вычислить

17. Найти острый угол между диагоналями параллелограмма, построенного на векторах , .

18. Даны три вектора: , , . Найти

19. Даны три вектора: , , . Найти

20. Найти острый угол между диагоналями параллелограмма, построенного на векторах и

21. Даны три вектора: , , . Вычислить

22. Найти вектор , зная, что он перпендикулярен векторам и

и удовлетворяет условию

23. Найти вектор , коллинеарный вектору и удовлетворяющий условию

24. Даны вершины треугольника: Определить внешний угол при вершине А.

25. Даны вершины треугольника: Определить внешний угол при вершине А.

26. Дан вектор и точки и Найти

27. В треугольнике с вершинами Определить внутренний угол при вершине А.

28. Даны векторы и Найти проекцию вектора на направление вектора

29. Даны вершины треугольника: Найти проекцию вектора на сторону

30. Даны векторы Найти проекцию вектора на вектор

Задача 10.Площадь параллелограмма, построенного на векторах

можно найти по формуле а площадь треугольника, построенного

на этих векторах:

Пример 10. Даны вершины треугольника Найти его площадь и длину высоты, опущенной из вершины С.

. Находим векторы

Векторное произведение

Так как где длина высоты, опущенной из вершины С на сторону АВ, .

Контрольные варианты к задаче 10

1. В параллелограмме ABCD даны векторы и Найти площадь параллелограмма, построенного на диагоналях параллелограмма

ABCD.

2. Даны три вершины параллелограмма , , . Найти длину высоты, опущенной из вершины С (через площадь

параллелограмма).

3. Найти площадь треугольника с вершинами , ,

(средствами векторной алгебры).

4. Найти площадь треугольника с вершинами , , (средствами векторной алгебры).

5. Даны три вершины треугольника: , , . Найти его высоту, приняв ВС за основание (через площадь треугольника).

6. На векторах и построен параллелограмм. Найти

площадь параллелограмма, сторонами которого являются диагонали данного параллелограмма.

7. Даны векторы и . Найти вектор перпендикулярный к векторам если модуль вектора численно равен площади треугольника, построенного на векторах и тройка векторов левая.

8. Даны точки , , Найти площадь параллелограмма, построенного на векторах и ( ).

9. На векторах и построен параллелограмм. Найти высоту, опущенную на основание (через площадь).

10. В треугольнике ABC, где , найти длину высоты, опущенной на сторону AB (через площадь треугольника; средствами векторной алгебры).

11. На векторах и построен параллелограмм. Найти площадь параллелограмма, построенного на диагоналях данного параллелограмма.

12. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника АСЕ (средствами векторной алгебры).

13. Найти площадь параллелограмма со сторонами если

14. Найти площадь треугольника со сторонами если ,

и

15. Дан треугольник с вершинами , и . Вычислить площадь треугольника и высоту, опущенную из вершины А (средствами векторной алгебры).

16. Даны векторы и Найти вектор , который пер-

пендикулярен векторам , если длина его численно равна площади треуго-

льника, построенного на векторах , и тройка векторов правая.

17. Даны точки , и . Вычислить площадь треугольника и высоту, опущенную из вершины С (средствами векторной алгебры).

18. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника ВСЕ (средствами векторной алгебры).

19. Даны точки , и . Найти площадь параллелограмма, построенного на векторах и

20. Даны три вершины треугольника: , , . Вычислить его высоту, опущенную из вершины В (через площадь, средствами векторной алгебры).

21. Дан треугольник с вершинами , и . Найти его высоту, опущенную из вершины А (через площадь, средствами векторной алгебры).

22. Даны векторы и Вычислить площадь треугольника, построенного на векторах

23. Даны векторы и Вычислить площадь треугольника, построенного на векторах

24. Найти площадь параллелограмма, построенного на векторах где

25. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника АСЕ (средствами векторной алгебры).

26. Даны векторы и Найти вектор , который перпендикулярен векторам если модуль вектора численно равен площади треугольника, построенного на векторах , и тройка векторов левая.

27. Даны точки , и . Найти длину высоты треугольника АВС, опущенной из вершины С (через площадь, средствами векторной алгебры).

28. Даны три вершины параллелограмма , и . Найти длину высоты, опущенной из вершины С (через площадь, средствами векторной алгебры).

29. На векторах и построен параллелограмм. Найти площадь параллелограмма, построенного на его диагоналях.

30. Даны векторы , и Вычислить площадь треугольника, построенного на векторах

Задача 11.Если даны координаты , то смешанное произведение векторов вычисляют по формуле

.

Объемы параллелепипеда и тетраэдра (треугольной пирамиды), построенных на векторах находятся с помощью смешанного произведения векторов:

,

Если > 0, то тройка векторов — правая.

Если < 0, то тройка левая.

Если = 0, то векторы компланарны.

Пример 11.Дан параллелепипед построенный на векторах и Найти высоту, проведенную из вершины на грань ABCD.

Объем равен произведению площади основания на высоту:

находится также по формуле , поэтому

.

Вычислим векторное произведение =

Тогда

Контрольные варианты к задаче 11

1. Найти объем треугольной пирамиды, построенной на векторах ,

и .

2. Найти объем треугольной пирамиды с вершинами ,

3. Найти значение , при котором векторы и образуют левую тройку, а объем параллелепипеда, построенного на них, равен 33.

4. Даны векторы Найти значение t, при котором выполняется равенство

5. Точки лежат в одной плоскости. Найти t .

6. Найти объем параллелепипеда, зная четыре его вершины:

7. Найти значение t, при котором векторы компланарны.

8. Точки служат вершинами параллелепипеда, объем которого равен 16. Найти t.

9. Даны векторы Найти значение t, при котором имеет место равенство

10. Векторы компланарны.

Найти t.

11. Даны векторы , Найти значение t, при котором имеет место равенство

12. Даны векторы Найти значение t, при котором имеет место равенство

13. Векторы образуют правую тройку, причем объем параллелепипеда, построенного на этих векторах, равен девяти. Найти t.

14. Векторы образуют левую тройку и служат ребрами параллелепипеда, объем которого равен 45. Вектор перпендикулярен плоскости ХОУ. Найти отличную от нуля координату вектора

15. Векторы образуют левую тройку. Объем построенного на них параллелепипеда равен 51. Найти t.

16. Найти объем треугольной пирамиды с вершинами в точках

и

17. Объем треугольной пирамиды равен пяти. Три его вершины находятся в точках Найти отличную от нуля координату четвертой вершины D, если она лежит на оси ОУ.

18. Точки и лежат в одной плоскости. Найти t.

19. Найти значение t, при котором векторы и компланарны.

20. Проверить, лежат ли точки и в одной плоскости.

21. Найти объем треугольной пирамиды, вершины которой находятся в точках

и

22. Даны векторы и Найти t, при котором имеет место равенство

23. Векторы образуют правую тройку. Объем построенной на них треугольной пирамиды равен . Найти t.

24. Вершины треугольной пирамиды находятся в точках и Найти значение t, если объем пирамиды равен 45.

25. Даны векторы Найти значение t, если имеет место равенство

26. Даны векторы Найти значение t, если имеет место равенство

27. Определить, при каком значении t векторы компланарны.

28. Даны векторы . Найти значение t, при котором имеет место равенство

29. Векторы образуют правую тройку, а объем построенного на них параллелепипеда равен 12. Найти значение t.

30. Даны векторы Найти значение t, если имеет место равенство

Задача № 12.Пусть вектор , причем векторы не образуют декартовый базис. Пусть известны тогда

Если векторы и , то

=

= +

Пример 12.При каком ненулевом значении t вектор будет еди-

ничным, если Вектор будет единичным, если его длина будет равна единице, т. е. .

Контрольные варианты к задаче 12

1. Даны векторы где Найти косинус угла между векторами

2. Найти если

3. Даны векторы найти если

4. Даны векторы Найти косинус угла между векторами если

5. При каком отличном от нуля значении параметра вектор будет единичным, если

6. Даны векторы найти если

7. Векторы служат сторонами параллелограмма. Найти косинус угла между диагональю и стороной если

8. Даны векторы . При каком значении параметра вектор , если

9. В параллелограмме АВСD найти длину диагонали , если

, .

10. В треугольнике АВС найти косинус внутреннего угла В, если

.

11. Даны векторы . Вычислить , если

,

12. При каком положительном значении параметра векторы имеют одинаковую длину, если

13. Даны векторы . Найти , если , .

14. В треугольнике АВС найти длину , если

15. Даны векторы . Найти , если

.

16. Дан вектор . Найти косинус угла между векторами , если .

17. Даны векторы . Найти , если , .

18. Даны векторы . Найти .

19. Даны векторы При каком значении параметра вектор , если

20. Дано: , . При каком значении параметра векторы и взаимно перпендикулярны?

21. Дан вектор — единичные векторы, образующие угол . Найти косинус угла между векторами .

22. Даны векторы . Найти , если ,

23. Дан вектор Найти , если .

24. Даны векторы . Найти длину вектора , если , .

25. Даны векторы . Найти , если , .

26. Векторы образуют угол . Зная, что найти длину вектора .

27. При каком значении параметра вектор будет единичным, если

28. При каком значении векторы имеют одинаковую длину, если ?

29. В треугольнике АВС найти косинус внутреннего угла при вершине В, если , где , .

30. Даны векторы . При каком значении параметра вектор , если , .

Задача 13. При решении этой задачи будем использовать свойства векторного произведения двух векторов. Модуль векторного произведения двух векторов

поэтому По свойствам векторного произведения

Площадь параллелограмма, постро-

енного на векторах , равна Площадь треугольника, построенного на векторах :

Пример 13.В параллелограмме ABCD даны векторы и Найти если Это условие в параллелограмме ABCD вектор Тогда Вектор



Использование закона косинусов и формулы скалярного произведения векторов для нахождения угла между тремя точками – Muthukrishnan

Для любых 3 точек A, B и C на декартовой плоскости. Если нам нужно найти угол между этими точками, есть много способов сделать это. В этой статье я расскажу о двух часто используемых методах:

  1. Формула закона косинусов
  2. Формула продукта Vector Dot

Закон косинусов

Для любого заданного треугольника ABC со сторонами AB, BC и AC угол, образованный прямыми AB и BC, определяется по формуле:

Вот как мы можем вывести эту формулу:

То же самое можно расширить и для других углов.

Теперь, если нам даны 3 точки на декартовой плоскости, мы можем найти расстояние между любыми двумя точками, используя формулу Евклидова расстояния:

Итак, чтобы найти угол между тремя точками A (x1,y1), B (x2,y2) и C (x3,y3), наша формула становится:

В Python мы можем представить приведенную выше формулу, используя код:

 импортировать numpy как np
импортировать математику
def angle_between_three_points (точка A, точка B, точка C):
    
    x1x2s = math.pow((точкаA[0] - точкаB[0]),2)
    x1x3s = math.pow((точкаA[0] - точкаC[0]),2)
    x2x3s = math.pow((точкаB[0] - точкаC[0]),2)
    
    y1y2s = math.pow((точкаA[1] - точкаB[1]),2)
    y1y3s = math.pow((точкаA[1] - точкаC[1]),2)
    y2y3s = math.pow((точкаB[1] - точкаC[1]),2)
    cosine_angle = np.arccos((x1x2s + y1y2s + x2x3s + y2y3s - x1x3s - y1y3s)/(2*math.sqrt(x1x2s + y1y2s)*math.sqrt(x2x3s + y2y3s)))
    вернуть np.степеней (косинус_угол)
A = np.массив ([2,4])
B = np. массив ([8,7])
C = np.массив ([9,1])
print("Угол между точками:", angle_between_three_points(A,B,C))
# дает 72,89
А = np.массив ([0,0])
B = np.массив ([0,4])
C = np.массив ([4,0])
print("Угол между точками:", angle_between_three_points(A,B,C))
# дает 45.0

Векторное скалярное произведение

Три точки также могут быть представлены в виде вектора, как показано ниже.

где,

Скалярное произведение или скалярное произведение двух векторов представлено формулой:

, где || * || — величина вектора, а θ — угол между двумя векторами.

Из приведенной выше формулы мы можем представить угол, используя формулу:

В Python мы можем представить приведенную выше формулу, используя код:

 def angle_between_three_points (точка A, точка B, точка C):
    ВА = точка А - точка Б
    ВС = точка C - точка B
    пытаться:
        cosine_angle = np.dot (BA, BC) / (np.linalg.norm (BA) * np.linalg.norm (BC))
        угол = np.arccos(cosine_angle)
    кроме:
        распечатать("отл")
        поднять исключение («неверный косинус»)
    вернуть np. степени (угол)

Выше приведен код из моего поста, где я говорил о нахождении коллинеарности трех точек на плоскости с помощью угла, образованного точками.

Каталожные номера:

  • http://mathworld.wolfram.com/DotProduct.html
  • https://en.wikipedia.org/wiki/Euclidean_distance
  • https://en.wikipedia.org/wiki/Law_of_cosines

Теги: Математика

Проверено 23 июня 2021 г., 1:35 (время сайта).

Доступно по адресу: 192.168.31.181/муту/?p=1106

Как вычислить подобие косинуса в R

[Эта статья была впервые опубликована на сайте Methods – finnstats и любезно предоставлена ​​R-блогерами]. (Вы можете сообщить о проблеме с содержанием на этой странице здесь)

Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.

Как вычислить косинусное сходство в R. Мерой сходства между двумя векторами в пространстве внутреннего произведения является косинусное сходство.

Формула для двух векторов, таких как A и B, и косинусного подобия может быть рассчитана следующим образом:

Косинусное сходство = ΣA i B i / (√ΣA i √Σ8 2 2 )

В основном косинусное сходство используется для измерения степени сходства документов независимо от их размера.

Другими словами, он вычисляет косинус угла, образованного двумя векторами, спроецированными в трех измерениях.

В этом руководстве описывается, как вычислить косинусное сходство между векторами в R при использовании функции косинуса().

Функцию cosine() можно загрузить из библиотеки lsa .

Сеть LSTM в R » Рекуррентная нейронная сеть »

Давайте создадим два вектора x и y и присвоим им некоторые значения.

#создать векторы

 x <- c(33, 33, 43, 55, 48, 37, 43, 24)
y <- c(37, 38, 42, 46, 46, 59, 41, 50)

#определить подобие косинуса

 библиотека (LSA)
косинус (х, у)
[1,] 0,9624844

На основании приведенного выше результата косинусное сходство между x и y составляет 0,9624844.

Повторные измерения ANOVA в R Полное руководство »

Мы можем вычислить косинусное сходство матрицы в R

Давайте создадим векторы x, y и z и создадим матрицу.

#define matrix

 x <- c(23, 24, 34, 35, 22, 25, 33, 24)
у <- с(10, 10, 22, 26, 16, 22, 11, 20)
z <- c(14, 15, 35, 16, 11, 23, 10, 41)
матрица <- cbind(x, y, z)

#рассчитать сходство косинуса

Корреляционный анализ в R? » Коэффициент корреляции Карла Пирсона »

 библиотека (LSA)
косинус (матрица)
x        y         z
х 1,0000000 0,9561517 0,8761308
у 0,9561517 1,0000000 0,9163248
z 0,8761308 0,9163248 1,0000000

Теперь вы можете увидеть косинусное сходство между x, y и z.

Косинусное сходство между векторами x и y составляет 0,9561517.

Косинусное сходство между векторами x и z составляет 0,8761308.

Косинусное сходство между векторами y и z составляет 0,9163248.

Для функции cosine() в качестве входных данных требовалась либо одна матрица, либо два вектора.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *