вычисление определителя 3 порядка
Вы искали вычисление определителя 3 порядка? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление определителя 3 порядка матрицы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление определителя 3 порядка».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление определителя 3 порядка,вычисление определителя 3 порядка матрицы,вычислить определители третьего порядка,вычислить определитель 3 порядка,вычислить определитель получив нули в какой либо строке или столбце,вычислить определитель третьего порядка по правилу треугольника,как вычислить определитель 3 порядка,как вычислить определитель второго порядка,как вычислить определитель третьего порядка,как вычислять определители,как найти определитель 3 порядка,как найти определитель матрицы 3х3 треугольником,как посчитать определитель 3 порядка,как решать определители,как решать определители 3 порядка,как решить определитель 3 порядка,как считать определитель 3 порядка,как считать определитель матрицы 3 порядка,матрица 3 порядка,матрица 3 порядка примеры,матрицы определитель 3 порядка,матрицы определитель третьего порядка,матрицы правило треугольников,матрицы третьего порядка,определители 3 порядка,определители 3 порядка как решать,определители 3 порядка примеры,определители как решать,определители примеры,определители третьего порядка,определитель 3 порядка,определитель 3 порядка как считать,определитель 3 порядка матрицы,определитель 3 порядка это,определитель матрицы первого порядка,определитель матрицы порядка 3,определитель матрицы третьего порядка,определитель первого порядка,определитель первого порядка матрицы,определитель правило треугольника,определитель правило треугольников,определитель третьего порядка,определитель третьего порядка вычислить,определитель третьего порядка как найти,определитель третьего порядка матрицы,определитель третьего порядка примеры,определитель третьего порядка это,правило саррюса вычисления определителя третьего порядка,правило треугольника определитель,правило треугольников определитель,примеры определители,примеры определитель,примеры определитель третьего порядка,способы вычисления определителей,способы вычисления определителя,формула определителя матрицы 3 порядка.
Решить задачу вычисление определителя 3 порядка вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Что такое определитель матрицы
Оглавление
Время чтения: 6 минут
417
Нередко при решении задач в высшей математике требуется провести вычисление определителя матрицы.
Что такое матрица?
На первом шаге стоит чётко понимать, что матрица — типичная таблица, внутри которой
расположены цифры. Размерность — основополагающая характеристика матрицы, которая говорит о
том, сколько столбцов и строк прописано в матричной структуре. При этом определитель можно посчитать для
квадратной матрицы.Принято говорить, что та или иная матрица А имеет размер
[m x n], когда в ней расположено m строчек и n столбиков. Визуально это
выглядит следующим образом: \[A=[m \times n]\].
В некоторых случаях запись такая: \[A=\left(a_{i j}\right), \quad 1 \leq i \leq m ; \quad 1 \leq j \leq
n\].
7 свойств определителя
- Когда 2 строчки/столбца меняются местами, меняется знак у определителя на противоположный;
- В случае умножения одной строки/столбца на число k, весь определитель также умножится на данное число;
- Определитель будет неизменным в случае, если взять одну строку и сложить/отнять её любое количество раз из другой;
- В целом определитель равен 0, когда 2 строчки определителя равны, или пропорциональны, или одна из строчек заполнена нулями;
- Столбцы также имеют все эти свойства;
- Определитель будет неизменным, если матрица транспонируется;
- Определитель произведения матриц численно равен произведению определителей.
Как можно найти определитель матрицы второго порядка?
В основном студенты и ученики получают от преподавателей задание вычислить определитель матрицы второго, третьего, иногда четвёртого порядка. В первом случае решение типовое и достаточно понятное. Детально это происходит следующим образом:
\[A=\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|\]
это квадратная матрица второго порядка, определителем которой называется число
\[|A|=\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|=a_{11} a_{22}-a_{12} a_{21}\]
Посчитать определитель подобной матрицы можно здесь так:
В матрице 2-го порядка n = 2, отсюда следует, что факториал n! = 2! = 2.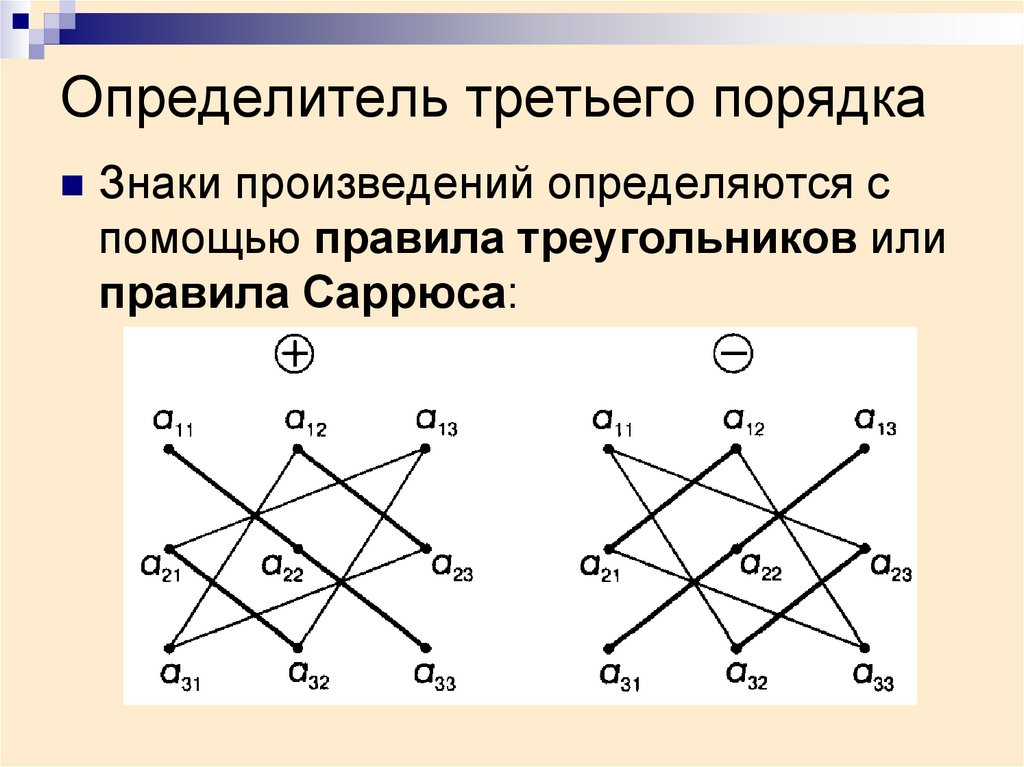
{N_{k}} * a_{1 j 1(k)} * a_{2 j 2(k)}=a_{11} * a_{22}-a_{12} * a_{21}\]
Проанализировав ранее сказанное, получаем типовой алгоритм для нахождения определителя матрицы 2-го порядка 2х2:
\[\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|=a_{11} * a_{22}-a_{12} * a_{21}\]
Если рассмотреть данную формулу на наглядном примере, то это будет вот так:
Пример
Вычислить определитель матрицы \[2 \times 2\]:
\[A=\left|\begin{array}{cc}2 & 3 \\-6 & 1\end{array}\right|\]
Решение:
Итак, у нас получается \[a_{11}=2, a_{12}=3, a_{21}=-6, a_{22}=1\].
Для решения необходимо воспользоваться ранее рассмотренной формулой:
\[A=\left|\begin{array}{ll}a_{11} & a_{12} \\a_{21} & a_{22}\end{array}\right|=a_{11} * a_{22}-a_{12} * a_{21}\]
Подставляем числа с примера и находим:
\[A=\left|\begin{array}{cc}2 & 3 \\-6 & 1\end{array}\right|=2 * 1-3 *(-6)=3-(-18)=21\]
Ответ:
Определитель матрицы второго порядка = 21.
Чтобы упростить понимание процесса, как в данном случае находится определитель матрицы, можно представить такой расчёт: от произведения элементов основной диагонали отнимается произведение элементов другой диагонали.
\[\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|=a_{11} \cdot a_{22}-a_{12} \cdot a_{21}\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Матрица 3-го порядка: методы нахождения ее определителя
Существует 2 способа, позволяющих быстро и точно решить уравнения. Определитель матрицы при этом находится по правилу треугольника или «параллельных полосок».
Правило треугольника
Визуальная схема действий здесь выглядит достаточно просто:
Произведения элементов в левом определителе, соединенные прямыми, суммируются; затем, перемноженные элементы правого определителя, связанные по прямой, вычитаются.
Происходит это таким образом:
\[\left|\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}\]
Правило Саррюса
Согласно правилу Саррюса («параллельных полосок»), матрица рассчитывается с учётом некоторых факторов и ряда операций:
- слева от определителя выписываются 2 первых столбца;
- элементы с основной диагонали и остальные, прописанные параллельно, перемножаются, произведения будут со знаком «+»;
- элементы с побочной диагонали и другие, которые ей параллельны, перемножаются, произведения будут со знаком «-».
Схематично это выглядит так:
Расчёт идёт по формуле:
Пример
Вычислить определитель \[\left|\begin{array}{rrr}3 & 3 & -1 \\4 & 1 & 3 \\1 & -2 & -2\end{array}\right|\] с
помощью правила Саррюса.
Решение:
\[\begin{array}{|rrr|rr}3 & 3 & -1 & 3 & 3 \\4 & 1 & 3 & 4 & 1 \\1 & -2 & -2 & 1 & -2\end{array} =3 \cdot 1
\cdot(-2)+3 \cdot 3 \cdot 1+\\+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4
\cdot(-2)=54\]
Ответ:\[\left|\begin{array}{rrr}3 & 3 & -1 \\4 & 1 & 3 \\1 & -2 & -2\end{array}\right|=54\]
Разложение определителя по элементам строки или столбца
Определитель матрицы четвёртого порядка вычисляется двумя способами: разложение по элементам строки или столбца. Это — способ рассчитать определитель n как нахождение определителя порядка n-1, достаточно представить определитель как итог сложения произведений элементов строки/столбца на их алгебраические дополнения.
Пример
\[|A|=a_{11} A_{11}+a_{12} A_{12}+a_{13} A_{13}\](разложение по элементам 1-ой строки)
\[|A|=a_{12} A_{12}+a_{22} A_{22}+a_{32} A_{32}\](разложение по элементам 2-го столбца)
Объяснение урока: Определитель треугольной матрицы
В этом объяснении мы узнаем, как найти определитель треугольной матрицы.
Начнем с того, что вспомним, как найти определитель обычной матрицы 3×3. Сделать это, нам нужно знать определения миноров и кофакторов.
Определение: Миноры
Пусть 𝐴=𝑎 — матрица порядка 𝑚×𝑚. Затем младших элементов 𝑎 (обозначается 𝐴) является определителем Полученная матрица (𝑚−1)×(𝑚−1) после удаления строки 𝑖 и столбца 𝑗 из 𝐴.
Определение: Кофакторы
Пусть 𝐴=𝑎 — матрица порядка 𝑚×𝑚. Затем кофактор элемента 𝑎 (обозначается 𝐶) 𝐶=(−1)𝐴, где 𝐴 — минор элемента 𝑎.
Определитель можно записать с использованием расширения кофактора следующим образом.
Определение: определитель матрицы 3 × 3 (разложение на кофакторы)
Пусть 𝐴=(𝑎) — матрица 3×3. Тогда для любого
фиксированный 𝑖=1,2 или 3, определитель 𝐴 равен
det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶,
где каждый 𝐶 является кофактором входа 𝑎. это известно
как 9Расширение кофактора 0009 (или расширение Лапласа) по строке 𝑖.
Это расширение кофактора по столбцу 𝑗.
Мы также отмечаем, что альтернативная, возможно, более удобная формулировка состоит в том, чтобы записать приведенные выше формулы явно в терминах определителей 2 × 2. Итак, для разложения первой строки имеем det(𝐴)=𝑎|||𝑎𝑎𝑎𝑎|||−𝑎|||𝑎𝑎𝑎𝑎|||+𝑎|||𝑎𝑎𝑎𝑎|||.
Важным аспектом расширения кофактора, который следует учитывать, является то, что мы можем выбирать, какую строку или столбец мы хотим расширяться вместе. Насколько это существенно, становится ясно, если мы рассмотрим, например, матрица как 𝐴=413100−3−24.
Если бы мы рассматривали первую строку, то вычисление определителя было бы det(𝐴)=4||00−24||−1||10−34||+3||10−3−2||.
Это выполнимо, но требует написания и вычисления трех определителей 2×2. С другой стороны, если бы мы использовали вместо этого вторую строку, мы бы просто получили
det(𝐴)=1||13−24||,
поскольку 𝑎 и 𝑎 равны 0.
Вспомним, что выбор строки или столбца с большим количеством нулей упрощает расчет при рассмотрении нашего первого примера.
Пример 1. Нахождение определителя матрицы, содержащей строку нулей
Найдите значение ||||5−180260000||||.
Ответ
Чтобы вычислить определитель матрицы 3×3, вспомните, что мы можем использовать разложение кофактора по любой строке по формуле det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶, где 𝑖=1,2 или 3, и по любому столбцу.
Хотя любой выбор строки или столбца даст нам одно и то же значение определителя, это всегда проще выбрать тот, который имеет наибольшее количество нулей. В частности, мы видим, что третий ряд сплошь нули:
Следовательно, если 𝑖=3, определитель
расчет будет
det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶=0×𝐶+0×𝐶+0×𝐶=0.
Как показано в последнем примере , так как в третьей строке матрицы для каждого элемента были нули, определитель был равен нулю. Естественно, так как расширение кофактора может быть применено к любой строке или столбцу, тот же результат будет верным, если вся строка или столбец матрицы равны нулю, и это можно обобщить. для матриц любого размера.
Свойство: определители с нулевыми строками или столбцами
Если 𝐴 — квадратная матрица, в которой каждый элемент в определенной строке или столбце равен нулю, тогда det(𝐴) равно нулю.
Некоторые примеры этого включают
Всякий раз, когда нас просят найти определитель, мы всегда должны помнить, чтобы проверить, есть ли какие-либо строки или столбцы нулевые, так как это позволяет нам сразу заключить, что определитель равен нулю, используя это свойство.
В следующем примере мы рассмотрим еще один частный случай вычисления определителя.
Пример 2: Нахождение значения определителя верхнетреугольной матрицы
Заполните пропуск: Значение определителя
||||30−2057004||||=.
Ответ
Когда вас попросят найти определитель матрицы 3×3, вспомните, что мы можем использовать разложение кофактора по любой строке по формуле det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶, где 𝑖=1,2 или 3, и по любому столбцу.
Для нас всегда выгодно выбрать для расширения строку или столбец с наибольшим числом нулевых записей, так как это приводит к меньшему количеству необходимых вычислений. Если мы исследуем данную матрицу, мы находим, что первый столбец и третья строка являются лучшими кандидатами, так как они оба содержат две записи, равные нулю:
Если мы выберем третью строку, то 𝑖=3. Итак, мы получаем det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶=0×𝐶−0×𝐶+4||3005||=4×3×5=60.
Давайте рассмотрим важный аспект этого примера. В итоге вычисление определителя
просто перемножал три записи по главной диагонали вместе. Как оказалось, причиной тому
расчет был настолько простым, потому что матрица была верхней треугольной матрицей.
Давайте
напомнить определение этого типа матрицы.
Определение: треугольная матрица
Если элементы под главной диагональю равны нулю, матрица является верхней треугольной матрицей .
Если элементы выше главной диагонали равны нулю, матрица является нижней треугольной матрицей .
Показаны верхняя и нижняя треугольные матрицы:
Матрица является треугольной , если она либо верхняя, либо нижняя треугольная (или обе).
Причина, по которой нахождение определителей треугольных матриц так просто, заключается в том, что нули в одной половине матрицы удалить большую часть вычислений. Чтобы убедиться в этом, рассмотрим расчет определитель общей верхней треугольной матрицы с использованием разложения на кофакторы по третьей строке: ||||𝑎𝑏𝑐0𝑑𝑒00𝑓||||=0×𝐶+0×𝐶+𝑓𝐶=𝑓|||𝑎𝑏0𝑑|||=𝑓(𝑎𝑑−0×𝑏)=𝑎𝑑𝑓.
Другими словами, конечный результат — это произведение трех элементов на главной диагонали. Точно так же для нижних треугольных матриц расширение кофактора по первой строке дает нам
|||| 𝑎00𝑏𝑐0𝑑𝑒𝑓 |||| = 𝑎𝐶+0 × 𝐶+0 × 𝐶 = 𝑎 ||| 𝑐0𝑒𝑓 ||| = 𝑎 (𝑐𝑓 -0 × 𝑒) = 𝑎𝑐𝑓.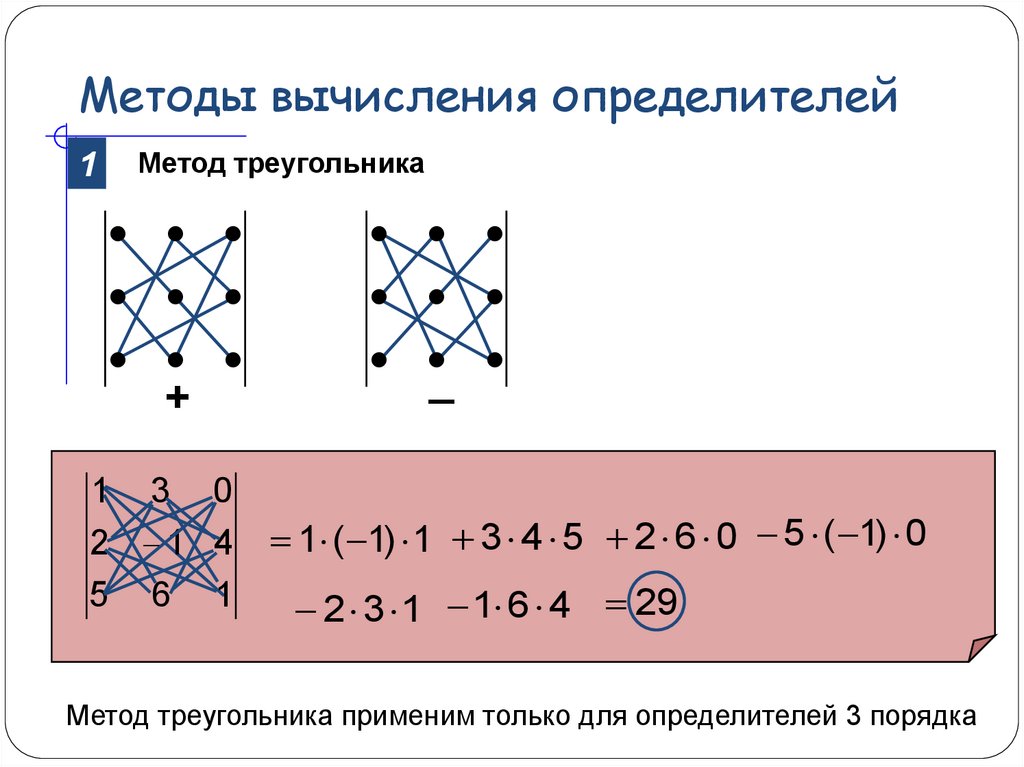
Это дает нам следующее свойство.
Свойство: определители треугольных матриц
Определитель треугольной матрицы является произведением элементов на главной диагонали:
В качестве примечания, это свойство также охватывает подкласс треугольных матриц: диагональные матрицы. Напомним, что диагональная матрица — это та, в которой только элементы на главной диагонали отличны от нуля. Поскольку диагональные матрицы являются и верхними, и нижними треугольными матрицами одновременно время, они, естественно, обладают одним и тем же свойством:
Это также относится к единичным матрицам (где произведение диагональных элементов всегда равно 1) и нулевые матрицы (где произведение всегда равно 0), так как это частные случаи диагонали, и, следовательно, треугольные матрицы.
Давайте посмотрим, как мы можем использовать это свойство для упрощения наших решений в следующем примере.
Пример 3. Сравнение значений определителей двух треугольных матриц
Верно или неверно: если
𝐴=142036004,𝐵=100530674,
тогда detdet(𝐴)=(𝐵).
Ответ
Один из способов ответить на этот вопрос — вычислить каждый определитель с помощью кофактора расширение по строкам или столбцам. Однако мы можем более эффективно ответить на этот вопрос, если обращаем внимание на то, что 𝐴 — верхнетреугольная матрица, а 𝐵 — нижняя треугольная матрица. Мы можем видеть это, потому что в 𝐴 записи ниже главная диагональ равна нулю, а в 𝐵 элементы над главной диагональю равны ноль:
Таким образом, мы можем воспользоваться тем свойством, что определитель треугольной матрицы равен произведению элементов на главной диагонали. Как видим, 𝐴 и 𝐵 имеют одинаковые диагональные элементы. Следовательно,
То есть detdet(𝐴)=(𝐵)=12, так что ответ верный.
Давайте подробнее рассмотрим примеры, в которых нам нужно найти определители треугольных матриц. В некоторых случаях легкой частью будет определить, что матрица является треугольной, и применить
свойство для определителей, а трудная часть будет включать дальнейшие вычисления для достижения
требуемый ответ.
Пример 4. Решение уравнений путем нахождения определителя диагональной матрицы
Рассмотрим уравнение ||||𝑥−1000𝑥+𝑥+10001||||=2.
Определите значение 𝑥.
Ответ
Первое, что бросается в глаза, когда мы видим эту матрицу, это то, что она диагональная, а это значит, что все элементы не на главной диагонали равны нулю: ||||𝑥−1000𝑥+𝑥+10001||||.
Диагональные матрицы представляют собой особый вид треугольных матриц, и мы можем вспомнить, что определитель такой матрицы находится путем произведения элементов на главной диагонали. Поэтому, определитель ||||𝑥−1000𝑥+𝑥+10001||||=(𝑥−1)×𝑥+𝑥+1×1=𝑥+𝑥+𝑥−𝑥−𝑥−1=𝑥+𝑥−𝑥+ 𝑥−𝑥−1=𝑥−1.
Теперь мы хотим найти 𝑥, используя тот факт, что этот определитель равен 2. То есть, 𝑥−1=2.
Отсюда можно найти 𝑥, используя свойства индексов, в частности что 𝑥=𝑥. Переставляя и возводя в квадрат обе стороны, мы имеем 𝑥=3𝑥=3𝑥=9.
В качестве последнего примера найдем определитель матрицы, заданной тремя переменными, которая
нам придется найти, найдя определители меньших матриц.
Пример 5. Нахождение значения определителя, включающего неизвестные, с использованием свойств
Если det𝑥44𝑦=0, det𝑦99𝑧=0, и det𝑥11𝑧=0, найти дет𝑥120𝑦300𝑧.
Ответ
Поскольку нам дано несколько уравнений с определителями и тремя неизвестными переменными, наиболее очевидным было бы найти эти детерминанты и посмотреть, дает ли это нам любую информацию о переменных, поэтому давайте сделаем это.
Прежде всего, для матриц 2×2 мы можем найти их определители по формуле дет𝑎𝑏𝑐𝑑=𝑎𝑑−𝑏𝑐.
Для первого уравнения имеем det𝑥44𝑦=0𝑥𝑦−4×4=0𝑥𝑦=16.
Для второго уравнения имеем det𝑦99𝑧=0𝑦𝑧−9×9=0𝑦𝑧=81.
Наконец, третье уравнение 2×2 дает нам det𝑥11𝑧=0𝑥𝑧−1×1=0𝑥𝑧=1.
Мы могли бы использовать эти уравнения сами по себе, чтобы найти 𝑥, 𝑦 и 𝑧, но это может быть больше работы, чем необходимо. Сначала найдем Определитель 3×3, чтобы мы могли видеть, какая информация от нас требуется. Мы можем упростить вычисление этой матрицы, заметив, что это верхняя треугольная матрица, так как записи ниже главной диагонали равны нулю:
Следовательно, определитель будет просто произведением элементов на главной диагонали, давая нам
Чтобы найти 𝑥𝑦𝑧, обратите внимание, что мы можем взять произведение 𝑥𝑦,
𝑦𝑧 и 𝑥𝑧 (поскольку мы уже вычислили эти значения)
а потом извлеките квадратный корень.
То есть у нас есть
(𝑥𝑦𝑧)=(𝑥𝑦)(𝑦𝑧)(𝑥𝑧)=16×81×1=1296.
Тогда, извлекая квадратный корень, получаем 𝑥𝑦𝑧=±36.
Мы должны знать, что здесь возможны как положительные, так и отрицательные 36. Эти разные значения возникают из-за различных возможных значений 𝑥, 𝑦 и 𝑧, поэтому значение определителя будет зависеть от значений переменных.
Следовательно, определитель равен либо −36, либо 36.
Давайте рассмотрим основные вещи, которые мы узнали из этого объяснения.
Ключевые моменты
- Мы можем упростить вычисление определителей в некоторых случаях, если некоторые элементы
нуль. В частности, это можно сделать следующим образом:
- Если матрица имеет нулевую строку или столбец, то ее определитель равен нулю:
- Если матрица верхнетреугольная, нижнетреугольная или диагональная, то ее определитель равен произведение элементов на главной диагонали:
Верхняя и нижняя треугольные матрицы — Krista King Math
Что такое верхние треугольные матрицы и нижние треугольные матрицы?
Верхние треугольные матрицы — это матрицы, в которых все элементы ниже главной диагонали равны ???0???.
Главная диагональ — это набор элементов, идущих от верхнего левого угла матрицы вниз к нижнему правому углу матрицы.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Нижние треугольные матрицы — это матрицы, в которых все элементы выше главной диагонали равны ???0???.
Вот главные диагонали в этих верхних треугольных матрицах,
и в этих нижних треугольных матрицах:
Мы обвели главную диагональ в каждой матрице, так что мы можем видеть, что все элементы в верхней треугольной матрице ниже главной диагонали равны ???0???, и что все элементы в нижней треугольной матрице матрицы выше главной диагонали равны ???0???.
Определитель треугольных матриц
Поскольку мы можем найти определитель матрицы в любой строке или столбце, который нам нужен, для верхних треугольных матриц всегда нужно выбирать первый столбец (или последнюю строку) , так как он включает в себя больше всего ???0??? записи.
Например, мы хотим найти определитель верхней треугольной матрицы ???A???:
Обратите внимание, что ???A??? включает ???0??? запись в ???a_{(2,3)}???. Это нормально. У нас могут быть нулевые значения на главной диагонали или выше нее. Чтобы считаться верхней треугольной матрицей, единственное, что имеет значение, это то, что все элементы ниже главной диагонали равны ???0???.
Определитель ???A??? по первому столбцу
Последние три члена обнуляются.
Упростим оставшиеся ???3\times3??? определитель снова по первому столбцу.
Последние два члена обнуляются.
???|A|=1\влево[-2((5)(-1)-(3)(0))\вправо]???
???|A|=1\влево[(-2)(5)(-1)\вправо]???
???|А|=(1)(-2)(5)(-1)???
???|А|=10???
В этом результате мы хотим отметить две вещи.
Во-первых, вычисление было намного проще, чем обычное ???4\times4??? определителя, поэтому работа с первым столбцом является хорошей стратегией, когда мы вычисляем определитель верхней треугольной матрицы.
Во-вторых, значением определителя было произведение ???(1)(-2)(5)(-1)???, которое является произведением всех элементов на главной диагонали ???A ???.
На самом деле, для всех верхних треугольных матриц это всегда будет верно! Учитывая любую верхнюю треугольную матрицу, вы можете найти значение определителя, просто перемножив вместе все элементы вдоль главной диагонали матрицы. Это также говорит вам, что если у вас есть ???0??? в любом месте на главной диагонали верхней треугольной матрицы определитель будет равен ???0???. Это означает, что если матрица содержит полную строку нулей в любом месте матрицы, то определитель будет равен ???0???.
То же верно и для нижних треугольных матриц.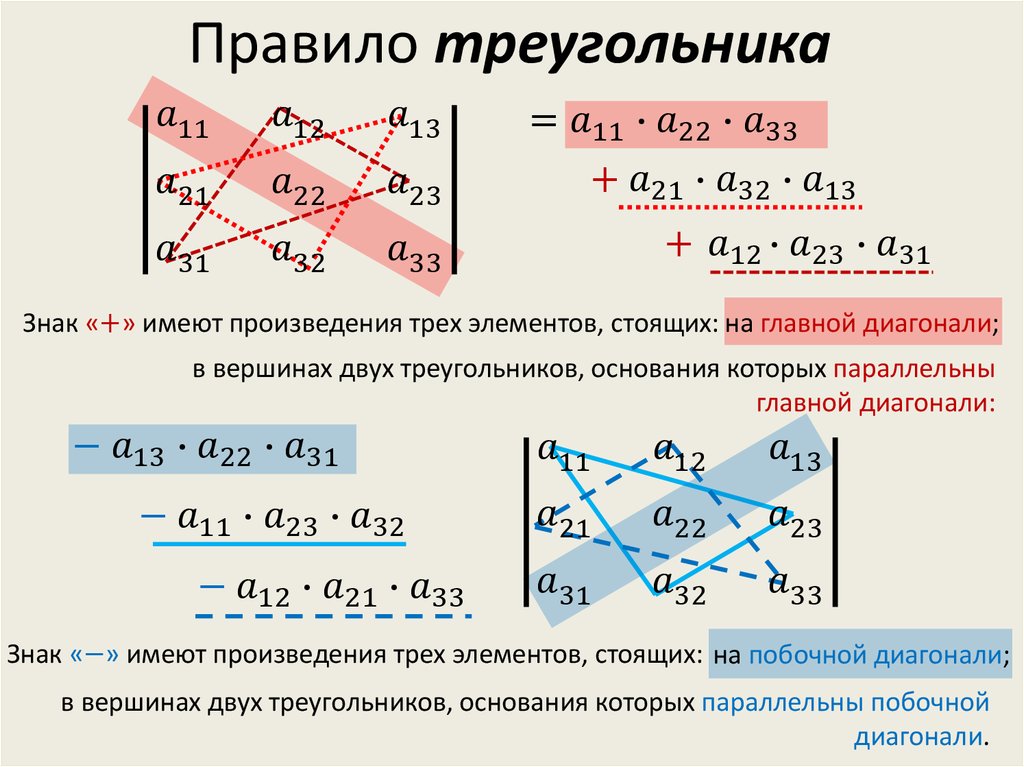
Если бы вы вычисляли определитель традиционным способом, вам нужно было бы вычислять его по первой строке или последнему столбцу, так как в них больше всего ???0??? записи.
Если бы вы сделали это, то обнаружили бы, что определитель нижней треугольной матрицы является произведением элементов вдоль главной диагонали, как мы это сделали для верхних треугольных матриц.
Преобразование матрицы в верхний треугольный или нижний треугольный вид — отличный способ быстро найти определитель.
Определение и построение верхних треугольных матриц и нижних треугольных матриц
Пройти курс
Хотите узнать больше о линейной алгебре? У меня есть пошаговый курс для этого. 🙂
Приведение матрицы к треугольной форме
Пример
Поставить ???A??? в верхний или нижний треугольный вид, чтобы найти определитель.
В ???A??? у нас не больше нулей ниже главной диагонали, чем над ней, или наоборот, так что мы действительно можем работать в любом направлении. Давайте начнем с того, что перепишем матрицу как определитель, который мы пытаемся найти.
Теперь поменяйте местами первую и вторую строки, чтобы у нас была сводная запись в первой строке. Помните, что когда мы меняем строки, определитель умножается на ???-1???.
Главная диагональ — это набор элементов, идущих от верхнего левого угла матрицы вниз к нижнему правому углу матрицы.
Теперь выполним ???2R_1+R_2\to R_2???.
Теперь выполните ???-3R_2+R_3\to R_3???.
Теперь, когда у нас есть ???A??? в верхнетреугольной форме определитель — это просто произведение элементов вдоль главной диагонали.