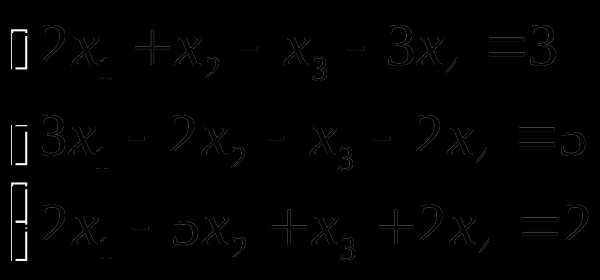2.4. Вычисление определителей

ai, j
Определители
2 0 0
det(2A) =det(2E) det A = 0 2 0 (−2) = 23 (−2) = −16 . 0 0 2
(d) Аналогично,
det(−3A) = det(−3E) det A = (−3)3 (−2) =54 .
(e) Сначала найдем матрицу ( A − 2E) , а затем ее определитель:
| 2 | 3 | 4 |
| 2 | 0 | 0 |
| 0 | 3 | 4 |
| |||
| 0 | 1 | 5 |
|
| 0 | 2 | 0 |
|
| 0 | −1 5 |
| , | |
A − 2E = |
| − |
| = |
| ||||||||||
| 0 | 0 |
|
|
| 0 | 0 | 2 |
|
| 0 | 0 |
|
|
|
| −1 |
|
|
| −3 |
| |||||||||
det(A − 2E) =0 (−1) (−3) =0 .
Здесь мы рассмотрим два метода вычисления определителей. Суть одного из них заключается в разложении определителя по элементам строки или столбца, в результате чего исходный определитель n-го порядка выражается через n определителей меньшего порядка. Другой метод основывается на свойствах определителей и связан с преобразованием определителя к более простому виду. Комбинация двух методов дает наиболее эффективный путь вычисления определителей.
2.4.1. Разложение определителя по элементам строки или столбца
Предварительно введем некоторые важные для последующего изложения понятия.
Рассмотрим квадратную матрицу n-го порядка. Выберем i,j-ый элемент этой матрицы и вычеркнем i-ую строку и j-ый столбец. В результате
мы получаем матрицу (n–1)-го порядка, определитель которой называется минором элемента ai, j и обозначается символом Mi, j .
Определители
Алгебраическое дополнение Ai, j элемента ai, j определяется формулой
Ai, j = (−1)i + j Mi, j .
Нетрудно заметить, что алгебраическое дополнение i,j-го элемента совпадает с минором этого элемента, если сумма индексов, нумерующих строку и столбец элемента, является четным числом. Для нечетных значений i+j алгебраическое дополнение отличается от минора только знаком.
Теорема о разложении определителя по элементам строки.
Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:
det A = ai,1 Ai,1 + ai,2 Ai,2 +K+ ai,n Ai,n =
n
= ∑ai, j Ai, j j =1
Доказательство: По определению, определитель матрицы A представляет собой сумму
det A = | ∑a1,k1 a2,k2 Kai,ki Kan,kn (−1)P{k1,k2 ,K,kn} | (*) |
| {k1,k2 ,Kki ,Kkn} |
|
по все возможным перестановкам индексов, нумерующих столбцы. Выберем произвольным образом некоторую строку, например, с
номером i. Один из элементов этой строки представлен в каждом произведении a1,k1 a2,k2 Kai,ki Kan,kn . Поэтому слагаемые суммы (*)
можно перегруппировать, объединив в первую группу те, что содержат элемент ai,1 в качестве общего множителя, во вторую группу – члены,
содержащие элемент ai,2 , и т.д.
Другими словами, выражение (*) можно представить в виде линейной комбинации элементов ai, j ( j =1,2,L,n ),
33
Определители
n |
| ∑a1,k1 a2,k2 Kai, j Kan,kn (−1)P{k1,k2 ,K,kn} = |
|
det A = ∑ |
|
| |
j =1{k1,k2 ,Kj,Kkn} |
| ||
n |
| ∑a1,k1 a2,k2 Kai −1,ki−1 ai +1,ki+1 an,kn (−1)P{k1,k2 ,K,kn} = | |
= ∑ai, j | |||
j =1 |
| {k1,k2 ,Kj,Kkn} |
|
n |
|
|
|
= ∑ai, j Ai, j = ai,1 Ai,1 + ai,2 Ai,2 +K+ai,n Ai,n , |
| ||
j =1 |
|
|
|
где | ∑a1,k1 a2,k2 Lai −1,ki−1 ai +1,ki+1 Kan,kn (−1)P(k1,L,ki−1, j,ki+1,L,kn ) . | ||
Ai, j = | |||
{k1,L,ki−1,ki = j,ki+1,L,kn} |
| ||
Покажем, что | Ai, j представляет собой алгебраическое | дополнение | |
элемента ai, j . |
|
|
|
Рассмотрим четность перестановки {k1,L, ki −1, j, ki +1,L, kn}. | |||
Во-первых, | требуется i–1 транспозиций элемента j с | соседними | |
элементами, чтобы получить перестановку { j, k1,L, ki −1, ki +1,L, kn}.
Во-вторых, в полученной перестановке, элемент j образует j–1 инверсий с другими элементами.
Следовательно,
(−1)P(k1,L,ki−1, j,ki+1,L,kn ) = (−1)i −1+ j −1 (−1)P(k1,L,ki−1,ki+1,L,kn ) =
= (−1)i + j (−1)P(k1,L,ki−1,ki+1,L,kn )
Однако
∑Lai −1,ki−1 ai +1,ki+1 K (−1)P(k1,L,ki−1,ki+1,L,kn ) = Mi, j {k1,L,ki−1,ki+1,L,kn}
представляет собой минор элемента ai, j .
Таким образом, Ai, j = (−1)i + j Mi, j , что и требовалось доказать.
Поскольку det A = det AT , то тем самым справедлива и следующая
Теорема о разложении определителя по элементам столбца.
Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:
det A = a1, j A1, j + a2, j A2, j +K+ an, j An, j
n
=∑ai, j Ai, j
i=1

Определители
Теоремы о разложении определителя имеют важное значение в теоретических исследованиях. Они устанавливает, что проблема вычисления определителя n-го порядка сводится к проблеме вычисления n определителей (n –1)-го порядка.
Примерs:
1) Вычислить определитель произвольной матрицы A =|| aij || третьего
порядка разложением по элементам |
|
|
|
|
|
|
|
|
|
| |||||||||||
(i) первой строки; |
| (ii) второго столбца. |
|
|
|
|
| ||||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| a11 | a12 | a13 |
|
|
| a22 | a23 |
| −a |
| a21 | a23 |
| +a |
| a21 | a22 | |||
|
|
|
|
|
|
| |||||||||||||||
|
|
|
|
|
|
|
| ||||||||||||||
det A = | a |
| a |
| a |
|
|
| = a |
|
|
|
| ||||||||
|
| 21 |
| 22 |
| 23 |
|
| 11 | a32 | a33 |
| 12 |
| a31 | a33 |
| 13 |
| a31 | a32 |
| a31 | a32 | a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
=a11(a22a33 −a23a32 ) −a12 (a21a33 −a23a31 ) +a13 (a21a32 −a22a31 )
=a11a22a33 +a12a23a31 +a13a21a32 −a11a23a32 −a12a21a33 −a13a22a31,
| a11 | a12 | a13 |
| a21 | a23 |
| +a |
| a11 | a13 |
| −a |
| a11 | a13 | |||
|
|
|
|
|
| ||||||||||||||
det A = | a |
| a |
| a |
| = −a |
|
|
|
| ||||||||
|
| 21 |
| 22 |
| 23 | 12 | a31 | a33 |
|
| 22 | a31 | a33 |
|
| 32 | a21 | a23 |
| a31 | a32 | a33 |
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
=−a12 (a12a33 −a23a31 ) +a22 (a11a33 −a13a31 ) −a32 (a11a23 −a13a21 )
=a11a22a33 +a12a23a31 +a13a21a32 −a11a23a32 −a12a21a33 −a13a22a31.
Результаты, полученные различными методами, идентичны.
| Вычислить определитель |
| 2 | −5 | 3 |
|
| разложением по элементам | |||||||||||
|
|
| |||||||||||||||||
2) |
| 1 | 4 | 0 |
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
| −3 | 7 | 5 |
|
|
|
|
|
| |
| (i) первой строки, | (ii) второго столбца. |
|
|
|
| |||||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
(i) | Разложение определителя по элементам первой строки дает | ||||||||||||||||||
|
|
| 2 | −5 | 3 |
|
| 4 0 |
|
| 1 |
|
| 0 |
| 1 4 |
| ||
|
|
|
|
|
|
|
|
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
| 1 | 4 | 0 |
| = 2 | −(−5) |
|
| +3 |
| |||||||
|
|
| −3 | 7 | 5 |
|
| 7 | 5 |
|
| −3 | 5 |
| −3 7 |
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
=2 4 5 +5 1 5 +3(7 +12) =122.
(ii)Тот же самый результат получается при разложении определителя по элементам второго столбца:
35

Определители
2 | −5 | 3 |
| 1 | 0 |
| 2 3 |
| 2 | 3 |
|
|
| ||||||||
|
|
| ||||||||
1 | 4 | 0 | = −(−5) | +4 | −7 | |||||
−3 | 7 | 5 |
| −3 | 5 |
| −3 5 |
| 1 | 0 |
|
|
|
|
|
|
|
|
=5(5 +0) +4 (10 +9) −7(0 −3) =122.
2.4.2.Вычисление определителей методом элементарных
преобразований
Под элементарными преобразованиями понимаются следующие операции.
N | Операция | Результат |
1 | Перестановка местами двух | Определитель изменяет свой |
| строк. | знак. |
2 | Умножение строки на ненулевое | Определитель умножается на это |
| число. | число. |
3 | Прибавление к строке другой | Определитель не изменяется. |
строки, предварительно | ||
| умноженной на любое число. |
|
С учетом равноправия строк и столбцов определителя подобные операции в полной мере применимы к столбцам.
Идея метода заключается в том, чтобы с помощью элементарных преобразований строк и столбцов привести определитель к треугольному виду, что решает проблему его вычисления.
Можно поступать и несколько иначе: с помощью элементарных преобразований получить строку (или столбец), содержащую только один ненулевой элемент, и затем разложить полученный определитель по элементам этой строки (столбца). Подобная процедура понижает порядок определителя на одну единицу.
Примеры. |
|
|
|
|
2 | −4 | 1 |
| |
| −3 | 2 |
| . Вычислить det A, приведя матрицу к |
1) Пусть A = | 5 | |||
| 1 | 2 |
|
|
| 3 |
| ||
треугольному виду.
Решение:
Определители
| 2 | −4 1 |
| r1 | →r1 −2r3 |
| 0 | −8 −5 |
|
|
|
| ||||||||
|
|
|
|
|
|
| ||||||||||||||
det A = |
| r2 | →r2 +3r3 |
|
|
|
|
| ||||||||||||
−3 | 2 |
|
| 5 |
|
| = |
|
|
| 0 | 8 | 14 |
|
|
|
| |||
| 1 | 2 |
|
| 3 |
|
|
|
|
|
| 1 | 2 | 3 |
|
|
|
| ||
r1 | ↔r3 | − |
| 1 |
| 2 |
| 3 |
| r3 | →r3 | +r2 | − |
| 1 | 2 | 3 |
| . | |
|
|
|
|
|
| |||||||||||||||
| = |
| 0 8 | 14 |
|
| = |
|
| 0 | 8 | 14 |
| |||||||
|
|
|
| 0 |
| −8 | −5 |
|
|
|
|
|
|
| 0 | 0 | 9 |
|
| |
Определитель матрицы треугольного вида равен произведению ее диагональных элементов:
det A = −1 8 9 = −72 . 2) Вычислить определитель матрицы
1 | 5 | −2 | 0 |
| |
| 3 | 1 | 6 |
|
|
| −1 | ||||
A = | 7 | 0 | 1 | 3 | . |
|
| ||||
| 4 | 5 | 2 | 1 |
|
|
| ||||
Решение: Сначала преобразуем первую строку с помощью элементарных операций над столбцами, стремясь получить в ней максимально возможное число нулей. С этой целью вычтем из второго столбца пятый столбец, предварительно умноженный на 5, а к третьему столбцу прибавим удвоенный второй столбец:
| 1 | 5 | −2 0 |
| c →c −5c |
| 1 | 0 | 0 0 |
|
| ||||
|
|
|
| ||||||||||||
| 3 | 1 | 6 | −1 |
| c2 | →c2 | +2c1 |
| 3 | −14 | 12 | −1 |
|
|
det A = |
| 3 | =3 | 1 |
|
| . | ||||||||
| 7 | 0 | 1 | 3 |
|
|
|
|
| 7 | −35 | 15 | 3 |
|
|
| 4 | 5 | 2 | 1 |
|
|
|
|
| 4 | −15 | 10 | 1 |
|
|
Теперь разложим определитель по элементам первой строки:
det A = |
| −14 | 12 | −1 |
|
|
| ||||
| −35 | 15 | 3 |
| |
|
| −15 | 10 | 1 |
|
Преобразуем строки, прибавляя к первой строке третью и вычитая из второй строки утроенную третью:
37
studfiles.net
разложение по строке — ПриМат
Дальнейшие преобразования будут проще, если элемент равен 1 или -1. Для этого из первой строки вынесем 3 за знак определителя:
Далее нам нужно получить нули в первом столбце. Домножим первую строку на -5 и прибавим ко второй, на 4 и прибавим к третей, на 7 и прибавим к четвертой:
Аналогично, дальнейшие вычисления будут проще, если элемент равен 1 или -1. Для этого вторую строку умножим на 2 и прибавим к четвертой строке. Далее поменяем вторую и последнюю строку местами. Перед определителем появится знак «-«.
Далее нам нужно получить нули во втором столбце под элементом . Для этого умножим вторую строку на 7 и прибавим к третей, на -7 и прибавим к четвертой.
Прибавим последнюю строку к третьей, потом умножим третью строку на 9 и прибавим к четвертой:
Привели определитель к треугольному виду. Его значение равно произведению элементов, стоящих на главной диагонали:
[свернуть]
ib.mazurok.com
Разложение определителя по строке.
Определение1. 7. Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.
Обозначение: выбранный элемент определителя, его минор.
Пример. Для
Определение1. 8. Алгебраическим дополнением элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.
Рассмотрим еще один способ вычисления определителей третьего порядка – так называемое разложение по строке или столбцу. Для этого докажем следующую теорему:
Теорема 1.1. Определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, т.е.
где i=1,2,3.
Доказательство.
Докажем теорему для первой строки определителя, так как для любой другой строки или столбца можно провести аналогичные рассуждения и получить тот же результат.
Найдем алгебраические дополнения к элементам первой строки:
Тогда
Таким образом, для вычисления определителя достаточно найти алгебраические дополнения к элементам какой-либо строки или столбца и вычислить сумму их произведений на соответствующие элементы определителя.
Пример. Вычислим определитель с помощью разложения по первому столбцу. Заметим, что при этом искать не требуется, так как следовательно, и Найдем и Следовательно,
=
Определители более высоких порядков.
Определение1. 9. Определитель n-го порядка
есть сумма n! членов каждый из которых соответствует одному из n! упорядоченных множеств полученных r попарными перестановками элементов из множества 1,2,…,n.
Замечание 1. Свойства определителей 3-го порядка справедливы и для определителей n-го порядка.
Замечание 2. На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и в конечном счете свести задачу к нахождению определителей 3-го порядка.
Пример. Вычислим определитель 4-го порядка с помощью разложения по 2-му столбцу. Для этого найдем и :
Следовательно,
Теоре́ма Лапла́са — одна из теорем линейной алгебры. Названа в честь французского математика Пьера-Симона Лапласа (1749 — 1827), которому приписывают формулирование этой теоремы в 1772 году[1], хотя частный случай этой теоремы о разложении определителя по строке (столбцу) был известен ещё Лейбницу.
олнение минора определяется следующим образом:
где , .
Справедливо следующее утверждение.
Число миноров, по которым берётся сумма в теореме Лапласа, равно числу способов выбрать столбцов из , то есть биномиальному коэффициенту .
Так как строки и столбцы матрицы равносильны относительно свойств определителя, теорему Лапласа можно сформулировать и для столбцов матрицы.
Разложение определителя по строке (столбцу) (Следствие 1)
Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.
Пусть — квадратная матрица размера . Пусть также задан некоторый номер строки либо номер столбца матрицы . Тогда определитель может быть вычислен по следующим формулам:
| Разложение по -й строке: Разложение по -му столбцу: |
где — алгебраическое дополнение к минору, расположенному в строке с номером и столбце с номером . также называют алгебраическим дополнением к элементу .
Утверждение является частным случаем теоремы Лапласа. Достаточно в ней положить равным 1 и выбрать -ую строку, тогда минорами, расположенными в этой строке будут сами элементы.
infopedia.su
вычисление определителей — ПриМат
Дальнейшие преобразования будут проще, если элемент равен 1 или -1. Для этого из первой строки вынесем 3 за знак определителя:
Далее нам нужно получить нули в первом столбце. Домножим первую строку на -5 и прибавим ко второй, на 4 и прибавим к третей, на 7 и прибавим к четвертой:
Аналогично, дальнейшие вычисления будут проще, если элемент равен 1 или -1. Для этого вторую строку умножим на 2 и прибавим к четвертой строке. Далее поменяем вторую и последнюю строку местами. Перед определителем появится знак «-«.
Далее нам нужно получить нули во втором столбце под элементом . Для этого умножим вторую строку на 7 и прибавим к третей, на -7 и прибавим к четвертой.
Прибавим последнюю строку к третьей, потом умножим третью строку на 9 и прибавим к четвертой:
Привели определитель к треугольному виду. Его значение равно произведению элементов, стоящих на главной диагонали:
[свернуть]
ib.mazurok.com
Решение. Разложим определитель по 4-й строке
Вычислить определитель:
 .
.
Решение.
Разложим определитель по 4-й строке:
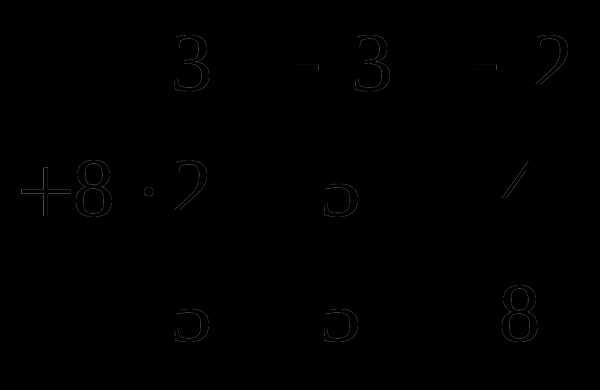
Разложим полученные определители по 3-й строке:
.
Осуществим следующие преобразования матрицы:
1 шаг
вычтем элементы 2-й строки из соответствующих элементов 3-й строки;
вычтем элементы 3-й строки из соответствующих элементов 1-й строки;
вычтем элементы 2-й строки из соответствующих элементов 3-й строки.
Затем сложим элементы 4-й строки с соответствующими элементами 2-й строки, умноженными на -5.
Сложим элементы 2-й строки с соответствующими элементами 3-й строки, умноженными на -2.
.
Переставим местами 1-ю и 3-ю строки, от этого определитель изменит знак.
Вынесем за знак определителя множитель -3 из 3-й строки и множитель -2 из 4-й строки.
Переставим местами 2-ю и 3-ю строки, от этого определитель изменит знак.
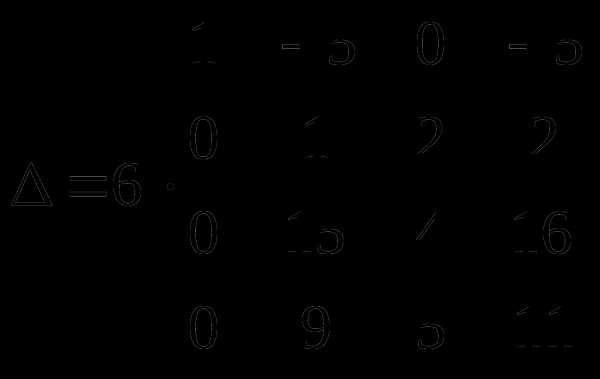
2 шаг. Сложим элементы 3-й строки с соответствующими элементами 2-й строки, умноженными на -15.
Вынесем за знак определителя множитель -2 из 3-й строки.

сложим элементы 3-й строки с соответствующими элементами 4-й строки
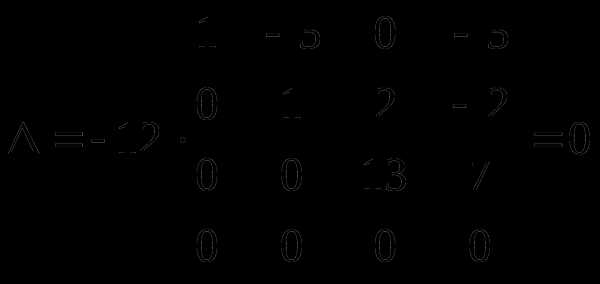
По свойству определителя, если матрица имеет нулевую строку, определитель равен 0.
Решение.
Обратная матрица находится по формуле
,
где  — присоединенная матрица, каждый элемент
которой – алгебраическое дополнение
элемента
— присоединенная матрица, каждый элемент
которой – алгебраическое дополнение
элемента  матрицы
матрицы  .
.
 .
.
Проверим условие невырожденности матрицы.
Определитель матрицы вычислим разложением по 1 строке.
Таким образом, матрица А является невырожденной, то есть имеет обратную. Вычислим матрицу, обратную для этой матрицы. Сначала найдем присоединенную матрицу из алгебраических дополнений.
Найдем алгебраические дополнения соответствующих элементов матрицы по формуле , где соответствующий минор получается вычеркиванием из определителя матрицы i строки и j столбца. Получим
; ; 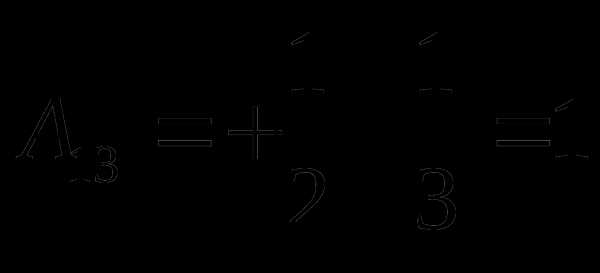
; 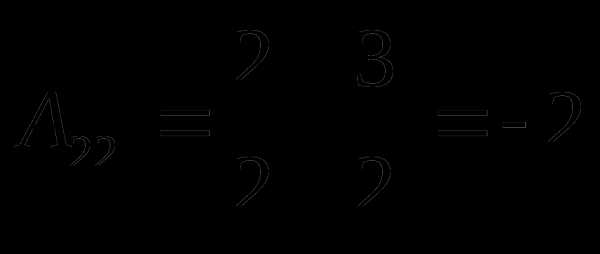 ;
; 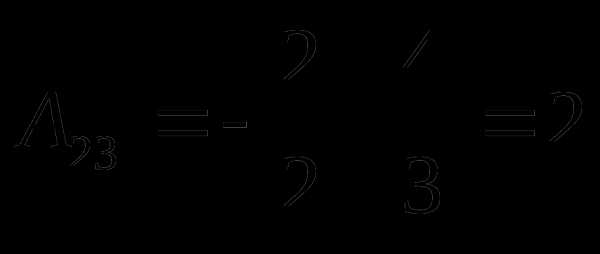
;  ;
;  .
.
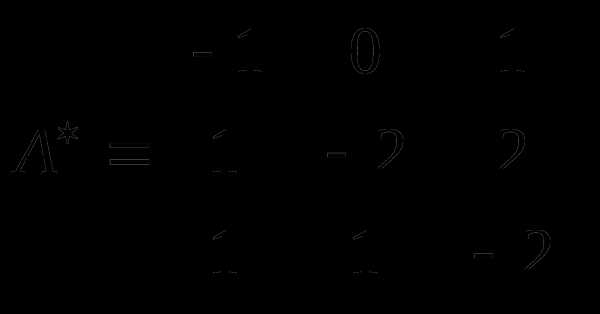 .
.
Таким образом, .
Найти ранг матрицы методом окаймляющих миноров и приведением к ступенчатому виду.
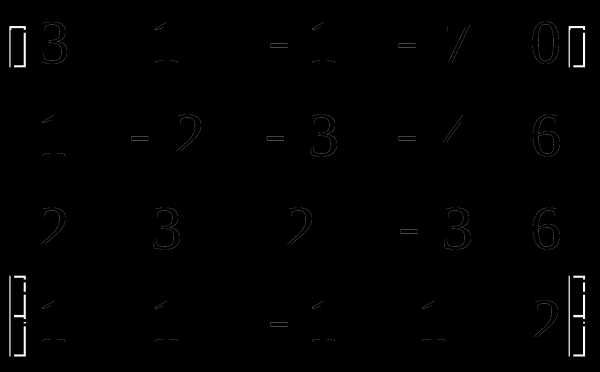 .
.
Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) .
Окаймляя при помощи второй строки и 5-го столбца, получаем минор
.
Переходим теперь к минорам 3-го порядка, окаймляющим М2.
Переходим теперь к минорам 4-го порядка, окаймляющим М3.
Ранг матрицы А равен 4.
Осуществим линейные преобразования, не изменяющие ранга матрицы.
Переставим местами 1-ю и 4-ю строки,
вычтем элементы 2-й строки из соответствующих элементов 1-й строки;
Получили матрицу, состоящую из 4 строк и 5 столбцов. Строки линейно независимы.
Ранг этой матрицы равен 4.
Решить матричное уравнение
Решение.
Решим уравнение: , где Х – матрица – решение.
Для
того, чтобы решить матричное уравнение,
сначала умножим обе части уравнения
слева на матрицу, обратную к матрице  .
.
По свойству обратной матрицы , где Е – единичная матрица. Получим
.
Обратная матрица находится по формуле .
Определитель матрицы вычислим разложением по 1 столбцу.
Таким образом, матрица А является невырожденной, то есть имеет обратную. Вычислим матрицу, обратную для этой матрицы. Сначала найдем присоединенную матрицу из алгебраических дополнений.
Найдем алгебраические дополнения соответствующих элементов матрицы по формуле , где соответствующий минор получается вычеркиванием из определителя матрицы i строки и j столбца. Получим
; ; 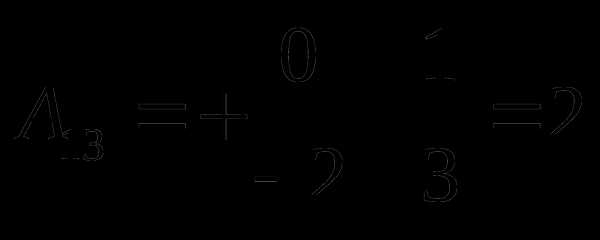
;  ;
; 
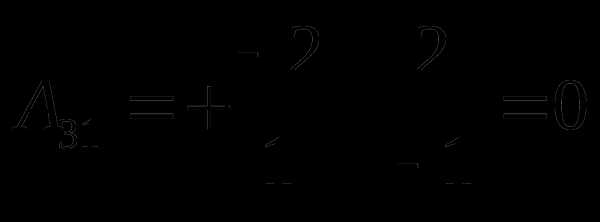 ;
; 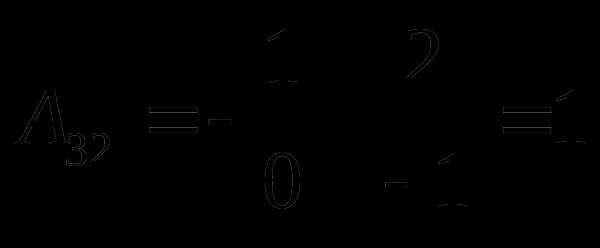 ;
;  .
.
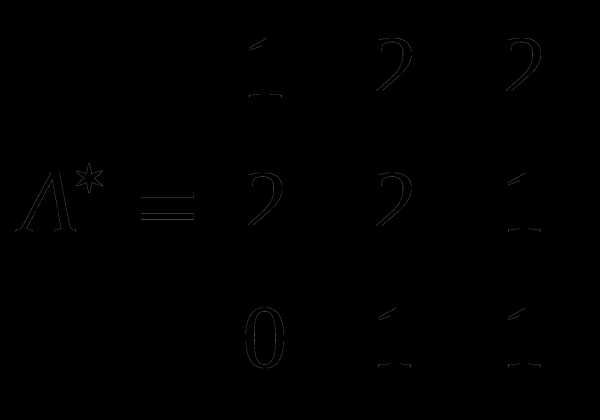 .
.
Таким образом,  .
.
Решить систему линейных уравнений по методу Крамера. Сделать проверку.
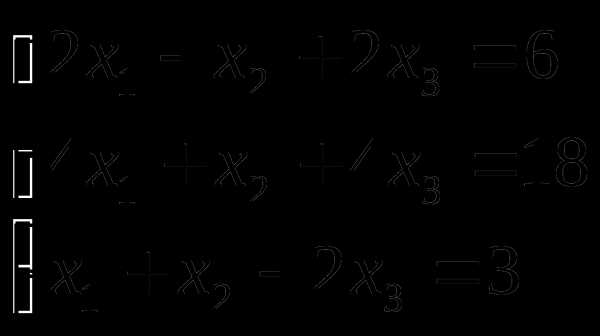
Решение.
Вычислим
определитель матрицы системы  по формуле:
по формуле:
.
.
Определитель  ,
следовательно, система совместна и
обладает единственным решением. Вычислим
определители
,
следовательно, система совместна и
обладает единственным решением. Вычислим
определители  ,
полученные путем замены J-го столбца
столбцом свободных членов.
,
полученные путем замены J-го столбца
столбцом свободных членов.
.
Аналогично вычисляем остальные определители:
.
Решение системы
найдем по правилу Крамера:  ;
;  ;
;  .
.
.
Проверка:
Решение найдено правильно.
Решить систему уравнений методом Гаусса. Сделать проверку.
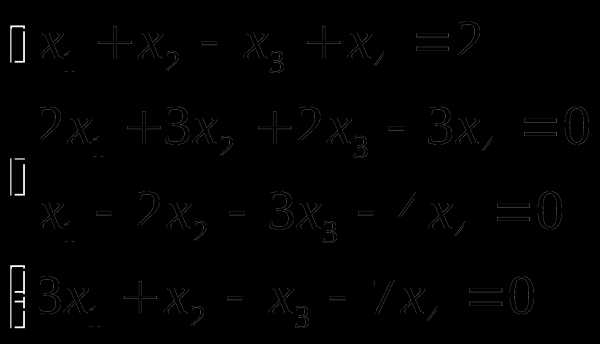
Решение.
Составим расширенную матрицу 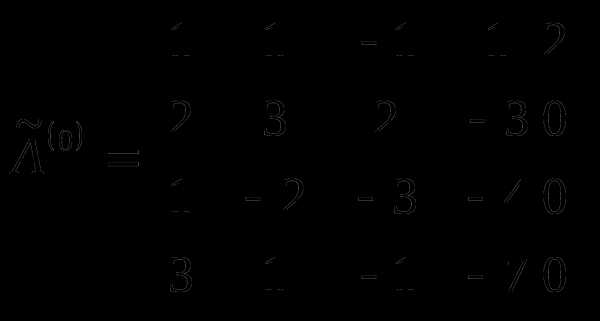 .
.
1 шаг.
В качестве направляющего элемента
выбираем элемент 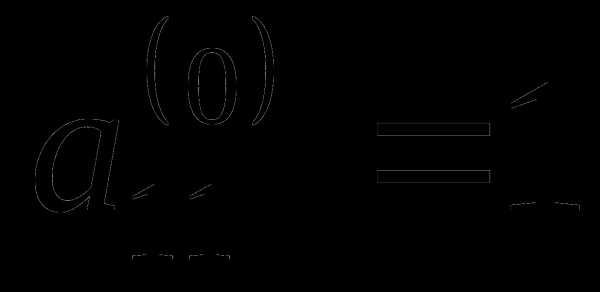 .
Главная строка – первая.
.
Главная строка – первая.
Преобразуем первый столбец в единичный. Для этого вычтем из 1-й строки 3-ю строку. Результат запишем на место 3-й строки.
Затем сложим элементы 2-й строки с соответствующими элементами 1-й строки, умноженными на -2.
Получим
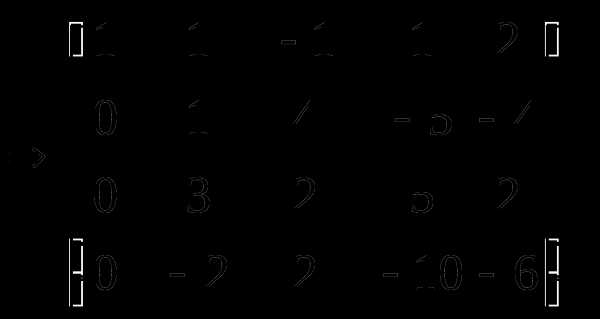
2 шаг.
В качестве направляющего элемента
выбираем элемент 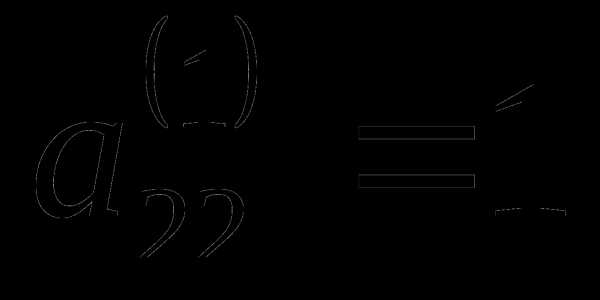 .
Главная строка – вторая.
.
Главная строка – вторая.
Сложим элементы 3-й строки с соответствующими элементами 2-й строки, умноженными на -3. Затем сложим элементы 4-й строки с соответствующими элементами 2-й строки, умноженными на 2.
.
3 шаг.
В качестве направляющего элемента
выбираем элемент 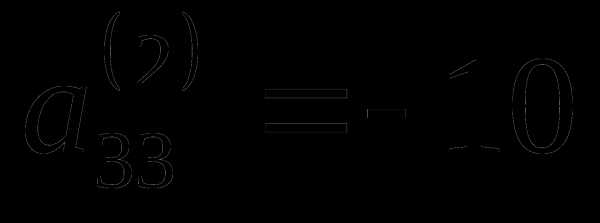 .
Главная строка – 3-я.
.
Главная строка – 3-я.
Сложим элементы 3-й строки с соответствующими элементами 4-й строки.
Нулевые строки удаляем.
Разделим 3-ю строку на -10.
Обратный ход метода Гаусса.
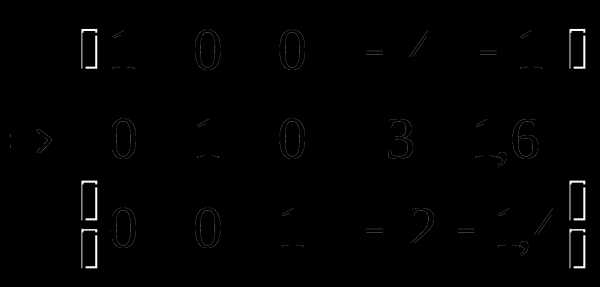
Исходная система эквивалентна следующей системе уравнений:
.
Это решение системы.
Проверка:
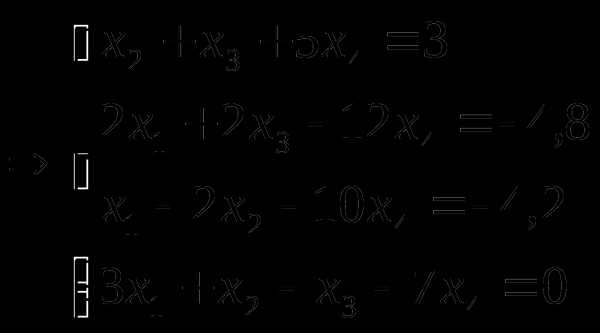 .
.
Найти фундаментальную систему решений:
 .
.
Решение.
Составим расширенную матрицу системы  .
.
Преобразуем расширенную матрицу
Исходная система эквивалентна следующей системе уравнений:
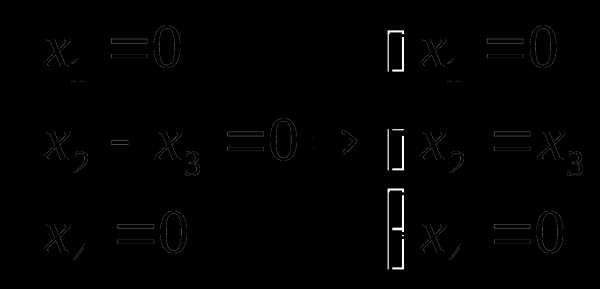 .
.
Возьмем . Тогда решение системы (0;0;0;0).
Возьмем . Тогда решение системы (0;1;1;0).
Два этих решения составляют фундаментальную систему.
Общее решение системы
Решение.
Найдём ранг расширенной матрицы системы уравнений
Следовательно, система является неопределённой (имеет бесконечно много решений), так как ранг расширенной матрицы равен 3 и ранг матрицы системы тоже равен 3.
Исходная система эквивалентна следующей системе уравнений:
Возьмем . Тогда решение системы (-1,4;-2;0;-2,6).
Возьмем . Тогда решение системы (-2,8;-3;1;-4,2).
gigabaza.ru

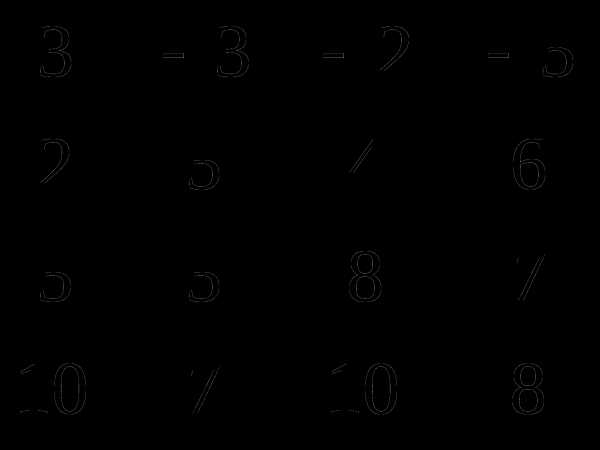 .
.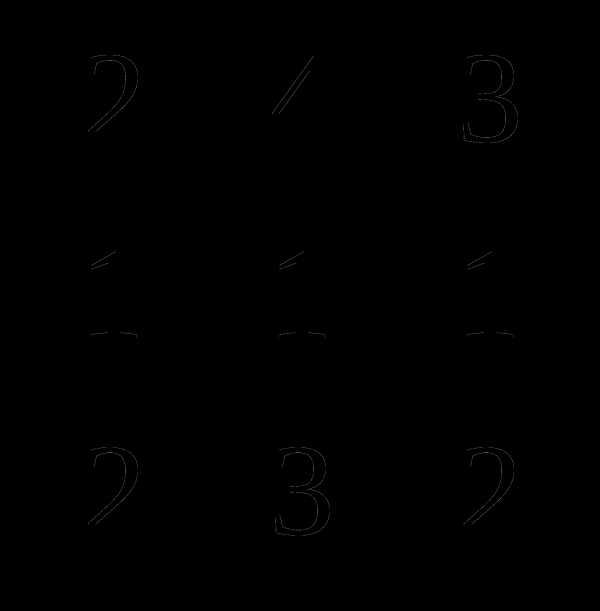
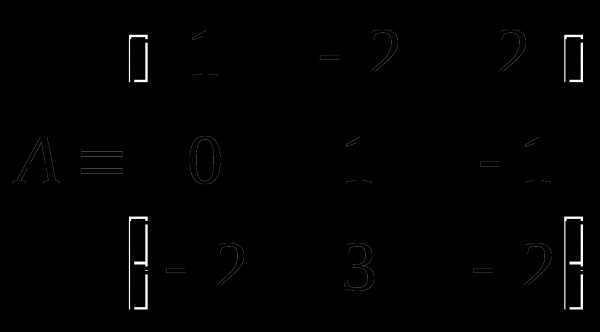 .
.  по формуле:
по формуле: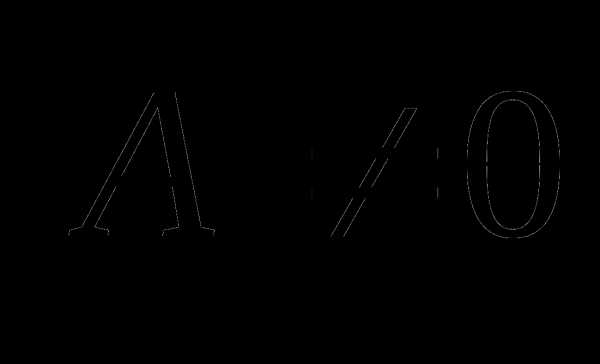 ,
следовательно, система совместна и
обладает единственным решением. Вычислим
определители
,
следовательно, система совместна и
обладает единственным решением. Вычислим
определители  ,
полученные путем замены J-го столбца
столбцом свободных членов.
,
полученные путем замены J-го столбца
столбцом свободных членов.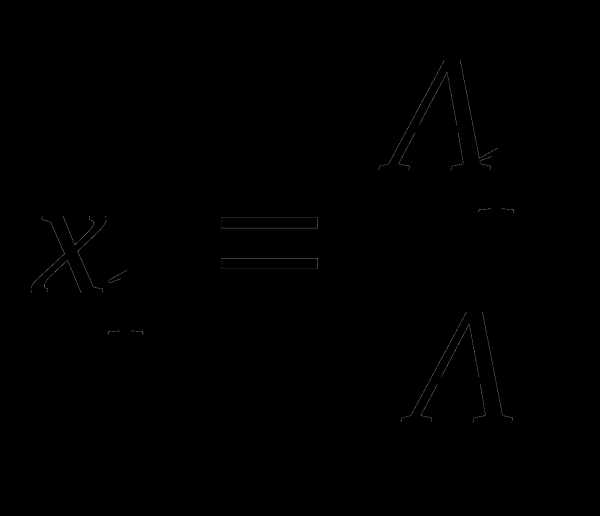 ;
; 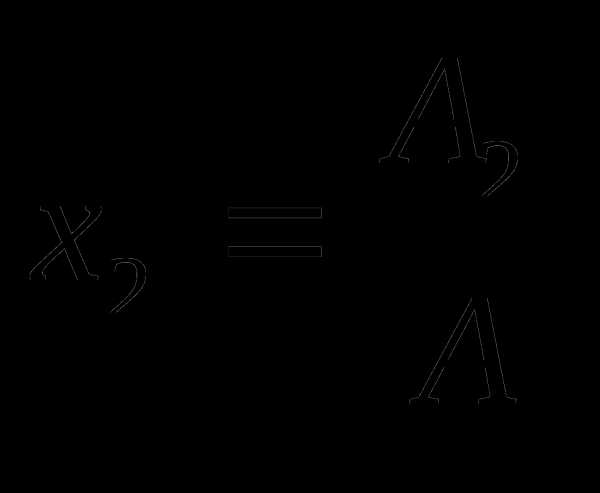 ;
; 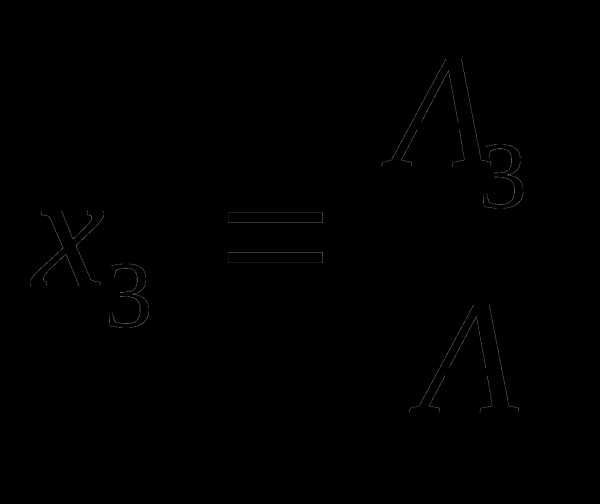 .
.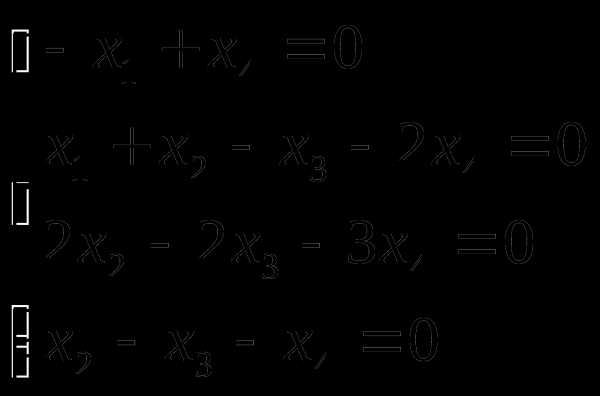 .
.