Вычисление площади криволинейной трапеции — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Вычисление площади криволинейной трапеции
Применение определенного интеграладля нахождения площади
криволинейной трапеции.
Найдите производную и одну из
первообразных функции
f'(x)
1
0
х
2Cos2x
22 ln2
х
f(x)
х
х
2х
Sin2x
F(x)
х3
12 2
х x
Соs2
2 ln22
x2
3
3.
 Определенный интегралb
Определенный интегралbf x dx F x
b
a
F b F a
a
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла
заключается в том, что определенный интеграл
равен площади криволинейной трапеции:
ограниченной кривой у = f(x),
прямыми х = а; х = b и осью Ох, у = 0 .
Криволинейная трапеция
Криволинейной трапецией называется фигура,
ограниченная графиком одной непрерывной
функцией f(х), прямыми х=а, x=b и отрезком
[а;b] на оси Ох.
У
0
a
x=b
х=а
y = f(x)
b
Х
На каком рисунке изображена
криволинейная трапеция?
y
1.
2.
y
x
x
3.
y
4.
x
y
x
6. Какие из данных фигур являются криволинейными трапециями?
12
3
у
y
y
y = f(x)
0
a
b
х
a
0
y
b
c
4
0
b
b x
y
y = f1(x)
b
x
0
0
a
y
a
a
x
y = f2(x)
0
x
5
a
b x
6
7.
 Площадь криволинейной трапецииy
Площадь криволинейной трапецииyD
C
b
S ABCD f x dx
a
a
b
B
x=b
x=a
0
A
F b F a
y=0
x
8. Площадь криволинейной трапеции
yB
b
y=0
x
b
S ABCD
f x dx
D
C
x=b
a
x=a
0
A
a
F b F a
y
Площадь криволинейной
трапеции
D
0
A
a
C
S PMCD S ABCD S ABMP
B
b
b
b
x
f x dx g x dx
a
a
b
b
а
a
f ( x)dx g ( x)dx
P
M
y
Площадь криволинейной
трапеции
D
C
S PMCD S ABCD S ABMP
P
0
Aa
M
b B
b
b
a
a
f x dx g x dx
f x g x dxx
b
a
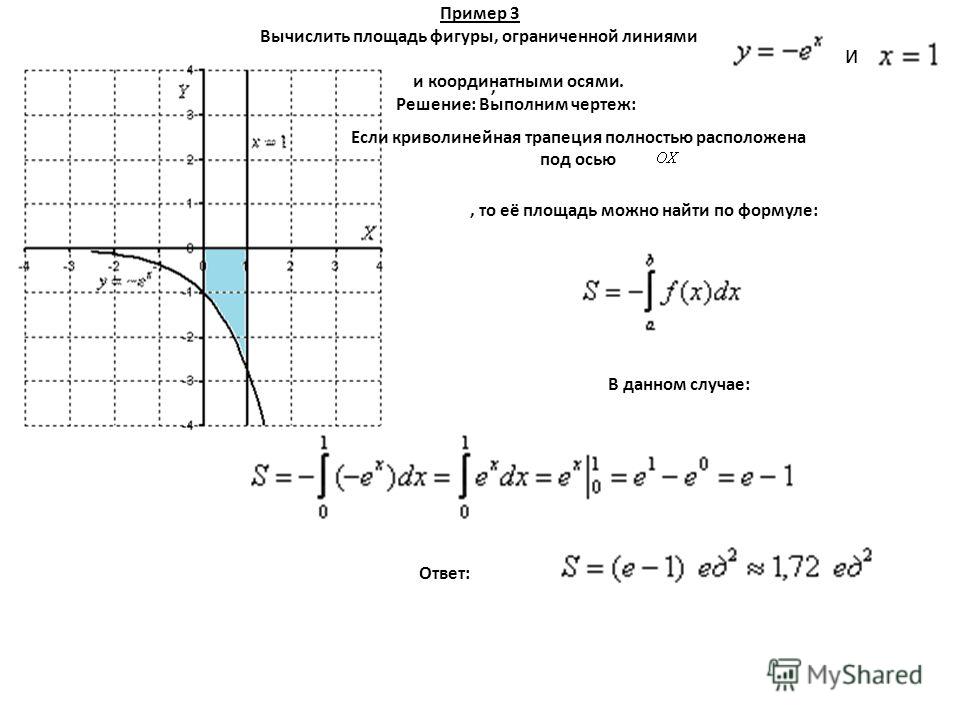
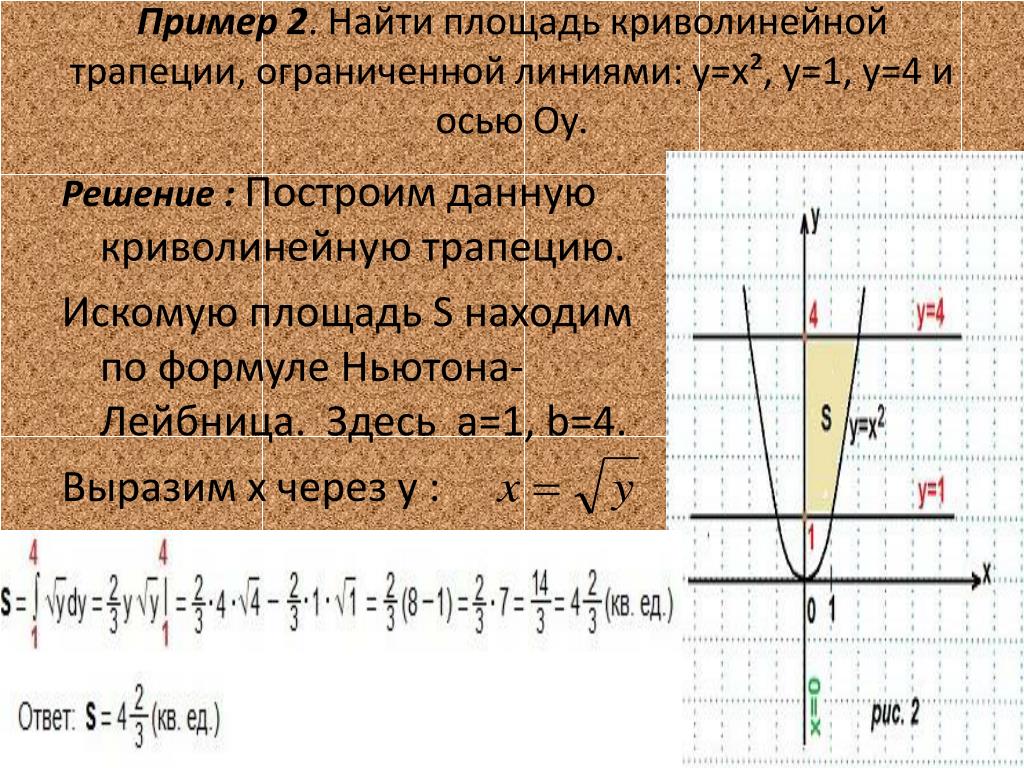
11. Пример 1:
вычислить площадь фигуры,ограниченной линиями y = x2, y = x + 2.
y
SВОС SABCD SABOCD
C
2
2
1
1
x 2 dx x 2 dx
B
A
-1
2
2
x
x
х 2 х 2 dx 2x
3
2
1
O
D
2
2
3
2
1
8 1
1
1
2 4 2 5 4,5
3 2
3
2
x
y
Площадь криволинейной
трапеции
SАЕDВ SAEDC SСDB
D
с
b
a
с
f x dx g x dx
Е
0
Aa
с
C
b
B
x
вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
y
4
0
SАDВ SADС SСDB
D
A
2
4
C
8
B
x
вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
4
8
x — 2 dx 2
2
2
3 4
x 2
8 — хdx
3
4
4 8 x 8 x
3
2
8
4
4 2 3 2 2 3 4 8 8 8 8 4 8 4 8 4
3
3
3
3
8 х t
dx dt
1
2
2 t dt 2 t dt
3
2
t
4
2 (8 x) 3
3
3
2
8 32 40
1
13
3 3
3
3
15.
 Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью Ox и прямой x=2.y x 1
Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью Ox и прямой x=2.y x 1 2
1
0
1
01
x=2
y
12
x
Найти площадь криволинейной трапеции,
изображенной на рисунке
У=х²
y
b
S
f ( x ) dx
a
3
S
х 2 dx F (3) F (1)
1
33 13
2
8 ( кв.ед)
3
3
3
1
0
1
3
x
Найдите площадь фигуры, ограниченной линиями
у
1
S ( x 2 2)dx
2
3
x
1
( 2 x) 2
3
1
8
2 ( 4)
3
3
х
-2
0
1
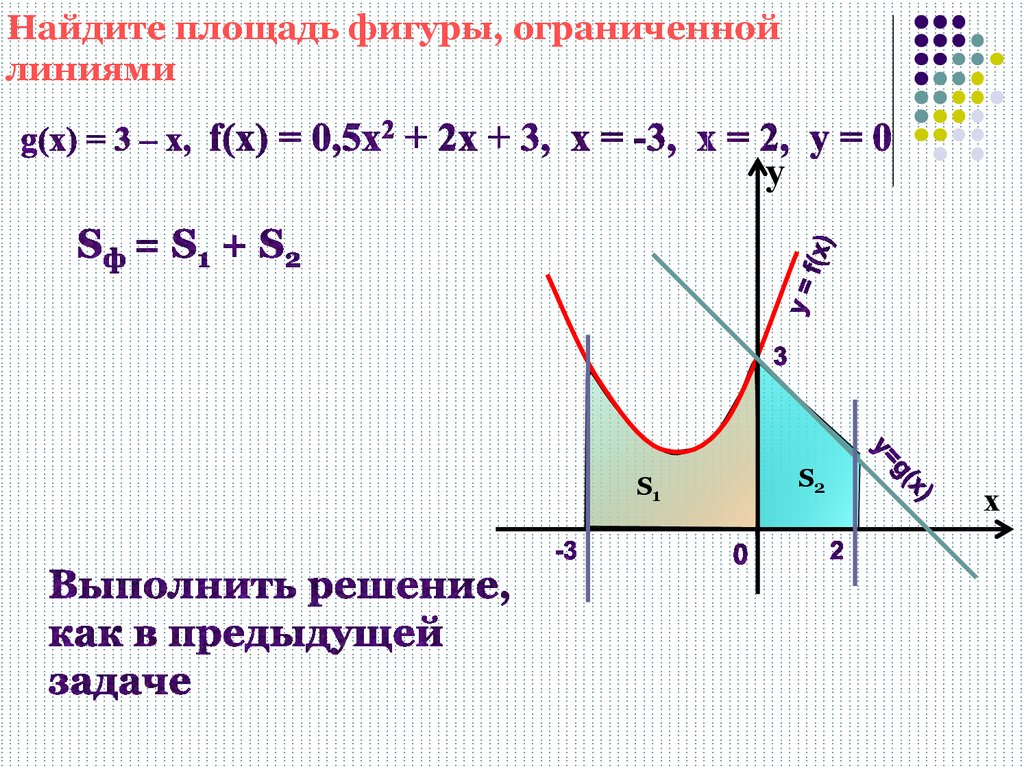
18. Вычисление площадей плоских фигур
Вычислить площадь фигуры, ограниченнойлиниями y=x-2 и y=x2-4x+2
y
1.
y=x2-
4x+2, xв =2, yв = -2
2. у=х-2: х=0, у=-2; х=2, у=0
3. Абсциссы точек пересечения:
x2- 4x+2=x-2
х1=1, х2=4
4
4. S= ((x 2)
( х 2 4 x 2))dx
1
4
2
3
4
5x
x
(5 x x 4)dx (
4 x) 4,5
2
3
1
1
1
2
-2
4
x
Найдите площадь фигуры, ограниченной
линиями
у
х
-2
3
у = х2 — 3
Найдите площадь фигуры, ограниченной
линиями
у
S1
S2
х
Найти площадь криволинейной трапеции,
изображенной на рисунке
y
I
1
0
I
-1
y=sinx
2
x
English Русский Правила
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
На полке было 12 книг. 2. Найдите площадь полной поверхности цилиндра.
2. Найдите площадь полной поверхности цилиндра.
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Пользуйтесь нашим приложением
Площадь криволинейной трапеции у х 2. Площадь криволинейной трапеции численно равна определенному интегралу. Применение интеграла к решению прикладных задач
Применение интеграла к решению прикладных задач
Вычисление площади
Определенный интеграл от непрерывной неотрицательной функции f(x) численно равен площади криволинейной трапеции, ограниченной кривой у = f(x), осью О х и прямыми х = а и х = b. Соответственно, формула площади записывается так:
Рассмотрим несколько примеров вычисления площадей плоских фигур.
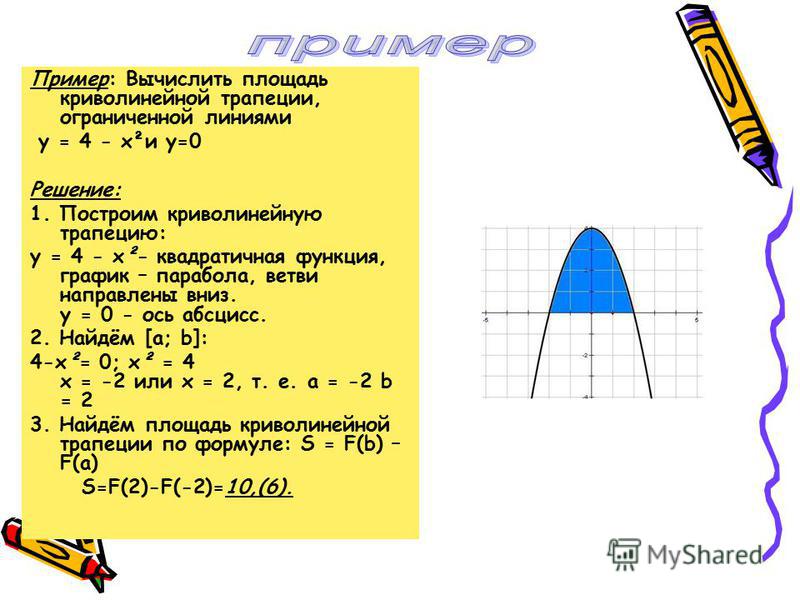
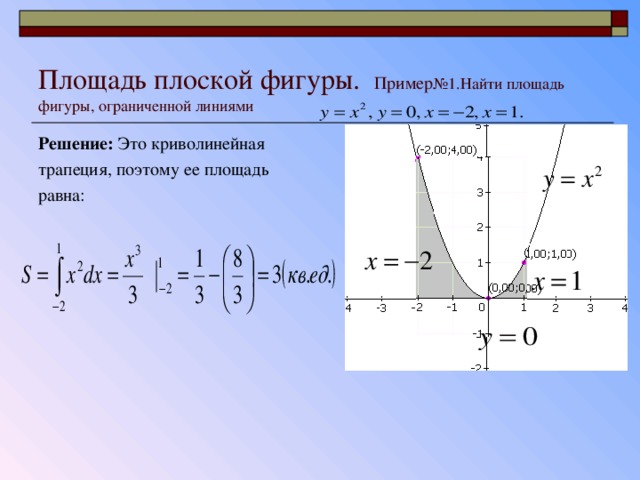
Задача №1. Вычислить площадь, ограниченную линиями y = x 2 +1, y = 0, x = 0, x = 2.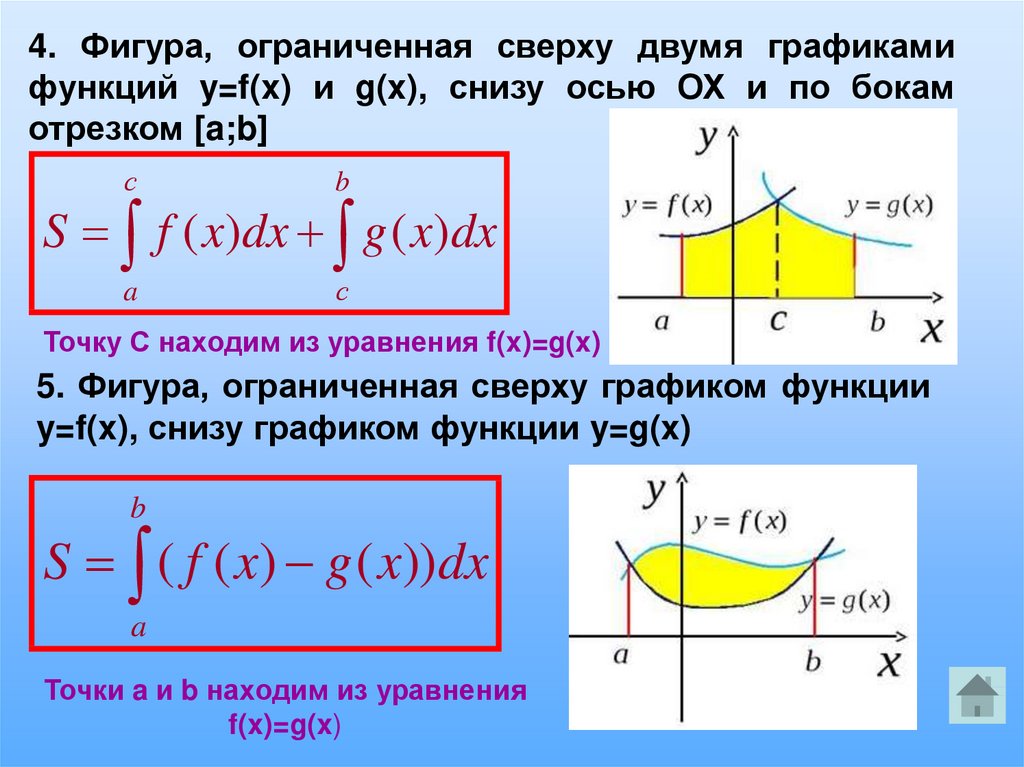
Решение. Построим фигуру, площадь которой нам предстоит вычислить.
у = х 2 + 1 — это парабола, ветви которой направлены вверх, причем парабола смещена вверх на одну единицу относительно оси О у (рис. 1).
Рис. 1. График функции y = x 2 + 1
Задание №2. Вычислить площадь, ограниченную линиями y = x 2 — 1, y = 0 в диапазоне от 0 до 1.
Раствор. График этой функции представляет собой параболу ветви, которая направлена вверх, а парабола смещена на единицу вниз относительно оси O y (рис. 2).
Рисунок 2. График функции y = x 2 — 1
Задание №3. Сделать чертеж и вычислить площадь фигуры, ограниченной линиями
y = 8 + 2x — x 2 и y = 2x — 4.
Решение. Первая из этих двух линий представляет собой параболу с ветвями, направленными вниз, так как коэффициент при x 2 отрицательный, а вторая линия представляет собой прямую, пересекающую обе оси координат.
Для построения параболы найдем координаты ее вершины: y’=2 – 2x; 2 – 2x = 0, x = 1 – абсцисса вершины; y(1) = 8 + 2∙1 – 1 2 = 9 – его ордината, N(1;9) – его вершина.
Теперь найдем точки пересечения параболы и прямой, решив систему уравнений:
Приравнивание правых частей уравнения, у которого равны левые части.
Получаем 8+2х — х 2 = 2х — 4 или х 2 — 12 = 0, откуда .
Итак, точки — это точки пересечения параболы и прямой (рисунок 1).
Рисунок 3 Графики функций y = 8 + 2x – x 2 и y = 2x – 4
Построим прямую y = 2x – 4. Она проходит через точки (0;-4), ( 2;0) на осях координат.
Для построения параболы можно также иметь ее точки пересечения с осью 0x, то есть корни уравнения 8 + 2x — x 2 = 0 или x 2 — 2x — 8 = 0. По теореме Виета, легко найти его корни: х 1 = 2, х 2 = четыре.
На рис. 3 изображена фигура (параболический отрезок M 1 N M 2), ограниченная этими линиями.
Вторая часть задачи — найти площадь этой фигуры.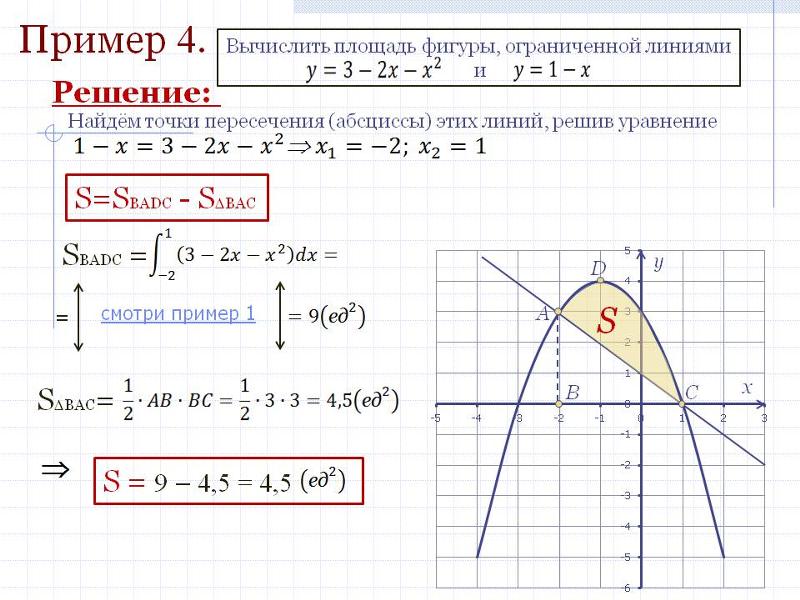 Его площадь можно найти с помощью определенного интеграла по формуле .
Его площадь можно найти с помощью определенного интеграла по формуле .
С учетом этого условия получаем интеграл:
2 Расчет объема тела вращения
Объем тела, полученный при вращении кривой y = f(x) вокруг оси О х, вычисляется по формуле:
При вращении вокруг оси О у формула имеет вид:
Задача № 4. Определить объем тела, полученного при вращении криволинейной трапеции, ограниченной прямыми х = 0 х = 3 и а кривая у = вокруг оси О х.
Раствор. Построим чертеж (рис. 4).
Рис. 4. График функции y =
Искомый объем равен
Задача № 5. Вычислить объем тела, полученного при вращении криволинейной трапеции, ограниченной кривой y = x 2 и прямые y = 0 и y = 4 вокруг оси O y .
Раствор. Имеем:
Контрольные вопросы
Рассмотрим криволинейную трапецию, ограниченную осью Ох, кривой у = f (х) и двумя прямыми: х = а и х = b (рис. 85).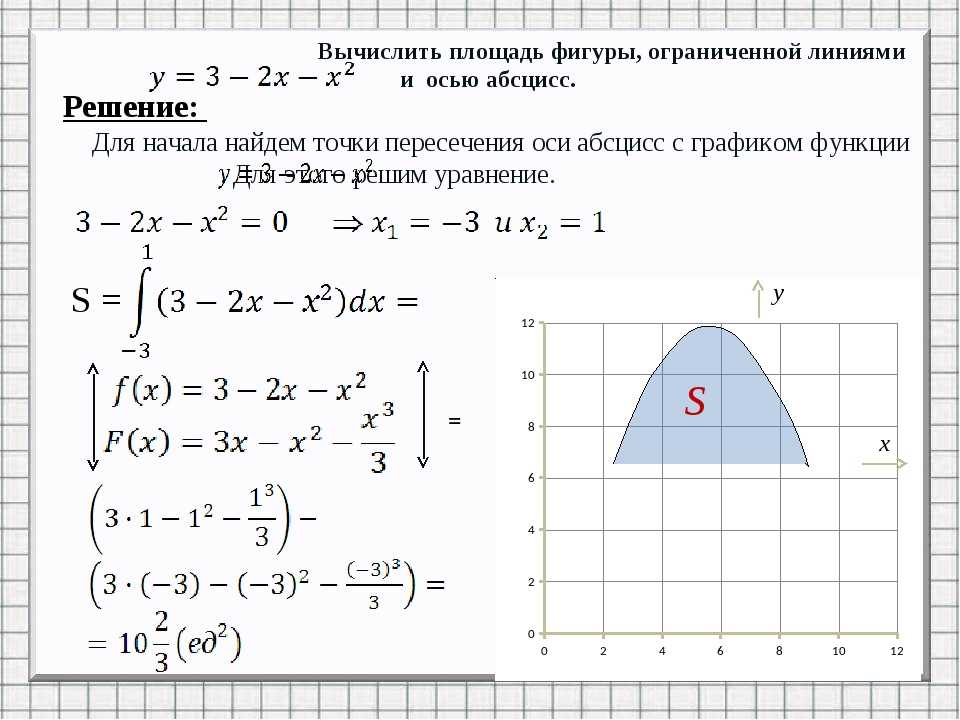 Возьмем произвольное значение x (только не a и не b). Зададим ей приращение h = dx и рассмотрим полосу, ограниченную прямыми AB и CD, осью Ox и дугой BD, принадлежащей рассматриваемой кривой. Эту полосу будем называть элементарной полосой. Площадь элементарной полосы отличается от площади прямоугольника ACQB на криволинейный треугольник BQD, а площадь последнего меньше площади прямоугольника BQDM со сторонами BQ = =h= dx) QD=Ay и площадь равна hAy = Ay dx. С уменьшением стороны h сторона Du также уменьшается и одновременно с h стремится к нулю. Следовательно, площадь БКДМ бесконечно мала второго порядка. Площадь элементарной полосы есть приращение площади, а площадь прямоугольника ACQB, равная AB-AC==/(x)dx>, есть дифференциал площади. Поэтому находим саму площадь, интегрируя ее дифференциал. В пределах рассматриваемого рисунка независимая переменная l: изменяется от а до b, поэтому искомая площадь 5 будет равна 5 = \f (x) dx. (I) Пример 1. Вычислить площадь, ограниченную параболой у — 1 -х*, прямыми Х = — Fj-, х = 1 и осью О* (рис.
Возьмем произвольное значение x (только не a и не b). Зададим ей приращение h = dx и рассмотрим полосу, ограниченную прямыми AB и CD, осью Ox и дугой BD, принадлежащей рассматриваемой кривой. Эту полосу будем называть элементарной полосой. Площадь элементарной полосы отличается от площади прямоугольника ACQB на криволинейный треугольник BQD, а площадь последнего меньше площади прямоугольника BQDM со сторонами BQ = =h= dx) QD=Ay и площадь равна hAy = Ay dx. С уменьшением стороны h сторона Du также уменьшается и одновременно с h стремится к нулю. Следовательно, площадь БКДМ бесконечно мала второго порядка. Площадь элементарной полосы есть приращение площади, а площадь прямоугольника ACQB, равная AB-AC==/(x)dx>, есть дифференциал площади. Поэтому находим саму площадь, интегрируя ее дифференциал. В пределах рассматриваемого рисунка независимая переменная l: изменяется от а до b, поэтому искомая площадь 5 будет равна 5 = \f (x) dx. (I) Пример 1. Вычислить площадь, ограниченную параболой у — 1 -х*, прямыми Х = — Fj-, х = 1 и осью О* (рис. y\ u003d sin jc, заключенный между двумя соседними точками пересечения с осью Ox (например, между началом координат и точкой с абсциссой i). Обратите внимание, что из геометрических соображений ясно, что эта площадь будет в два раза больше площади предыдущего примера. Однако проведем расчеты: i 5= | s\nxdx=[-cosx)*—cosi-(-cos0)=1+1=2. o Действительно, наше предположение оказалось справедливым. Пример 4. Вычислить площадь, ограниченную синусоидой и осью Ох на одном периоде (рис. 88). Предварительные рас-фигурные суждения предполагают, что площадь получится в четыре раза больше, чем в пр. 2. Однако проделав вычисления, получим «i G, * i S — \sin x dx = [- cos x] 0 = = — cos 2n — (-cos 0) = — 1 + 1 = 0. Этот результат требует уточнения. Для пояснения сути дела вычисляем также площадь, ограниченную той же синусоидой y = sin l: и осью Ох в пределах от l до 2n. Применяя формулу (I), получаем Таким образом, мы видим, что эта площадь оказалась отрицательной. Сравнивая его с площадью, рассчитанной в упр.
y\ u003d sin jc, заключенный между двумя соседними точками пересечения с осью Ox (например, между началом координат и точкой с абсциссой i). Обратите внимание, что из геометрических соображений ясно, что эта площадь будет в два раза больше площади предыдущего примера. Однако проведем расчеты: i 5= | s\nxdx=[-cosx)*—cosi-(-cos0)=1+1=2. o Действительно, наше предположение оказалось справедливым. Пример 4. Вычислить площадь, ограниченную синусоидой и осью Ох на одном периоде (рис. 88). Предварительные рас-фигурные суждения предполагают, что площадь получится в четыре раза больше, чем в пр. 2. Однако проделав вычисления, получим «i G, * i S — \sin x dx = [- cos x] 0 = = — cos 2n — (-cos 0) = — 1 + 1 = 0. Этот результат требует уточнения. Для пояснения сути дела вычисляем также площадь, ограниченную той же синусоидой y = sin l: и осью Ох в пределах от l до 2n. Применяя формулу (I), получаем Таким образом, мы видим, что эта площадь оказалась отрицательной. Сравнивая его с площадью, рассчитанной в упр.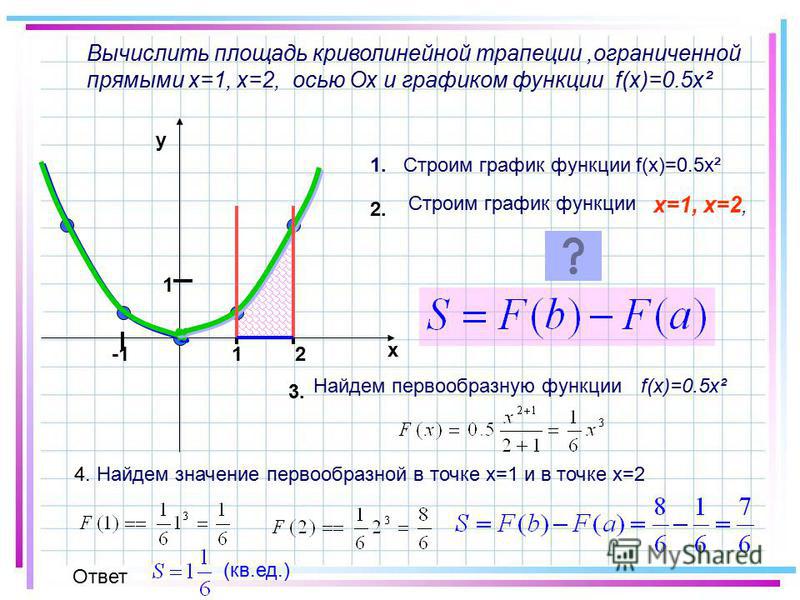 x = [замена:
x = [замена:
] =
Следовательно, несобственный интеграл сходится и его значение равно .
Глава V
Глава VГлава В
ОПРЕДЕЛЕННО ИНТЕГРАЛ
5.1 Определенный интеграл как предел суммы
5.1.1 Интегральная сумма: Пусть функция f ( x ) быть определенным на интервале a х б, и а = х 0 < х 1 < < x н .= б ан произвольное разбиение этого интервала на n подинтервалов (рис. 37). Сумма вида
где
называется интегралом сумма функции f ( х ) на ( а, б ) . Геометрически говоря, S n является
алгебраическая площадь ступенчатой фигуры (рис.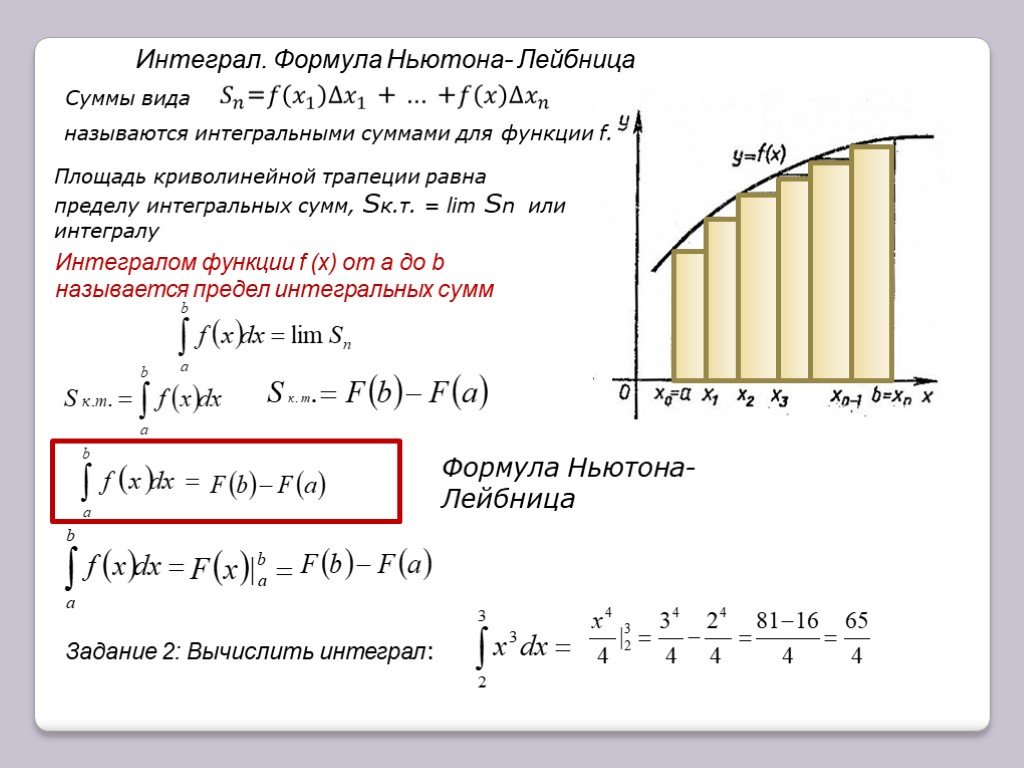 37).
37).
5.1.2 Определенный интеграл : Предел суммы S n , при условии, что количество подразделений n стремится к бесконечность и самый большой из них, D x и , к нулю, называется определенным интегралом функция f ( x ) в пределах от x = a от до x = b, т. е.
Если функция f ( x )
непрерывная на ( а , б ) , интегрируема на [ а , b ], т. е. предел (2) существует и не зависит от
режим разбиения интервала интегрирования [ и , b ] на подинтервалы и не зависит от выбора
точки x i в этих подинтервалах.
С геометрической точки зрения определенный интеграл (2) есть
алгебраическая сумма площадей фигур, составляющих
криволинейной трапеции aABb, , в которой площади
части, расположенные над осью x , являются положительными, а те
ниже оси x- отрицательны
(рис.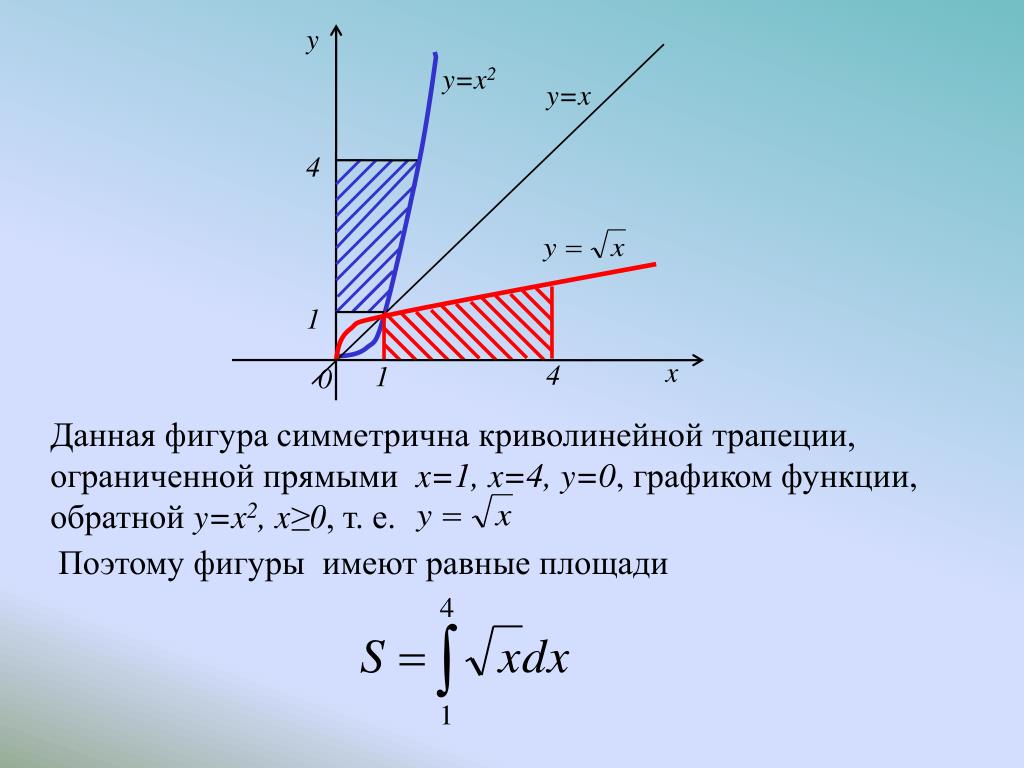 37).
37).
Определения интегральных сумм и определенных интегралы естественным образом обобщаются на случай отрезка [ а, b ] , где a > b.
Пример 1. Составление интегральной суммы S n для функции
на отрезке [1, 10], разделив интервал в n равные части и выбор точек x i которые совпадают с левыми концами подинтервалов [ x i , х я+1 ]. Найдите предел
Решение: У нас есть D x i = (10 — 1)/ n = 9/ n и x i = x i = x 0 + i D x i = 1 + 9 i / n , откуда f ( x i )
= 1 + 1 + 9 i / n = 2 + 9 i / n (Рис.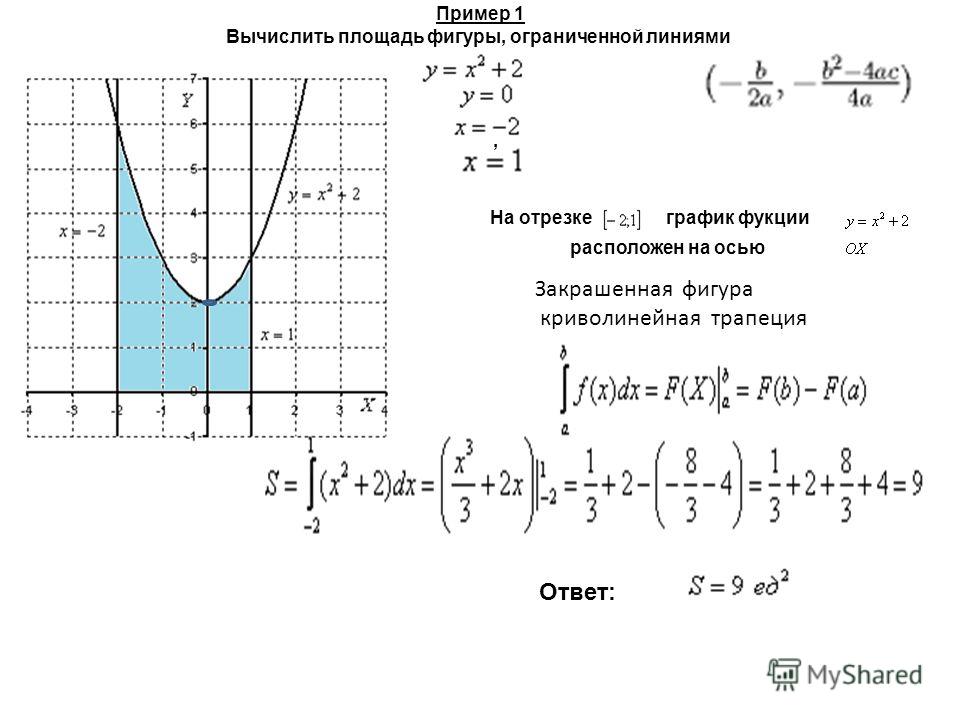 38)
38)
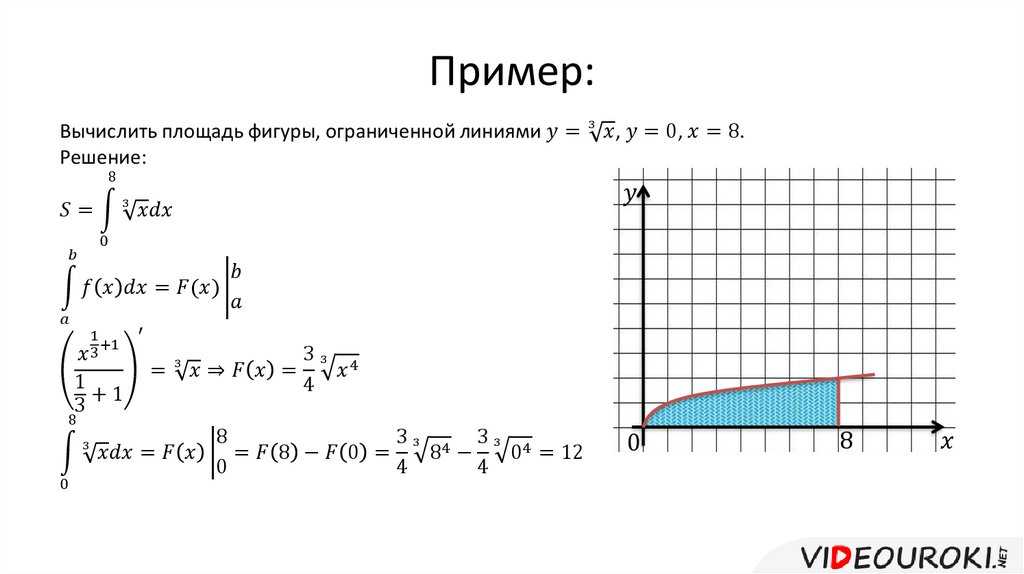
Пример 2: Найти площадь ограничен дугой параболы y = x , x -ось и ординаты x= 0 , x = a ( a > 0).
Решение: Раздел основание a в n равные части D x = a / n . Выбор значения функции в начале каждого подинтервал, у нас есть
Площади прямоугольников получаются умножение каждого y k по основанию D x = a / n (рис. 39). Суммируя, получаем площадь ступенчатой фигуры
Используя формулу суммы квадратов целые числа
находим
и, переходя к пределу,
УПРАЖНЕНИЯ 1501 — 1507
Оцените следующие определенные интегралы, рассматривая их как пределы соответствующих интегральных сумм:
Советы и ответы 1501 — 1507
5. 2 Вычисление определенных интегралов с помощью
Неопределенные интегралы
2 Вычисление определенных интегралов с помощью
Неопределенные интегралы
5.2.1 Определенный интеграл с переменной верхней лимит: . Если функция f ( t ) непрерывна на отрезке [ a , b ], то функция
— антипроизводная от . функция f ( x ), т. е.
5.2.2 Формула Ньютона-Лейбница: . Если F’ ( x ) = f ( x ) , , то
Антипроизводная F ( x ) это вычисляется путем нахождения неопределенного интеграла
Пример 1. Найти интеграл
Решение:
УПРАЖНЕНИЯ 1508 — 1545
Советы и ответы 1508 — 1545
5. 3.1 Интегралы от неограниченных функций: Если функция f ( x ) не ограничена в любом
окрестность точки c интервала [ a,b ]
и является непрерывным для a x < с и с < х б,
то по определению пишем
3.1 Интегралы от неограниченных функций: Если функция f ( x ) не ограничена в любом
окрестность точки c интервала [ a,b ]
и является непрерывным для a x < с и с < х б,
то по определению пишем
Если пределы в правой части (1) существуют и конечны, говорят, что несобственный интеграл сходится , иначе это расходится. Когда c = a или c = b, определение соответственно упрощается.
Если есть непрерывная функция F ( x ) на [ a , b ] такие, что F ‘( x ) = f ( x ), когда x c ( обобщенный антипроизводная ) , затем
Если f ( x ) F ( x ) когда a x ~ J ~ b и
сходится, то интеграл (1) тоже сходится ( сравнение проверка ) .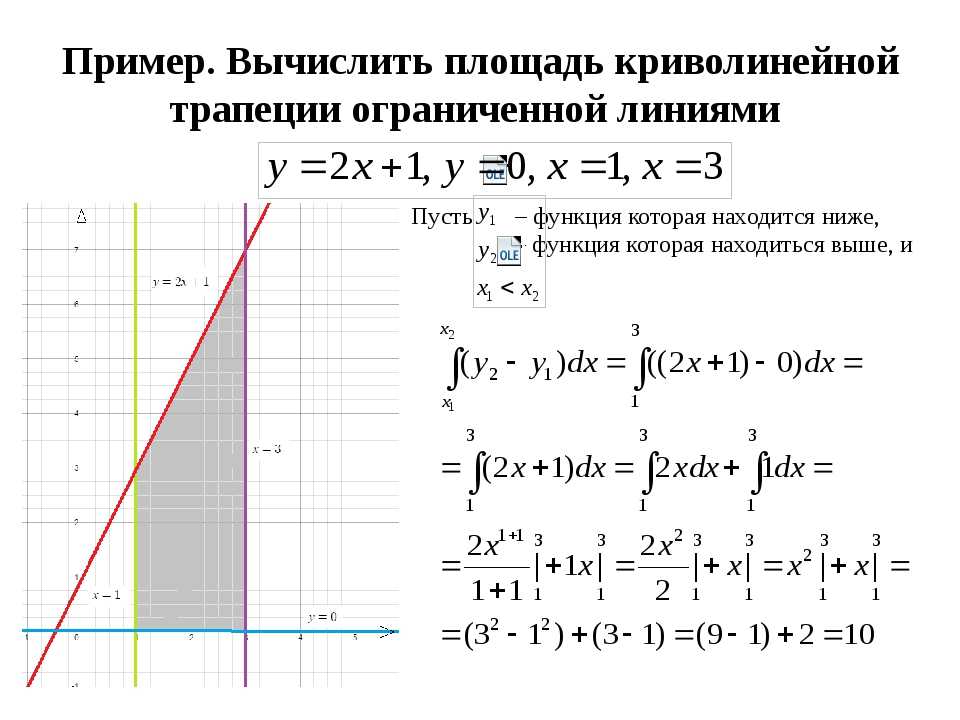
Если f ( x ) 0 и
как х c , то а) интеграл (1) сходится для m < l, б) интеграл (1) расходится на м л.
5.3.2. Интегралы с бесконечными пределами: . Если функция f ( x ) непрерывна когда a x < , то мы предполагаем, что
и, в зависимости от наличия конечного предел или нет в правой части, соответствующий интеграл равен говорят, что сходятся или расходятся.
Аналогично,
Если f ( x ) F ( x ) и интеграл
сходится, то сходится и интеграл (3).
Если f ( x ) 0 и
как х , то а) Интеграл (3) сходится на м > 1, б) для м<л Интеграл (3) расходится на м 1.
Пример 1.
и интеграл расходится.
Пример 2.
Пример 3. Проверка сходимости вероятности встроенный
Решение: Ставим
Первый из двух интегралов справа сторона не несобственная, а вторая сходится, так как e -x е -х при х л и
откуда сходится интеграл (4).
Пример 4. Проверка сходимости интеграла
Решение: Когда x + , мы имеем
Так как интеграл
сходится, интеграл (5) аналогично
сходится.
Пример 5: Тест сходимость эллиптического интеграла
Решение: Точка разрыв подынтегральной функции равен х = л . Применение Лагранжа формула , находим
где x < x 1 < 1, откуда для х 1,
Так как интеграл
тоже самое (6).
УПРАЖНЕНИЯ 1546 — 1575
Оцените неправильные интегралы или установите их расхождение
): 1546.~. D Проверка сходимости интегралов
1574*. Докажите, что интеграл Эйлера от первый вид ( бета-функция )
сходится, когда p > 0 и q > 0.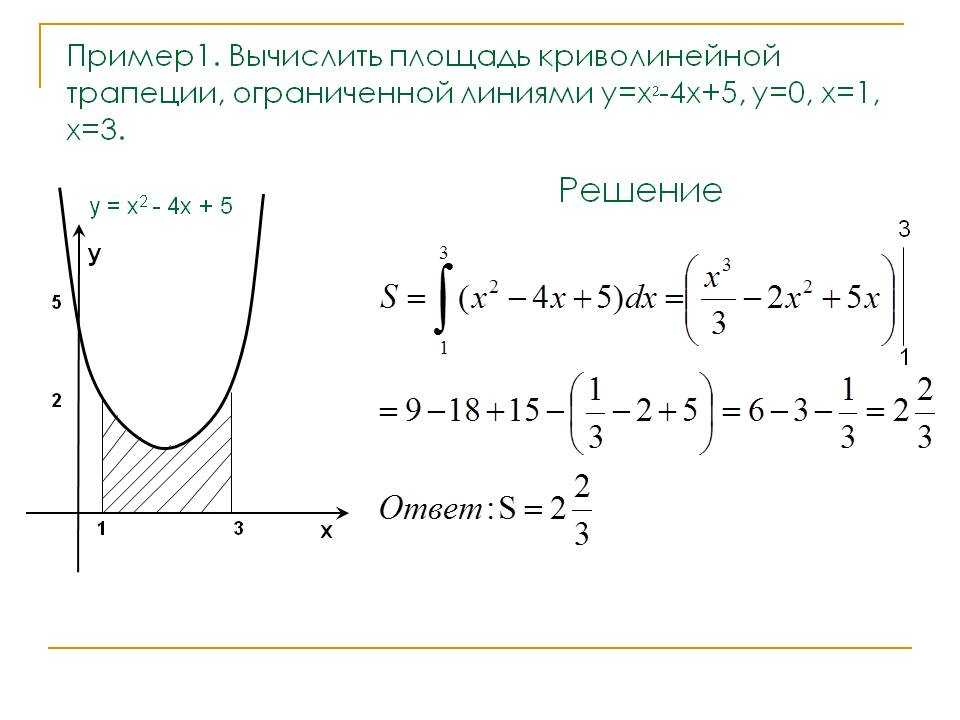
1575*. Докажите, что интеграл Эйлера от второй вид ( гамма-функция )
сходится к р > 0.
Советы и ответы 1546 — 1575
5.4 Замена переменной в определенном интеграле
Если функция f ( x ) непрерывна более a x b и x = j ( t ) является a функция, непрерывная вместе со своей производной j ‘ ( t ) свыше а т б , где а = j ( а ) и б = й ( б ), и f [ j ( t )] определенная и непрерывная на интервале a t b , затем
Пример 1.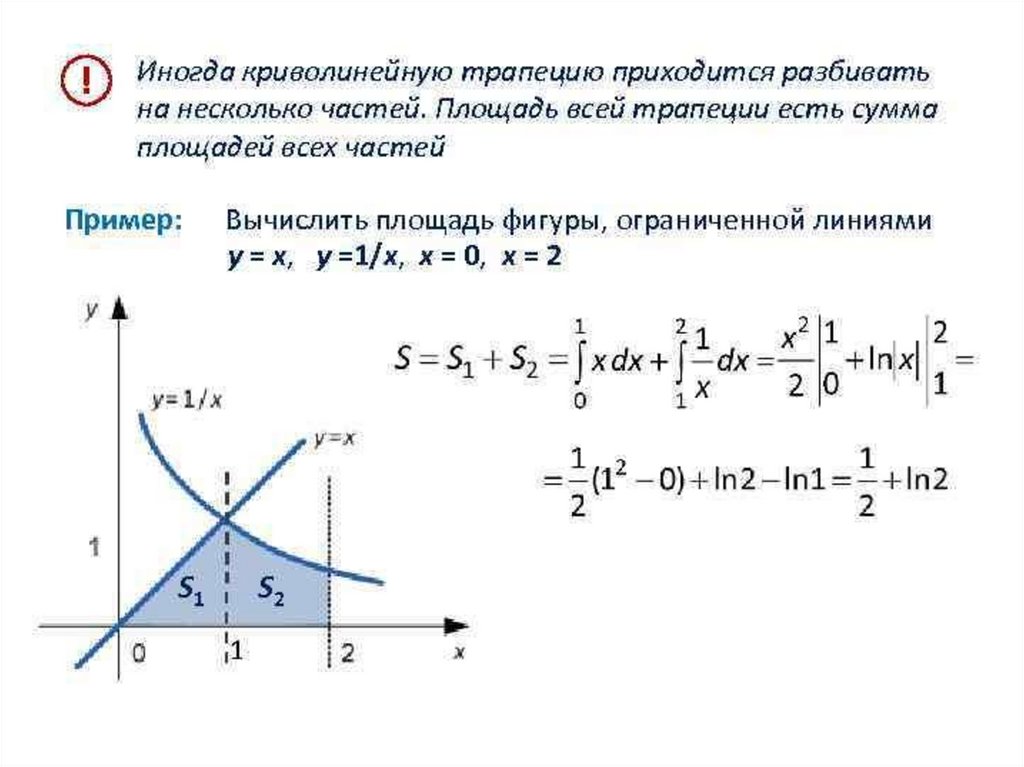 Найти
Найти
Раствор. Ставим
Тогда t = arsin x / a и, следовательно, можно взять a = arsin 0 = 0, б = арсин л = p /2, откуда
. Упражнения 1576 — 1598
1576. Можно заменить х = cos т изготавливаться в Интеграле
Преобразование определенных интегралов с помощью указанные замены:
Найдите целочисленную линейную замену
в результате чего лимиты интегрирование будет равно 0 и 1 соответственно. Применение указанных замены, вычислить интегралы:
Оценить с помощью соответствующих замен интегралы:
Вычисление интегралов:
1595.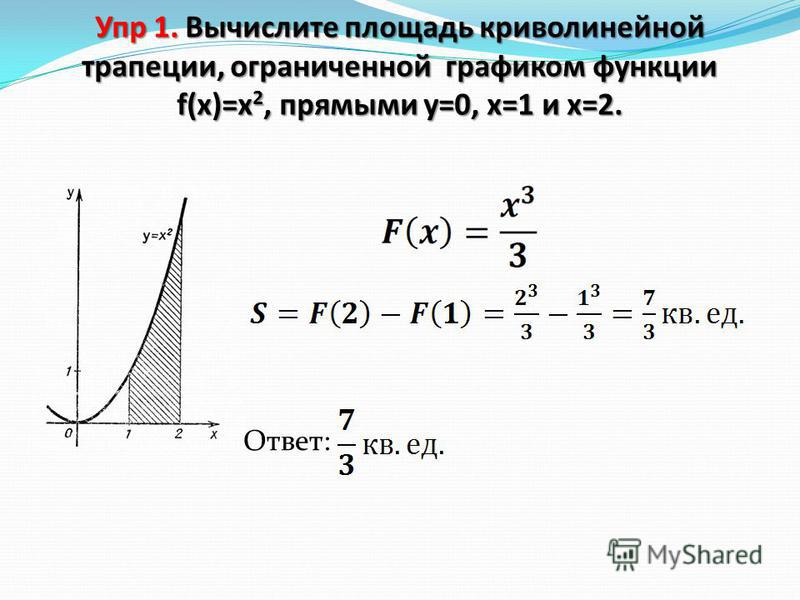 Докажите, что если f ( x )
— четная функция, то
Докажите, что если f ( x )
— четная функция, то
Но, если ф ( х ) нечетная функция, то
Советы и ответы 1576 — 1598
5,5 Интеграция с помощью Детали
Если функции u ( x ) и v ( x ) непрерывно дифференцируемы на отрезке [a, b ] , затем
УПРАЖНЕНИЯ 1599 — 1609
Вычисление интегралов по частям:
Советы и ответы 1599 — 1609
5,6 Теорема о среднем значении
5. 6.1
Оценка интегралов: . Если ф ( х ) Ф ( х )
для a x b , затем
6.1
Оценка интегралов: . Если ф ( х ) Ф ( х )
для a x b , затем
Если f ( x ) и j ( x ) непрерывный для a x b и, кроме того, j ( x ) 0, затем
, где m — наименьшее, а M — наименьшее. наибольшее значение функции f ( x ) в интервале [ а , б ].
В частности, если j ( x ) = l, затем
Неравенства (2) и (3) можно заменить, соответственно эквивалентными равенствами
где c и x точно числа, лежащие между a и b.
Пример 1. Оценить интеграл
Решение: Поскольку 0 sin x 1 , имеем
5. 6.2
Среднее значение функции: 90 130
Номер
6.2
Среднее значение функции: 90 130
Номер
называется средним значением функция f ( x ) на интервале a x b.
УПРАЖНЕНИЯ 1610 — 1622
1610*. Определите признаки следующих интегралы без их вычисления:
Советы и ответы 1510 — 1622
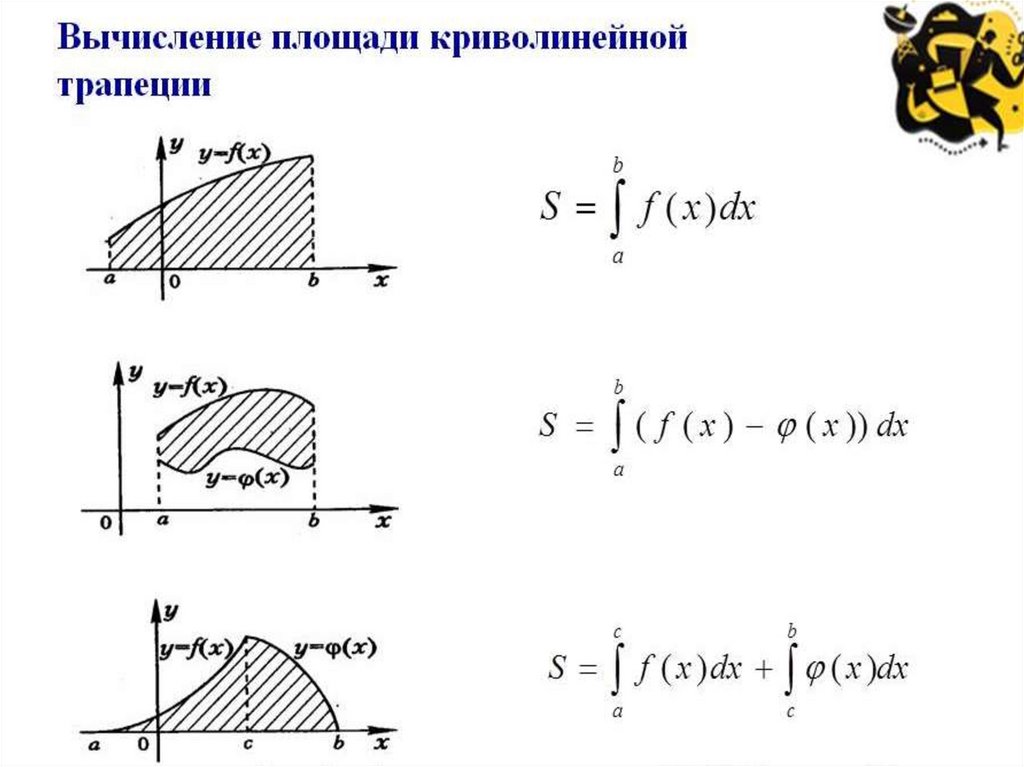
5.7 Площади плоских фигур
5.7.1 Площадь в прямоугольных координатах : . Если непрерывная кривая определена в прямоугольные координаты по уравнению
площадь криволинейной
трапеция, ограниченная этой кривой двумя вертикальными линиями в
баллы x = a и x = b и сегментом оси x а х б (рис.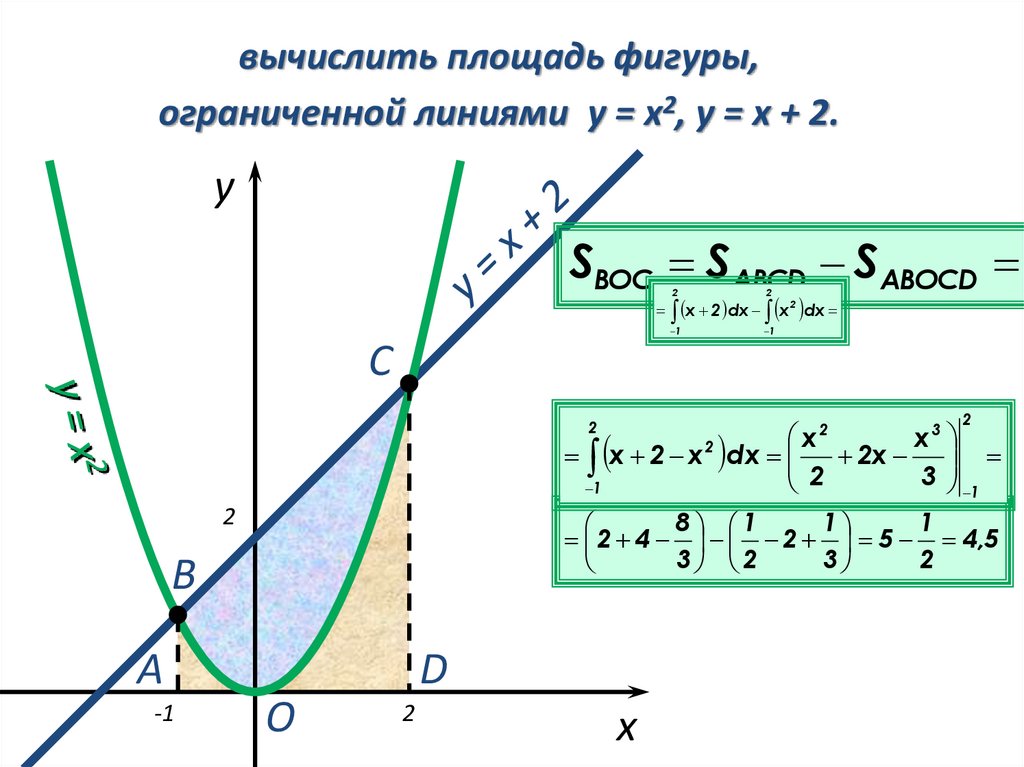 40), определяется как
40), определяется как
Пример 1. Вычислите площадь, ограниченную параболой y = x /2 , прямые линии x = 1 и x = 3 , и ось x (Рис.41).
Решение: В площадь выражается интегралом
Пример 2. Оценить площадь ограничен кривой x = 2 — y — y и осью y- (рис. 42).
Решение: Роли координатные оси здесь поменялись местами, поэтому искомая площадь выражается интегралом
где пределы интегрирования г 1 = — 2 и y 2 = l — ординаты точки пересечения кривой y- с осью .
В более общем случае, если область S ограничен двумя непрерывными кривыми y=f 1 ( x , y = f 2 ( x ) и двумя вертикальными
строки x=a и x=b, где f 1 ( x ) ф 2 ( х )
когда а х b (рис.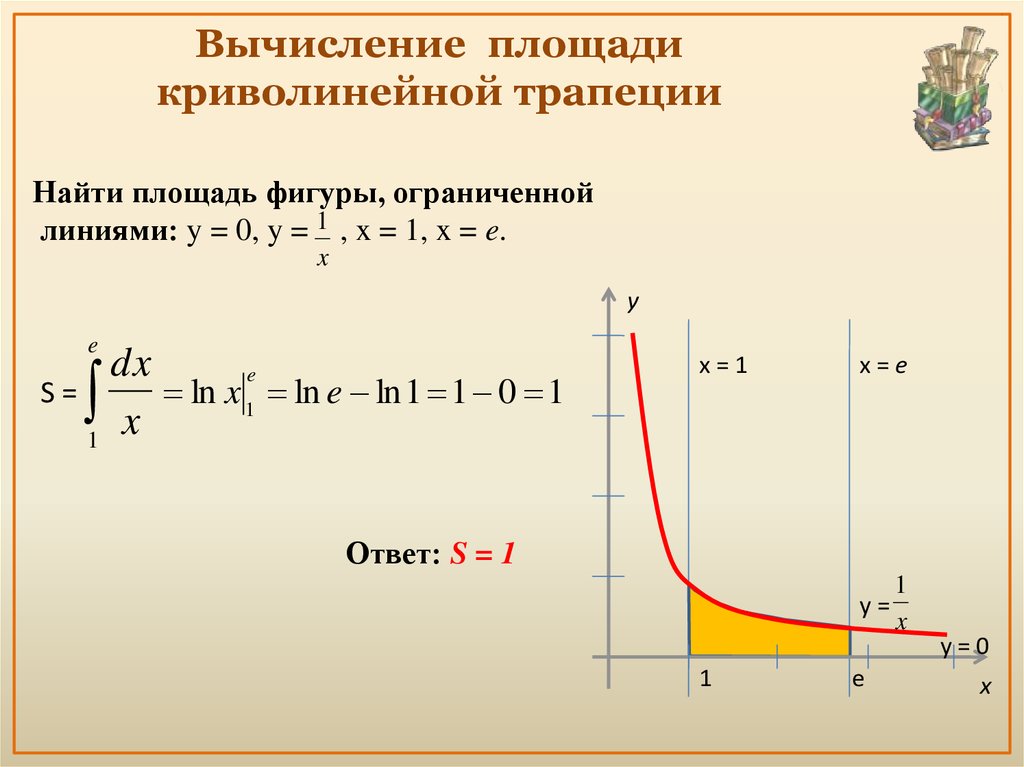 43), тогда у нас будет
43), тогда у нас будет
Пример 3. Оценка площади S содержится между кривыми
Решение: Решение уравнений (3} одновременно находим пределы интегрирования х 1 = — 1 и х 2 = л. По (2) получаем
Если кривая определяется уравнениями в параметрическая форма: x = j ( t ) , y = y ( t ), площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикальные линии ( x = a и x = b ) и сегмент x — ось задается интегралом
где т 1 и t 2 определяются из уравнений
Пример 4. Найти
площади эллипса (рис.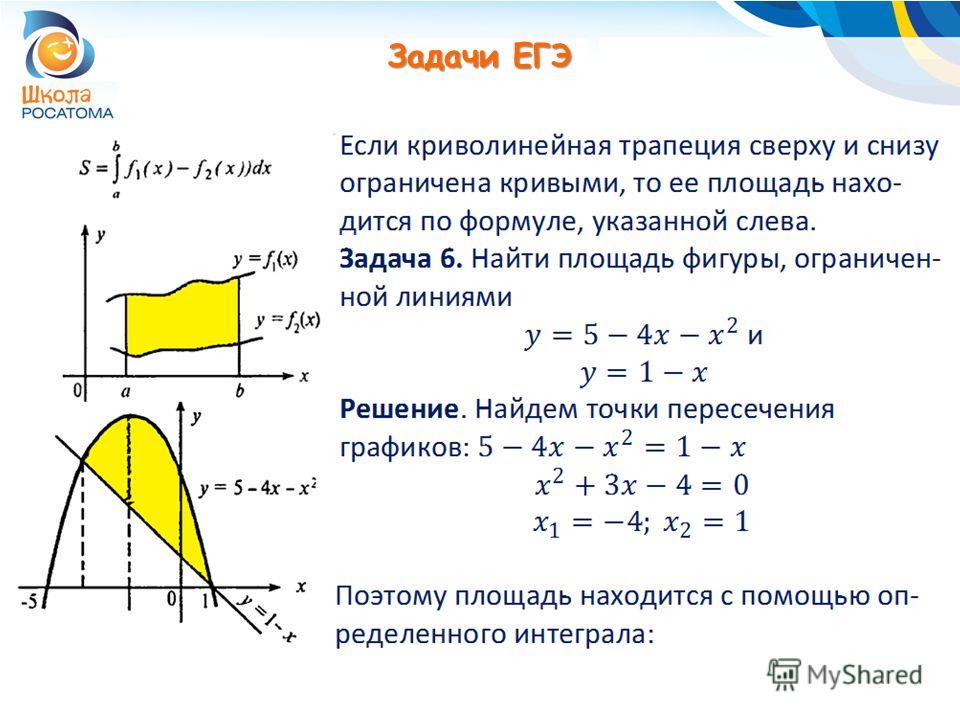 45) с помощью его параметрического
уравнения
45) с помощью его параметрического
уравнения
Решение: Из-за симметрии, достаточно вычислить площадь одного квадрант, а затем умножьте результат на четыре. Если мы сначала установим х = 0 в уравнении x = a cos t и затем x = a, получаем пределы интегрирования t 1 = р /2 и т 2 = 0 , откуда
и, следовательно, S = p аб.
5.7.2 Район в полярных координатах: . Если кривая — это , определенная в полярных координатах как уравнение r = f ( j ), тогда площадь сектора АОБ (рис. 46), ограничен дугой кривой и двумя радиус-векторами OA и ОВ, , которые соответствуют значениям j 1 = a и j 2 = b, дается интегралом
Пример 5.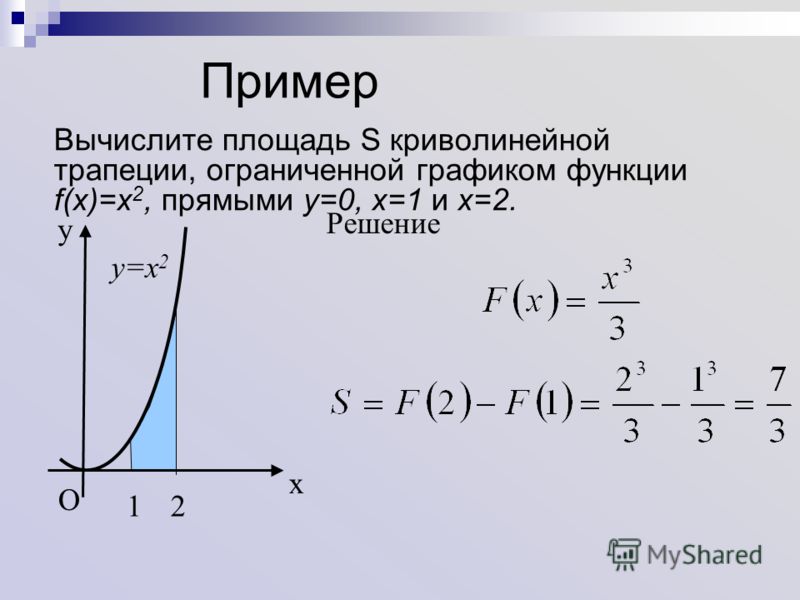 Найти
область внутри лемниската Бернулли
Найти
область внутри лемниската Бернулли
Раствор. В силу симметрии кривой, мы определяем первый квадрант требуемая площадь:
УПРАЖНЕНИЯ 1623 — 1664
Советы и ответы 1623 — 1664
5,8 Дуга Длина из a Кривая
5.8.1. Длина дуги в прямоугольных координатах: Длина дуги с кривой y=f ( x ), содержится между двумя точками с абсциссами x = a и x = б это
Пример 1. Найдите длину астроид x 2/3 + у 2/3 = а 2/3 (рис. 49).
Решение: Отличие уравнение астроиды, получаем
откуда для длины дуги четверть астроида:
5. 8.2 Длина дуги представленной кривой
параметрически: . Если кривая
представлены уравнениями в параметрической форме х= j ( т ), у = y ( t ), тогда длина дуги s кривой задана
к
8.2 Длина дуги представленной кривой
параметрически: . Если кривая
представлены уравнениями в параметрической форме х= j ( т ), у = y ( t ), тогда длина дуги s кривой задана
к
где т 1 и т 2 значения параметра, соответствующие оконечности дуги.
Пример 2. Найдите длину одна дуга циклоиды (рис. 50)
Решение: У нас есть
Пределы интегрирования т 1 = 0 и t 2 = 2 p соответствуют крайние точки дуги циклоиды.
Если кривая определяется уравнением r = f ( j ) В полярных координатах длина дуги с
, где a и b значения полярного угла в крайних точках дуги.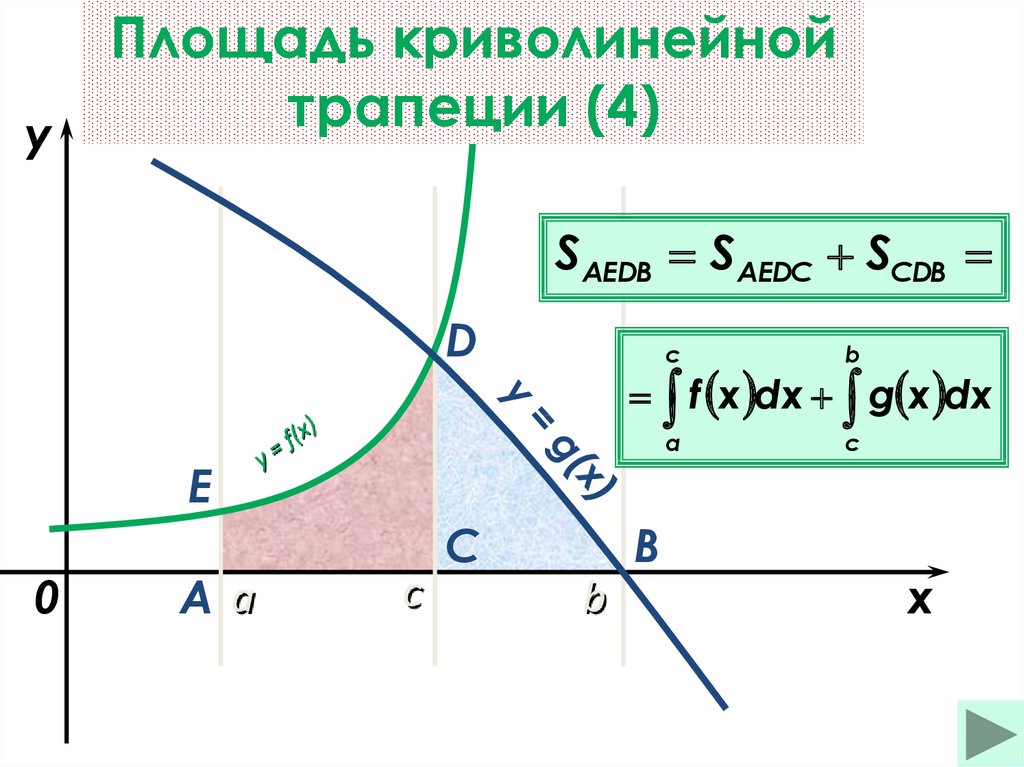

 .. — Учеба и наука
.. — Учеба и наука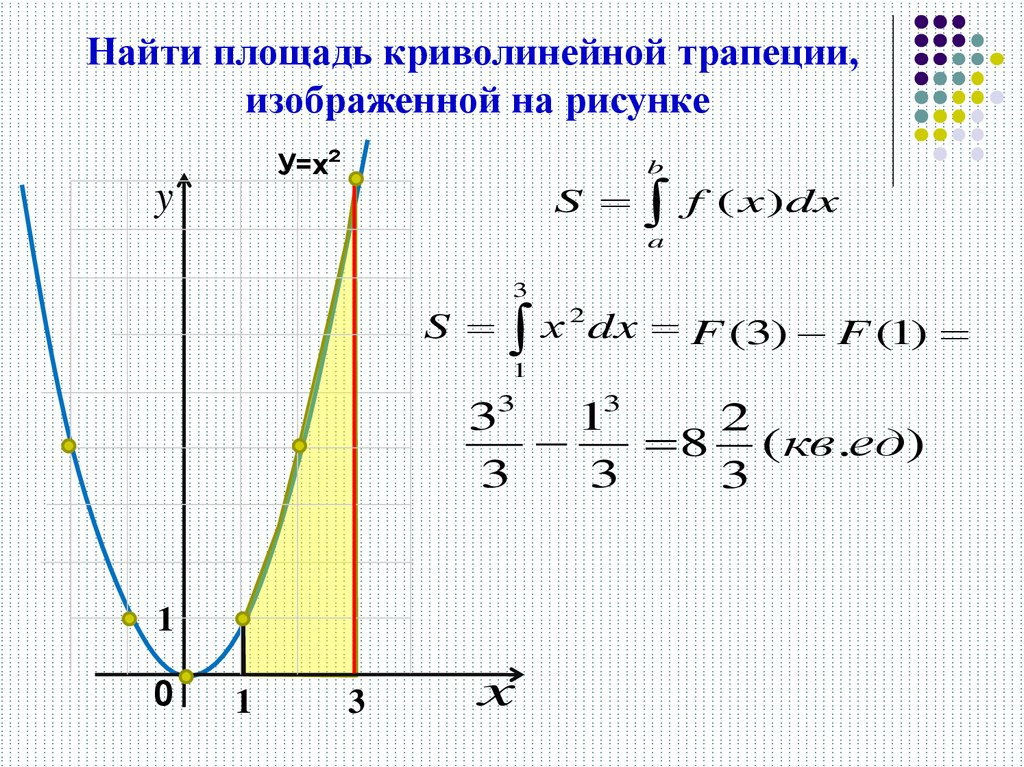 02.18
02.18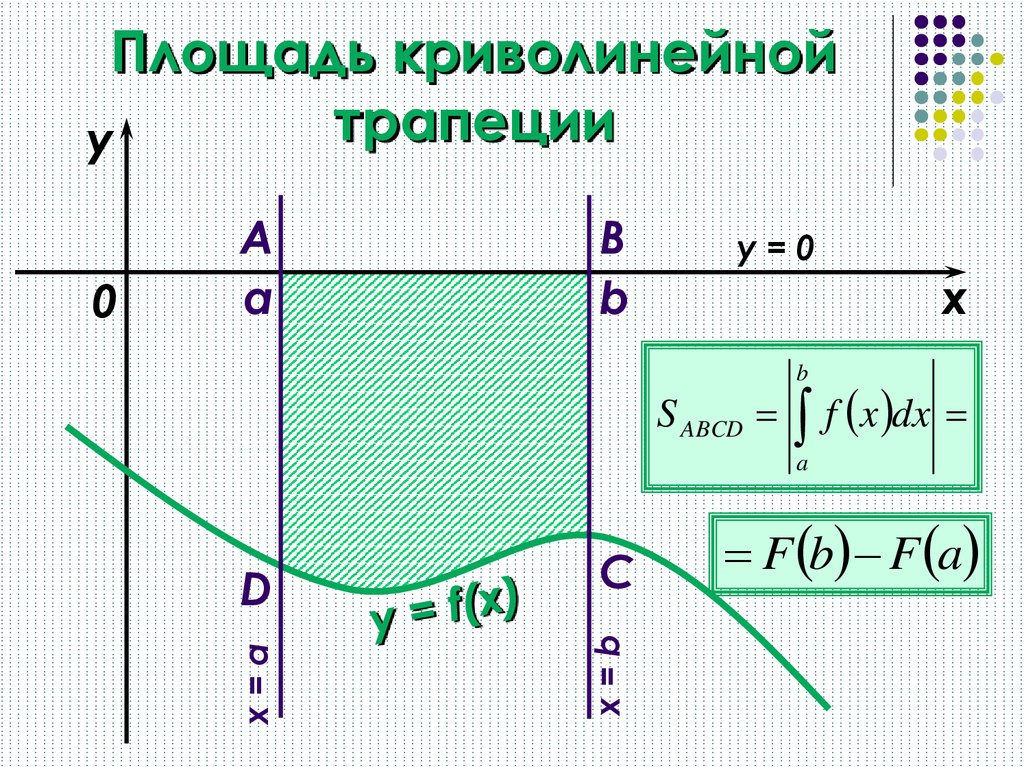 02.18
02.18