Вычислить площадь области ограниченной линиями: Вычислить площадь фигуры, ограниченной линиями

Площадь фигуры ограниченной линиями с примерами решения

 

Расчет площади фигуры является, пожалуй, одной из самых сложных задач теории площадей. В школьной геометрии учат находить области базовых геометрических фигур, таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т. д. Однако часто приходится иметь дело с вычислением площадей более сложных форм. Именно при решении таких задач очень удобно использовать интегральное исчисление.

Пример 1.

Найти площадьфигуры,офаниченной линиями Построить чертеж.

Решение:

Найдем точки пересечения параболы и прямой. Приравняем правые части уравнений, задающих функции, и решим полученное уравнение

Фигура, площадь которой нужно найти, изображена на рисунке. Используя приведенную формулу, получим

Ответ: площадь фигуры равна 13,5 кв. ед.

Вычисление площадей плоских фигур в полярной системе координат

Пусть плоская фигура ограничена линией и лучами

тогда ее площадь можно найти по формуле

Если же фигура ограничена линиями и лучами как на рисунке, то площадь фигуры равна

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Пример 2.

Найти площадь фигуры, ограниченной линией, заданной в полярной системе координат уравнением

Решение:

Ответ: площадь данной фигуры 9,5л кв. ед.

Пример З.

Найти площадь фигуры, ограниченной линиями, заданными в полярной системе координат

Решение:

Фигура, площадь которой требуется найти, показана на рисунке.

Найдем точки пересечения окружности и кардиоиды. Решая совместно данные уравнения, получим точки

По рисунку видно, что фигура симметрична. Вычислим площадь половины фигуры, учитывая, что она в свою очередь разделена на части и (см. рисунок).

Ответ: площадь фигуры

Возможно вам будут полезны данные страницы:

Метод неопределенных коэффициентов

Вычислить площадь фигуры ограниченной линиями

Правило Лопиталя: пример решения

Признак Лейбница

Пример 4.

3.

Найти площадь фигуры, ограниченной линиями

Решение:

Из чертежа (см. рис. 7) видно, что искомая площадь криволинейного треугольника равна разности двух площадей: каждая из которых находится по геометрическому смыслу определенного интеграла. Решая систему

получаем, что точка В пересечения прямой и кривой имеет координаты (2;4)

Тогда Окончательно,

Данная задача может быть также решена другим способом. По определению определенного интеграла

Если на то интеграл численно равен площади

криволинейной трапеции, ограниченной кривой и прямыми

Другими словами, в данном случае площадь вычисляется посредством проецирования криволинейной трапеции на ось ординат). Теперь возвращаясь к задаче нашего примера, можем записать:

Если криволинейная трапеция ограничена кривой, заданной в параметрическими уравнениями

прямыми и и отрезком оси то ее площадь вычисляется по формуле где и определяются из равенства

Пример 4.

5.

1. Вычислить площадь фигуры, ограниченной линиями: и

Решение:

Решая систему уравнений, находим абсциссы точек пересечения эллипса и параболы Каждое из уравнений разрешаем относительно и учетом симметрии области получаем:

Для вычисления первого интеграла применяем подстановку

Второй интеграл вычисляется непосредственно.

Ответ:

Пример 4.6

Вычислить площадь области, ограниченной эллипсом

Решение:

В силу симметричности эллипса относительно координатных осей вычислим часть области, лежащей в первой четверти, кода и следовательно По формуле а) вычисления площади находим

Пример 4.7

Вычислить площадь области, ограниченной лемнискатой

Решение:

Принимая во внимание симметрию линии относительно полярной оси, получаем:

Пример 4.8

Вычислить площадь фигуры, ограниченной прямыми и кривыми

Решение:

Так как максимум функции достигается в точке и равен а функция на отрезке то

Пример 4.

9

Вычислить площадь фигуры, лежащей в первом квадранте, ограниченной линиями и осью

Решение:

Функция

составной график которой ограничивает трапецию сверху, является непрерывной на промежутке

Площадь криволинейной трапеции равна

Пример 5.0

Найти площадь астроиды

Решение:

Запишем уравнение астроиды в параметрическом виде

Здесь удобнее вычислить сначала Отсюда

4.I. Вычисление площадей

Внимательно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 193—196. Разберите примеры, приведенные в п° 196. При решении задач с геометрическим содержанием всегда старайтесь сопроводить решение чертежом.

I. Уравнения кривых заданы в декартовой системе координат.

443. Вычислить площадь фигуры, ограниченной дугой параболы, прямыми X=I9 х — А и отрезком

оси абсцисс.

Решение. В теоретическом курсе показано, что площадь криволинейной трапеции численно равна определенному интегралу

В данном случае (рис. 5) криволинейная трапеция ABDC9 площадь которой мы вычисляем, ограничена параллельными прямыми AB и CD, отрезком прямой AC и отрезком кривой линии BD.

Искомая площадь равна:

444. Вычислить площадь трапеции, ограниченной дугой параболы и отрезком прямой х = 2.

Решение. Из рисунка 6 видно, что искомая площадь расположена симметрично относительно оси абсцисс и, следовательно,

445. Вычислить площадь фигуры, ограниченной кривыми;

Решение. На рисунке 7 изображена фигура, площадь которой мы должны вычислить. Как видно из рисунка, площадь фигуры OBMAO можно представить как разность двух площадей (пл. OBMPO и OAMPU1 где MP — перпендикуляр, опущенный из точки M на ось Ох).

Найдем координаты точки Al. Решая систему уравнений

получимСледов ат ельн о,

Легко видеть, что данную задачу можно решить и другим путем. Искомую площадь можно представить в виде разности двух площадей—пл. OAMNO и пл. OBMNO (MN — перпендикуляр, опущенный из точки M на ось Oy):

Тогда

Ясно, что значение площади OBMAO не зависит от способа ее вычисления.

446. Вычислить площадь фигуры, ограниченной петлей кривой:

Решение. Из уравнений кривой видно, что она расположена симметрично относительно оси Ох. Следовательно, можно легко вычислить половину искомой площади (см. рис. 8).

Рекомендуем провести самостоятельно подробное исследование кривой.

Записав уравнение кривой в виде легко найдем точки пересечения кривой с осью Ох, положив у = 0. Мы получим.Учитывая все сказанное, окончательно найдем:

447. Вычислить площадь фигуры, ограниченной синусоидой wИ осью Ох, если

Вся площадь петли равна:

Решение. Из рисунка 9 видно, что искомая площадь на сегментеРасположена над осью Ох, а на сегменте

Под осью Ох. Следовательно, достаточно вычислить площадь, ограниченную полуволной синусоиды на отрезке|, и удвоить полученный результат:

448. Найти всю площадь фигуры, ограниченной кривыми, прямыми X = 3, X = —2 и осью Ох.

Решение. Из рисунка 10 видно, что искомая площадь может быть представлена как сумма площадей:

где BA и MN—перпендикуляры, опущенные из точек В и Al на ось Ох.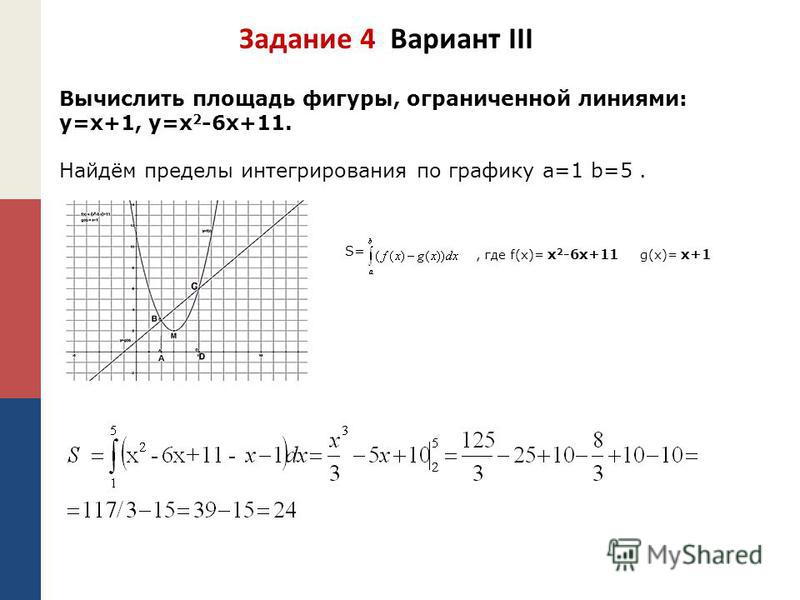

Определим координаты точек В, С, М, Р. Для этого решим следующие системы уравнений:

Решая систему (I) уравнений, найдем координаты точек В и M : В (I, 2), M {— I, 2).

Решая систему (2) уравнений, найдем координаты точки С : С (3, К».

Решая систему (3) уравнений, найдем координаты точки P : Р(— 2, 5).

Найдем теперь значения промежуточных площадей:

Отсюда

449. Найти площадь фигуры, ограниченной линиями:

450. Найти площадь фигуры, ограниченной линиями:

451. Найти площадь фигуры, ограниченной параболами:

452. Найти площадь фигуры, ограниченной линиями:

453. Найти площадь фигуры, ограниченной линиями:

454. Найти площадь «Ьигуоы. огоаниченной линиями:

455. Найти площадь круга:

456. Найти площадь эллипса

457. Найти площадь, заключенную между кривыми

458. Найти площадь фигуры, ограниченной гипоци-лоидой

459. Найти площадь фигуры, ограниченной гиперболой

И прямой

460.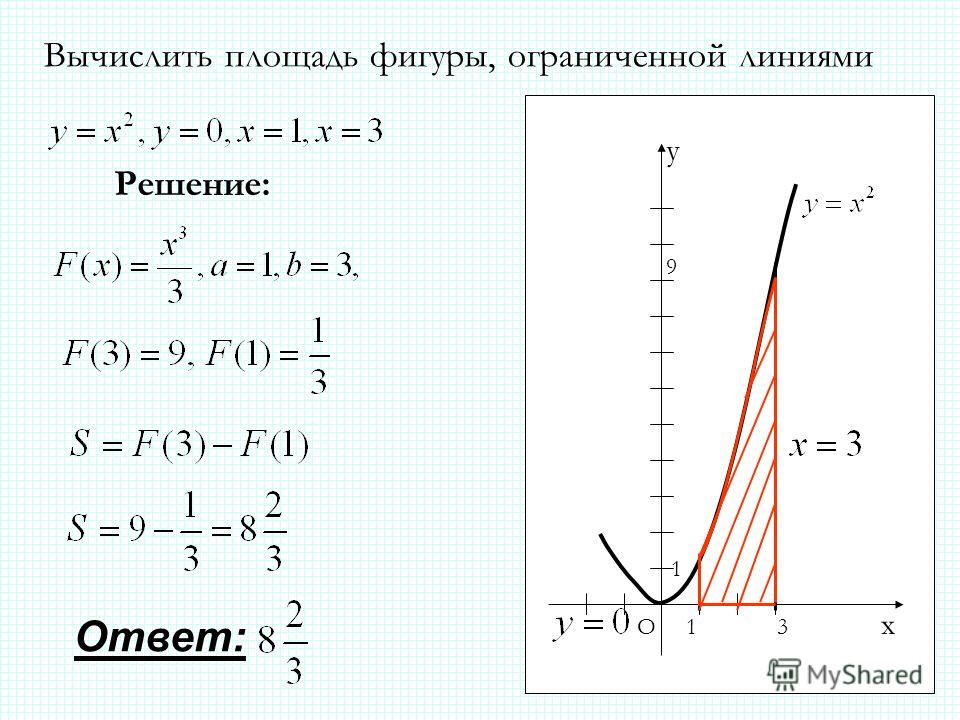 Вычислить площадь фигуры, заключенной между параболой, осями координат и прямой х=3,5.

461. Найти площадь фигуры, заключенной между кривыми:

462. Найти площадь частей эллипса отсеченных гиперболой

463. Найти площадь фигуры, ограниченной кривой

464. Найти площадь фигуры, заключенной между кривыми

2. Кривые заданы параметрическими уравнениями. Если кривая, ограничивающая площадь плоской фигуры, задана параметрическими уравнениями:

где функцииНепрерывны вместе со своими про

изводными наТо для вычисления площади

плоской фигуры следует в определенном интеграле произвести замену переменной:

465. Вычислить площадь, ограниченную эллипсом!

Решение. Эллипс расположен симметрично относительно обеих осей (рис. Последовательно, можно вычислить сначала• часть площади данной фигуры. Вычислим площадь той части плоской фигуры, которая расположена в первом квадранте:

Найдем пределы интегрирования для переменной t из условий:

Имеем:

466. Найти площадь фигуры, ограниченной астроидой:

PsP ш е н и е. Искомая площадь изображена на рисунке 12. Вычислим сначала площадь тсй части плоской фигуры, которая расположена в первом квадранте, это будет

Рис. 12.

часть всей искомой площади. Найдем пределы интегрирования для переменной / из условий:

Следовательно,

467. Вычислить площадь, ограниченную одной аркой циклоиды:И осью Ох.

Решение. Из рисунка 13 видно, что при изменении параметра t от 0 до 2л точка (ху у) обегает всю арку циклоиды, причем х изменяется в промежутках от 0 до 2т. Следовательно,

Вся площадь, ограниченная астроидой, равна:

о

468. Вычислить площадь четверти круга: x = 2cos t, y = 2sint.

469. Найти площадь, ограниченную эволютой эллипса:

(.Эволютой кривой называется геометрическое место её центров кривизны. Эволютой эллипса является деформированная астроида.)

470. Найти площадь, ограниченную кардиоидой:

х = a(2cost — cos 21), у = a (2sin/— sin 2/).

3. Кривые заданы в полярной системе координат. Из

теоретического курса известно, что площадь S1 ограниченная неподвижным полярным радиусом г0, подвижным полярным радиусом г и кривой г — /(ф), может быть вычислена по следующей формуле:

<Р> Ч, г

S = — j J/-2 Лр = J — j /(<р)]2<*Ф.

90

471. Вычислить площадь, ограниченную первым витком спирали Архимеда г — а<р (рис. 14).

Решение. Найдем пределы интегрирования. Первый виток спирали образуется при изменении параметра t от О до 2зх. Следовательно,

,12*

D3 Д

472. Найти площадь, ограниченную одним лепестком кривой г = a sin 2<р.

Решение. Пределы интегрирования для <р найдем из условий:

О < 2<р<я.

Отсюда

и, следовательно,

473. Вычислить площадь, ограниченную кривой г = = a cos ф.

Решение. Данная кривая—окружность радиуса у,

проходящая через полюс, расположенная симметрично относительно полярной оси. Эго легко увидеть, если перейти к декартовым координатам. (Проделайте это самостоя-

а2 I

тельно.) Тогда S = я — — = —я;а2.

7 4 4

Можно было найти искомую площадь, используя полярное уравнение данной кривой. Пределы для q> найдут* ся из условия cos ф> 0, следовательно,

1C

T

S = J a® cos2 ф dq> =

TC TC

—< ф < —.

2 Y 2

Таким образом, имеем:

474. Вычислить площадь OAB (см. рис. 15), ограниченную полярными радиусамиг, = OA и r2 = OB и дугой логарифмической спирали

Решение. Будем считать, что полярному радиусу г, соответствует полярный угол фг, а полярному радиусу г2 соответствует полярный угол ф2. Тогда

475. Найти площадь петли листа Декарта:

Решение. Перейдем к полярным координатам с помощью известных соотношений:

Уравнение данной кривой в полярных координатах примет вид:

откуда

На получим

откуда

, в этом промежутке изменения полярного

углаф кривая опишет петлю. ПриИли

знаменатель стремится к нулю и, следовательно, р —» оо. Это значит, что существует асипмтота данной кривой. Найдем ее, пользуясь исходным уравнением кривой в лекап-товых координатах. Разделив обе части равенства

Из полученного уравнения кривой видно, чтоПри

HO

и, следовательно, таким образом,

Уравнение асимптоты:

Подставляя вместо k и b найденные значения, получим искомое уравнение асимптоты данной кривой:

Для построения данной кривой совместим полюс с началом декартовых координат и будем считать положительное направление оси Ox совпадающим с направлением полярной оси. Составим таблицу значений

Соединяя теперь плавной кривой полученные точки, получим петлю данной кривой (рис. 16).

Найдем площадь, ограниченную петлей листа Декарта. Из геометрических соображений видно, что полярный угол <р

изменяется от 0 до.Tаким образом, находим:

476. Вычислить площадь круга

477. Найти площадь, ограниченную петлей лемнискаты>

Построив предварительно данную кривую.

478. Найти площадь, ограниченную кривой:

P = a cos 4<р.

479. Найти площадь, ограниченную одним лепестком кривой:

P = a cos 2ф.

480. Найти площадь фигуры, ограниченной вторым витком спирали Архимеда р = аф и отрезком полярной оси, соединяющим концы первого и второго витков (см. рис. 14).

481. Найти площадь, ограниченную улиткой Паскаля:

P = 2а (2 cos ф).

482. Вычислить площадь, ограниченную кардиоидой:

P = а (I — cos ф).

< Предыдущая		Следующая >

Объяснение урока: Площадь между кривой и линией

В этом объяснении мы узнаем, как применить интегрирование, чтобы найти площадь между кривой функции и горизонтальной или вертикальной прямой линией.

Нахождение площади под кривой функции — очень полезный метод, имеющий множество применений.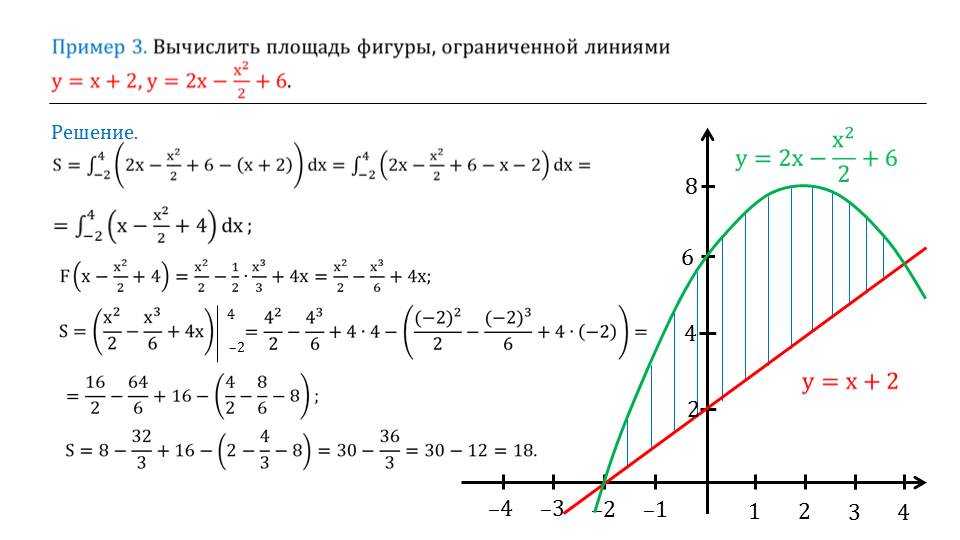 Например, нахождение площади под графиком скорость-время объекта между двумя моментами времени дает общее расстояние, пройденное за это время.

Площадь под прямолинейным графиком вычислить достаточно просто. Например, рассмотрим площадь, ограниченную кривой функции, 𝑓(𝑥)=4𝑥+7, и осью 𝑥 между двумя точками, 𝑥=𝑎 и 𝑥=𝑏.

Замкнутую площадь можно найти по стандартной формуле площади трапеции: площадь трапеции=𝑝+𝑞2⋅ℎ, где 𝑝 и 𝑞 — длины двух параллельных сторон, а ℎ — расстояние между ними. Применяя эту формулу к замкнутой области на графике, наши две параллельные стороны имеют длины 𝑓(𝑎) и 𝑓(𝑏), а высоту ℎ=𝑏−𝑎. Следовательно, мы имеем площадь трапеции = 𝑓(𝑎)+𝑓(𝑏)2⋅(𝑏−𝑎).

При 𝑓(𝑥)=4𝑥+7 площадь трапеции=4𝑎+7+4𝑏+72⋅(𝑏−𝑎)=(2𝑎+2𝑏+7)(𝑏−𝑎)=2𝑎𝑏−2𝑎+2𝑏− 2𝑎𝑏+7𝑏−7𝑎=2𝑏+7𝑏−2𝑎+7𝑎.

Этот подход прекрасно работает, когда у нас есть линейная функция 𝑓(𝑥), и мы можем использовать простую геометрию, но он не будет работать для более сложных функций. Например, если скорость объекта не меняется с постоянной скоростью (т. е. его ускорение непостоянно), то график скорость-время не будет прямой линией, и таким образом мы не сможем легко найти площадь.

Для общей кривой функции 𝑦=𝑓(𝑥) площадь между кривой и осью 𝑥 и между вертикальными линиями 𝑥=𝑎 и 𝑥=𝑏 определяется основной теоремой исчисления .

Мы определяем новую функцию 𝐴(𝑥) как площадь между кривой, 𝑓(𝑥), осью 𝑥 и вертикальными линиями 𝑥=0 и 𝑥=𝑥, общим значением 𝑥.

Увеличивая верхнюю границу площади на небольшую величину, d𝑥, приращение функции площади d𝐴 определяется выражением dd𝐴=𝑓(𝑥)𝑥.

Перестановка дает изменение в 𝐴, деленное на изменение в 𝑥: dd𝐴𝑥=𝑓(𝑥).

Это производная от 𝐴 относительно 𝑥. Исходная функция площади 𝐴(𝑥), площадь под кривой между 0 и 𝑥, определяется инвертированием операции дифференцирования в обеих частях уравнения. В правой части это дает первообразную , 𝐹, 𝑓: 𝐴(𝑥)=𝐹(𝑥), где dd𝐹𝑥=𝑓(𝑥).

Теперь рассмотрим точно такой же сценарий, но оценивая площадь под кривой между двумя конкретными значениями 𝑥, 𝑥=𝑎 и 𝑥=𝑏.

Площадь 𝛽 под кривой и между 𝑥=𝑎 и 𝑥=𝑏 определяется выражением 𝛽=𝐹(𝑏)−𝐹(𝑎).

Вычисление первообразной 𝐹 в двух точках 𝑥=𝑎 и 𝑥=𝑏 и получение разности называется определенным интегралом между 𝑎 и 𝑏 и обозначается 𝐹(𝑏)−𝐹(𝑎)=𝑓(𝑥)𝑥 .d

Следовательно, площадь 𝛽=𝐹(𝑏)−𝐹(𝑎) под кривой и между 𝑥=𝑎 и 𝑥=𝑏 определяется выражением 𝛽=𝑓(𝑥)𝑥=𝐹(𝑏)− 𝐹(𝑎).d

Правая часть часто обозначается 𝐹(𝑏)−𝐹(𝑎)=[𝐹(𝑥)],, где квадратные скобки с 𝑎 внизу справа и 𝑏 на вверху справа указано, что 𝐹(𝑥) оценивается при 𝑥=𝑎 и 𝑥=𝑏, а затем берется разница 𝐹(𝑏)−𝐹(𝑎). Произвольная константа интегрирования +𝐶 опускается для определенного интеграла, поскольку она одинакова как для 𝐹(𝑎), так и для 𝐹(𝑏) и, следовательно, сокращается.

Теорема: основная теорема исчисления

Площадь, заключенная между кривой 𝑓(𝑥), осью 𝑥 и двумя вертикальными линиями 𝑥=𝑎 и 𝑥=𝑏, определяется как aread=𝑓(𝑥) 𝑥=𝐹(𝑏)−𝐹(𝑎),, где 𝐹 — первопроизводная 𝑓. Правая часть часто обозначается 𝐹(𝑏)−𝐹(𝑎)=[𝐹(𝑥)],, где квадратные скобки с 𝑎 внизу справа и 𝑏 вверху справа указывают, что 𝐹(𝑥) оценивается при 𝑥=𝑎 и 𝑥=𝑏, тогда берется разница 𝐹(𝑏)−𝐹(𝑎).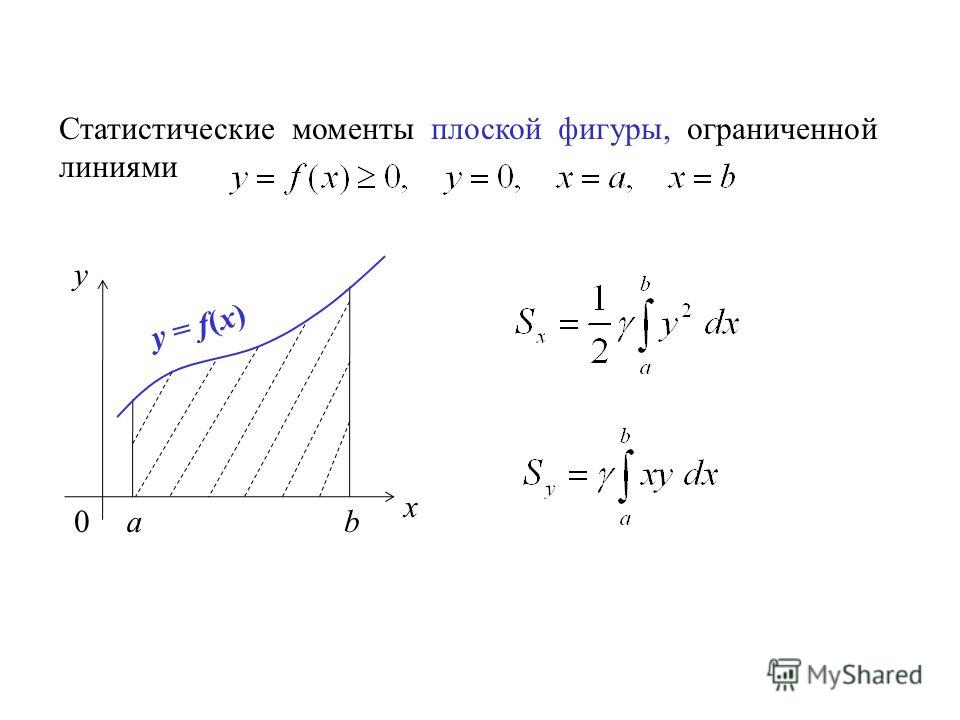

Вернемся к функции из предыдущего примера, 𝑓(𝑥)=4𝑥+7, и на этот раз мы будем использовать интегрирование, чтобы найти площадь под кривой между двумя точками 𝑥=𝑎 и 𝑥=𝑏, как показано на диаграмме ниже .

Используя формулу площади под кривой, 𝑓(𝑥), между 𝑥=𝑎 и 𝑥=𝑏, aread=𝑓(𝑥)𝑥=𝐹(𝑏)−𝐹(𝑎)=[𝐹(𝑥) ].

В этом случае имеем 𝑓(𝑥)=4𝑥+7, что дает площадь=4𝑥+7𝑥.

Интегрирование по 𝑥 дает площадь=2𝑥+7𝑥. 

Оценив при 𝑥=𝑏 и 𝑥=𝑎 и взяв разность, площадь=2𝑏+7𝑏−2𝑎+7𝑎.

Этот результат точно согласуется с результатом, полученным ранее для площади трапеции . Однако огромное преимущество использования интегрирования для нахождения площади под кривой заключается в том, что оно распространяется на гораздо более сложные функции, для которых иначе было бы невозможно вычислить площадь.

Давайте рассмотрим пример использования интегрирования для нахождения площади под более сложной кривой.

Пример 1. Нахождение площади под кривой квадратичной функции

Пусть 𝑓(𝑥)=2𝑥+3. Определите площадь, ограниченную кривой 𝑦=𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=−1 и 𝑥=5.

Ответ

Может быть полезно набросать площадь, которую нас просят рассчитать. В данном случае это площадь, ограниченная прямыми 𝑥=−1 и 𝑥=5 и кривой 𝑦=2𝑥+3.

Напомним, что площадь между кривой 𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=𝑎 и 𝑥=𝑏 задается определенным интегралом aread=𝑓(𝑥)𝑥=𝐹(𝑏)−𝐹( 𝑎),, где 𝐹 — первообразная 𝑓 такая, что dd𝐹𝑥=𝑓(𝑥). Подставляя в заданную функцию 𝑓(𝑥)=2𝑥+3 и пределы 𝑥=−1 и 𝑥=5: aread=2𝑥+3𝑥.

Интегрирование по 𝑥 дает area= 23𝑥+3𝑥, и оценивая это между пределами 𝑥=−1 и 𝑥=5, получаем площадь квадрата единиц =23⋅5+3⋅5−23⋅(−1)+3(−1) =2503+15−−23−3=102.

Для некоторых функций существуют области, для которых кривая лежит ниже по оси 𝑥. По характеру того, как мы оцениваем площадь между кривой и 𝑥-осью, поскольку приращение d𝑥 всегда положительно, элемент площади dd𝐴=𝑓(𝑥)𝑥, конечно, будет отрицательным , если функция 𝑓(𝑥 ), в этот момент отрицательный.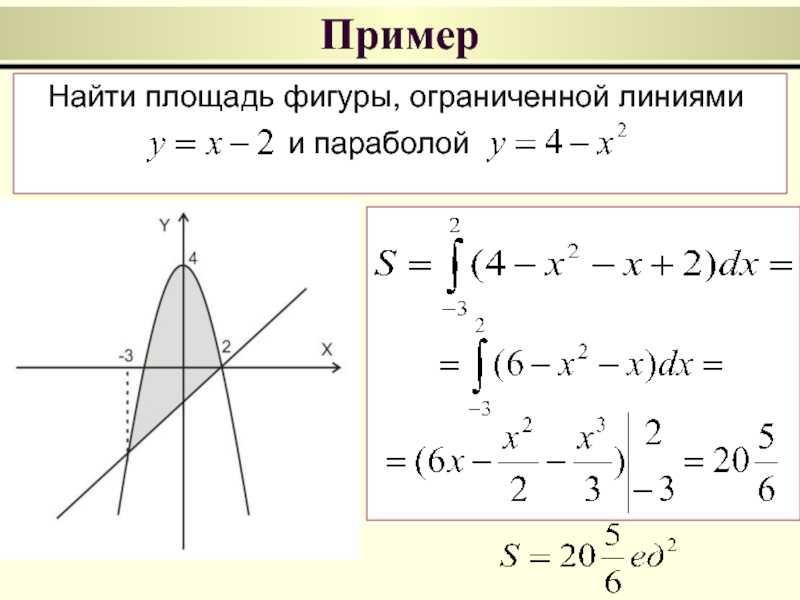

Следовательно, любая область, заключенная в ниже по оси 𝑥 кривой, будет оцениваться как минус . Поскольку площадь является строго положительной величиной, это часто решается путем взятия абсолютного значения определенного интеграла для каждой области.

Давайте рассмотрим пример того, как мы можем использовать интегрирование, чтобы найти площадь, ограниченную кривой ниже оси 𝑥.

Пример 2. Использование определенного интегрирования для нахождения площади между двумя линиями и ниже Горизонтальная ось

Показанная кривая 𝑦=1𝑥. Чему равна площадь заштрихованной области? Дайте точный ответ.

Ответ

Напомним, что площадь между кривой 𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=𝑎 и 𝑥=𝑏 задается определенным интегралом aread=𝑓(𝑥)𝑥=𝐹(𝑏 )−𝐹(𝑎), где 𝐹 — первообразная 𝑓 такая, что dd𝐹𝑥=𝑓(𝑥). Подставляя в заданную функцию 𝑓(𝑥)=1𝑥 и пределы 𝑥=−1 и 𝑥=−13: aread=1𝑥𝑥.

Интегрирование по 𝑥 дает arean=[|𝑥|]; мы помним, что натуральный логарифм ln(𝑥) не определен для отрицательных значений 𝑥, поэтому мы берем абсолютное значение.

Оценивая это между пределами 𝑥=−1 и 𝑥=−13: =|||−13|||−|−1|=3−0=−(3)≈−1,099().lnlnlnlnto3d. p.

Обратите внимание, что результат отрицательный. Это связано с тем, что площадь между кривой и 𝑥-осью составляет ниже 𝑥-оси. Взяв абсолютное значение, мы находим, что истинное значение для площадь заштрихованной области составляет ln(3)≈1,099 (до 3 д.п.) квадратных единиц.

Иногда вычисление истинного значения площади, ограниченной кривой, не так просто, как получение абсолютного значения определенного интеграла. Давайте рассмотрим пример, где нам нужно быть более осторожными с этим методом.

Пример 3: Использование определенного интегрирования для нахождения площади областей выше и ниже горизонтальной оси

На рисунке показан график функции 𝑓(𝑥)=2𝑥−8𝑥. Оцените площадь заштрихованной области.

Ответ

Напомним, что площадь между кривой 𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=𝑎 и 𝑥=𝑏 задается определенным интегралом aread=𝑓(𝑥)𝑥=𝐹(𝑏 )−𝐹(𝑎), где 𝐹 — первообразная 𝑓 такая, что dd𝐹𝑥=𝑓(𝑥).

В этом примере функция 𝑓(𝑥)=2𝑥−8𝑥 является нечетной функцией. То есть он совершенно антисимметричен относительно оси 𝑦, поэтому 𝑓(−𝑥)=−𝑓(𝑥). Это, в свою очередь, означает, что площадь между 𝑥=0 и любым значением 𝑥=𝑎 будет точно такой же, как площадь между 𝑥=−𝑎 и 𝑥=0. Однако при использовании определенного интегрирования для нахождения площади интеграл на одной стороне оси 𝑦 будет иметь напротив знака интеграла с другой стороны.

Это означает, что при интегрировании между двумя равными и противоположными значениями, как здесь, между −2 и +2, мы обнаружим, что интеграл на одной стороне оси 𝑦 уравновешивает интеграл на другой стороне, давая всего ноль: aread=2𝑥−8𝑥𝑥.

Интегрирование по 𝑥 дает area=12𝑥−4𝑥.

Теперь мы оцениваем четную функцию (т.е. , 𝑓(−𝑥)=𝑓(𝑥)) при двух равных и противоположных значениях перед взятием разности, поэтому результат будет равен нулю: площадь = 12⋅2−4⋅2−12⋅(−2)−4⋅ (−2)=8−16−(8−16)=0,

Однако ясно, что площадь полностью заштрихованной области не равна нулю.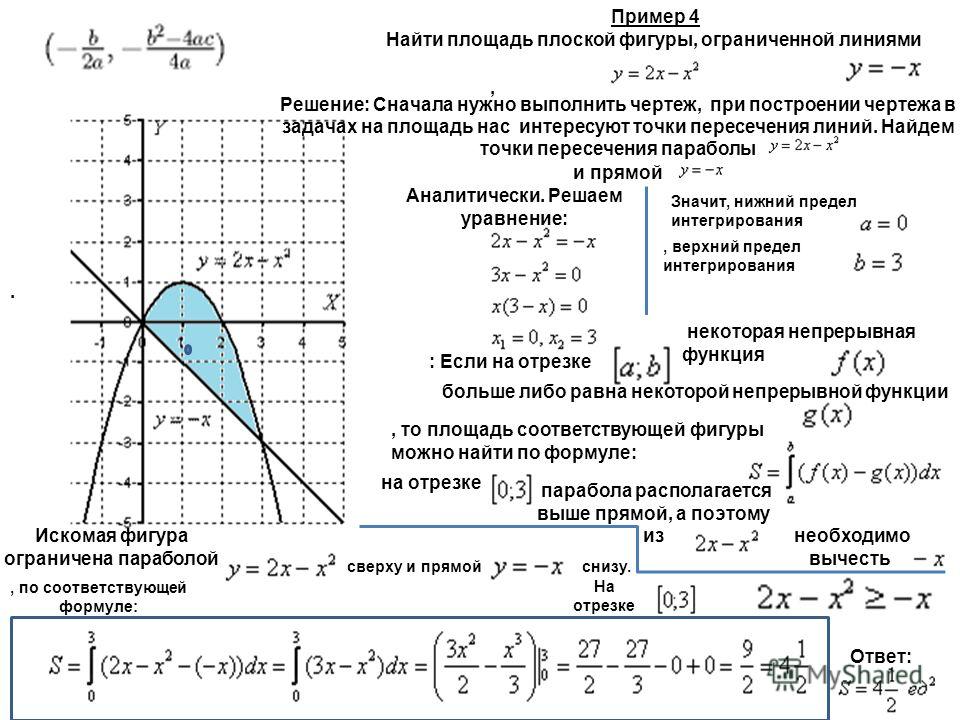 Чтобы исправить эту проблему, нам нужно оценить площадь каждой части заштрихованной области отдельно .

В этом примере у нас есть две отдельные области, окруженные кривой, 𝑓(𝑥), и осями 𝑥 и 𝑦.

Итак, нам нужно вычислить интеграл между 𝑥=−2 и 𝑥=0 и интеграл между 𝑥=0 и 𝑥=2 отдельно, взять абсолютное значение каждого интеграла, чтобы получить площадь, а затем сложить их вместе чтобы дать площадь полной заштрихованной области.

Для первой области площадь1=12𝑥−4𝑥=0−12⋅(−2)−4⋅(−2)=0−(8−16)=8. 

А для второй области: area2=12𝑥−4𝑥=12⋅2−4⋅2−0=8−16−0=−8.

Отрицательное значение ожидается, поскольку область между 𝑥=0 и 𝑥=2 находится ниже оси 𝑥. Взяв абсолютное значение, чтобы получить площадь: area2=|−8|=8.

Таким образом, общая площадь полностью заштрихованной области представляет собой сумму этих двух площадей: площадьплощадьплощадьквадратединицы=1+2=8+8=16.

Основная теорема исчисления, конечно, не ограничивается функциями независимой переменной (обычно 𝑥).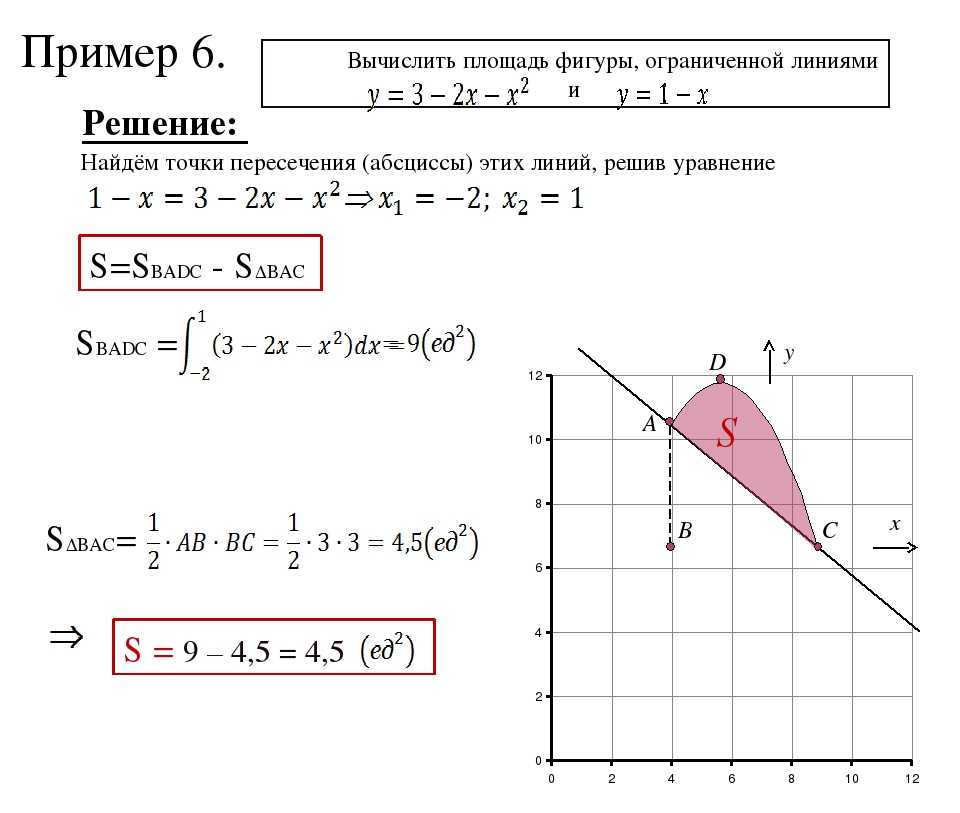 Его также можно использовать для нахождения площади, ограниченной функцией 𝑦.

Теорема: площадь, ограниченная кривой функции 𝑦

Площадь, заключенная между кривой 𝑓(𝑦), осью 𝑦 и двумя горизонтальными линиями 𝑦=𝑎 и 𝑦=𝑏, определяется выражением aread= 𝑓(𝑦)𝑦=𝐹(𝑏)−𝐹(𝑎),, где 𝐹 — первообразная 𝑓. Правая часть часто обозначается 𝐹(𝑏)−𝐹(𝑎)=[𝐹(𝑦)],, где квадратные скобки с 𝑎 внизу справа и 𝑏 справа вверху указывают, что 𝐹(𝑦) оценивается при 𝑦=𝑎 и 𝑦=𝑏, тогда берется разница 𝐹(𝑏)−𝐹(𝑎).

В нашем следующем примере искомая область ограничена функцией 𝑦 и двумя горизонтальными линиями.

Пример 4. Использование метода определенного интегрирования для нахождения площади между неявной функцией и двумя горизонтальными линиями

Найдите площадь, ограниченную графиком 𝑥=9−𝑦, осью 𝑦 и линиями 𝑦=−3 и 𝑦=3.

Ответ

Может быть полезно набросать площадь, которую нас просят рассчитать. В данном случае это площадь, ограниченная прямыми 𝑦=−3 и 𝑦=3 и кривой 𝑥=9−𝑦.

𝑥 является отрицательной квадратичной функцией от 𝑦, поэтому кривая представляет собой n-образную параболу вокруг оси 𝑥. Чтобы найти 𝑥-перехват, подставляем 𝑦=0 в уравнение функции и решаем его относительно 𝑥, что дает 𝑥=9.

Итак, кривая пересекает ось 𝑥 в точке 𝑥=9. Далее, чтобы найти 𝑦-пересечения кривой, подставляем 𝑥=0 в уравнение функции и решаем его относительно 𝑦, что дает 0=9−𝑦𝑦=±3.

Следовательно, кривая пересекает ось 𝑦 в точках 𝑦=3 и 𝑦=−3. Теперь у нас достаточно информации, чтобы нарисовать кривую.

Напомним, что площадь между кривой 𝑓(𝑥), осью 𝑥 и двумя прямыми 𝑥=𝑎 и 𝑥=𝑏 определяется определенным интегралом: aread=𝑓(𝑥)𝑥=𝑓(𝑏)−𝑓(𝑎), где 𝐹 — первообразная 𝑓 такая, что dd𝐹𝑥=𝑓(𝑥).

Однако в этом случае мы не можем просто перестроить функцию кривой для 𝑦 и проинтегрировать по 𝑥, так как площадь над осью 𝑥 равна площади под ней, и результат интегрирования будет нуль.

Если мы попытаемся действовать таким образом, мы начнем с 𝑦=±√9−𝑥, так, aread=±√9−𝑥𝑥. 

Проблема в данном конкретном случае заключается в том, что функция 𝑦=√9−𝑥 не соответствует уникальному значению 𝑦, поскольку квадратный корень может быть как положительным, так и отрицательным; поэтому невозможно узнать, какую область мы оцениваем.

В этом случае 𝑦=√9−𝑥 сопоставляет заданное значение 𝑥 с , как — положительный квадратный корень +√9−𝑥  , так и — отрицательный квадратный корень −√9−𝑥.

Извлечение положительного квадратного корня дает площадь, ограниченную кривой над осью 𝑥.

Поскольку мы изменили функцию на строго взаимооднозначную, теперь мы можем оценить эту площадь обычным способом с определенным интегралом: aread=+√9−𝑥𝑥=−23(9−𝑥)=18.

Аналогично, извлечение отрицательного квадратного корня дает площадь, ограниченную кривой под осью 𝑥.

Еще раз, мы можем оценить эту площадь с помощью определенного интеграла: aread=−√9−𝑥𝑥=23(9−𝑥)=−18.

Сложение этих площадей вместе дает результат 0, но мы можем использовать наши знания о том, что истинная площадь определяется суммой этих абсолютных значений: квадратные единицы площади=|18|+|−18|=36.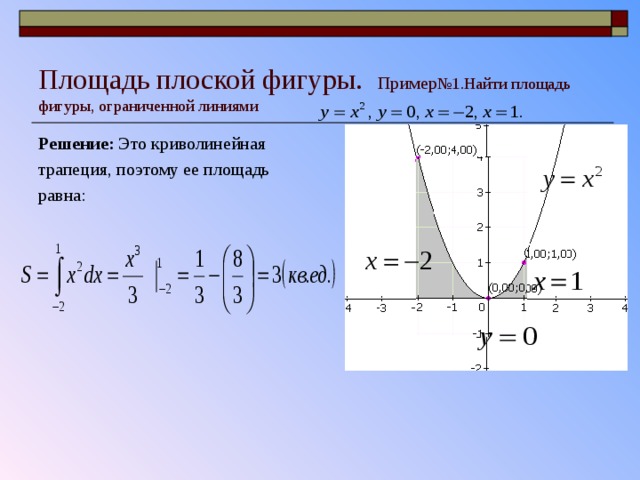

Более простой альтернативой является интегрирование по 𝑦. По сути, это переключает переменные. Рассмотрим горизонтальную полосу площади, ограниченную 𝑥=9−𝑦 и осью 𝑦, с шириной 𝑥 и высотой d𝑦.

Функция 𝑥=𝑓(𝑦)=9−𝑦 может быть проинтегрирована по y между 𝑦=−3 и 𝑦=3, так как нет внутренней разницы между 𝑥 и 𝑦 как переменными, и это просто соглашение что 𝑥 обычно является независимой переменной. Кроме того, эта функция соответствует одному значению 𝑥, поэтому ее можно интегрировать без необходимости разбивать интеграл на отдельные области. Таким образом, у нас есть aread=9−𝑦𝑦.

Интегрирование по 𝑦 дает квадратные единицы площади =9𝑦−13𝑦=9⋅3−13⋅3−9⋅(−3)−13⋅(−3)=27−9−(−27+9)=36.

Определенные интегралы также можно использовать для нахождения площади, заключенной между кривой функции 𝑦=𝑓(𝑥) и кривой другой функции 𝑦 =𝑔(𝑥), используя тот факт, что интегральный оператор, как и дифференциальный оператор, является линейным оператором , что означает, что он замкнут относительно сложения : 𝑓(𝑥)𝑥+𝑔(𝑥)𝑥 =𝑓(𝑥)+𝑔(𝑥)𝑥. ddd

Это распространяется и на вычитание, так как интегрирование также закрыто при скалярном умножении : 𝛼𝑓(𝑥)𝑥=𝛼𝑓(𝑥)𝑥,dd, где 𝛼 — скаляр. Взяв частный случай 𝛼=−1, −𝑓(𝑥)𝑥=-𝑓(𝑥)𝑥,dd и объединив это с первым свойством, мы можем выразить разницу между двумя интегралами как один интеграл: 𝑓 (𝑥)𝑥−𝑔(𝑥)𝑥=𝑓(𝑥)𝑥+−𝑔(𝑥)𝑥=𝑓(𝑥)−𝑔(𝑥)𝑥.ddddd

Для более простого случая второй функции будучи постоянной горизонтальной линией 𝑦=𝑔(𝑥)=𝑐, тогда мы имеем 𝑓(𝑥)𝑥−𝑐𝑥=𝑓(𝑥)−𝑐𝑥.ddd

Следовательно, мы можем найти площадь, заключенную в кривую 𝑦=𝑓(𝑥) и горизонтальную линию 𝑦=𝑐 между двумя точками 𝑥=𝑎 и 𝑥=𝑏 по формуле aread=𝑓(𝑥)−𝑐𝑥.

Давайте рассмотрим пример того, как мы используем это, чтобы найти площадь, заключенную между кривой и прямой линией.

Пример 5. Использование метода интегрирования для нахождения площади, ограниченной кривой и горизонтальной линией

Найдите площадь заштрихованной области.

Ответ

Площадь этой заштрихованной области может быть найдена вычислением определенного интеграла кривой 𝑦=3𝑥+4𝑥−2 между пределами 𝑥=1 и 𝑥=2, а затем вычитанием площади прямоугольника под ним , который мы можем легко найти с помощью стандартной формулы площади прямоугольника.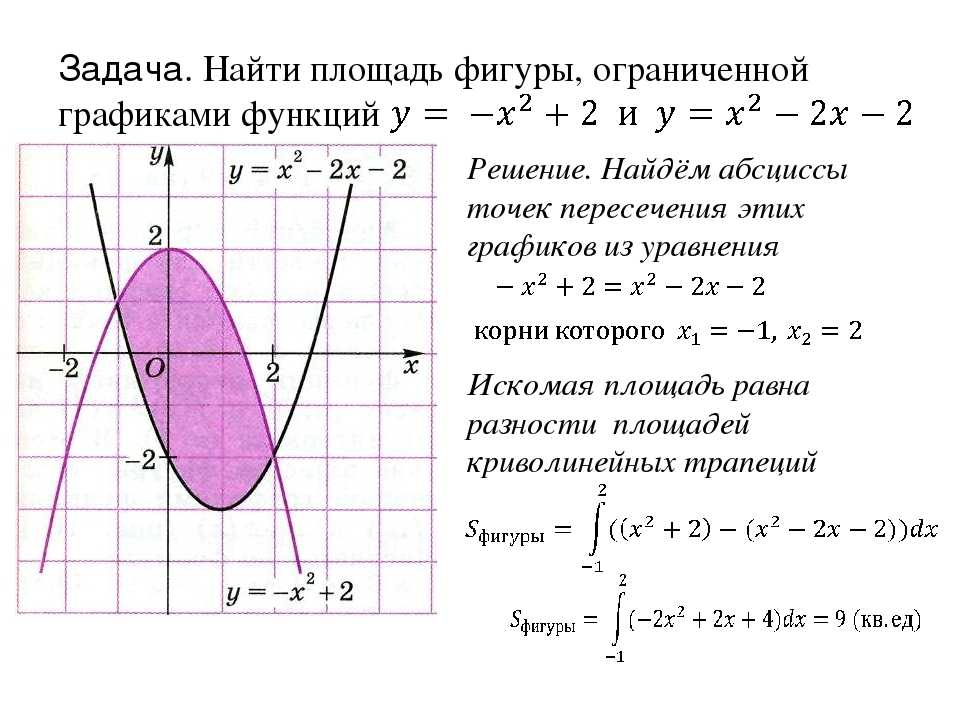

Однако напомним, что мы также можем найти площадь, ограниченную кривой 𝑦=𝑓(𝑥) и горизонтальной линией 𝑦=𝑐 между двумя точками 𝑥=𝑎 и 𝑥=𝑏, используя формулу aread=𝑓(𝑥)− 𝑐𝑥.

В этом случае у нас есть кривая 𝑓(𝑥)=3𝑥+4𝑥−2 и горизонтальная линия 𝑦=5. Подстановка их в приведенную выше формулу дает areadd=3𝑥+4𝑥−2−5𝑥=3𝑥+4𝑥−7𝑥.

. 2+2⋅2−7⋅2−1+2⋅1−7⋅1=8+8−14−(1+2−7)=6.

Давайте закончите повторением некоторых ключевых моментов из этого объяснения.

Ключевые точки

• Площадь, ограниченная кривой 𝑦=𝑓(𝑥), осью 𝑥 и двумя горизонтальными линиями 𝑥=𝑎 и 𝑥=𝑏, определяется выражением 𝐴=𝑓(𝑥)𝑥. d
• Площадь, ограниченная кривой 𝑥=𝑓(𝑦), осью 𝑦 и двумя вертикальными линиями 𝑦=𝑎 и 𝑦=𝑏, равна 𝐴=𝑓(𝑦)𝑦.d
• A область, заключенная над осью 𝑥/осью 𝑦, дает положительный интеграл, а область, заключенная под осью 𝑥/осью 𝑦, дает отрицательный интеграл. Так как площадь является строго положительной величиной, чтобы найти замкнутую площадь, мы берем абсолютное значение интеграла для каждой отдельной замкнутой области.
• Площадь, ограниченная кривой 𝑦=𝑓(𝑥), другой горизонтальной линией 𝑦=𝑐 и двумя линиями 𝑥=𝑎 и 𝑥=𝑏, равна 𝐴=𝑓(𝑥)−𝑐𝑥.d

Нахождение области, ограниченной 2 линиями/кривыми путем интегрирования

спросил 11 лет, 1 месяц назад

Изменено 6 лет, 9 месяцев назад

Просмотрено 13 тысяч раз 92-x)\;dx$

Добавлено: Нет, если вы начертите две кривые, которые я дал, между двумя кривыми будет область в форме линзы. Если вам нужна площадь между двумя кривыми, вы делаете $\int y_2-y_1 \;dx$. Область между кривой и осью x является частным случаем $y_2=0$

В исходной задаче имеет смысл говорить об области, ограниченной осью $x$ и двумя кривыми. Вы могли видеть этот сюжет. $\sqrt{1+x}$ поднимается над осью в точке $x=-1$.