Лучший ответ по мнению автора
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
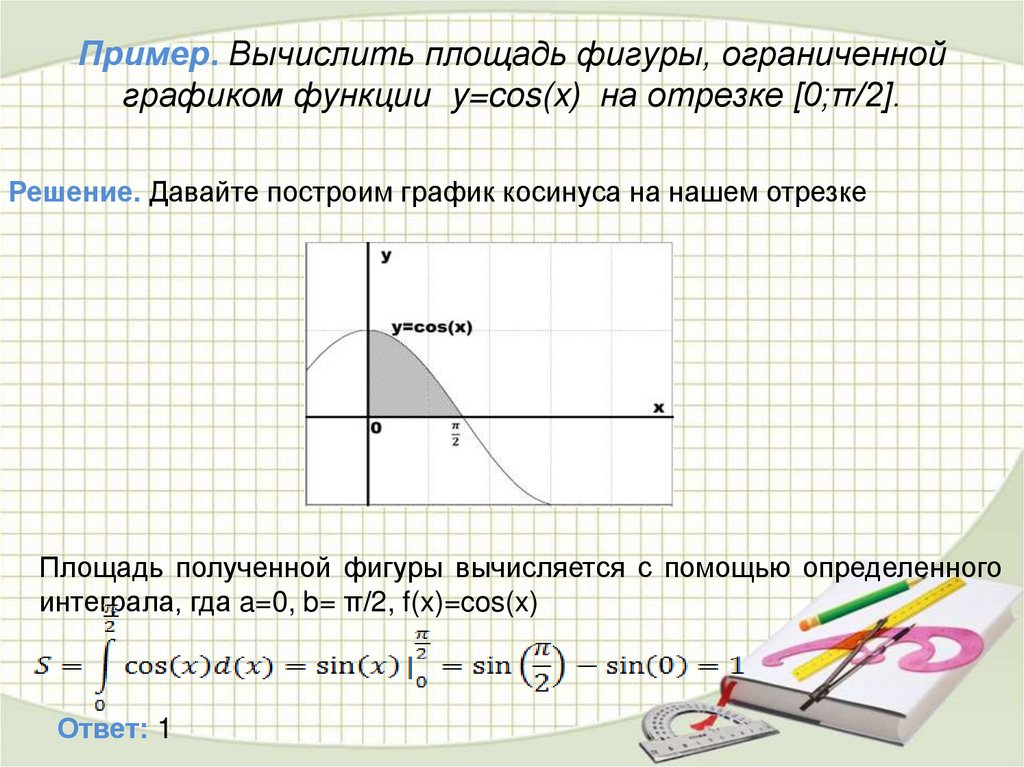
Вычислим площадь фигуры.
 Колмогоров Алгебра 10-11 класс упр 368 параграф 8 – Рамблер/класс Вычислим площадь фигуры. Колмогоров Алгебра 10-11 класс упр 368 параграф 8 – Рамблер/класс
Колмогоров Алгебра 10-11 класс упр 368 параграф 8 – Рамблер/класс Вычислим площадь фигуры. Колмогоров Алгебра 10-11 класс упр 368 параграф 8 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Помогаю брату с домашкой! Подскажете?
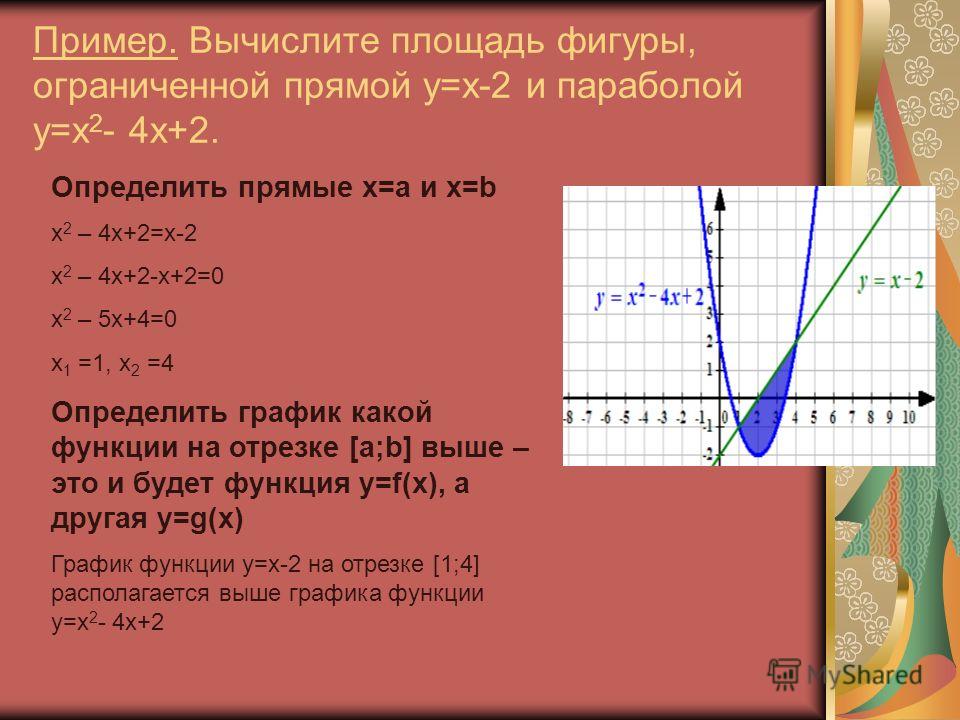
Вычислите площадь фигуры, ограниченной графиком функции f (х) = 8 — 0,5х2, касательной к нему в точке с абсциссой х = -2 и прямой х = 1
ответы
Хорошее дело! Подскажу)
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Юмор
Олимпиады
ЕГЭ
10 класс
похожие вопросы 5
В какой момент времени ускорение движения будет наименьшим? Колмогоров Алгебра 10-11 класс Упр 309
Привет! Поможете с решением?)
Скорость изменяется по закону
(скорость измеряется в метрах в секунду). В какой момент времени (Подробнее…)
В какой момент времени (Подробнее…)
ГДЗ11 классКолмогоров А.Н.10 классАлгебра
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
С чем связано окончание приема учащихся в Московский институт телевидения и радиовещания «Останкино»? (Подробнее…)
ВузыПоступление11 классНовости
Какой был проходной балл в вузы в 2017 году?
Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)
Поступление11 классЕГЭНовости
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых).
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
6.1: Области между кривыми — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2519
- Гилберт Странг и Эдвин «Джед» Герман
- ОпенСтакс
Цели обучения
- Определить площадь области между двумя кривыми путем интегрирования по независимой переменной.
- Найдите площадь составной области.

- Определить площадь области между двумя кривыми путем интегрирования по зависимой переменной.
В разделе «Введение в интегрирование» мы разработали концепцию определенного интеграла для вычисления площади под кривой на заданном интервале. В этом разделе мы расширим эту идею, чтобы вычислить площадь более сложных регионов. Начнем с нахождения площади между двумя кривыми, являющимися функциями \(\displaystyle x\), начиная с простого случая, когда значение одной функции всегда больше другого. Затем рассмотрим случаи, когда графики функций пересекаются. Наконец, мы рассмотрим, как вычислить площадь между двумя кривыми, которые являются функциями \(\displaystyle y\).
Площадь области между двумя кривыми
Пусть \(\displaystyle f(x)\) и \(\displaystyle g(x)\) — непрерывные функции на интервале \(\displaystyle [a,b]\), такие что \(\displaystyle f(x)≥g(x)\) на \(\displaystyle [a,b]\). Нам нужно найти площадь между графиками функций, как показано на рисунке \(\PageIndex{1}\).
Эти результаты резюмируются в следующей теореме.
Нахождение площади между двумя кривыми
Пусть \(\displaystyle f(x)\) и \(\displaystyle g(x)\) — непрерывные функции такие, что \(\displaystyle f(x)≥g(x) \) на интервале [\(\displaystyle a,b]\). Обозначим через R область, ограниченную сверху графиком \(\displaystyle f(x)\), снизу графиком \(\displaystyle g(x)\), а слева и справа линиями \(\ displaystyle x=a\) и \(\displaystyle x=b\) соответственно. Тогда площадь \(\textbf{R}\) равна 9b_a[f(x)−g(x)]dx. \nonumber \]
Применим эту теорему в следующем примере.
Пример \(\PageIndex{1}\): нахождение площади области между двумя кривыми I
Если \(\textbf{R}\) — это область, ограниченная сверху графиком функции \(\displaystyle f(x)=x+4\) и ниже по графику функции \(\displaystyle g(x)=3−\dfrac{x}{2}\) на интервале \(\displaystyle [1,4 ]\), найдите площадь области \(\textbf{R}\).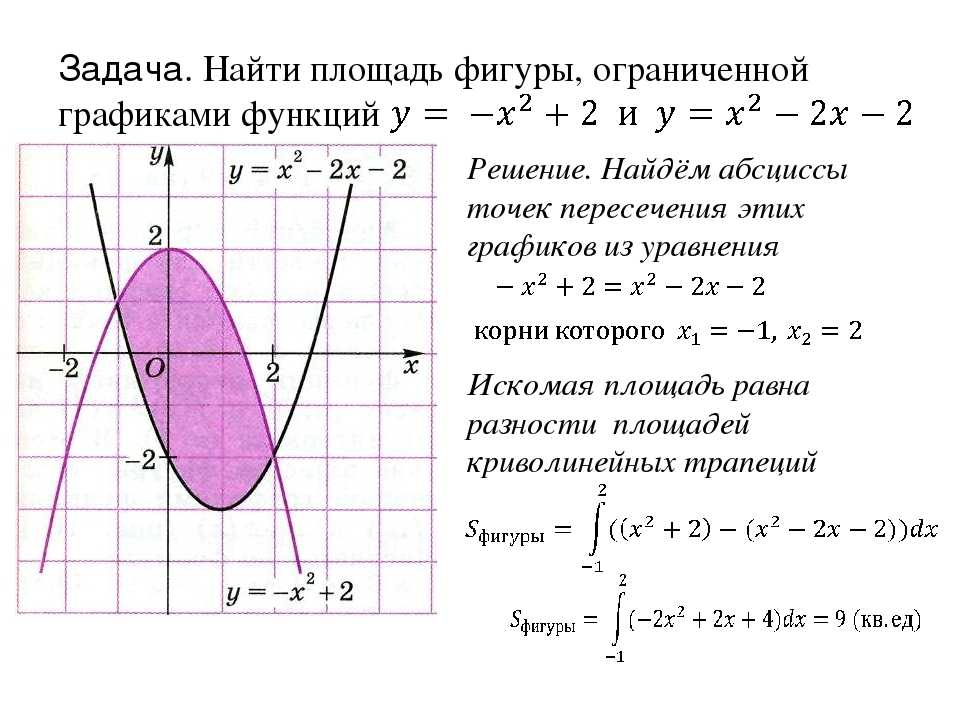
Раствор
92\).Упражнение \(\PageIndex{1}\)
Если \(\textbf{R}\) область, ограниченная графиками функций \(\displaystyle f(x)=\dfrac{x}{2 }+5\) и \(\displaystyle g(x)=x+\dfrac{1}{2}\) на интервале \(\displaystyle [1,5]\), найти площадь области \(\textbf {Р}\).
- Подсказка
Нарисуйте графики функций, чтобы определить, график какой функции образует верхнюю границу, а график нижней границы, затем выполните процесс, описанный в примере.
- Ответить
\(\displaystyle 12\) единиц 2
В примере \(\PageIndex{1}\) мы определили интересующий интервал как часть условия задачи. Однако довольно часто мы хотим определить интересующий нас интервал на основе того, где пересекаются графики двух функций. Это показано в следующем примере.
Пример \(\PageIndex{2}\): нахождение площади области между двумя кривыми II 92\) и ниже по графику функции \(\displaystyle g(x)=6−x\) найти площадь области \(\textbf{R}\).

Решение
Область изображена на следующем рисунке.
Рисунок \(\PageIndex{4}\): на этом графике показана область ниже графика \(\displaystyle f(x)\) и выше графика \(\displaystyle g(x).\)\[ \begin{align*} \displaystyle f(x) =g(x) \\[4pt] 94\), найдите площадь области \(\textbf{R}\).
- Подсказка
Используйте процесс из примера \(\PageIndex{2}\).
- Ответить
\(\displaystyle \dfrac{3}{10}\) ед. 2
Площади составных областей
До сих пор нам требовалось \(\displaystyle f(x)≥g(x)\) на всем интересующем интервале, но что, если мы хотим посмотреть на области, ограниченные графами пересекающиеся друг с другом функции? В этом случае мы модифицируем процесс, который мы только что разработали, используя функцию абсолютного значения. 9b_a|f(x)−g(x)|dx. \nonumber \]
9b_a|f(x)−g(x)|dx. \nonumber \]
На практике применение этой теоремы требует, чтобы мы разбивали интервал \(\displaystyle [a,b]\) и вычисляли несколько интегралов, в зависимости от того, какое из значений функции больше на данной части интервал. Изучим этот процесс на следующем примере.
Пример \(\PageIndex{3}\): нахождение площади области, ограниченной пересекающимися функциями
Если \(\textbf{R}\) — это область между графиками функций \(\displaystyle f (x)=\sin x \) и \(\displaystyle g(x)=\cos x\) на интервале \(\displaystyle [0,π]\), найти площадь области \(\textbf{R }\).
Решение
Область изображена на следующем рисунке.
Рисунок \(\PageIndex{5}\): Область между двумя кривыми может быть разбита на две подобласти.Графики функций пересекаются в точке \(\displaystyle x=π/4\). Для \(\displaystyle x∈[0,π/4], \cos x≥\sin x,\) поэтому
\(\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\cos x−\sin x . \)
\)
С другой стороны, для \(\displaystyle x∈[π/4,π], \sin x ≥\cos x,\), поэтому
9π_{π/4} \\[4pt] =(\sqrt{2}−1)+(1+\sqrt{2})=2\sqrt{2}. \end{align*}\]Площадь области составляет \(\displaystyle 2\sqrt{2}\) единиц 2 .
Упражнение \(\PageIndex{3}\)
Если \(\textbf{R}\) область между графиками функций \(\displaystyle f(x)=\sin x \) и \( \displaystyle g(x)=\cos x\) на интервале \(\displaystyle [π/2,2π]\), найти площадь области \(\textbf{R}\).
- Подсказка
Две кривые пересекаются в точке \(\displaystyle x=(5π)/4.\)
- Ответить
\(\displaystyle 2+2\sqrt{2}\) единиц 2
Пример \(\PageIndex{4}\): определение площади сложной области
Рассмотрим область, изображенную на рисунке \(\PageIndex{6}\). Найдите площадь \(\textbf{R}\).
Рисунок \(\PageIndex{6}\): Для вычисления площади этой области требуются два интеграла. 92_1=\dfrac{1}{2}.\)
92_1=\dfrac{1}{2}.\)Складывая эти области вместе, мы получаем
\(\displaystyle A=A_1+A_2=\dfrac{1}{3}+\dfrac{1}{2 }=\dfrac{5}{6}.\)
Площадь региона составляет \(\displaystyle 5/6\) единиц 2 .
Упражнение \(\PageIndex{4}\)
Рассмотрим область, изображенную на следующем рисунке. Найдите площадь \(\textbf{R}\).
- Подсказка
Две кривые пересекаются в точке х=1
- Ответить
\(\displaystyle \dfrac{5}{3}\) единиц 2
Области, определенные относительно y
В примере \(\PageIndex{4}\) нам пришлось вычислить два отдельных интеграла для вычисления площади области. Однако существует и другой подход, требующий только одного интеграла. Что, если мы будем рассматривать кривые как функции \(\displaystyle y\), а не как функции \(\displaystyle x\)? Просмотрите рисунок. 2\) как функции \(\displaystyle y \).Однако, судя по графику, нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией \(\displaystyle y=g(x)=2−x\), но также легко может быть представлен функцией \(\displaystyle x=u(y)=2−y\). Когда графики представлены как функции \(\displaystyle y\), мы видим, что область ограничена слева графиком одной функции и справа графиком другой функции. Следовательно, если мы интегрируем по \(\displaystyle y\), нам нужно вычислить только один интеграл. Разработаем формулу для этого типа интеграции.
2\) как функции \(\displaystyle y \).Однако, судя по графику, нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией \(\displaystyle y=g(x)=2−x\), но также легко может быть представлен функцией \(\displaystyle x=u(y)=2−y\). Когда графики представлены как функции \(\displaystyle y\), мы видим, что область ограничена слева графиком одной функции и справа графиком другой функции. Следовательно, если мы интегрируем по \(\displaystyle y\), нам нужно вычислить только один интеграл. Разработаем формулу для этого типа интеграции.
Пусть \(\displaystyle u(y)\) и \(\displaystyle v(y)\) — непрерывные функции на интервале \(\displaystyle [c,d]\) такие, что \(\displaystyle u(y) )≥v(y)\) для всех \(\displaystyle y∈[c,d]\). Мы хотим найти площадь между графиками функций, как показано на рисунке \(\PageIndex{7}\).
Рисунок \(\PageIndex{7}\): Мы можем найти площадь между графиками двух функций, \(\displaystyle u(y)\) и \(\displaystyle v(y)\). На этот раз мы собираемся разбить интервал на 9d_c[u(y)−v(y)]dy.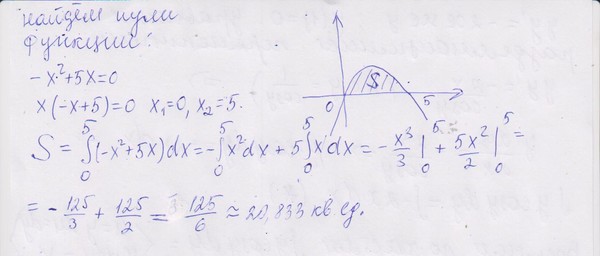 \end{align*}\]
\end{align*}\]
Эти результаты резюмируются в следующей теореме.
Нахождение площади между двумя кривыми, интегрирование по оси Y
Пусть \(\displaystyle u(y)\) и \(\displaystyle v(y)\) — непрерывные функции, такие что \(\displaystyle u( y)≥v(y) \) для всех \(\displaystyle y∈[c,d]\). Пусть \(\textbf{R}\) обозначает область, ограниченную справа графиком \(\displaystyle u(y)\), слева графиком \(\displaystyle v(y)\ ), а сверху и снизу строками \(\displaystyle y=d\) и \(\displaystyle y=c\) соответственно. Тогда площадь \(\textbf{R}\) равна 9d_c[u(y)−v(y)]dy. \nonumber \]
Пример \(\PageIndex{5}\): интегрирование по y
Вернемся к примеру \(\PageIndex{4}\), только на этот раз интегрируем по \(\displaystyle y \). Пусть \(\textbf{R}\) будет регионом, изображенным на рисунке \(\PageIndex{9}\). Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).
Рисунок \(\PageIndex{9}\): Площадь области \(\textbf{R}\) можно вычислить с помощью одного интеграла, только если кривые рассматриваются как функции \(\displaystyle y\).
Решение
Сначала мы должны представить графики как функции \(\displaystyle y\). Как мы видели в начале этого раздела, кривая слева может быть представлена функцией \(\displaystyle x=v(y)=\sqrt{y}\), а кривая справа может быть представлена функцией функция \(\displaystyle x=u(y)=2−y\).
Теперь нам нужно определить пределы интегрирования. Область ограничена снизу осью x, поэтому нижний предел интегрирования равен \(\displaystyle y=0\). Верхний предел интегрирования определяется точкой пересечения двух графиков, которая является точкой \(\displaystyle (1,1)\), поэтому верхний предел интегрирования равен \(\displaystyle y=1\). Таким образом, мы имеем \(\displaystyle [c,d]=[0,1]\). 91_0\\[4pt] =\dfrac{5}{6}. \end{align*}\]
Площадь области составляет \(\displaystyle 5/6\) единиц 2 .
Упражнение \(\PageIndex{5}\)
Давайте вернемся к контрольной точке, связанной с примером \(\PageIndex{4}\), только на этот раз давайте проинтегрируем относительно \(\displaystyle y\). Пусть \(\textbf{R}\) будет областью, изображенной на следующем рисунке. Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).
Пусть \(\textbf{R}\) будет областью, изображенной на следующем рисунке. Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).
- Подсказка
Повторите процесс из предыдущего примера.
- Ответить
\(\displaystyle \dfrac{5}{3}\) единиц 2
Ключевые понятия
- Точно так же, как определенные интегралы можно использовать для нахождения площади под кривой, их также можно использовать для нахождения площади между двумя кривыми.
- Чтобы найти площадь между двумя кривыми, заданными функциями, проинтегрируйте разность функций.
- Если графики функций пересекаются или область является сложной, используйте абсолютное значение разности функций. В этом случае может потребоваться вычислить два или более интеграла и сложить результаты, чтобы найти площадь области.
- Иногда бывает проще интегрировать по y, чтобы найти площадь.
 Принципы одни и те же независимо от того, какая переменная используется в качестве переменной интегрирования.
Принципы одни и те же независимо от того, какая переменная используется в качестве переменной интегрирования.
Ключевые уравнения
- 9d_c[u(y)−v(y)]dy\)
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- ОБЛАСТЬ МЕЖДУ ДВУМЯ КРИВЫМИ
- Площадь между двумя кривыми, интегрированная по оси x
- Площадь между двумя кривыми, интегрированными по оси Y
- Площади составных областей
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1
Пример 2: Найдите площадь под кривой для области, заключенной в эллипс x 2 /36 + y 2 /25 = 1.
Решение:
Данное уравнение эллипса ис.х 2 9{-1}1) — 0]\\&=\frac{20}{6}.\frac{36}{2}.\frac{\pi}{2}\\&=30\pi \end{ align}\)
Ответ: Следовательно, площадь эллипса равна 30π квадратных единиц.
Эта страница под названием 6.1: Области между кривыми распространяется по лицензии CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Германом (OpenStax) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
Площадь под кривой — метод, формула, примеры решений, часто задаваемые вопросы
Площадь под кривой рассчитывается разными методами, из которых наиболее популярен первообразный метод нахождения площади. Площадь под кривой можно найти, зная уравнение кривой, границы кривой и ось, охватывающую кривую. Как правило, у нас есть формулы для нахождения площадей правильных фигур, таких как квадрат, прямоугольник, четырехугольник, многоугольник, круг, но нет определенной формулы для нахождения площади под кривой. Процесс интегрирования помогает решить уравнение и найти искомую площадь.
Для нахождения площадей неправильных плоских поверхностей очень полезны методы первообразных. Здесь мы научимся находить площадь под кривой относительно оси, находить площадь между кривой и прямой и находить площадь между двумя кривыми.
1. | Как найти площадь под кривой? |
| 2. | Различные методы поиска площади под кривой |
| 3. | Формула площади под кривой |
| 4. | Область под кривой — круг |
| 5. | Площадь под кривой — парабола |
| 6. | Область под кривой — эллипс |
| 7. | Область между кривой и трапецеидальной линией |
| 8. | Область между двумя кривыми |
| 9. | Решенные примеры |
| 10. | Практические вопросы |
| 11. | Часто задаваемые вопросы по Area Under The Curve |
Как найти площадь под кривой?
Площадь под кривой можно рассчитать за три простых шага. Во-первых, нам нужно знать уравнение кривой (y = f(x)), пределы, в которых должна быть рассчитана площадь, и ось, охватывающую площадь. Во-вторых, мы должны найти интегрирование (первообразную) кривой. Наконец, нам нужно применить верхний предел и нижний предел к интегральному ответу и взять разницу, чтобы получить площадь под кривой. 9б_а\)
Во-вторых, мы должны найти интегрирование (первообразную) кривой. Наконец, нам нужно применить верхний предел и нижний предел к интегральному ответу и взять разницу, чтобы получить площадь под кривой. 9б_а\)
=\( г(б) — г(а)\)
Различные методы нахождения площади под кривой
Площадь под кривой можно вычислить тремя способами. Кроме того, метод, используемый для нахождения площади под кривой, зависит от необходимости и доступных входных данных для нахождения площади под кривой. Здесь мы рассмотрим три метода, чтобы найти площадь под кривой.
9нф(х).\дельта х\). Метод — II: В этом методе также используется процедура, аналогичная описанной выше, для нахождения площади под кривой. Здесь область под кривой разделена на несколько прямоугольников. Далее площади этих прямоугольников складываются, чтобы получить площадь под кривой. Этот метод представляет собой простой способ найти площадь под кривой, но он дает только приблизительное значение площади под кривой.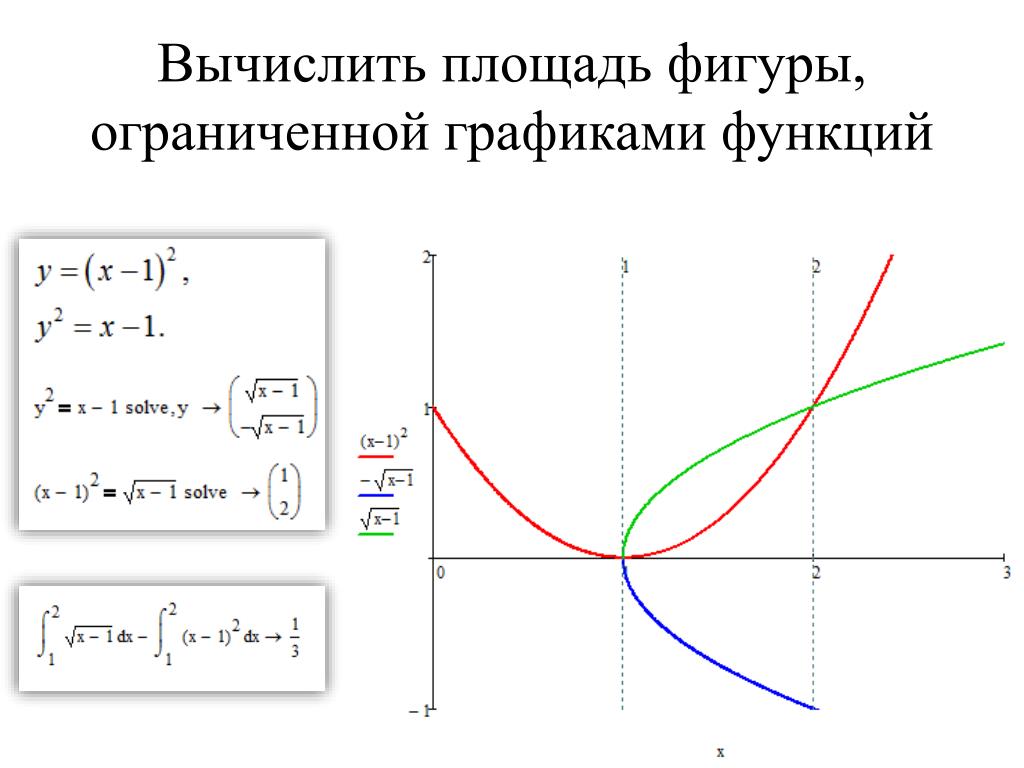 b f(x ).dx\)
b f(x ).dx\)
Формула площади под кривой
Площадь кривой может быть рассчитана относительно различных осей как граница данной кривой. Площадь под кривой можно рассчитать относительно оси x или оси y. Для особых случаев кривая находится ниже осей и частично ниже осей. Для всех этих случаев у нас есть производная формула для нахождения площади под кривой.
Площадь по оси x: 9cf(x).dx\)
Область под кривой — круг
Площадь круга рассчитывается путем вычисления площади части круга в первом квадранте. Здесь уравнение окружности x 2 + y 2 = a 2 заменяется уравнением кривой вида y = √(a 2 — x 2 ). Это уравнение кривой используется для нахождения площади относительно оси x и пределов от 0 до a. 9а_0\)
= 4[((a/2)× 0 + (a 2 /2)Sin -1 1) — 0]
= 4(а 2 /2)(π/2)
= 2π r
Следовательно, площадь круга равна π a 2 квадратных единиц.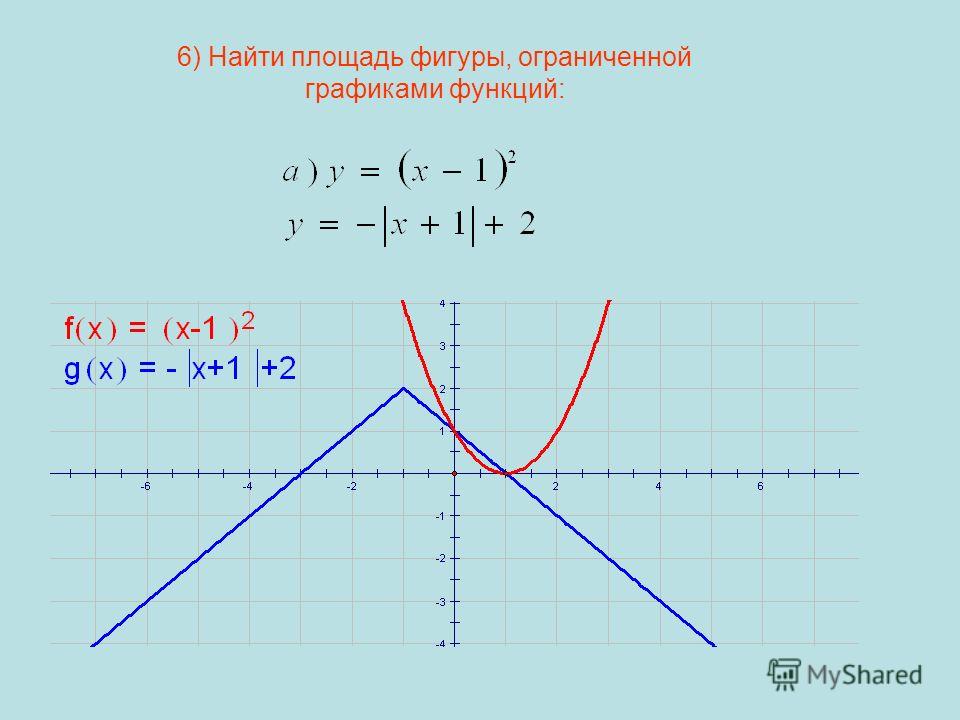
Площадь под кривой — парабола
Парабола имеет ось, которая делит параболу на две симметричные части. Здесь мы берем параболу, симметричную относительно оси x и имеющую уравнение y 92}{3}\) квадратных единиц.
Область под кривой — эллипс
Уравнение эллипса с большой осью 2a и малой осью 2b: x 2 /a 2 + y 2 /b 2 = 1. Это уравнение можно преобразовать в виде y = b/a .√(a 2 — x 2 ). Здесь мы вычисляем площадь, ограниченную эллипсом по первой координате и по оси x, и далее умножаем на 4, чтобы получить площадь эллипса. Граничные пределы, взятые по оси x, составляют от 0 до a. Вычисления площади эллипса следующие. 92}{2}.\frac{\pi}{2}\\&=\pi ab\end{align}\)
Следовательно, площадь эллипса составляет πab кв. единиц.
Область под кривой — между кривой и трапецеидальной линией
Площадь между кривой и линией можно удобно рассчитать, взяв разность площадей одной кривой и площади под линией.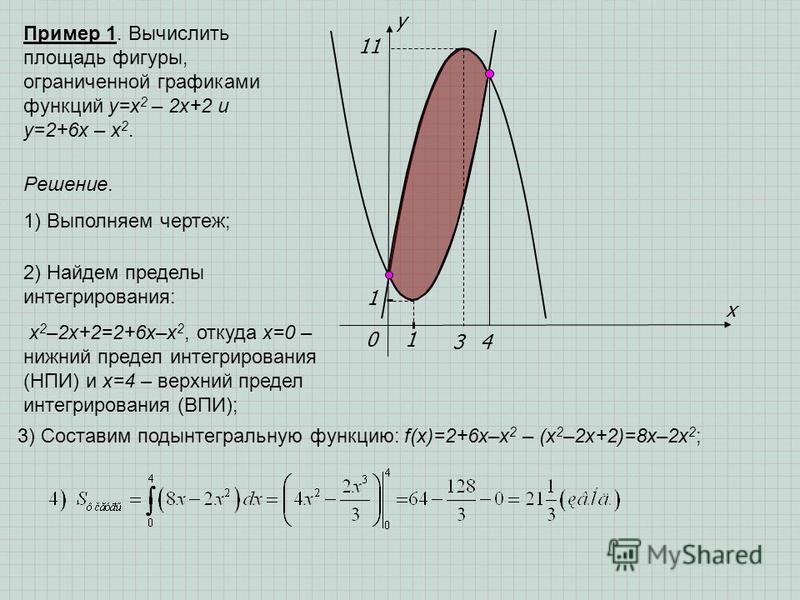 Здесь граница относительно оси и для кривой, и для линии одинакова. На рисунке ниже показаны кривая \(y_1\) = f(x) и линия \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между кривой и линией. Здесь мы берем интеграл от разности двух кривых и применяем границы, чтобы найти результирующую площадь. 9b_a [f(x) — g(x)].dx\)
Здесь граница относительно оси и для кривой, и для линии одинакова. На рисунке ниже показаны кривая \(y_1\) = f(x) и линия \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между кривой и линией. Здесь мы берем интеграл от разности двух кривых и применяем границы, чтобы найти результирующую площадь. 9b_a [f(x) — g(x)].dx\)
Область под кривой — между двумя кривыми
Площадь между двумя кривыми удобно вычислять, взяв разность площадей одной кривой из площади другой кривой. Здесь граница по оси для обеих кривых одинакова. На приведенном ниже рисунке показаны две кривые \(y_1\) = f(x) и \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между этими двумя кривыми. Здесь мы берем интеграл от разности двух кривых и применяем границы, чтобы найти результат. 94_0\)
= [((4/2)× 0 + (16/2)Sin-11) — 0]
= (16/2)(π/2)
= 4π
Ответ: Следовательно, площадь области, ограниченной кругом в первом квадранте, составляет 4π квадратных единиц
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
9b y.dx\)
Какие существуют методы нахождения площади под кривой?
Существует три основных метода нахождения площади под кривой. Площадь под кривой рассчитывается путем деления пространства площади на множество маленьких прямоугольников, а затем площади складываются для получения общей площади. Второй метод заключается в разделении области на несколько прямоугольников, а затем области складываются для получения необходимой площади. Третий способ – найти площадь с помощью интегрирования.
Второй метод заключается в разделении области на несколько прямоугольников, а затем области складываются для получения необходимой площади. Третий способ – найти площадь с помощью интегрирования.
Что означает площадь под кривой?
Площадь под кривой означает площадь, ограниченную кривой, осью и граничными точками. Площадь под кривой представляет собой двумерную площадь, рассчитанную с помощью осей координат и формулы интегрирования.
Что представляет площадь под кривой?
Площадь под кривой представляет собой площадь, заключенную под кривой и осью, которая отмечена ограничивающими точками. Эта площадь под кривой дает площадь неправильной плоской формы в двумерном массиве.
Что такое площадь под кривой на графике скорости во времени?
На графике скорость-время скорость отложена по оси у, а время отложено по оси х. При этом предполагается, что площадь является произведением скорости и времени, и это дает пройденное расстояние. Следовательно, площадь под кривой графика зависимости скорости от времени дает пройденное расстояние.
Как интерпретировать площадь под кривой?
Площадь под кривой — это площадь между кривой и осью координат. Дальнейшие границы накладываются поперек кривой относительно оси, чтобы получить требуемую площадь. Площадь под кривой обычно представляет собой площадь неправильных форм, для которых нет формул площади в геометрии.
Как рассчитать площадь под кривой без интегрирования?
Площадь под кривой можно рассчитать даже без использования интегрирования. Площадь под кривой можно разбить на меньшие прямоугольники, а затем суммирование этих площадей дает площади под кривой. Также другой метод состоит в том, чтобы разбить область под кривой на несколько прямоугольников, а затем мы можем взять соответствующие области, чтобы получить площадь под кривой.
Как приблизительно определить площадь под кривой?
Площадь под кривой можно приблизительно рассчитать, разбив площадь на небольшие части в виде небольших прямоугольников. И площади этих прямоугольников можно вычислить, и их суммирование дает площадь под кривой. Другой способ найти приблизительную площадь под кривой — нарисовать набор из нескольких больших прямоугольников, а затем суммировать их площади. Далее мы можем просто найти точную площадь под кривой с помощью определенных интегралов.
Другой способ найти приблизительную площадь под кривой — нарисовать набор из нескольких больших прямоугольников, а затем суммировать их площади. Далее мы можем просто найти точную площадь под кривой с помощью определенных интегралов.
Когда использовать площадь под кривой?
Площадь под кривой полезна для нахождения площади неправильной формы на плоскости. Обычно мы находим формулы для нахождения площади круга, квадрата, прямоугольника, четырехугольника, многоугольника, но у нас нет никаких средств для нахождения площади неправильной формы. Здесь мы используем концепцию определенных интегралов для получения значений площадей.
Когда площадь под кривой имеет отрицательное значение?
Площадь под кривой отрицательна, если кривая находится под осью или в отрицательных квадрантах оси координат. Для этого также вычисляется площадь кривой с использованием нормального метода, и к окончательному ответу применяется модуль. Даже при отрицательном ответе берется только значение площади, без учета отрицательного знака ответа.

 10.17
10.17
 Принципы одни и те же независимо от того, какая переменная используется в качестве переменной интегрирования.
Принципы одни и те же независимо от того, какая переменная используется в качестве переменной интегрирования. org/details/books/calculus-volume-1
org/details/books/calculus-volume-1