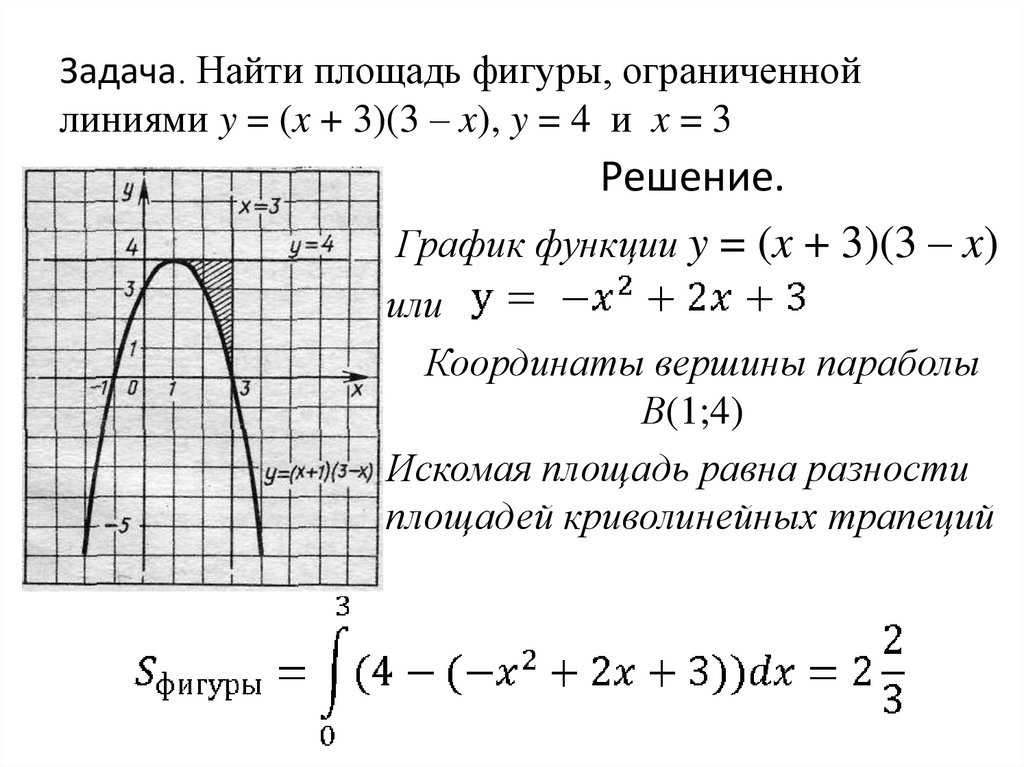
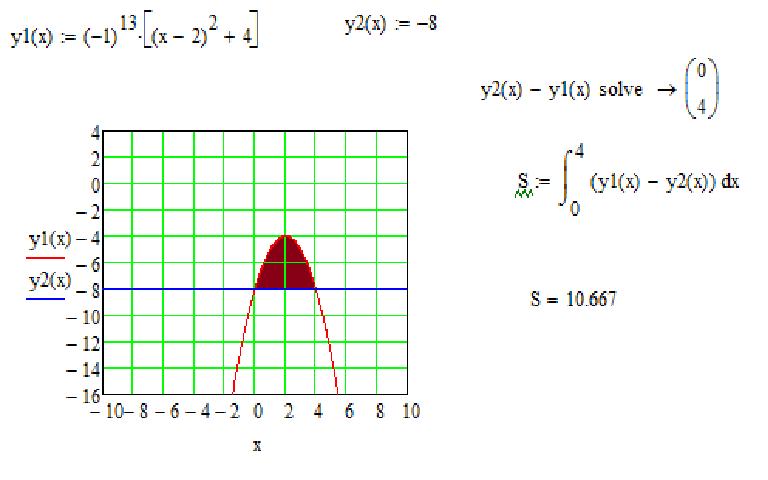
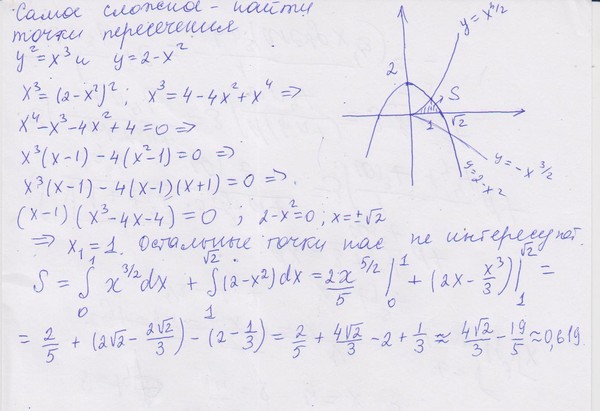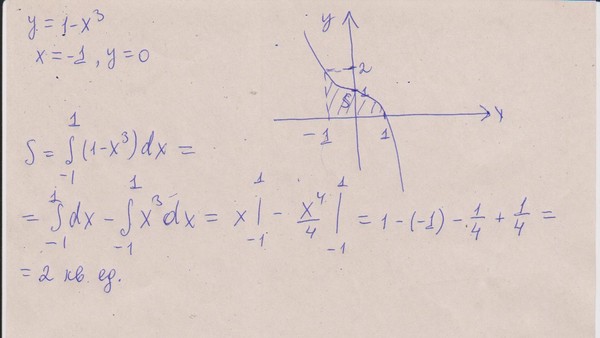Вычислите площадь фигуры ограниченной линиями y 4 x 2 y 0: Найдите площадь фигуры,ограниченной линиями y=4-x^2 и y=0

alexxlab / / Разное

Урок алгебры в 11-м классе на тему: «Вычисление площадей фигур»

Цели урока:

1) Повторить, закрепить и расширить знания по заданной теме.

2) Уметь самостоятельно применять полученные знания по теме к решению задач.

3) Уметь рационально решать задачи.

4) Творчески подходить к решению конкретной задачи.

1. Повторение теоретического материала

Фронтальный опрос (по таблице “Площади фигур”)

Вопрос: Как найти площади изображенных фигур?

Ответ:

2. Разминка (на 3 мин., в тетрадях только решение)

Задача. Найти площади изображенных фигур. Ответы с комментариями.

3. Программированный контроль

Задания

Ответы

Вычислить площадь фигуры, ограниченной линиями:

        

I вариант

II вариант

1

2

3

4

y=x2+2, y=x+2

y=-x2+4, y=-x+4

7

1/6

2/3

1/3

y=sin2x,y=0

x=0, x=/4

y=cos2x, y=0

x=-/4, x=/4

2

-1

1/2

1

y=-2/х, y=2

x=-4, x=-1

y=-1/х, y=1

x=-3, x=-1

 6-4ln2

2-ln3

2ln2

2-3ln2

Верные ответы: I вариант: 2,3,1 II вариант: 2,4,2

4. Решение задач на закрепление (с проверкой у доски)

1) Найти площадь фигуры, ограниченной линиями

2) Фигура, ограниченная линиями y=x+6, x=1, y=0 делится параболой y=x2+2x+4 на две части. Найти площадь каждой части.

3) Найти ту первообразную F(x) функции f(x)=2x+4, график которой касается прямой у=6х+3. Вычислить площадь фигуры, ограниченной графиком найденной первообразной и прямыми у=6х+3 и у=0.

4) Составить формулы для нахождения площадей фигур, изображенных на таблице:

Ответы с комментариями:

5) Интересная задача. Найти сумму площадей бесконечного количества фигур, заштрихованных на рисунках:

(Аргумент каждой следующей функции увеличивается в 2 раза)

Указания к решению: sin nx=0 ; x=/n;

где n=1,2,4,8,16…;

S=2+1+1/2+1/4+1/8+…=2/(1-1/2)=4

Ответ: 4.

5. Задачи с индивидуальным подходом

Задачи, которые прокомментируют сейчас ученики, имеют индивидуальный подход. Поэтому, прежде чем приступить к их решению, надо проанализировать заданную ситуацию. Решения этих задач в тетрадях не пишутся, дома же вы их решите, по возможности, несколькими способами.

1) Найти площадь фигуры, ограниченной линиями y=x2-4x+8 и y=3x2-x3, если х[-2;3]

Решение:

  • Если не рисовать графиков данных функций, то надо узнать имеют ли эти графики общие точки на (-2;3).Для этого надо решить уравнение:

3x2-x3= x2-4x+8. Итак, х=2 и х=-2. 2(-2;3).

Не зная, график какой из функций находится выше другого на (-2;2) и (2;3], площадь фигуры находится так

 

  • Если же нарисовать графики данных функций (что очень не сложно), то замечаем, что всюду на [-2;3] выполняется неравенство: х2-4x+83х2-х3

    • Сравнивая формулы, полученные для вычисления площади S, видим, что в данном примере значительно легче искать площадь после того, как нарисованы графики функций. А можно ли всё-таки решить задачу, не делая рисунка? Найдите ещё один способ решения! Но есть задачи, в которых построение графиков затруднено.

2) Найти площадь фигуры, ограниченную линиями: y=x2-4x+sin2x/2 и y=-3-cos2x/2, если х[2;3].

Решение:

Так как графики данных функций построить трудно, то можно выяснить соотношение между функциями, не используя графиков. Исследуем разность данных функций:

x2-4x+sin2x/2-(-3-cos2x/2)=x2-4x+4=(х-2)2 0

Следовательно, x2-4x+sin2x/2>-3-cos2x/2 на [2;3], а, значит, график первой функции лежит выше графика второй функции и

3) Вычислить площадь фигуры, ограниченной данными линиями:y=x2 при x0, y=1, y=4, x=0

Решение:

Данная фигура симметрична криволинейной трапеции, ограниченной прямыми х=1, х=4, у=0, графиком функции , обратной у=х2, x0. Поэтому эти фигуры имеют равные площади и .

А всегда ли рационально использовать интеграл при нахождении площади фигуры?

4) Найти площадь фигуры, ограниченной прямыми у=3х+1, у=9-х, у=х+1.

Решение:

Вершины полученного ABC имеют координаты: А(0;1), В(2;7), С(4;5).

Можно заметить, что ABC — прямоугольный (произведение угловых коэффициентов прямых у=х+и у=9-х равно -1). Поэтому применение интеграла для вычисления S(ABC) не рационально. Её всегда можно найти как разность площадей треугольников, у которых известны высота и основание или же можно использовать координатный метод.

6. Домашнее задание

Найти площади фигур, ограниченных линиями (1-7)

  1. у=х2 (х0), у=1, у=4, х=0
  2. у=х2-4х+8, 3х2-х3, если если х[-2;3]
  3. у=х2-4х+sin2(x/2), y=-3-cos2(x/2), если х[2;3]
  4. у=3х+1, у=9-х, у=х+1
  5. у=|x-2|,
  6. x|y|=2;x=1;x=3
  7. y= arcsin x; у=0; x=0,5; x=1
  8. При каком значении а прямая х=а делит площадь фигуры, ограниченной линиями у=2/х; х=1; х=3 в отношении 1:3?
  9. Вычислить   исходя из его геометрического смысла.

Составить карточку (можно несколько) для зачета, в которой должны быть:

  1. Теоретический вопрос: (определение, свойств без доказательства)
  2. Теоретический вопрос: (с доказательством)
  3. Пример на вычисление неопределенного интеграла (одним из методов)
  4. Пример на вычисление определённого интеграла.
  5. Пример на нахождение первообразной сложной функции.
  6. Пример на нахождение площади фигуры.

7. Итог урока

1402 — Стр 9

4. Вычислить длину кривой, заданной уравнением в декартовой системе координат

 

1

3

 

y

1 2x

 

4 x 0 .

2

 

3

 

 

 

 

 

Вариант 9

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y x2; y x2 ; x 2. 4

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

xt sint; y 1 cost 0 t 2 .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r sin6 .

4. Вычислить длину кривой, заданной уравнением в декартовой системе координат

y 1 ex e x 0 x 3 . 2

Вариант 10

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

yx2; y x; x 2.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x5 t sint ; y 5 1 cost 0 t 10 .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r cos6 .

4. Вычислить длину кривой, заданной уравнением в декартовой системе координат

y ex e ln3 x ln15 .

83

Вариант 11

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

ysin x;y x; x .

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

 

 

2

 

2

 

x cost;

y sint

 

t

 

.

2

2

 

 

 

 

3. Вычислить площадь фигуры, ограниченной линией, заданной уравнением в полярных координатах

r sin5 .

4. Вычислить длину кривой, заданной уравнением в декартовой системе координат

y 10 ln x2 1 2 x 5 .

Вариант 12

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

yx3;y x .

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

 

 

 

x 2cost; y 2sint

0 t

 

.

4

 

 

 

3. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

 

 

 

 

 

 

 

 

 

 

r

3cos ;

r sin

0

 

.

2

 

 

 

 

 

 

4. Вычислить длину кривой, заданной уравнением в декартовой системе координат

 

 

 

 

7

 

 

1 x2

 

y

arcsinx

0 x

 

.

9

 

 

 

 

 

84

Вариант 13

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y ln x; x 1; x e; y 0.

2.Вычислить площадь фигуры, ограниченной петлей линии

x2t2 1; y t3 t .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r6 1 cos .

4.Вычислить длину кривой, заданной уравнением в декартовой системе координат

 

 

 

y lnsinx

 

x

 

.

4

 

 

2

 

Вариант 14

1.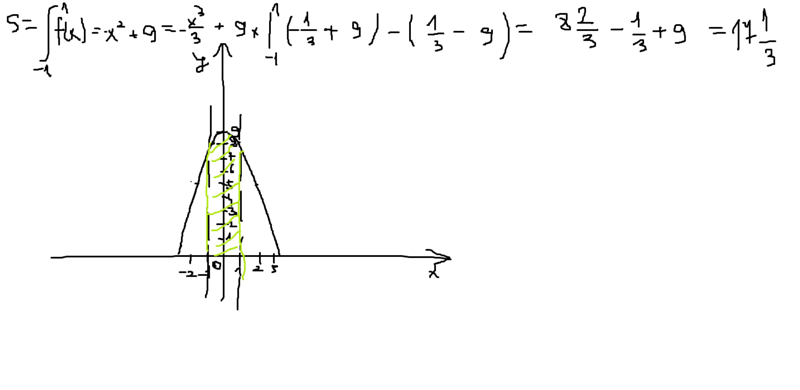 Вычислить площадь фигуры, ограниченной графиками функ-

ций

y x2; y x 6.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x2 t sint ; y 2 1 cost ; y 0.

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r 2cos ; r 3cos .

4. Вычислить длину кривой, заданной уравнением в декартовой системе координат

y ln x2 1 2 x 3 .

Вариант 15

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

85

y4x x2;y 0.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x9cost; y 4sint 0 t .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r 1,5cos ;

r 2cos .

4. Вычислить длину кривой, заданной уравнением в декартовой системе координат

 

 

 

y 1 lncosx

0 x

 

.

4

 

 

 

Вариант 16

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y tgx; x ;y 0. 4

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

xt sint; y 1 cost 0 t .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r1 cos .

4.Вычислить длину кривой, заданной уравнением в декартовой системе координат

y 0,25x 0,5lnx 1 x 2 .

Вариант 17

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y = (x – 2)3; y = 4x – 8.

2. Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат:

x 4 t sint ; y 4 1 cost 0 t 2 .

86

3. Вычислить площади фигуры, ограниченной линией, заданной уравнением в полярных координатах:

r4cos3 .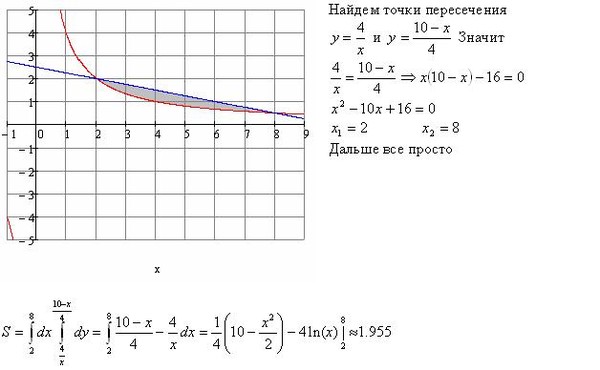

4.Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат:

y 25 x 4x 23 4×3 0 x 2 .

Вариант 18

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y = 4 – x2; y = x2 – 2x.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x2cost; y 6sint 0 t .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

 

 

 

 

 

 

 

 

x

3cos ; y sin

0

 

.

2

 

 

 

 

 

4. Вычислить длину дуги кривой, заданной уравнениями в прямоугольной системе координат

y x2 lnx 1 x 2 . 4 2

Вариант 19

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y

 

1

 

; y = 0; x= 1; x = e3.

 

 

 

x

1 ln x

 

 

 

2.Вычислить площадь фигуры, ограниченной петлей линии

x3t2 1; y t4 t2 .

3.Вычислить площадь фигуры, ограниченной линией, заданной уравнением в полярных координатах

r 6sin3 .

4. Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат

87

x x

0 x 2 .

y e2 e 2

Вариант 20

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y = (x + 1)2; y2 = x + 1.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x22cost; y 32sint 0 x 4 .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

xcos ; y 2cos .

4.Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат

y 4 2lnsin0,5x 0,75 x 1,5 .

Вариант 21

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y7 x2; y x 5.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x6 t sint ; y 6 1 cost 0 t 2 .

3.Вычислить площадь фигуры, ограниченной линией, заданной уравнением в полярных координатах

r 1 2cos .

4. Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат

 

1

3

 

 

 

 

.

y

x2 2

 

 

x

 

 

2

7

2

 

3

 

 

 

 

 

 

 

Вариант 22

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

88

y = 2x – x2 + 3; y = x2 – 4х + 3.

2. Вычислить площадь области, ограниченной кривой, заданной в

параметрической системе координат

 

 

 

 

x 6cost; y 4sint

0 t

 

.

 

 

 

2

3. Вычислить площадь фигуры, ограниченной линией, заданной уравнением в полярных координатах

r1 2sin .

4.Вычислить длины дуг кривых, заданных уравнениями в прямоугольной системе координат

y2 x 1 3 2 x 5 .

Вариант 23

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y lnx; x e; x e2 .

2.Вычислить площадь фигуры, ограниченной линией, заданной уравнением в параметрической системе координат

xcost; y 2sint 0 t 2 .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

x 3cos ; y 5cos .

22

4.Вычислить длину дуги кривой, заданной уравнением в прямо-

угольной системе координат

y1 x2 1 2

между точками пересечения с осью 0х.

Вариант 24

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y x2 1; y x.

2. Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

89

x 3cost; y 4sint 0 t .

3. Вычислить площадь фигуры, ограниченной линией, заданной уравнением в полярных координатах

rsin6 .

4.Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат

9y2 4×3 0 x 3 .

Вариант 25

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y = (x – 1)2; y2 = x – 1.

 

 

2. Вычислить площадь области, ограниченной кривой, заданной в

параметрической системе координат

 

 

 

 

x 4cost; y 2sint

0 t

 

.

 

 

 

2

3. Вычислить площадь фигуры, ограниченной линией, заданной уравнением в полярных координатах

r2cos6 .

4.Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат

x2 2y 3 0

между точками ее пересечения с осью 0х.

Вариант 26

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

xy 1; x 2; y x.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x6cost; y 2sint 0 t .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r 3cos ;

r 5sin .

90

4. Вычислить длины дуги кривой, заданной уравнением в прямоугольной системе координат

y 2 ex ln3 x ln8 .

 

Вариант 27

1.

Вычислить площадь фигуры, ограниченной графиками функ-

ций

y2 2x 4; x 0.

 

2.

Вычислить площадь области, ограниченной кривой, заданной в

параметрической системе координат

 

 

r 3cost;

r 8sint .

3.

Вычислить площадь фигуры, ограниченной линией, заданной

уравнением в полярных координатах

 

rcos sin .

4.Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат

 

 

 

 

 

1

 

 

 

 

 

2

 

 

 

 

y 5 arccos

x

x x

 

 

 

x 1 .

 

9

 

 

 

 

 

 

 

Вариант 28

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y2 x2; y 2x 1.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

 

 

 

 

x 3cost;

y 2sint

0 t

 

.

2

 

 

 

 

3. Вычислить площадь фигуры, ограниченной линией, заданной уравнением в полярных координатах

r cos2 .

4. Вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат

y 26 ex ln8 x ln24 .

91

Библиографический список

1.Пискунов Н.С. Дифференциальное и интегральное исчисления для вту-

зов. – М.: Наука,1970. – 1985. – Т.1.

2.Шипачев В.С. Высшая математика. – М.: Высшая школа, 1985.

3.Бугров Я.С. Высшая математика. Дифференциальное и интегральное исчисления/ Я.С.Бугров, С.Н.Никольский. – М.: Наука, 1989.

4.Данко П.Е. Высшая математика в упражнениях и задачах/ П.Е. Данко, А.Г.Попов. – М.: Высшая школа, 1989. – Т.1.

5.Бугров Я.С. Высшая математика: Задачник/ Я.С.Бугров, C.М. Никольский. – М.: Наука, 1982.

92

volume of solid of revolution

AlleBilderVideosNewsMapsShoppingBücher

Suchoptionen

Scheibenmethode (Disc integration)

Alle anzeigen

Scheibenintegration, in der Integralrechnung auch als Scheibenmethode bekannt, ist eine Methode zur Berechnung des Volumens eines Rotationskörpers eines Festkörpermaterials, wenn entlang einer Achse «parallel» zur Rotationsachse integriert wird. Wikipedia (на английском языке)

Rotationskörper

Rotationskörper wird in der Geometrie ein Körper genannt, dessen Oberfläche durch Rotation einer erzeugenden Kurve um eine …

Исчисление I — Объемы тел вращения / Метод колец

tutorial.edmathlache calci › volumewithrings

16.11.2022 · В этом разделе мы начнем рассматривать объем тела вращения. Сначала мы должны определить, что такое тело вращения.

Ähnliche Fragen

Как найти объем твердого тела?

Что такое формула тела вращения?

Какова формула объема твердого тела?

Каков объем вики-тела вращения?

Volumes of Solids of Revolution — Cliffs Notes

www.cliffsnotes.com › исчисление › исчисление › объем…

Если поперечные сечения тела взяты параллельно оси вращения, то цилиндрическая оболочка Метод будет использоваться для нахождения объема твердого тела.

[PDF] Объемы тел вращения — Mathcentre

www. mathcentre.ac.uk › ресурсы › загружено › mc-ty-volumes-2009-1

Теперь эта формула дает нам способ расчета объемов тел вращения вокруг оси x. Ключевой момент. Если y задан как функция x, объем …

Вычисление объема тела вращения интегрированием

www.youtube.com › смотреть

30.05.2018 · Мы можем найти объем вещей, называемых телами вращения, опять же путем интегрирования, это просто…
Dauer: 11:20
Прислано: 30.05.2018

Объем тела вращения: диски и шайбы — Math34.net

math34.net

Вычислите объем твердого тела, полученного путем вращения области, ограниченной параболой и функцией квадратного корня, вокруг оси. Решение.

Solid of Revolution — Википедия

en.wikipedia.org › wiki › Solid_of_revolution

Репрезентативный диск представляет собой трехмерный объемный элемент тела вращения. Элемент создается путем вращения отрезка линии (длиной w) вокруг …

3.3 Объем вращения: дисковый метод

www. sfu.ca › math-coursenotes › sec_volume

Поскольку объем твердого тела вращения рассчитывается с использованием дисков, этот тип вычислений часто называют дисковым методом. 🔗. Захватываем наш …

Объем тела вращения | Математические примеры — LAKschool

lakschool.com › математика › применение интегрального исчисления

Объем тела вращения Другим применением интегрального исчисления является вычисление объема тела вращения. Тела вращения …

Объяснение урока: Объемы тел вращения — Nagwa

www.nagwa.com › объяснители

Определение: Объем тел вращения · 𝑦 = 𝑓 ( 𝑥 ) · 𝑥 · 𝑥 = 𝑎 · 𝑥 = 𝑏 · 𝑥 · 𝑉 = 𝜋 [ 𝑓 ( 𝑥 ) ] 𝑥 .

1.1: Объемы тел вращения — сечения — Math LibreTexts

math.libretexts.org › … › 1: Applications of Integration

18.02.2022 · Тело, показанное на рисунке, является примером цилиндра с некруглым основанием. Чтобы вычислить объем цилиндра, мы просто умножаем …

Ähnlichesuchanfragen

Тела вращения вокруг оси Y

Интеграл объема сферы

Метод оболочки

Объем дискового калькулятора

Дисковый метод

Объем вращения Wolfram Alpha

4a.

Объем тела вращения путем интегрирования (дисковый метод)

М. Борн

Токарный станок

Многие твердые предметы, особенно изготовленные на токарном станке , имеют круглое поперечное сечение и изогнутые стороны. На этой странице мы видим, как найти объем таких объектов с помощью интеграции.

Изделия, изготовленные на токарном станке…

Пример 1

приложений

Не пропустите приложения для винных бочек и арбузов в этом разделе.

Рассмотрим область, ограниченную прямой линией «y = 3x», осью «x» и «x = 1»:

12-1-2123-1xyОткрыть изображение на новой странице

График `y=3x` с заштрихованной областью под «кривой» между `x=0` и `x=1`.

Когда заштрихованная область поворачивается на 360° вокруг оси `x`, создается объем.

Полученное твердое тело представляет собой конус:

123-3xy1Открыть изображение на новой странице

Область под кривой `y=3x` от `x=0` до `x=1`, повернутая вокруг оси `x`, показывает типичный диск.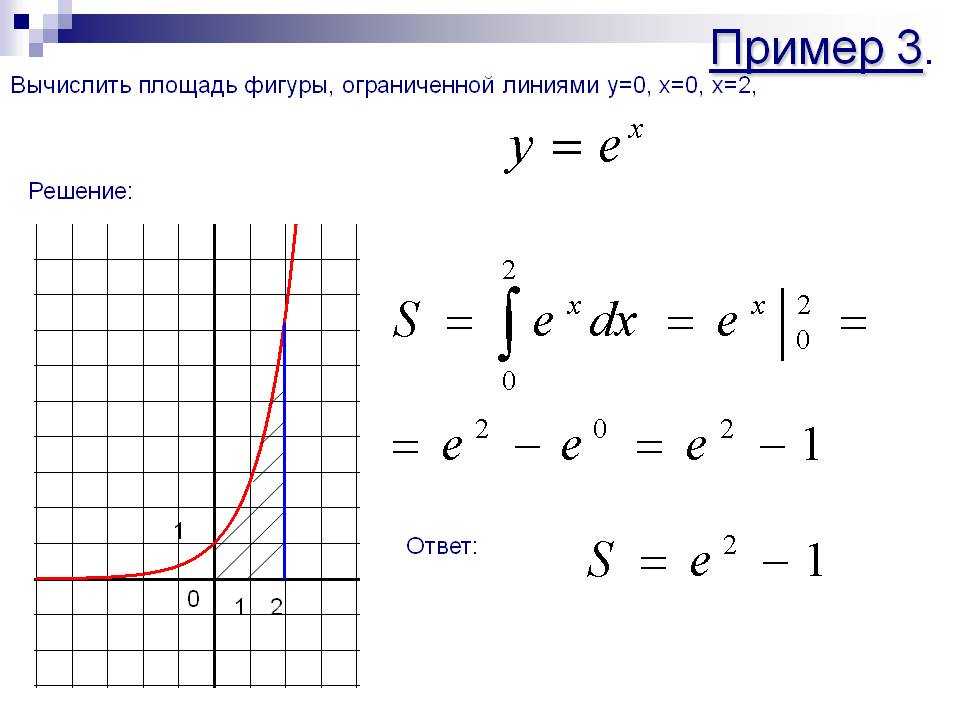 2dx` к предыдущему примеру, мы получаем: 92]dx`

На следующем общем графике `y_2` выше `y_1`. Нижний и верхний пределы области, подлежащей вращению, обозначены вертикальными линиями в точках ‘x = a’ и ‘x = b’.

Область, ограниченная кривыми y_1 и y_2 и линиями x=a и x=b, включая типичный прямоугольник.xyab

`y_2`

`у_1`

Область, ограниченная кривыми `y_1` и `y_2` и линиями `x=a` и `x=b`.

Когда мы вращаем такую ​​фигуру вокруг оси и делаем срезы, получается 92` (нижняя кривая), `y = x+1` (линия выше) и `x = 0`, показывая типичный прямоугольник.

Нижний предел интегрирования `x = 0` (поскольку в вопросе сказано `x ≥ 0`).

Далее нам нужно найти место пересечения кривых, чтобы мы знали верхний предел интегрирования.

Приравнивание двух выражений и решение:

2 х 2 = х + 1

2 х 2 — х — 1 = 0

93`

Упражнения

Найти объем, образованный площадями, ограниченными данными кривыми, если они вращаются вокруг заданной оси:

(1) Прямая `y = x` между `y = 0` и `x = 2` вращается вокруг оси `x`.

Ответ

Это область, которую нужно повернуть вокруг оси x:

12-112-1xyОткрыть изображение на новой странице

График `y=x`, с областью под «кривой» между `x=0` и `x=2` заштриховано.

Следовательно, образовавшийся объем можно найти по формуле объема тела вращения: 92 = 4` в квадранте I вращается вокруг оси y.

Ответ

Мы признаем, что это эллипс. Вопрос говорит нам, что область интереса находится только в первом квадранте.

121xyyΔxy = f(x)Открыть изображение в новой странице = 2 и ось x .

Из диаграммы видно, что границы ограниченной области равны 93`

Приложения

1. Объем винной бочки

Винная бочка имеет радиус в верхней части 30 см и радиус в середине 40 см. Высота бочки 1м. Каков объем бочки (в л), если предположить, что форма стенок параболическая?

Ответ

Положим бочку на бок, чтобы упростить алгебру:

2550-25-5010203040-10-20-30-40xyОткрыть изображение на новой странице

Парабола с вершиной в `(0, 40)` и проходящей через ` (50, 30)`.


Нам нужно найти уравнение параболы с вершиной в точке `(0, 40)` и проходящей через `(50, 30)`.

Используем формулу:

( x − h ) 2 = 4 a ( y − k )

Теперь ( h , k ) равно (0, 40), поэтому мы имеем: x 2 = 4 a ( y − 40) и парабола проходит через 0 (50, 3) , так что

92ч`.

Интересно, что Архимед (тот самый, который, как известно, выпрыгнул из ванны и побежал по улице с криком «Эврика! Я понял») использовал этот подход для нахождения объемов сфер около 200 г. до н.э. Этот метод был почти забыт до начала 1700-х годов, когда исчисление было разработано Ньютоном и Лейбницем.

Мы видим, как решить задачу, используя оба подхода.

Объем с использованием исторического метода:

Ответ

Поскольку дыня симметрична, мы можем определить объем половины дыни, а затем удвоить наш ответ.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *