Курс высшей математики, Т.2
Курс высшей математики, Т.2
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТНАДЦАТОМУ ИЗДАНИЮГЛАВА I. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2.  (n)=f(x). (n)=f(x).19. Системы обыкновенных дифференциальных уравнений. 20. Примеры. 21. Системы уравнений и уравнения высших порядков. 22. Линейные уравнения с частными производными. 23. Геометрическая интерпретация. 24. Примеры. ГЛАВА II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 25. Линейные однородные уравнения второго порядка. 26. Линейные неоднородные уравнения второго порядка. 27. Линейные уравнения высших порядков. 28. Однородные уравнения второго порядка с постоянными коэффициентами. 29. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. 30. Частные случаи. 31. Корни решений и колеблющиеся решения 32. Линейные уравнения высших порядков с постоянными коэффициентами. 33. Линейные уравнения и колебательные явления. 34. Собственные и вынужденные колебания. 35. Синусоидальная внешняя сила и резонанс.  36. Предельные задачи. 37. Примеры. 38. Символический метод. 39. Линейные однородные уравнения высших порядков с постоянными коэффициентами. 40. Линейные неоднородные уравнения с постоянными коэффициентами. 41. Пример. 42 Уравнение Эйлера. 43. Системы линейных уравнений с постоянными коэффициентами. 44. Примеры § 4. ИНТЕГРИРОВАНИЕ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ 45. Интегрирование линейного уравнения с помощью степенного ряда 46. Примеры. 47. Разложение решения в обобщенный степенной ряд. 48. Уравнение Бесселя 49. Уравнения, приводящиеся к уравнению Бесселя § 5. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ПО ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 50. Метод последовательных приближений для линейных уравнений. 51. Случай нелинейного уравнения. 52. Дополнения к теореме существования и единственности. 54. Особые точки дифференциальных уравнений первого порядка. 55. Автономные системы. 56. Примеры.  ГЛАВА III. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА § 6. КРАТНЫЕ ИНТЕГРАЛЫ 58. Двукратный интеграл. 59. Вычисление двукратного интеграла. 60. Криволинейные координаты. 61. Трехкратный интеграл 62. Цилиндрические и сферические координаты. 63. Криволинейные координаты в пространстве. 64. Основные свойства кратных интегралов. 65. Площадь поверхности. 66. Интегралы по поверхности и формула Остроградского. 67. Интегралы по определенной стороне поверхности. 68. Моменты. § 7. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ 69. Определение криволинейного интеграла. 70. Работа силового поля. Примеры. 71. Площадь и криволинейный интеграл. 72. Формула Грина 73. Формула Стокса. 74. Независимость криволинейного интеграла от пути на плоскости. 75. Случай многосвязной области. 76. Независимость криволинейного интеграла от пути в пространстве. 77. Установившееся течение жидкости. 78.  Интегрирующий множитель. Интегрирующий множитель.79. Уравнение в полных дифференциалах для случая трех переменных. 80. Замена переменных в двойном интеграле. § 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 81. Интегрирование под знаком интеграла. 82. Формула Дирихле. 83. Дифференцирование под знаком интеграла 84. Примеры. 85. Несобственные интегралы. 86. Неабсолютно сходящиеся интегралы. 87. Равномерно сходящиеся интегралы. 88. Примеры. 89. Несобственные кратные интегралы. 90. Примеры. § 9. МЕРА И ТЕОРИЯ ИНТЕГРИРОВАНИЯ 92. Основные теоремы. 94. Мера Жордана. 95. Квадрируемые множества. 96. Независимость от выбора осей. 97. Случай любого числа измерений. 98. Интегрируемые функции. 99. Вычисление двойного интеграла. 100. n-кратные интегралы. 101. Примеры. 102. Внешняя мера Лебега. 103. Измеримые множества. 104. Измеримые функции. 105.  Дополнительные сведения. Дополнительные сведения.106. Интеграл Лебега. 107. Свойства интеграла Лебега. 108. Интегралы от неограниченных функций. 109. Предельный переход под знаком интеграла. 110. Теорема Фубини. 111. Интегралы по множеству бесконечной меры. ГЛАВА IV. ВЕКТОРНЫЙ АНАЛИЗ И ТЕОРИЯ ПОЛЯ 112. Сложение и вычитание векторов. 113. Умножение вектора на скаляр. Компланарность векторов. 114. Разложение вектора по трем некомпланарным векторам. 115. Скалярное произведение. 116. Векторное произведение. 117. Соотношения между скалярным к векторным произведениями. 118. Скорости точек вращающегося твердого тела; момент вектора. § 11 ТЕОРИЯ ПОЛЯ 119. Дифференцирование вектора 120. Скалярное поле и его градиент. 121. Векторное поле; расходимость и вихрь. 122. Потенциальное и соленоидальное поля. 123. Направленный элемент поверхности. 124. Некоторые формулы векторного анализа. 125. Движение твердого тела и малая деформация. 126.  Уравнение непрерывности. Уравнение непрерывности.127. Уравнения гидродинамики идеальной жидкости. 128. Уравнения распространения звука. 129. Уравнение теплопроводности. 130. Уравнения Максвелла. 131. Выражение оператора Лапласа в ортогональных координатах. 132. Операция дифференцирования для случая переменного поля. ГЛАВА V. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ 134. Эвольвента. 135. Естественное уравнение кривой. 136. Основные элементы кривой в пространстве. 137. Формулы Френе. 138. Соприкасающаяся плоскость. 139. Винтовые линии. 140. Поле единичных векторов. § 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОВЕРХНОСТЕЙ 141. Параметрические уравнения поверхности. 142. Первая дифференциальная форма Гаусса. 143. Вторая дифференциальная форма Гаусса. 144. О кривизне линий, начерченных на поверхности. 145. Индикатриса Дюпена и формула Эйлера. 146. Определение главных радиусов кривизны и главных направлений. 147.  Линии кривизны. Линии кривизны.148. Теорема Дюпена. 149. Примеры. 150. Гауссова кривизна. 151. Вариация элемента площади и средняя кривизна. 152. Огибающая семейства поверхностей и кривых. 153. Развертывающиеся поверхности. ГЛАВА VI. РЯДЫ ФУРЬЕ 154. Ортогональность тригонометрических функций. 155. Теорема Дирихле. 156. Примеры. 157. Разложение в промежутке (0, п). 158. Периодические функции периода 2l. 159. Средняя квадратичная погрешность. 160. Общие ортогональные системы функций. 161. Класс L2 162. Сходимость в среднем. 163. Ортонормированные системы в L2. § 15. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ ФУРЬЕ 164. Разложение в ряд Фурье. 165. Вторая теорема о среднем. 166. Интеграл Дирихле. 167. Теорема Дирихле. 168. Приближение к непрерывной функции полиномами. 169. Формула замкнутости. 170. Характер сходимости рядов Фурье. 171. Улучшение сходимости рядов Фурье. 172. Пример. § 16. ИНТЕГРАЛ ФУРЬЕ И КРАТНЫЕ РЯДЫ ФУРЬЕ 173.  Формула Фурье. Формула Фурье.174. Ряды Фурье в комплексной форме. 176. Кратные ряды Фурье. ГЛАВА VII. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 177. Решение Даламбера. 178. Частные случаи. 179. Ограниченная струна. 180. Способ Фурье. 181. Гармоники и стоячие волны. 182. Вынужденные колебания. 183. Сосредоточенная сила. 184. Формула Пуассона. 185. Цилиндрические волны. 186. Случай n-мерного пространства. 187. Неоднородное волновое уравнение. 188. Точечный источник. 189. Поперечные колебания мембран. 190. Прямоугольная мембрана. 191. Круглая мембрана. 192. Теорема единственности. 193. Применение интеграла Фурье. § 18. ТЕЛЕГРАФНОЕ УРАВНЕНИЕ 195. Установившиеся процессы. 196. Устанавливающиеся процессы. 197. Примеры. 198. Обобщенное уравнение колебаний струны. 199. Неограниченная цепь в общем случае. 200. Способ Фурье для ограниченной цепи. 201.  Обобщенное волновое уравнение. Обобщенное волновое уравнение.§ 19. УРАВНЕНИЕ ЛАПЛАСА 202. Гармонические функции. 203. Формула Грина. 204. Основные свойства гармонических функций. 205. Решение задачи Дирихле для круга. 206. Интеграл Пуассона. 207. Задача Дирихле для сферы. 208. Функция Грина. 209. Случай полупространства. 210. Потенциал объемных масс. 211. Уравнение Пуассона. 212. Формула Кирхгофа. § 20. УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ 214. Неограниченный стержень. 215. Стержень, ограниченный с одного конца. 216. Стержень, ограниченный с обоих концов. 217. Дополнительные замечания. 218. Случай сферы. 219. Теорема единственности. |
Сложение и вычитание векторов
Определение
Сложение векторов иосуществляется поправилу треугольника.
Суммой двух
векторов иназывают
такой третий вектор,
начало которого совпадает с началом,
а конец — с концомпри
условии, что конец вектораи
начало векторасовпадают
(рис.
Для сложения векторов применяется также правило параллелограмма.
Определение
Правило параллелограмма — если два неколлинеарных вектора ипривести к общему началу, то векторсовпадает с диагональю параллелограмма, построенного на векторахи(рис. 2). Причем начало векторасовпадает с началом заданных векторов.
Определение
Вектор называетсяпротивоположным вектором к вектору , если онколлинеарен вектору , равен ему по длине, но направлен в противоположную сторону вектору.
Операция сложения векторов обладает следующими свойствами:
— коммутативность
— ассоциативность
Определение
Разностью векторов иназывается вектортакой, что выполняется условие:(рис. 3).
Умножение вектора на число
Определение
Произведением вектора на число называется вектор, удовлетворяющий условиям:
, если ,, если.

Свойства умножения вектора на число:
Здесь и- произвольные векторы,,- произвольные числа.
Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3.
В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов: конечномерное вещественное векторное пространство с введённым на нём положительно определённымскалярным произведением, либо метрическое пространство, соответствующее такому векторному пространству. В этой статье за исходное будет взято первое определение.
-мерное
евклидово пространство обозначается
также
часто используется обозначение(если
из контекста ясно, что пространство
обладает евклидовой структурой).
Для определения евклидова пространства проще всего взять в качестве основного понятие скалярного произведения. Евклидово векторное пространство определяется как конечномерное векторное пространство над полем вещественных чисел, на векторах которого задана вещественнозначная функция обладающая следующими тремя свойствами:
Билинейность: для любых векторов и для любых вещественных чисели
Симметричность: для любых векторов
Положительная определённость: для любого причём
Аффинное пространство, соответствующее такому векторному пространству, называется евклидовым аффинным пространством, или просто евклидовым пространством[1].
Пример евклидова пространства — координатное пространство состоящее из всевозможныхn-ок вещественных чисел скалярное произведение в котором определяется формулой
Базис и координаты вектора
Ба́зис (др. -греч. βασις, основа) — множество таких векторов в векторном
пространстве,
что любой вектор этого пространства
может быть единственным образом
представлен в виде линейной
комбинации векторов из этого множества — базисных
векторов.
-греч. βασις, основа) — множество таких векторов в векторном
пространстве,
что любой вектор этого пространства
может быть единственным образом
представлен в виде линейной
комбинации векторов из этого множества — базисных
векторов.
В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:
Базис Га́меля, в определении которого рассматриваются только конечные линейные комбинации. Базис Гамеля применяется в основном в абстрактной алгебре (в частности в линейной алгебре).
Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды. Это определение применяется в основном в функциональном анализе, в частности для гильбертова пространства,
В конечномерных пространствах обе разновидности базиса совпадают.
Координа́ты
ве́ктора ― коэффициенты единственно возможной линейной
комбинации базисных векторов в выбранной системе
координат,
равной данному вектору.
где — координаты вектора.
Скалярное произведение.
операция над двумя векторами, результатом которой является число [когда рассматриваются векторы, числа часто называют скалярами], не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.
Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:
Векторное произведение
это псевдовектор, перпендикулярный плоскости, построенной по двум
сомножителям, являющийся результатом бинарной
операции «векторное умножение» над векторами в трёхмерном евклидовом
пространстве. Векторное произведение не обладает
свойствами коммутативности и ассоциативности (является антикоммутативным)
и, в отличие от скалярного
произведения векторов,
является вектором. Широко используется
во многих технических и физических
приложениях. Например, момент
импульса и сила
Лоренца математически записываются в виде
векторного произведения. Векторное
произведение полезно для «измерения»
перпендикулярности векторов — модуль
векторного произведения двух векторов
равен произведению их модулей, если они
перпендикулярны, и уменьшается до нуля,
если векторы параллельны либо
антипараллельны.
Векторное произведение не обладает
свойствами коммутативности и ассоциативности (является антикоммутативным)
и, в отличие от скалярного
произведения векторов,
является вектором. Широко используется
во многих технических и физических
приложениях. Например, момент
импульса и сила
Лоренца математически записываются в виде
векторного произведения. Векторное
произведение полезно для «измерения»
перпендикулярности векторов — модуль
векторного произведения двух векторов
равен произведению их модулей, если они
перпендикулярны, и уменьшается до нуля,
если векторы параллельны либо
антипараллельны.
где
Смешанное произведение
Сме́шанное произведе́ние векторов —скалярное произведение вектора навекторное произведение векторов и:
.
Иногда
его называют тройным
скалярным произведением векторов, по всей видимости из-за того,
что результатом является скаляр (точнее — псевдоскаляр).
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами .смешанное произведение трех векторов можно найти через определитель
Плоскость в пространстве
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
Некоторые характеристические свойства плоскости
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;
Две плоскости являются либо параллельными, либо пересекаются по прямой.
Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.
Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.
Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.

Аналогично отрезку и интервалу, плоскость, не включающую крайние точки, можно назвать интервальной плоскостью, или открытой плоскостью.
где и— постоянные, причёмиодновременно не равны нулю; ввекторной форме:
где — радиус-вектор точки, векторперпендикулярен к плоскости (нормальный вектор).Направляющие косинусы вектора :
где ,,— отрезки, отсекаемые плоскостью на осяхи.
в векторной форме:
Нормированное уравнение плоскости
нормальное уравнение плоскости вида задает в прямоугольной системе координатOxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости .
Прямая в пространстве
Прямая
в пространстве может быть задана как
линия пересечения двух плоскостей.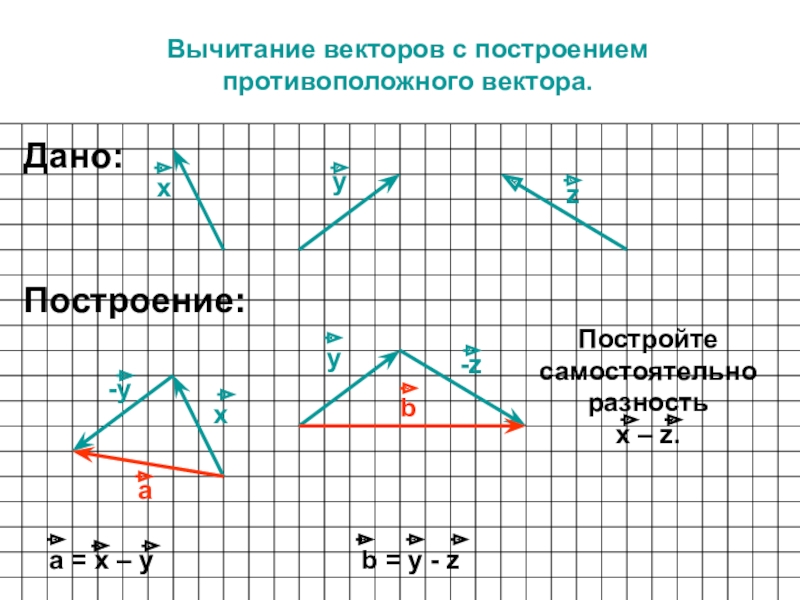 Так
как точка прямой прнадлежит каждой из
плоскостей, то ее координаты обязаны
удовлетворять уравнениям обеих
плоскостей, то есть удовлетворять
системе из двух уравнений.
Так
как точка прямой прнадлежит каждой из
плоскостей, то ее координаты обязаны
удовлетворять уравнениям обеих
плоскостей, то есть удовлетворять
системе из двух уравнений.
итак, если уравнения двух непараллельных плоскостей — и, то прямая, являющаяся их линией пересечения, задается системой уравнений
(11.11) |
И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.
Уравнения (11.11) называют общими уравнениями прямой в пространстве.
Уравнение окружности
Уравнение окружности радиуса с центром вначале координат:
Эллипс. Каноническое уравнение. Эксцентриситет, фокальный радиус.
Э́ллипс — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек и(называемыхфокусами) постоянна и больше расстояния между фокусами, то есть
причем
Окружность является частным случаем эллипса. Наряду
с гиперболой и параболой,
эллипс является коническим
сечением и квадрикой.
Наряду
с гиперболой и параболой,
эллипс является коническим
сечением и квадрикой.
Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
Вычитание векторов – Практические задачи от Ведущего урока
Учебное пособие и 20 практических задач по:
Вычитание векторов
Учебное пособие
$\langle y_1, y_2\rangle — \langle x_1, x_2\rangle = \langle y_1-x_1, y_2-x_2\rangle$.
(3 задачи)
Вектор из $\bfx$ в $\bfy$ задается как $\bfy — \bfx$.
(14 задач)
Вычитание вектора аналогично сложению отрицательного значения вектора: $$\bfy — \bfx = \bfy + (- \bfx).$$
(1 проблема)
Похожие темы
Река течет со скоростью $10$ м/с в северо-восточном направлении.
 Конкретная лодка может двигаться со скоростью $20$ м/с относительно воды. В каком направлении должна быть направлена лодка, чтобы двигаться строго на запад?
Конкретная лодка может двигаться со скоростью $20$ м/с относительно воды. В каком направлении должна быть направлена лодка, чтобы двигаться строго на запад?Решение
Решение
Найдите длину вектора от $(2,4,5)$ до $(3, -1, -2)$.
Решение
Векторы $\mathbf{a}$, $\mathbf{b}$, $\mathbf{c}$ и $\mathbf{d}$ показаны ниже. Используя только векторное сложение и вычитание, выразите $\mathbf{b}$ через $\mathbf{a}$, $\mathbf{c}$ и $\mathbf{d}$.
Решение
Пусть $\mathbf{z}$ — точка, находящаяся на одной трети пути от $\mathbf{x}$ до $\mathbf{y}$. Используя векторную арифметику, выразите $\mathbf{z}$ через $\mathbf{x}$ и $\mathbf{y}$.
Решение
Предположим, что две противоположные стороны четырехугольника параллельны и имеют одинаковую длину.
 Докажите, что четырехугольник является параллелограммом.
Докажите, что четырехугольник является параллелограммом.Решение
Рассмотрим произвольный четырехугольник. Два синих отрезка соединяют середины соседних сторон. Используя только сложение векторов и умножение на константы, покажите, что эти отрезки параллельны и имеют одинаковую длину.
Решение
Докажите, что прямая, соединяющая середины двух сторон треугольника, параллельна третьей стороне и составляет половину ее длины.
Решение
Используйте векторное сложение, вычитание и скалярное умножение, чтобы показать, что средняя точка между двумя точками $\mathbf{x}$ и $\mathbf{y}$ равна $\frac{\mathbf{x} + \mathbf{y} {2}$.
Решение
Пусть $\mathbf{O}, \mathbf{N}, \mathbf{B}$ — три точки, как показано.
(a) Каков знак скалярного произведения $(\mathbf{B} — \mathbf{O}) \cdot (\mathbf{N} — \mathbf{O})$?
(b) Каков знак скалярного произведения $(\mathbf{B} — \mathbf{N}) \cdot (\mathbf{N} — \mathbf{O})$?Решение
- больше проблем
Аналитические методы – Колледж физики
Резюме
- Понимание правил сложения и вычитания векторов с использованием аналитических методов.

- Применение аналитических методов для определения векторов вертикальной и горизонтальной составляющих.
- Применение аналитических методов для определения величины и направления результирующего вектора.
Аналитические методы сложения и вычитания векторов используют геометрию и простую тригонометрию, а не линейку и транспортир графических методов. Часть графической техники сохранена, потому что векторы по-прежнему представлены стрелками для облегчения визуализации. Однако аналитические методы более лаконичны, точны и точны, чем графические методы, которые ограничены точностью, с которой может быть выполнен чертеж. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.
Аналитические методы и прямоугольные треугольники идут рука об руку в физике, потому что (среди прочего) движения вдоль перпендикулярных направлений независимы. Нам очень часто нужно разделить вектор на перпендикулярные компоненты. Например, имея вектор, как на рисунке 1, мы можем захотеть найти, какие два перпендикулярных вектора и , добавить, чтобы получить его.
Например, имея вектор, как на рисунке 1, мы можем захотеть найти, какие два перпендикулярных вектора и , добавить, чтобы получить его.
и определяются как компоненты осей x и y. Три вектора и образуют прямоугольный треугольник:
Обратите внимание, что эта связь между компонентами вектора и результирующим вектором сохраняется только для векторных величин (которые включают как величину, так и направление). Отношения не применимы только к величинам. Например, если восток, север и северо-восток, то верно, что векторы Однако это не правда, что сумма модулей векторов тоже равна. То есть
Таким образом,
Если известен вектор, то известны его модуль и угол (направление). Чтобы найти его x- и y-компоненты, мы используем следующие соотношения для прямоугольного треугольника.
Чтобы найти его x- и y-компоненты, мы используем следующие соотношения для прямоугольного треугольника.
и
Рисунок 2. Величины компонентов вектора A x и A y можно отнести к результирующему вектору A и угол θ с тригонометрическими тождествами. Здесь мы видим, что A x =A cos θ и A y =A sinθ .Предположим, например, что это вектор, представляющий полное перемещение человека, идущего по городу, который рассматривался в главе 3.1 «Кинематика в двух измерениях: введение» и главе 3.2 «Сложение и вычитание векторов: графические методы».
Рисунок 3. Мы можем использовать соотношения A x =A cos θ и A y =A sinθ для определения величины векторов горизонтальной и вертикальной составляющих в этом примере.
Тогда и так
Если известны перпендикулярные компоненты и вектора, то их можно найти и аналитически. Чтобы найти величину и направление вектора по его перпендикулярным компонентам, мы используем следующие соотношения:
Рисунок 4. Величина и направление результирующего вектора могут быть определены после того, как горизонтальная и вертикальная составляющие A x и A y .Обратите внимание, что это уравнение — всего лишь теорема Пифагора, связывающая катеты прямоугольного треугольника с длиной гипотенузы. Например, если и составляют 9 и 5 кварталов соответственно, то кварталы, опять же, соответствуют примеру человека, идущего по городу. Наконец, направление прежнее.
ОПРЕДЕЛЕНИЕ ВЕКТОРОВ И КОМПОНЕНТОВ ВЕКТОРОВ С ПОМОЩЬЮ АНАЛИТИЧЕСКИХ МЕТОДОВ
Уравнения и используются для нахождения перпендикулярных компонентов вектора, то есть для перехода от и к и Уравнения и используются для нахождения вектора по его перпендикулярным компонентам, то есть для перехода от и к и Оба процесса имеют решающее значение для аналитические методы сложения и вычитания векторов.
Чтобы увидеть, как складывать векторы, используя перпендикулярные компоненты, рассмотрите рисунок 5, на котором векторы и складываются для получения результирующего числа
. Рисунок 5. Векторы A и В — две ноги прогулки, а R — равнодействующее или полное перемещение. Вы можете использовать аналитические методы для определения величины и направления R . Если и представляют собой два этапа ходьбы (два перемещения), то это общее перемещение. Человек, совершающий прогулку, оказывается на вершине. Есть много способов добраться до одной и той же точки. В частности, человек мог пройти сначала в направлении x , а затем в направлении y 9.0123 -направление. Этими путями являются x — и y -компоненты равнодействующей, и Если мы знаем и можем найти и используя уравнения и Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.
Шаг 1. Определите оси X и Y, которые будут использоваться в задаче. Затем найдите компоненты каждого добавляемого вектора вдоль выбранных перпендикулярных осей . Используйте уравнения и, чтобы найти компоненты. На рисунке 6 эти компоненты равны и Углы, которые векторы и образуют с осью x , равны и соответственно.
Рисунок 6. Чтобы добавить векторы A и B , сначала определите горизонтальную и вертикальную составляющие каждого вектора. Это точечные векторы A x , A y , B x и B y показаны на изображении.Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси, складывая компоненты отдельных векторов вдоль этой оси . То есть, как показано на рисунке 7,
и
Рисунок 7.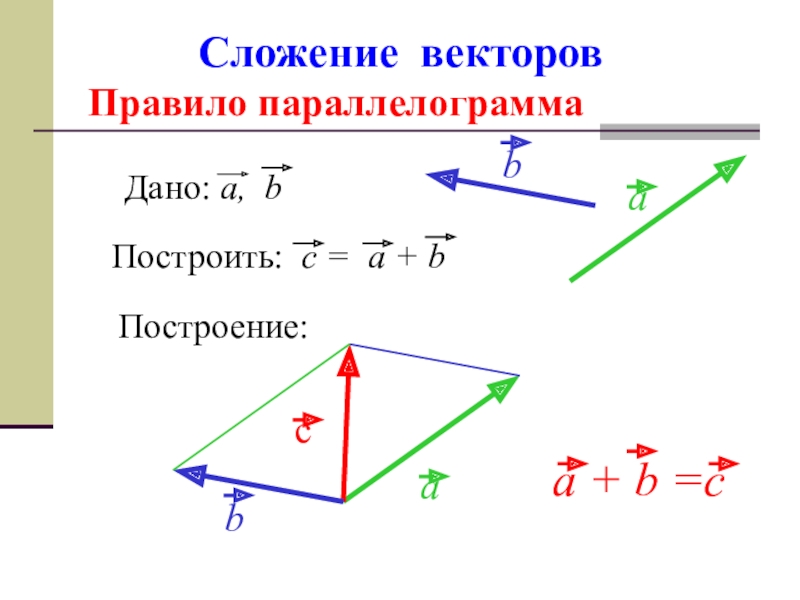 Величина векторов A x и B x суммируйте, чтобы получить величину R x результирующего вектора в горизонтальном направлении. Точно так же величины векторов A y и B y складываются, чтобы получить величину R y 3 в вертикальном направлении результирующего вектора.
Величина векторов A x и B x суммируйте, чтобы получить величину R x результирующего вектора в горизонтальном направлении. Точно так же величины векторов A y и B y складываются, чтобы получить величину R y 3 в вертикальном направлении результирующего вектора. Компоненты вдоль одной и той же оси, скажем, оси x , являются векторами вдоль одной и той же прямой и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль и -ось. (Например, пройти 9 кварталов на восток можно двумя этапами: первые 3 квартала на восток и вторые 6 кварталов на восток, всего 9, потому что они идут в одном направлении.) Таким образом, разложение векторов на компоненты вдоль общие оси облегчают их добавление. Теперь, когда компоненты известны, можно найти его величину и направление.
Теперь, когда компоненты известны, можно найти его величину и направление.
Шаг 3. Чтобы получить величину равнодействующей, используйте теорему Пифагора:
Шаг 4. Чтобы получить направление равнодействующей:
В следующем примере показан метод сложения векторов с использованием перпендикулярных компонентов.
Пример 1. Добавление векторов с помощью аналитических методов
Добавьте вектор к вектору, показанному на рис. 8, используя перпендикулярные компоненты вдоль осей x и y . Оси 90 122 x 90 123 и 90 122 y 90 123 проходят соответственно с востока на запад и с севера на юг. Вектор представляет собой первый этап прогулки, когда человек идет в направлении к северу от востока. Вектор представляет второй отрезок, смещение направления к северу от востока.
Рисунок 8. Вектор A имеет звездную величину 53,0 м и направление 20,0 0 к северу от оси x. Вектор B имеет величину 34,0 м и направление 63,0 0 к северу от оси x. Вы можете использовать аналитические методы для определения величины и направления R .
Вектор B имеет величину 34,0 м и направление 63,0 0 к северу от оси x. Вы можете использовать аналитические методы для определения величины и направления R .Стратегия
Компоненты осей x и y и вдоль них представляют ходьбу строго на восток и строго на север, чтобы добраться до одной и той же конечной точки. После обнаружения они объединяются для получения результирующего.
Решение
Следуя описанному выше методу, мы сначала находим компоненты и вдоль осей x и y . Обратите внимание, что и Мы находим x -компоненты, используя которые, получаем
и
Аналогично, y -компоненты находятся с помощью
и
x — и y -компоненты результатов таким образом,
и
Теперь мы можем найти величину равнодействующей, используя теорему Пифагора:
так что
Наконец находим направление равнодействующей:
Таким образом,
Рис. 0 к северу от востока.
0 к северу от востока.Обсуждение
Этот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание векторов осуществляется добавлением отрицательного вектора. Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты являются минусами компонентов x — и y -компоненты равнодействующей, таким образом,
и
, а остальная часть метода, описанного выше, идентична методу сложения. (См. рис. 10.)
Анализ векторов с использованием перпендикулярных компонент очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга. Следующий модуль, Глава 3.4 Движение снаряда, является одним из многих, в которых использование перпендикулярных компонентов помогает сделать картинку более ясной и упростить физику.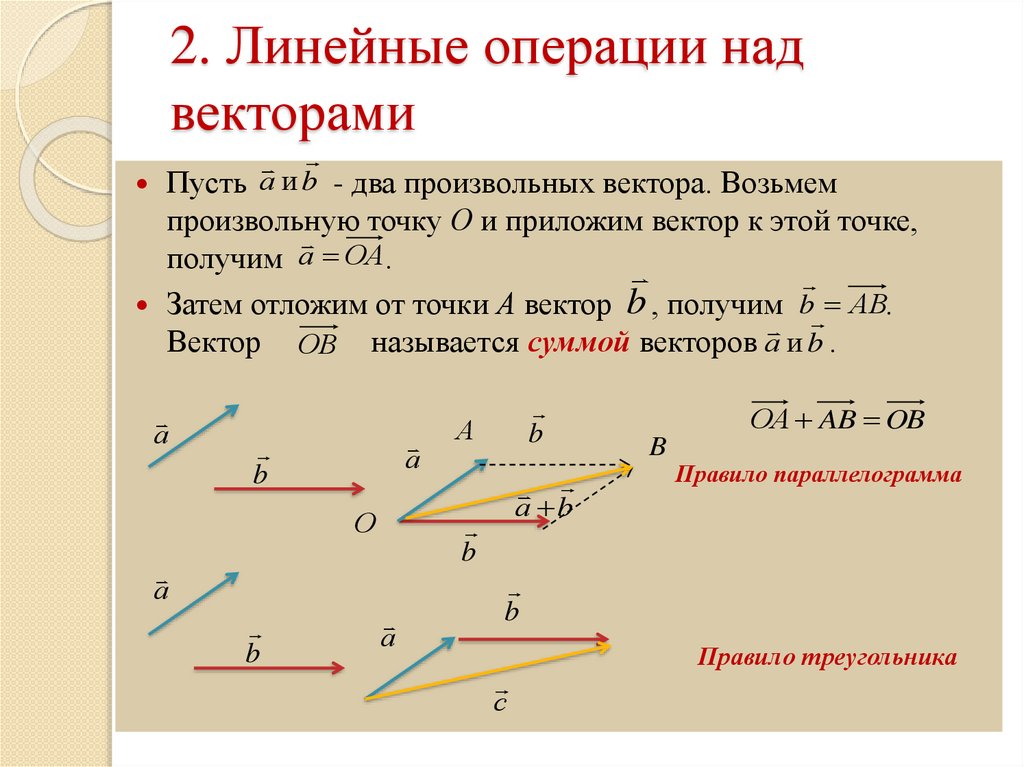



 Конкретная лодка может двигаться со скоростью $20$ м/с относительно воды. В каком направлении должна быть направлена лодка, чтобы двигаться строго на запад?
Конкретная лодка может двигаться со скоростью $20$ м/с относительно воды. В каком направлении должна быть направлена лодка, чтобы двигаться строго на запад? Докажите, что четырехугольник является параллелограммом.
Докажите, что четырехугольник является параллелограммом.