Векторы в пространстве (равенство векторов, коллинеарность векторов, компланарність векторов). Сложение, вычитание векторов, умножение вектора на число, свойства действий над векторами — ГЕОМЕТРИЯ — Планы-конспекты уроков для 10 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
Урок 58
Тема. Векторы в пространстве (равенство векторов, коллинеарность векторов, компланарність векторов).
Сложение, вычитание векторов, умножение вектора на число, свойства действий над векторами
Цель урока: формирование знаний учащихся о векторах в пространстве, действия над векторами, заданными координатами, Формирование умений применять изученный материал к решению задач.
Оборудование: схема «Векторы в пространстве».
Ход урока
записями на доске.
Решение задачи № 63
Пусть SOα, SAO = 45°, OAB = 45° (рис. 292). Проведем SOОА. Пусть SO = а; тогда ОА = а, OB = a. ΔOSA = ΔOSB = ΔОАВ (за двумя катетами). Из равенства треугольников следует, что SA = SB = AB, т.е. ΔSAB — равносторонний; следовательно, SAB = 60°.
Ответ. 60°.
II. Восприятие и осознание нового материала
Ученикам предлагается прочитать в учебнике п. 35 и 36 и познакомиться с векторами в пространстве и действиями над векторами в пространстве.
Далее предлагается фронтально обсуждать вопросы и выполнять дополнительные задания.
1. Что такое вектор? Что такое абсолютная величина вектора? Какие векторы называются одинаково напрямленими? противоположно напрямленими?
Задачи.
а) Укажите одинаково направлены, противоположно направленные векторы среди векторов, которые указаны на изображении прямоугольного параллелепипеда (рис. 293).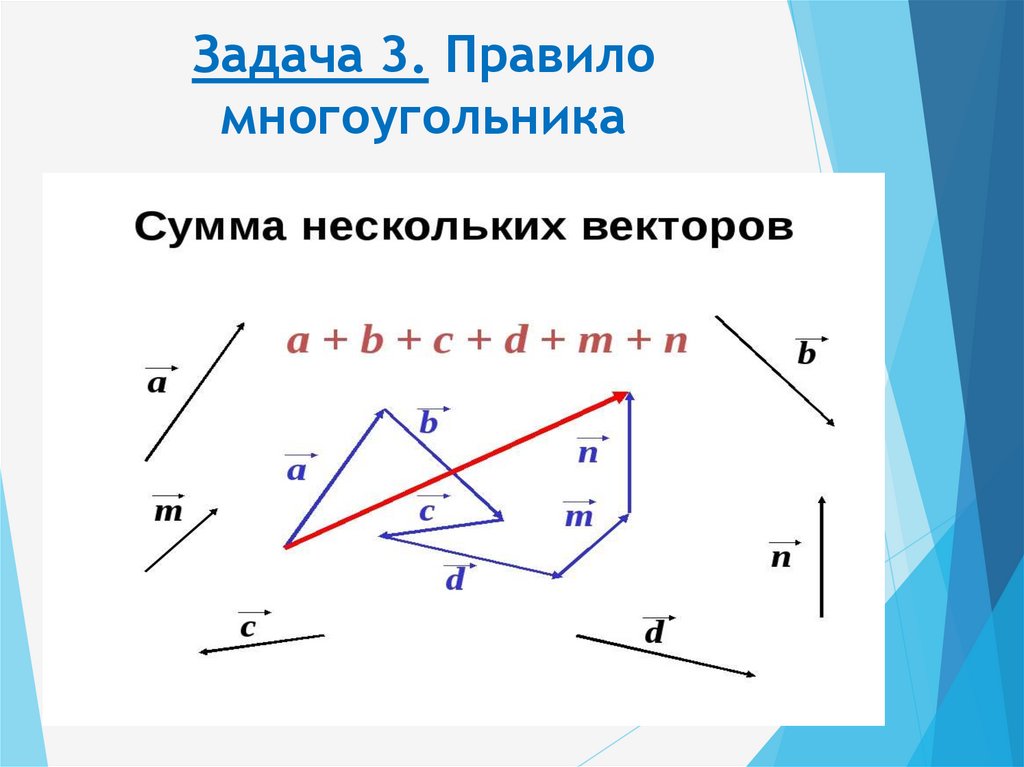
б) Найдите ||, ||,|| (рис. 294), если на рисунке изображен куб с ребром 5 см.
2. Какие векторы называются равными? противоположными?
Задачи.
а) ABCD — параллелограмм (рис. 295). Какие векторные равенства можно записать?
б) возможно Ли равенство векторов АВ и ВА ?
в) Укажите равные и противоположные векторы, если на рис.296 изображен прямоугольный параллелепипед.
3. Дайте определение координат вектора с началом в точке А (а1; а2; а3) и концом В точке В (b1; b2; b3). Условие равенства векторов, заданных координатами?
Задачи.
а) Даны точки А (2; 3; 4), B(1; 1; 1). Какие координаты векторов , ?
б) координаты вектора , если А (5; 1; -3), точка О — начало координат?
в) Когда вектор (1; 2; 3) отложили от начала координат, то получили вектор ОА.
Какие координаты точки А?
г) Найти ||, если А (1; 2; 3), В (3; 2; 1).
д) Даны точки А(3; -2; 5), В(-4; 6; 1), С(-2; — 6; -11), D(х; у; z). Найдите х, у, z, если .
е) Абсолютная величина вектора (5; 3; z) равна 9. Найдите z.
4. Что называется суммой (разностью) векторов (аx; y; z) и (bx; by; bz)? Условие принадлежности точек А, В, С прямой?
Задачи.
а) Даны векторы (4; -5; 6), (-1; 2; 5). Найдите: +, — , |+ |, | — |.
б) лежат Ли на одной прямой точки А, В, С, если А(3; -7; 8), В(-5; 4; 1), С (27; -40; 29)?
в) Найдите координаты точки C такой, что СА + СВ = 0, если А(-5; 7; 12), В(4; -8; 3).
г) Найдите координаты векторов и , если = + , = — , (4; -1; 5), (6; 3; 1).
д) может быть нулевым вектором сумма трех векторов, модули которых равны 7; 1; 8?
е) Упростите: +++++; +++++.
5. Что называется произведением вектора (аx; y; z) на число λ? Какие векторы называются коллинеарными? Условие колінеарності ненулевых векторов?
Задачи.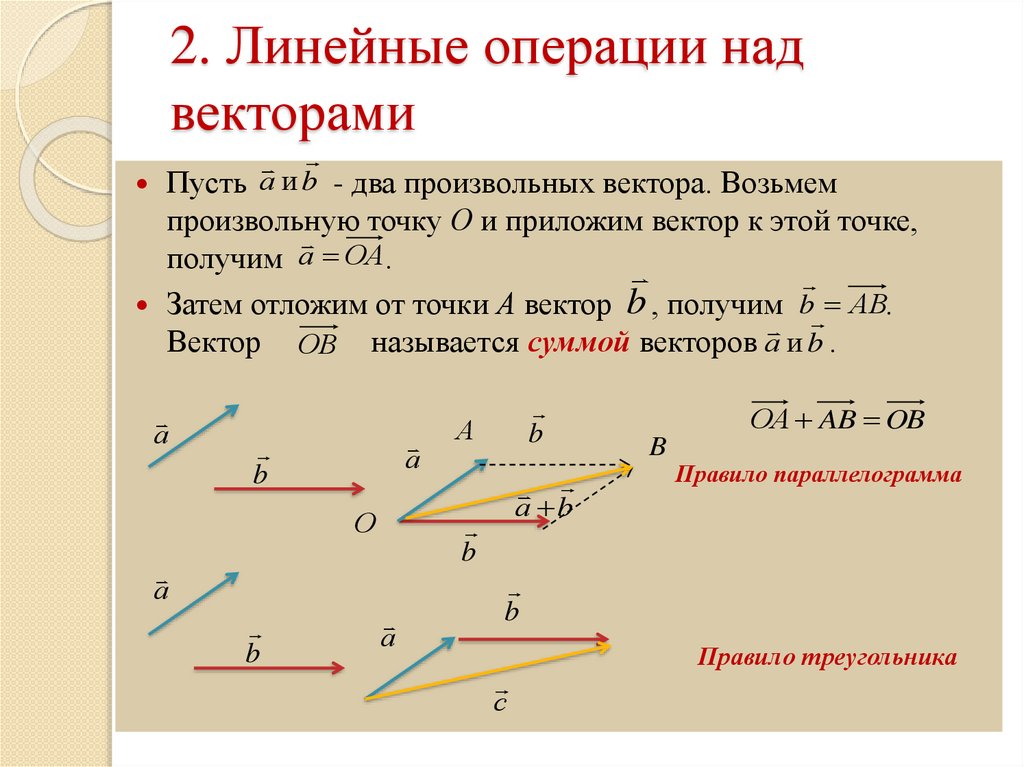
а) Дано (1; -2; 3), (-2; 1; -3). Найдите координаты векторов 2; — 3; 2 + 3; 2 — 3.
б) Найдите |2|, если (1; 2; 2).
в) коллинеарны Ли векторы (2; 3; 8) и (-4; 6; — 16) ?
г) При каком значении т и п векторы (15; т; 1) и (18; 12; п) коллинеарны?
д) коллинеарны Ли векторы АВ и CD, если А(3; -2; 5), B(-1; 4; 7), C(1; 3; 6), D(-3; 9; 18)?
е) При каких значениях т и п векторы АВ и CD коллинеарны, если A(1; 0; 2), B(3; n; 5), C(2; 2; 0), D(5; 4; m)?
6. Три вектора называют компланарними, если соответствующие им направленные отрезки размещены в параллельных плоскостях. Векторы , и компланарні только при условии, что точки О, А, В, С лежат в одной плоскости.
Задачи.
а) компланарні векторы (3; 2; 0), (6; 3; 0), (8; 1; 0)?
б) ABCD — тетраэдр, К, Р, Т — середины его ребер АВ, АС и AD. Или компланарні векторы , и ; , и ?
III. Домашнее задание
§4, п.
35-36; контрольные вопросы № 18-20; задачи № 51-53 (с. 58).
IV. Подведение итога урока
Подведение итога урока целесообразно провести с использованием данной схемы.
Векторы в пространстве |
|
Координаты вектора (рис. а) (хВ — хА; уВ — уА; zВ — zА) |
|
Длина вектора(аx; y; z): |
|
Равенство векторов(аx; y; z) = (bx; by; bz) |
|
Сумма векторов (рис. (аx; y; z) + (bx; by; bz) = (аx + bx; y + by; z + bz). + + = |
|
Разница векторов (рис. в) (аx; y; z) — (bx; by; bz) = (аx — bx; y — by; z — bz). — = |
|
Произведение вектора на число |
|
Коллинеарны векторыи коллинеарны, если = λ· |
|
б)
| Назад | Содержание | Вперед |
Геометрия. 10 класс. Понятие вектора в пространстве. Сложение и вычитание векторов
 Программа 10 и 11 класса
Смотрите все серииГеометрия. Программа 10 и 11 класса
|
Если вам пишется что ролик удалён, напишите нам в комментариях об этом.
Интеллект-видео. 2010.RSS |
- $a-b$ как о том, насколько похожи два вектора?
- $a + b$ как перемещение вектора $a$ в направлении вектора $b$?
- исчисление
- линейная алгебра
- векторные пространства
- векторы
$\endgroup$
3
$\begingroup$
Сложение векторов $\vec a + \vec b$ можно рассматривать как описание точки в конце $\vec b$, если $\vec b$ начинается в конце $\vec a$. На рисунке ниже красный вектор — это $\color{red}{\vec{a}}$, синий вектор — это $\color{blue}{\vec b}$, а желтый вектор — это $\vec a. + \vecb$:
При вычитании векторов лучше думать о сложении. Во-первых, поймите, что $-\vec a$ — это просто $\vec a$, отраженное относительно начала координат.
Затем обработайте $\vec{a} — \vec{b}$ как $\vec{a} + (-\vec{b})$ и визуализируйте это как сложение.
Если вы ищете меру сходства векторов, мы обычно используем внутренний продукт или скалярный продукт : $\vec{a}\cdot \vec{b}$. Это связано с тем, что мы хотели бы думать о «сходстве» как о скалярной величине, а не как о целом векторе. Если вы изучили взаимосвязь между скалярным произведением и косинусом, это имеет немного больше смысла:
$$\vec a \cdot \vec b = \|\vec a\|\|\vec b\|\cos\theta$$ …где $\theta$ — это угол между двумя векторами, как на изображении ниже:
Таким образом, векторы, указывающие в одном направлении, «подобны», а векторы, указывающие в противоположных направлениях, «несходны». Здесь полезна нормализация, потому что тогда $+1$ означает «идентичные векторы», а $-1$ означает «отраженные векторы». Значение $0$ означает перпендикуляр.
$\endgroup$
$\begingroup$
Когда я хочу изобразить сложение векторов, $v+w$, и вычитание, $v-w$, я просто помню, что они являются диагоналями параллелограмма со сторонами $v$ и $w$:
Вот способ физической визуализации сложения векторов.
Представьте себе птицу (или самолет), летящую в ветреный день. Если вектор $v$ представляет собой скорость птицы без ветра, а $w$ представляет собой скорость ветра, то $v+w$ является фактической скоростью птицы. Так что представьте себе это: в день с сильным ветром направление, в котором указывает птица, не обязательно будет направлением, в котором она на самом деле летит.
Для вычитания векторов просто подумайте о смещениях. Если вы находитесь в начале вектора $w$ и перемещаетесь в начало вектора $v$, то вектор, по которому вы двигаетесь, равен $v-w$.
Я не знаю, как количественно определить сходство двух векторов, но, например, вы можете количественно определить, насколько они параллельны/перпендикулярны.
Чем ближе к параллельности два вектора, тем ближе к $\|v\|\|w\|$ скалярное произведение $v$ и $w$.
Чем ближе к перпендикуляру два вектора, тем ближе к $\|v\|\|w\|$ величина векторного произведения $v$ и $w$. 9n$ является нормированным пространством, а не его алгебраическими свойствами.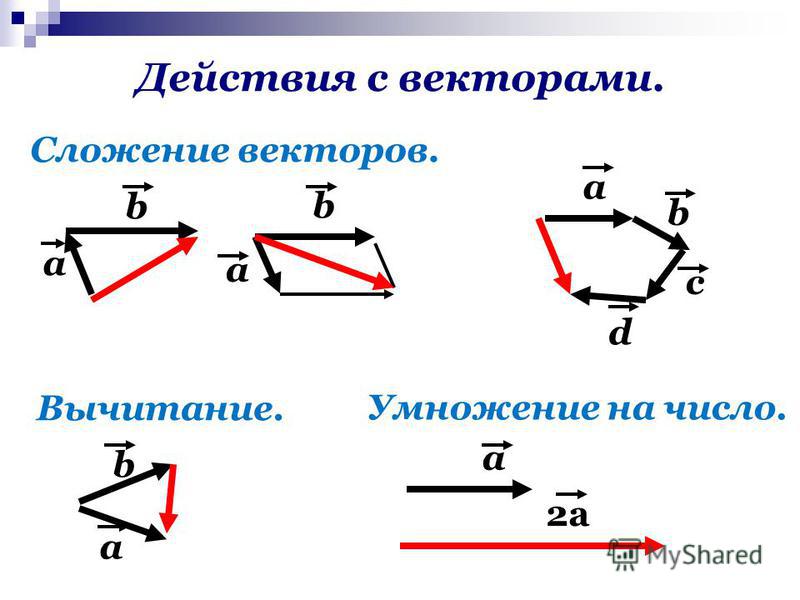
Это означает, что в абстрактном векторном пространстве вы не можете сказать, что означает для вектора быть «маленьким», если у вас нет нормы или чего-то подобного.
$\endgroup$
7
$\begingroup$
Да. Евклидово пространство естественным образом обобщается на n измерений.
Во-первых, евклидово пространство допускает метрику L-2, поэтому при вычислении разностей и сложений то, насколько они «похожи» или «сколько вы переместились», зависит от расстояний между ними, которые вы вычисляете с помощью метрики.
Евклидова метрика дает естественную меру «расстояния», к которой мы привыкли в одно-, двух-, трехмерном пространстве. С другой стороны, если вы переключитесь на другое метрическое пространство, смысл будет потерян. Итак, метрика имеет значение.
Во-вторых, вы можете видеть объекты более низкого измерения как проекции их, находящиеся в более высоком измерении.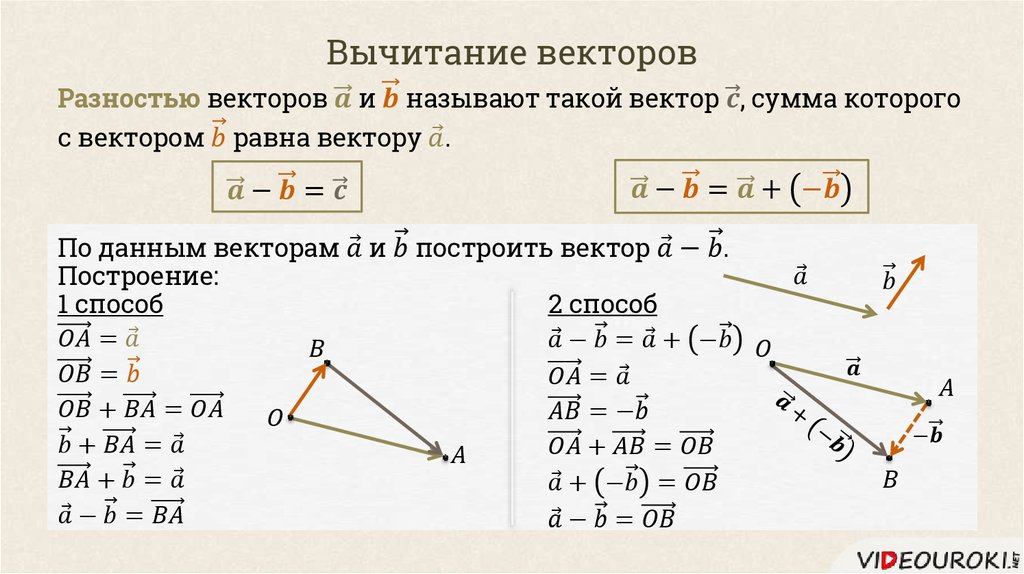
Представьте себе трехмерный куб, изначально находящийся в пятимерном пространстве с осями v,w,x,y,z; но его длина, ширина и высота совпадают с осями x, y, z, поэтому мы можем естественно рассматривать куб в нашей естественной системе отсчета.
$\endgroup$
векторов, часть 5
векторов, часть 5Векторы в двух и трех измерениях
Часть 5: Векторы в космосе
Мы думаем о трехмерном пространстве, начиная с горизонтального ху -самолет
и расширение вверх и вниз с использованием третьей координаты, z . В этом
В трехмерном пространстве мы можем создавать векторы так же, как мы это делали на плоскости.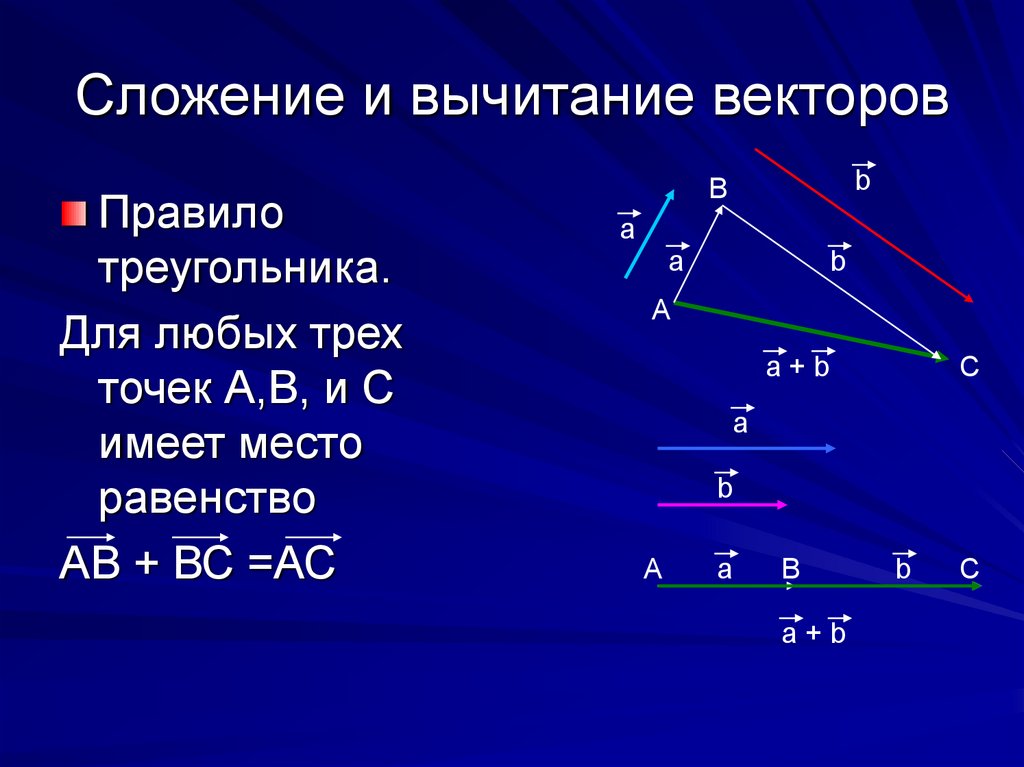
Векторы в пространстве могут быть описаны по упорядоченные тройки координат ( a, b, c ) . Геометрически, определенный таким образом вектор можно рассматривать как стрелку, указывающую из начала координат к этой точке пространства.
Как и с векторами на плоскости, мы определить сложение и вычитание покоординатно:
( а,б,в ) + ( г,д,е ) = ( а+г,б+е,в+е )
( а,б,в ) — ( г,д,е ) = ( а-г, б-е, в-ф )
- Вычислить сумму и разность из (1,2,-3) и (-7,1,0). Нарисуйте эти векторы, их сумму и разность, как на бумаге, так и на рабочем листе.
Векторы в пространстве тоже имеют направление и длина. Их можно вычислить так же, как и для двумерных векторов, взяв дополнительная координата учитывается в наших формулах. Таким образом, величина или длина вектора v = (a,b,c) равна
и скалярное произведение двух векторов v = ( a,b,c ) и w = ( d,e,f ) равно
< v , w > = объявления
+ быть + ср.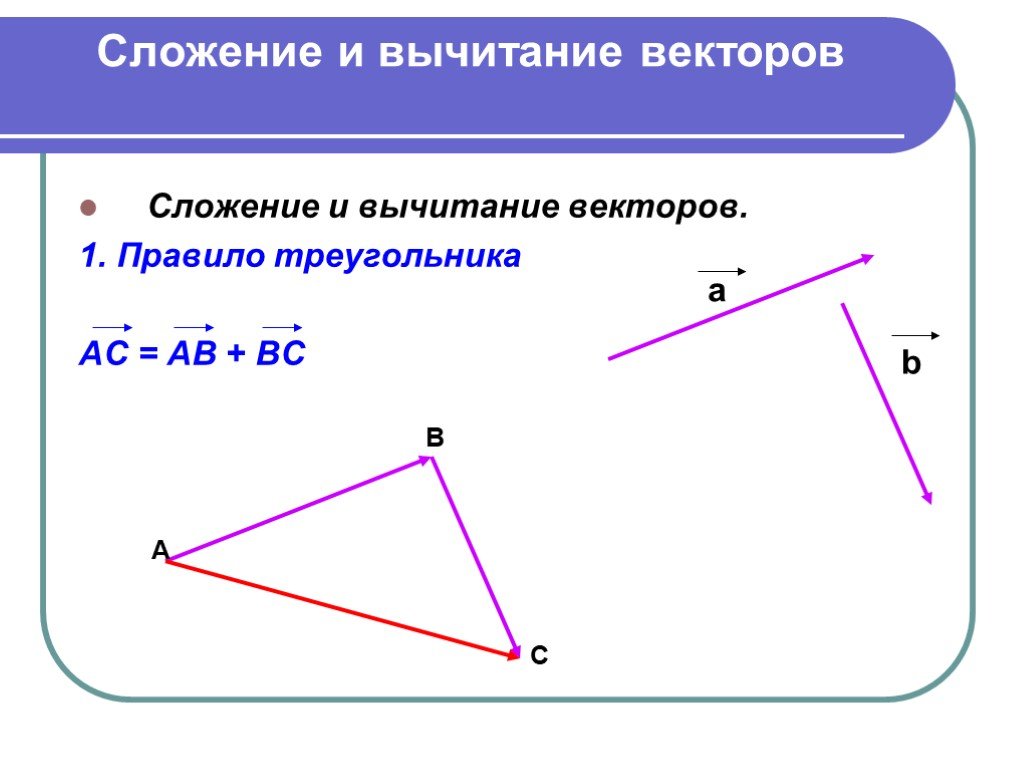
Как и раньше, скалярное произведение говорит нам об относительном направлении двух векторов.
Выразите косинус угла между векторами v и w с точки зрения их скалярного произведения и их длин. (Намекать: Просмотрите свои 2D-расчеты в Части 2 и определите, что изменится при каждом изменении. вектор имеет третий компонент.)
- Вычислить скалярное произведение (1,2,-3) и (-7,1,0) и вычислить угол между ними.
- Постройте векторы (-2,3,1) и (1,5,3) на вашем листе и вычислите угол между их.
В самолете мы увидели, что можем
выразить вектор как сумму кратных горизонтального единичного вектора, i ,
и кратное вертикальному единичному вектору, j . Мы можем сделать то же самое в
пространство, но теперь нам нужны три единичных вектора — те же самые два вектора i = (1,0,0)
и j = (0,1,0), лежащие в xy -плоскости, и новый вектор k = (0,0,1) перпендикулярно этой горизонтальной плоскости.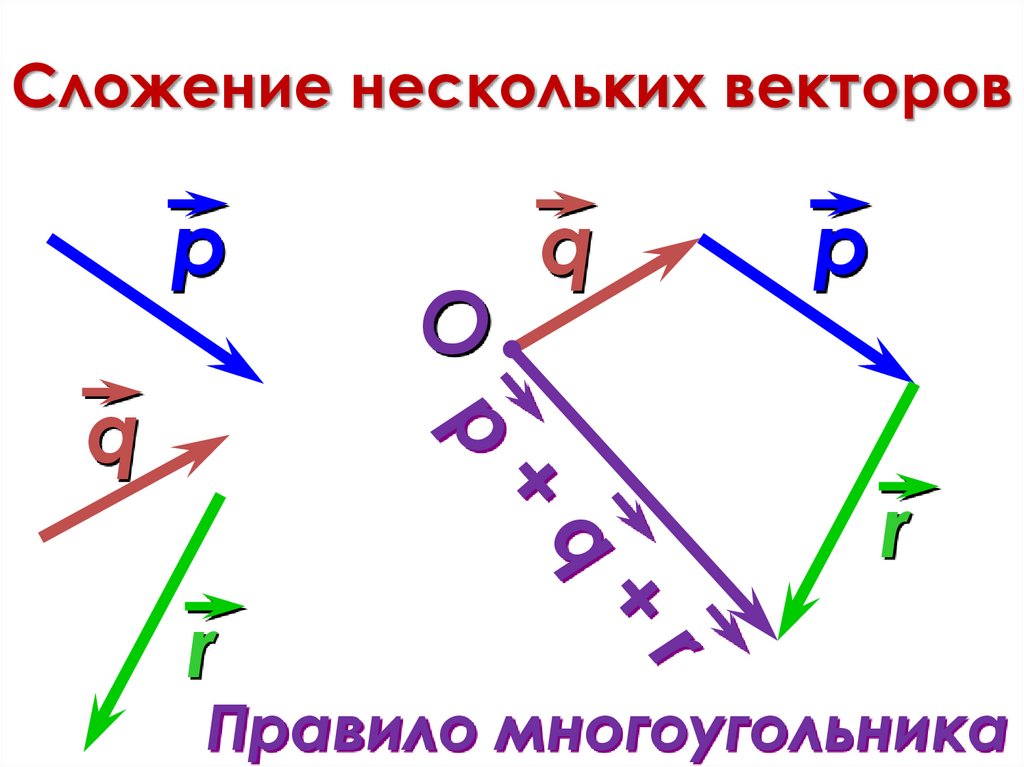
- Выразите вектор (-1,5,2) как сумма скалярных множителей i , j и k .
Умножение векторов в пространстве имеет больше возможностей, чем в самолете. Как мы увидим в части 7, существует второе понятие умножения векторов в пространстве, имеющее геометрическое значение. В частности, он выражает отношение векторов i , j , и k довольно красиво.
| КПК Главная | Материалы | Многовариантный Исчисление | Содержание модуля | Назад | Вперед |
| модулей на math.duke.edu | Авторское право
КПК и автор(ы), 2001-2002 гг. |