Вычитание матрицы из числа: Онлайн калькулятор. Сложение и вычитание матриц

Вычитание матриц — определение с примерами

Содержание:

1. Сложение матриц
2. Вычитание для матриц

Определение 1. Суммой двух матриц одинакового размера и называется третья матрица того же размера, каждый элемент которой равен сумме соответствующих элементов матриц-слагаемых: для всех и

Таким образом, сложение матриц сводится к сложению соответствующих элементов матриц-слагаемых. Не все матрицы можно складывать, а только те, которые имеют одинаковый размер, и матрица-сумма тоже будет того же размера, что и матрицы-сла-гаемые.

В этом случае говорят, что матрицы согласованы для сложения.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Сложение матриц

Сложение матриц обладает обычными свойствами аддитивности и коммутативности:

• Свойство 1. Коммутативность: А + В = В + А, т.е. матрицы, согласованные для сложения можно складывать в любом порядке.
• Свойство 2. Ассоциативность: А+(В+С) = (А+В)+С, т.е., как и в обычной алгебре, можно вначале сложить В и С, а затем прибавить к ним А, или же вначале сложить А и В, а кним прибавить С. Результат сложения будет один и тот же.

Определение 2. Разностью двух матриц и называется третья матрица того же размера, каждый элемент которой равен разности соответствующих элементов матриц — уменьшаемого и вычитаемого: для всех ,

Вычитание матриц также сводится к вычитанию соответствующих элементов матриц. Как и в случае сложения матрицы должны быть согласованы для действия вычитания, т.е. должны иметь одинаковый размер.

Определение. Суммой двух матриц А и В одинакового типа называется матрица С = А + В того же типа, элементы которой равны суммам соответствующих (т. е. имеющих одинаковые двойные индексы) элементов матриц А и В .

Элементы матрицы С = А + В определяются, следовательно, формулами

где и — элементы матриц А и В соответственно. Таким образом, если

Подчеркнем еще раз, что складывать можно только матрицы с одинаковым числом строк и с одинаковым числом столбцов.

Вычитание для матриц

Вычитание для матриц (как и для чисел) определяется как действие, обратное сложению. Пример с решением таким образом, при вычитании матриц вычитаются соответствующие элементы этих матриц, т. е.

Определение. Для того чтобы сложить две матрицы одинаковой размерности нужно к каждому элементу первой матрицы прибавить соответствующий (то есть расположенный на том же месте) элемент второй матрицы.

Так как вычесть из матрицы А матрицу В означает — умножить матрицу В на (-1), а затем сложить матрицу А с матрицей (-В), то вычитание А — В производится так же поэлементно, как и сложение.

Возможно вам будут полезны данные страницы:

Вычислить определитель матрицы

Сложение матриц: примеры решения

Матрица математика: примеры решения

Единичная матрица: вид, примеры, онлайн

Итак, если заданы две матрицы одинаковой размерности и то их суммой (разностью) будет матрица той же размерности , элементы которой равны

Сумма (разность) матриц — Мегаобучалка

Сумма матриц — действие несложное.

НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой.

— Такое действие не определено для этих матриц!

 

Определение: Для того чтобы получить матрицу, равную сумме (разности) двух исходных матриц, необходимо сложить (вычесть) их соответствующие элементы:

Пример:

Сложить матрицы и

В соответствии с определением, запишем:

.

Для разности матриц, аналогично, находим разность соответствующих элементов:

Пример:

Найти разность матриц и .

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу H:

Примечание: В теории высшей математики школьного понятия «вычитание» нет.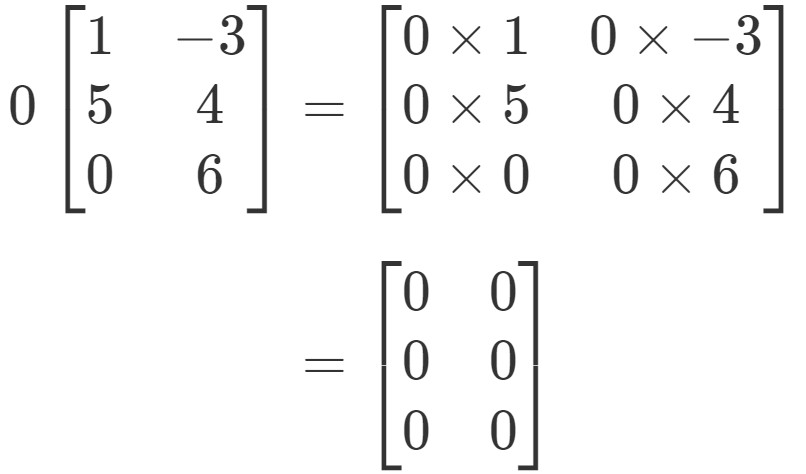 Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

 

 

Умножение матриц.

Скажем сразу, правило умножения матриц (есть в любом учебнике по алгебре) выглядит очень странно для неподготовленного слушателя, но мы объясним это на конкретных примерах. Прежде всего: «Какие матрицы можно умножать?»

Следствие (из строгого определения): Для умножения матрицы K на матрицу L слева необходимо, чтобы число столбцов матрицыKравнялось числу строк матрицыL.

 

Пример:

Можно ли умножить матрицу

на матрицу ?

, значит, умножать данные матрицы можно.

А вот если, в данном случае, матрицы переставить местами, то умножение уже невозможно!

, значит, выполнить умножение нельзя, и, вообще, такая запись не имеет смысла:

Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так, но с разным результатом, т. к. в общем случае KL ¹ LK. Например, для матриц

и существует как произведение , так и .

 

Как умножать матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

Пример:

Умножить матрицу на матрицу
Мы будем сразу приводить формулу для каждого случая:

– попытайтесь сразу уловить закономерность. Поэтому:

 

 

Пример сложнее:

Умножить матрицу на матрицу

Формула: . В таком случае произведение:

.

В результате мы получили так называемую нулевую матрицу.

Попробуйте самостоятельно выполнить умножение . Правильный ответ — .

Обратите внимание, что! Это почти всегда так!

 

Таким образом, переставлять матрицы в произведении нельзя!Если в задании предложено умножить матрицу M на матрицу N, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

 

Примеры с матрицами третьего порядка:

Умножить матрицу на матрицу .

Формула умножения очень похожа на предыдущие формулы:

.

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу на матрицу .

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

.

 

 

матриц — Вычесть матрицу из скаляра

спросил 10 лет, 3 месяца назад

Изменено 8 лет, 10 месяцев назад

Просмотрено 35 тысяч раз

$\begingroup$

Это вообще возможно? Поскольку вы можете вычитать с правой стороны, я думаю, должен быть способ сделать это и с левой стороны.

Я хотел бы рассчитать это:

3 — [2 1] = ??

• матрицы

$\endgroup$

5

$\begingroup$

Вы не можете сложить скаляр и матрицу. В общем, вы не можете добавить две матрицы, если они не имеют одинакового размера. Однако часто мы обозначаем скалярную матрицу (диагональную матрицу, все элементы которой одинаковы) скаляром. Например, вы можете написать $4$ для обозначения матрицы $\begin{bmatrix}4 & 0 \\ 0 & 4\end{bmatrix}$. Размерность матрицы следует понимать из контекста. Это обозначение позволяет записать, например, $$ 4-\begin{bmatrix}1 и 2 \\ 3 и 4\end{bmatrix}=\begin{bmatrix}4 и 0 \\ 0 и 4\end{bmatrix}-\begin{bmatrix}1 и 2 \\ 3 & 4\end{bmatrix}=\begin{bmatrix}3 & -2 \\ -3 & 0\end{bmatrix} $$ Однако в вашем случае я никогда не видел скаляр, используемый для обозначения неквадратной матрицы.

$\endgroup$

5

$\begingroup$

Предыдущие ответы, которые в основном говорят: «Нет, сложение/вычитание не определено между матрицами разных размеров», являются правильным ответом на ваш вопрос.

На самом деле нечто подобное делается формально в алгебрах Клиффорда. Есть элементы алгебры, идентифицированные со скалярами, элементы, идентифицированные как векторы (и даже больше элементов с различными идентификациями). Поскольку все они живут в алгебре, между ними определены сложение, вычитание и умножение.

Однако этот последний пункт, вероятно, не является ответом, который вы ищете, потому что добавление чисто формальное: скаляр $\lambda$ плюс вектор $v$ просто «$\lambda +v$», а там это не формула, которая представляет его как другой скаляр или другой вектор.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

матриц.

Можете ли вы добавить скаляр к матрице?

спросил 7 лет, 3 месяца назад

Изменено 3 года назад

Просмотрено 49 тысяч раз

$\begingroup$

Если я добавлю скаляр к каждому элементу матрицы, например. для матрицы $2\times2$

$$ \begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix} + b \overset{?}{=} \begin{pmatrix}a_ {11}+b & a_{12}+b \\ a_{21}+b & a_{22}+b\end{pmatrix},$$

, где $b$ — скаляр, тогда какое обозначение правильное ? Сложение и вычитание матриц определены только для матриц одинакового размера. Однако кажется утомительным сначала умножать $b$ на матрицу из единиц, чтобы сложить две матрицы одинакового размера:

$$ J_2 = \begin{pmatrix} 1 & 1 \\ 1 & 1\end{pmatrix} . $$

Таким образом, записать:

$$ \begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix} + bJ_2 = \begin{pmatrix}a_{ 11}+b & a_{12}+b \\ a_{21}+b & a_{22}+b\end{pmatrix}.$$

Вы всегда пишете $A+bJ_d$ (с $d$ размеры $A$)? Другим обозначением будет $A+\mathbf{b}$ (жирный шрифт $b$), подразумевающий матрицу размера $A$. Однако это обозначение также используется для умножения $b$ на единичную матрицу $bI_d$, которая отличается и, следовательно, сбивает с толку.

Почему прибавление скаляра к матрице не определяется просто как скалярное умножение, то есть операция над каждым элементом матрицы? Примером, где это разрешено , является язык MATLAB, где вы можете добавить скаляр к матрице $A$ просто путем добавления: например. А+3 . Мне кажется, это логичный выбор. Добавление скаляра к матрице может быть определено как $A+b = A+bJ_d$, где $d$ размерность $A$. Это коммутативно и ассоциативно, как обычное сложение матриц. Тогда $A+\mathbf{b}$ будет сложением $A$ и $bI_d$, а $A+B$ — сложением матриц в известном нам виде, действительным только для матриц одинаковой размерности.

Почему это не определения?

• матрицы
• обозначения
• арифметика

$\endgroup$

1

$\begingroup$

Вероятно, это потому, что это не имеет геометрического смысла; линейное преобразование, матрица которого в одном базисе равна всем единицам, имеет другую матрицу в другом базисе.

Всякий раз, когда я встречал обозначение $A+b$ в математике, оно означало $A+bI$ (где $A$ — квадратичная матрица, а $I$ — единичная матрица того же размера). Например, некоторые пишут $\det(A-\lambda)$ для характеристического многочлена.

$\endgroup$

2

$\begingroup$

Пояснение:

$I$ Обычно относится к идентификационной матрице https://en. T}}$$

Правильно?

Точно не знаю. В любом случае я бы не стал использовать в документе $A+\lambda$, где A — матрица, а $\lambda$ — скаляр, потому что мне лично кажется, что это выглядит странно и труднее увидеть, как уравнение работает с измерениями.

Тем не менее, он отлично работает в Matlab, например:

 magic(3) + 1
ответ =
       9 2 7
       4 6 8
       5 10 3
 

Рекомендация:

9 таджикских долларов

$A+\лямбда J$

В обоих случаях вам, вероятно, потребуется объяснить, что $e$ — это вектор-столбец всех единиц или что $J$ — это матрица всех единиц. Подразумевая, что $I$ или $J$ имеют правильную размерность, это нормально, лично мне не нравятся ни $I_\text{dim}$, ни $J_\text{dim}.$

$\endgroup$

2

$\begingroup$

матричное скалярное сложение математически неверно.