| 1вариант. Выполните действия: а) 12,533 б) 1,6 7,125 в) 254,32-68 г) 53,82:6,9 д) 1,47:4,2 е) 2,8623+4,06 Найти значение выражения: А) 90-16,2:9+0,08 Б) 0,96:0,16+0,04·2,5 Решите уравнение 2•х+0,49=7,23 Найти значение выражения: 6,56 4,36-3,36:(0,736+2,464)-20,0424 Решите задачу На автомобиль погрузили 6 контейнеров и 8 одинаковых ящиков по 0,28т каждый. Какова масса одного ящика, если масса всего груза 2,4т? 2 вариант. Выполните действия: а) 2,46 45 б) 3,2 5,125 в) 277,02-57 г) 60,03:8,7 д) 5,6994:8,05 е) 9,315+2,3 Найти значение выражения: А) 40-23,2:8+0,07 Б) 1,83:0,61+0,4·0,0025 Решите уравнение 2·х-6,25=3,8 Найти значение выражения: (32,24 0,32+366,032 0,1):2,3-18,6388 Решите задачу Из 7,7м ткани сшили 7 платьев для кукол и 9 одинаковых полотенец.  Сколько ткани пошло на одно полотенце, если на каждое платье потребовалось 0,65 м ткани? 1вариант. Выполните действия: а) 12,533 б) 1,6 7,125 в) 254,32-68 г) 53,82:6,9 д) 1,47:4,2 е) 2,8623+4,06 Найти значение выражения: А) 90-16,2:9+0,08 Б) 0,96:0,16+0,04·2,5 Решите уравнение 2•х+0,49=7,23 Найти значение выражения: 6,56 4,36-3,36:(0,736+2,464)-20,0424 Решите задачу На автомобиль погрузили 6 контейнеров и 8 одинаковых ящиков по 0,28т каждый. Какова масса одного ящика, если масса всего груза 2,4т? 2 вариант. Выполните действия: а) 2,46 45 б) 3,2 5,125 в) 277,02-57 г) 60,03:8,7 д) 5,6994:8,05 е) 9,315+2,3 Найти значение выражения: А) 40-23,2:8+0,07 Б) 1,83:0,61+0,4·0,0025 Решите уравнение 2·х-6,25=3,8 Найти значение выражения: (32,24 0,32+366,032 0,1):2,3-18,6388 Решите задачу Из 7,7м ткани сшили 7 платьев для кукол и 9 одинаковых полотенец.  Сколько ткани пошло на одно полотенце, если на каждое платье потребовалось 0,65 м ткани?Выполните действия: а) 12,533 б) 1,6 7,125 в) 254,32-68 г) 53,82:6,9 д) 1,47:4,2 е) 2,8623+4,06 Найти значение выражения: А) 90-16,2:9+0,08 Б) 0,96:0,16+0,04·2,5 Решите уравнение 2•х+0,49=7,23 Найти значение выражения: 6,56 4,36-3,36:(0,736+2,464)-20,0424 Решите задачу На автомобиль погрузили 6 контейнеров и 8 одинаковых ящиков по 0,28т каждый. Какова масса одного ящика, если масса всего груза 2,4т? 2 вариант. Выполните действия: а) 2,46 45 б) 3,2 5,125 в) 277,02-57 г) 60,03:8,7 д) 5,6994:8,05 е) 9,315+2,3 Найти значение выражения: А) 40-23,2:8+0,07 Б) 1,83:0,61+0,4·0,0025 Решите уравнение 2·х-6,25=3,8 Найти значение выражения: (32,24 0,32+366,032 0,1):2,3-18,6388 Решите задачу Из 7,7м ткани сшили 7 платьев для кукол и 9 одинаковых полотенец.  Сколько ткани пошло на одно полотенце, если на каждое платье потребовалось 0,65 м ткани? 1вариант. Выполните действия: а) 12,533 б) 1,6 7,125 в) 254,32-68 г) 53,82:6,9 д) 1,47:4,2 е) 2,8623+4,06 Найти значение выражения: А) 90-16,2:9+0,08 Б) 0,96:0,16+0,04·2,5 Решите уравнение 2•х+0,49=7,23 Найти значение выражения: 6,56 4,36-3,36:(0,736+2,464)-20,0424 Решите задачу На автомобиль погрузили 6 контейнеров и 8 одинаковых ящиков по 0,28т каждый. Какова масса одного ящика, если масса всего груза 2,4т? 2 вариант. Выполните действия: а) 2,46 45 б) 3,2 5,125 в) 277,02-57 г) 60,03:8,7 д) 5,6994:8,05 е) 9,315+2,3 Найти значение выражения: А) 40-23,2:8+0,07 Б) 1,83:0,61+0,4·0,0025 Решите уравнение 2·х-6,25=3,8 Найти значение выражения: (32,24 0,32+366,032 0,1):2,3-18,6388 Решите задачу Из 7,7м ткани сшили 7 платьев для кукол и 9 одинаковых полотенец.  Сколько ткани пошло на одно полотенце, если на каждое платье потребовалось 0,65 м ткани?Скачать 19.68 Kb. Поделитесь с Вашими друзьями: |
Законы Ньютона — простыми словами. Объяснение с примерами
С помощью законов Ньютона можно описать движение любой механической системы, будь то старушка, переходящая дорогу, или робот-пылесос. А может быть, это девятиклассница Соня, которая едет в поезде метро на занятия. При торможении электропоезда на станции Соня некоторое время продолжает по инерции двигаться вперед.
Инерция — явление сохранения постоянной скорости тела при отсутствии действия на него других тел.
С инерцией мы сталкиваемся каждый день:
- велосипед движется, если перестать крутить педали;
- бегун не может остановиться сразу после финиша, а пробегает некоторое расстояние;
- чай в кружке продолжает вращаться, если перестать его размешивать и убрать ложку;
- дверь способна сама захлопнуться после толчка.
Объяснить это явление можно с помощью первого закона Ньютона, который также называют законом инерции.
Первый закон Ньютона: формулировка
Существуют системы отсчета, называемые инерциальными (ИСО), в которых тело находится в состоянии покоя (V = 0) или движется равномерно и прямолинейно (V = const), если на тело не действуют силы (F = 0) или действие этих сил скомпенсировано (F = 0).
Инерциальные системы отсчета окружают нас повсюду. Например, равномерно спускающийся лифт или тот самый поезд метро, в котором Соня равномерно движется между станциями.
Инерциальные системы отсчета обладают следующими свойствами:
- тела в таких системах движутся равномерно или находятся в состоянии покоя;
- при одинаковых начальных условиях тела движутся одинаково;
- изменение скорости тела происходит в результате действия на него других тел.
Остановимся на последнем свойстве подробнее и рассмотрим пример.
Кот Василий неподвижно спит на батарее. На него определенно действуют силы: со стороны Земли — сила тяжести, направленная вниз, а со стороны батареи — сила реакции опоры, направленная вертикально вверх. Однако изменения скорости Василия не происходит потому, что действие вышеупомянутых сил скомпенсировано.
1-й закон Ньютона не имеет формулы, однако математически его можно описать следующим образом:
,
где — скорость тела [м/с],
— равнодействующая сила [Н].
Равнодействующая сила — векторная сумма всех сил, действующих на тело. При равномерном прямолинейном движении или в состоянии покоя равнодействующая сила равна нулю.
Вернемся к примеру с котом Василием. До тех пор, пока кота никто не трогает, он находится в состоянии покоя. Когда Соня толкнет Василия с некоторой силой, его скорость изменится.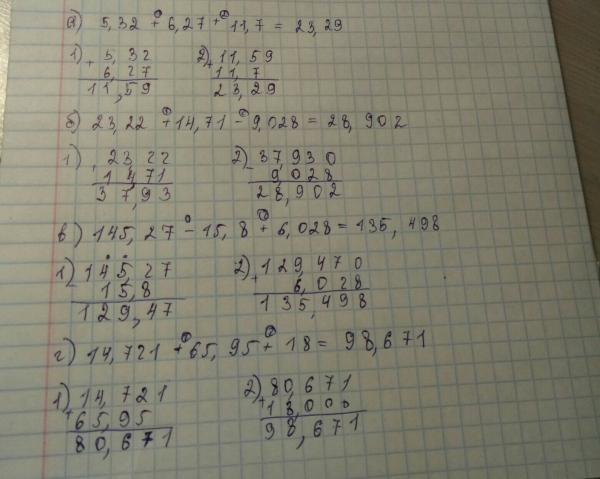
Причем чем большую силу приложит Соня, тем большее ускорение приобретет Василий. Связь между ускорением тела и приложенной силой устанавливает 2-й закон Ньютона.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Второй закон Ньютона: формулировка
В ИСО ускорение, с которым движется тело, прямо пропорционально равнодействующей всех сил и обратно пропорционально массе этого тела.
Вспомним Соню в поезде метро. Рассмотрим участок разгона электропоезда под действием равнодействующей силы. Согласно 2-му закону Ньютона, чем больше равнодействующая сила, тем большее ускорение приобретет поезд. Под действием той же силы более легкий поезд будет двигаться с бóльшим ускорением.
Второй закон Ньютона: формула
,
где — ускорение [м/с2],
— равнодействующая сила [Н],
— масса [кг].
Важно
Сила и ускорение — величины векторные, их направления всегда совпадают.
Рассмотрим примеры решения задач с использованием второго закона Ньютона.
Задача 1
Уставший Аркаша пришел домой после школы и с силой 4,5 Н горизонтально бросил в сторону кровати рюкзак массой 6 кг. Какое ускорение приобрел рюкзак? Силой сопротивления воздуха можно пренебречь.
Решение.
Сила воздействия Аркаши на рюкзак при горизонтальном броске равна равнодействующей силе. Подставим в формулу 2-го закона Ньютона числа:
м/с2.
Ответ: рюкзак приобрел ускорение 0,75 м/с2.
Задача 2
На рисунке отмечены все силы, действующие на тело. Чему равна равнодействующая сила, если одной клетке соответствует 1 Н?
Решение.
Для определения равнодействующей силы необходимо найти векторную сумму F1, F2 и F3 с помощью правил сложения векторов. Согласно правилу треугольника, чтобы сложить два вектора, нужно последовательно отложить их друг от друга (т. е. начало второго вектора должно совпадать с концом первого).
Сложим силы F2 и F3, лежащие в горизонтальной плоскости. Их сумма имеет длину 3 клетки и направлена вправо в сторону большей силы.
Затем полученную сумму сложим с силой F1 по правилу параллелограмма. Отложим силы F1 и F23 от одной точки, достроим до параллелограмма. Диагональ параллелограмма является искомой суммой ΣF.
По теореме Пифагора найдем гипотенузу:
И вычислим:
Ответ: равнодействующая сила равна 34.
Хотите найти универсальный способ решения всех задач по динамике, успешно справляться с заданиями ОГЭ и даже освоить самую сложную задачу № 30 из ЕГЭ? Тогда записывайте алгоритм.
Вот 7 шагов к успеху!
Алгоритм решения задач с использованием 2-го закона Ньютона
Выбрать ИСО.
Отметить на рисунке все силы, действующие на тело.
Записать 2-й закон Ньютона в векторном виде.
Найти проекции сил на координатные оси.
Записать 2-й закон Ньютона в проекциях на координатные оси.
Составить и решить систему уравнений.
Выполнить расчет и записать ответ.
Попробуем применить алгоритм прямо сейчас, чтобы лучше разобраться в каждом шаге.
Задача 3
Серёжа с силой F = 12 Н, приложенной под углом 30°, тянет машинку массой 600 г по шероховатому ламинату, как показано на рисунке.
С каким ускорением движется машинка? Коэффициент трения равен 0,1.
Решение.
При решении задачи будем считать машинку материальной точкой. Выберем направления осей, как показано на рисунке, и отметим все действующие в системе силы. На машинку действуют сила тяги Серёжи F, сила тяжести mg, сила трения Fтр, сила реакции опоры N.
Запишем 2-й закон Ньютона в векторном виде:
Определим проекции силы на координатные оси и запишем 2-й закон Ньютона в проекциях на эти оси.
Ox: ma = Fcosα − Fтр; (1)
Oy: 0 = N + Fsinα − mg. (2)
Запишем формулу для силы трения скольжения: Fтр = μN. (3)
Решим полученную систему из трех уравнений. Для этого подставим выражение для силы трения (3) в уравнение (1) и получим:
ma = Fcosα − μN; (1)
0 = N + Fsinα − mg.
(2)
Затем выразим в уравнении (2) силу реакции опоры N = mg − Fsinα и подставим полученное выражение в уравнение (1):
ma = Fcosα − μ(mg − Fsinα).
Выразим искомое ускорение:
И вычислим:
м/с2.
Ответ: машинка движется с ускорением 17,3 м/с2.
Как мы уже заметили, тела постоянно взаимодействуют друг с другом. Именно об этом говорит 3-й закон Ньютона.
Третий закон Ньютона: формулировка
Тела действуют друг на друга с силами, направленными вдоль одной прямой, противоположными по направлению и разными по модулю.
Суть закона в том, что сила действия равна силе противодействия. Причем силы имеют одну природу, а приложены они к разным телам.
Действие и противодействие встречаются повсюду:
мы притягиваем к себе Землю с той же силой, с какой она притягивает нас;
боксер носит перчатки потому, что груша ударяет его с той же силой, что и он;
ноутбук давит на стол с той же силой, что и стол на ноутбук;
прыжок гребца из лодки непременно вызовет движение лодки в противоположную сторону;
лебедь плавает по озеру за счет взаимодействия с водой.
Третий закон Ньютона: формула
,
где — сила, с которой тело 1 действует на тело 2 [Н],
— сила, с которой тело 2 действует на тело 1 [Н].
Для решения задач часто используют комбинацию 2-го и 3-го законов Ньютона, которая имеет следующий вид:
,
где — масса тела 1 [кг],
— масса тела 2 [кг],
— ускорение тела 1 [м/с2],
— ускорение тела 2 [м/с2].
Задача 4
Во время веселых стартов две команды перетягивают канат. Команда «Чемпионы» тянет с максимальной силой 240 Н, а команда «Апельсинки» — с силой 280 Н. С какой силой команды могут натянуть канат, стоя неподвижно на одном месте?
Решение.
Поскольку сила действия равна силе противодействия, а «Чемпионы» могут действовать с силой не более 240 Н, то именно с такой силой команды могут натягивать канат, удерживая его неподвижно.
Ответ: команды могут натягивать канат, стоя неподвижно, с силой 240 Н.
Вот мы и рассмотрели три закона Ньютона. С их помощью любая задача по динамике теперь вам по плечу!
Но это еще не все. Мы подготовили подарок — готовые схемы и формулы по наиболее часто встречающимся типам задач на законы Ньютона.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи. На уроках вы изучите немало любопытных физических явлений и научитесь решать самые разнообразные задачи. Ждем вас!
Пересечение наклона регрессии: как найти его в простых шагах
Вероятность и статистика > Анализ регрессии > Поиск пересечения наклона регрессии
Пересечение наклона регрессии: обзор
Пересечение наклона регрессии используется в линейной регрессии.
Формула пересечения наклона регрессии, b 0 = y – b 1 * x на самом деле просто алгебраическая вариация уравнения регрессии, y’ = b 0 + b 1 x где «b 0 ” — точка пересечения с осью y, а b 1 x — наклон.
После того, как вы нашли уравнение линейной регрессии, все, что требуется, — это немного алгебры, чтобы найти точку пересечения по оси y (или наклон).
Примечание: Вы также можете увидеть формулу пересечения наклона регрессии, записанную как a = y’ + bx. Это та же самая формула с другими переменными: a используется для b 0 и b используется для b 1 .
Пересечение наклона регрессии: Шаги
Пример вопроса: Найдите точку пересечения наклона регрессии для следующего набора данных:
| Субъект | Возраст х | Уровень глюкозы y | ху | х 2 | г 2 | 1 | 43 | 99 | 4257 | 1849 | 9801 |
|---|---|---|---|---|---|
| 2 | 21 | 65 | 1365 | 441 | 4225 | 3 | 25 | 79 | 1975 | 625 | 6241 |
| 4 | 42 | 75 | 3150 | 1764 | 5625 | 5 | 57 | 87 | 4959 | 3249 | 7569 |
| 6 | 59 | 81 | 4779 | 3481 | 6561 |
| Σ | 247 | 486 | 20485 | 11409 | 40022 |
Шаг 1: Найдите уравнение линейной регрессии (возможно, оно уже было дано вам в вопросе).
Если вы не знаете, как это сделать, см.: Найдите уравнение линейной регрессии. Для этого примера вопроса уравнение линейной регрессии имеет вид: y’ = 65,14 + 0,385225x
Шаг 2: Преобразуйте уравнение линейной регрессии с помощью алгебры, чтобы оно соответствовало формуле пересечения наклона регрессии, b 0 = y – b 1 * х:
65,14 = у’ + 0,385225 х
Это y-перехват!
Совет: Вы также можете определить наклон по формуле, которая равна 0,385225.
Посетите наш канал на Youtube, чтобы получить дополнительные советы и помощь. Вы найдете видео о том, как найти уравнение линейной регрессии вручную или с помощью технологий (например, Excel).
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Пересечение наклона регрессии: как найти его простыми шагами» Из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/find-regression-slope-intercept/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Решение квадратных уравнений
Терминология
1. Квадратное уравнение – это уравнение, которое содержит член второй степени и не содержит члена более высокой степени.
2. Стандартная форма квадратного уравнения имеет вид , где a, b и c — действительные числа, а .
Этапы решения квадратных уравнений с помощью Factorin g
1. Запишите уравнение в стандартной форме:
2. Полностью факторизируйте.
3. Примените правило нулевого произведения, установив каждый фактор, содержащий переменную, равным нулю. Если ab = 0, то a = 0 или b = 0.
4. Решить линейные уравнения на шаге 3.
5. Проверить.
Примечание : Большинство квадратных уравнений имеют 2 решения.
2 решения соответствуют точкам пересечения по оси x графика квадратичной функции.
Смотреть видео: Решение квадратных уравнений с помощью факторизации основных примеров от Патрика ДжМТ
| |
Смотреть видео: Решение квадратных уравнений с помощью факторизации другого примера от Патрика ДжМТ
| |
Смотреть видео: Математическая помощь Квадратичные уравнения: решение с помощью факторинга, Пэт МакКег
|
Проверьте себя: нажмите на действие
Сопоставьте элементы.
Задача состоит в том, чтобы сопоставить элементы с буквами и элементами с правильными номерами. Ниже показан список обозначенных буквами элементов.
Далее следует список пронумерованных элементов. За каждым пронумерованным элементом следует раскрывающийся список. Выберите букву в раскрывающемся списке, которая лучше всего соответствует пронумерованному элементу с буквенными альтернативами.
| а. | |
| б. 7 и -4 | |
| c. -4 и -6 | |
| д. | |
| 1. | a b c d |
| 2. | a b c d |
| 3. | a b c d |
| 4. | a b c d |
Этапы решения квадратных прикладных задач:
1. При необходимости нарисуйте и подпишите картинку.
2. Определите все переменные.
3. Определите, нужна ли специальная формула. Подставьте полученную информацию в уравнение.
4. Запишите уравнение в стандартной форме.
5. Фактор.
6. Установите каждый коэффициент равным 0. И решите линейное уравнение. Исключите любые необоснованные ответы. ( Подсказка: У нас не может быть -5 футов ковра.)
7. Проверьте свои ответы.
Площадь прямоугольника и задачи Ландшафтный дизайн/граница/рамка .
Пример 1: Пустующий участок прямоугольной формы превращается в общественный огород размером 8 на 12 метров. Дорожка одинаковой ширины должна окружать сад. Если площадь участка 140 квадратных метров, найдите ширину дорожки, окружающей сад.
Пример 2: Каждая сторона квадрата удлиняется на 7 дюймов. Площадь этого нового большего квадрата составляет 81 квадратный дюйм.
Найдите длину стороны исходного квадрата.
Теорема Пифагора Задачи:
Пример 3: К дереву прикреплена растяжка, чтобы оно росло прямо. Длина проволоки на 2 фута больше, чем расстояние от основания дерева до столба. Высота деревянной части дерева на 1 фут больше, чем расстояние от основания дерева до кола.
Пример 5: Кусок провода длиной 20 футов прикреплен к телефонному столбу в качестве растяжки. Расстояние по земле от нижней части столба до конца провода на 4 фута больше, чем высота, на которой провод прикреплен к столбу. Как далеко до столба доходит растяжка?
Задачи движения по формуле
Пример 4: Вы бросаете мяч прямо вверх с крыши высотой 384 фута с начальной скоростью 3 фута в секунду.