Помогите решить Самостоятельная работа 1. Вариант 3. № 1 Геометрия 8 класс Зив Б.Г. – Рамблер/класс
Помогите решить Самостоятельная работа 1. Вариант 3. № 1 Геометрия 8 класс Зив Б.Г. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Выпуклый четырехугольник ABCD имеет две пары рав-
ных между собой смежных сторон: АВ = AD, ВС = CD,
Сравните периметры пятиугольников ABCOD и
ABOCD.
ответы
Помогу:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Психология
Химия
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт.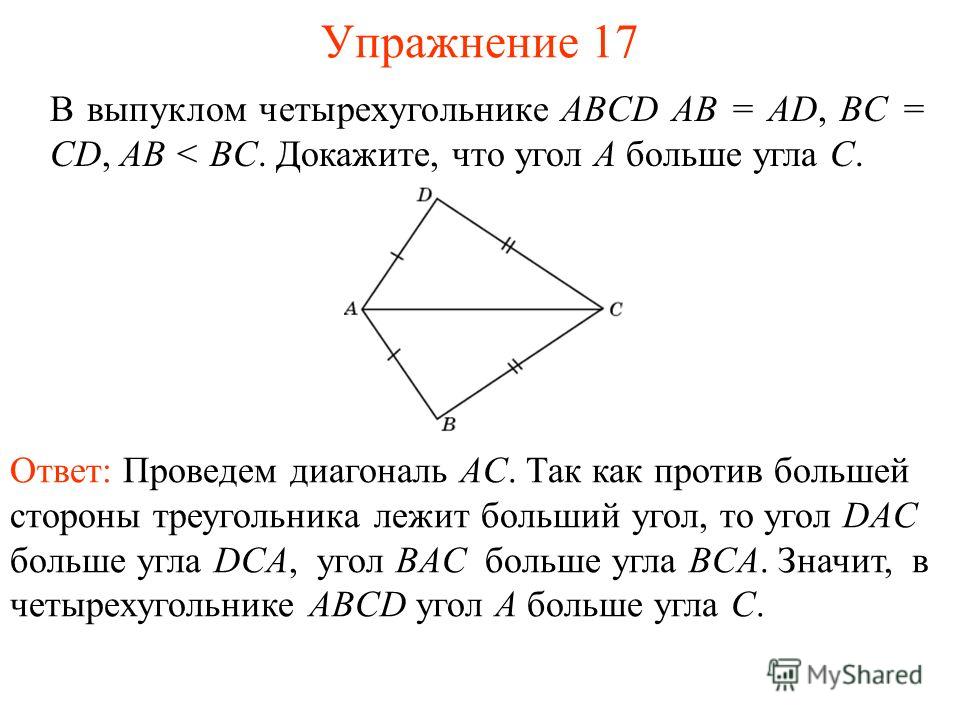
Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых).
..
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
04.22
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
tga-? Если sina=-5/корень 26 и a пренадлежит (pi;3pi/2)
В треугольнике ABC угол A равен 45 градусов, угол B равен 60 градусов, BC= 6√6.
Найдите AC.
Решено
У ході лабораторної роботи учень рівномірно тягне по столу дерев’яний брусок, діючи на нього з горизонтальною силою 1,2 H. Визначте коефіцієнт тертя ковзання бруска по столу, якщо маса бруска
Решено
Число 4 -является корнем уравнения 3х в квадрате+вх+4=0.Найти значение в и второй корень уравнения.
Решено
В треугольнике ABC известно, ЧТО AB=5, BC=7, AC=9. Найдите cos угла ABC
Пользуйтесь нашим приложением
геометрия — пусть $ABCD$ будет выпуклым четырехугольником, докажите, что неравенство верно AB}{AE}=\frac{DC}{DF}=n\right)$ само по себе не приведет нас к требуемому доказательству. Вы должны ввести в картину площадь четырехугольника $S$, используя определенные теоремы, неравенства и другие наблюдения. Начнем с доказательства простой леммы, которая понадобится нам позже.
Мы также предполагаем, что $\infty\ge n\ge 1$.$\underline{\mathrm{1.\space Лемма}}$
$TUVW$ — выпуклый четырехугольник (см. $\mathrm{Рис.\space 1.1}$). Точки $X$ и $Y$ делят его стороны $TU$ и $VW$ соответственно, так что $\frac{TU}{TX}=\frac{WV}{WY}=n$. Следующее неравенство верно для всех $n$, тогда как равенство выполняется только тогда, когда две стороны $UV$ и $WT$ параллельны друг другу. $$\left(\frac{n-1}{n}\right)WT+\left(\frac{1}{n}\right)UV\ge XY \tag{1}$$
$\underline{ \mathrm{1.1.\space Доказательство}}$
Проведите прямую, параллельную $WT$, через $X$, чтобы пересечь диагональ $UW$ в точке $Z$. Это делает $\frac{WU}{WZ}=n$. Теперь проведите еще одну линию, на этот раз параллельную $UV$, через $Y$, чтобы пересечься с диагональю $UW$ в некоторой точке $Z_1$. Это дает нам $\frac{WU}{WZ_1}=n$. Так как $\frac{WU}{WZ_1} = \frac{WU}{WZ}$, две точки $Z_1$ и $Z$ совпадают.
Когда мы применяем неравенство треугольника к треугольнику $XYZ$, мы получаем $ZX+YZ\gt XY$.
Если $WT$ параллелен $UV$, то очевидно, что $Z$ лежит на $XY$. Следовательно, только в этом конкретном случае мы можем написать $ZX+YZ= XY$. Поэтому в целом верно, что
$$ZX+YZ\ge XY. \тег{2}$$
Мы знаем, что $ZX= \left(\frac{n-1}{n}\right)WT$ и $YZ=\left(\frac{1}{n}\right)UV$. Подставив эти значения в неравенство (2), получим
$$\left(\frac{n-1}{n}\right)WT+\left(\frac{1}{n}\right)UV\ge XY.$$
$\underline{\mathrm{2.\space Теорема Птолемея\space and\space Неравенство}}$
Рассмотрим $\mathrm{Рис.\space 1.2}$. Теорема Птолемея утверждает, что для вписанного четырехугольника, изображенного на этой диаграмме, сумма произведений двух пар противоположных сторон равна произведению его диагоналей, то есть $AC\times BD = AB\times CD + BC\times DA$. Однако для четырехугольника, который не является вписанным, теорема Птолемея становится неравенством, т. е. $AC\times BD \lt AB\times CD + BC\times DA$. Поэтому в целом верно, что
$$AC\times BD \le AB\times CD + BC\times DA. \tag{3}$$ 92}≥С.
\tag{6}$$
Неравенство (6) по-прежнему сохраняет свою справедливость, однако становится слабее неравенства (5).
ABCD — выпуклый четырехугольник, вписанный в окружность. AB=10, AD=24 и m∠BAD=90 градусов. Найдите наибольшую возможную площадь ABCD. В этой задаче нет изображения.
РЕШЕНИЕ: ABCD — выпуклый четырехугольник, вписанный в окружность. AB=10, AD=24 и m∠BAD=90 градусов. Найдите наибольшую возможную площадь ABCD. В этой задаче нет изображения.Алгебра -> Формулы -> РЕШЕНИЕ: ABCD — выпуклый четырехугольник, вписанный в окружность. AB=10, AD=24 и m∠BAD=90 градусов. Найдите наибольшую возможную площадь ABCD. В этой задаче нет изображения. Войти
|
AB=10, AD=24 и m∠BAD=90 градусов. Найдите наибольшую возможную площадь ABCD. 