Выпуклый четырехугольник параллелограмм: Выпуклый четырехугольник, параллелограмм, ромб, квадрат, трапеция

Определение четырехугольника, выпуклые четырехугольники, сумма углов выпуклого четырехугольника

Запомнить

Восстановить пароль

Регистрация

Конспект

Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

• Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.
• Вершины, не являющиеся соседними, называются противоположными.
• Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями.
• Стороны четырехугольника, исходящие из одной вершины, называются соседними сторонами.
• Стороны, не имеющие общего конца, называются противолежащими сторонами.
• Сумма углов выпуклого четырехугольника равна 360°.

Че­ты­рех­уголь­ник на­зы­ва­ет­ся вы­пук­лым, если можно через любую его сто­ро­ну про­ве­сти пря­мую, и че­ты­рех­уголь­ник пол­но­стью ока­жет­ся в одной из двух об­ра­зо­вав­ших­ся по­лу­плос­ко­стей.

Виды четырехугольников

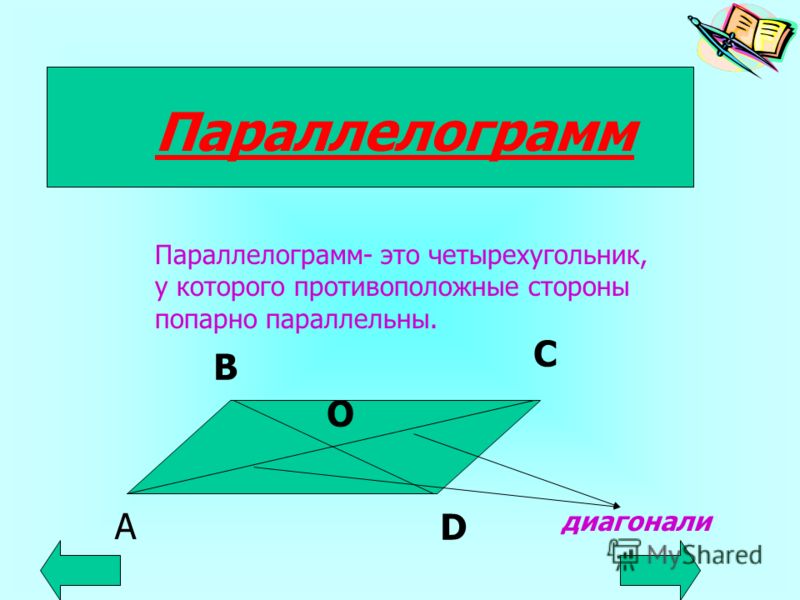
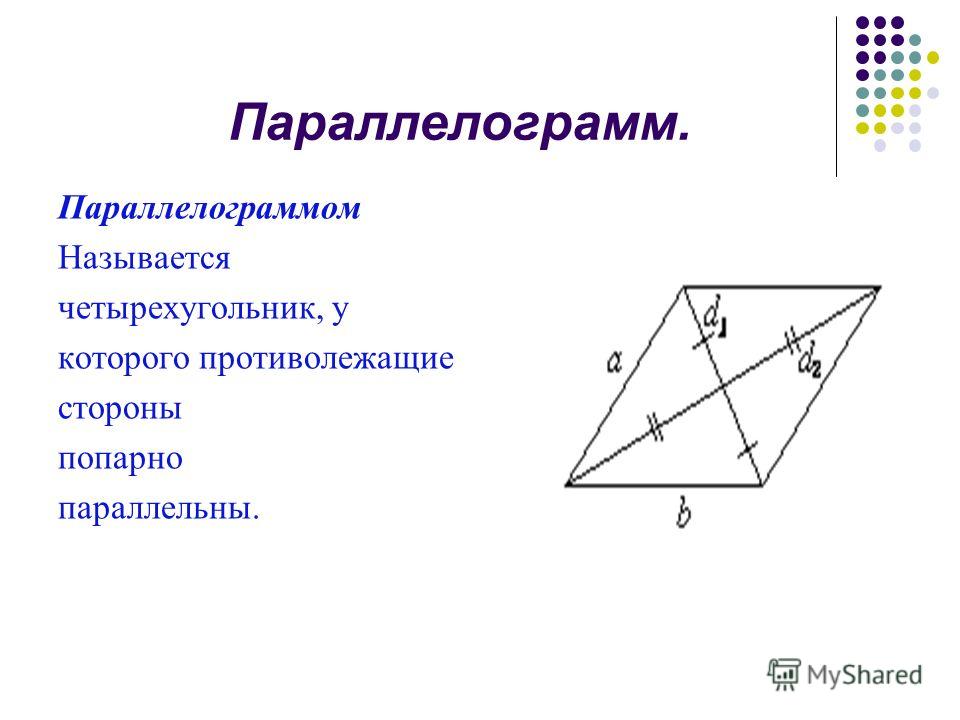
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.

Прямоугольник – параллелограмм, у которого все углы прямые.

Ромб – параллелограмм, у которого все стороны равны.

Квадрат – прямоугольник, у которого все стороны равны.

Трапеция – четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Дельтоид – четырехугольник, у которого две пары смежных сторон равны.

Вопросы

1. Укажите пары противоположных сторон четырехугольника.

2. Найдите периметр четырехугольника ABCD, если АВ = 16 см, ВС = 12 см, СD = 8 см и АD = 18 см.

3. Дан выпуклый четырехугольник АВСD. \(∠А = 61º,  ∠В = 110º, ∠С = 92º\). Найдите градусную меру угла \(∠D\).

    

4. В выпуклом четырехугольнике ABCD диагонали АС = 12 и BD = 10. Найти периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

5. Найдите периметр четырехугольника ABCD, если АВ = 12 см, ВС = 17 см, CD = 5 см и AD = 14 см.

6. Найдите большую сторону четырехугольника, если его периметр равен 66 см, а одна из сторон больше второй на 8 см и на столько же меньше третьей, а четвертая – в три раза больше второй.

7. Расстояния от середины стороны АD выпуклого четырехугольника ABCD до середин сторон АВ и CD равны соответственно 6 и 12. Найдите длину большей диагонали четырехугольника ABCD.

8. В выпуклом многоугольнике три угла по 80 градусов, а остальные – 150 градусов. Сколько углов в выпуклом многоугольнике?

9. Найдите наибольший угол выпуклого четырехугольника, если его углы пропорциональны числам 1, 2, 4, 5.

10. Какие из наборов углов могут быть углами четырехугольника?

Сообщить об ошибке

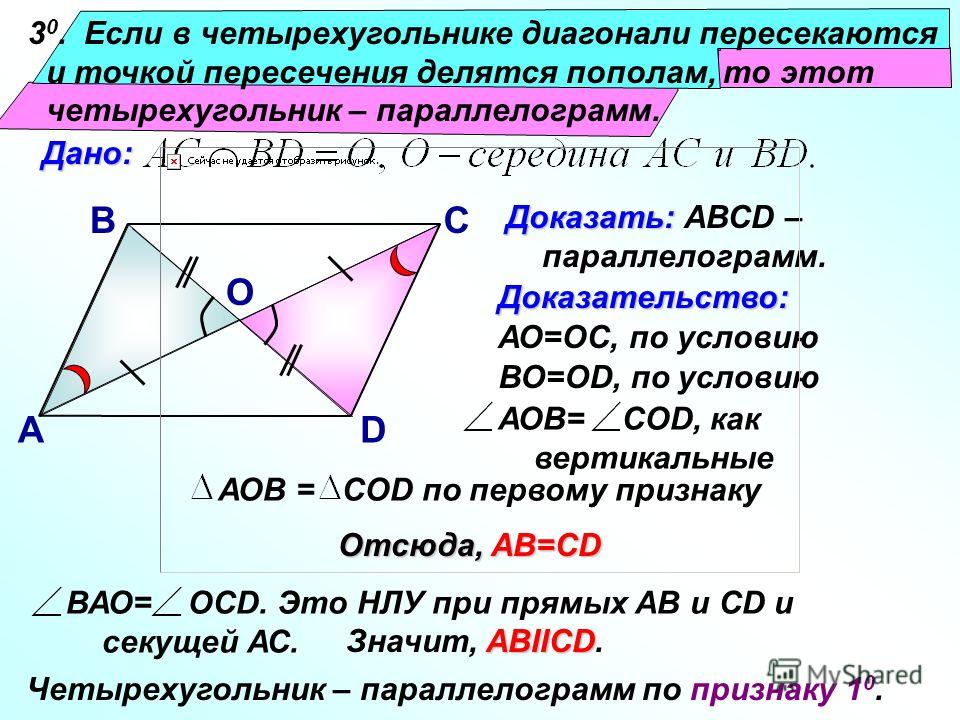
Параллелограмма — Определение и Доказательство

Главная » геометрия

Обновлено 28. 02.2022

Параллелограмм — это выпуклый четырехугольник, у которого

две любые стороны равны и параллельны.

На рисунке 1 изображен выпуклый четырехугольник MNPQ, со сторонами MN, PQ, MQ, NP. Чтобы доказать, что это параллелограмм, посмотрим
какие у него стороны. Итак, по рисунку 1 видно, что у этого выпуклого четырехугольника в первую очередь противоположные стороны равны: MN = PQ и NP = MQ.
Но нам этого еще недостаточно,так как равные противоположные стороны могут быть и у прямоугольника. Для того, чтобы можно было окончательно сказать,
что этот выпуклый четырехугольник — параллелограмм, надо во вторую очередь посмотреть параллельны, ли эти стороны. Сторона MN параллельна стороне PQ,
а сторона NP параллельна стороне MQ.

Следовательно, у этого выпуклого четырехугольника две стороны равны и параллельны,а это значит, что это параллелограмм.

Докажем признак, который мы использовали для доказательства — о том, что если в четырехугольнике
две любые стороны равны и параллельны, то это параллелограмм.

На рисунке 2 изобразим выпуклый четырехугольник CPED. По условию CP = ED, CP || ED. Докажем, что CPED — параллелограмм.

1. Проведем диагональ CE, которая разделит выпуклый четырехугольник на два треугольника.
2. Рассмотрим два треугольника: CPE и EDC.
3. По условию CP = ED.
   Сторона CE — общая.
   ∠ECP=∠CED, так как накрест лежащие углы при СP || ED и секущей CE.Следовательно, по двум сторонам и углу между ними — треугольник
   CPE равен треугольнику EDC.
4. Из этого всего следует, что соответствующие углы ∠ECD=∠CPE.
   А так как эти углы — накрест лежащие при прямых PE, CD и секущей CE, то прямые PE и CD параллельны.

   5) PE || CD, CP || ED и PE = CD, CP = ED, следовательно CPED — параллелограмм, ч.т.д.

   Признак доказан.
   

Кроме признака параллелограмма, который мы сейчас доказали, существует еще несколько признаков,
которые мы рассмотрим и докажем в следующих статьях.

Разница между параллелограммом и четырехугольником

Параллелограмм и четырехугольник
 

Четырехугольники и параллелограммы — это многоугольники, встречающиеся в евклидовой геометрии. Параллелограмм является частным случаем четырехугольника. Четырехугольники могут быть либо плоскими (2D), либо трехмерными, тогда как параллелограммы всегда плоские.

Четырехугольник

Четырехугольник — это многоугольник с четырьмя сторонами. У него четыре вершины, а сумма внутренних углов равна 3600 (2π рад). Четырехугольники подразделяются на категории самопересекающихся и простых четырехугольников. Самопересекающиеся четырехугольники имеют две или более сторон, пересекающих друг друга, и меньшие геометрические фигуры (например, треугольники) образуются внутри четырехугольника.

Простые четырехугольники также делятся на выпуклые и вогнутые четырехугольники. Вогнутые четырехугольники имеют смежные стороны, образующие рефлекторные углы внутри фигуры. Простые четырехугольники, не имеющие внутренних углов отражения, являются выпуклыми четырехугольниками. Выпуклые четырехугольники всегда могут иметь замощения.

Большая часть геометрии четырехугольников на начальных уровнях касается выпуклых четырехугольников. Некоторые четырехугольники хорошо знакомы нам со времен начальной школы. Ниже приведена диаграмма, показывающая различные выпуклые четырехугольники.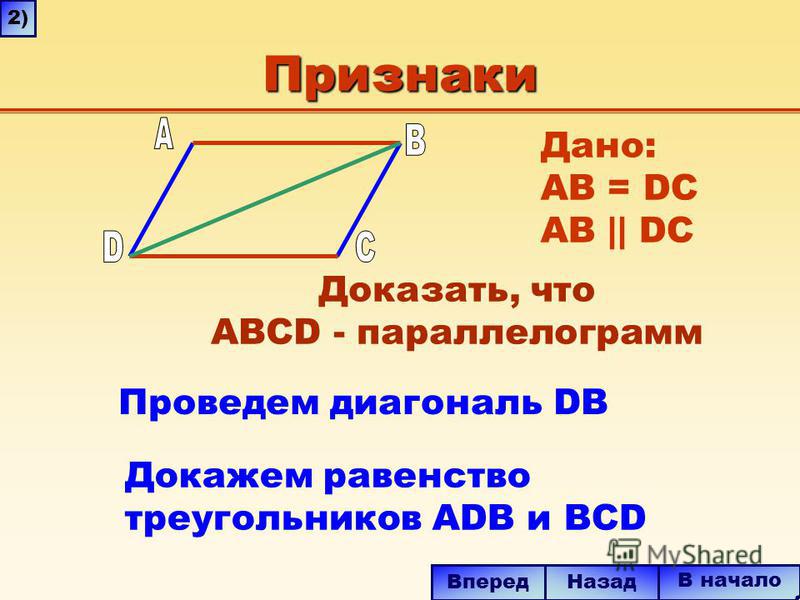

Параллелограмм

Параллелограмм можно определить как геометрическую фигуру с четырьмя сторонами, противоположные стороны которых параллельны друг другу. Точнее, это четырехугольник с двумя парами параллельных сторон. Эта параллельная природа придает параллелограммам множество геометрических характеристик.

          

Четырехугольник является параллелограммом, если обнаружены следующие геометрические характеристики.

• Две пары противоположных сторон имеют одинаковую длину. (АВ = DC, AD = ВС) 9{\circ} = \pi rad[/latex]

• Пара сторон, противостоящих друг другу, параллельна и имеет одинаковую длину. ( AB = DC и AB∥DC)

• Диагонали делят друг друга пополам (AO = OC, BO = OD)

• Каждая диагональ делит четырехугольник на два равных треугольника. (∆ADB ≡ ∆BCD, ∆ABC ≡ ∆ADC)

Далее, сумма квадратов сторон равна сумме квадратов диагоналей. Иногда его называют 9. 0036 закон параллелограмма и имеет широкое применение в физике и технике. (AB ²  + BC ²  + CD ²  + DA ²  = AC ²  + BD ² )

Каждая из вышеперечисленных характеристик может быть использована в качестве свойства четырехугольника. является параллелограммом.

Площадь параллелограмма можно вычислить произведением длины одной стороны и высоты противоположной стороны. Следовательно, площадь параллелограмма можно определить как

Площадь параллелограмма = основание × высота = AB × h

Площадь параллелограмма не зависит от формы отдельного параллелограмма. Она зависит только от длины основания и высоты перпендикуляра.

Если стороны параллелограмма могут быть представлены двумя векторами, площадь может быть получена по величине векторного произведения (перекрестного произведения) двух соседних векторов.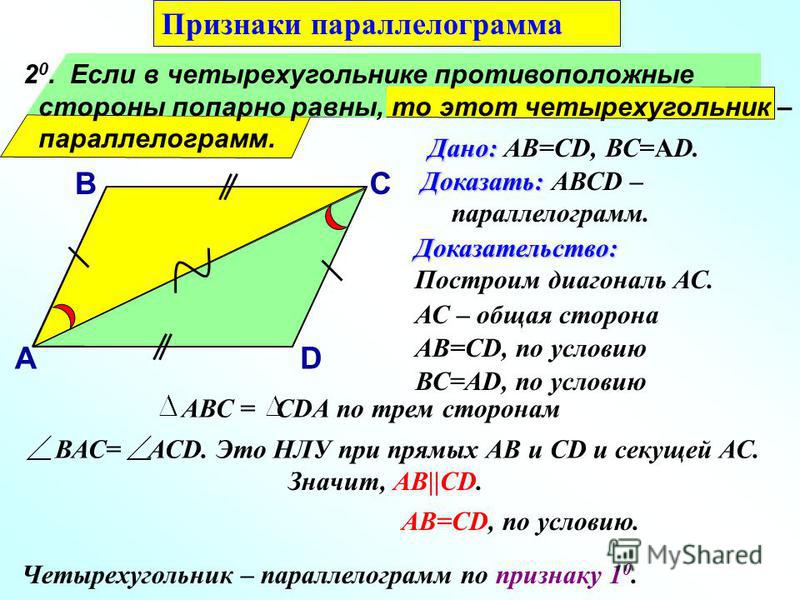

Если стороны AB и AD представлены векторами ([latex]\overrightarrow{AB}[/latex]) и ([latex]\overrightarrow{AD}[/latex]) соответственно, площадь параллелограмма задана by [латекс]\left | \overrightarrow{AB}\times \overrightarrow{AD} \right | = AB\cdot AD \sin \alpha [/latex], где α — угол между [латекс]\overrightarrow{AB}[/латекс] и [латекс]\overrightarrow{AD}[/латекс].

Ниже приведены некоторые дополнительные свойства параллелограмма.

• Площадь параллелограмма вдвое больше площади треугольника, образованного любой из его диагоналей.

• Площадь параллелограмма делится пополам любой линией, проходящей через его середину.

• Любое невырожденное аффинное преобразование переводит параллелограмм в другой параллелограмм

• Параллелограмм имеет вращательную симметрию порядка 2

• Сумма расстояний от любой внутренней точки параллелограмма до сторон не зависит от положения точки

В чем разница между параллелограммом и четырехугольником?

• Четырехугольники — это многоугольники с четырьмя сторонами (иногда называемые четырехугольниками), а параллелограмм — это особый тип четырехугольника.

• Четырехугольники могут иметь стороны в разных плоскостях (в трехмерном пространстве), в то время как все стороны параллелограмма лежат в одной плоскости (плоскостной/двумерной).

• Внутренние углы четырехугольника могут принимать любое значение (включая углы отражения), так что в сумме они составляют 3600. Параллелограммы могут иметь только тупые углы в качестве максимального типа угла.

• Четыре стороны четырехугольника могут быть разной длины, а противоположные стороны параллелограмма всегда параллельны друг другу и равны по длине.

• Любая диагональ делит параллелограмм на два конгруэнтных треугольника, а треугольники, образованные диагоналями общего четырехугольника, не обязательно конгруэнтны.

Урок Середины четырехугольника являются вершинами параллелограмма

Урок Середины четырехугольника являются вершинами параллелограмма

Алгебра -> Настраиваемые средства решения задач Word -> Геометрия -> Урок Середины четырехугольника являются вершинами параллелограмма Войти

Объявление: Более 600 словесных задач по алгебре на edhelper. com

Задачи Word: GeometryWord РешателиРешатели УрокиУроки Архив ответовОтветы     Этот урок (Середины четырехугольника являются вершинами параллелограмма) был создан пользователем ikleyn(46512)   : Просмотр исходного кода, Показать Об ikleyn : Теорема В произвольном выпуклом четырехугольнике середины сторон являются вершинами параллелограмма. Доказывать. Доказательство Пусть ABCD — произвольный выпуклый четырехугольник ( рис. 1 ),                          , и пусть точки E , F , G и H являются серединами его сторон AB , BC , CD и AD соответственно. Нам нужно доказать, что четырехугольник EFGH является параллелограммом. Проведите диагонали AC и BD в четырехугольнике ABCD ( рис. 2 ). Отрезок HG является средним отрезком треугольника ACD . Следовательно, сегмент HG параллельна стороне AC треугольника ACD в соответствии с уроком Отрезок, соединяющий середины двух сторон треугольника (по теме Треугольники раздела Геометрия на этом сайте).          Рисунок 1 . К теореме          Рисунок 2 . К доказательству Теорема Отрезок EF является средним отрезком треугольника ABC . Следовательно, отрезок EF параллелен стороне AC треугольника ABC . Поскольку отрезки HG и EF параллельны диагонали AC , они параллельны друг другу. Точно так же отрезок GF является средним отрезком в треугольнике ДКБ . Следовательно, отрезок GF параллелен стороне DB треугольника DCB . Отрезок HE является средним сегментом треугольника ABD . Следовательно, отрезок НЕ параллелен стороне DB треугольника ABD . Поскольку отрезки GF и HE параллельны диагонали DB , они параллельны друг другу. Итак, мы доказали, что в четырехугольнике EFGH противоположные стороны HG и EF , HE и GF попарно параллельны. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт