Учебные материалы по математике | Первообразная функция и неопределенный интеграл
СОДЕРЖАНИЕ
1. Первообразная функция и неопределенный интеграл
2. Таблица простейших интегралов
3. Интегрирование методом замены переменной
4. Метод интегрирования по частям
5. Понятие о неберущихся в конечном виде интегралах
6. Интегрирование рациональных функций
7. Интегрирование тригонометрических рациональных выражений
8. Интегрирование простейших иррациональных выражений
Н Е О П Р Е Д Е Л Ё Н Н Ы Й И Н Т Е Г Р А Л
1. Первообразная функция и неопределенный интеграл
Восстановление функции F(x) по известной производной этой функции F’(x)=f (x) (или по известному ее дифференциалу dF(x)=f(x)dx) называется интегрированием, а искомая функция F(x) называется первообразной функцией.
Всякая функция f(x) имеет бесчисленноемножество различных первообразных функций, отличающихся друг от друга на постоянное слагаемое, т.
[F(x)+C]’=F‘(x)=f(x). Cовокупность всех первообразных F(x)+C одной и той же функции f(x) называется неопределенным интегралом этой функции и обозначается символом
, (1)
где x — переменная интегрирования, f(x) — подынтегральная функция, f(x)dx — подынтегральное выражение.
Геометрически, графики всех первообразных функций для f(x) представляют в системе координат XOY семейство кривых, которые получаются одна из другой путем параллельного переноса вдоль оси Y на величину С.
Как следует из понятия неопределенного интеграла, интегрирование и нахождение дифференциала являются обратными действиями.
Действительно, если первообразная, а значит и неопределенный интеграл для функции f(x) существует, то подынтегральное выражение представляет собой дифференциал любой из этих первообразных
f(x)dx=F'(x)d(x)=dF(x),
тогда
d∫f(x)dx=d[F(x)+C]=F'(x)dx=f(x)dx, (2)
∫dF(x)=∫ f(x)dx=F(x)+C, (3)
т. е. знаки d и ∫ взаимно сокращаются.
Укажем основные свойства неопределенного интеграла, правильность которых можно проверять дифференцированием.
І. Постоянный множитель выносится за знак интеграла.
∫Af(x)dx=A∫ f(x)dx (4)
2. Интеграл от алгебраической суммы (разности) функций равен сумме (разности) интегралов.
∫[f(x)± φ(x)]dx=∫f(x)dx ±∫φ(x)dx . (5)
3. Неопределенный интеграл не зависит от выбора переменной интегрирования.
∫f(u)du= F(u)+C, (6)
где u — независимая переменная или функция x, u=u(x). Этот результат следует непосредственно из правила дифференцирования сложной функции
; , ,
тогда
.
4. Интеграл ∫udv может быть сведен к интегралу ∫vdu.
Из формулы дифференцирования произведения двух функций d(uv)=udv
+vduинтегрированием получается следующее равенство
∫udv = uv – ∫vdu, (7)
которое называется формулой интегрирования по частям.
2. Таблица простейших интегралов
Пользуясь тем, что интегрирование – операция обратная вычислению дифференциала можно записать основные формулы интегрирования
1. α ≠ -1
2.
3.
4.
5.
6.
7.
8.
9.
Для полноты таблицы добавим еще две формулы.
10.
11.
В этих формулах u — независимая переменная или функция от независимой переменной, a – постоянная (в формуле 7 а ).
Приведем простейшие примеры вычисления интегралов:
Пример 1.
Пример 2.
Пример 3.
1.Разлагая интеграл 1 по свойству 2 на три интеграла и вынося постоянный множитель за знак интеграла (свойство 1), приведем интеграл к следующему виду:
далее первый и второй интегралы вычисляются по формуле 1 таблицы, а
в третьем — знаки ∫ и d взаимно сокращаются (интегрирование и взятие дифференциала – обратные действия).
.
2.Интеграл табличный, формула 3.
3.Подынтегральная функция (пр.3) может быть преобразована и сведена к разности двух функций, а значит к двум интегралам, интегрируемых по формуле 1 таблицы.
Для вычисления различных интегралов дополним таблицу определенными приёмами и методами интегрирования.
3. Интегрирование методом замены переменной.
Метод замены переменной или подстановки является одним из самых эффективных приемов интегрирования и вытекает из свойства 3.
Пусть требуется вычислить , во многих случаях удается в качестве новой переменной выбрать такую функцию u=u(x) , чтобы подынтегральное выражение представилось в виде
,
тогда достаточно найти интеграл
чтобы из него подстановкой u=u(x) получить искомый интеграл, т. е.
(9)
Рассмотрим частный случай замены переменной, если ∫ f(x)dx=F(x)+C, то
(8)
Действительно, , тогда
т. е. и функция оказывается первообразной
для f(ax+b).
Пример 4.
Пример 5. .
Пример 6.
Пример 7.
так как , то полагая , получим
При выборе подстановки , упрощающей подынтегральное выражение, нужно помнить, что в его составе должен найтись множитель , дающий дифференциал новой переменной.
Приведем ряд примеров на вычисление интегралов, которые заменой переменной сводятся к табличным.
Пример 8.
полагаем тогда и
Пример 9.
Замена подставляя новую переменную в исходный интеграл, получим
Пример 10.
В состав подынтегрального выражения входит множитель , являющийся
дифференциалом функции lnx , отсюда подстановка u=lnx, du=d(lnx) т. е.
Пример 11.
Подстановка x3 = u, du=3x2dx сводит искомый интеграл к другому интегралу, который является табличным.
ΩΩΩ
Интегрирование дробей, содержащих квадратный трехчлен
(10)
при условии, что квадратный трехчлен x2 +px+q не имеет действительных корней .
Для вычисления интеграла из квадратного трехчлена выделяется полный квадрат двучлена т.
к. , то подстановка приводит к следующей замене
Искомый интеграл принимает следующий вид:
Первый интеграл аналогичен интегралу из примера 8, второй табличный
/формула 6/.
Пример 12.
Выделяем полный квадрат x2 +4x+10=(x2+4x+4)+(10-4), делаем замену x+2=u, тогда 3x-1=3u-7, du=dx, подставляем в интеграл
4. Метод интегрирования по частям
Согласно свойству 4 вычисление интеграла может быть сведено к отысканию другого интеграла . Применение формулы целесообразно, если будет проще, чем или подобен ему. Для применения формулы интегрирования по частям к интегралу следует подынтегральное выражение представить в виде произведения двух множителей
д.Пример 13.
Примем за , тогда , подставляя в формулу (7), получим
Второй интеграл вычисляется подстановкой , окончательный результат
Пример 14.
Принимаем за , находим подставляем в (7)
Интеграл Мора (сопромат)
Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.
Получение формулы интеграла Мора
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки () в точке K.
Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.
Внутренние усилия, возникающие во вспомогательной балке, обозначим и .
Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .
При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).
Тогда, учитывая, что , окончательно получим формулу интеграла Мора: .
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора, а саму формулу – интегралом Мора.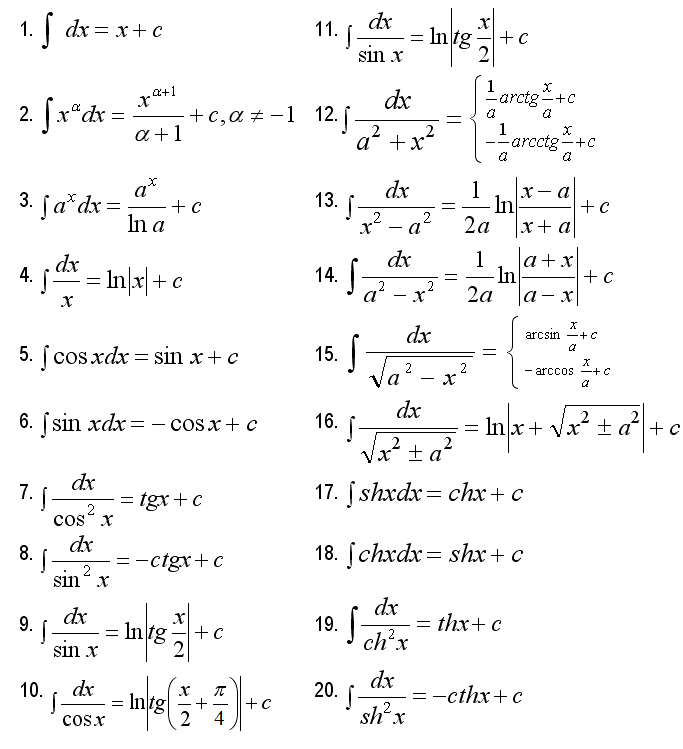
Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 15.6, в).
порядок вычисления перемещений методом Мора:
· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;
· вычисляем интеграл Мора для всей балки по соответствующим участкам;
· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия.
Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.
Вычисление интеграла Мора пример
Пусть для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета () и угол поворота на левой опоре ().
определение прогиба с помощью интеграла Мора
В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.7, б).
Записываем выражения для изгибающих моментов для каждого из двух участков () заданной и вспомогательной балок:
.
.
Вычисляем интеграл Мора. Учитывая симметрию балки, получим:
.
Определение угла поворота методом Мора
Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ():
;
.
Тогда интеграл Мора будет иметь вид:
.
Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .
Indefinite Integrals Calculator & Solver
Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора
Indefinite Integrals . Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Проверьте все наши онлайн-калькуляторы здесь!1
2
3
4
5
6
7
8
A
B
C
D
F
B
C
D
F
B
C
D
F
B
C
D
F
B
.0007
g
m
n
u
v
w
x
y
z
7.
(◻)
+
—
×
◻/◻
/
÷
◻ 2
◻ ◻
√◻
√
◻ √ ◻
◻ √
∞e
π
ln
журнал
журнал ◻
LIM
D/DX
D □ x
∫
∫ ◻
| ◻ |
θ
=
>
<
>=
<=
sin
cos
tan
cot
sec
csc
asin
acos
atan
acot
asec
acsc
sinh
cosh 9{n-1}$
$2x$
3
Теперь, чтобы переписать $dx$ через $du$, нам нужно найти производную от $u$.
Нам нужно рассчитать $du$, мы можем сделать это, выведя приведенное выше уравнение
$du=2xdx$
4
Изолировать $dx$ в предыдущем уравнении
$\frac{du}{2x}=dx$
Промежуточные шаги
Упростить дробь $\frac{xu}{2x}$ на $x$
$\int\frac{u}{2}du$
5
Подставим $u$ и $dx$ в интеграл и упростим
$\int\frac{u}{2}du$
Промежуточные шаги
Возьмем константу $\frac{1}{2}$ из интеграла
$\frac{1}{2}\int udu$
Разделить $1$ на $2$
$\frac{1}{2}\int udu$
6
Вынести константу $\frac{1}{2}$ из интеграла 92-sin(x)+ln(2x)
| x | Y | π | E | 1 | 2 | 3 | 2 | 3 | 2 | 3 | 40357 | 40357 | 40357 | 2 | 3 | 2 | . «> а б | а б | эксп | 4 | 5 9093800324 | 6 | × | удалить | |||||||||||||
| ( | ) | |а| | пер. | 7 | 8 | 9 | — | ↑ | ↓ | ||||||||||||||||||||||||||||
| √ | 3 √ | C | журнал a | 0 | . | ↵ | + | ← | → | ||||||||||||||||||||||||||||
Этот калькулятор для решения неопределенных интегралов взят от ООО «Вольфрам Альфа». Все права принадлежат владельцу!
Неопределенный интеграл
Нахождение неопределенного интеграла — очень распространенная задача в математике и других технических науках.
На самом деле решение простейших физических задач редко обходится без нескольких вычислений простых интегралов. Поэтому со школьного возраста нас обучают приемам и методам решения интегралов , приводятся многочисленные таблицы интегралов простых функций. Но со временем все благополучно забывается или у нас нет времени на расчеты или нужно найти неопределенный интеграл от очень сложной функции. Наш сервис идеально подойдет для решения этих проблем. Он позволяет точно находить неопределенные интегралы онлайн.
Решить неопределенный интеграл
Онлайн-сервис OnSolver.com позволяет быстро и бесплатно решить интеграл онлайн. Вы можете заменить наш сервис на поиск нужного интеграла в таблицах. Здесь вы получите решение неопределенного интеграла в табличном виде, просто набрав нужную функцию. Не все математические сайты могут быстро и качественно вычислить неопределенные интегралы от функций онлайн, особенно если вы хотите найти неопределенный интеграл от сложных функций или функций, которые не входят в общий курс высшей математики.