Пусть заданы точки м1(x1, y1, z1), m2(x2, y2, z2) и вектор .
Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору .
Векторы и вектор должны быть компланарны, т.е.
( ) = 0
Уравнение плоскости:
Уравнение плоскости по одной точке и двум векторам,
коллинеарным плоскости.
Пусть заданы два вектора и , коллинеарные плоскости. Тогда для произвольной точки м(х, у, z), принадлежащей плоскости, векторы должны быть компланарны.
Уравнение плоскости:
Уравнение плоскости по точке и вектору нормали.
Теорема. Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C
A(x – x0) + B(y – y0) + C(z – z0) =
0.
Доказательство. Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор . Т.к. вектор — вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору . Тогда скалярное произведение
= 0
Таким образом, получаем уравнение плоскости
Теорема доказана.
Уравнение плоскости в отрезках.
Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на -D
,
заменив , получим уравнение плоскости в отрезках:
Числа a, b, c являются точками пересечения плоскости соответственно с осями х, у, z.
Уравнение плоскости в векторной форме.
где
— радиус- вектор текущей точки М(х, у, z),
— единичный вектор, имеющий направление,
перпендикуляра, опущенного на плоскость
из начала координат.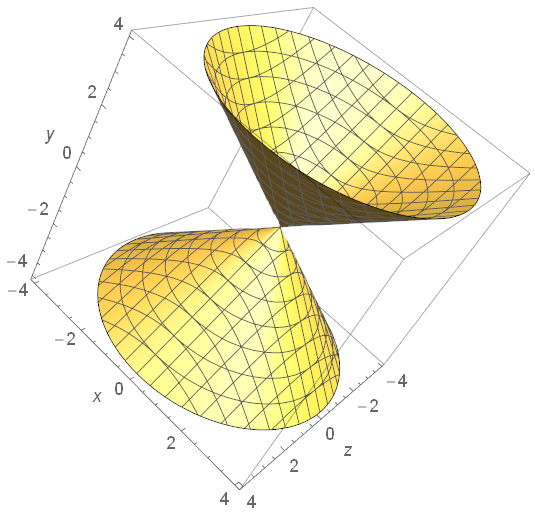
, и — углы, образованные этим вектором с осями х, у, z.
p – длина этого перпендикуляра.
В координатах это уравнение имеет вид:
xcos + ycos + zcos — p = 0.
Расстояние от точки до плоскости.
Расстояние от произвольной точки М0(х0, у0, z0) до плоскости Ах+Ву+Сz+D=0 равно:
Уравнение линии на плоскости.
Как известно, любая точка на плоскости определяется двумя координатами в какой- либо системе координат. Системы координат могут быть различными в зависимости от выбора базиса и начала координат.
Определение. Уравнением линии называется соотношение y = f(x) между координатами точек, составляющих эту линию.
Отметим, что
уравнение линии может быть выражено
параметрическим способом, то есть каждая
координата каждой точки выражается
через некоторый независимый параметр t.
Характерный пример – траектория движущейся точки. В этом случае роль параметра играет время.
Уравнение прямой на плоскости.
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка
А х + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 0. Это уравнение первого порядка называют общим уравнением прямой.
В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
C = 0, А 0, В 0 – прямая проходит через начало координат
А = 0, В 0, С 0 { By + C = 0}- прямая параллельна оси Ох
В = 0, А 0, С 0 { Ax + C = 0} – прямая параллельна оси Оу
В = С = 0, А 0 – прямая совпадает с осью Оу
А = С = 0, В 0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено
в различном виде в зависимости от каких
– либо заданных начальных условий.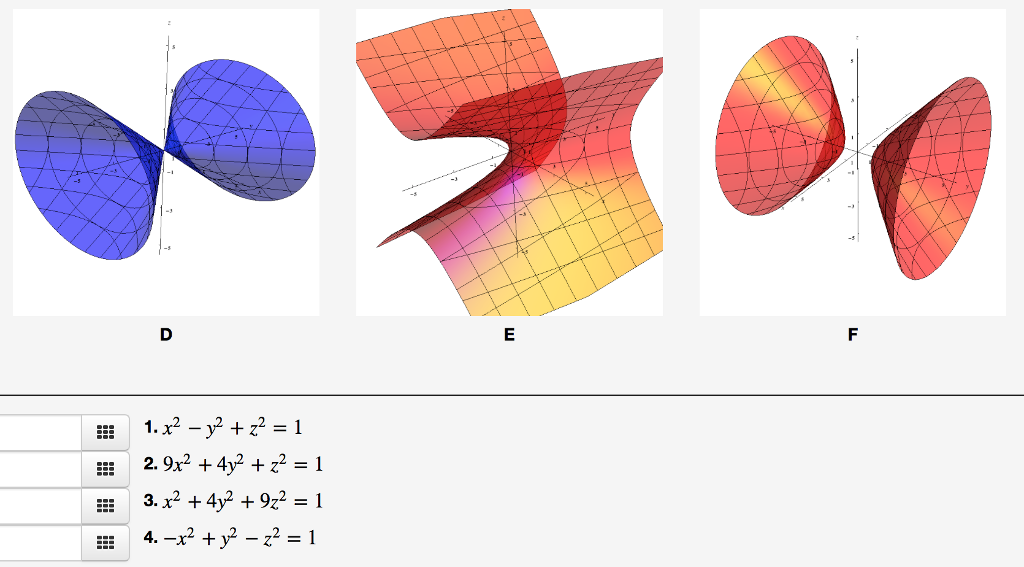
Уравнение прямой по точке и вектору нормали.
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).
Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.
Получаем: 3 – 2 + C = 0, следовательно С = -1.
Итого: искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки.
Пусть в пространстве заданы две точки M1(x1
, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки: Если
какой- либо из знаменателей равен нулю,
следует приравнять нулю соответствующий
числитель.
На плоскости записанное выше уравнение прямой упрощается:
если х1 х2 и х = х1, еслих1 = х2.
Дробь = k называется угловым коэффициентом прямой.
Уравнение прямой по точке и угловому коэффициенту.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить , то полученное уравнение называется уравнением прямой с угловым коэффициентом
Уравнение прямой по точке и направляющему вектору.
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор (1, 2), компоненты которого удовлетворяют условию А1 + В2 = 0 называется направляющим вектором прямой
Ах + Ву + С = 0.
Уравнение прямой в отрезках.
Если в общем уравнении прямой Ах + Ву + С = 0 С 0, то, разделив на –С, получим: или
, где
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Нормальное уравнение прямой.
Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется нормирующем множителем, то получим
xcos + ysin — p = 0 — нормальное уравнение прямой.
Знак нормирующего множителя надо выбирать так, чтобы С < 0.
р – длина перпендикуляра, опущенного из начала координат на прямую, а — угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Угол между
прямыми на плоскости.
Определение. Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как
.
Две прямые параллельны, если k1 = k2.
Две прямые перпендикулярны, если k1 = -1/k2.
Теорема. Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = А, В1 = В. Если еще и С1 = С, то прямые совпадают.
Координаты точки пересечения двух прямых находятся как решение системы двух уравнений.
Уравнение прямой, проходящей через данную точку
перпендикулярно данной прямой.
Определение. Прямая, проходящая через точку М1(х1, у1) и перпендикулярная к прямой у = kx + b представляется уравнением:
Расстояние от точки до прямой.
Т еорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как
.
Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
(1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
Второе
уравнение системы – это уравнение
прямой, проходящей через заданную точку
М
Если преобразовать первое уравнение системы к виду:
A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,
то, решая, получим:
Подставляя эти выражения в уравнение (1), находим:
.
Аналитическая геометрия в пространстве.
Уравнение линии в пространстве.
Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:
F(x, y, z) = 0.
Это уравнение называется уравнением линии в пространстве.
Кроме того,
линия в пространстве может быть определена
и иначе. Ее можно рассматривать как
линию пересечения двух поверхностей,
каждая из которых задана каким- либо
уравнением.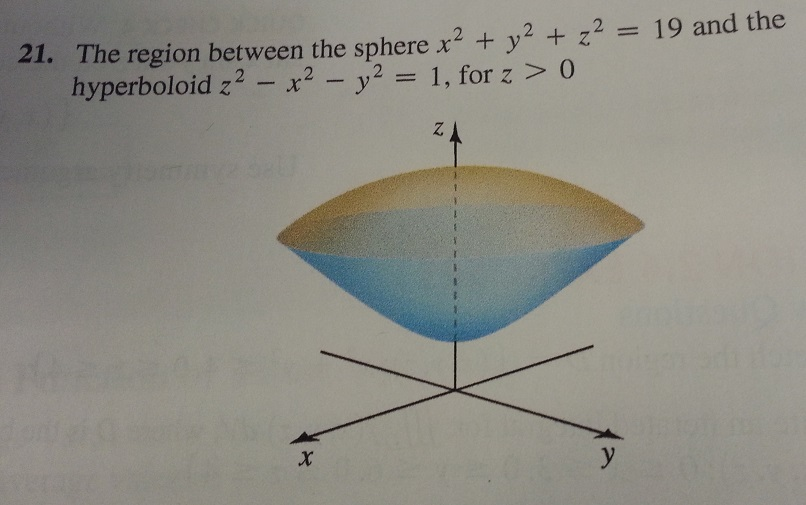
Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.
Тогда пару уравнений
назовем уравнением линии в пространстве.
5$$Есть ли простой способ решить эту проблему? Я перепробовал все свои уловки, пытался перемножить два уравнения, заменить $z=1-x-y$, но все запуталось, кажется, ничего не получается.
- абстрактная алгебра
- системы уравнений
- симметричные полиномы
$\endgroup$
3
$\begingroup$
Эта форма уравнений может быть решена систематически с использованием тождеств Ньютона. 93$$ и выше
$\endgroup$
2
Поверхности
Поверхности
Самолеты
Так же, как линии — самые простые и важные кривые, плоскости — самые
важные поверхности.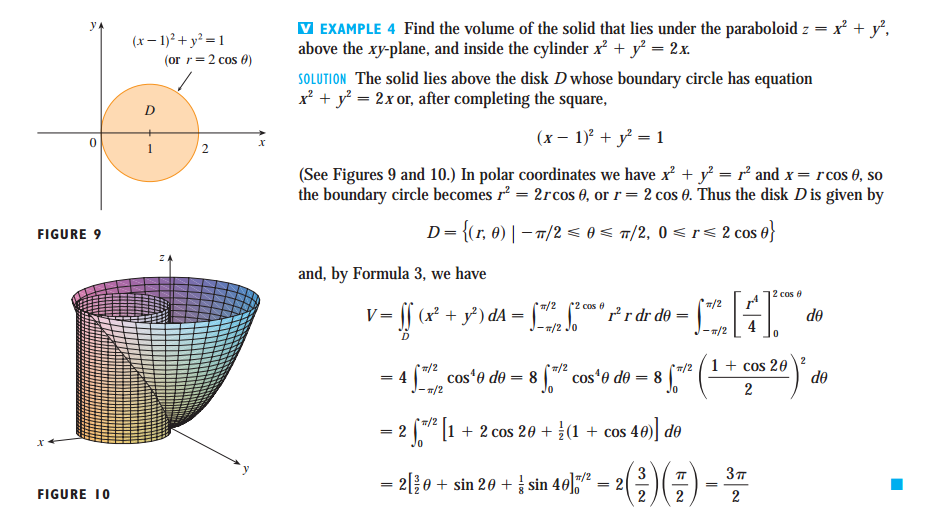
Общая плоскость имеет уравнение
топор + by + cz = д
Чтобы нарисовать плоскость со всеми положительными коэффициентами, мы просто нанесем три точки, где плоскость пересекает оси и соединяют точки.
Пример
График
2x + 3y + 4z = 12
Раствор
Сначала мы устанавливаем y и z равно 0, чтобы получить точку
(6,0,0)
Аналогично находим два других отрезка
(0,4,0) и (0,0,3)
Теперь нанесите три точки и соедините их, как показано на рисунке ниже.
Квадратные поверхности
В плоскости xy следующим шагом после изучения прямых является изучение коник:
параболы, эллипсы и гиперболы. Все их уравнения имеют x 2 или y 2 терминов или оба. Через три
Поверхности размеров, уравнения которых имеют только линейные и квадратичные члены, называются
называются квадратичными поверхностями.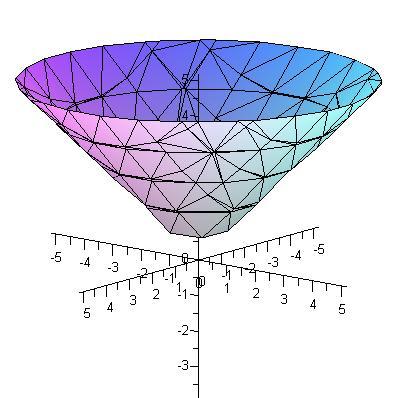
Именование
использует суффикс «-oid», чтобы указать, что поверхности имеют след в
форму эллипса. Обратите внимание, что круг — это особый эллипс.
Ниже приведены имена некоторых из них:
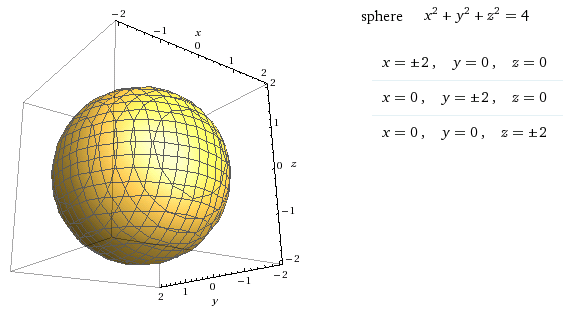
x 2 /a 2 + y 2 /b 2 + z 2 /c 2 = 1 является эллипсоидом
-x 2 /a 2 — y 2 /b 2 + z 2 /c 2 = 1 представляет собой гиперболоид из 2 листов , а
х 2 /а 2 + у 2 /б 2 — z 2 /c 2 = 1 представляет собой гиперболоид из 1 листа
z = x 2 /a 2 + y 2 /b 2 это параболоид
г = x 2 /a 2 — у 2 /б 2 является гиперболическим параболоидом
х 2 /а 2 + у 2 /б 2 — z 2 /c 2 = 0 конус
Пример
Назовите следующую квадрику
Решение
Обратите внимание, что трассировка на плоскости xy
x 2 — y 2 = 1
гипербола и на плоскости xz
х 2 — 4z 2 = 1
также гипербола и не плоскость yz
x 2 + 4z 2 = 1
эллипс.