| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Параметрические уравнения кривых
Параметрические уравнения кривыхпараметрических уравнений
Каждое значение параметра t дает значения для
х и у; точка является соответствующей точкой на
Кривая.
Например, рассмотрим параметрические уравнения
Вот некоторые моменты, которые возникают в результате подключения некоторые значения для t:
График кривой выглядит так:
Это параметрические уравнения для окружности:
Иногда вы можете восстановить уравнение xy параметрической кривой с помощью исключение t из параметрических уравнений. В таком случае,
Обратите внимание, что график круга равен , а не 9.0908 график функция. Параметрические уравнения могут представлять более общие кривые, чем графы функций могут, что является одним из их преимуществ.
Эти параметрические уравнения представляют собой спираль:
Это также не график функции.
Пример. Найдите уравнение x-y для
Решите x-уравнение для t:
Подставьте это выражение для t в уравнение y:
Пример.
Найдите уравнение x-y для
Заметь
Так
Это стандартная форма уравнения эллипса.
В некоторых случаях восстановление уравнения x-y может быть затруднено или невозможно. Например, это параметрические уравнения для гипоциклоиды с четырьмя точками возврата :
В этом случае было бы трудно исключить t, чтобы получить x-y уравнение.
А если пойти другим путем? Если у вас есть кривая (или x-y уравнение), как вы получаете параметрические уравнения?
Заметим сначала, что данная кривая может быть представлена бесконечным числом системы параметрических уравнений. Например, все эти наборы параметрические уравнения представляют единичный круг:
Даже в этом случае может быть трудно найти параметризацию для кривых.
Начнем с простого случая. Если у вас есть уравнения x-y, в которых x
или у решается для, это легко.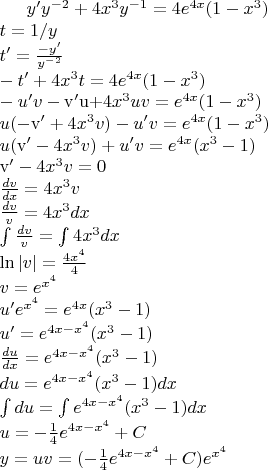
Например, для параметризации установите . Затем . Параметризация задается
Для параметризации установите . Тогда, так
Это параметризация . (Это как вы можете построить график уравнений x в терминах y на вашем калькуляторе.)
Вот еще один важный случай. Если и точки, то линия через и может быть параметризовано
Легче всего запомнить это в векторе форма
Обратите внимание, что когда , у меня есть , и когда , . Таким образом, если вы позволите, вы получите сегмент от до .
Пример. Найдите параметрические уравнения для линия через и .
Таким образом,
Аналогичный результат справедлив для линий в трех измерениях (или в любом количестве). размеров).
В качестве примера более общего метода параметризации кривых я приведу
рассмотрим параметризацию по наклону .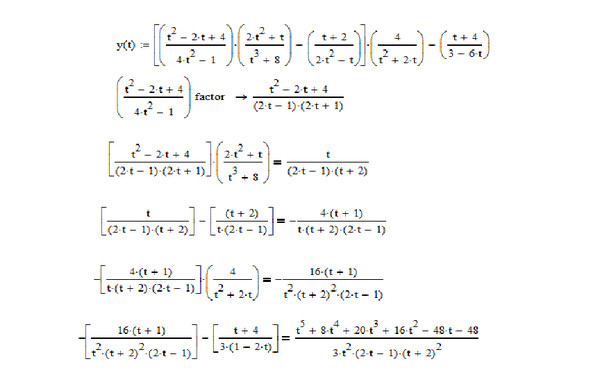
Идея в том,
рассматривать точку на кривой как
точка пересечения кривой и прямой:
Наклон t будет параметром кривой.
Пример. Найдите параметрические уравнения для Фолиума Декарта :
Установлен . затем
Следовательно, . А параметризация задается
Первая и вторая производные дают информацию о форме кривая. Вот как найти производные для параметрической кривой.
Во-первых, по цепному правилу,
Решение для дает
Пример. Найдите уравнение касательной к кривой
Когда и . Касательная линия
Пример. В каких точках на следующей кривой касательная горизонтальна?
Найдите производную:
Касательная горизонтальна при , при и при .
Когда и .