Решение уравнений 3-й и 4-й степеней
Цели:
- Систематизировать и обобщить знания и умения по теме: Решения уравнений третьей и четвертой степени.
- Углубить знания, выполнив ряд заданий, часть из которых не знакома или по своему типу, или способу решения.
- Формирование интереса к математике через изучение новых глав математики, воспитание графической культуры через построение графиков уравнений.
Тип урока: комбинированный.
Оборудование: графопроектор.
Наглядность: таблица «Теорема Виета».
Ход урока
1. Устный счет
Вопросы:
а) Чему равен остаток от деления многочлена рn (х) = аnхn + аn-1хn-1 + … + а1х1 + a0на двучлен х-а?
б) Сколько корней может иметь кубическое уравнение?
в) С помощью чего мы решаем уравнение третьей и четвертой степени?
г) Если b четное число в квадратном уравнение, то чему равен Д и х1;х2
2. Самостоятельная работа (в группах)
Самостоятельная работа (в группах)
Составить уравнение, если известны корни (ответы к заданиям закодированы) Используется «Теорема Виета»
3 |
2 |
-4 |
8 |
-18 |
7 |
1 |
-1 |
-10 |
-5 |
ы |
п |
ф |
р |
й |
л |
0 |
н |
и |
ь |
1 группа
Корни: х1 = 1; х2 = -2; х3 = -3; х4 = 6
Составить уравнение:
— b=1 -2-3+6=2; b=-2
с=-2-3+6+6-12-18= -23; с= -23
d=6-12+36-18=12; d= -12
е=1(-2)(-3)6=36
х4 — 2 х3 — 23х2 — 12 х + 36 = 0 (это уравнение решает потом 2 группа на доске)
Решение. Целые корни ищем среди делителей числа 36.
Целые корни ищем среди делителей числа 36.
р = ±1;±2;±3;±4;±6…
р4(1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, следовательно, =1 корень уравнения. По схеме Горнера
|
1 |
-2 |
-23 |
-12 |
36 |
1 |
1 |
-1 |
-24 |
-36 |
0 |
-2 |
1 |
-3 |
-18 |
0 |
|
р3(x) = х3 -х2 -24x -36
р3(-2) = -8 -4 +48 -36=0, х2=-2
р2(x) = х2 -3х -18=0
х3=-3, х4=6
Ответ: 1;-2;-3;6 сумма корней 2 (П)
2 группа
Корни: х1 = -1; х2 = х3 =2; х4 =5
Составить уравнение:
— b=-1+2+2+5-8; b= -8
с=2(-1)+4+10-2-5+10=15; с=15
-d=-4-10+20-10= -4; d=4
е=2(-1)2*5=-20;е=-20
р = ±1;±2;±4;±5;±10;±20.
|
1 |
-8 |
15 |
4 |
-20 |
-1 |
1 |
-9 |
24 |
-20 |
0 |
2 |
1 |
-7 |
10 |
0 |
|
р4(1)=1-8+15+4-20=-8
р4(-1)=1+8+15-4-20=0
р3(x) = х3 -9х2 +24x -20
р3(2) = 8 -36+48 -20=0
р2(x) = х2 -7х +10=0 х1=2; х2=5
Ответ: -1;2;2;5 сумма корней 8(Р)
3 группа
Корни: х1 = -1; х2 =1; х3 =-2; х4 =3
Составить уравнение:
-в=-1+1-2+3=1;в=-1
с=-1+2-3-2+3-6=-7;с=-7
-d=2+6-3-6=-1; d=1
е=-1*1*(-2)*3=6
х4 — х3 — 7х2 + х + 6 = 0 (это уравнение решает потом на доске 4 группа)
 Целые корни ищем среди делителей числа 6.
Целые корни ищем среди делителей числа 6.р = ±1;±2;±3;±6
|
1 |
-1 |
-7 |
1 |
6 |
1 |
1 |
0 |
-7 |
-6 |
0 |
| 1 |
1 |
-1 |
-6 |
0 |
|
р4(1)=1-1-7+1+6=0
р3(x) = х3 — 7x -6
р3(-1) = -1+7-6=0
р2(x) = х2 -х -6=0; х1=-2; х2=3
Ответ:-1;1;-2;3 Сумма корней 1(О)
4 группа
Корни: х1 = -2; х2 =-2; х3 =-3; х4 =-3
Составить уравнение:
-b=-2-2-3+3=-4; b=4
с=4+6-6+6-6-9=-5; с=-5
-d=-12+12+18+18=36; d=-36
е=-2*(-2)*(-3)*3=-36;е=-36
х4 + 4х3 – 5х2 – 36х -36 = 0 (это уравнение решает потом 5 группа на доске)
 Целые корни ищем среди делителей числа -36
Целые корни ищем среди делителей числа -36
р = ±1;±2;±3…
|
1 |
4 |
-5 |
-36 |
-36 |
-2 |
1 |
2 |
-9 |
-18 |
0 |
-2 |
1 |
0 |
-9 |
0 |
|
р(1)= 1 + 4-5-36-36 = -72
р4 (-2) = 16 -32 -20 + 72 -36 = 0
р3(х) = х3+2х2-9х-18 = 0
р3(-2)= -8 + 8 + 18-18 = 0
р2(х) = х2 -9 = 0; x=±3
Ответ: -2; -2; -3; 3 Сумма корней-4 (Ф)
5 группа
Корни: х1= -1; х2 =-2; х3 =-3; х4 =-4
Составить уравнение
-b=-10;b=10
с=35
-d= -50; d=50
е=24
х4+ 10х3 + 35х2 + 50х + 24 = 0 (это уравнение решает потом 6группа на доске)
Решение.
р = ±1;±2;±3
|
1 |
10 |
35 |
50 |
24 |
-1 |
1 |
9 |
26 |
24 |
0 |
-2 |
1 |
7 |
12 |
0 |
|
p4 (1)≠0
р4 (-1) = 1 -10 + 35 -50 + 24 = 0
р3(х) = x-3 + 9х2 + 26x+ 24 = 0
p3(-2) = -8 + 36-52 + 24 = О
р2(х) = x2 + 7x+ 12 = 0
Д=49-48=1
Ответ:-1;-2;-3;-4 сумма-10 (И)
6 группа
Корни: х1 = 1; х2 = 1; х3 = -3; х4 = 8
Составить уравнение
-b=1+1-3+8=7;b=-7
с=1 -3+8-3+8-24= -13
-d=-3-24+8-24= -43; d=43
е= -24
х4 — 7х3— 13х2 + 43x — 24 = 0 (это уравнение решает потом 1 группа на доске)
Решение. Целые корни ищем среди делителей числа -24.
Целые корни ищем среди делителей числа -24.
|
1 |
-7 |
-13 |
43 |
-24 |
1 |
1 |
-6 |
-19 |
24 |
0 |
1 |
1 |
-5 |
-24 |
0 |
|
р = +1;±2;±3
р4(1)=1-7-13+43-24=0
р3(1)=1-6-19+24=0
р2(x)= х2 -5x — 24 = 0
х3=-3, х4=8
Ответ: 1;1;-3;8 сумма 7 (Л)
3. Решение уравнений с параметром
Решение уравнений с параметром
1. Решить уравнение х3 + 3х2 + mх — 15 = 0; если один из корней равен (-1)
Ответ записать в порядке возрастания
Решение:
|
1 |
3 |
-13 |
-15 |
-1 |
1 |
2 |
-15 |
0 |
R=Р3(-1)=-1+3-m-15=0
-m- 13=0
m=-13
х3 + 3х2 -13х — 15 = 0; -1+3+13-15=0
По условию х1 = — 1; Д=1+15=16
Р2(х) = х2+2х-15 = 0
х2=-1-4 = -5;
х3=-1 + 4 = 3;
Ответ:- 1;-5; 3
В порядке возрастания: -5;-1;3. ( Ь Н Ы)
( Ь Н Ы)
2. Найти все корни многочлена х3 — 3х2 + ах — 2а + 6, если остатки от его деления на двучлены х-1 и х +2 равны.
Решение: R=Р3(1) = Р3(-2)
Р3(1) = 1-3 + а- 2а + 6 = 4-а
Р3(-2) = -8-12-2а-2а + 6 = -14-4а
4-a=-14-a
3a=-18
a=-6
x3 -Зх2 -6х + 12 + 6 = х3 -Зх2 -6х + 18
x2(x-3)-6(x-3) = 0
(х-3)(х2-6) = 0
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из этих множителей равен нулю, а другой при этом имеет смысл.
х1=3 или х2 — 6 = 0
;
Ответ: -; ; 3 (Произведение 18) (Й)
4. Домашнее задание
1. Решить уравнение х3 — (2а + 1)х2 + (а2 + а)х — (а2 — а) = 0 , где а — параметр.
Решение:
Подбором находим х1 = 1 корень, а — любое число.
Р3 (1)=1-2а-1+ а2+а-а2 =0
|
1 |
-2а-1 |
а²+а |
-а²+а |
1 |
1 |
-2а |
а²-а |
0 |
Р2(х) = х2 -2ах+(а2 – а)=0
Р2(х) = 0;Д = а2 -а2 +а = а, Д >0
1)если а<0, то корней нет
2) а>0, х2 = а — √а; х3 = а + √а
3) а=0, х2 -0*х2 +0 = 0; х2 =0; х4=0
Ответ:
а<0; х=1
а=0; х=0; х=1
а>0; х=1; х=а ± √а
2. Составить уравнение
Составить уравнение
1 группа. Корни: -4; -2; 1; 7;
2 группа. Корни: -3; -2; 1; 2;
3 группа. Корни: -1; 2; 6; 10;
4 группа. Корни: -3; 2; 2; 5;
5 группа. Корни: -5; -2; 2; 4;
6 группа. Корни: -8; -2; 6; 7.
Сколько будет x в 3 степени + x в 4 степени… -reshimne.ru
Новые вопросы
Ответы
Х в седьмой степени…….
«Х» в седьмой степени
х*х*х*х*х*х*х
первые три это Х в третей степени, а остальные это Х в четвёртой
Похожие вопросы
Алгебра 7 класс (упростить выражение)…
Упростите выражение и найдите его значение а)-6(0,5-1,5)-4,5x-8, при x=5…
Найдите нули функции y=3-2x. 2-6x-7=0…
2-6x-7=0…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Сколько будет 3 в 3-й степени?
Математика касается не только чисел, но и различных вычислений с использованием чисел и переменных. Это то, что в основном известно как алгебра. Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Числа могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
Это то, что в основном известно как алгебра. Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Числа могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
Показатели и степени
Экспоненты и степени — это основные операторы, используемые в математических вычислениях, экспоненты используются для упрощения сложных вычислений, включающих многократное самоумножение, самоумножение — это в основном числа, умноженные сами на себя. Например, 7 × 7 × 7 × 7 × 7 можно просто записать как 7 5 . Здесь 7 — базовое значение, 5 — показатель степени, а значение равно 16807. 11 × 11 × 11 можно записать как 11 3 , здесь 11 — базовое значение, а 3 — показатель степени или степень числа 11. Значение 11 3 равно 1331.
Показатель степени определяется как степень, заданная числу, сколько раз оно умножается само на себя. Если выражение записано как cx y , где c — константа, c — коэффициент, x — основание, а y — показатель степени. Если число, например p, умножить n раз, то n будет показателем степени p. Это будет записано как
Если выражение записано как cx y , где c — константа, c — коэффициент, x — основание, а y — показатель степени. Если число, например p, умножить n раз, то n будет показателем степени p. Это будет записано как
p × p × p × p … n раз = p n
Основные правила экспонент с другими математическими операциями, например, если есть произведение двух показателей, его можно упростить, чтобы упростить вычисления, и оно известно как правило произведения, давайте рассмотрим некоторые из основных правил показателей,
- Правило продукта ⇢ A N + A M = A N + M
- Правило коэффициента ⇢ N / A M = A N — M
- Правило мощности ⇢ (A A A A N — M
- N ) M = A N × M или M √a N = A N/M
- Отрицательное правило показания ⇢ -M = 1/A M
- Нулевое правило ⇢ a 0 = 1
- Одно правило ⇢ a 1 = a
Сколько будет 3 в степени 3
rd ?Решение:
Любое число, имеющее степень 3, можно представить в виде куба этого числа.
Куб числа — это число, умноженное само на себя дважды, куб числа представлен как показатель степени 3 этого числа. Если нужно записать куб x, это будет x 3 . Например, куб числа 5 представлен как 5 3 и равен 5 × 5 × 5 = 125. Другим примером может быть куб числа 12, представленный как 12 3 , равно 12 × 12 × 12 = 1728.
Давайте вернемся к постановке задачи и поймем, как она будет решаться, постановка задачи просила упростить 3 до степени 3 rd . Это означает, что задача состоит в том, чтобы решить куб числа 3, который представлен как 3 3 ,
3 3 = 3 × 3 × 3
= 27
. из 3.
Пример задачи
Вопрос 1: Решите выражение, 9 2 – 7 2 .
Решение:
Чтобы решить выражение, сначала решите 2 -й степени чисел, а затем вычтите второй член из первого члена.
Однако ту же задачу можно решить проще, просто применив формулу:
x 2 – y 2 = (x + y)(x – y)
9 2 – 7 2 = (9 + 7)(9 – 7)
= 17 × 2
= 34
Вопрос 2: Решите выражение, 11 2 – 5 2 .
Решение:
Чтобы решить выражение, сначала решите вторую степень чисел, а затем вычтите второй член из первого. Однако ту же задачу можно решить проще, просто применив формулу:
x 2 – y 2 = (x + y)(x – y)
11 2 – 5 2 = (11 + 5)(11 – 5)
= 16 × 6
= 96
Вопрос 3: Решите выражение 3 2 + 2 2 .
Решение:
Чтобы решить выражение, сначала решите числа во второй степени, а затем прибавьте второй член к первому.
3 2 + 2 2 = (3 х 3) + (2 х 2)
= 9 + 4
- numpy.
сила( x1 , x2 , / , out=None , * , where=True , casting=’same_kind’ , order=’K’ , dtype=None , subok=True [ подпись , extobj ]) =
Элементы первого массива возведены в степени из второго массива, поэлементно.
Возвести каждое основание в x1 в соответствующую степень в х2 . x1 и x2 должны транслироваться в одинаковую форму.
Целочисленный тип, возведенный в отрицательную целочисленную степень, повысит
ЗначениеОшибка.Отрицательные значения, увеличенные до нецелого значения, вернут
nan. Чтобы получить сложные результаты, приведите вход к комплексному или укажитеdtypeдолжен бытьсложным(см. пример ниже).
- Параметры
- x1 array_like
Базы.
- x2 array_like
Показатели. Если
x1.shape != x2.shape, они должны транслироваться на общий форма (которая становится формой вывода).- out ndarray, None или кортеж из ndarray и None, необязательный
Местоположение, в котором сохраняется результат. Если он предусмотрен, он должен иметь форма, на которую транслируются входные данные. Если не указано или Нет, возвращается только что выделенный массив. Кортеж (возможен только как аргумент ключевого слова) должен иметь длину, равную количеству выходов.
- где array_like, необязательный
Это условие передается по входу. В местах, где Если условие равно True, массив из будет установлен на результат ufunc. В другом месте массив из сохранит исходное значение. Обратите внимание, что если неинициализированный массив из создается по умолчанию
out=None, места внутри него, где условие равно False, будут остаются неинициализированными.- **kwargs
Другие аргументы, содержащие только ключевые слова, см. документы ufunc.
- Возвращает
- y ndarray
Базы в x1 возведены в экспоненты в x2 . Это скаляр, если и x1 , и x2 являются скалярами.
См. также
float_powerстепенная функция, переводящая целые числа в число с плавающей запятой
Примеры
Кубировать каждый элемент массива.
>>> x1 = np.arange(6) >>> х1 [0, 1, 2, 3, 4, 5] >>> np.power(x1, 3) массив([ 0, 1, 8, 27, 64, 125])Возведение оснований в разные степени.
>>> x2 = [1,0, 2,0, 3,0, 3,0, 2,0, 1,0] >>> np.power(x1, x2) массив([ 0., 1., 8., 27., 16., 5.])Эффект трансляции.
>>> x2 = np.array([[1, 2, 3, 3, 2, 1], [1, 2, 3, 3, 2, 1]]) >>> х2 массив([[1, 2, 3, 3, 2, 1], [1, 2, 3, 3, 2, 1]]) >>> np.

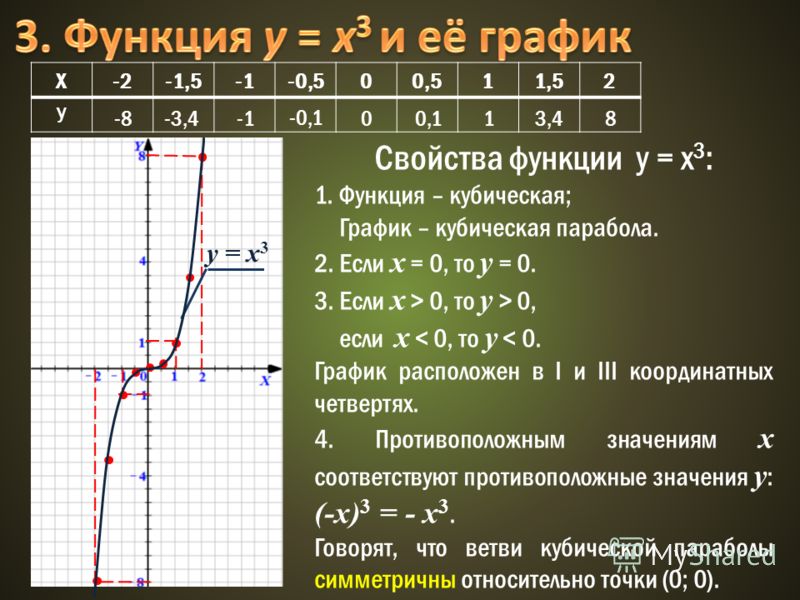 Куб числа — это число, умноженное само на себя дважды, куб числа представлен как показатель степени 3 этого числа. Если нужно записать куб x, это будет x 3 . Например, куб числа 5 представлен как 5 3 и равен 5 × 5 × 5 = 125. Другим примером может быть куб числа 12, представленный как 12 3 , равно 12 × 12 × 12 = 1728.
Куб числа — это число, умноженное само на себя дважды, куб числа представлен как показатель степени 3 этого числа. Если нужно записать куб x, это будет x 3 . Например, куб числа 5 представлен как 5 3 и равен 5 × 5 × 5 = 125. Другим примером может быть куб числа 12, представленный как 12 3 , равно 12 × 12 × 12 = 1728. Однако ту же задачу можно решить проще, просто применив формулу:
Однако ту же задачу можно решить проще, просто применив формулу: сила( x1 , x2 , / , out=None , * , where=True , casting=’same_kind’ , order=’K’ , dtype=None , subok=True [ подпись , extobj ]) =
сила( x1 , x2 , / , out=None , * , where=True , casting=’same_kind’ , order=’K’ , dtype=None , subok=True [ подпись , extobj ]) = 
