X1 x2 формула корней: Теорема Виета

Погружаемся в мир формул. Мастерская квадратных уравнений. Статья 2 – Учительская газета

Сегодня мы будем говорить о теореме Виета. Попутно надо сказать, что главное открытие Франсуа Виета вовсе не теорема Виета, а сама наука алгебра. Дело в том, что алгебру открывали дважды. Первый раз (и мы уже говорили об этом) – Мухаммед аль-Хорезми. Но и после аль-Хорезми формул в алгебре еще не было. Как так не было? А вот так: общие формулы выражали словами. Помните, как вы заучивали, например, формулу квадрата суммы? Квадрат первого плюс удвоенное произведение первого на второе плюс квадрат второго. Вот примерно так же. Только сейчас, изучая формулу, мы можем ее записать буквами, а тогда буквенной записи не было вообще!

Смешно, но факт: записывать формулы буквами придумал только Виет – и вот это-то и было его главным открытием. А ведь Виет был современником королевы Марго. Посмотрим даты его жизни: он родился в 1540 году и умер в 1603-м. Всего за 8 лет до рождения знаменитого Д’Артаньяна – да это же почти наше время! Столько понадобилось человечеству, чтобы догадаться о такой «простой» вещи, как буквенная запись формул (хотя по поводу ее простоты могут быть сомнения). Итак, вот что придумал Виет.Предположим, есть приведенное (то есть с первым коэффициентом, равным 1) квадратное уравнение x2+3x-29=0. Можно его решать, а можно рассматривать в общем виде: x2+px+q=0                (1) Виет стал использовать буквы как параметры, превращающие конкретную формулу в целый класс формул (то, что мы выражаем словами «в общем виде»). Поэтому следующее рассмотрение будем вести именно по Виету – в общем виде. Рассуждения о формулах непривычны и для начинающих математиков, а подчас и для опытных непросты. Поэтому выдающийся современный математик Пенроуз дает такой совет: сначала, при первом чтении, текст читать подряд, минуя формулы, и ухватить только общий смысл, так как смысл формул объясняется в тексте словами (и таким образом, добавлю я, нас возвращают к математике до Виета). Если этого общего понимания достаточно, то к тексту уже можно не возвращаться. Если же требуется полное понимание, то надо вернуться, внимательно и медленно разобраться. Итак, дано приведенное квадратное уравнение (1), и мы заранее знаем, что оно имеет два различных корня x1, x2. Это означает, что верны равенства: x12+px1+q=0                  (2)иx22+px2+q=0                 (3)Почленно вычитая из (2) (3), получаем: (x12 – x22) + p (x1 – x2) = 0. Затем раскладываем квадрат разности в левой части и делим на (x1 – x2):p = – (x1 + x2)                 (4)Теперь подставим это в (1) и получим: x12 – (x1 + x2) x1 + q = 0, откуда q = x1 x2                  (5) Эти две формулы (4) и (5), выражающие коэффициенты p и q через значения корней, и есть теорема Виета. Напомню, что мы сейчас рассмотрели тот случай, когда корней два, причем различных. Можно доказать, что трех корней в квадратном уравнении не бывает. Ведь в этом случае, например, p = – (x1 + x2) = – (x1 + x3), т.е. x2 = x3. Дальше. Пусть в приведенном квадратном уравнении есть два корня (равные или разные; в случае равенства мы говорим также об одном корне). Рассмотрим выражение (x1-x2)2. Оно равно:(x1-x2)2=x12-2x1x2+x22=(x1+x2)2-4x1x2=(-p)2-4c=p2-4c               (6) Поэтому равенство нулю выражения p2 – 4c «сигнализирует» нам о количестве корней. Если p2 – 4c = 0, то (x1 – x2)2 = 0 и х1=х2 – корень один. И наоборот, если корень один, то х1=х2 и p2 – 4c = 0.Если уравнение имеет всего один корень х1, то формулы (4) и (5) дают: p=-2×1 и q=x12. Верно это в общем случае или нет? «Сигнал», что имеется один корень – равенство p2-4q=0. Выразим q из p2-4q=0 и подставим в исходное уравнение (1). Получим:  . То есть  . Это уравнение имеет один корень                 (7) Отсюда сразу получаем p=-2×1 и  . То есть формулы (5) и (6) работают верно, и теорема Виета распространяется и на случай двух совпадающих корней.Теперь еще один способ вывести формулу для решения квадратных уравнений.Будем считать, что , ведь мы вправе выбирать, какому корню дать какой индекс. Согласны ли вы, что выполняется такая формула?             (8)Естественно – да, достаточно раскрыть скобки с плюсом и с минусом.Мы нашли формулу для решения квадратного уравнения в случае… если мы заранее знаем это решение! Но не спешите: давайте воспользуемся плодами теоремы Виета.Т. к.  , выполняется равенство , и это можно подставить в формулу (8). Получим И теперь применим формулы (6) и (4):            (9) Получается обычная формула решения приведенного квадратного уравнения. При положительном p2 – 4q она дает два корня, при p2 – 4q = =0 – один. При отрицательном p2-4q корней нет, т. к. при этом , то есть , чего не может быть. Формула (9) выведена чисто алгебраическим способом, без обращения к геометрической интуиции. Только логика. Вот почему эта страница может показаться сложной. На самом деле это не сложно, а, скорее, непривычно. Со временем математики научились преобразовывать головоломные формулы, пользуясь определенным набором правил и не очень-то задаваясь вопросом о том, что все это означает.Первым же был Франсуа Виет. Это феноменальная личность. Будучи сыном прокурора маленького городка на юге Франции, он стал главным помощником короля (сначала Генриха III, потом Генриха IV). Он разгадал сложнейший шифр, которым пользовались в переписке испанский и нидерландский короли. Он мог работать по трое суток без сна! И все-таки делом его жизни была математическая книга, своеобразный набор трактатов по формальной математике. Ведь на самом деле он был первым математиком в современном смысле слова, то есть преобразователем формул. В математике было не так много абсолютно звездных мгновений. Одно из них – открытие аксиоматического метода (принадлежит Евклиду или Евдоксу). Второе – открытие возможностей мыслить с помощью игры формул. И это открытие принадлежит Виету.Формальный аппарат – это великолепный инструмент. Это своего рода игра с заданными правилами. Мы погружаемся в мир формул, изучаем их, комбинируем, выводим одни из других, причем совершенно забыв подчас, что они означают: все равно результат оказывается правильный, даже если дорога к нему была пройдена с завязанными глазами. Отсюда все трудности в понимании. Со временем, однако, вы научитесь действовать по правилам, «отключив» геометрическую интуицию, и откроете неожиданные новые возможности формального метода мышления. Часто с помощью быстрого и оригинального «шахматного хода» в преобразованиях формул результат может быть достигнут во много раз быстрее, чем при блуждании впотьмах при попытках решить ту или иную задачу с помощью простых или хитрых рассуждений. Кстати, с этим вы уже много раз сталкивались при решении задач «на уравнения».

Теорема Виета, формулы Виета

В квадратных уравнениях существует целый ряд соотношений. Основными являются отношения между корнями и коэффициентами. Также в квадратных уравнениях работает ряд соотношений, которые задаются теоремой Виета.

В этой теме мы приведем саму теорему Виета и ее доказательство для квадратного уравнения, теорему, обратную теореме Виета, разберем ряд примеров решения задач. Особое внимание в материале мы уделим рассмотрению формул Виета, которые задают связь между действительными корнями алгебраического уравнения степени n и его коэффициентами.

Формулировка и доказательство теоремы Виета

Формула корней квадратного уравнения a·x2+b·x+c=0 вида x1=-b+D2·a, x2=-b-D2·a, где D=b2−4·a·c, устанавливает соотношения x1+x2=-ba, x1·x2=ca.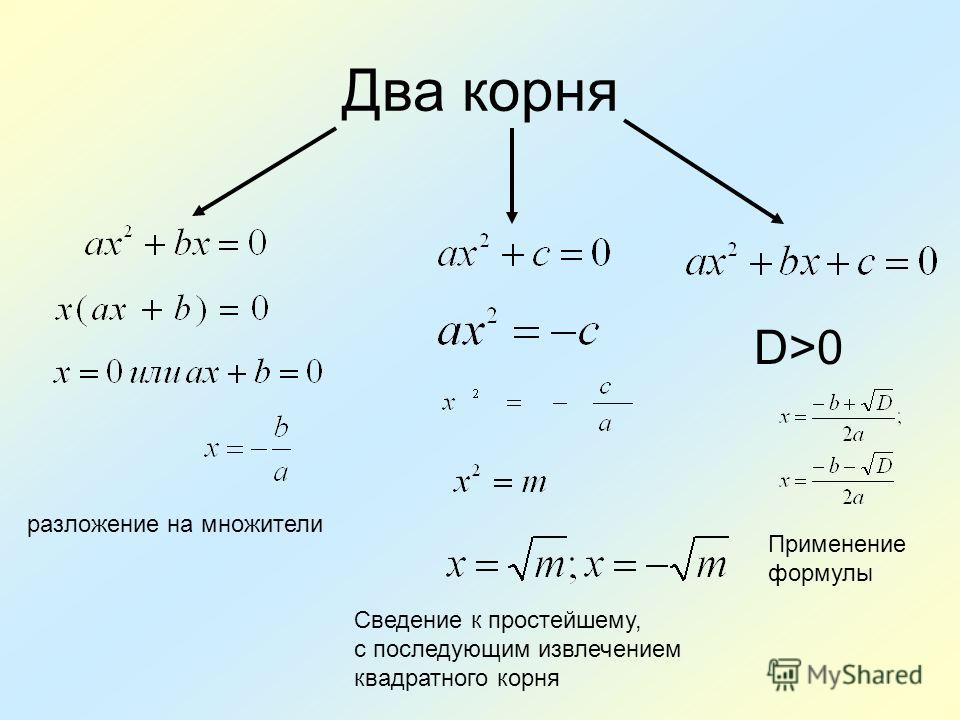 Это подтверждает и теорема Виета.

Теорема 1

В квадратном уравнении a·x2+b·x+c=0, где x1 и x2 – корни, сумма корней будет равна соотношению коэффициентов b и a, которое было взято с противоположным знаком, а произведение корней будет равно отношению коэффициентов c и a, т. е. x1+x2=-ba, x1·x2=ca.

Доказательство 1

Предлагаем вам следующую схему проведения доказательства: возьмем формулу корней, составим суму и произведение корней квадратного уравнения и затем преобразуем полученные выражения для того, чтобы убедиться, что они равны -ba и ca соответственно.

Составим сумму корней x1+x2=-b+D2·a+-b-D2·a. Приведем дроби к общему знаменателю -b+D2·a+-b-D2·a=-b+D+-b-D2·a. Раскроем скобки в числителе полученной дроби и приведем подобные слагаемые: -b+D+-b-D2·a=-b+D-b-D2·a=-2·b2·a. Сократим дробь на: 2-ba=-ba.

Так мы доказали первое соотношение теоремы Виета, которое относится к сумме корней квадратного уравнения.

Теперь давайте перейдем ко второму соотношению.

Для этого нам необходимо составить произведение корней квадратного уравнения: x1·x2=-b+D2·a·-b-D2·a.

Вспомним правило умножения дробей и запишем последнее произведение следующим образом: -b+D·-b-D4·a2.

Проведем в числителе дроби умножение скобки на скобку или же воспользуемся формулой разности квадратов для того, чтобы преобразовать это произведение быстрее: -b+D·-b-D4·a2=-b2-D24·a2.

Воспользуемся определением квадратного корня для того, чтобы осуществить следующий переход: -b2-D24·a2=b2-D4·a2. Формула D=b2−4·a·c

отвечает дискриминанту квадратного уравнения, следовательно, в дробь вместо D можно подставить b2−4·a·c:

b2-D4·a2=b2-(b2-4·a·c)4·a2

Раскроем скобки, приведем подобные слагаемые и получим: 4·a·c4·a2. Если сократить ее на 4·a, то остается ca. Так мы доказали второе соотношение теоремы Виета для произведения корней.

Запись доказательства теоремы Виета может иметь весьма лаконичный вид, если опустить пояснения:

x1+x2=-b+D2·a+-b-D2·a=-b+D+-b-D2·a=-2·b2·a=-ba,x1·x2=-b+D2·a·-b-D2·a=-b+D·-b-D4·a2=-b2-D24·a2=b2-D4·a2==D=b2-4·a·c=b2-b2-4·a·c4·a2=4·a·c4·a2=ca.

При дискриминанте квадратного уравнения  равном нулю уравнение будет иметь только один корень. Чтобы иметь возможность применить к такому уравнению теорему Виета, мы можем предположить, что уравнение при дискриминанте, равном нулю, имеет два одинаковых корня. Действительно, при 

D=0 корень квадратного уравнения равен: -b2·a, тогда x1+x2=-b2·a+-b2·a=-b+(-b)2·a=-2·b2·a=-ba и x1·x2=-b2·a·-b2·a=-b·-b4·a2=b24·a2, а так как D=0, то есть, b2-4·a·c=0, откуда b2=4·a·c, то b24·a2=4·a·c4·a2=ca.

Чаще всего на практике теорема Виета применяется по отношению к приведенному квадратному уравнению вида x2+p·x+q=0, где старший коэффициент a равен 1. В связи с этим и формулируют теорему Виета именно для уравнений такого вида. Это не ограничивает общности в связи с тем, что любое квадратное уравнение может быть заменено равносильным уравнением. Для этого необходимо поделить обе его части на число a, отличное от нуля.

Приведем еще одну формулировку теоремы Виета.

Теорема 2

Сумма корней в приведенном квадратном уравнении x2+p·x+q=0  будет равна коэффициенту при x, который взят с противоположным знаком, произведение корней будет равно свободному члену, т.

е. x1+x2=−p, x1·x2=q.

Теорема, обратная теореме Виета

Если внимательно посмотреть на вторую формулировку теоремы Виета, то можно увидеть, что для корней x1 и x2 приведенного квадратного уравнения x2+p·x+q=0 будут справедливы соотношения x1+x2=−p, x1·x2=q. Из этих соотношений x1+x2=−p, x1·x2=q следует, что x1 и x2 – это корни квадратного уравнения x2+p·x+q=0. Так мы приходим к утверждению, которое является обратным теореме Виета.

Предлагаем теперь оформить это утверждение как теорему и провести ее доказательство.

Теорема 3

Если числа x1 и x2 таковы, что x1+x2=−p и x1·x2=q, то x1 и x2 являются корнями приведенного квадратного уравнения x2+p·x+q=0.

Доказательство 2

Замена коэффициентов p и q на их выражение через x1 и x2 позволяет преобразовать уравнение x2+p·x+q=0 в равносильное ему x2−(x1+x2)·x+x1·x2=0

.

Если в полученное уравнение подставить число x1 вместо x, то мы получим равенство x12−(x1+x2)·x1+x1·x2=0. Это равенство при любых x1 и x2 превращается в верное числовое равенство 0=0, так как x12−(x1+x2)·x1+x1·x2=x12−x12−x2·x1+x1·x2=0. Это значит, что x1 – корень уравнения x2−(x1+x2)·x+x1·x2=0, и что x1 также является корнем равносильного ему уравнения x2+p·x+q=0.

Подстановка в уравнение x2−(x1+x2)·x+x1·x2=0  числа x2вместо x позволяет получить равенство x22−(x1+x2)·x2+x1·x2=0. Это равенство можно считать верным, так как x22−(x1+x2)·x2+x1·x2=x22−x1·x2−x22+x1·x2=0. Получается, что x2  является корнем уравнения x2−(x1+x2)·x+x1·x2=0, а значит, и уравнения x2+p·x+q=0.

Теорема, обратная теореме Виета, доказана.

Примеры использования теоремы Виета

Давайте теперь приступим к разбору наиболее типичных примеров по теме. Начнем с разбора задач, которые требуют применения теоремы, обратной теореме Виета. Ее можно применять для проверки чисел, полученных в ходе вычислений, на предмет того, являются ли они корнями заданного квадратного уравнения. Для этого необходимо вычислить их сумму и разность, а затем проверить справедливость соотношений x1+x2=-ba, x1·x2=ac.

Выполнение обоих соотношений свидетельствует о том, что числа, полученные в ходе вычислений, являются корнями уравнения. Если же мы видим, что хотя бы одно из условий не выполняется, то данные числа не могут быть корнями квадратного уравнения, данного в условии задачи.

Пример 1

Какая из пар чисел 1) x1=−5, x2=3, или 2) x1=1-3, x2=3+3, или 3) x1=2+72, x2=2-72 является парой корней квадратного уравнения 4·x2−16·x+9=0?

Решение

Найдем коэффициенты квадратного уравнения 4·x2−16·x+9=0. Это a=4, b=−16, c=9. В соответствии с теоремой Виета сумма корней квадратного уравнения должна быть равна -ba, то есть, 164=4, а произведение корней должно быть равно ca, то есть, 94.

Проверим полученные числа, вычислив сумму и произведение чисел из трех заданных пар и сравнив их с полученными значениями.

В первом случае x1+x2=−5+3=−2. Это значение отлично от 4, следовательно, проверку можно не продолжать. Согласно теореме, обратной теореме Виета, можно сразу сделать вывод о том, что первая пара чисел не является корнями данного квадратного уравнения.

Во втором случае x1+x2=1-3+3+3=4.  Мы видим, что первое условие выполняется. А вот второе условие нет: x1·x2=1-3·3+3=3+3-3·3-3=-2·3. Значение, которое мы получили, отлично от 94. Это значит, что вторая пара чисел не является корнями квадратного уравнения.

Перейдем к рассмотрению третьей пары. Здесь x1+x2=2+72+2-72=4 и x1·x2=2+72·2-72=22-722=4-74=164-74=94. Выполняются оба условия, а это значит, что  x1 и x2 являются корнями заданного квадратного уравнения.

Ответ: x1=2+72, x2=2-72

Мы также можем использовать теорему, обратную теореме Виета, для подбора корней квадратного уравнения. Наиболее простой способ – это подбор целых корней приведенных квадратных уравнений с целыми коэффициентами. Можно рассматривать и другие варианты. Но это может существенно затруднить проведение вычислений.

Для подбора корней мы используем тот факт, что если сумма двух чисел равна второму коэффициенту квадратного уравнения, взятому со знаком минус, а произведение этих чисел равно свободному члену, то эти числа являются корнями данного квадратного уравнения.

Пример 2

В качестве примера используем квадратное уравнение x2−5·x+6=0. Числа x1 и x2 могут быть корнями этого уравнения в том случае, если выполняются два равенства x1+x2=5 и x1·x2=6. Подберем такие числа. Это числа 2 и 3, так как 2+3=5 и 2·3=6. Получается, что 2 и 3 – корни данного квадратного уравнения.

Теорему, обратную теореме Виета, можно использовать для нахождения второго корня, когда первый известен или очевиден. Для этого мы можем использовать соотношения x1+x2=-ba, x1·x2=ca.

Пример 3

Рассмотрим квадратное уравнение 512·x2−509·x−3=0. Необходимо найти корни данного уравнения.

Решение

Первым корнем уравнения является 1, так как сумма коэффициентов этого квадратного уравнения равна нулю. Получается, что x1=1.

Теперь найдем второй корень. Для этого можно использовать соотношение 

x1·x2=ca. Получается, что 1·x2=−3512, откуда x2=-3512.

Ответ: корни заданного в условии задачи квадратного уравнения 1 и -3512.

Подбирать корни, используя теорему, обратную теореме Виета, можно лишь в простых случаях. В остальных случаях лучше проводить поиск с использованием формулы корней квадратного уравнения через дискриминант.

Благодаря теореме, обратной теореме Виета, мы также можем составлять квадратные уравнения по имеющимся корням x1 и x2. Для этого нам необходимо вычислить сумму корней, которая дает коэффициент при x с противоположным знаком приведенного квадратного уравнения, и произведение корней, которое дает свободный член.

Пример 4

Напишите квадратное уравнение, корнями которого являются числа −11 и 23.

Решение

Примем, что x1=−11 и x2=23. Сумма и произведение данных чисел будут равны: x1+x2=12 и x1·x2=−253. Это значит, что второй коэффициент -12, свободный член −253.

Составляем уравнение: x2−12·x−253=0.

Ответ: x2−12·x−253=0.

Мы можем использовать теорему Виета для решения заданий, которые связаны со знаками корней квадратных уравнений. Связь между теоремой Виета связана со знаками корней приведенного квадратного уравнения x2+p·x+q=0 следующим образом:

• если квадратное уравнение имеет действительные корни и если свободный член q является положительным числом, то эти корни будут иметь одинаковый знак «+» или «-»;
• если квадратное уравнение имеет корни и  если свободный член q является отрицательным числом, то один корень будет «+», а второй «-».

Оба этих утверждения являются следствием формулы x1·x2=q и правила умножения положительных и отрицательных чисел, а также чисел с разными знаками.

Пример 5

Являются ли корни квадратного уравнения x2−64·x−21=0положительными?

Решение

По теореме Виета корни данного уравнения не могут быть оба положительными, так как для них должно выполняться равенство x1·x2=−21. Это невозможно при положительных x1 и x2.

Ответ: Нет

Пример 6

При каких значениях параметра r квадратное уравнение x2+(r+2)·x+r−1=0будет иметь два действительных корня с разными знаками.

Решение

Начнем с того, что найдем значения каких r, при которых в уравнении будет два корня. Найдем дискриминант и посмотрим, при каких r он будет принимать положительные значения. D=(r+2)2−4·1·(r−1)=r2+4·r+4−4·r+4=r2+8. Значение выражения r2+8 положительно при любых действительных r, следовательно, дискриминант будет больше нуля при любых действительных r. Это значит, что исходное квадратное уравнение будет иметь два корня при любых действительных значениях параметра r.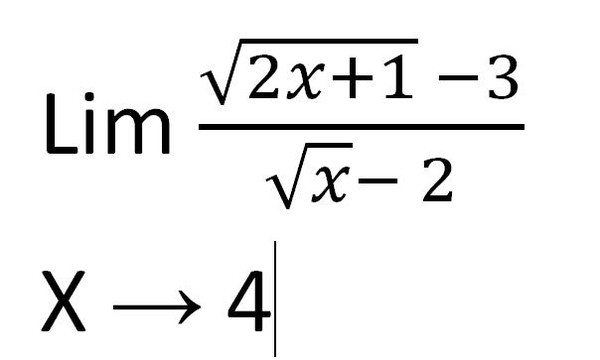

Теперь посмотрим, когда корни будут иметь разные знаки. Это возможно в том случае, если их произведение будет отрицательным. Согласно теореме Виета произведение корней приведенного квадратного уравнения равно свободному члену. Значит, правильным решением будут те значения r, при которых свободный член r−1 отрицателен. Решим линейное неравенство r−1<0, получаем r<1.

Ответ: при r<1.

Формулы Виета

Существует ряд формул, которые применимы для осуществления действий с корнями и коэффициентами не только квадратных, но также кубических и других видов уравнений. Их называют формулами Виета.

Для алгебраического уравнения степени n вида a0·xn+a1·xn-1+…+an-1·x+an=0  считается, что уравнение имеет nдействительных корней x1, x2, …, xn , среди которых могут быть совпадающие:
x1+x2+x3+…+xn=-a1a0,x1·x2+x1·x3+…+xn-1·xn=a2a0,x1·x2·x3+x1·x2·x4+…+xn-2·xn-1·xn=-a3a0,…x1·x2·x3·…·xn=(-1)n·ana0

Определение 1

Получить формулы Виета нам помогают:

• теорема о разложении многочлена на линейные множители;
• определение равных многочленов через равенство всех их соответствующих коэффициентов.

Так, многочлен a0·xn+a1·xn-1+…+an-1·x+an  и его разложение на линейные множители вида a0·(x-x1)·(x-x2)·…·(x-xn) равны.

Если мы раскрываем скобки в последнем произведении и приравниваем соответствующие коэффициенты, то получаем формулы Виета. Приняв n=2, мы можем получить формулу Виета для квадратного уравнения: x1+x2=-a1a0, x1·x2=a2a0.

Определение 2

Формула Виета для кубического уравнения:
x1+x2+x3=-a1a0,x1·x2+x1·x3+x2·x3=a2a0,x1·x2·x3=-a3a0

Левая часть записи формул Виета содержит так называемые элементарные симметрические многочлены.

2} + px + 12 = 0$, таковы, что ${x_2}

Дата последнего обновления: 25 января 2023 г.

•

Всего просмотров: 292,2 тыс.

•

Просмотров сегодня: 7,87 тыс.

3

3

Проверено

292.2k+ просмотров

Подсказка: Решим задачу, используя свойства квадратного уравнения: —
Сумма корней общего квадратного уравнения $\dfrac{{ — b}}{a}$ а произведение корней общего квадратного уравнения равно $\dfrac{c}{a}$. 92} + bx + c = 0$, а корни равны ${x_1}\& {x_2}$.
Тогда сумма корней $\left( {{x_1} + {x_2}} \right) = \dfrac{{ — b}}{a}$
И произведение корней $\left( {{x_1} \ раз {x_2}} \right) = \dfrac{c}{a}$
Сравнивая данное уравнение с общим уравнением, мы имеем
$a = 1,b = p,c = 12$
Также$\left( {{x_1} + {x_2}} \right) = \dfrac{{ — p}}{1} = — p$ — (1)
И учитывая, что $\left( {{x_2} — {x_1}} \ справа) = 1$ — (2)
Прибавляя уравнение 2 к уравнению 1 получаем:
\[
   \Стрелка вправо \влево( {{x_2} + {x_1}} \вправо) — \влево( {{x_2} — {x_1}} \вправо) = — p + 1 \\
   \Стрелка вправо 2{x_2 } = — p + 1 \\
   \Rightarrow {x_2} = \dfrac{{1 — p}}{2} \\
\]
Из уравнения 2 получаем:
\[
   \Rightarrow {x_1} = { x_2} — 1 \\
   \Стрелка вправо {x_1} = \dfrac{{1 — p}}{2} — 1 \\
   \Стрелка вправо {x_1} = \dfrac{{1 — p — 2}}{2} \\
   \Rightarrow {x_1} = \dfrac{{ — 1 — p}}{2} \\
\]
Используя далее второе свойство, получаем: 92} = 49 \\
   \Rightarrow p = \pm 7 \\
\]
Следовательно, p имеет 2 значения: +7 и -7.

Примечание: Всякий раз, решая квадратное уравнение, мы всегда должны сохранять как решение, так и свойства корней квадратного уравнения, упомянутые выше в разделе подсказок, чтобы решить задачу легко и быстро.

Недавно обновленные страницы

Если пружина имеет период T и разрезана на n равный класс 11 по физике CBSE

Планета движется вокруг Солнца по почти круговой орбите 11 класс физики CBSE

В любом треугольнике AB2 BC4 CA3 и D является серединой 11 класса математики JEE_Main

В треугольнике ABC 2asin dfracAB+C2 соответствует классу IIT Screening 11 maths JEE_Main

Если в треугольнике ABCangle A 45circ угол C 60circ тогда класс 11 maths JEE_Main

Если в треугольнике rmABC сторона a sqrt 3 + 1rmcm и угол class 11 maths JEE_Main

Если пружина имеет период T и разрезана в n равный класс 11 физика CBSE

Планета движется вокруг Солнца по почти круговой орбите 11 класс физики CBSE

В любом треугольнике AB2 BC4 CA3 и D является серединой 11 класса математики JEE_Main

В треугольнике ABC 2asin dfracAB+C2 соответствует классу IIT Screening 11 maths JEE_Main

Если в треугольнике ABCangle A 45circ угол C 60circ тогда класс 11 maths JEE_Main

Если в треугольнике rmABC сторона a sqrt 3 + 1rmcm и угол class 11 maths JEE_Main

2

0003

Квадратные уравнения | Суперпроф

Все вопросы по математике

Как найти корни квадратного уравнения?

Ответы

Используйте формулы, чтобы найти корни квадратного уравнения. 2-4x1x(-1)))/2×1=(-1+/-sqrt5)/2 Таким образом, первый корень будет (-1+sqrt5)/2, а второй (-1-sqrt5)/ 2.Надеюсь помог 🙂 92+bx+c=0 просто подставьте свои значения и готово!

IXL_-_Решение_а_квадратичного_уравнения_использованием_квадратных_корней__Оценка_10_maths_practice_.pdf

IXL_-_Решение_а_квадратичного_уравнения_использованием_квадратных_корней__Оценка_10_maths_practice_.pdf

Вы можете найти x в квадратном уравнении, разложив его на множители.

Есть несколько вариантов: Разложить на множители [Заключить их в две пары скобок, например (x+2)(x+3)] Заполнить квадрат Формула квадрата Начертить график 92-4ач)/2а)

Квадратное уравнение — это любое уравнение в форме ax2 + bx + c = 0, где a ≠ 0. Любое квадратное уравнение можно решить по формуле x = (-b +/-√(b2 — 4ac))/2a. Запишите уравнение в квадратной форме. Официальное определение квадратного уравнения — это полиномиальное уравнение второго порядка, выраженное одной переменной x, где a ≠ 0. [1] Проще говоря, это просто означает, что это уравнение с одной переменной (обычно x), где старший показатель степени переменной равен 2. В общих чертах мы можем записать это как ax2 + bx + c = 0, чтобы получить уравнение в квадратичной форме. , просто получите все условия с одной стороны знака равенства, чтобы у вас был 0 с другой стороны. Например, если мы хотим получить уравнение 2×2 + 8x = -5×2 — 11 в квадратичной форме, мы можем сделать это так: 2×2 + 8x = -5×2 + 112×2 + 5×2 + 8x = + 112×2 + 5×2 + 8x — 11 = 07×2 + 8x — 11 = 0 . Обратите внимание, что это в стандартной форме ax2+ bx + c = 0, упомянутой выше. Затем найдите значение a, b, c, а затем примените формулу, чтобы найти значение x. 92-4ac)Шаг 2- Проверить, если D>0, то корни вещественные и равные,              если D=0, то корни вещественные и различные,             , если D<0, то корни комплексные и сопряженные. Шаг 3- найти x1= - b +sqrt(D)/2aStep4- find x2= -b-sqrt(D)/2a Это корни.

Рассмотрим_the_quadratic_equation.

No related posts.