Функции y=x2 и y=x3 и их графики.
Конспект урока алгебра 7 класс «Функции y= х2 и y= х3 »
Тип урока: изучение новых знаний и способов действий
Вид урока: проблемно — поисковый
Цели урока:
помочь учащимся на основе имеющихся у них знаний о линейной функции, представить графики функций у=х2 , у=х3 и указать их свойства
содействовать развитию логического мышления, умений сравнивать и обосновывать свою точку зрения;
способствовать формированию навыков бережного отношения к своему здоровью.
Оборудование: раздаточный материал, презентация.
Ход урока.
1. Организационный момент.
2.
Упростить: (0,75 су4)
Найдите значение выражения: а) ; б)
(а- 49; б- 2)
1) Какая функция называется линейной?
2) Что является графиком линейной функции и сколько точек достаточно для
ее построения?
3) Какая функция называется прямой пропорциональностью?
4) Что является графиком прямой пропорциональности и сколько точек
достаточно для ее построения?
5) Как определить принадлежит ли точка М (-2; 6) графику функции у = 4х – 2?
6) Это были вопросы, ответы на которые мы знаем. А что делать, если мне
нужно построить график функции, ранее мне не встречавшейся
2. Построить график функции у=2х+1 и описать её свойства (1уч-ся у доски)
Свойства функции:
Область определения: ___________________ ;
Область соответсвующих значений ________________________ ;
У=0, если х = ___;
График функции расположен в ______и__________ координатных четвертях;
У больше 0 при х _________ 0, у меньше 0 при х _____________ 0;
6. Убывающая или возрастающая функция? __________________________
Убывающая или возрастающая функция? __________________________
Принадлежит ли графику функции у=2х-3 точка:
а)А (0, -3), б) В (3,2) ( А – да, В – нет)
3.Определение темы и цели урока
Является ли функция y = x2 линейной?
Ребята, сегодня мы познакомимся с функциями, которые не являются линейными.
Рассмотрим примеры этих функций.
-Задайте формулой зависимость площади квадрата от его стороны (S= a2
-Объёма куба от его ребра (V= a3)
-Укажите в обеих формулах независимую переменную? Зависимую?
Запишите данные функции с помощью переменных х и у
— С какими же функциями мы сегодня ознакомимся?
— Запишем тему урока
4. Работа по изучению новых знаний и способов действий.
Работа по изучению новых знаний и способов действий.
Мини-исследование по таблице
исследовать свойства функций у=х2 и у= х3.
Исследование проводим в группах
Вам предстоит: а) заполнить таблицу;
б) построить график функции;
в) указать свойства
Вопросы | у=х2 | у= х3 | ||||||||||||||||||||||||||||
Заполните таблицу |
|
| ||||||||||||||||||||||||||||
По данным таблицы построить график | ||||||||||||||||||||||||||||||
Свойства функции | 1. Если х≠0, то у ____ 0 Противоположным значениям х соответствует _____________ значение у 4. График функции симметричен_________________________ и расположен в_____________________ координатных четвертях | 1. Область определения _____________ у больше 0 при х ________ 0, у меньше 0 при х __________0 Противоположным значениям х соответствует _____________ значения у 4. График функции симметричен_________________________ | ||||||||||||||||||||||||||||
Функция возрастает | При х | При х | ||||||||||||||||||||||||||||
Функция убывает | При х |
| ||||||||||||||||||||||||||||
Название функции |
|
| ||||||||||||||||||||||||||||
Название графика |
6. Сравнение двух функций
Сравнение двух функций
Сравните в чем сходство и в чем различие данных функций?
у = х2 | у = х3 |
Квадратичная функция. Графиком является парабола. | Кубическая функция. Графиком является кубическая парабола. |
Свойства функции у = х2: 1. Если х = 0, то у = 0 2. Если х 0, то у 0 3. Противоположным значениям аргумента соответствуют равные значения функции. | Свойства функции у = х3: 1. 2. Если х 0, то у 0 3. Если х 0, то у 0 4. Противоположным значениям аргумента соответствуют противоположные значения функции. |
5. Минутка психологической разгрузки
7. Закрепление изученного материала
Стр. 105-109
№ 484, № 488
у= -х3 (1 группа)
у= -х2 (2 группа)
Вопросы | у= -х2 | ||||||||||||||||
Заполните таблицу |
| ||||||||||||||||
По данным таблицы построить график | |||||||||||||||||
Свойства функции | 1. Если х≠0, то у ____ 0 Противоположным значениям х соответствует _____________ значение у 4. График функции симметричен_________________________ и расположен в_____________________ координатных четвертях | ||||||||||||||||
Функция возрастает | При х | ||||||||||||||||
Функция убывает | При х | ||||||||||||||||
Название функции |
| ||||||||||||||||
Название графика |
Вопросы | у= — х3 | ||||||||||||
Заполните таблицу |
| ||||||||||||
По данным таблицы построить график | |||||||||||||
Свойства функции | 1. У больше 0 при х ________ 0, у меньше 0 при х __________0 Противоположным значениям х соответствует _____________ значения у 4. График функции симметричен_________________________ | ||||||||||||
Функция возрастает | При х | ||||||||||||
Функция убывает |
| ||||||||||||
Название функции |
| ||||||||||||
Название графика |
Проверка выполнения работы (отчёт – по 1 выступающему от группы)
8. Домашняя работа
Задание на дом: № 485, № 489, № 490 (б)
9.Итог урока. Выставление оценок.
10. Рефлексия
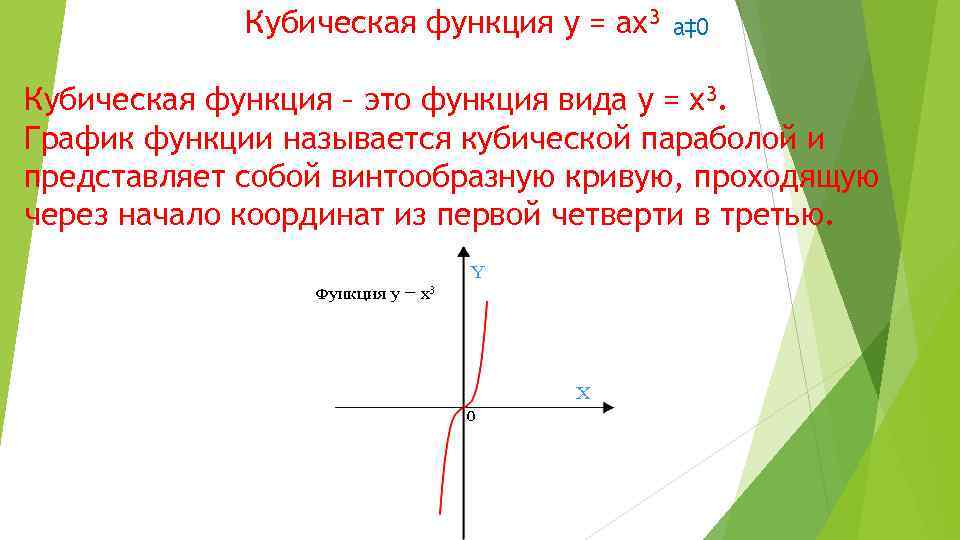
Объяснение урока: Кубические функции и их графики
В этом объяснении мы научимся строить графики кубических функций, записывать их правила на основе графиков и определять их свойства.
Мы сосредоточимся на стандартной кубической функции, 𝑓(𝑥)=𝑥. Создание таблицы значений с целыми значениями 𝑥 из −2≤𝑥≤2, тогда мы можем график функции.
| 𝑥 | −2 | −1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| 𝑓 (𝑥) = 𝑥 | −8 | −1 | 0 | 1 | 8 |
Основные характеристики Кубической функции являются следующими:
- Как функция с нечетной степенью (3), она имеет противоположное поведение конца. Его конечное поведение таково, что по мере увеличения 𝑥 до бесконечности 𝑓(𝑥) также увеличивается до бесконечности. В качестве 𝑥 убывает, 𝑓(𝑥) также уменьшается до отрицательной бесконечности.
- Это странная функция,
𝑓(−𝑥)=−𝑓(𝑥), для всех значений
𝑥 в домене 𝑓, и, как таковой, его
граф инвариантен относительно поворота
180∘ о происхождении.

- 1
2. функция положительна, когда 𝑥 равно положительный, отрицательный, когда 𝑥 отрицательный, и 0, когда 𝑥=0.
Когда мы преобразуем эту функцию, определение кривой сохраняется. Мы будем посмотрите на ряд различных преобразований, и мы можем считать их два типа:
- Изменения на входе, 𝑥, например, 𝑥⟶𝑥+3 или 𝑥⟶4𝑥
- Изменения в выводе, 𝑓(𝑥), например, 𝑓(𝑥)⟶𝑓(𝑥)−3 или 𝑓(𝑥)⟶2𝑓(𝑥)
Кроме того, мы можем рассмотреть изменения на входе, 𝑥, и результат, 𝑓(𝑥), состоящий из
- сложения,
- умножения,
- отрицания.
Теперь мы можем исследовать, как изменяется график функции, когда мы добавляем или вычесть значения из вывода.
Допустим, у нас есть функции 𝑔(𝑥) и ℎ(𝑥) такое, что 𝑔(𝑥)=𝑓(𝑥)+2 и ℎ(𝑥)=𝑓(𝑥)−1, тогда 𝑓(𝑥)=𝑥,𝑔(𝑥)=𝑥+2,ℎ(𝑥)=𝑥−1.
Чтобы построить графики этих функций, мы можем расширить таблицу значения выше, чтобы рассмотреть значения 𝑓(𝑥) для одинаковые значения 𝑥. Таким образом, мы имеем таблицу ниже.
| 𝑥 | −2 | −1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| 𝑓(𝑥)=𝑥 | −8 | −1 | 0 | 1 | 8 |
| 𝑔(𝑥)=𝑥+2 | −6 | 1 | 2 | 3 | 10 |
| ℎ(𝑥)=𝑥−1 | −9 | −2 | −1 | 0 | 7 |
The outputs of 𝑔 are always 2 крупнее, чем у
𝑓. Точно так же каждый из выходов ℎ на 1 меньше, чем у
𝑓. Мы можем изобразить эти три функции рядом друг с другом
как показано.
Точно так же каждый из выходов ℎ на 1 меньше, чем у
𝑓. Мы можем изобразить эти три функции рядом друг с другом
как показано.
Заметим, что эти функции представляют собой вертикальный перевод 𝑓(𝑥)=𝑥.
В общем случае график функции 𝑓(𝑥)+𝑘 для константы 𝑘∈ℝ, представляет собой вертикальный сдвиг графика функции 𝑓(𝑥)=𝑥. Если 𝑘>0, то его график представляет собой сдвиг на 𝑘 единиц вверх график 𝑓(𝑥)=𝑥. Если 𝑘0, то его график является переводом |𝑘| единиц вниз по графику 𝑓(𝑥)=𝑥.
Далее мы можем исследовать, как функция 𝑓(𝑥)=𝑥 изменяется, когда мы добавляем значения в вход. На этот раз мы берем функции 𝑔(𝑥) и ℎ(𝑥) такие, что 𝑔(𝑥)=𝑓(𝑥+2) и ℎ(𝑥)=𝑓(𝑥−1): 𝑓(𝑥)=𝑥,𝑔(𝑥)=(𝑥+2),ℎ(𝑥)=(𝑥−1).
Мы можем составить таблицу значений этих функций и построить график эти функции.
| 𝑥 | −2 | −1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| 𝑓(𝑥)=𝑥 | −8 | −1 | 0 | 1 | 8 |
| 𝑔(𝑥)=(𝑥+2) | 0 | 1 | 8 | 27 | 64 |
| ℎ (𝑥) = (𝑥 -1) | −27 | −8 | —1 | 0 | 1 |
We ObsEREBER WE ObsERE.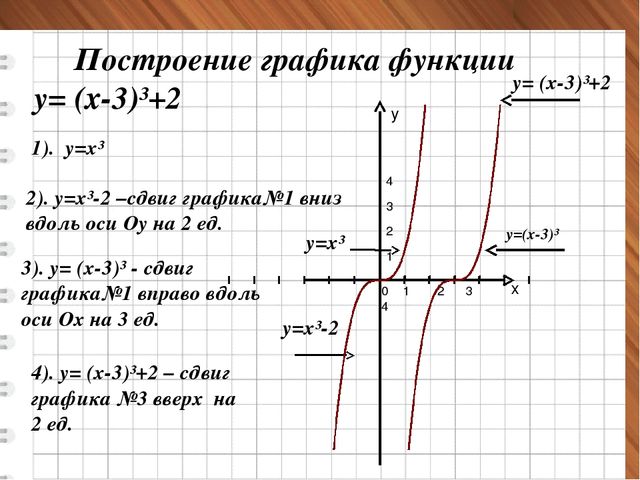 функция
𝑔(𝑥)=(𝑥+2) — это горизонтальный перевод
𝑓(𝑥)=𝑥 осталось две единицы. Сходным образом,
ℎ(𝑥)=(𝑥−1) — это горизонтальный перевод
𝑓(𝑥)=𝑥 на одну единицу вправо.
функция
𝑔(𝑥)=(𝑥+2) — это горизонтальный перевод
𝑓(𝑥)=𝑥 осталось две единицы. Сходным образом,
ℎ(𝑥)=(𝑥−1) — это горизонтальный перевод
𝑓(𝑥)=𝑥 на одну единицу вправо.
Это может быть нелогичным преобразованием, чтобы вспомнить, как мы часто считаем дополнение в переводе как производящее движение в положительном направлении. В этом случае верно обратное. Чтобы помочь вспомнить это свойство, считаем, что функция перенесена по горизонтали ℎ единиц сразу после изменения ввода, 𝑥⟶𝑥−ℎ. Поэтому, например, в функции 𝑓(𝑥)=(𝑥+1), ℎ=−1, а функция 𝑓(𝑥)=𝑥 переводится влево на 1 единицу.
Мы можем обобщить, как сложение изменяет функцию 𝑓(𝑥)=𝑥 ниже.
| Операция | Преобразованное уравнение | Геометрическое изменение |
|---|---|---|
| 𝑓 (𝑥) ⟶𝑓 (𝑥)+𝑘 | 𝑓 (𝑥) = 𝑥+𝑘 | Вертинический , 𝑘 единиц вверх. Если 𝑘0, |𝑘| единиц вниз. |
| 𝑥⟶𝑥−ℎ | 𝑓(𝑥)=(𝑥−ℎ) | Горизонтальный перевод: Если ℎ>0, ℎ единиц вправо.  Если ℎ0, |ℎ| остались единицы. |
Далее мы можем исследовать, как умножение меняет функцию 𝑓(𝑥)=𝑥, начиная с изменений на выходе, 𝑓(𝑥).
Рассмотрим функции 𝑓(𝑥)=𝑥, 𝑔(𝑥)=3𝑓(𝑥) и ℎ(𝑥)=12𝑓(𝑥): 𝑓(𝑥)=𝑥,𝑔(𝑥)=3𝑥,ℎ(𝑥)=12𝑥.
Мы можем заметить, что функция 𝑓(𝑥)=3𝑥 была растянута вертикально или расширено в 3 раза. Функция 𝑓(𝑥)=12𝑥 имеет вертикальное растяжение в 12. Таким образом, для любого положительного значения 𝑎, когда 𝑓(𝑥)⟶𝑎𝑓(𝑥), есть вертикаль растяжение фактора 𝑎.
Если мы изменим ввод, 𝑥⟶𝑏𝑥, на 𝑏>0, мы получим функция вида ℎ(𝑥)=(𝑏𝑥). Следующий график сравнивает функция 𝑓(𝑥)=𝑥 с ℎ(𝑥)=(2𝑥).
Если рассматривать координаты (1,1) в функции
𝑓(𝑥)=𝑥, мы обнаружим, что это когда
input, 1, производит выход 1. Чтобы получить такое же выходное значение 1 в
функция ℎ(𝑥)=(2𝑥), 2𝑥=1; так
𝑥=12. То же верно и для координат (2,8) в
𝑓(𝑥)=𝑥. Тот же выход 8 в
ℎ(𝑥)=(2𝑥) получается, когда
2𝑥=2, поэтому 𝑥=1. Таким образом, когда мы умножаем каждый
𝑥 значение в
𝑓(𝑥) на 2, чтобы получить функцию
ℎ(𝑥)=(2𝑥), график
𝑓(𝑥)=𝑥 расширяется по горизонтали в раз
12, при этом каждая точка перемещается на половину своего
предыдущее расстояние от оси 𝑦.
Тот же выход 8 в
ℎ(𝑥)=(2𝑥) получается, когда
2𝑥=2, поэтому 𝑥=1. Таким образом, когда мы умножаем каждый
𝑥 значение в
𝑓(𝑥) на 2, чтобы получить функцию
ℎ(𝑥)=(2𝑥), график
𝑓(𝑥)=𝑥 расширяется по горизонтали в раз
12, при этом каждая точка перемещается на половину своего
предыдущее расстояние от оси 𝑦.
Для любого положительного 𝑏∈ℝ, когда 𝑥⟶𝑏𝑥, график 𝑦=(𝑏𝑥) является горизонтальное растяжение 𝑓(𝑥)=𝑥 в раз 1𝑏.
Мы можем обобщить эти результаты ниже, для положительного 𝑎 и 𝑏.
| Операция | Преобразованное уравнение | Геометрическое изменение | ||
|---|---|---|---|---|
| 𝑓 (𝑥) ⟶𝑎𝑓 (𝑥) | 𝑓 (𝑥) = 𝑎𝑥 | . | 𝑓(𝑥)=(𝑏𝑥) | Горизонтальное расширение коэффициента 1𝑏 |
Наконец, мы можем исследовать изменения стандартной кубической функции с помощью
отрицание, для функции
𝑔(𝑥)=−𝑓(𝑥). Это дает нам функцию
𝑔(𝑥)=−𝑥. Каждое выходное значение
𝑔(𝑥) будет отрицательным значением в
𝑓(𝑥)=𝑥. Например, координаты
(2,8) в исходной функции будет
(2,−8) в преобразованной функции.
Каждое выходное значение
𝑔(𝑥) будет отрицательным значением в
𝑓(𝑥)=𝑥. Например, координаты
(2,8) в исходной функции будет
(2,−8) в преобразованной функции.
Создает эффект отражения по горизонтальной оси.
Поскольку кубический граф является нечетной функцией, мы знаем, что 𝑓(−𝑥)=−𝑓(𝑥). Таким образом, изменение введите 𝑥⟶−𝑥 в функцию 𝑓(𝑥)=𝑥 также преобразует функцию в 𝑓(𝑥)=−𝑥. В общем, для любой функции 𝑓(𝑥), 𝑓(𝑥)⟶−𝑓(𝑥) создает отражение в горизонтальной оси и изменение ввода 𝑥⟶−𝑥 создает отражение 𝑓(𝑥) по вертикальной оси. Тот факт, что кубическая функция, 𝑓(𝑥)=𝑥, нечетна, означает, что отрицание ввода или вывода дает тот же графический результат.
| Операция | Преобразованное уравнение | Геометрическое изменение | ||
|---|---|---|---|---|
| 𝑓 (𝑥) ⟶ — 𝑓 (𝑥) | 𝑓 (𝑥) = — 𝑥 | . ⟶−𝑥 | 𝑓(𝑥)=(−𝑥) | Отражение по вертикальной оси |
Мы можем составить полную таблицу изменений функции
𝑓(𝑥)=𝑥 ниже, для положительного
𝑎 и 𝑏.
| Эксплуатация | Преобразованное уравнение | Геометрическое изменение |
|---|---|---|
| 𝑓 (𝑥) ⟶𝑓 (𝑥)+𝑘 | 𝑓 (𝑥) = 𝑥+𝑘 | Вертикальный трансляция: , если 𝑘> 0, 𝑘 поднимает. Если 𝑘0, |𝑘| единиц вниз. |
| 𝑥⟶𝑥−ℎ | 𝑓(𝑥)=(𝑥−ℎ) | Горизонтальный перевод: Если ℎ>0, ℎ единиц вправо. Если ℎ0, |ℎ| остались единицы. |
| 𝑓 (𝑥) ⟶𝑎𝑓 (𝑥) | 𝑓 (𝑥) = 𝑎𝑥 | Вертикальная дилатация фактора 𝑎 |
| 𝑥⟶𝑏𝑥 | 𝑓(𝑥)=(𝑏𝑥) | Horizontal dilation of factor 1𝑏 |
| 𝑓(𝑥)⟶−𝑓(𝑥) | 𝑓(𝑥)=−𝑥 | Reflectioninthehorizontalaxis |
| 𝑥 ⟶−𝑥 | 𝑓(𝑥)=(−𝑥) | Отражение по вертикальной оси |
Мы можем объединить ряд этих различных преобразований со стандартным кубическая функция, создающая функцию в виде 𝑓(𝑥)=𝑎(𝑥−ℎ)+𝑘.
Определение: преобразования кубической функции
Если 𝑎, ℎ и
𝑘∈ℝ, где 𝑎≠0, тогда
график
𝑓(𝑥)=𝑎(𝑥−ℎ)+𝑘
является преобразованием графа 𝑦=𝑥. Мы перечисляем
преобразований, которые нам нужны, чтобы преобразовать график 𝑦=𝑥 в
𝑦=𝑓(𝑥) следующим образом:
Мы перечисляем
преобразований, которые нам нужны, чтобы преобразовать график 𝑦=𝑥 в
𝑦=𝑓(𝑥) следующим образом:
- Если 𝑎>0, то график 𝑦=𝑥 есть вертикально расширен в 𝑎 раз.
- Если 𝑎0, то график 𝑦=𝑥 есть отражается по горизонтальной оси и расширяется по вертикали в множитель |𝑎|.
- Если ℎ>0, то график 𝑦=𝑥 есть переведено по горизонтали ℎ единиц вправо.
- Если ℎ0, то график 𝑦=𝑥 есть переведено горизонтально |ℎ| единицы оставил.
- Если 𝑘>0, то график 𝑦=𝑥 это переведено по вертикали на 𝑘 единиц вверх.
- Если 𝑘0, то график 𝑦=𝑥 есть переведено вертикально |𝑘| единиц вниз.
Порядок, в котором мы выполняем преобразования функции, важен, даже если иногда мы получаем один и тот же график независимо. Мы используем следующий порядок:
- Вертикальное расширение, 𝑎
- Горизонтальное перемещение, ℎ
- Вертикальное перемещение, 𝑘
Если нам дан график неизвестной кубической функции, мы можем использовать форму
родительской функции, 𝑓(𝑥)=𝑥, чтобы установить
какие преобразования были применены к нему и, следовательно, установить
функция. Давайте посмотрим на примере того, как мы можем это сделать.
Давайте посмотрим на примере того, как мы можем это сделать.
Пример 1. Написание уравнения графика путем распознавания преобразования эталона Кубическая функция
Какое уравнение соответствует графику?
- 𝑦=(𝑥−2)−1
- 𝑦=(𝑥+2)−1
- 𝑦=(𝑥+2)+1
- 𝑦=(𝑥4−2)+14−29+014−2
Ответ
Можно заметить, что эта функция похожа по форме на стандартную кубическая функция, 𝑓(𝑥)=𝑥, иногда пишется как уравнение 𝑦=𝑥. На самом деле, мы можем отметить, что нет расширение функции, либо глядя на ее форму, либо отмечая коэффициенты при (𝑥−ℎ) в данных вариантах равны 1. график 𝑦=𝑥 проходит через начало координат и может быть изображен на том же графике, что и ниже.
Точка перегиба 𝑦=𝑥 находится в координате
(0,0), а точка перегиба неизвестного
функция находится в точке (−2, −1). Следовательно, функция 𝑦=𝑥
был переведен на две единицы влево и на 1 единицу вниз. Поскольку обе функции имеют
такая же крутизна и они не нашли отражения, значит нет
дальнейшие преобразования.
Поскольку обе функции имеют
такая же крутизна и они не нашли отражения, значит нет
дальнейшие преобразования.
Кубическая функция вида 𝑦=𝑎(𝑥−ℎ)+𝑘 является преобразование 𝑦=𝑥 для 𝑎, ℎ и 𝑘∈ℝ, с 𝑎≠0. В таком виде значение 𝑎 указывает масштабный коэффициент расширения, а отражение, если 𝑎0; есть горизонталь перевод ℎ единиц вправо и вертикальный перевод 𝑘 единиц вверх. Выполняем эти преобразования с помощью сначала вертикальное растяжение, затем горизонтальное перемещение и вертикальное перевод третий.
В этом вопросе график не отражен и не расширен, поэтому
𝑎=1. И нам не нужно выполнять какую-либо вертикальную дилатацию. Следующий,
у функции осталось горизонтальное смещение на 2 единицы, поэтому
ℎ=−2. Вертикальный перевод на 1 единицу вниз означает, что
𝑘=−1. Мы можем заполнить их в уравнении
𝑦=𝑎(𝑥−ℎ)+𝑘, что дает
𝑦=1(𝑥−(−2))+(−1)=(𝑥+2)−1.
Следовательно, уравнение графика таково, как указано в варианте B: 𝑦=(𝑥+2)−1,
В следующем примере мы определим правильную форму графика кубическая функция.
Пример 2. Идентификация графика кубической функции путем идентификации преобразований стандартной кубической функции
Что из следующего является графиком 𝑓(𝑥)=−(𝑥−2)?
Ответ
Мы можем сравнить функцию 𝑓(𝑥)=−(𝑥−2) со своим родителем функция 𝑓(𝑥)=𝑥, которую мы можем нарисовать ниже.
Кубическая функция в виде
𝑓(𝑥)=𝑎(𝑥−ℎ)+𝑘 является преобразованием
из 𝑓(𝑥)=𝑥, для 𝑎,
ℎ и 𝑘∈ℝ, с
𝑎≠0. Здесь 𝑎 представляет расширение
или отражение, ℎ дает количество единиц, которые график
переводится в горизонтальном направлении, а 𝑘 — это
количество единиц, на которые график смещается в вертикальном направлении. Мы
выполнить эти преобразования сначала с вертикальным расширением, горизонтальным
перевод второй, а вертикальный перевод третий.
В функции 𝑓(𝑥)=−(𝑥−2), значение 𝑎=−1. Это свидетельствует об отсутствии дилатации (вернее, расширение масштабного коэффициента 1). Однако, поскольку 𝑎 отрицательный, это означает, что есть отражение графика в 𝑥-ось. Следовательно, мы могли бы выполнить отражение 𝑓(𝑥)=𝑥, как показано ниже, создавая функцию 𝑓(𝑥)=−𝑥.
Далее в заданной функции 𝑓(𝑥)=−(𝑥−2), значение ℎ равен 2, что указывает на то, что есть перевод 2 единицы Правильно. Это смещает точку перегиба от (0,0) до (2,0). Функция 𝑓(𝑥)=−(𝑥−2) можно нарисовать как показано.
Таким образом, график, показывающий функцию 𝑓(𝑥)=−(𝑥−2) — это вариант E.
В следующем примере мы увидим, как можно записать функцию, зная ее график.
Пример 3. Написание уравнения графика путем распознавания преобразования эталона Кубическая функция
Выберите уравнение этой кривой.
- 𝑦 = 𝑥 -3
- 𝑦 = −𝑥 -3
- 𝑦 = 2𝑥+3
- 𝑦 = −2𝑥 -3
- 𝑦 = 𝑥+3
.0002 Мы можем сравнить эту функцию с функцией 𝑦=𝑥 по формуле построить график этой функции на тех же осях.
Мы отмечаем, что не было никакого расширения или отражения с тех пор, как крутизна и конечное поведение кривых идентично. Нет горизонтального перевод, но есть вертикальный перевод на 3 единицы вниз. Для любого значения 𝑘∈ℝ функция 𝑦=𝑥+𝑘 — перевод функции 𝑦=𝑥 на 𝑘 единиц по вертикали. Поскольку перевод здесь в отрицательном направлении, значение 𝑘 должен быть отрицательным; следовательно, 𝑘=−3.
Таким образом, уравнение этой кривой является ответом, данным в варианте А: 𝑦=𝑥−3.
Теперь мы рассмотрим пример, в котором нам нужно идентифицировать три отдельных преобразования стандартной кубической функции.
Пример 4. Идентификация графика кубической функции путем идентификации преобразований стандартной кубической функции
Какой из следующих графиков представляет 𝑓(𝑥)=2−(𝑥−5)?
Ответ
Кубическая функция в виде 𝑦=𝑎(𝑥−ℎ)+𝑘
является преобразованием 𝑦=𝑥, для 𝑎,
ℎ и 𝑘∈ℝ, с
𝑎≠0.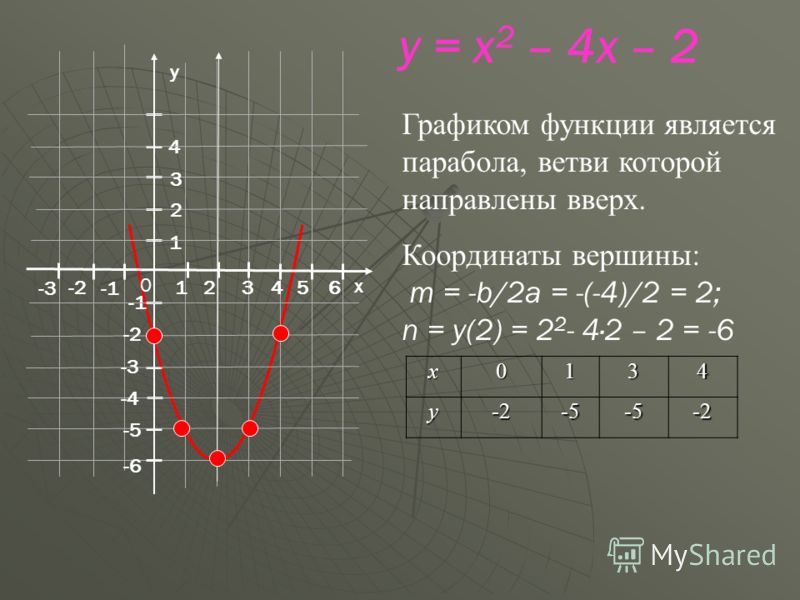 Здесь 𝑎 представляет расширение
или отражение, ℎ дает количество единиц, которые график
переводится в горизонтальном направлении, а 𝑘
количество единиц, на которые график смещается в вертикальном направлении. Сначала мы выполняем эти преобразования с вертикальным растяжением,
горизонтальный перевод второй, а вертикальный перевод третий.
Здесь 𝑎 представляет расширение
или отражение, ℎ дает количество единиц, которые график
переводится в горизонтальном направлении, а 𝑘
количество единиц, на которые график смещается в вертикальном направлении. Сначала мы выполняем эти преобразования с вертикальным растяжением,
горизонтальный перевод второй, а вертикальный перевод третий.
Функция 𝑓(𝑥)=2−(𝑥−5) может быть записано как 𝑓(𝑥)=−(𝑥−5)+2.
Поскольку значение 𝑎=−1 является отрицательным, график должен быть отражается на оси 𝑥. С |𝑎|=1, график 𝑦=𝑥 имеет вертикальное расширение с масштабным коэффициентом 1; таким образом, он будет иметь такую же форму.
Поскольку ℎ=5, горизонтальный сдвиг вправо составляет 5 единиц.
Наконец, 𝑘=2, поэтому график также имеет вертикальное перемещение на 2 единицы вверх.
Мы можем визуализировать переводы поэтапно, начиная с графика
𝑓(𝑥)=𝑥.
Объединение двух переводов и отражения дает нам решение что график, показывающий функцию 𝑓(𝑥)=2−(𝑥−5) — вариант B.
Кстати, вариант A представляет функцию 𝑓(𝑥)=2+(𝑥+5), вариант C представляет функцию 𝑓(𝑥)=2−(𝑥+5), а вариант D есть функция 𝑓(𝑥)=2+(𝑥−5).
Теперь рассмотрим пример с расширением.
Пример 5. Написание уравнения графика путем распознавания преобразования эталона Кубическая функция
Какое уравнение соответствует графику?
- 𝑦=(𝑥-1)+4
- 𝑦=2(𝑥-1)+4
- 𝑦=3(𝑥-1)+4
- 𝑦=13()+4
- 𝑦=13() 4
- 𝑦=12(𝑥−1)+4
Ответ
Показанная функция является преобразованием графика
𝑦=𝑥. Мы можем написать уравнение графика в виде
форма 𝑦=𝑎(𝑥−ℎ)+𝑘, которая является
преобразование 𝑦=𝑥 для 𝑎,
ℎ и 𝑘∈ℝ, с
𝑎≠0. Здесь 𝑎 представляет расширение
или отражение, ℎ дает количество единиц, которые график
перемещается в горизонтальном направлении и
𝑘 — количество единиц, на которое график переводится в
вертикальное направление. Выполняем эти преобразования с вертикальным
сначала растягивание, затем горизонтальное перемещение и вертикальное перемещение
в третьих.
Выполняем эти преобразования с вертикальным
сначала растягивание, затем горизонтальное перемещение и вертикальное перемещение
в третьих.
Мы можем нарисовать график 𝑦=𝑥 рядом с данным изгиб.
Если мы сравним точку поворота 𝑦=𝑥 с точкой поворота данного графа имеем (0,0)⟶(1,4). Это указывает на горизонтальный перевод на 1 единицу вправо и вертикальный перевод на 4 единиц вверх.
Заметим, что данная кривая круче, чем у функции 𝑦=𝑥. Мы можем сравнить перевод 𝑦=𝑥 на 1 единицу вправо и на 4 единицы вверх с заданным изгиб.
Ввод 𝑥 0 в транслируемой функции производит
выход, 𝑦, из 3. Однако аналогичный ввод 0 на данной кривой
производит выход 1. Существует расширение масштабного коэффициента 3 между
две кривые. Так как данная кривая круче кривой функции
𝑓(𝑥)=𝑥, то он был расширен
по вертикали с масштабным коэффициентом 3 (вместо расширения с масштабом
коэффициент 13, что дает
«сжатый» график).
Теперь мы можем заменить 𝑎=3, ℎ=1 и 𝑘=4 в 𝑦=𝑎(𝑥−ℎ)+𝑘 дать 𝑦=3(𝑥−1)+4.
Это ответ, данный в варианте C.
Мы рассмотрим последний пример, включающий одну из особенностей кубического функция: точка симметрии.
Пример 6. Определение точки симметрии кубической функции
Рассмотрим график функции 𝑦=(𝑥+2)−2.
Запишите координаты точки симметрии графика, если она существует.
Ответ
Данный график представляет собой перевод 𝑦=𝑥 на 2 единицы влево и на 2 единицы вниз. Так как 𝑦=𝑥 имеет точку вращательная симметрия при (0,0), то после перевода переведенное график будет иметь точку вращательной симметрии на 2 единицы влево и на 2 единицы вниз от (0,0).
Следовательно, мы можем определить точку симметрии как (−2,−2).
Подведем итоги.
Ключевые моменты
- Стандартная кубическая функция — это функция
𝑓(𝑥)=𝑥.
 Она имеет следующие свойства:
Она имеет следующие свойства:- Выходы функции положительны, когда 𝑥 положительный, отрицательный, когда 𝑥 отрицательный, и 0, когда 𝑥=0.
- Его конечное поведение таково, что по мере увеличения 𝑥 до бесконечность, 𝑓(𝑥) также увеличивается до бесконечности. По мере уменьшения 𝑥 𝑓(𝑥) также уменьшается до отрицательной бесконечности.
- Это странная функция, 𝑓(−𝑥)=−𝑓(𝑥), и поэтому его график имеет вращение на 180∘ симметрия относительно происхождения.
- Если 𝑎, ℎ и
𝑘∈ℝ, где 𝑎≠0, то график
𝑓(𝑥)=𝑎(𝑥−ℎ)+𝑘
является преобразованием графа 𝑦=𝑥. Мы перечисляем
преобразований, которые нам нужны, чтобы преобразовать график 𝑦=𝑥
в 𝑦=𝑓(𝑥) следующим образом:
- Если 𝑎>0, то график 𝑦=𝑥 вертикально расширен в 𝑎 раз.
- Если 𝑎0, то график 𝑦=𝑥 отражается по горизонтальной оси и расширяется по вертикали в множитель |𝑎|.
- Если ℎ>0, то график 𝑦=𝑥
переводится по горизонтали на ℎ единиц вправо.

- Если ℎ0, то график 𝑦=𝑥 переводится горизонтально |ℎ| остались единицы.
- Если 𝑘>0, то график 𝑦=𝑥 переводится вертикально на 𝑘 единиц вверх.
- Если 𝑘0, то график 𝑦=𝑥 переводится вертикально |𝑘| единиц вниз.
- Для функции 𝑓(𝑥)=𝑎(𝑥−ℎ)+𝑘,
выполняем преобразования кубической функции в следующем порядке:
- Вертикальное расширение, 𝑎
- Горизонтальное перемещение, ℎ
- Вертикальное перемещение, 𝑘
Кубические функции (ответы на 10 часто задаваемых вопросов) — JDM Educational
Кубические функции полезны для моделирования объема объектов (например, сфер или коробок). Однако многое нужно знать об этих полиномах третьей степени, их корнях и графиках.
Итак, что вам нужно знать о кубических функциях? Кубическая функция имеет вид f(x) = ax 3 + bx 2 + cx + d, где a, b, c и d действительны, а a не равно нулю. Некоторые кубические функции являются один к одному, а некоторые имеют нечетную симметрию, но ни одна кубическая функция не имеет четной симметрии. Кубическая функция имеет 3 корня и либо ноль, либо два комплексных, либо мнимых корня.
Некоторые кубические функции являются один к одному, а некоторые имеют нечетную симметрию, но ни одна кубическая функция не имеет четной симметрии. Кубическая функция имеет 3 корня и либо ноль, либо два комплексных, либо мнимых корня.
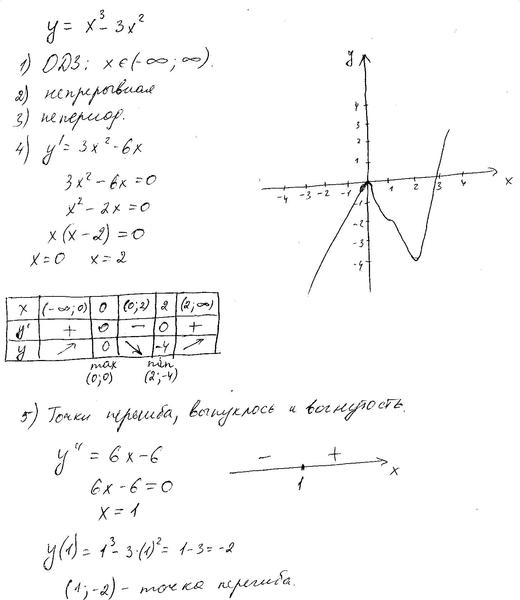
Конечно, кубическая функция может иметь до двух локальных экстремумов (максимумов или минимумов) и всегда имеет точку перегиба (поскольку вторая производная линейна).
В этой статье мы более подробно рассмотрим кубические функции и ответим на некоторые распространенные вопросы о них. Мы также рассмотрим несколько примеров, включая графики различных кубических функций.
Начнем.
Что такое кубическая функция?
Кубическая функция имеет стандартный вид
- f(x) = ax 3 + bx 2 + cx + d
где a, b, c и d действительны, с не равным нулю.
Кубическую функцию также называют полиномом третьей степени или полиномиальной функцией степени 3. Это означает, что x 3 является наибольшей степенью x с ненулевым коэффициентом.
Это означает, что x 3 является наибольшей степенью x с ненулевым коэффициентом.
Это также означает, что кубический многочлен можно описать как многочлен нечетной степени. Это означает, что у него всегда будет по крайней мере один действительный корень, и у него всегда будет нечетное количество действительных корней (и четное количество комплексных корней, которые входят в сопряженные пары).
Область определения кубической функции — это множество всех действительных чисел. Диапазон кубической функции также является набором всех действительных чисел.
Если мы приравняем кубическую функцию к нулю, то получим кубическое уравнение:
- f(x) = 0
или
- ax 0 1 0 6 90 906 + bx = 0
Это уравнение имеет 3 решения. Некоторые из решений могут повторяться, а некоторые из них могут быть комплексными или мнимыми числами.
Вот несколько примеров кубических функций и их графиков.
Пример 1. Кубическая функция и ее график
Рассмотрим кубическую функцию
- f(x) = x 3 + 3x 2 + 2x
Обратите внимание, что a = 1, b = 3, c = 0 и 9003.
Мы можем установить эту функцию равной нулю и разложить ее на множители, чтобы найти корни, что поможет нам изобразить ее в виде графика: = 0
Итак, корни x = 0, x = -1 и x = -2. Это означает, что график касается оси x в трех местах: при x = 0, -1 и -2.
Мы будем использовать эти значения для построения графика функции:
Кубическая функция f(x) = x 3 + 3x 2 + 2x имеет нули при x = 0, x = -1 и x = — 2. Обратите внимание, что функция приближается к отрицательной бесконечности по мере того, как x становится более отрицательным. Функция приближается к положительной бесконечности по мере того, как x становится более положительным.
Пример 2. Кубическая функция и ее график
Рассмотрим кубическую функцию
- f(x) = x 3 – x 2 + x – 1
Мы можем установить эту функцию равной нулю и факторизовать ее, чтобы найти корни, что поможет нам построить ее график: х – 1 = 0
Итак, корни равны x = 1, x = i и x = -i (где I = √-1). Итак, эта кубическая имеет только один реальный нуль, а это означает, что график касается оси x только один раз (при x = 1).
График функции показан ниже:
Кубическая функция f(x) = x 3 – x 2 + x – 1 имеет нули при x = 1, x = i и x = -i. Мнимые нули на графике не появляются.
Обратите внимание, что функция приближается к отрицательной бесконечности по мере того, как x становится более отрицательным. Функция приближается к положительной бесконечности по мере того, как x становится более положительным.
Для чего кубическая функция используется в реальной жизни?
Во-первых, кубическую функцию можно использовать для моделирования объема объектов, включая коробки и сферы.
Пример 1: Объем коробки с квадратным основанием
Допустим, у нас есть коробка с квадратным основанием. Длина стороны квадратного основания равна х.
Мы хотим, чтобы коробка была в два раза больше в высоту, чем в ширину. Тогда высота коробки умножится на 2.
Объем коробки:
- V = (длина)*(ширина)*(высота)
В этом случае у нас есть длина и ширина x (квадратное основание) и высота в 2 раза (в два раза больше ширины). Итак, наш объем становится:
- V = (x)*(x)*(2x)
- V = 2x 3
Итак, мы можем выбрать значение x и найти соответствующий объем коробки, которую мы описали.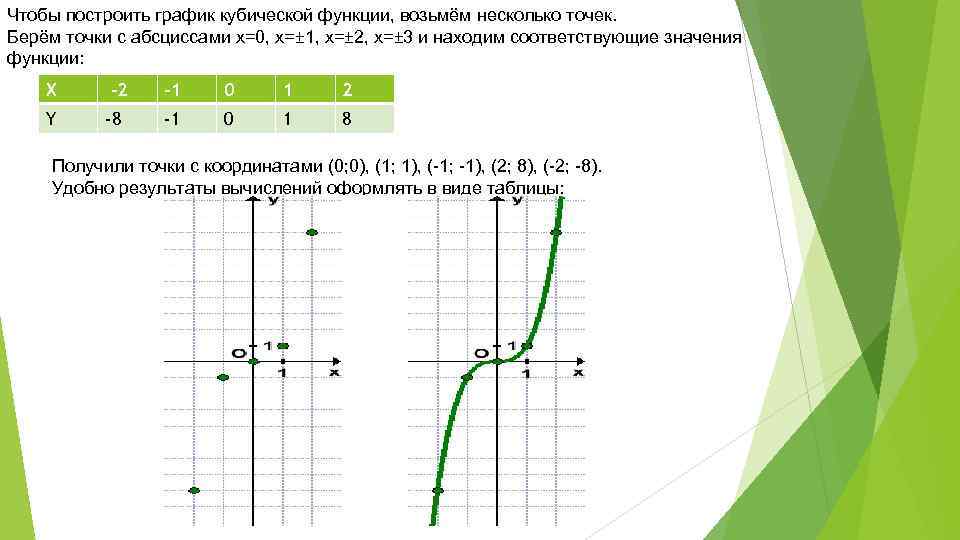 Например, если длина стороны x = 3 фута, то объем V = 2(3) 3 = 54 кубических фута.
Например, если длина стороны x = 3 фута, то объем V = 2(3) 3 = 54 кубических фута.
Мы также можем выбрать объем для этого ящика и работать в обратном порядке, чтобы найти размеры. Например, предположим, что мы хотим, чтобы этот тип коробки имел объем 128 кубических футов.
Нам нужно решить уравнение объема для 128:
- V = 2x 3
- 128 = 2x 3
- 64 = x 3
- 4 = x
So, the length and width of the box равно 4 (основание площадью 16 квадратных футов). Высота 2х=8 футов.
Пример 2: Объем сферы
Если сфера имеет радиус x, то ее объем определяется уравнением0047
Это кубическая функция, поскольку x 3 является максимальной степенью x с ненулевым коэффициентом в многочлене.
Как узнать, является ли график кубическим?
Есть несколько признаков, по которым можно определить, является ли граф кубическим:
- Первая производная f’(x) будет квадратичной.
 Таким образом, он будет равен нулю для 0, 1 или 2 действительных значений. Это означает, что кубика f(x) может иметь ноль, один или не более двух локальных экстремумов (максимумов или минимумов).
Таким образом, он будет равен нулю для 0, 1 или 2 действительных значений. Это означает, что кубика f(x) может иметь ноль, один или не более двух локальных экстремумов (максимумов или минимумов). - Вторая производная f’’(x) будет линейной. Таким образом, кубическая функция f(x) будет иметь единственную точку перегиба, в которой она меняет вогнутость. https://jdmeducational.com/when-is-a-function-concave-or-convex-4-key-ideas/
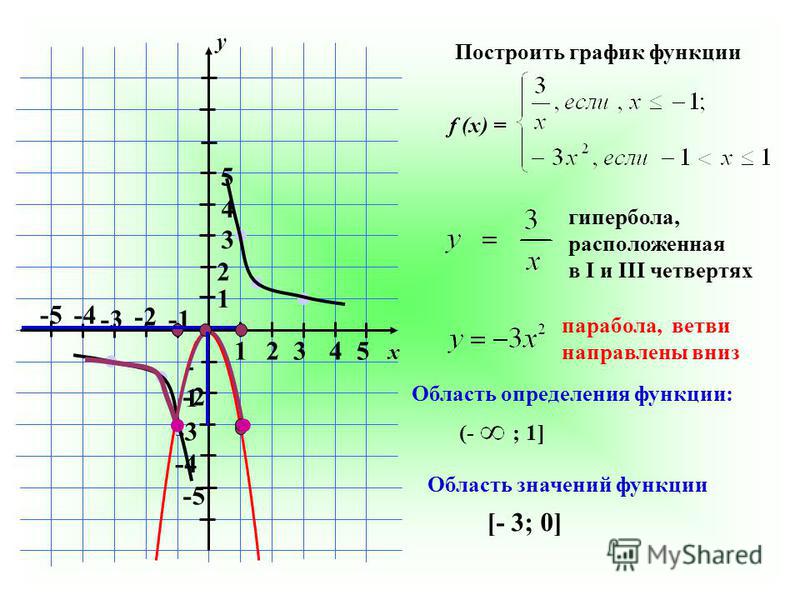
- Форма графика: см. примеры ниже для a > 0 и a < 0
Как сдвинуть кубическую функцию?
Чтобы сдвинуть кубическую функцию вверх или вниз на k единиц (вертикальный сдвиг), просто прибавьте или вычтите k из функции.
Например, если f(x) = x 3 это наша исходная кубическая функция, то:
- g(x) = f(x) + k = x 3 + k является графиком f (x) сдвинут вверх на k единиц.

- h(x) = f(x) – k = x 3 – k – график f(x), сдвинутый вниз на k единиц.
Чтобы сдвинуть кубическую функцию влево или вправо на h единиц (горизонтальный сдвиг), просто вычтите или прибавьте h к каждому x в функции.
Например, если f(x) = x 3 — исходная кубическая функция, то:
- g(x) = f(x + h) = (x + h) 3 — график f(x), сдвинутой влево на h единиц.
- h(x) = f(x – h) = (x – h) 3 – график f(x), сдвинутый вправо на h единиц.
Если вы хотите сдвигать график и по горизонтали, и по вертикали, то комбинируйте оба типа сдвигов. Например, функция j(x) = f(x – h) + k представляет собой график f(x), сдвинутый на h единиц вправо и k единиц вверх.
Как по таблице узнать, является ли функция кубической?
Чтобы узнать, является ли функция кубической из таблицы, расширьте таблицу, добавив 5 столбцов: первые разности y, первые разности x, частное первых разностей y с первыми разностями x, а затем еще два столбца: 2-я и 3-я разности частного.
Посмотрите на последние 3 столбца таблицы. Если все значения в этом последнем столбце одинаковы, но в двух других столбцах значения различаются, то таблица составлена из кубической функции.
Example 1: A Cubic Function From A Table
Consider the following table of values:
| x | f(x) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 29 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | . We will extend the table as follows:
 Теперь смотрим на последние 3 столбца. Обратите внимание, что все значения в последнем столбце одинаковы, а значения в двух других столбцах различаются. Это означает, что третья производная постоянна, что говорит нам о том, что таблица получена из кубической функции: f(x) = x 3 + 2. Пример 2: некубическая функция из таблицыРассмотрим следующую таблицу значений:
из кубической функции? Расширим таблицу следующим образом:
 Теперь смотрим на последние 3 столбца. Обратите внимание, что все значения в последнем столбце одинаковы, как и значения в предпоследнем столбце. Это означает, что вторая и третья производные постоянны, что говорит нам о том, что таблица составлена из квадратичной функции: f(x) = 2x 2 – 1. Является ли кубическая функция взаимно однозначной?Не все кубические функции взаимно однозначны, но некоторые из них. Пример 1. Кубическая функция, являющаяся взаимно однозначной ниже:Кубическая функция f(x) = x 3 равна один к одному, так как она проходит тест горизонтальной линии.Мы также можем увидеть это алгебраически, используя тест горизонтальной линии. Любая горизонтальная линия имеет уравнение y = k. Если k действительное число, то оно имеет действительный кубический корень, r = k 1/3 . Затем мы можем установить кубическое значение равным k и решить, сколько точек пересечения имеется:
Отсюда следует, что x = r или x 2 + rx + r 2 = 0. В этом случае дискриминант (выражение под радикалом в квадратной формуле):
Поскольку дискриминант отрицателен, мы знаем, что квадратное число имеет два комплексно-сопряженных корня и не имеет действительных корней. Таким образом, существует только одно действительное решение кубика и только одна точка, где горизонтальная линия y = k пересекает кубику f(x) = x 3 . Пример 2. Кубическая функция, которая не является взаимно однозначной к единице, так как он не прошел тест горизонтальной линии. Это легко увидеть, если мы возьмем горизонтальную прямую y = 0.Решив пересечение кубика и прямой, получим:
Это означает, что кубический равен нулю, когда x = 0 или x = 1. Таким образом, есть два действительных корня. Однако x = 0 является повторяющимся (двойным) корнем. Кубическая функция f(x) = x 3 – x 2 имеет два нуля: x = 0 (двойной корень) и x = 1. Точно так же кубическая функция имеет один нуль, если она является тройным корнем (повторяется трижды). Например, f(x) = x 3 имеет один нуль (x = 0) и является тройным корнем. Может ли кубическая функция иметь три мнимых корня? (Нет действительных корней)Кубическая функция не может иметь три мнимых корня. Это означает, что кубическая функция должна иметь хотя бы один действительный корень. Может иметь либо два мнимых корня (комплексно-сопряженная пара), либо не иметь комплексных корней. Согласно основной теореме алгебры многочлен степени n с вещественными коэффициентами имеет n комплексных корней (с учетом повторяющихся корней). Применяя это к кубику с действительными коэффициентами (n = 3), мы видим, что такая функция имеет 3 корня (возможно, повторяющиеся корни). В некоторых случаях кубическая функция может иметь мнимые корни. Кубическая функция всегда будет иметь либо 0, либо 2 мнимых корня, которые должны быть комплексно-сопряженными друг другу (согласно теореме о комплексно-сопряженных корнях). Например, если x = 2i является корнем куба f(x), то x = -2i (комплексное сопряжение 2i) также является корнем f(x). Третий корень из этой кубы будет действительным. В таблицах ниже приведены возможные значения действительных и комплексных или мнимых корней кубических функций.
нулей кубического числа и сколько корней являются действительными или комплексными. 
 Есть ли у кубической функции асимптоты?Кубическая функция не имеет асимптот. Кубическая функция не имеет вертикальных асимптот, поскольку в кубическом полиноме не может быть нулевого знаменателя. Кубическая функция не имеет горизонтальных асимптот, так как областью значений кубического многочлена являются все действительные числа. Имеет ли кубическая функция симметрию? (Четные/Нечетные)Некоторые кубические функции обладают симметрией, но не все. Не существует четной кубической функции, поскольку гарантируется нечетная степень x (в частности, x 3 ). Итак, кубическая функция не может быть четной. Кубическая функция является нечетной, если она не имеет ни квадратичного члена, ни постоянного члена (то есть, если коэффициент при x 2 равен нулю и постоянный член также равен нулю). Пример 1. Нечетная кубическая функцияРассмотрим кубическую функцию
Мы можем показать, что f(-x) = -f(x):
Итак, f(x) = x 3 + x — нечетная кубическая функция. Пример 2. Нечетная кубическая функцияРассмотрим кубическую функцию
Мы можем показать, что f(x) не нечетна f(-x) = (-x) 3 + 1Поскольку f(-x) = -(x 3 – 1) и -f(x) = -(x 3 + 1), мы видим, что f(-x) не равно –f(x). Итак, f(x) = x 3 + 1 не нечетно. Кубическая функция f(x) = x 3 + 1 не имеет ни четной, ни нечетной симметрии.ЗаключениеТеперь вы знаете больше о кубических функциях, их корнях и о том, как выглядят их графики. Вы также знаете немного больше об их симметрии. Вы также можете прочитать мою статью о решениях кубических функций, мою статью о функциях четвертой степени или мою статью о функциях пятой степени. |

 Область определения _____________
Область определения _____________ Если х = 0, то у = 0
Если х = 0, то у = 0 Область определения _____________
Область определения _____________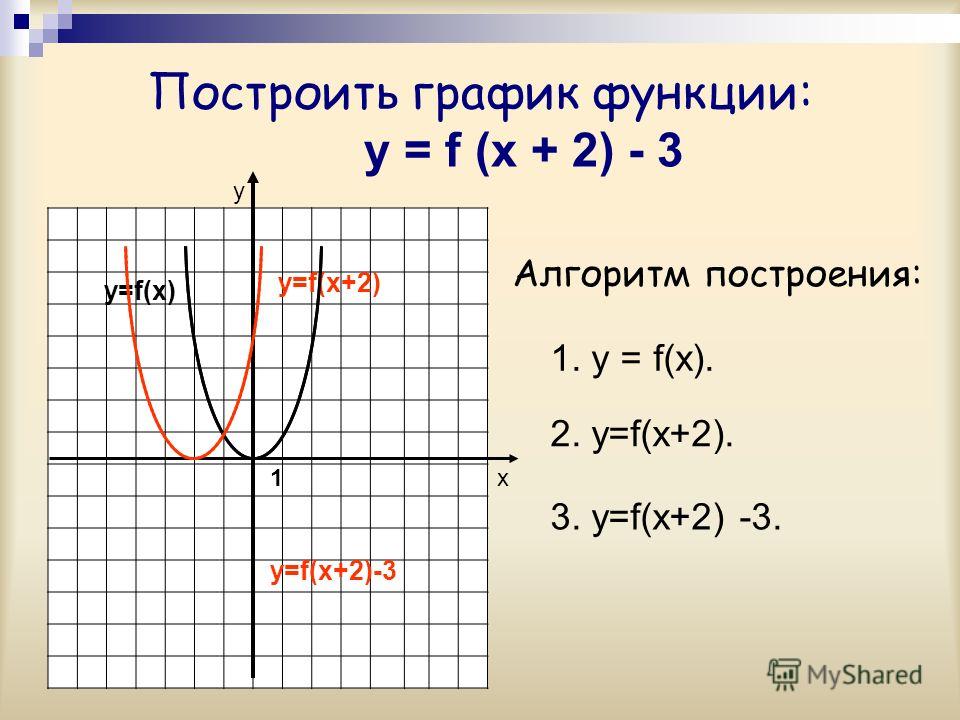 Область определения _____________
Область определения _____________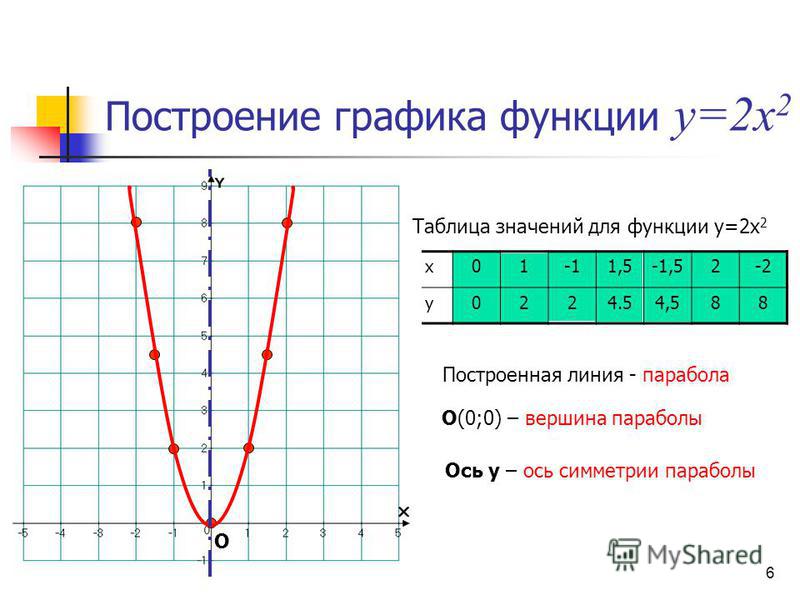
 Она имеет следующие свойства:
Она имеет следующие свойства:
 Таким образом, он будет равен нулю для 0, 1 или 2 действительных значений. Это означает, что кубика f(x) может иметь ноль, один или не более двух локальных экстремумов (максимумов или минимумов).
Таким образом, он будет равен нулю для 0, 1 или 2 действительных значений. Это означает, что кубика f(x) может иметь ноль, один или не более двух локальных экстремумов (максимумов или минимумов). 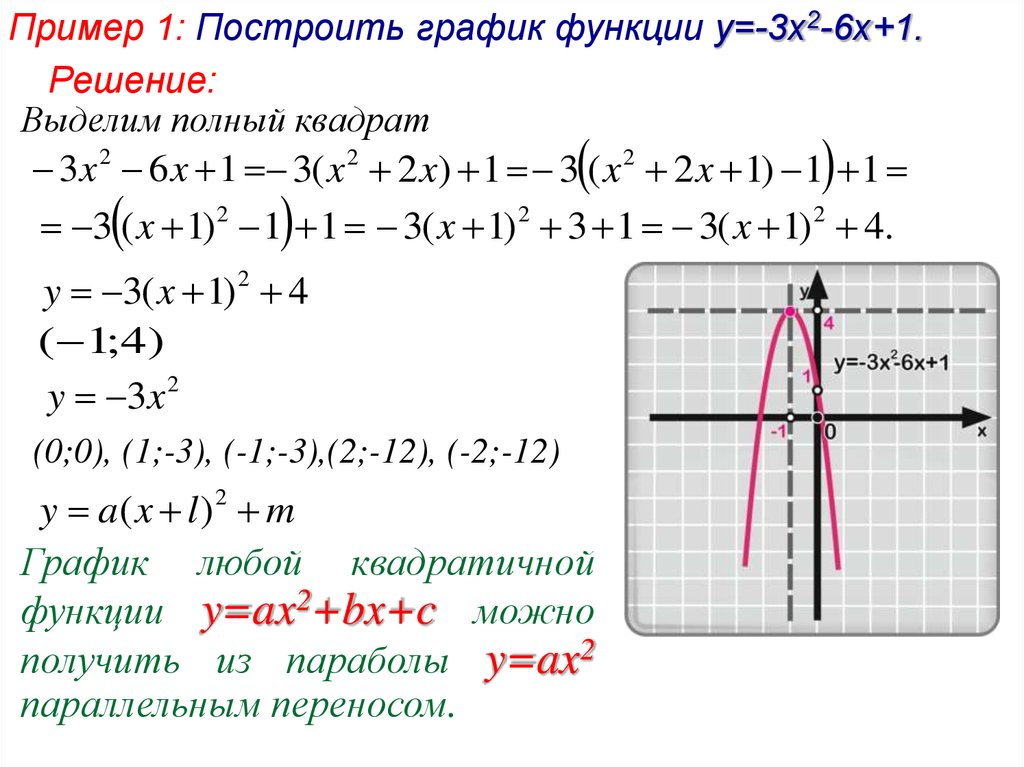
 Вторая возможность представляет собой квадратное уравнение с a = 1, b = r и c = r 2 .
Вторая возможность представляет собой квадратное уравнение с a = 1, b = r и c = r 2 . Итак, горизонтальная линия y = 0 пересекает кубику f(x) = x 3 + 3x 2 + 2x в трех точках: (0, 0), (-1, 0) и (-2, 0). ). Кубическая функция f(x) = x 3 + 3x 2 + 2x не является один к одному, так как горизонтальная линия y = 0 пересекает график три раза.
Итак, горизонтальная линия y = 0 пересекает кубику f(x) = x 3 + 3x 2 + 2x в трех точках: (0, 0), (-1, 0) и (-2, 0). ). Кубическая функция f(x) = x 3 + 3x 2 + 2x не является один к одному, так как горизонтальная линия y = 0 пересекает график три раза.