Y 1 2 sinx: построить график y=1/2sin — Школьные Знания.com

Содержание

Свойства функций y=sin x, y=cos x и их графики. Преобразование графиков на примере тригонометрических функций

Тема урока: Свойства функций y=sin x, y=cos x и их графики. Преобразование графиков на примере тригонометрических функций (практическое занятие)

Цели урока: Вспомнить тригонометрические функции, их графики; рассмотреть геометрические преобразования графиков функций Научится строить графики сложных функций с использованием параллельного переноса, растяжения, сжатия, симметрии относительно осей координат графиков известных функций, показать построение графиков, содержащих модуль, а также с последовательным применением нескольких способов. прививать интерес к математике; воспитывать графическую культуру, умение видеть красоту математики.

0 х у Параллельный перенос вдоль оси OX

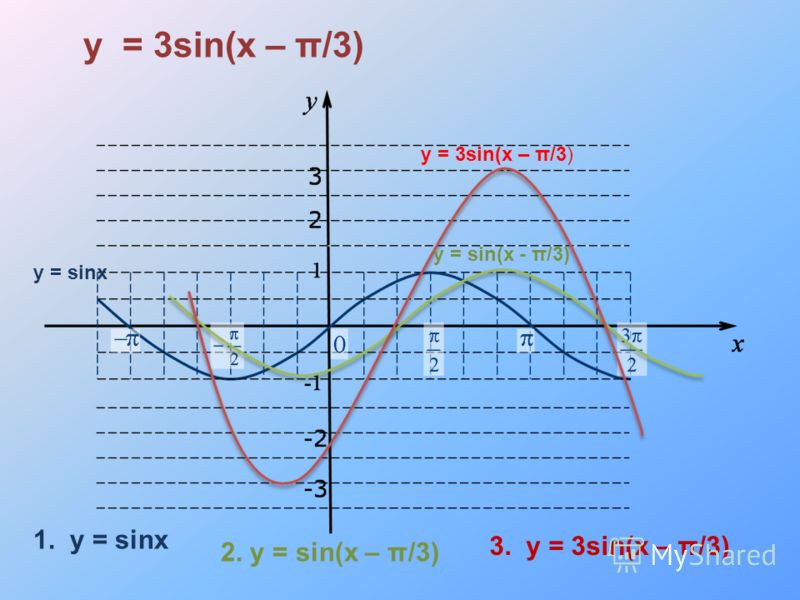
0 1 x y -1 ) 3 sin( p + = x y

1 -1 y x ) 3 tg( p - = x y

0 х у Параллельный перенос вдоль оси Oy

0 1 x y -1

0 1 -1 y x

0 х у a > 1 Растяжение (сжатие) в a раз вдоль оси OX 0 < a < 1

0 1 x y -1 2 cos = x y

0 1 x y -1

0 х у 0 < a < 1 Растяжение (сжатие) в а раз вдоль оси Oy a> 1

0 1 x y -1

1 -1 y x

0 х у Преобразование симметрии относительно оси Оy

у = sin (-x) у = sin x у = sin (-x)

0 х у Преобразование симметрии относительно оси Оx

y= tg x y= — tg x y= — tg x

0 х у Cправа от оси Оу график без изменений, а слева – симметрично правому относительно оси Оу

у = sin │x│ у = sin x

0 х у Выше оси Ох график без изменений, а ниже – симметрично относительно оси Ох

y= tg x y=│ tg x │

0 1 x y -1 sin = x y -2 3 sin = x y 3 sin = x y -2 3 sin = x y

0 1 x y -1 Y=cosx Y=cos2x Y=-cos2x Y=-cos2x+3 Y=-cos2x+3

Самостоятельная работа

Критерий оценки С/Р 3-5 баллов – 1 задание «построить» По1баллу за правильную формулу (1б. 5) – 2 задание «определить формулу» По 2 балла (2б.4)– 3 задание «определить вид преобразования» max=18 баллов

1в) y = 2sinx-1 Построить самостоятельно:

0 1 x y -1

0 х у 4 1 2 3 5 1 -1 Определите формулы, соответствующие графикам функций

X Y 1 2 -2 -1 - X Y 1 2 -1 -2 X Y 1 2 -1 -2 Определить вид преобразований. Назвать формулу функции по графику X Y 1 1 2 -2 -1 а) б) в) г)

Критерий оценки С/Р 3-5 баллов – 1 задание «построить» По1баллу за правильную формулу (1б.5) – 2 задание «определить формулу» По 2 балла (2б.4)– 3 задание «определить вид преобразования» max=18 баллов

Проверка результатов работы Слайд 1 Слайд 2 — растяжение по оси ОУ в 2 раза — сжатие по оси ОУ в 2 раза — сжатие по оси ОХ в 2 раза — растяжение по оси ОХ в 2 раза

Выставление оценок по критериям 9-12 баллов – «3» 13-16 баллов – «4» 17-18 баллов – «5»

Подведение итогов урока Графики функций широко используются в различных областях науки, поэтому умение строить, “читать”, прогнозировать их “поведение”, имеет огромную роль в практической деятельности разных специальностей.

Домашнее задание Построить графики, найти D(y), E(y)

Методическая разработка урока по теме: «Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения» | Методическая разработка по алгебре (10 класс) по теме:

Предмет: алгебра, класс: 10 класс. В Классе 2 ученика.

Тема урока: «Преобразование графика тригонометрической функции у = sin x путем сжатия и расширения»

Тип урока: комбинированный.

Продолжительность занятия: 45 минут.

Цели урока:

Систематизировать знания и умения по теме: “Преобразование графиков тригонометрических функций вида: y = f (x) + m, y = f (x + t), y = к f (x), y = f (к x),

научиться строить графики вида: y = f (x + t) + m;

Задачи урока.

Образовательные — научиться строить графики тригонометрической функции с помощью геометрических преобразований.

Развивающие – формировать логическое мышление, умение анализировать, обобщать полученные знания, способствовать развитию самостоятельной творческой исследовательской деятельности ученика.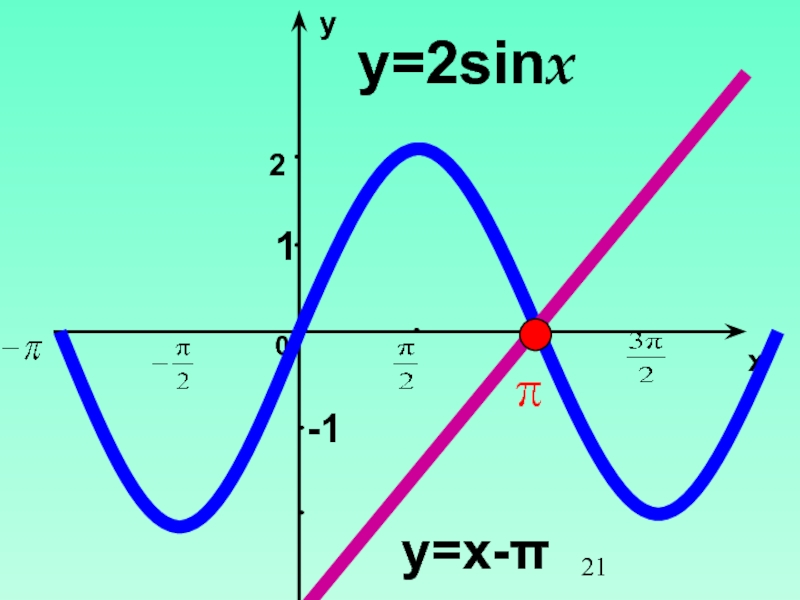

Воспитательные – активизировать интерес к получению новых знаний, воспитывать графическую культуру, формирование точности, внимательности и аккуратности при выполнении чертежей, чувство уважения к науке.

Оснащение: нетбук у каждого ученика, ноутбук у учителя, операционная система Microsoft Windows 98/Me/2000/XP, программа MS Office 2003: Power Point, Microsoft Word.

Литература: учебник Алимов Ш.А. и др. Алгебра и начала анализа 10-11 кл.

Технологии: ИКТ, взаимопроверка, энергосберегающая.

Вначале урока выдается лист контроля учащегося.

Ход урока

№

Этап урока

Действие учителя

Действия учащихся

Организационный момент

Приветствие учащихся, проверка готовности учащихся к уроку, определение отсутствующих.

Умение строить графики нам нужны при:

решении уравнений;

решении неравенств;

решении заданий, связанных с исследованием свойств функций.

Подготовка тетрадей, учебников к уроку

Объявление темы и цели урока.

Объявляет тему и цели урока.

ИКТ Слайд № 1,2

Слушают и записывают тему урока в тетрадях.

Повторение и закрепление знаний, умений и навыков

Фронтальный опрос

Повторить правила преобразования графиков функций:

y = f(x) + m,

y = f(x + t),

y = к f(x),

y = f (к x) с помощью чертежей.

ИКТ Слайд № 3 — 15

Проговаривают алгоритм.

Просматривают преобразование графиков на по готовым чертежам.

Сравнивают свой вывод с алгоритмом на слайде.

Выполняют задание.

Взаимопроверка.

Изложение нового материала

Вывести алгоритм построения графика функции у=а(х+t)2+m, если известен график функции у=ах2.

Сформулировать и проверить гипотезу построения графика функции у=а(х+t)2+m.

ИКТ Слайд № 16 — 18

Просит сделать вывод.

ИКТ Слайд № 19

Диалоговый режим работы.

Выполняют построение графиков схематично.

Физкультминутка

ИКТ энергосберегающая.

Закрепление и контроль знаний, умений и навыков изученного материала;

с последующей взаимопроверкой.

Вопрос:

Какое преобразование необходимо выполнить, чтобы построить графики функций:

1. у = 2sinх +3

2. у = 2sin(х +)

3. y = sin- 2?

Практическая работа

ИКТ Слайд № 20

Выдают Лист контроля

Проговаривают алгоритм последовательногопостроения графиков.

Выполняют работу

(взаимопроверка).

Выставляют баллы в листе контроля.

Домашнее задание

Дифференцированное и разноуровневое домашнее задание:

Записывают в дневник.

Подведение итогов.

Итоги урока.

На уроке повторили правила построения графиков функций с помощью геометрических преобразований, научились строить график функции

y = f (x + t) + m.

Выставление оценок (подсчет баллов в листе контроля).

Рефлексия.

Тригонометрическая функция

Тригонометрическая функция. Продолжаем рассматривать задачи связанные с нахождением точек максимума (минимума). Советую повторить теорию необходимую для решения задач на нахождение наибольшего (наименьшего) значения функции на интервале и на нахождение точек максимума (минимума) функции. В этой статье разберём две задачи в этой теме, рассмотрим тригонометрические функции. Задачи с логарифмами уже были нами рассмотрены ранее.

Ещё раз запишем алгоритм нахождения точек максимума (минимума) функции:

1. Вычисляем производную функции.

2. Приравниваем её к нулю, решаем уравнение.

3. Полученные корни разбивают числовую ось на интервалы, отмечаем их.

4. Определяем знаки производной на этих интервалах (подставляем произвольные значения из интервалов в производную).

5. Делаем вывод.

77492. Найдите точку максимума функции y = (2x –3) cos x – 2sin x + 5

принадлежащую промежутку (0;П/2).

Найдём производную функции:

Решаем уравнение:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, и другие при этом не теряют смысла. Следовательно:

Решаем уравнение – sin x = 0:

В условии дан промежуток (0;П/2). Ему не принадлежит ни один из полученных корней. *Обратите внимание, что указанные границы исключены (скобки круглые).

Решаем уравнение: 2х – 3 = 0, получим х = 1,5.

Запишем данный промежуток в радианах, получим: (0;1,57), так как

Следовательно полученное значение принадлежит промежутку (0;П/2):

Конечно, нам интуитивно понятно, что полученная точка это и есть точка максимума, и казалось бы в дальнейших вычислениях и рассуждениях нет необходимости. Но любая задача данного типа должна быть решена до конца по указанному алгоритму. Это важно!

Полученное значение х разбивает данный промежуток на два других. Определим знаки производной функции, подставляя произвольные значения из полученных промежутков (0;1,5) и (1,5;1,57) в найденную производную, и изобразим на рисунке поведение функции:

*В подобных случаях необязательно вычислять значения выражений. Важно установить их знаки (положительный либо отрицательный). Например, мы видим, что выражение:

(3,14/2) – 3 имеет отрицательный знак

3,14 – 3 имеет положительный знак

В целом этого достаточно для определения знака выражения.

Таким образом, в точке х = 1,5 функция меняет знак с положительного на отрицательный. Это означает, что данная точка является точкой максимума функции на заданном промежутке.

Ответ: 1,5

77493. Найдите точку минимума функции y = (0,5 – x) cos x + sin x

принадлежащую промежутку (0;П/2).

Найдём производную функции:

Решаем уравнение:

Решаем уравнение – sin x = 0:

В условии дан промежуток (0;П/2). Ему не принадлежит ни один из полученных корней.

Решаем уравнение: 0,5 – х = 0, получим х = 0,5.

Запишем данный промежуток в радианах: (0;1,57).

*Показано в предыдущем примере.

Следовательно полученное значение принадлежит промежутку (0;П/2):

Найденное значение х разбивает данный промежуток на два других. Определим знаки производной функции, подставляя произвольные значения из полученных промежутков (0;0,5) и (0,5;1,57) в найденную производную, и изобразим на рисунке поведение функции:

*Синус 0,3 радиана и синус 1 радиана имеют положительные знаки, так как оба эти угла лежат в пределах от 0 до 90 градусов. А мы знаем, что синусы углов лежащих в первой четверти имеют положительные значения.

Таким образом, в точке х = 0,5 функция меняет знак с отрицательного на положительный. Это означает, что данная точка является точкой минимума функции на заданном промежутке.

Ответ: 0,5

Как видите всё просто. Необходимо понимать свойства производной для исследования функций, понимать как «работать» с мерами углов, знать основы тригонометрии.

В будущем мы рассмотрим задачи на нахождение наибольшего (наименьшего) значения тригонометрических функций на заданном интервале, не пропустите!

Посмотрите, что нашёл в интернете. Оказывается, что при извержении вулканов тоже молнии бывают. Да ещё какие!

На том всё. Успехов Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

y = 1 / 2sin x. найти домен, диапазон, амплитуду и период

Фабай Дж.
задано • 29.03.17
y = 1 / 2sin x
домен =?
диапазон =?
амплитуда =?
период =?
Артуро О. ответил • 29.03.17
Опытный учитель физики Репетиторство по физике
Я полагаю, вы имеете в виду
y = (1/2) sinx
Домен — это все реальные числа.

Диапазон: от -1/2 до 1/2
Амплитуда: 1/2
Период: 2π
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈〉 ◊

график y = 1/2 sin (x pi / 2)
график y = 1/2 sin (x pi / 2) | математикатестподготовка.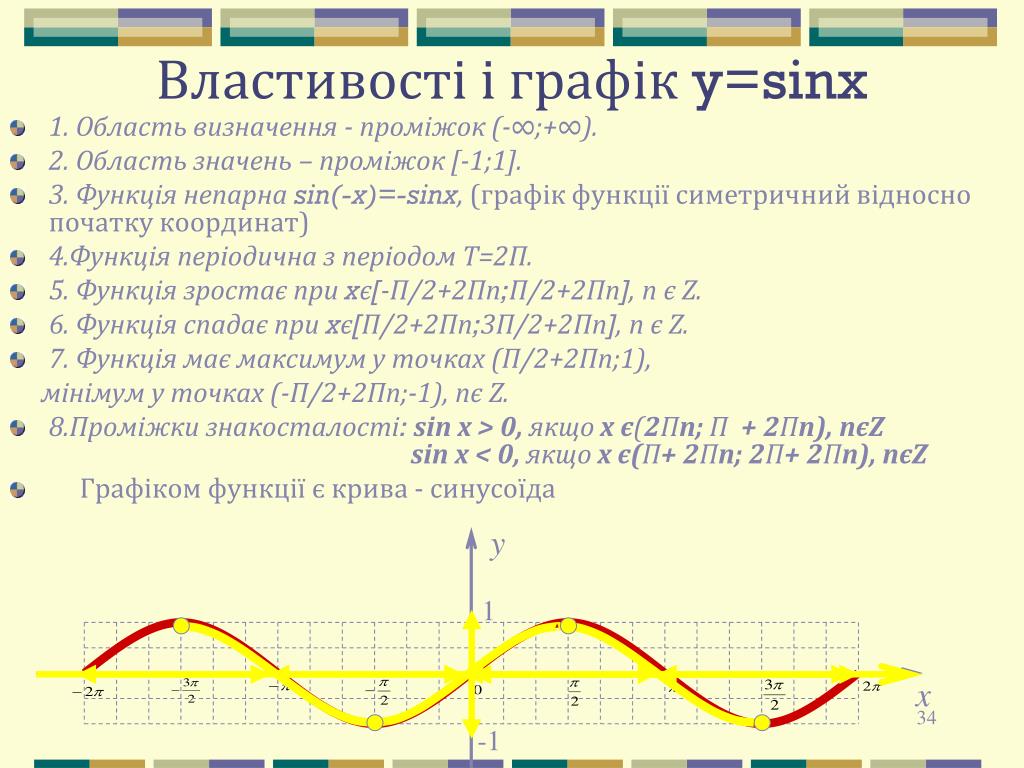 ком назад к
математический вопрос и ответ
График y = A sin Bx имеет свойство
(1). амплитуда = | A |
(2). период = 2pi / B
Для y = 1/2 sin [(pi / 2) x],
, поскольку A = 1/2, поэтому его амплитуда = | 1/2 |
, так как B = pi / 2, поэтому его период = 2pi / B = 2pi и делим pi / 2 = 2pi и умножаем на 2 / pi = 4
Таким образом, его амплитуда 1/2 и период 4
Найдите пять точек за один период
один период — 4, полупериод — 2, квартальный период — 1
делим пять точек поровну за период [0, 4]
Пять точек на оси x: x ₁ = 0, x ₂ = 1, x ₃ = 2, x ₄ = 3, x ₅ = 4
, поэтому пять точек в плоскости xy: (0,?), (1,?), (2,?), (3,?), (4,?)

Теперь найдите значения функции y = 1 / 2sin (x pi / 2) в пяти точках
, когда x = 0, y = 1/2 sin [(pi / 2) & times 0] = 1/2 sin (0) = 0, то есть точка (0, 0)
, когда x = 1, y = 1/2 sin [(pi / 2) & times 1] = 1/2 sin (pi / 2) = 1/2, то есть точка (1, 1/2)
, когда x = 2, y = 1/2 sin [(pi / 2) & times 2] = 1/2 sin (pi) = 0, поэтому точка равна (2, 0)
, когда x = 3, y = 1/2 sin [(pi / 2) & times 3] = 1/2 sin (3pi / 2) = — 1/2, то есть точка (3, — 1/2)
, когда x = 4, y = 1/2 sin [(pi / 2) & times 4] = 1/2 sin (2 pi) = 0, поэтому точка равна (4, 0)
Пять точек: (0, 0), (1, 1/2), (2, 0), (3, -1/2), (4, 0)
Нарисуйте график y = 1 / 2sin (x pi / 2) на основе пяти точек
Обратите внимание, что значения функции синуса для специальных углов:

грех (0) = 0
sin (пи / 2) = 1
sin (пи) = 0
sin (3pi / 2) = -1
sin (2pi) = 0
Анализ графика:
х = 0, у = 0.
x = 2 — его полупериод, в этот момент его значение y равно 0.
x = 1 — его период четверти, в этот момент его значение y равно 1/2, что является максимальным.
x = 3 — это его три четвертых периода, в этот момент его значение y равно -1/2, что является минимумом.
x = 4 — его конечная точка первого периода, в этот момент его значение y равно 0.
Кривая y = 1/2 sin (x pi / 2) непрерывна, она будет повторяться с периодом 4.

Лекция 39: Построение графика функции y = — (1/2) sinx
1: Что такое единичный круг? 2: Единичный круг и угол (Часть 1 из 2) 3: Единичный круг и угол (Часть 2 из 2) 4: Единичный круг и угол (30 и 60 градусов) 5: Единичный круг и знаки x и y 6: функция тригонометрии: объяснение синуса 7: функция тригонометрии: объяснение косинуса 8: функция тригонометрии: объяснение тангета 9: функция тригонометрии: объяснение котангета 10: функция тригонометрии: объяснение секант 11: тригонометрия Функция: объяснение косеканса 12: Что такое отрицательные углы? 13: Как преобразовать углы больше 360? 14: Что такое четные и нечетные функции? 15: Основные триггерные идентификации16: Использование единичной окружности для оценки триггерных функций 17: Использование единичной окружности для оценки Триггерные функции 18: Использование единичного круга для оценки триггерных функций 19: Формула сокращения (1 из 4) Сложение / вычитание 2 pi20: Формула сокращения (2 из 4) Сложение / вычитание pi21: Формула сокращения (3 из 4) Добавить pi / 222: Формула сокращения (4 из 4) Вычтем pi / 223: график y = sin (theta) (1 из 2) 24 : График y = sin (theta) (2 из 2) и единичный круг 25: график y = cos (theta) 26: график y = tan (theta) 27: период графиков синуса и косинуса 28: общее уравнение для синуса и Косинус 29: Общее уравнение для синуса и косинуса: Амплитуда 30: Общее уравнение для синуса и косинуса: Период 31: Общее уравнение для синуса и косинуса: Сдвиг влево / вправо 32: Общее уравнение для синуса и косинуса: Сдвиг вверх / вниз 33: Графическая сумма функций тригонометрии (1 из 2) 34: Графическая сумма функций тригонометрии (2 из 2) 35: График отрицательной функции триггера 36: Графическое изображение произведения тригонометрической функции (без калькуляторов!) 37: Графическое изображение произведения триггера Функция (без калькуляторов!) 38: Построение графика произведения триггерной функции (без калькуляторов!) 39: Построение графика функции y = — (1/2) sinx40: Построение графика функции y = 2 + 2cosx41: определение амплитуды, периода, и график y = -3sin3x42: найти амплитуду, период и график y = 4cos [(1/2) x] 43: найти амплитуду, период и график y = cos [x- (pi / 2)] 44: Найдите амплитуду Pe riod и График y = 3sin [(2x / 3) — (pi / 6)] 45: Найдите амплитуду, период и график y = 2cos [3x + (pi / 4)] — 146: Найдите амплитуду, период, Фазовый угол и напишите уравнение 47: Найдите амплитуду, период, фазовый угол и запишите уравнение 48: Найдите амплитуду, период, фазовый угол и запишите уравнение49: График y = tan4x50: График y = csc2x51: Функция обратного синуса52: Функция обратного косинуса53 : Функция обратной касательной 54: функция обратной тригонометрии: не запутайтесь! 55: угол в радианах 56: длина дуги (окружность) 57: площадь сектора (окружность) 58: основы тригонометрии 59: основы тригонометрии: пример 60: основы тригонометрии : Упражнение 161: Основы тригонометрии: Упражнение 262: Основы тригонометрии: Упражнение 363: Основы тригонометрии: Упражнение 464: Функции обратного триггера: Найти угол 65: Функции обратного триггера: Упр. 166: Обратные триггерные функции: Пример. 267: Обратные триггерные функции: Сводка 68: Найти все неизвестные (Adj =? Opp =?) 69: Найти все неизвестные (Adj =? Hyp =?) 70: Найти все неизвестные (Adj =? Angle =?) 71: Вызов Задача № 172: Задача № 273: Задача № 374: Задача № 475: Высота флага =? 76: Расстояние до ближайшей звезды =? 77: Высота здания =? 78: Расстояние между Венерой и Солнцем =? 79: Окружность планеты =? 80: Угол геосинхронного спутника =? 81: Определение закона синуса 82: Доказанный закон синуса 83: Пример SSA (сторона-сторона-угол) 84: Пример AAS (угол-угол-сторона ) 85: Осторожно: НЕТ случаев решения с законом синуса 86: множественные решения с законом синуса 87: определение высоты спутника 88: определение высоты горы 89: что такое закон косинусов? 90: поиск трех углов с тремя сторонами91: Доказанный закон косинусов92: Найдите расстояние и пеленг самолета93: Найдите расстояние между кораблями94: Формула Герона: Введение95: Доказанная формула Герона96: Каковы основные тригонометрические тождества? 97: Cofunction Trigonometric Identities98: Упростить тригонометрическое выражение: 199: Упростить тригонометрическое выражение: 2100: Проверить идентичность: 1101: Подтвердить идентичность: 2102: Проверить идентичность: 3103: Подтвердить идентичность: 4104: Формулы сложения и вычитания 105: Доказательство сложения Формула (косинус) 106: доказательство формулы вычитания (косинус) 107: доказательство идентичности кофункции 108: доказательство формулы сложения (синус) 109: доказательство формулы вычитания (синус) 110: доказательство формулы сложения (касательная) 111: доказательство Формула вычитания (касательная) 112: Найдите sin75 ,. 3 (тета) = загар (тета), тета =? 148: вычислить sin (2theta) + cos (theta) = 0, theta =? 149: решить sin (theta) + sin (3theta) = 0, theta =? 150 : Решить 2cos (3theta) = 1, theta =? 151: Решить sin (2theta) = 3cos (2theta), theta =? 152: Решить 2sin (x) tan (x) -tan (x) = 1-2sin (x ), x =?
Производные от тригонометрических функций
Основные тригонометрические функции включают следующие \ (6 \) функции: синус \ (\ left (\ sin x \ right), \) косинус \ (\ left (\ cos x \ right), \) касательная \ (\ left (\ tan x \ right), \) котангенс \ (\ left (\ cot x \ right), \) секанс \ (\ left (\ sec x \ right) \) и косеканс \ (\ left (\ csc x \ верно).2} x}}}
= {- \ frac {{\ cos x}} {{\ sin x}} \ cdot \ frac {1} {{\ sin x}}}
= {- \ cot x \ csc x.}
\]
Таблица производных тригонометрических функций
В таблице ниже приведены производные от \ (6 \) основных тригонометрических функций:
В приведенных ниже примерах найдите производную заданной функции. \ prime} = {1 \ cdot \ sin x + x \ cdot \ cos x + \ left ({- \ sin x} \ right)} = {\ cancel {\ sin x} + x \ cos x — \ cancel { \ грех х}} = {х \ соз х.} \]
Вертикальный сдвиг синусоидальной диаграммы
Craphil’l? Три? Fundions: Sine и Cosine Определите части каждого уравнения и опишите преобразование. Затем нарисуйте график функции. кричать каждое преобразование. amp: период: фазовый сдвиг: вертикальный сдвиг: преобразования: amp: период: фазовый сдвиг: вертикальный сдвиг: преобразования: sin amp: период: фазовый сдвиг: вертикальный сдвиг:
Нарисуйте одну полную кривую следующего на представленных графиках: l . y = 4sin (x) +2 3. y = sin x + — Вертикальное и горизонтальное смещение триггерных графиков 2.y = -cos (x) —3 600 60 2 4. Укажите диапазон каждой из следующих синусоидальных функций в форме интервала. (c) y = 22sin (x) +30 5.
y = A sin (Bx C) + D. Эти значения можно найти, используя рисунок 4.77. Начнем с D. Чтобы найти D, мы используем вертикальный сдвиг. Поскольку глубина воды колеблется от минимум 5 футов до максимум 13 футов, кривая колеблется около среднего значения, 9 футов. Таким образом, D = 9, что ЕСТЬ вертикальный сдвиг. На максимальной глубине вода составляет 4 фута выше 9 футов.
период и вертикальный сдвиг исходного графика.= −sin (1 3) −2 Амплитуда: Частота: Период: Вертикальный сдвиг: 6. Для данного уравнения найдите амплитуду, частоту, период и вертикальный сдвиг исходного графика. = −2cos (2𝜃) +6 Амплитуда: Частота: Период: Вертикальный сдвиг: Вместе: 7.
Раздел 4.4 Таблица преобразований синуса и косинуса Определите для каждого из них амплитуду, период, частоту, фазовый сдвиг и вертикальный сдвиг. Опишите преобразования, необходимые для получения триггерной функции, начиная с родительской функции.1. y = 2 sin 3x 2. y = -sin (x — π) 3. y = 3 cos 4x 4. y = 3 sin 6x — 3 5. y = -cos 2x — 5 6.
Графики синуса и Косинусные функции. Опишите, как связаны графики f (x) и g (x). Затем найдите амплитуду g (x) и нарисуйте два периода обеих функций на одних и тех же осях координат. Укажите амплитуду, период, частоту, фазовый и вертикальный сдвиг каждого из них.
Графические функции синуса и косинуса. Опишите, как связаны графики f (x) и g (x). Затем найдите амплитуду g (x) и нарисуйте два периода обеих функций на одних и тех же осях координат.Укажите амплитуду, период, частоту, фазовый и вертикальный сдвиг каждого из них.
График синуса и косинуса с вертикальным сдвигом. Рабочий лист
Ползунки изменяют параметры a, b, h и k в тригонометрических функциях y = a sin [b (x — h¹)] + d и y = a cos [b ( х — h¹)] + d. Выберите функцию синуса или косинуса, нажав соответствующую кнопку. Перетащите ползунок, чтобы изменить значение параметра.
Графики y A sin k и y A cos k показаны ниже. Вы можете использовать родительский график функций синуса и косинуса, а также амплитуды и периода для построения графиков y A sin k и y A cos k.Укажите амплитуду и период функции y 1 2 sin 4. Затем изобразите функцию. Поскольку A 1 2, амплитуда равна 1 2 или 1 2
Рабочий лист графиков родительских функций
Функции синуса и косинуса имеют несколько отличительных характеристик: Они являются периодическими функциями с периодом 2π.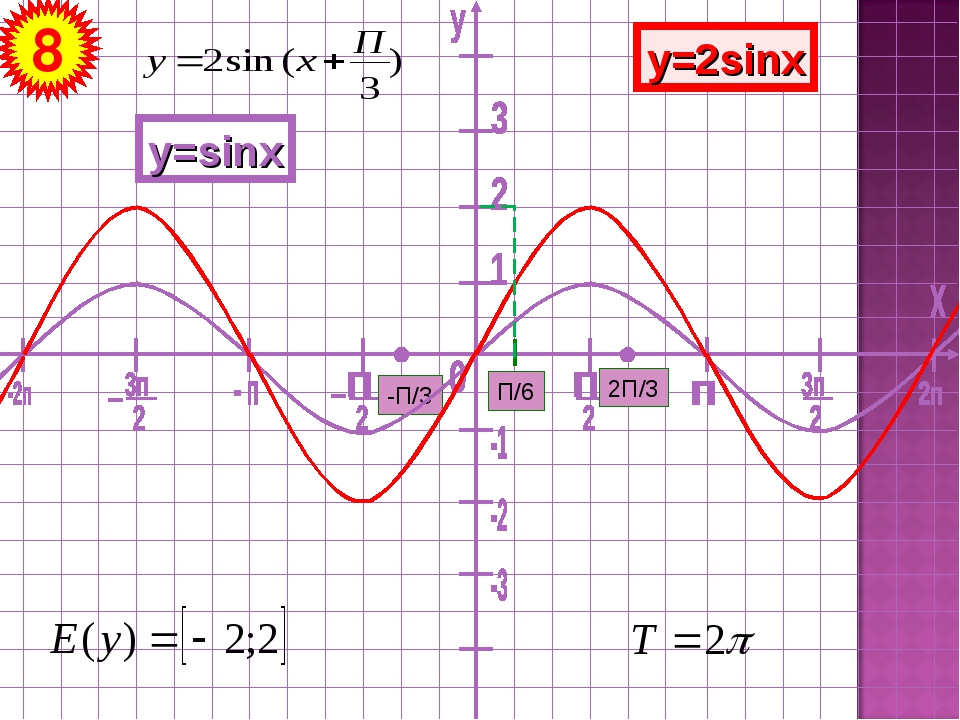 Область каждой функции — Шаг 5. D = 3, поэтому средняя линия равна y = 3, а вертикальный сдвиг — 3. Поскольку A отрицательно, график функции косинуса отражен относительно оси x.
При построении графика преобразованной функции синуса или косинуса выполните следующие действия: 1. Нарисуйте базовую функцию. 2. Примените вертикальное растяжение или сжатие для достижения желаемой амплитуды. 3. Примените вертикальный сдвиг. Используйте горизонтальную справочную линию, чтобы помочь вам. 4. Примените горизонтальную растяжку или сжатие, чтобы достичь желаемого периода. 5. Примените фазовый сдвиг.
Если смотреть на фазовый сдвиг, + будет двигаться влево — будет двигаться вправо, ноя 116: 27 PM 1. Напишите уравнение синусоидальной функции с амплитудой 4, периодом π, фазовым сдвигом -π / 8 и вертикальным сдвиг 6.2. Напишите уравнение функции косинуса с амплитудой 5, периодом 4π, фазовым сдвигом -π и вертикальным сдвигом -2.
Тригонометрия (10-е издание) отвечает на главу 4 — Графики круговых функций — Раздел 4.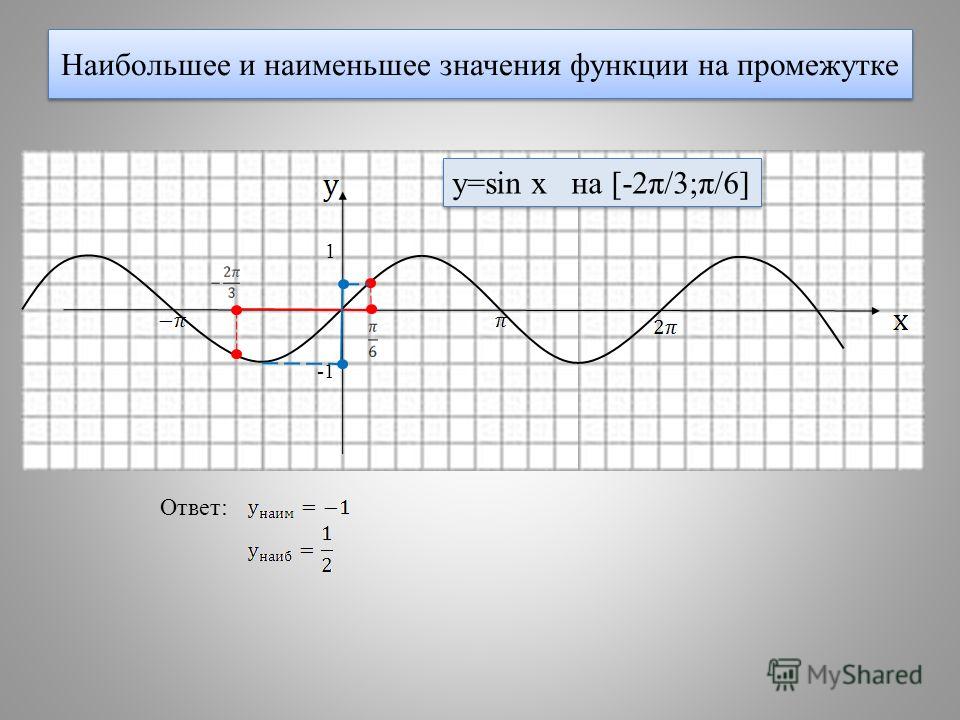 2. Переводы графиков функций синуса и косинуса — 4.2 Упражнения — Page 156 31 включая пошаговую работу, написанную такими членами сообщества, как вы. Авторы учебника: Лиал, Маргарет Л .; Хорнсби, Джон; Шнайдер, Дэвид I .; Дэниэлс, Калли, ISBN-10: 0321671775, ISBN-13: 978-0-32167-177-6…
Графическое изображение функций синуса и косинуса Преобразования функций синуса и косинуса Синусоида — это преобразование графика функции синуса. Общая форма синусоидальных функций синуса и косинуса: y = a sin (bx + c) + d или y = a cos (bx + c) + d. Графики
задач тригонометрических тождеств с решениями pdf
Обратные тригонометрические функции: • Области тригонометрических функций ограничены так, что они становятся взаимно однозначными, и их обратные могут быть определены.• Поскольку определение обратной функции говорит, что -f 1 (x) = y => f (y) = x У нас есть обратная синусоидальная функция, -sin 1x = y — π => sin y = x и π / 2 <= y <= / 2
Precalculus: An Investigation of Functions — бесплатный открытый учебник, охватывающий последовательность двух четвертей перед исчислением, включая тригонометрию. Первая часть книги посвящена исследованию функций, изучению графического поведения, интерпретации и решений задач, включающих линейные, полиномиальные, рациональные, экспоненциальные и…
функций. Мы также тщательно определяем соответствующие однозначные главные значения обратных тригонометрических и гиперболических функций, следуя соглашениям Абрамовица и Стегуна (см. Ссылку 1). 1. Обратные тригонометрические функции: arctan и arccot Мы начинаем с изучения решения уравнения z = tanw = sinw cosw = 1 i eiw …
5 января 2019 г. · 4 Trig Excellent Страница рабочего листа Parabola Загрузить Pdf с 4 из таблицы доказательств тригонометрической идентичности с ответами, источник: glasgowmajorevents.com У вас есть все материалы. Бумага — не редкость в компаниях, когда они пытаются найти лекарство и должны получить все возможные перспективы и доступные данные.
Тригонометрические интегралы В этом разделе мы используем тригонометрические тождества для интегрирования определенных комбинаций тригонометрических функций.
No related posts.