Mathway | Популярные задачи
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |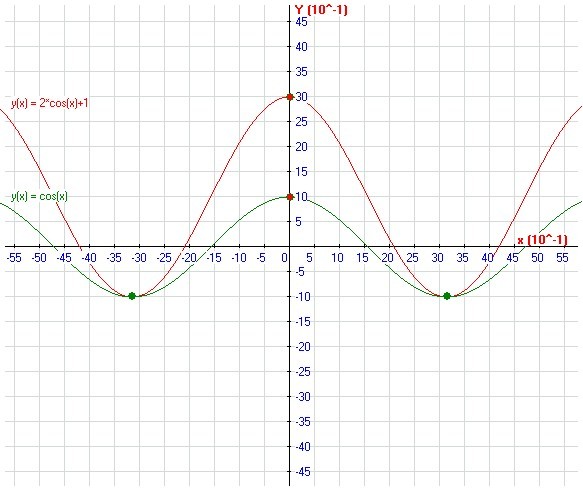
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |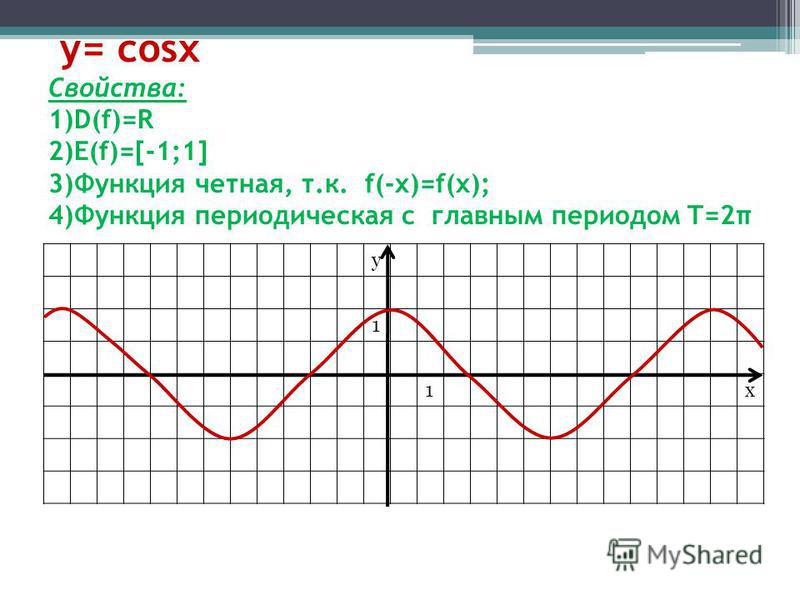
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град. ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Найдите нули функции:1) 1/2 cos x; 2) y=5 sin x. — Учеба и наука
Лучший ответ по мнению автора | |||
| |||||||||||||||||
05.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Отрезок длиной 13 см не пересекает плоскость.
Концы отрезка удалены от плоскости на 2 и 7 см. Найдите длину проекции отрезка на плоскость.
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81%
Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площад
Решено
С помощью циркуля и линейки постройте угол 150’
Пользуйтесь нашим приложением
3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 922017-2018 学年 赤峰 市 松山区 高 一 一 （）） 期末 数学 试卷 （） 含 详细 _ _ 文库 文库
《2017-2018 学年 赤峰 市 高 （上） （）） 详细 解答》 由 会员 分享 ， 可 在线 阅读 ， 多 相关 《《2017-2018 学年 赤峰 市 松山区 一 （（）） 期末 数学在 七七 文库 搜索。。
1、1 (5 分） 在 ABCD 中 ， 等于 等于 （（（（（（（（abcd2 (5 分) 2018 角 象限 是 是 （（第一 b 第二 象限 c 第三 d象限 3 (5 分) 设函数 f (x） sin (2x) ， xr ， 则 f (x) 是 （（） 最 小 周期 为 的 奇函数 b 最 正 周期 为 的 奇函数 c 最 小 周期函数 d 最 正 周期 为 的 偶函数 4 (5 分） 已 知 ， ， ， 知 为 偶函数 4 (5 分） 已 知 ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， ， 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知 知.
分）函数yx2sinx，x，的大致图象是（）ABCD8（5分）已知sin（+），则sin（2）的值是（）ABCD9（5 分） 已 知 abc 中 ， sina ， cosb ， 则 的 值 等于 （（） 或 或 或 bcd 或
2、10 (5 分） 已 知函数 f （） ， 又 为 锐角 两 （（（（（（（（（（（（ ）Af（sin）f（cos）Bf（sin）f（cos）Cf（sin）f（sin）Df（cos）f（cos）11（5分）在平行四边形ABCD中，AC与BD交O，E是线段OD的中点，AE的延长线与CD交于点F若，则（）A+B+C+D+12（5分）定义运算：a1a4a2a3，将函数f（f（f（f（ 0) 的 向 左平 移 个 单位 ， 所得 图象 对应 的 为 偶函数 ， 则 的 最 小值 是 （） 的 为 偶函数 ， 的 最 小值 是 是）） 二 、 偶函数 题 ： 最 小值 是 （）） 二 填 空 题 ： 小值 题 共 4 小 题 ， 小 题 5 分. 5分）已知向量，不共线，若向量k+与+2平行，则实数k 14（5分）已知f（x），则f（6）+f（39） 1 90分）已知函数f（x）cos（x+）（0）在区间上的值域为1，则的取值范围为 16（5分）已知函数f（s|+x）|s|+x） ， 有 以下 结论 ： ： f （x） 是 周期 函数 ， 且 小 正 周期 为 ； f (x） 的 称 轴 方程 为 为 ， ； f (x） 的 称 轴 方程 为 为 ， ； f （x） 在 （（） 上 增函数 方程 f （（区间 （） 增函数 ； 方程 f x) 在 区间 ， 0 上 有 6 个根 其中 正确 的 序号 是 （出 所有 正确 答案） 三 、 解答 ： ： 解答应 必要 的 文字 说明 证明 过程 或 演算 .17 （10 分 f （（证明 或 演算. ）（1）化简f（）；（2）若（0，），且sin（），求f（）的值18（12分）已知函数f（x（sin（1+xsinxco ）求函数f（x）的最小正周期和最大值；（2
4 、) 求函数 f (x)求f（x）的解析式；（2）设g（x）+lg，求g（x）的定义域20（12分）已知函数f（x）asinxcosxacos2x+a+b（a0（a0） ）若xR，求函数f（x）图象的对称轴方程；（2）若f（x）的最小值是2，最大值是4，求实称数a（2）b）函数f（x）2cos（x+）（0，0）为奇函数，且函数yf（x）图象的两相邻对称轴间的距离为（2３弉（f（1３函）f（ x ， 时 方程 f (x） k 有 两 个 不同 实根 实根 求实数 求实数 k 的 范围 范围 22 (12 分） 已 知函数 f (x) cos2x+4
5 、 sinxsin2 （) (1 ) 设 0 ， 若函数 f (x） 在 区间 ， 上 是 增函数 ， 在 区间 0 ， 上 恰好 取得 次 最 大 值 ， 求 取值 范围 ； （2)点 的 标变 为 原来 的 倍 （（不 变）） 再 将 向 右平 移 个 单位 ， 所 得到 图象 对应 的 函数 为 为 （x） ， 对于 的 的 x ， 式 | g （X） m | 2 恒 成立 ， 求实数 m 的 取值 范围 2017-2018 学年 赤峰 二 中 高 一 一 上） 期末 数学 试卷 （）） 答案 与 试题 解析 一小 题 ， 小 题 5 分.
，两对对边平行且相等，以一对对边所在的线段构成向
6 、 量 ， 得到 的 要么 相 等 ， 要么 是 相反 向量 ， 根据 本题所 给 的 个 向量 来 ， 它们 一 对 相反 相反 向量 ， 为 零向量 ， 得到 ： Abcd 中 与 是 一 对 相反 向量 ，+， 故选 ： ： 【】 本 题 考查向量 的 加减 运算 ， 一 个 基础 ， 用 一 向量 来 表示 一 个 向量 ， 以后 过程 见到 的 来 表示 一 向量 是 解题 常 的 的 表示 一 一 的 的， 向量 加减 运 算是 用向量 解决 问题 的 基础 2 (5 分）） 角 所在 象限 是 是 是 是 （第一 象限 B 第二 象限 C 第三 D 第四 象 【分析】 由 2018218+5360 ， 知 限 分析】 由 由 由 由 由 由 由 由 由 由 由 由与 2018 角 相同 的 角 是 是 218 角 ， 由 此 能够 知道 知道 角 所在 的 象限 【解答】 解 ： 2018218+5360 ， 与 ： ： 相同 的 角 是 218 角 是 ： idp C 【点评 本 题 考查 考查
7 、 的 概念 ， 解题 时 要 熟练 掌握 象 限角 判断 方法 ， 是 基础 3 （5 分 设函数 f （x） sin （2x) ， ， 则 f f （X） 是 （） 最 小 正 周期 为 的 奇函数 b 最 正 周期 为 奇函数 奇函数 c 最 小 周期 为 的 偶函数 d 最 正 周期 的 偶函数 【分析 直接 直接 诱导 公式 简函数 表达式 为 偶函数 【】 直接 诱导 公式 简函数 表达式 为 【分析 直接 利用 公式 化 的， 然后 函数 的 奇偶性 ， 求出函数 的 周期 即 可 【解答】 解 ： 函数 f (x） sin (2x） cos2x ， 函数 是 偶函数 函数 的 是 t 故选 ： C 【】 本 ， 函数考查 三角函数 周期性 以及 求法 ， 函数 的 奇偶性 的 应用 ， 考查 能力 能力 4 (5 分） 已 知 ， ， 3sin22cos ， cos （） （）） 【分析】 由 求 得 得 的 值 ， ， ， ， ， ， ， ， ，再根据cos（）cos求得结果【解答】解：
8 、 ， 3sin22cos ， sin ， coscos (） （）） 故选 故选 ： ： 【点评】 题 主要 考查 二 公式 、 诱导 公式 的 应用 ， 属于 题 5 （5 分 若 则 则 则 则 （（（（（））） （ 【分析 利用 二 倍 角 的 正弦 函数 公式 ， 同角 三角函数 关系 式 化 简所求 ， 结合 知即 可 计算 【解答】 解 ： ， ， ： 计算 点评】 题 解 考查 ， 二 ： ： 点评】 题 考查 了 二 二 二 了 考查 主要 主要 主要 主要 主要 主要 主要 主要 主要 主要 主要 主要 ：倍角 的 函数 公式 ， 同角 三角函数 基本 关系式 在 三角函数 化 简求值 的 应用 ， 属于 基础 题 6 (5 分） 的 值 是 （（【【】 首先 把 10 角 3020 引出 特殊 特殊 特殊角 ， 两 角 和 公式 进一步化简 ， 最后 约 分 得出 【解答】 解 ： 原式 ： ： C 【点评】 题 主要 考查 了 两 角 的 和 差 注意 利用 特殊 角 角 考查 了 两 的 和 与 注意 利用 特殊 角 70907
9、（5分）函数yx2sinx，x，的大致图象是（）ABCD【分析】f（x）x+2sinx（x2sinx）f（x），所以函数为奇函数，故函数的图象关于原 点 称 ， 只 有 有 CD 适合 由于 由于 Cd 图象 中 值点 不同 ， 可 再 求函数 的 极值点 选择 【解答】 解 ： ： 可 再 求函数 极值点 选择 答案 解答】 解 ： ： （再 求函数 的 极值点 答案 【解答】 ： ： ： （再 求函数 极值点 选择 答案 解答】 解 ： ： ： （求函数 的 极值点 选择 【解答】 ： ： ： （（求函数 的 极值点 答案 【解答】 ： ： ： （（求函数 的 极值点奇函 数 ， 的 图象 关于 原点 对 称 ， 只 有 有 Cd 适合 ， y12cosx ， 由 y0 解 得 ， 当 x 时 ， 函数取 值 ， 故 d 适合 ， ： h ： 点评】 题 研究 函数奇偶性 ， 利用 研究 函数 的 极值点 ， 属于 基本 题 8 （5 分） 知 知 sin (+) грех (2) грех2 (9)0907
10 、+) 的 值 【解答】 解 ： sin (+) ， sin (2) sin2 (+) sin2 (+)+cos2 (+）） 、 、 、 、 、 、 、 、 、 、 公式 公式 公式 公式 公式 公式 公式 公式 公式 公式 公式 公式 公式 公式 公式 公式 公式 公式二 倍角 的 应用 ， 属于 基础 题 9 (5 分） 已 知 知 abc 中 ， sina ， cosb ， 则 的 值 等于 等于 （） 或 或 或 【分析】 由 由 的 及 及 及 三角形 ， 同角 同角 同角 同角 同角 同角 同角 利用 利用 同角三角函数 间 的 关系 求出 求出 sinb 的 值 ， 由 sinb 大于 sina ， 得到 为 锐角 ， 由 sina 的 值求出 的 值 值 将 将 后 利用 角 和 与 差 余弦函数 公式化简 ， 将 各自 利用 两 和 差 余弦函数 公式化简 ， 将 各自 各自 各自 各自 各自 ， ， ， 各自 各自的 值代入 计算 可求 出值 【解答】 解 ： 在 abc 中 ， sina ， cosb ， sinbsina ， a 为 锐角 ， cosa ， 则 Cosccos (a+b is Cosacos
11 、 B+Sinasinb+： obrycos
点评】 题 考查 了 两 角 和 与 差 的 余弦函数 公式 ， 掌握 公式 是 解本 的 的 关键 关键 （余弦函数 ， 熟练 掌握 是 解本 题 的 关键 10 (5 分） 知函数 知函数 f (x） 又 ， 为 锐角 形 两 锐角 （（） （（又 为 三角 形 锐角 则 （） （（， 为 三角 两) F (cos) bf (sin) f (cos) cf (sin) f (sin) df (cos) f (cos） 【分析】 判断 函数 f (x） 的 单调性 由 ， 为 三角形 的 两 两 两 两 两 两 两 两 两 两 两 两 两 两 两个锐角 ， 可 得+， 进而 ， 且 ， 均 为 锐角 ， 正 弦函数 的 单调性 和 诱导 公式 5 ， 可 结论 【解答 解 ： 作出函数 f （x） 的 ， 则 函数 单调 递减函数 递减函数 ： （图象 ， 则 函数 单调 递减函数 递减函数 ： ： ， 为 三角形 的 两 个 锐角 ， ，+， 且 ， 均 锐角 ， ， Sinsin () cos ， Coscos (（） sin ， f (sin） f (cos） ： ： ： 【】 本 题 考查函 考查函 考查函 12 、 的 大小 比较 ， 根据 数形 结合 判断 函数 的 单调性 ， 结合 三角函数 的 公式 进行 化简 解决 本 题 的 关键 结合 三角函数 的 诱导 进行 化简 是 本 题 的 关键 11 （5 分） 在 四边 形 形 形 中 ， 与 交于 点 分 在O，E是线段OD的中点，AE的延长线与CD交于点F若，则（）A+B+C+D+【分析】根据DEFBEA得对应边成毰侔，丗得，丗做 fg 平行 bd 交 ac 于点 g ， 使用 已 知向量 表示 出 要求 向量 ， 即 可 得出 结论 解答】 ： ： defbea ， df ： Bade ： be1 ： 3 ； fg 平行 bd 交 a g ， bade.
Fg ： do2 ： 3 ， cg ： CO2 ： 3 ，+，+， ： ： D 【点评】 题 考查向量 的 线性 运算 及 其 几何 意义 考查 学生 计算 能力 能力 灵活 运用 题目 的 是 的 关键 的 能力 ， 运用 的 条件 解题 的 关键 关键 灵活 灵活 的 解题 解题， 属于 中档 题 12 (5 分
13 、） 运算 ： ： a1a4a2a3 ， 将函数 f (x） （） 的 向 左平 移 个 单位 所得 图象 对应 的 函数 偶函数 的 最 小 小 小 小 小 小 小 小 值 值 值是 （） abcd 【】 化函 数 数 f (x） 为 函数 ， 写 出 f （x） 图象 左平 移 个 单位 后 的 函数 y ， 由 y 为 偶函数 求出 的 最 小 【， 由 函数 偶函数 ， 求出 最 小 值 【【【的 的 的 对应 对应 的解答】 解 ： 函数 f (x) cosxsinx2cos (x+） （0) ， f (x） 的 图象 向 左平 个 单位 ， 所得 图象 对应 函数 为 y2cos (x+）+2cos （x ； 函数为 偶函数 ，+k ， kz ， 解 得 ， kz ； 当 k1 时 取得 最 小值 是 故选 ： b 【点评 本 题 考查 了 的 化简 与 平移 平移 应用 问题 ， 是 题 二 、 与 平移 的 问题 ， 基础 题 二 二 二 二 二 是 是填空题：本大题共4小题，每小题5分.13（5分）已知向量，不共线，若向量k
14 、+与 +2 平行 ， 则 实数 k 【】 利用 向量 线 定理 、 平面 向量 基本 定理 可 得出 【解答 ： ： 、 平面 向量 定理 即 可 【解答】 ： ： 、 平面 基本 定理 即 得出 【解答 ： ： 向量 k+与 +2 ） ， ， 不 共 线 ， 解 得 k 故 答案 为 ： ： 点评】 题 考查 了 向量 线 线 定理 平面 向量 基本 ， 题 考查 推理 能力 与 能力 ， 属于 题 题 题 （分 已 知 与 计算 ， 中档 题 （（） 知（X） 则 f ()+f （（）） 2 【分析】 分段函数 的 函数 值 ， 先 判断 自 变量 什么 范围 范围 然后 代入 的 解析式 进行 【【】 ： ： 0f （（（相应 的 进行 【 （）x0时，f（x）f（x1）1f（）f（1）1f（）1f（）2sin（）22f（）+f（）2故答案为：2【点评】本题䦘丘段函数 的 值 ， 要 注意 判断 自 变量 的 范围 才 求解 ， 同时 考查 了 能力 能力 ， 属于
15 、 题 15 （5 分 已 知函数 f (x） cos （x+） （0））） 在 已区间 上 值域 为 为 1 ， 则 的 取值 范围 为 ， 1 【】 求出 x0 ， 时 x+的 范围 ， 根据 f (x) 的 ， 结合 余弦函数 图象 和 性质 的 取值 取值 取值 取值 值域 ， 余弦函数 图象 和 性质 的 的 的 的范围 【解答】 ： ： 在 区间 0 ， 上 ， x+，+， f (x） Cos （x+） 的 为 1 ， 由 的 图象知 ，+， 解 得 ， 1 故 ： ： ， 1 【点评】 题 考查 了 余弦函数 的 图象 和 性质 的 应用 问题 ， 基础 题 题 16 (5 分） 已 知函数 f （x） | sinx |+| cosx | ， 有 相关 ： qti周期 函数 ， 最 小 正 周期 为 ； f (x) 的 称 轴 方程 为 x ， kz ； f (x） 在 区间 （（） 为 增函数 方程 方程 f (x) 在 区间 0 上 有 个根 增函数其中正确的序号是（写出所有正确答案）【分
16 、】 首先 把 三角函数 变形成 f （x 形式 ， 进一步 的 的 最 小 周期 ， 确定 最 值 对 称 方程 方程 ， 作出 ， 即 判断 判断 结论 【： idp函数 f (x) | sinx |+| cosx | ， 最 小 正 周期 t 不 ； ； sin2x1 或 0 时 ， 2xk+或 k ， x+或 ， kz 是 的 对 称轴 所以 正确 ； ； （） 函数 不 是 对 ， 正确 ； （（函数 不 是单调函数 ， 不 正确 ； 函数 的 周期 为 ， 函数 的 最 值 为 ， 小值 为 为 1 ， 方程 方程 f (x） 在 ， 0 上 有 6 个根 有 6 个根 ， ； 为 ： ： ： 上 有 有 个根 ： 【点评 本 题 主要 考查 了 三角函数恒 等 变换 应用 应用 ， 了 三角 函数 周期性 周期性 及 求 法函数 的 单调性 函数 的 对称性 ， 命题 的 真假 的 与 应用 ， 属于 知识 考查 考查 的 的 判断 应用 ， 基本 的 考查 考查三 、 解答 ： ： 解答应 写出 的 文字 文字 说明
17 、、 过程 或 演算 步骤.