404 — Страница не найдена
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||
§3. Логико-дидактический анализ содержания темы
Анализ теоретического материала
В учебнике Алгебра и начала анализа: Учеб. для 10 кл. общеобразоват. учреждений/Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров и др. — М.: Просвещение, 2003.
тема «Функция y=cos x, ее свойства и график» представлена в последней главе после темы «Функция y=sin x, ее свойства и график».Основными дидактическими единицами темы «Функция y=cos x, ее свойства и график»:
— определения: периодическая функция
-тригонометрические неравенства
-функции арксинус, арккосинус, арктангенс, арккотангенс
-свойства функций (их области определения, множества значений, четность/нечетность функций, промежутки монотонности, ограниченность, наибольшие и наименьшие значения, непрерывность и их периодичность) : y = sin x, y = cos x, y = tg x, y = ctg x, y = arcsin x, y = arccos x, y = arctg x, y = arcctg x
—
графики: y
= sin
x,
y
= cos
x,
y
= tg
x,
y
= ctg
x,
y
= arcsin
x,
y
= arccos
x,
y
= arctg
x,
y
= arcctg
x.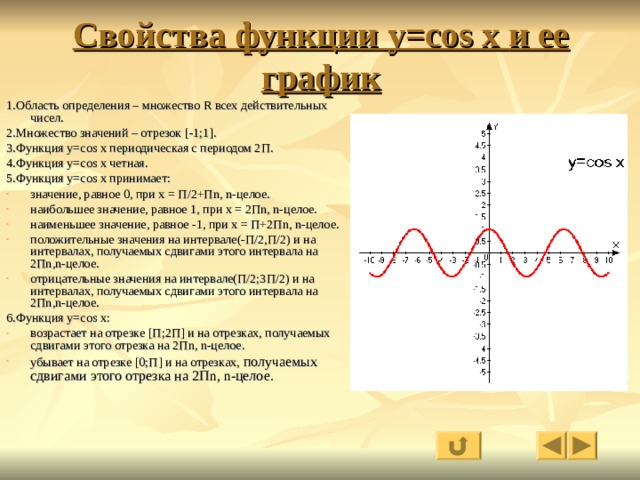
Так как начало тригонометрии, а именно тригонометрические уравнения и неравенства, изучалось в 9 классе, то в 10 вводится понятие тригонометрической функции. Способом получения новых знания может быть самостоятельное «открытие» учениками: нахождение области определения и множества значений функций y= sin x, y = cos x, y = tg x, y = ctg x; проведение доказательства четности/нечетности функции; с помощью учителя воспроизведение свойств функции y = cosx аналогичных свойствам функции y = sinx.
Автор сначала в первом параграфе главы вводит периодичность тригонометрических функций, в нем автор вводит определение периодичной функции. Затем вводит функцию y = sin x, отмечает ее свойства и график. Потом вводится функция y =cos x на основе уже известной функции y = sinx, отмечаются ее свойства, и строится график.
Отдельны
параграф отводиться тригонометрическим
неравенствам, при решении которых
используются свойства тригонометрических
функций, которые были пройдены, и их
графики.
После этого, необходимо отметить, что в учебнике Ш.А.Алимов в теме тригонометрические функции уделяется внимание обратным тригонометрическим функциям: y = arcsin x, y = arcos x, y = arctg x, y = arcctg x, что нет у А.Г.Мордковича, их свойствам и графикам. На них и заканчивается изучение данной главы.
Основные цели – ввести: понятие тригонометрической функции, так как в учебнике не дается четкой формулировки понятия, но вместо определения дается словесное описание; понятие области определения и множества значений тригонометрический функций; свойств тригонометрических функций.
Анализ задачного материала
При изучение темы «Функция y=cos x, ее свойства и график» можно выделить следующие группы задач:
Работа с возрастанием и убыванием функции: №959, №960, №961
Ключевая задача №959.
Решение:
1)[3
;4
]-возрастает,
2)[-2
;-
]-убывает,
3)[2
;
]-убывает,
4)[
;
]-возрастает,
5)[1;3]-убывает, 6)[-2;-1]-возрастает.
Выяснить при каких значениях х, принадлежащих отрезку, функция принимает значения: №958(она же и ключевая)
Решение:
1)при ; 1 при 0,2 ; -1 при
2)положительные значения при
3)отрицательные значения при
Найти все решения неравенства, принадлежащие интервалу: №962, №966
Ключевая задача: №962
Приведу решение одного примера: 1)cosx
График функции y =cos x лежит не ниже графика у= при . Значит решением неравенства будет .
Найти область определения функции: №963, №969-970
Ключевая задача: №963
Найти множество значений функции: №964, №968, №971
Ключевая задача: №968
Решение:
1)Так
как cos
x
убывает ,
то ,
т. е. -1
е. -1
Построить график: №967, №972
Ключевая задача: №967
Решение:
1)у=1+cosx
-область определения:
-множество значений:
-периодическая с периодом 2
-четная
-принимает наименьшее значение, равное 0, при , принимает наибольшее значение, равное 2, при , не отрицательная.
-возрастает при
убывает при
по этим свойствам строим график.
Выражая синус через косинус по формулам приведения, сравнить числа: №965(она же и ключевая).
Решение:
Так как убывает на и , то , т.е.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | арктан(-1) | ||
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.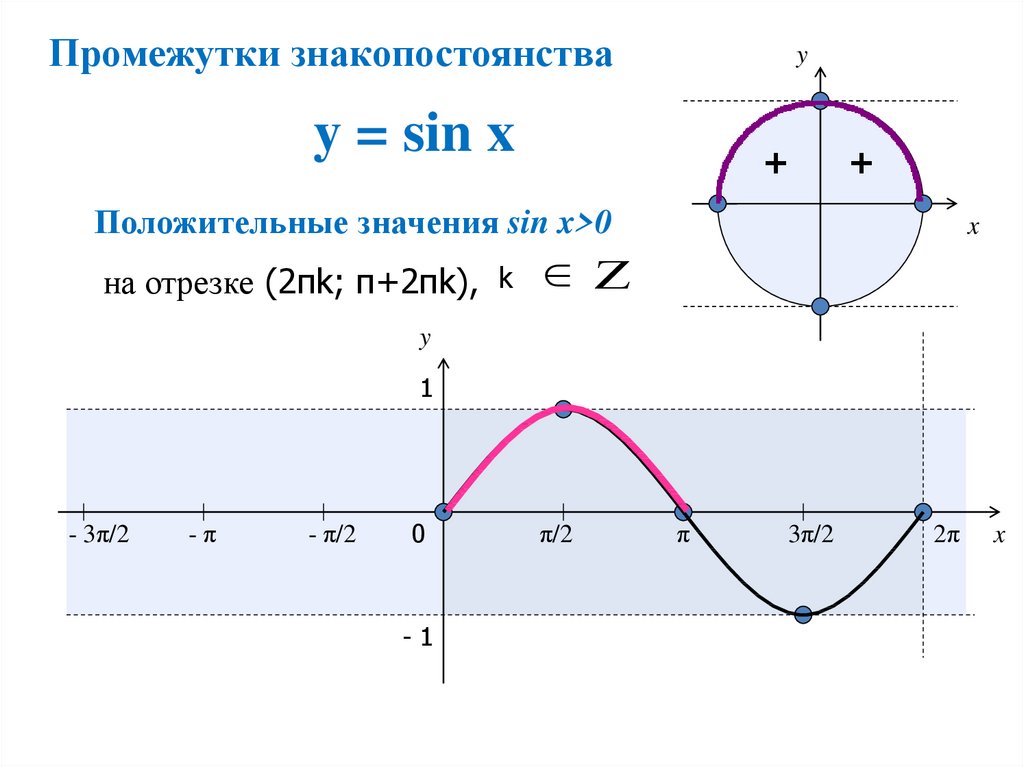 |

 by/algebra/funkcii/funkcija-ycosx] не найдена.
by/algebra/funkcii/funkcija-ycosx] не найдена.
 05.13
05.13  by 2013-2016
by 2013-2016