Построить график функции y 2×2 5x 3. Строим график функций онлайн
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком.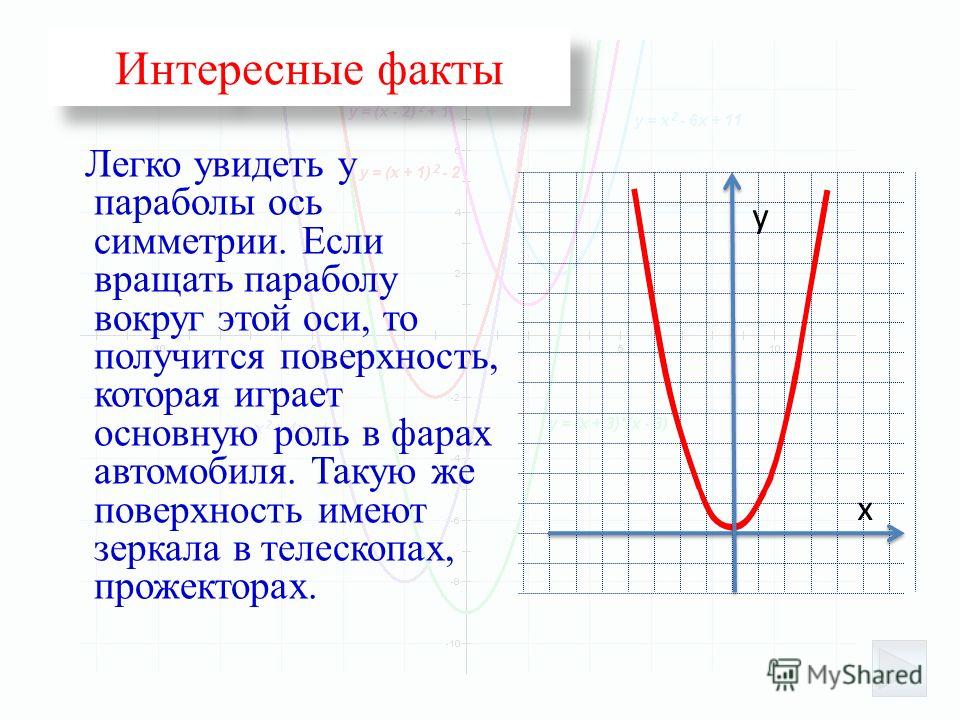
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .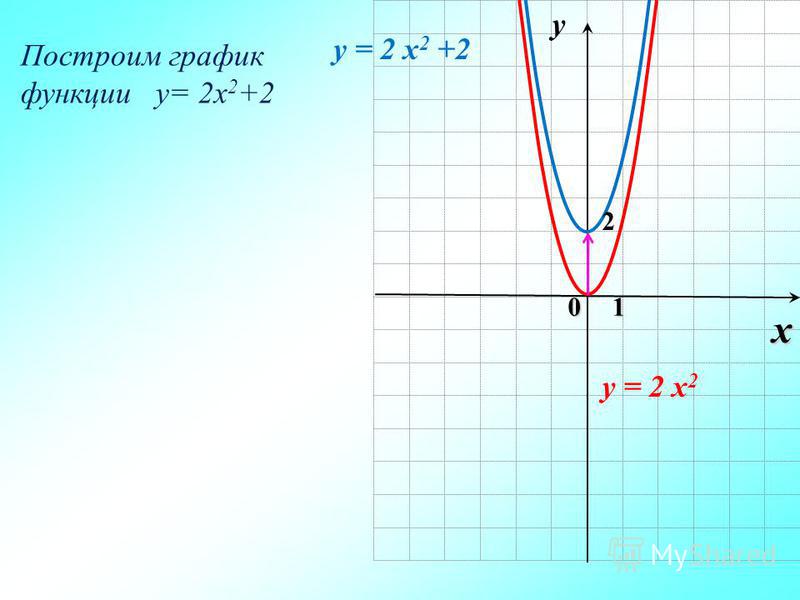
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).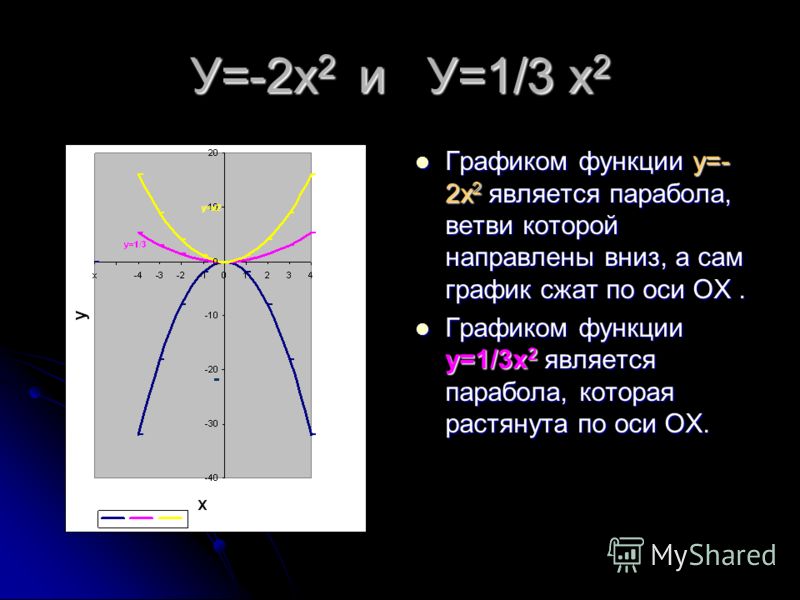
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Как найти ординату вершины параболы — Dudom
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
- 1 — первый корень;
- 5 — второй корень.
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
- Записываем производную и приравниваем к нулю.
f'(x) = (4x²+16x-17)’ = 8x+16 =0
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
| X | 5,5 |
| Y |
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Видео
Это видео поможет вам научиться находить вершину параболы
Парабола – это геометрическое множество точек, равноудалённых от точки F, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$. 2 – 5 cdot 2.5 + 7$
2 – 5 cdot 2.5 + 7$
Вершина кубической параболы
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Чтобы найти вершины (точки локальных минимумов и максимумов) кубической параболы, необходимо найти её производную, приравнять её к нулю и затем вычислить $x$ и $y$.
Если же необходимо найти точку перегиба кубической параболы, необходимо найти вторую производную и также приравнять её к нулю.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Как найти координаты вершины параболы? Для этого достаточно запомнить всего одну короткую формулу (она же — корень квадратного уравнения для случая, если дискриминант равен нулю).
I. Абсциссу координаты вершины параболы — графика квадратичной функции y=ax²+bx+c, где a, b, c — числа, причем a≠0, находят по формуле
Для нахождения ординаты достаточно подставить в формулу функции xₒ вместо каждого x:
Можно также найти ординату вершины параболы, воспользовавшись формулой
(минус дискриминант, деленный на 4a).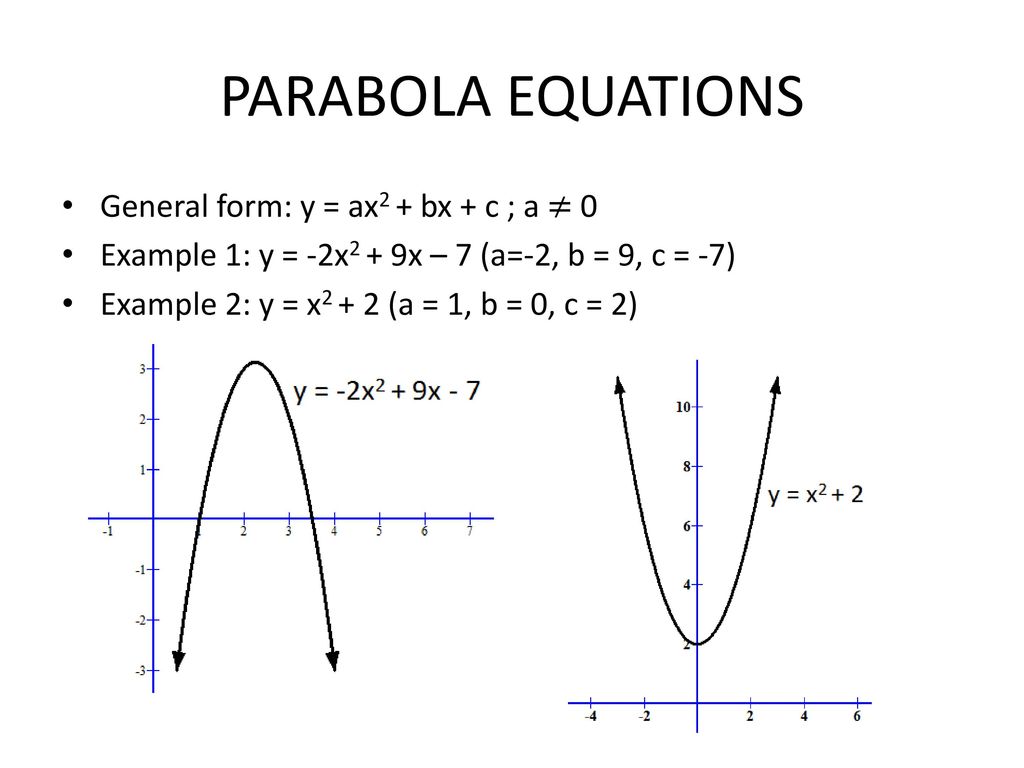
Найти координаты вершины параболы:
Вершина параболы y=x²-7x+3 — точка (3,5; -9,25).
Вершиной параболы y= -x²+8x+2 является точка (4; 18).
(-2; 8) — вершина параболы y= -3x²-12x-4.
Следовательно, (-2,5; 3,75) — вершина параболы y=0,2x²+x+5 .
II. Абсциссу вершины параболы можно также найти как среднее арифметическое между нулями функции (в том случае, если функция имеет нули):
Этим способом удобно находить вершину параболы, когда квадратичная функция задана в виде y=a(x-x1)(x-x2).
Найдём координаты вершины параболы y=5(x-1)(x+7). Ищем нули функции:
Точка (-3; -80) — вершина параболы y=5(x-1)(x+7).
III. Если функция задана в виде
то её вершина — точка ( xₒ; y ₒ ). Например, вершиной параболы
является точка (-3; -1).
2 комментария
При исследовании квадратичной функции, графиком которой является парабола, в одном из пунктов необходимо найти координаты вершины параболы. Как это сделать аналитически, используя заданное для параболы уравнение?
Как это сделать аналитически, используя заданное для параболы уравнение?
Надежда, в статье выше как раз описывается, как найти координаты вершины параболы. Абсциссу находят по формуле x0=-b/2a. Чтобы найти ординату, достаточно в формулу функции вместо каждого x подставить найденное значение x0 и вычислить.
Конспект обобщающего урока Квадратичная функция
Тема урока «Квадратичная функция, ее график и свойства».
Тип урока: Повторительно – обобщающий.
Цели урока: Обобщить и систематизировать основные знания, умения и навыки по теме «Квадратичная функция и её график», используя возможности ИКТ технологий и использовать эти знания для решения задач, входящих в раздел «Алгебра » ОГЭ .
Задачи урока:
Образовательные задачи:
1. Повторить изученный материал и устранить пробелы в знаниях.
2. Совершенствовать навыки построения графиков, исследования функций и умения переносить знания в новые условия.
Развивающие задачи:
1.Формировать умения сравнивать, обобщать, делать выводы;
2.Развивать у учащихся самостоятельность в мышлении и учебной деятельности;
Воспитательные задачи:
1.Воспитывать аккуратность в работе при построении графиков;
2.Стимулировать учащихся к самооценке своей образовательной деятельности;
3.Совершенствовать умения, навыки учащихся при работе в группе.
Здоровьесберегающие задачи:
1.Создать здоровьесберегающие моменты, направленные на укрепление глаз и улучшения мозгового кровообращения.
Оборудование урока:
Компьютеры и мультимедийный проектор
Интерактивные задания
Карточки с заданиями
Ход урока
1. Организационный момент.
Организационный момент.
2. Постановка целей урока.
3.Актуализация знаний учащихся .
1.Фронтальная работа с использованием интерактивной доски.
Слайд 2
Вспомним: Какой формулой задается квадратичная функция?
Как называются коэффициенты а,b,c в данной формуле?
Что является графиком функции?
Слайд 3
Среди данных графиков определите графики квадратичной функции и объясните,
почему вы так считаете.
Слайд 4
Как определить квадратичную функцию по формуле функции? Как найти коэффициенты данных функций?
Поставить проблемный вопрос: какую информацию можно получить о графике квадратичной функции, зная коэффициенты квадратного трёхчлена.
Слайд 5
Как связан коэффициент а с направлением ветвей параболы?
Слайд 6
Определите знак коэффициента а для данных функций
Слайд 7
При каком значении аргумента графики функций пересекают ось ординат?
Какой коэффициент квадратичной функции можно определить используя данный факт?
Слайд 8
Определите чему равен коэффициент с ?
Слайд 9
На интерактивной доске установите соответствие между знаками коэффициентов а и с с расположением графика функции на координатной плоскости.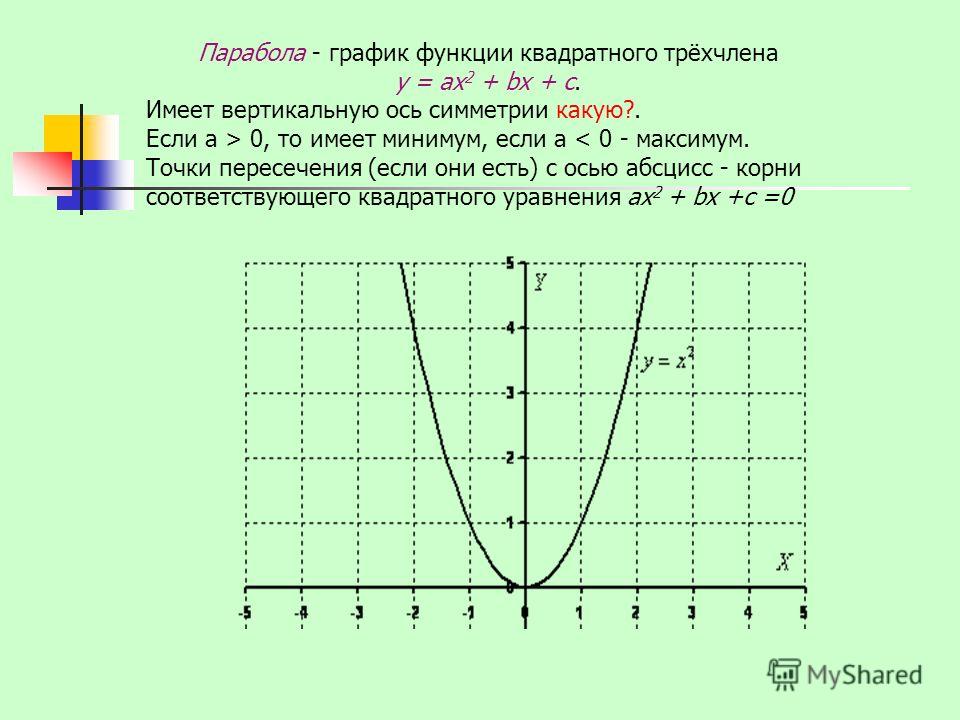
Слайд 10
Вспомним формулы для определения координат вершины параболы и ее оси симметрии.
Слайд 11
Определите координаты вершины парабол и назовите уравнения осей симметрии парабол.
Слайд 12
Какую информацию о графике квадратичной функции можно получить, вычислив дискриминант квадратного уравнения?
Слайд 13
Для каждого графика укажите соответствующие ему значения коэффициента a и дискриминанта D.
Какую еще дополнительную информацию по графику можно получить? Как с помощью графиков функции решить квадратное неравенство?
Слайд 14
При каких значениях х выполняется неравенство а) у 0; б) у 0?
Работа в группах по карточкам
1 задание Установите соответствие между графиками функций и формулами, которые их задают.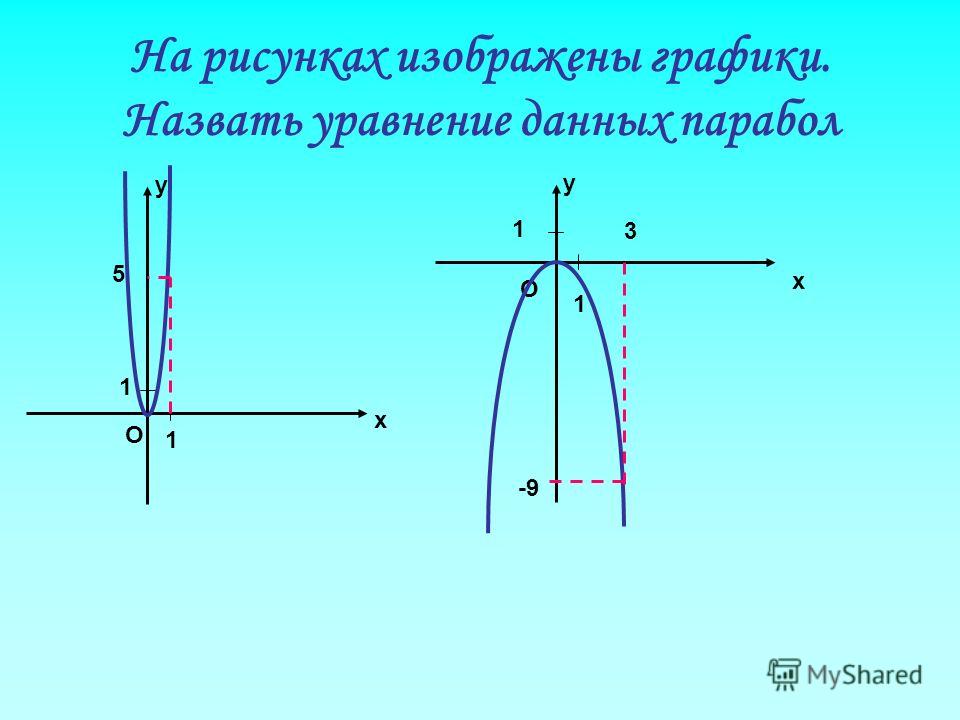 Запишите название функции и графика (Карточка 1)
Запишите название функции и графика (Карточка 1)
2 задание Установите соответствие между графиками функций и знаками коэффициентов a и c.(Карточка 2)
3 задание Установите соответствие между графиками функций и формулами, которые их задают (карточка 3)
Взаимопроверка по слайдам 15-17
Физкультурная минутка для глаз и для улучшения мозгового кровообращения.
Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5. Повторить 4-5 раз.
Крепко зажмурить глаза (считая до 3), открыть, посмотреть вдаль (считая до 5). Повторить 4-5 раз.
Исходное положение -сидя на стуле, 1-2-плавно наклонить голову назад, 3-4 голову наклонить вперед, плечи не поднимать. Повторить 4-6 раз. Темп медленный.
Теоретический зачёт в форме «Заполни пропуски».

Каждый ученик получает зачётный лист, содержащий десять основных теоретических положений темы. Ключевое слово или формула в каждом правиле заменено пропуском , который необходимо заполнить.
Вариант 1
1. График функции у = ах2 , при а_______ и____ координатных четвертях.
2. Ветви параболы у = ах2 +bх + с направлены вверх если а______
3. Абсцисса вершины параболы у = ах2 +bх + с равна_____
4. Квадратичная функция у = ах2 +bх + с убывает на промежутке _______при а0.
5. График функции у = ах2 +с, где с из графика функции у = ах2 параллельным переносом вдоль оси_ ____ на_ ____ единиц _ ______.
6. График функции у = а(х — с)2, где с может быть получен из графика функции у=ах2 параллельным переносом вдоль оси__ _______ на _ ____единиц __ _____ .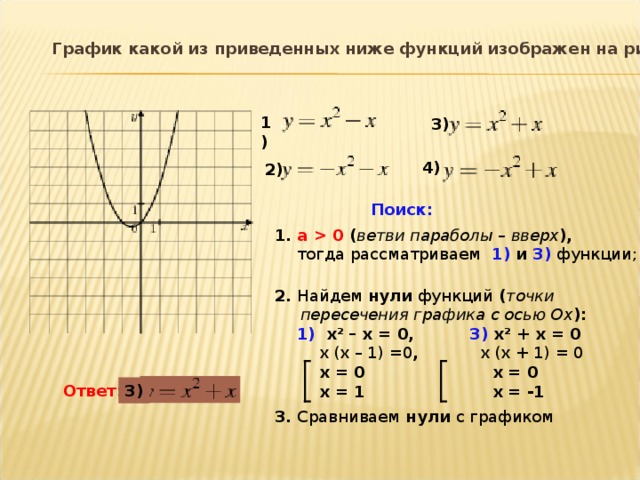
7. Если числа т и п являются корнями трёхчлена ах2 +bх + с , то его можно разложить на множители:
ах2 + bх + с =
8. Параболу y = х2 растянули в три раза от оси OХ, сместили вдоль оси OX вправо на 5 и вдоль OY вниз на 7. Получили график функции y = _______________
Вариант 2
1. График функции у = ах2 , при а0 расположен в _ __ и _____координатных четвертях
2. Ветви параболы у = ах2 +bх + с направлены вниз если а _____
3. Абсцисса вершины параболы у = ах2 + bх + с равна _____
4. Функция у = ах2 +bх + с возрастает на промежутке ____ при а
5. График функции у = ах2 +с, где с0, может быть получен из графика функции у = ах2 параллельным переносом вдоль оси __ ___на _ ____ единиц _ ____.
6. График функции у = а(х — с)2,где с0 может быть получен из графика функции у = ах2 параллельным переносом вдоль оси_ __ на __ ___ единиц __ ___.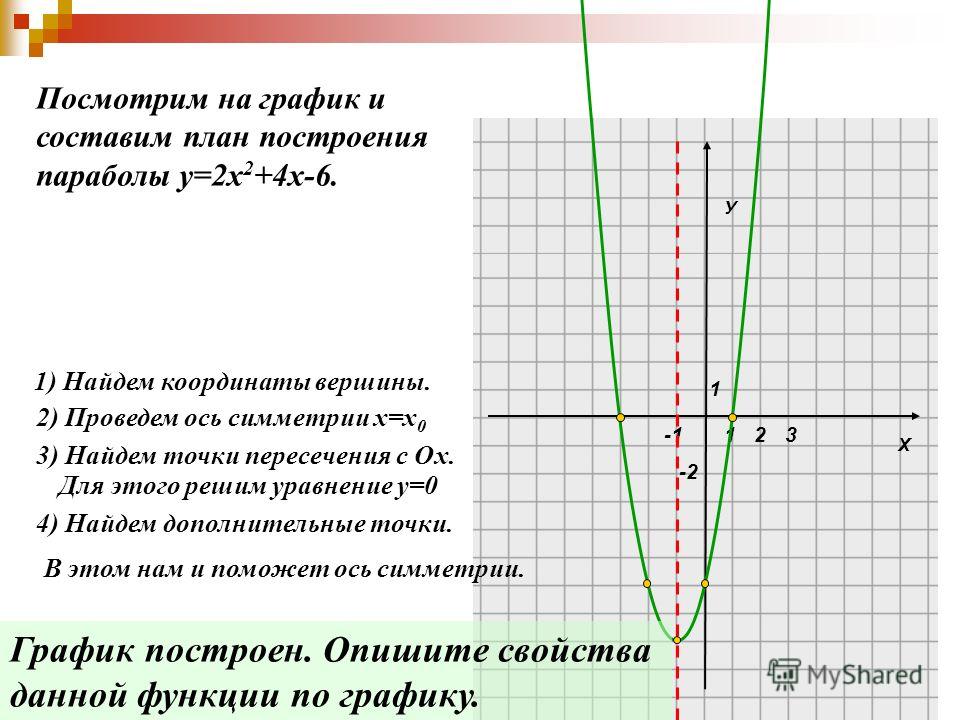
7. Если числа m и п являются корнями трёхчлена ах2 +bх + с , то его можно разложить на множители: ах2 + bх + с = _____________________.
8. Параболу y = х2 сжали в 3 раза к оси OХ, сместили вдоль оси OX влево на 5 и вдоль OY вверх на 7. Получили график функции y = _____________
Итог урока
Выставить оценки за урок (самооценка, оценка учителя)
Рефлексия
Кто доволен свой работой на уроке? Почему? Удалось ли достичь поставленной цели?
Сегодняшный урок мне позволил…
Интересным на уроке было…
Меня огорчило только…
8.Домашнее задание: повторить теоретический материал главы 2, выполнить задания стр.138,139, «Это надо уметь»
Вариант 1
1. График функции у = ах2 , при а3 и 4 координатных четвертях.
2. Ветви параболы у = ах2 +bх + с направлены вверх если а_0
3. Абсцисса вершины параболы у = ах2 +bх + с равна
Абсцисса вершины параболы у = ах2 +bх + с равна
4. Квадратичная функция у = ах2 +bх + с убывает на промежутке __при а0.
5. График функции у = ах2 +с, где с из графика функции у = ах2 параллельным переносом вдоль оси_у на_с единиц _вниз.
6. График функции у = а(х — с)2, где с может быть получен из графика функции у=ах2 параллельным переносом вдоль оси__х_ на _с_единиц __влево .
7. Если числа т и п являются корнями трёхчлена ах2 +bх + с , то его можно разложить на множители: ах2 + bх + с =а(х-m)(х-n)
8. Параболу y = х2 растянули в три раза от оси OХ, сместили вдоль оси OX вправо на 5 и вдоль OY вниз на 7. Получили график функции y = 3(х-5)2-7
Вариант 2
1. График функции у = ах2 , при а0 расположен в _1 и 2координатных четвертях
2. Ветви параболы у = ах2 +bх + с направлены вниз если а
Ветви параболы у = ах2 +bх + с направлены вниз если а
3. Абсцисса вершины параболы у = ах2 + bх + с равна
4. Функция у = ах2 +bх + с возрастает на промежутке при а
5. График функции у = ах2 +с, где с0, может быть получен из графика функции у = ах2 параллельным переносом вдоль оси __у___на _с____ единиц _вверх____.
6. График функции у = а(х — с)2,где с0 может быть получен из графика функции у = ах2 параллельным переносом вдоль оси_х__ на __с___ единиц __вправо___.
7. Если числа m и п являются корнями трёхчлена ах2 +bх + с , то его можно разложить на множители: ах2 + bх + с =а(х-m)(х-n)_____________________.
8. Параболу y = х2 сжали в 3 раза к оси OХ, сместили вдоль оси OX влево на 5 и вдоль OY вверх на 7. Получили график функции y = (х+5)2+7_____________
Приложение 1
Тема урока «Квадратичная функция, ее график и свойства».
Тип урока: Повторительно – обобщающий.
Цели урока: Обобщить и систематизировать основные знания, умения и навыки по теме «Квадратичная функция и её график», используя возможности ИКТ технологий и использовать эти знания для решения задач, входящих в раздел «Алгебра » ОГЭ .
Задачи урока:
Образовательные задачи:
1. Повторить изученный материал и устранить пробелы в знаниях.
2. Совершенствовать навыки построения графиков, исследования функций и умения переносить знания в новые условия.
Развивающие задачи:
1.Формировать умения сравнивать, обобщать, делать выводы;
2.Развивать у учащихся самостоятельность в мышлении и учебной деятельности;
Воспитательные задачи:
1.Воспитывать аккуратность в работе при построении графиков;
2.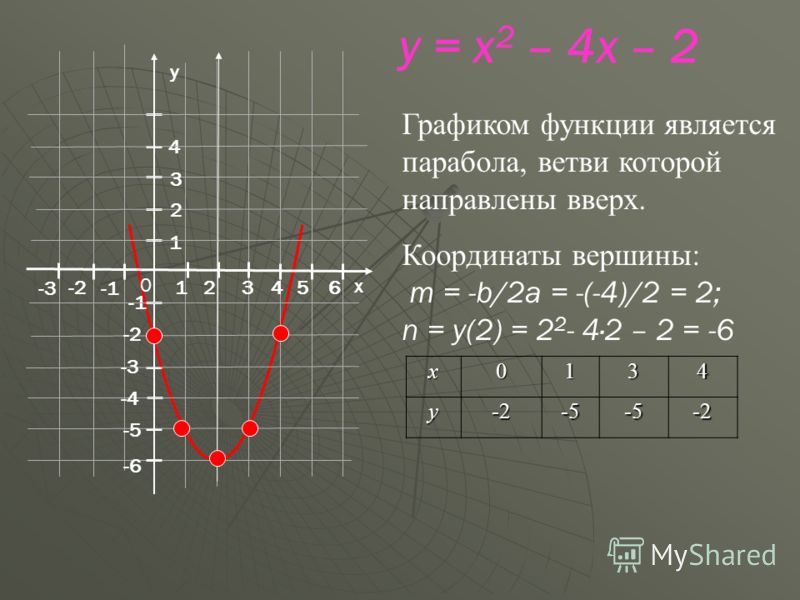 Стимулировать учащихся к самооценке своей образовательной деятельности;
Стимулировать учащихся к самооценке своей образовательной деятельности;
3.Совершенствовать умения, навыки учащихся при работе в группе.
Здоровьесберегающие задачи:
1.Создать здоровьесберегающие моменты, направленные на укрепление глаз и улучшения мозгового кровообращения.
Оборудование урока:
Компьютеры и мультимедийный проектор
Интерактивные задания
Карточки с заданиями
Ход урока
1.Организационный момент.
2. Постановка целей урока.
3.Актуализация знаний учащихся .
1.Фронтальная работа с использованием интерактивной доски.
Слайд 2
Вспомним: Какой формулой задается квадратичная функция?
Как называются коэффициенты а,b,c в данной формуле?
Что является графиком функции?
Слайд 3
Среди данных графиков определите графики квадратичной функции и объясните,
почему вы так считаете.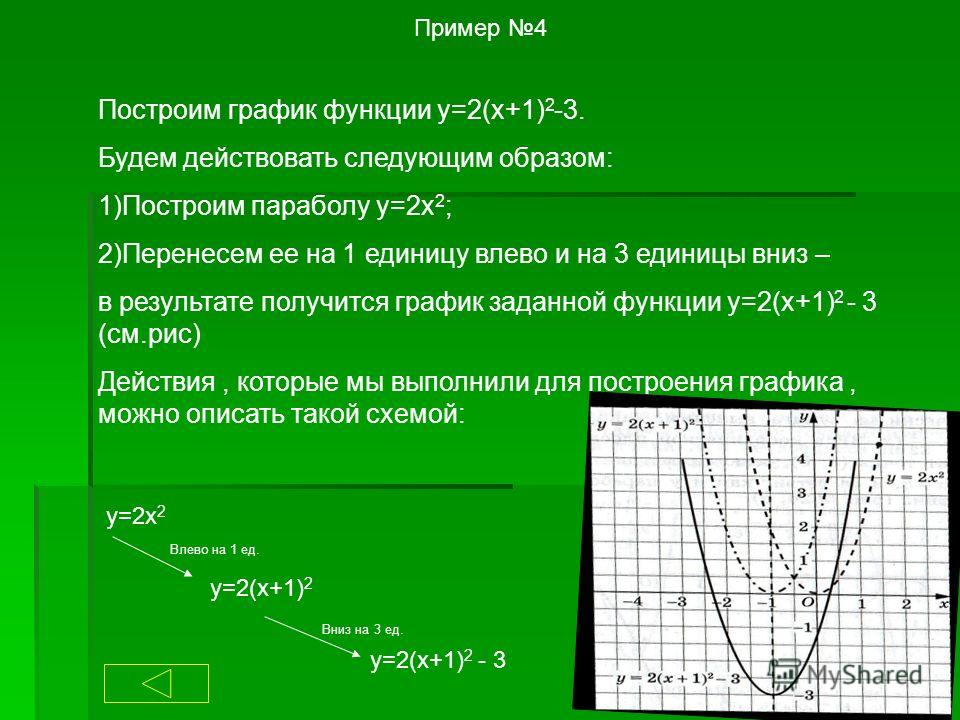
Слайд 4
Как определить квадратичную функцию по формуле функции? Как найти коэффициенты данных функций?
Поставить проблемный вопрос: какую информацию можно получить о графике квадратичной функции, зная коэффициенты квадратного трёхчлена.
Слайд 5
Как связан коэффициент а с направлением ветвей параболы?
Слайд 6
Определите знак коэффициента а для данных функций
Слайд 7
При каком значении аргумента графики функций пересекают ось ординат?
Какой коэффициент квадратичной функции можно определить используя данный факт?
Слайд 8
Определите чему равен коэффициент с ?
Слайд 9
На интерактивной доске установите соответствие между знаками коэффициентов а и с с расположением графика функции на координатной плоскости.
Слайд 10
Вспомним формулы для определения координат вершины параболы и ее оси симметрии.
Слайд 11
Определите координаты вершины парабол и назовите уравнения осей симметрии парабол.
Слайд 12
Какую информацию о графике квадратичной функции можно получить, вычислив дискриминант квадратного уравнения?
Слайд 13
Для каждого графика укажите соответствующие ему значения коэффициента a и дискриминанта D.
Какую еще дополнительную информацию по графику можно получить? Как с помощью графиков функции решить квадратное неравенство?
Слайд 14
При каких значениях х выполняется неравенство а) у 0; б) у 0?
Работа в группах по карточкам
1 задание Установите соответствие между графиками функций и формулами, которые их задают.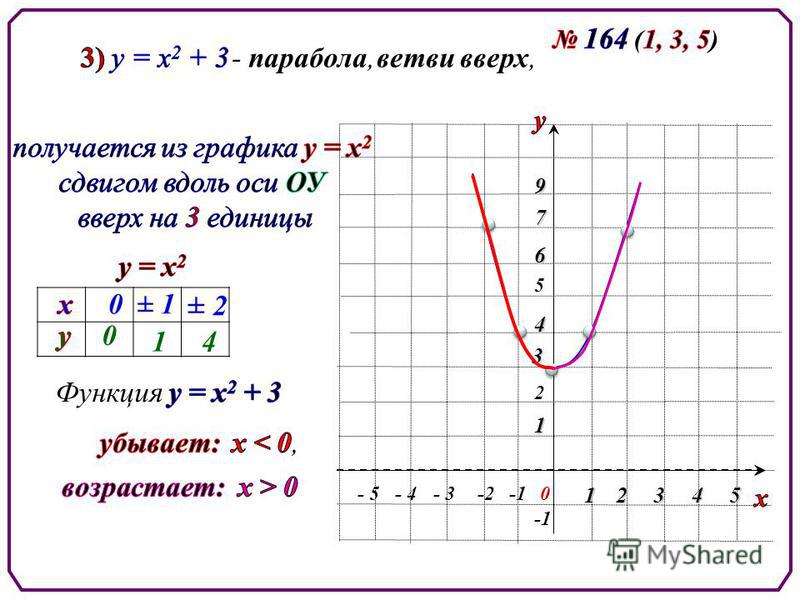 Запишите название функции и графика (Карточка 1)
Запишите название функции и графика (Карточка 1)
2 задание Установите соответствие между графиками функций и знаками коэффициентов a и c.(Карточка 2)
3 задание Установите соответствие между графиками функций и формулами, которые их задают (карточка 3)
Взаимопроверка по слайдам 15-17
Физкультурная минутка для глаз и для улучшения мозгового кровообращения.
Быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5. Повторить 4-5 раз.
Крепко зажмурить глаза (считая до 3), открыть, посмотреть вдаль (считая до 5). Повторить 4-5 раз.
Исходное положение -сидя на стуле, 1-2-плавно наклонить голову назад, 3-4 голову наклонить вперед, плечи не поднимать. Повторить 4-6 раз. Темп медленный.
Теоретический зачёт в форме «Заполни пропуски».

Каждый ученик получает зачётный лист, содержащий десять основных теоретических положений темы. Ключевое слово или формула в каждом правиле заменено пропуском , который необходимо заполнить.
Вариант 1
1. График функции у = ах2 , при а_______ и____ координатных четвертях.
2. Ветви параболы у = ах2 +bх + с направлены вверх если а______
3. Абсцисса вершины параболы у = ах2 +bх + с равна_____
4. Квадратичная функция у = ах2 +bх + с убывает на промежутке _______при а0.
5. График функции у = ах2 +с, где с из графика функции у = ах2 параллельным переносом вдоль оси_ ____ на_ ____ единиц _ ______.
6. График функции у = а(х — с)2, где с может быть получен из графика функции у=ах2 параллельным переносом вдоль оси__ _______ на _ ____единиц __ _____ .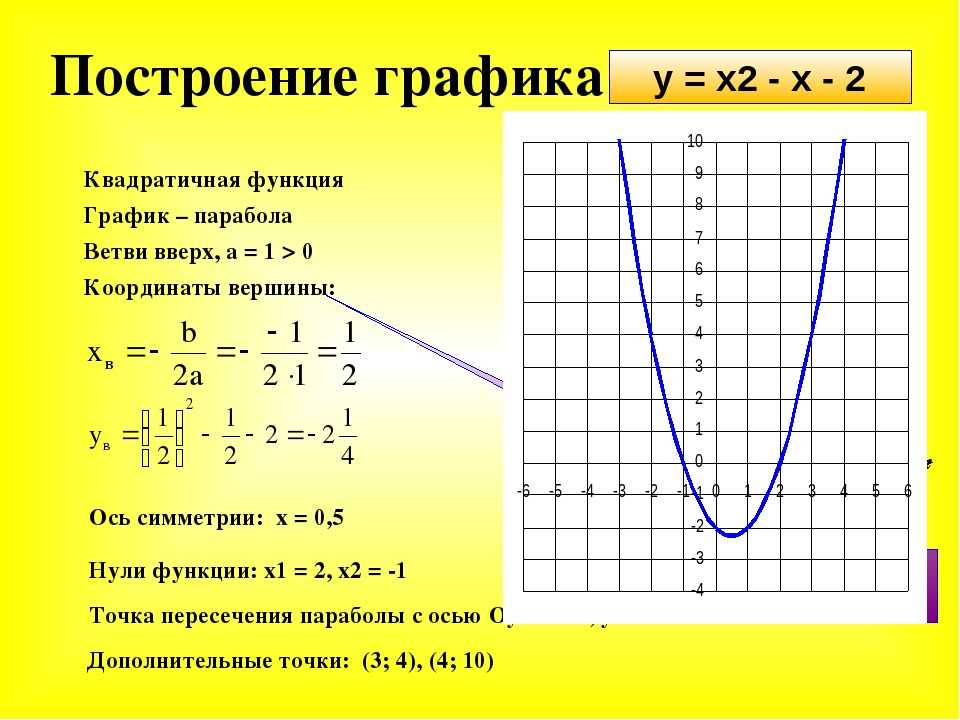
7. Если числа т и п являются корнями трёхчлена ах2 +bх + с , то его можно разложить на множители:
ах2 + bх + с =
8. Параболу y = х2 растянули в три раза от оси OХ, сместили вдоль оси OX вправо на 5 и вдоль OY вниз на 7. Получили график функции y = _______________
Вариант 2
1. График функции у = ах2 , при а0 расположен в _ __ и _____координатных четвертях
2. Ветви параболы у = ах2 +bх + с направлены вниз если а _____
3. Абсцисса вершины параболы у = ах2 + bх + с равна _____
4. Функция у = ах2 +bх + с возрастает на промежутке ____ при а
5. График функции у = ах2 +с, где с0, может быть получен из графика функции у = ах2 параллельным переносом вдоль оси __ ___на _ ____ единиц _ ____.
6. График функции у = а(х — с)2,где с0 может быть получен из графика функции у = ах2 параллельным переносом вдоль оси_ __ на __ ___ единиц __ ___.
7. Если числа m и п являются корнями трёхчлена ах2 +bх + с , то его можно разложить на множители: ах2 + bх + с = _____________________.
8. Параболу y = х2 сжали в 3 раза к оси OХ, сместили вдоль оси OX влево на 5 и вдоль OY вверх на 7. Получили график функции y = _____________
Итог урока
Выставить оценки за урок (самооценка, оценка учителя)
Рефлексия
Кто доволен свой работой на уроке? Почему? Удалось ли достичь поставленной цели?
Сегодняшный урок мне позволил…
Интересным на уроке было…
Меня огорчило только…
8.Домашнее задание: повторить теоретический материал главы 2, выполнить задания стр.138,139, «Это надо уметь»
Вариант 1
1. График функции у = ах2 , при а3 и 4 координатных четвертях.
2. Ветви параболы у = ах2 +bх + с направлены вверх если а_0
3. Абсцисса вершины параболы у = ах2 +bх + с равна
Абсцисса вершины параболы у = ах2 +bх + с равна
4. Квадратичная функция у = ах2 +bх + с убывает на промежутке __при а0.
5. График функции у = ах2 +с, где с из графика функции у = ах2 параллельным переносом вдоль оси_у на_с единиц _вниз.
6. График функции у = а(х — с)2, где с может быть получен из графика функции у=ах2 параллельным переносом вдоль оси__х_ на _с_единиц __влево .
7. Если числа т и п являются корнями трёхчлена ах2 +bх + с , то его можно разложить на множители: ах2 + bх + с =а(х-m)(х-n)
8. Параболу y = х2 растянули в три раза от оси OХ, сместили вдоль оси OX вправо на 5 и вдоль OY вниз на 7. Получили график функции y = 3(х-5)2-7
Вариант 2
1. График функции у = ах2 , при а0 расположен в _1 и 2координатных четвертях
2. Ветви параболы у = ах2 +bх + с направлены вниз если а
Ветви параболы у = ах2 +bх + с направлены вниз если а
3. Абсцисса вершины параболы у = ах2 + bх + с равна
4. Функция у = ах2 +bх + с возрастает на промежутке при а
5. График функции у = ах2 +с, где с0, может быть получен из графика функции у = ах2 параллельным переносом вдоль оси __у___на _с____ единиц _вверх____.
6. График функции у = а(х — с)2,где с0 может быть получен из графика функции у = ах2 параллельным переносом вдоль оси_х__ на __с___ единиц __вправо___.
7. Если числа m и п являются корнями трёхчлена ах2 +bх + с , то его можно разложить на множители: ах2 + bх + с =а(х-m)(х-n)_____________________.
8. Параболу y = х2 сжали в 3 раза к оси OХ, сместили вдоль оси OX влево на 5 и вдоль OY вверх на 7. Получили график функции y = (х+5)2+7_____________
парабол y=−2×2 и y=2×2+k пересекаются в точках A и B, которые находятся в третьем и четвертом квадранте соответственно.
 Найдите k, если длина отрезка AB равна 5.
Найдите k, если длина отрезка AB равна 5.Геометрия
Джек К.
спросил 31.01.20Параболы y = −2 x 2 и y = 2 x 2 + k , пересекающиеся в четвертых точках A и B соответственно. Найти тыс. если длина отрезка AB равна 5.
Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Джозеф Д. ответил 31.01.20
Репетитор
5,0 (488)
Репетитор по геометрии с необходимой помощью.
Смотрите таких репетиторов
Смотрите таких репетиторов
Привет, Джек К. ,
,
Парабола (1) y = -2x 2 — это парабола, которая открывается вниз с вершиной в (0, 0).
Парабола (2) y = 2x 2 + k — это парабола, которая открывается вершиной в точке (0, k).
Нам нужно найти k, чтобы два пересечения (A и B) этих двух парабол находились на расстоянии 5 единиц друг от друга. При пересечении в III и IV квадрантах параболе (2) потребуется, чтобы вершина смещалась вниз по оси Y.
Расстоянием пересечения будет горизонтальная линия от A до B. Таким образом, расстояние представляет собой изменение значения x без изменения значения y (|x 2 — x 1 | = |B х — А х | = расстояние).
Поскольку обе параболы имеют вершину на оси Y, половина расстояния будет в квадранте III, а другая половина расстояния в квадранте IV. Таким образом, ось Y разделяет расстояние, и, поскольку расстояние представляет собой только значения x, половина расстояния составляет 5/2 = 2,5. Теперь мы знаем, что пересечение будет в (-2,5, y) и
(2,5 года).
Также значения y на пересечении должны быть равными. Мы можем установить два уравнения равными друг другу (y = y), и с x = 2,5 или -2,5 мы можем найти k .
-2x 2 = 2x 2 + K
-25 = K, (я позволю вам сделать математику)
Поэтому Y = 2x 2 -25 сдвиг вершины параболы вниз до -25 по оси Y с пересечением двух парабол в точках (-2,5, -12,5) и (2,5, -12,5).
Надеюсь, это поможет, Джо.
Голосовать за 0 голос против
Подробнее
Отчет
Тейлор С. ответил 31.01.20
Репетитор
5,0 (119)
Терпеливый и опытный репетитор по количественной математике
См. таких репетиторов
таких репетиторов
Смотрите таких репетиторов
Допустим,
f(x)= -2x 2 и g(x)= 2x 2 +k
Пусть A и B — их точки пересечения, такие что;
A= (x 1 ,y 1 ) и B= (x 2 ,y 2 )
Обе функции являются параболами.
Согласно преобразованиям, f(x) открывается вниз и имеет вершину в 0.
Согласно преобразованиям, g(x) очень похож на f(x), за исключением того, что он открывается и смещается по вертикали (из-за k) .
В обеих функциях нет смещения по горизонтали, поэтому на их пересечениях, A и B, значения y одинаковы (поскольку они являются параболами).
Отсюда следует, что;
A= (x 1 ,y) и B= (x 2 ,y)
Поскольку сдвиг по горизонтали отсутствует, обе функции симметричны относительно оси y.
Это означает, что если два x имеют одинаковое значение y, они являются положительной и отрицательной версиями друг друга.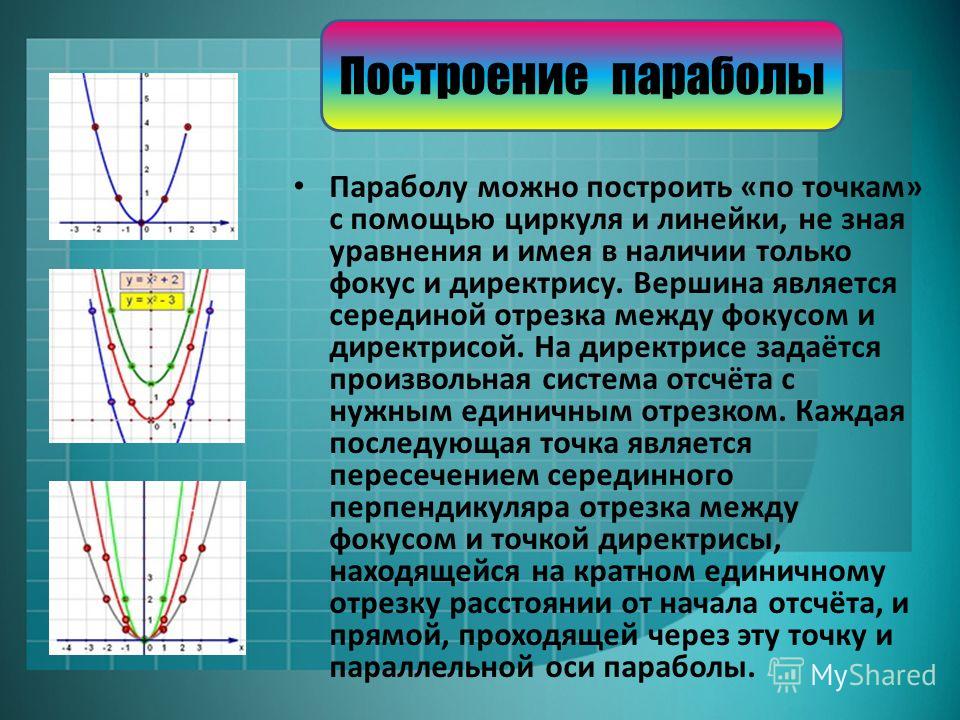
Отсюда следует, что;
i) x 1 = -x 2
Поскольку расстояние между A и B равно 5, а линия, соединяющая их, абсолютно горизонтальна (поскольку значения y одинаковы), это означает, что расстояние между x 1 и x 2 равно 5.
Таким образом,
ii) x 2 — x 1 = 5
Используя уравнения (i) и (ii) x 2 x 2 — x 1 = 5
найти одну из переменных
x 1 = -x 2 x 1 = x 2 — 5
Установите каждое уравнение, равное друг другу и решайте
2 = x 2 — 5
2 = x 2 — 52 = x 2 — 5
. x 2 = 2,5, так как x 2 и x 1 имеют противоположные знаки,
x 1 = -2,5
Теперь, когда у нас есть значения x, давайте найдем k.
Поскольку пересечение происходит там, где f(x) = g(x), мы можем подставить любое из наших значений x в это уравнение.
F (x) = G (x)
-2x 2 = 2x 2 + K
Подключение x 1 или x 2
-2 (2,5) 2 = 2 (2.5) 2 + k
-12,5 = 12,5 + k
k = -25
Голосовать за 0 голос против
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
92-5*x-(3)=0
Никаких пакетов или подписок, платите только за то время, которое вам нужно.
92-5*x-(3)=0
Пошаговое решение :
Шаг 1 :
Уравнение в конце шага 1 :
(2x 2 - 5x) - 3 = 0
Шаг 2 :
Попытка разложения путем разделения среднего члена
2.1 Разложение на множители 2x 2 -5x-3
Первый член равен 2x 2 , его коэффициент равен 2 .
Средний член равен -5x, его коэффициент равен -5.
Последний член, «константа», равен -3
Шаг-1: умножьте коэффициент первого члена на константу 2 • -3 = -6
Шаг 2. Найдите два множителя -6 , сумма которых равна коэффициенту среднего члена, который равен -5 .
| -6 | + | 1 | = | -5 | . шаг 2 выше, -6 и 1 2x 2 — 6x + 1x — 3 Шаг-4: Сложите первые 2 члена, выделив одинаковые множители : Уравнение в конце шага 2 :(2 x 3) ) = 0 Шаг 3 :Теория — корни продукта: 3. Если произведение двух или более слагаемых равно нулю, то хотя бы одно из слагаемых должно быть равно нулю. Теперь мы будем решать каждый термин = 0 отдельно Другими словами, мы собираемся решить столько уравнений, сколько членов в произведении Любое решение термина = 0 также решает произведение = 0. Решение уравнения с одной переменной :3.2 Решение : x-3 = 0 Добавить 3 к обеим сторонам уравнения: Решение единого переменного уравнения:3,3 Решение: 2x+1 = 0 Вычтите 1 с обеих сторон уравнения: Дополнение: Решение квадратного уравнения напрямуюРешение 2x 2 -0x-9 напрямую0304
Графики квадратичных функцийВ предыдущих уроках мы обсуждали стандартную форму квадратичной функции : f(x)=ax 2 +bx+c. Возможно, вы видели другие формы, такие как вершинная форма или факторизованная форма . Почему существует так много распространенных способов записи одних и тех же уравнений? Зачем нам изучать все эти разные формы, если стандартная форма и так самая распространенная? 9 квадратичная функция . Определяющей характеристикой квадратичной функции является то, что это полином, старший показатель которого равен 2. Существует несколько способов записи квадратичной функции:
y− пересечение квадратичной функции в стандартной форме равно (0,c) и находится путем замены x в f(x)=ax 2 +bx+c. Резюме вершинной формыДана квадратичная функция в вершинной форме : f(x)=a(x−h) 2 +k:
Вершина параболыВ стандартной форме квадратичной функции координата x вершины параболы задается уравнением: \(\ x=-\frac{b}{2 a}\) Координата y вершины находится с помощью: \(\ y=f\left(-\frac{b}{2 a}\right)\) Ось симметрии параболы Парабола имеет отражательная симметрия относительно вертикальной линии, проходящей через вершину. Вертикальная линия \(\ x=-\frac{b}{2 a}\) также является девяткой параболы{2}\) в правую часть уравнения: g(x)=x 2 +6x+7 =x 2 +6x+9+7−9 правая часть: g(x)=(x+3) 2 −2 Таким образом, a=1 и вершина этой параболы равна (-3, -2). Мы знаем, что парабола раскрывается с той же шириной, что и y=x 2 , и имеет минимальное значение в вершине. График параболы ниже. Пример 2Найти вершину и построить график квадратичной функции g(x)=x 2 −8x+12. Решение Координата x вершины равна \(\ x=-\frac{-8}{2}=4\). Координата y вершины равна g(4)=(4) 2 −8(4)+12=16−32+12=−4 Таким образом, вершина находится в точке (4, -4) . Чтобы построить параболу, мы составим таблицу точек с координатой x, равной 4:
Теперь мы можем использовать симметрию g(x), чтобы заполнить эту таблицу для g(3). Пример 3Нарисуйте график функции y=f(x)=x 2 +2x−3. Решение Давайте сначала найдем точки пересечения. Для y-пересечения, если x=0, то f(0)=-3 или y=-3, поэтому точка y-пересечения равна (0, -3). Теперь для точек пересечения x, если y=f(x)=0, то x 2 +2x−3=0 или x 2 +2x−3=(x+3)(x− 1)=0 , так что x=-3 и x=1 являются точками пересечения x, то есть (-3, 0) и (1, 0). Вершина (крайняя точка) находится на \(\ x=\frac{-b}{2 a}=\frac{-2}{2(1)}=-1\) Начиная с \(\ \begin{выровнено} 9{2}+2(-1)-3 \\ Вершина (-1, -4). Поскольку коэффициент при x 2 положительный, a>0, экстремум является минимумом и парабола раскрывается. Из этой информации мы можем сделать грубый набросок параболы, содержащей точки, определенные выше. Пример 4Нарисуйте график квадратичной функции f(x)=−x 2 +4x. Решение Чтобы найти точку пересечения с осью y, установите x=0 и f(0)=−(0) 2 +4(0)=0 Таким образом, парабола пересекает ось y в начале координат. Пересечение x получается установкой y=0. Таким образом, −x 2 +4x=0. Факторинг, −x 2 +4x=−x(x−4)=0 , так что x=0 и x=4 являются точками пересечения x. У нас есть a=−1 и b=4, так что крайняя точка возникает, когда \(\ x=\frac{-b}{2 a}=\frac{-4}{2(-1) }=2\) Поскольку f(2)=−(2) 2 +4(2)=−4+8=4, то (2, 4) является крайней точкой. Это максимальных точек, поскольку a=−1<0 и парабола раскрывается вниз. Наконец, график можно получить, начертив параболу через определенные выше точки. Судя по графику, диапазон функции равен y≤4. Пример 5 Нарисуйте график y=−3(x−2) 2 +1. Решение Уравнение y=−3(x−2) 2 +1 уже находится в вершинной форме, поэтому построить график относительно просто: Вспомните, когда уравнение записывается в форме вершины, как эта, вершина является точкой (h,k): форма вершины: y=a(x−h) 2 +k Наше уравнение : y=−3(x−2) 2 +1 Исследуя наше уравнение, мы видим, что вершина параболы находится в точке (2, 1). Чтобы найти другую точку на параболе, найдите значение x. Поскольку вершина находится в точке x = 2, попробуем на одну единицу вправо: x = 3. −3(3−2) 2 +1=−2 ∴ На параболе есть точка (3, -2) Поскольку ось параболы равна симметрии, проходящей через его вершину, мы можем отразить точку (3, -2) через ось симметрии, чтобы получить другую точку, (1, -2) также на параболе. График y=−3(x−2)2+1 показан ниже с использованием вершины (2, 1) и точек (3, -2) и (1, -2). Обзор
Нарисуйте график каждой функции:
Квадратичная функция y=−0,05x 2 +1,5x может использоваться для представления траектории футбольного мяча, отброшенного на 30 ярдов дальше по полю. Переменная x представляет расстояние в ярдах, которое мяч прошел по полю. Высота футбольного мяча в воздухе в ярдах представлена переменной (y). Используйте квадратичную функцию, чтобы вычислить высоту мяча, когда он движется по полю. Ответы округлите до сотых долей ярда.
Обзор (ответы)Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 2.2. Словарь
Эта страница под названием 2.1.2: Графики квадратичных функций распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, который был отредактирован в соответствии со стилем и стандартами LibreTexts. |

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

 1 Произведение нескольких слагаемых равно нулю.
1 Произведение нескольких слагаемых равно нулю. точка, называемая вершиной . Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили "у", потому что коэффициент первого члена, 2 , положителен (больше нуля).
точка, называемая вершиной . Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили "у", потому что коэффициент первого члена, 2 , положителен (больше нуля). 2500 для x Мы можем рассчитать y -координату:
2500 для x Мы можем рассчитать y -координату:  Так как
Так как  3 Решение 2x 2 -5x-3 = 0 с помощью квадратной формулы .
3 Решение 2x 2 -5x-3 = 0 с помощью квадратной формулы . 1.2: Графики квадратичных функций
1.2: Графики квадратичных функций
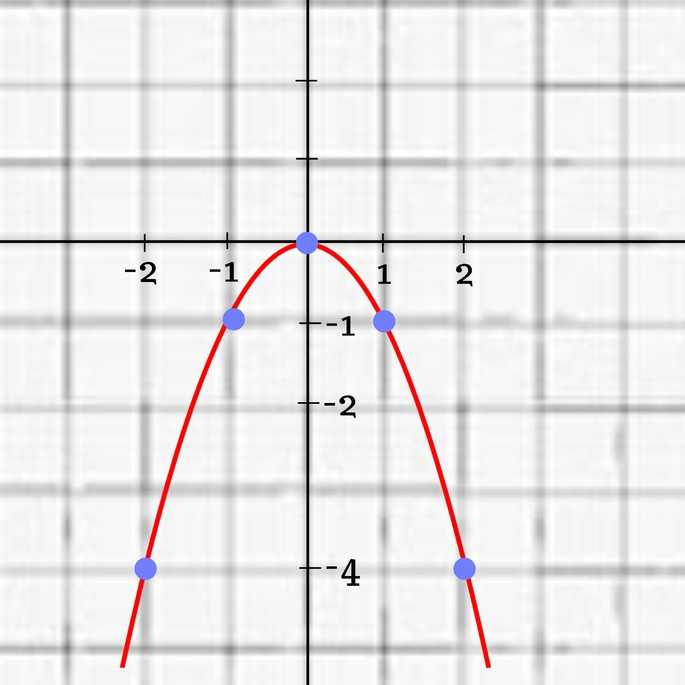
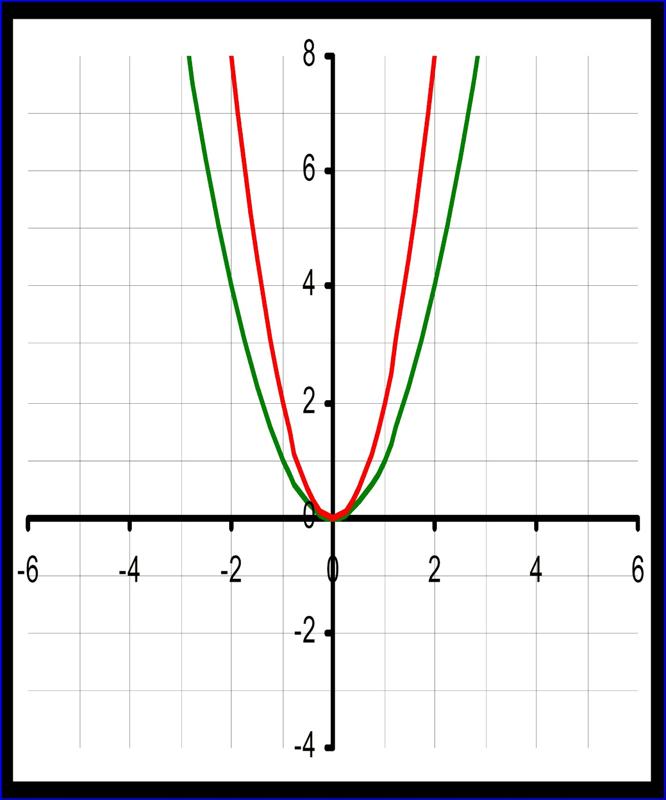 Обратите внимание, что g(3)=g(5)=-3. Аналогично, г(2)=г(6)=0. Окончательный график ниже.
Обратите внимание, что g(3)=g(5)=-3. Аналогично, г(2)=г(6)=0. Окончательный график ниже. Обратите внимание, что диапазон функции равен y≥−4.
Обратите внимание, что диапазон функции равен y≥−4.
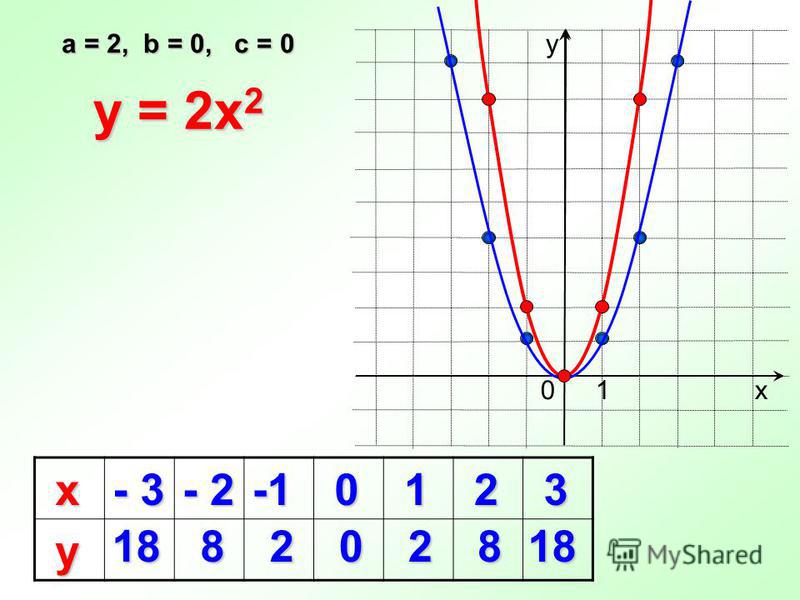

 Точка пересечения x — это точка, в которой кривая пересекает ось x. Точка пересечения y — это точка, в которой кривая пересекает ось y.
Точка пересечения x — это точка, в которой кривая пересекает ось x. Точка пересечения y — это точка, в которой кривая пересекает ось y.