Графические функции, такие как y = a sin(k(x-b)) и y = a cos(kx+b)
В предыдущем разделе были рассмотрены (основные) графики
$\,y = \sin x\,$ и $\,y = \cos x\,$.
Однако эти тригонометрические функции часто
появляются в «преобразованных» версиях.
Вы можете увидеть, например,
$\,y = -1,5\sin \frac{1}{2}(x — \pi)\,$ или $\,y = \frac{1}{3}\cos (4x + 5)\,$ .
Наблюдения и методы, обсуждаемые в этом разделе, позволят вам надежно, быстро и эффективно график любой функции следующих форм, не запоминая кучу разных формул :
Обратите внимание, в частности, что аргументы $\,k(x\pm b)\,$ (первая строка) и $\,kx\pm B\,$ (вторая строка) различны .
Например, $\,2(x-5)\,$ отличается от $\,2x — 5\,$.
В математике слово «аргумент» часто используется для обозначения входных данных.
функции.
Например, аргумент функции синуса в выражении ‘$\,\sin k(x\pm b)\,$’ равен $\,k(x\pm b)\,$.
В качестве второго примера, аргумент функции косинуса в выражении ‘$\,\cos (kx\pm B)\,$’ равен $\,kx\pm B\,$.
Любой аргумент только с двумя типами термов: $\,x\,$-терм и постоянный терм
можно обрабатывать с помощью четырехэтапного графического процесса, обсуждаемого ниже.
С помощью этой четырехэтапной техники вам не нужно определять с каким типом аргумента вы работаете;
вам нужно только определить коэффициент $\,x\,$-члена.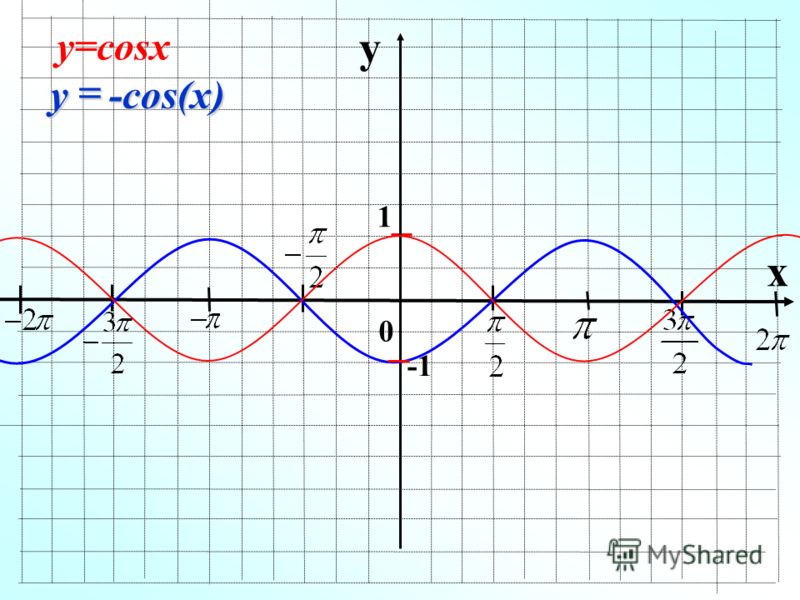
В этом разделе
коэффициент при $\,x\,$ -термине в аргументе всегда обозначается $\,k\,$.
Например, четырехэтапный метод можно использовать для построения графика, скажем, $\displaystyle\,y = -9\sin\frac{\pi + 5x}{8}\,$.
Почему?
Аргумент имеет только член $x$ и постоянный член.
Здесь $\,k = \frac 58\,$.
Почему?
Перепишите аргумент (при необходимости), чтобы увидеть, что коэффициент $\,x\,$ равен $\,\color{red}{\frac 58}\,$:
$$\cssId{s27}{\frac{\pi +\color{red}{5}x}{\color{red}{8}} = \frac{\pi}8 + \color{red}{\ дробь{5}{8}}x}\,$$
Следующие два ключевых наблюдения приведут к эффективному подходу.
Нажмите кнопку показать/скрыть для получения дополнительной информации.
- Наблюдение №1:
Каждая обобщенная функция является результатом графических преобразований, выбранных из:- горизонтальное растяжение/усадка
- сдвиг вправо/влево
- вертикальное растяжение/усадка
- отражение вокруг оси $x$
- Наблюдение №2:
Единственное преобразование, которое изменяет период, — это горизонтальное растяжение/сжатие.
Горизонтальное растяжение/сжатие вызвано заменой каждого $\,x\,$ на $\,kx\,$,
что заставляет точки $\,(x,y)\,$ перемещаться в новые точки $\displaystyle\,(\frac{x}{k},y)\,$.Для $\,k > 0\,$ горизонтальное растяжение/сжатие изменяет исходный период $\,2\pi\,$ на новый период $\displaystyle\,\frac{2\pi}{k} \, $.
Если $\,k
- синус нечетный:
$\,\sin(-x) = -\sinx\,$
- косинус четный:
$\,\cos (-x) = \cos x$
Это приводит нас к:
ЧЕТЫРЕХЭТАПНЫЙ ГРАФИЧЕСКИЙ ПРОЦЕСС:
Вы нарисуете только один период .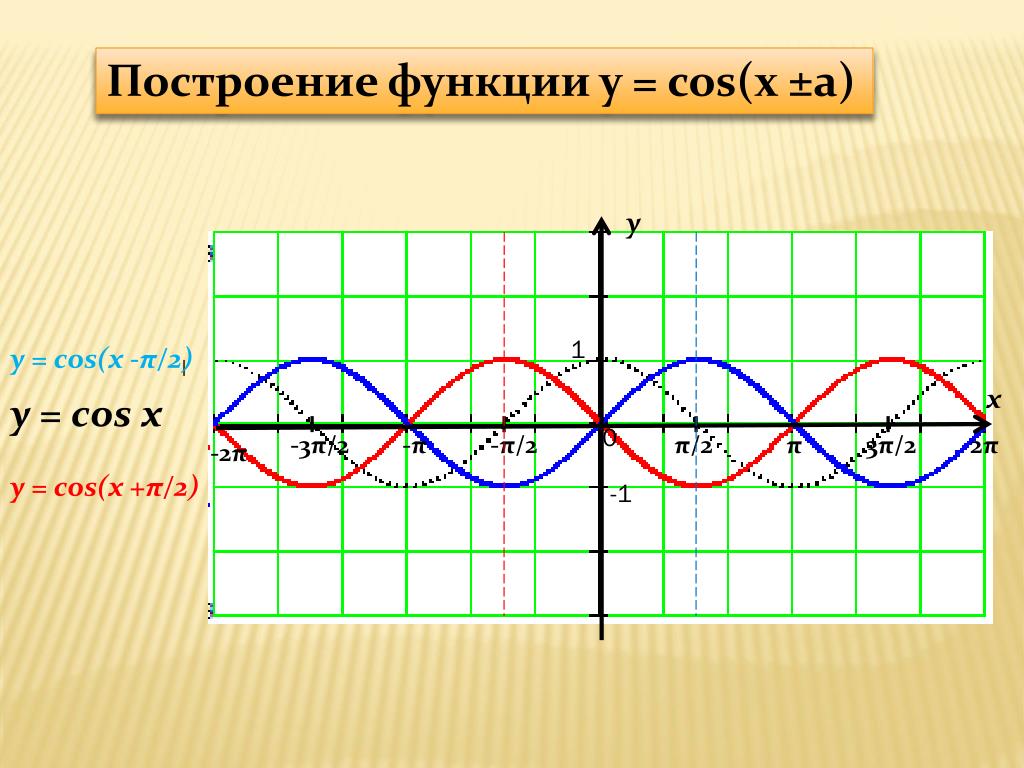
Периодически расширяясь, это однозначно определяет всю кривую.
| ОБЩАЯ ПРОЦЕДУРА | ПРИМЕР: График $\,y = -7\cos (3-5x)\,$ | ||||
| ШАГ 1: ПРОВЕРИТЬ, ЧТО $\,k\,$ ПОЗИТИВНО Коэффициент при $\,x\,$-члене в аргументе обозначается $\,k\,$. | Изначально коэффициент при члене $\,x\,$ равен $\,-5\,$. Переписать: (Таким образом, $\,k = 5\,$.  ) | ||||
| ШАГ 2: НАЧАЛЬНАЯ ТОЧКА Каждая кривая синуса/косинуса начинает «естественный» цикл, когда ее аргумент равен нулю. | Найдите $\,S\,$:
$$
\начать{собирать}
\cssId{s74}{5x-3 = 0}\cr
\cssId{s75}{5x = 3}\cr
\cssId{s76}{x = \frac{3}{5}}
\конец{собрать}
$$
Итак, $\,S = \frac{3}{5}\,$. | ||||
| ШАГ 3: КОНЕЧНАЯ ТОЧКА Вычислите новый период, $\displaystyle\,\frac{2\pi}{k}\,$. Цикл, который начинается в $\,S\,$, заканчивается в $\displaystyle\,E := S +\frac{2\pi}{k}\,$. Отметьте конечную точку $\,E\,$ на числовой прямой. Разделите интервал от НАЧАЛЬНОЙ ТОЧКИ до КОНЕЧНОЙ ТОЧКИ на четыре равные части, чтобы было проще рисовать в основном цикле. | $\,k = 5\,$ $\cssId{s85}{\displaystyle\text{period} = \frac{2\pi}{k} = \frac{2\pi}{5}}$ $\cssId{s86}{\displaystyle E := S + \frac{2\pi}{k} = \frac{3}{5} + \frac{2\pi}{5}}$ | ||||
| ШАГ 4: РИСОВАНИЕ В БАЗОВОМ ЦИКЛЕ; ОТРЕГУЛИРОВАТЬ (ПО НЕОБХОДИМОСТИ) ДЛЯ АМПЛИТУДЫ/ПЕРЕВЕРТКИ Как обсуждается в следующем разделе, амплитуда — это расстояние от оси $x$ к самой высокой (или самой низкой) части графика. 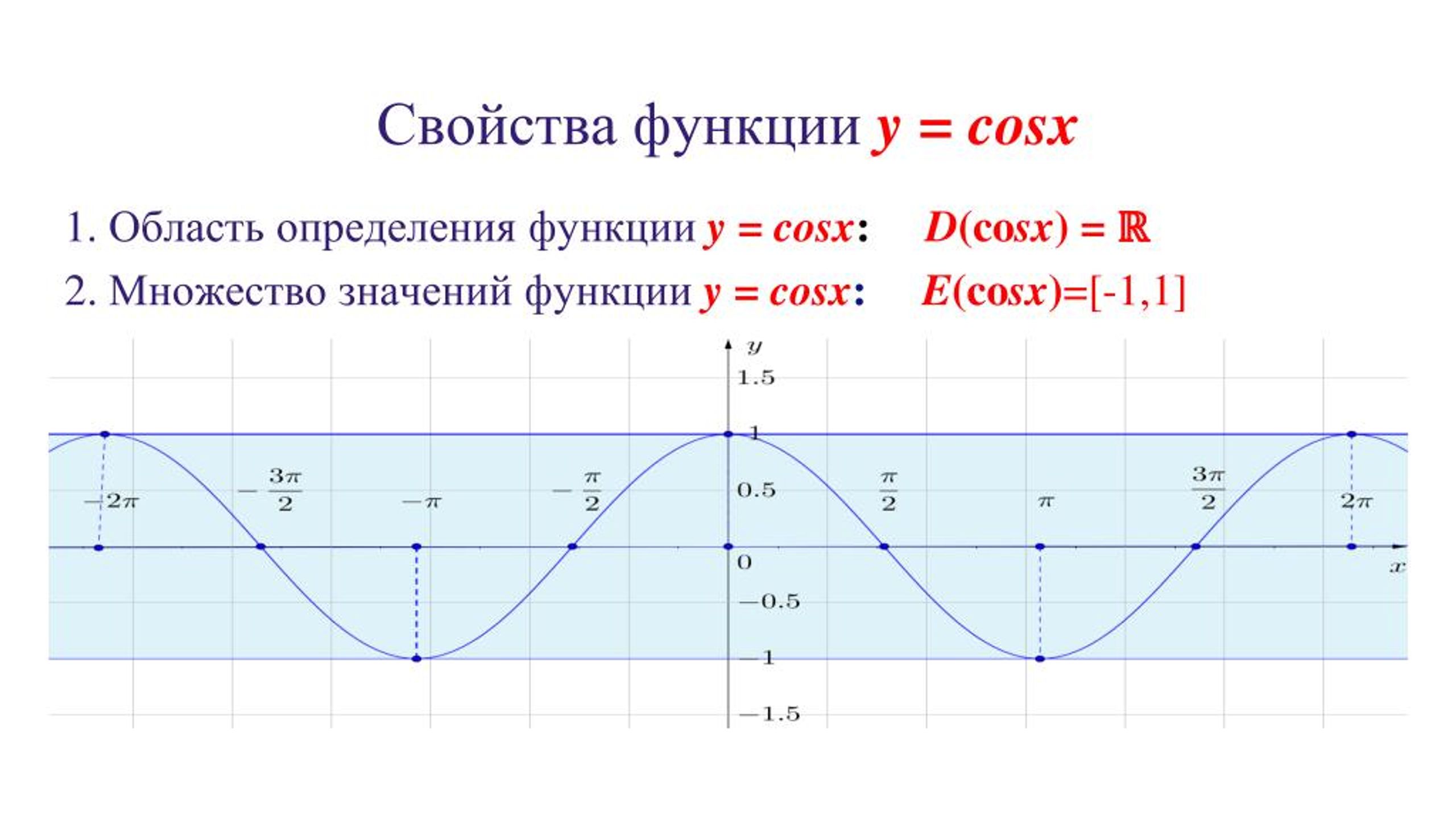 Амплитуда $\,y = \sin x\,$ и $\,y = \cos x\,$ равна $\,1\,$. Вертикальное масштабирование с коэффициентом $\,-1\,$ вызывает отражение около ось $x$ (т. е. «флип»). | Нарисуйте базовый косинусный цикл, перевернутый.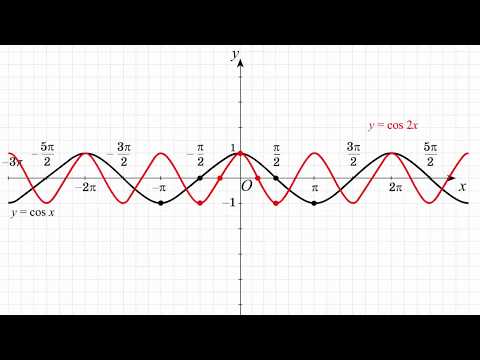 Амплитуда $\,7\,$. Чтобы подчеркнуть: На этом графике (один цикл) $y = -7\cos (5x-3)$:
|
Ваш браузер не поддерживает аудио элементы.
ПРОЧТЕНИЕ, ЧАСТЬ 2
ПРИМЕРЫ
Три предыдущих примера повторяются с использованием компактной версии четырехшагового графического процесса.
Также приводится новый пример.
Посмотрите, как это быстро и просто!
В этих примерах циклы показаны в стандартном окне просмотра.
($\,x\,$ между $\,-20\,$ и $\,20\,$; $\,y\,$ между $\,-10\,$ и $\,10\,$ ),
для облегчения сравнения графиков.
Цикл, отображаемый с помощью четырехэтапного процесса, показан темно-зеленым цветом.
Дополнительные циклы показаны для заполнения окна просмотра.
Включены десятичные приближения до десятых долей.
Не забудьте сначала получить точных ответов, затем приблизительных!
График $\,y = -1,5\sin\frac12(x-\pi)\,$ с использованием четырехэтапного процесса
- $k = \frac 12 = 0,5$
- $S = \pi \примерно 3,1$
(мысленно приравнять $\,\frac 12(x-\pi)\,$ к нулю) - $\displaystyle\text{период} = \frac{2\pi}{k} = \frac{2\pi}{0,5} = 4\pi \приблизительно 12,6 $
$E = S + \text{период} = \pi + 4\pi = 5\pi \примерно 15,7$ - основной синусоидальный цикл, перевернутый, примерно на $\,[3. 1,15.7]\,$, амплитуда $\,1.5\,$:
1,15.7]\,$, амплитуда $\,1.5\,$:График $\,y = \frac13\cos (4x+5)\,$ с использованием четырехшагового процесса
- $k = 4$
- $S = -\frac{5}{4} = -1,25$
(мысленно приравнять $\,4x+5\,$ к нулю) - $\displaystyle\text{период} = \frac{2\pi}{k} = \frac{2\pi}{4} = \frac{\pi}{2} \приблизительно 1,6$
$\displaystyle\displaystyle E = S + \text{period} = -1,25 + \frac{\pi}2 \приблизительно 0,3$ - базовый косинусный цикл на (около) $\,[-1.25,0.3]\,$, амплитуда $\displaystyle\,\frac{1}{3}\,$:
График $\,y = -7\cos (3 — 5x)\,$ с использованием четырехэтапного процесса
- Переписать:
$-7\cos(3-5x) = -7\cos(-(5x-3)) = -7\cos(5x-3)$
(косинус четный)
$к = 5$ - $S = \frac{3}{5} = 0,6$
(мысленно приравнять $\,5x-3\,$ к нулю) - $\displaystyle\text{период} = \frac{2\pi}{5} = 0,4\pi \примерно 1,3 $
$E = S + \text{период} = 0,6 + 0,4\пи \приблизительно 1,9$ - базовый косинусоидальный цикл, перевернутый, около $\,[0,6,1,9]\,$, амплитуда $\,7\,$:
График $\displaystyle\,y = -4\sin\frac{\pi-3x}{8} \,$ с использованием четырехэтапного процесса
- Переписать:
$\displaystyle -4\sin\frac{\pi-3x}{8} = -4\sin (-\frac 18(3x-\pi)) = 4\sin\frac18(3x — \pi)$
(синус нечетный)
$\displaystyle k = \frac38 \примерно 0,4$ - $\displaystyle S = \frac{\pi}{3} \примерно 1,0$
(мысленно приравнять $\displaystyle\,\frac18(3x-\pi)\,$ к нулю) - $\displaystyle\text{период} = \frac{2\pi}{3/8} = \frac{16\pi}3 \приблизительно 16,8 $
$\displaystyle E = S + \text{период} = \frac{pi}3 + \frac{16\pi}3 = \frac{17\pi}3 \примерно 17,8$ - основной синусоидальный цикл около $\,[1. 0,17.8]\,$, амплитуда $\,4\,$:
0,17.8]\,$, амплитуда $\,4\,$:График Cos — GCSE по математике
Введение
Что такое график cos?
Как построить график cos
Круг агрегата
Когда мы получаем положительные и отрицательные значения для cos(θ)?
График функции косинуса
Обратная величина cos(θ)
Сравнение графиков cos(θ) и sin(θ)
Как использовать графики косинусов
График косинуса
Распространенные заблуждения
Похожие уроки
Практика косинусных графиков вопросы
Косинусные графики GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Еженедельные онлайн-уроки повторения математики GCSE теперь доступны
Узнать больше
Введение
Что такое график cos?
Как построить график cos
Круг агрегата
Когда мы получаем положительные и отрицательные значения для cos(θ)?
График функции косинуса
Обратная величина cos(θ)
Сравнение графиков cos(θ) и sin(θ)
Как использовать графики косинусов
График косинуса
Распространенные заблуждения
Похожие уроки
Практика косинусных графиков вопросы
Косинусные графики GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о диаграммах косинуса, в том числе о том, как распознавать график функции косинуса, рисовать кривую косинуса и обозначать важные значения, а также интерпретировать график косинуса.
Есть также co синусоидальных графиков рабочих листов, основанных на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое график cos?
График косинуса — это визуальное представление функции косинуса для заданного диапазона углов.
Горизонтальная ось тригонометрического графика представляет собой угол, обычно обозначаемый как \theta , а ось Y представляет собой синусоидальную функцию этого угла.
- 9о
- Максимальное значение равно 1, а минимальное значение равно -1.
В этом уроке мы рассмотрим график функции косинуса только для углов в градусах, хотя его также можно представить в радианах.
Что такое график cos?
Как построить график косинуса
Помните, что \cos(\theta) – это отношение между прилежащей стороной и гипотенузой прямоугольного треугольника:
вычислить размер угла \theta .
Для каждого треугольника гипотенуза одинакова, но длина прилежащей стороны и связанный с ней угол меняются.
Здесь мы видим, что для \cos(\theta)=\frac{adj}{hyp} по мере увеличения угла \theta длина стороны, прилегающей к углу, также увеличивается, чтобы сохранить прямой угол. Итак, для каждого треугольника имеем:
- Треугольник 1: \cos(\theta)=\frac{7}{10}=0,7
- Треугольник 2: \cos(\theta)=\frac{5}{10}=0,5
- Треугольник 3: \cos(\theta)=\frac{1}{10}=0,1
Итак, что произойдет, если сторона, примыкающая к углу, будет равна 10?
9о . Для любых больших или меньших углов нам нужно смотреть на единичный круг.Объясните, как построить график cos
Единичная окружность
Единичная окружность — это окружность радиусом 1 с центром в начале координат. Мы можем пометить значения, в которых окружность пересекает оси, потому что мы знаем, что радиус единичной окружности равен 1 единице.
Мы все еще можем построить треугольник внутри единичного круга с углом, начинающимся с положительной оси x.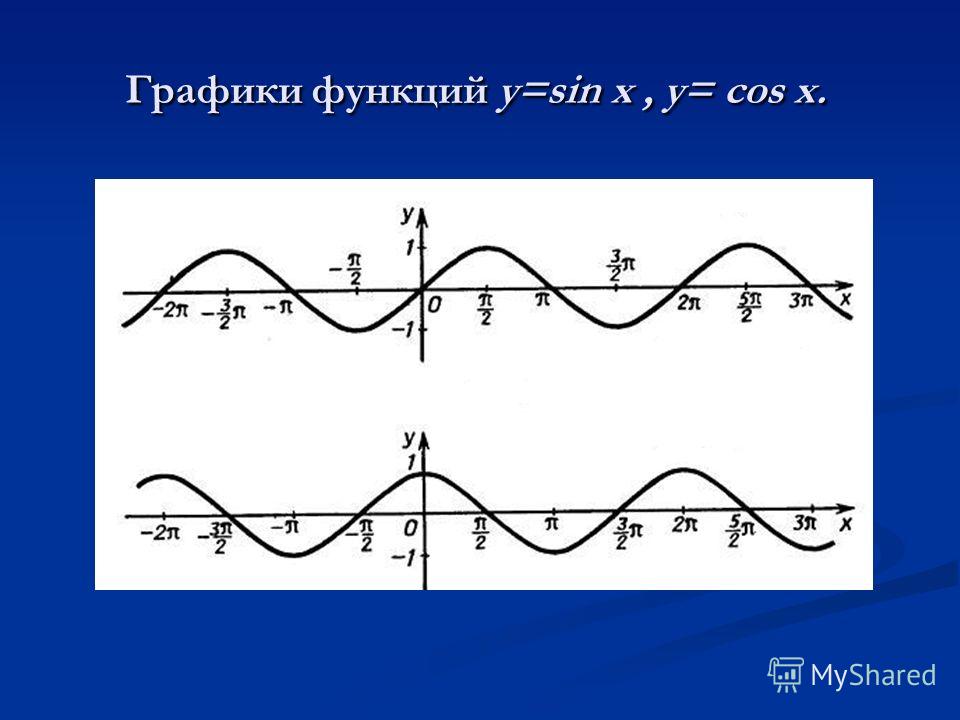
Глядя на тригонометрические отношения синуса и косинуса, мы можем сказать, что:
- \sin(\theta)=\frac{a}{1} \; \текст{так} \; а=\грех(\тета)
- \cos(\theta)=\frac{b}{1} \; \текст{так} \; б = \ соз (\ тета)
- \tan(\theta)=\frac{a}{b} \; \текст{так} \; \ загар (\ тета) = \ гидроразрыва {\ грех (\ тета)} {\ соз (\ тета)}
Это означает, что ширина треугольника равна \cos(\theta) и высота треугольника равна \sin(\theta) . Таким образом, точка на единичной окружности является координатой ( \cos(\theta) , \; \sin(\theta) ): 9o , значение x отрицательное, поэтому \cos(\theta) равно отрицательному .
Визуализируя это с помощью осей координат, мы можем показать, когда \cos(\theta) является положительным и отрицательным:
Мы больше не ограничены диапазоном значений для \theta, поскольку мы можем продолжать поворачивать любой угол положительное или отрицательное направление и получить значение для \cos(\theta) .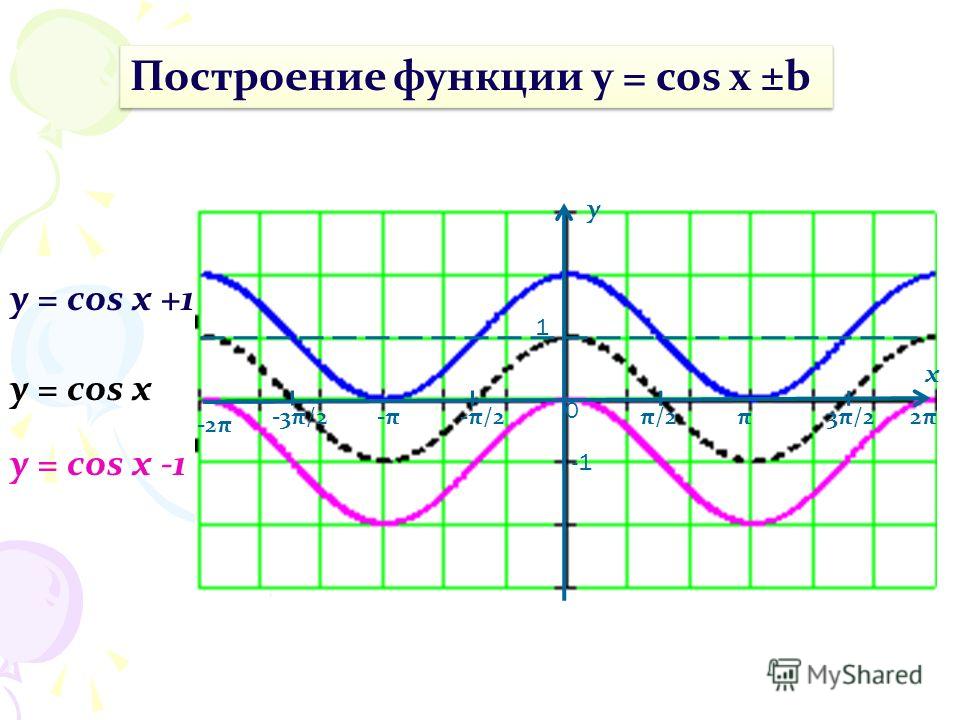
Поэтому мы можем расширить нарисованный ранее график, чтобы представить этот новый набор значений на графике для углов между -360° и 360°. 9о).
Вы должны уметь интерпретировать единичный круг, чтобы определить значение \theta. Вот несколько примеров, чтобы помочь вам. 9{-1}(\тета) .
Обозначения, используемые для обратных функций, не следует путать с обратной функцией . На уровне математики мы узнаем, что функция , обратная к \cos(\theta), называется секансом или \sec(\theta), где \sec(\theta)=\frac{1}{\cos(\theta) )} .
Сравнение графиков cos(θ) и sin(θ)
Графики \sin\theta и \cos\theta очень похожи.
На самом деле, если вы примените фазовый сдвиг к любому графику, вы получите график другой функции.
График функций y=\sin(\theta) (красный) и y=\cos(\theta) (синий):
Если мы переместим график \sin\theta, вычитая 90 градусов из каждого угол (sin(90-\theta)) мы получаем \cos(\theta) . Этот горизонтальный сдвиг может быть в любом направлении. Мы также можем выполнять вертикальное смещение, горизонтальное растяжение, вертикальное растяжение, вращение и многое другое!
Дополнительную информацию по этой теме смотрите в уроке Преобразование тригонометрических графов .
Как использовать графики косинуса
Чтобы использовать графики синуса:
- Проведите прямую линию от оси известного значения до кривой косинуса .
- Нарисуйте прямую перпендикулярную линию в точке пересечения с другой осью .
- Считайте значение, где перпендикулярная линия пересекает другую ось .
Графики синуса, косинуса и тангенса
Получите бесплатный лист графика косинуса, содержащий более 20 вопросов и ответов по графикам синуса, косинуса и тангенса. Включает рассуждения и прикладные вопросы. 9o считывается с графика.
- Графики синусоиды и косинуса переключаются
Графики синуса и косинуса очень похожи, и их легко спутать друг с другом. Совет, который следует помнить, заключается в том, что вы «синусируете вверх» от 0 для синусоидального графика, поэтому линия увеличивается, тогда как вы «косинусируете вниз» от 1, поэтому линия уменьшается для косинусного графика.
- Неправильно построены асимптоты для графика функции тангенса 9049о и так далее.
- Графики построены с помощью линейки
Каждый тригонометрический график представляет собой кривую, поэтому единственный раз, когда вам требуется использовать линейку, — это провести набор осей.
