Y cos x y 0 2 y 0: найдите площадь фигуры ограниченную линиями y=cosx, y=0, x=0, x=П/2

alexxlab / / Разное
2+1, y=5. — вопрос №2457795 — Учеба и наука

Лучший ответ по мнению автора

17. 05.17
Лучший ответ по мнению автора

Ответ понравился автору вопроса

Михаил Александров
Читать ответы

Андрей Андреевич
Читать ответы

Eleonora Gabrielyan
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.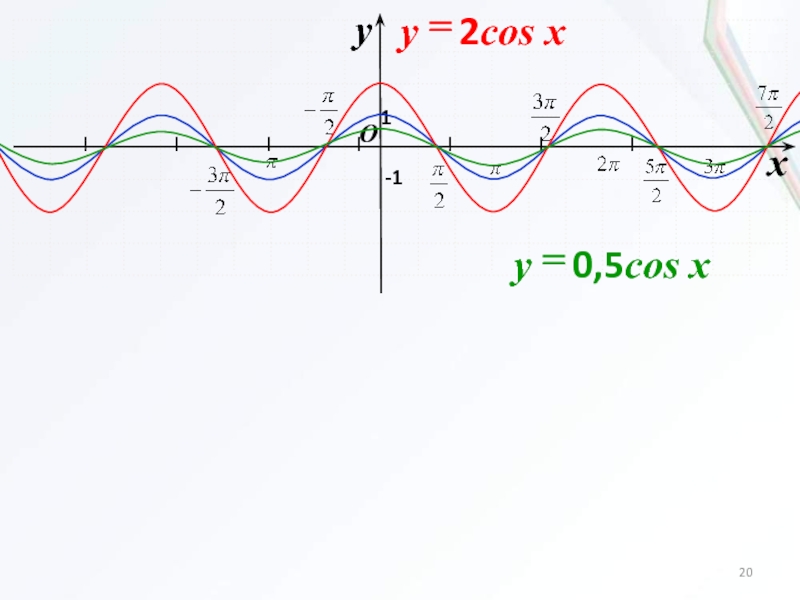 75 . Найдите АС.

Решено

Высота проведённая к основанию равнобедренного треугольника равна 9 см,а само основание равно 24 см.Найдите градусы вписанной в треугольник и описанной около треугольника окружность(и чертёж)

хорды АВ и СД пересекаются в точке Е так,что АЕ=3см,ВЕ=36см,СЕ:ДЕ=3:4.найти СД и наименьшее значение радиуса этой окружности

Параллельные прямые а и в пересечены двумя параллельными секущими АВ и СД, причем А и С принадлежат прямой а , В и Д – прямой в .Докажите, что АС=ВД.

Лестница соединяет точки A и B и состоит из 25 ступеней. Высота каждой ступени равна 14 см, а длина – 48 см. Найдите расстояние между точками A и B (в метрах).

Пользуйтесь нашим приложением

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )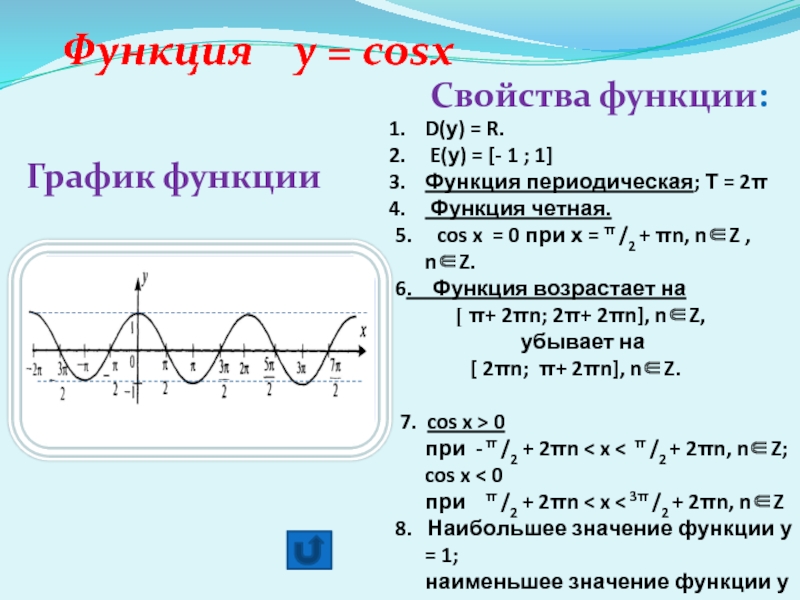
4Найти точное значениеsin(60 град. )
5
Найти точное значение		tan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8Найти точное значениеcos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значение
cos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18
Найти точное значение		cos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значение csc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значение
tan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )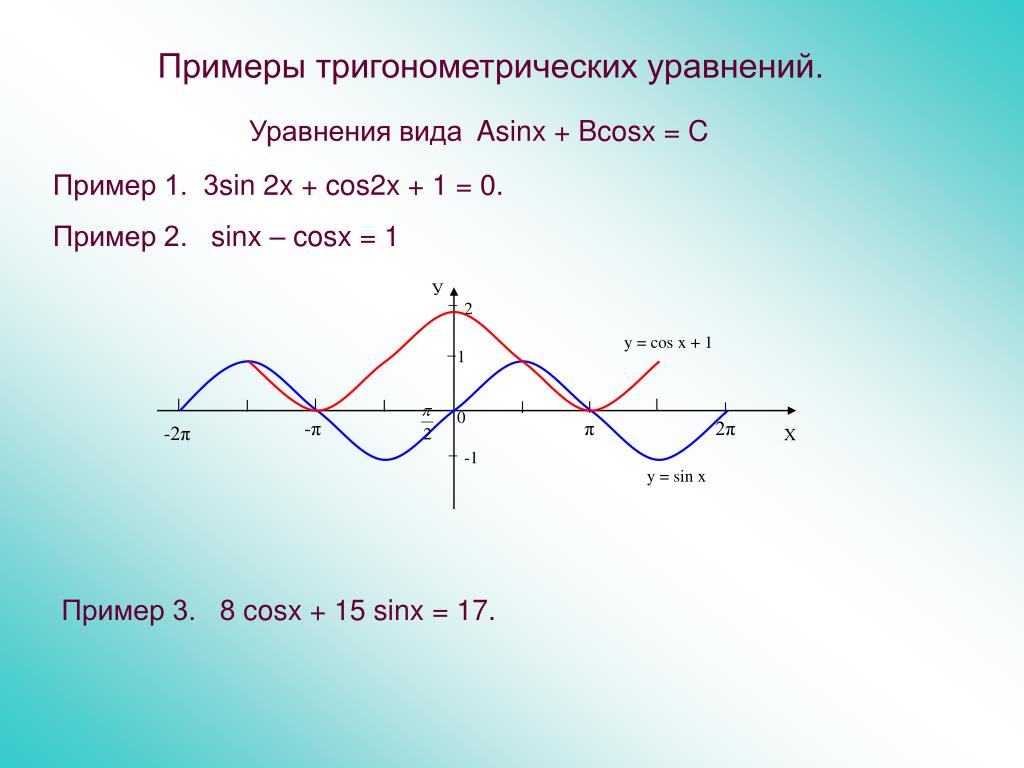
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )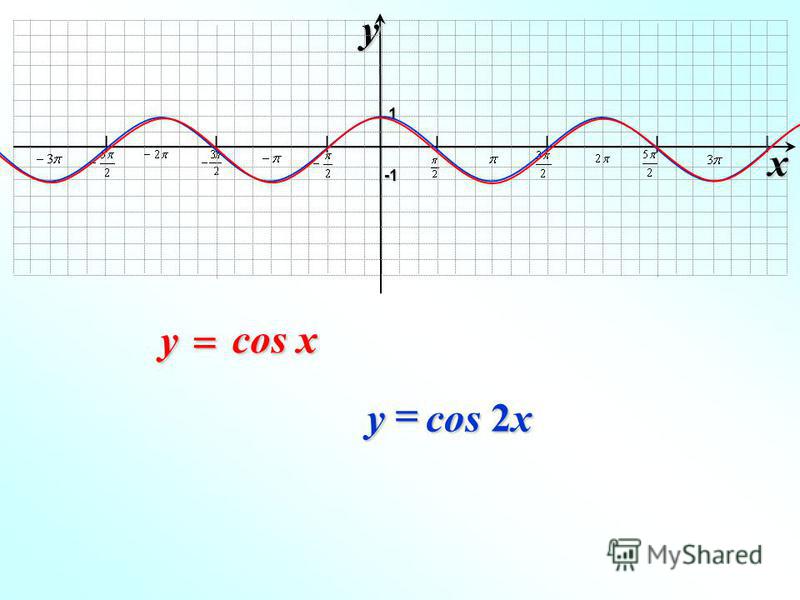
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

тригонометрия — Почему $\cos(x) + \cos(y) — \cos(x + y) = 0$ выглядит как эллипс?

спросил

Изменено 2 года, 1 месяц назад

Просмотрено 4к раз

$\begingroup$

Множество решений $\cos(x) + \cos(y) — \cos(x + y) = 0$ выглядит как эллипс. Действительно ли это эллипс, и если да, то есть ли способ записать его уравнение (без каких-либо триггерных функций)?

Это мотивирует следующий пример. Множество решений $\cos(x) — \cos(3x + 2y) = 0$ выглядит как две прямые линии, и мы действительно можем определить уравнения этих линий.

$$ \начать{выравнивать} \cos(x) &= \cos(3x + 2y) \\ \подразумевает x &= \pm (3x + 2y) \\ \подразумевается x + y &= 0 \text{ или } 2x + y = 0 \end{выравнивание} $$

Можем ли мы сделать то же самое для первого уравнения?

  • тригонометрия
  • конические сечения

$\endgroup$ 92=Д,$$ эллипс с центром в $(a,b)$. (При условии, что квадратичная форма положительно определена, т. е. не является седловой точкой.)

Чем ближе вы подходите к экстремуму, тем более точным будет эллипс. Эффект более выражен, а кривые более симметричны, когда производные третьего порядка малы.

В случае заданной тригонометрической функции, переводя координаты в $(\pi,-\pi)$ для приведения максимума в начало координат, получаем

$$z=\cos(x) +\cos(y)+\cos(x+y). $$ 94}{12}.$$

На приведенном ниже графике показана изокривая $z=0$, рассчитанная с помощью квадрической (коричневатой) и четвертой (розоватой) аппроксимаций; последняя неотличима от истинной кривой, квазиэллипса.

$\endgroup$

3

$\begingroup$

Используя формулу суммы к произведению для косинуса

$$ \cos s + \cos t = 2\cos \tfrac{s+t}{2}\cos \tfrac{s-t}{2} = \cos (с+т)$$

сейчас самое время сделать поворот на 45 градусов $u = \tfrac{s+t}{2}:, v=\tfrac{s-t}{2}, s+t = 2u$

$$ 2 \cos u\cos v = \cos 2u \hspace{0,25 дюйма}\text{or}\hspace{0,25 дюйма} \bbox[5px,border:2px solid #F5A029]{2\cos v = \frac{\cos 2u}{\cos u}}$$

Wolfram Alpha не предлагает значительного упрощения, кроме это .

 импортировать numpy как np
импортировать matplotlib.pyplot как plt
%matplotlib встроенный
х = 2*np. 2-\ квадрат {19}=0.$$
Но при осмотре мы видим, что кривизна графиков не равна.
 Фактически, вот анимация, показывающая полиномиальные отношения от $k=0$ до $k=20.$
 «Эллипсы» расположены вдоль линий $y=\pm x.$
 Кроме того, как предположил мой @MathGemini в комментариях выше, ваш график может быть скоплением конусов в $(x,y,z),$, где $$z=\cos x+\cos y-\cos(x+y).$ $ Однако это не так, потому что поверхность, которую вы получаете, является одной из периодических максимумов и минимумов, что является ожидаемым поведением, заданным уравнением.
 (Это поверхность и ее пересечение с плоскостью $xy$, если смотреть с положительной оси $z-$.)
 (Это поверхность и ее пересечение с плоскостью $xy$, если смотреть с точки $ x>0,y>0,z>0.$)
 (Это поверхность и ее пересечение с плоскостью $xy$, если смотреть снизу плоскости $xy-$.)
 $\endgroup$
 2
 $\begingroup$
 9{-1}\!\!\left(\dfrac{-1+\sqrt{3}}{2}\right)$ и $\beta = \dfrac{2\pi}{3}$, поэтому они должны быть конечными точками большой и малой осей. 2]$$ 
 На контурных графиках ниже вы можете видеть силуэты «эллипсов».
 $\endgroup$
 $\begingroup$
 Из-за симметрии по осям x,y мы можем сделать поворот на 45 градусов, чтобы совместить оси "эллипса" вдоль $x$ и $y$. Пусть используется вращательное преобразование $ x_1 = x-y, y_1 = x+y $ и игнорирует масштабирование осей.
 Контур представляет собой топографию холмов и долин.
 Вблизи точек "Col" (более пологое место для отдыха при альпинизме) между центрами "эллипсов" кривые уровня более гиперболические с седловыми точками.
 На больших высотах они более эллиптичны, а пересекающиеся овалы кажутся эллипсами, но на самом деле это не так.
 Эллипсы являются  непериодическими  , что означает, что они имеют  однократное появление  во всем интервале $x,y$ $ -\infty< x < \infty, -\infty< y < \infty $ размерности 2.
 Но данные кривые представляют собой полиномиальный тригонометрический массив бесконечной степени,  размерность которого не может быть равна двум , как это имеет место для конического сечения. 92 + х\, у =1 $ и $ х\, у + 1 =0 $ . Принимая 3,4,5 числа терминов, можно аппроксимировать «эллипс» или «гиперболу». Итак, то, что вы сейчас видите, это  эллипсов более высокого порядка /гипербол.
 По центру овала выглядит как эллипс. Что касается центральной точки овалов как центра, вы заметите, что..
 профиль, похожий на гиперболу, игнорируется, поскольку, возможно, люди смотрят только на более круглый профиль. Различные центры точек обзора показаны на последней иллюстрации для графиков уровня $ \cos x + \cos y $. 92$. Но он проходит через точки $(\pm1,0)$ и $(0,\pm1)$.
 $\endgroup$
 Решить (dy)/(dx) = cos x, y(0) = 1 2 
  •  Класс 9
  •  Класс 8
  •  Класс 7
  •  Класс 6
  •  IIT JEE
    •  Экзамен
      •  JEE MAINS
      •  JEE ADVANCED 900 22
      •  X ПЛАТЫ
      •  XII BOARDS
      •  NEET
        •  Новый Предыдущий год (по годам)
        •  Физика Предыдущий год
        •  Химия Предыдущий год
        •  Биология Предыдущий год
        •  Чистый Все образцы статей
        •  Образец статей по биологии
        •  Образец статей по физике
        •  Образец Документы Химия
    •  Скачать PDF-файлы
      •  Класс 12
      •  Класс 11
      •  Класс 10
      •  Класс 9
      •  Класс 8
      •  Класс 7
      •  Класс 6
    •  Экзаменационный уголок
    •  Онлайн-класс
    •  Викторина
    •  Ask Doubt в WhatsApp
    •  Поиск Doubtnut
    •  Английский словарь
    •  Toppers Talk
    •  Блог
    •  О нас
    •  Карьера
    •  Скачать
      •  9002 5
         9(2)y=tan y(dy)/(dx)
         6729
         09:08
         Решите:
1. (х+1)dydx=2xy
2.cosx(1+cosy)dx−s∈y(1+sinx)dy=0
         26783
         05:46
         Решить: dydx=−x+ycosx1+sinx
         26996
         9 0002 02:57
         Решите: xdydx=y+cos(1x)
         8491423
         03:22
         हल कीजिए- 
         dydx=−x+ycosx1+sinx.
         112161029
         04:47
         अवकल समीकरण को हल कीजिए- 
         co sx(1+cosy)dx−siny(1+sinx)dy=0
         112161114
         Текстовое решение
         Решить y(1+x)dx+x(1+y)dy=0
         116068925
         02:48
         हल कीजिए dydx+cosxsinycosy=0
         226111264
         02:56
         हल कीजिए dydx=cosxsinycosy
         226111267
         02:28
         সমাধান কর ো : y(1+x)dx+x(1+y)dy=0
         352282362
         02:25
         সমাধান করো: dydx +y(y−1)(x−1)=0
         352282427
         05:35
         Решите дифференциальное уравнение:
(i) (1+y2)+(x−этан−1y)dydx=0
(ii) xdydx+cos2y=tanydydx
         642583417
         08:23
         Решить (x-y+1)dx-(x+y+5)dy=0
         643478313
         02:29
         90 002 Решить (x-y + 1) dx - (x+ y -: 5 )dy = 0.
        No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *