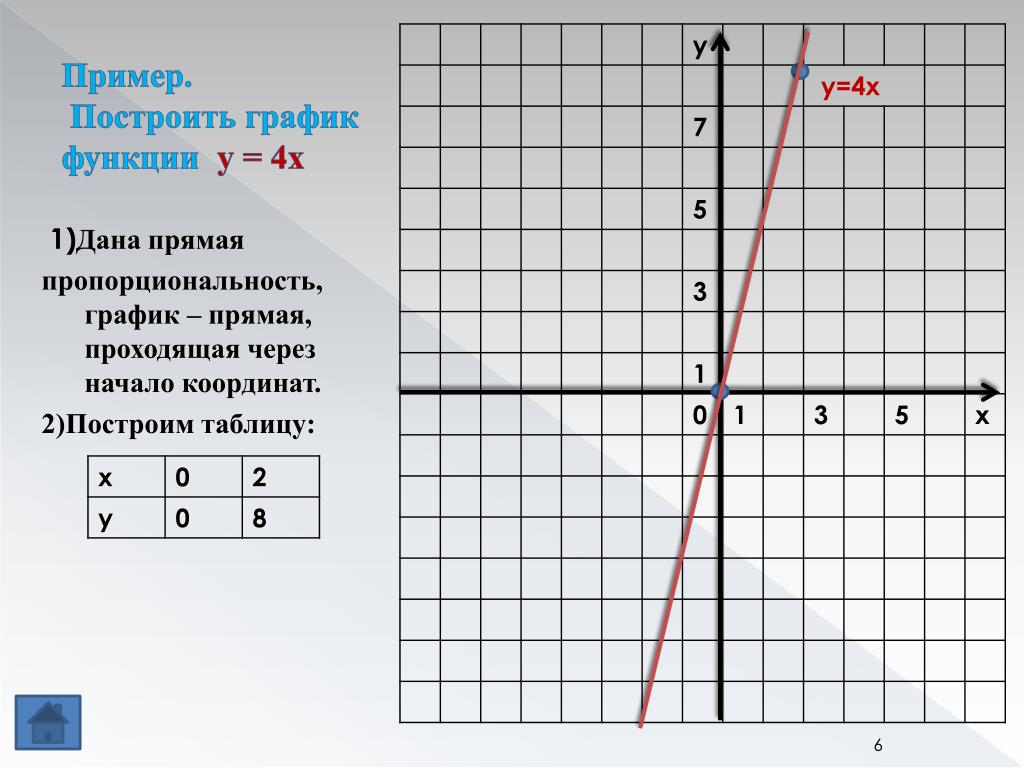
Y x 4 2 график функции: Постройте график функции y = (x-4)^2

Чтобы построить график y = ( x − 4 ) 2, вы сдвинете график y = x 2 на _ на расстояние __ единиц. (pp. 106-108)

Literature guidesConcept explainersWriting guidePopular textbooksPopular high school textbooksPopular Q&ABusinessAccountingBusiness LawEconomicsFinanceLeadershipManagementMarketingOperations ManagementEngineeringAI and Machine LearningBioengineeringChemical EngineeringCivil EngineeringComputer EngineeringComputer ScienceCybersecurityData Structures and AlgorithmsElectrical EngineeringMechanical EngineeringLanguageSpanishMathAdvanced MathAlgebraCalculusGeometryProbabilityStatisticsTrigonometryScienceAdvanced PhysicsAnatomy and PhysiologyBiochemistryBiologyChemistryEarth ScienceHealth ScienceHealth & NutritionNursingPhysicsSocial ScienceAnthropologyGeographyHistoryPolitical SciencePsychologySociology

Learn

Написать

плюс

Precalculus Enhanced с графическими утилитами

6th Edition

ISBN: 9780321795465

Автор: Michael Sullivan, Michael III Sullivan

: Невозможно. См. похожие книги

Precalculus Enhanced with Graphing Utilities

Линейные и квадратичные функции. 4AYU

Глава 3.3, Задача 4AYU

К графику у «=» ( Икс − 4 ) 2 вы сдвинете график у «=» Икс 2 до _______ на расстоянии ________ единиц. (стр. 106-108)

Заполнить: Пропуск данного утверждения «Чтобы построить график y = (x − 4)2, вы сдвинете график y = x2 на _______ на расстояние ______ единиц».

«Чтобы построить график y = (x − 4)2, вы сдвинете график y = x2 вправо на расстояние 4 единицы».

Дано:

Данное утверждение является

«Чтобы построить график y = (x − 4)2, вы сдвинете график y = x2 на _______ расстояние в ______ единиц».

График функции f(x + h), где h положительно, представляет собой график функции f(x) с h единицами, сдвинутыми по горизонтали влево.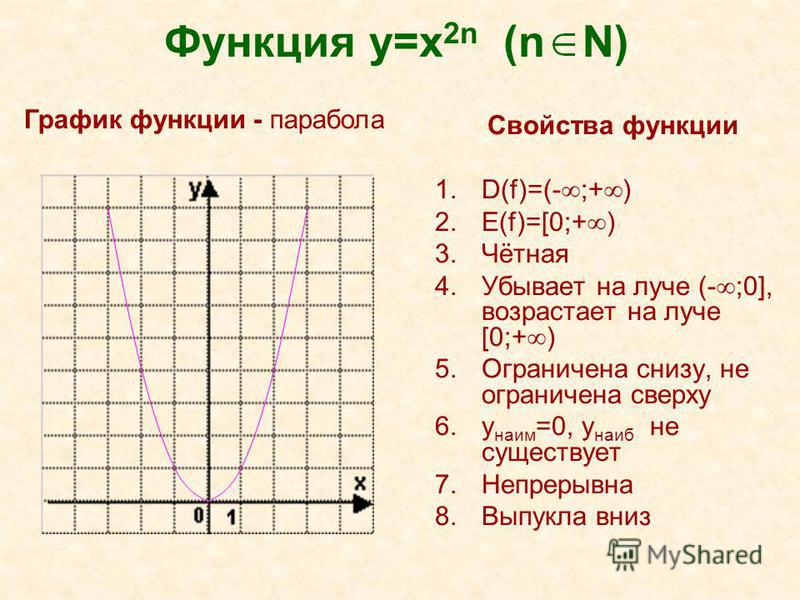

Точно так же график f (x − h), где h положительно, является графиком функции f(x) с h единицами, сдвинутыми по горизонтали вправо.

Следовательно, график y = (x − 4)2 — это график y = x2 с 4 единицами, сдвинутыми по горизонтали вправо.

Глава 3.3, задача 3AYU

ГЛАВА 3.3, Задача 5AYU

. III Sullivan

Издатель: PEARSON

Бесполезно? См. похожие книги

Precalculus Enhanced with Graphing Utilities

Линейные и квадратичные функции. 4АЮ

Lessons 5

Conic Sections

Anatomy of a Parabola

y = ax ² + bx + c y = a(x h) ² + k y = a(x z ₁ )(x z ₂ )

(то же функция, но разные формы уравнения. )

x = ay ² + by + c x = a(y h) ² + k x = a(y z ₁ )(y z ₂ )

_______________________________________________________________

Парабола — это множество точек в плоскости, равноудаленной от фиксированной прямой и фиксированной точки, не лежащей на этой прямой. Эта линия называется директриса . Эта точка называется фокусом .
Графики квадратичных полиномы ( полиномов в одной переменной степени 2 ) являются параболы.

_____________________________________________________________
Как найти вершину: Вершина будет минимальной точкой , если парабола открывается вверх. Вершина будет максимальной точкой если парабола направлена вниз.
o       Если формула написана при заполнении квадратная форма, y = a( x h) ² + k:
вершина прямая (h, k). .
Пример: y = 0,55 ( x 12) ²
+ 17.8. Вершина – это точка (12, 17.8)
Пример: y = -3( х + 15,4) ² 12 Вершина – точка (-15,4, -12)
или Если формула в стандартной форме, y = а х ² + б х + с:
Координата x вершины . Координата затем найти, подставив это значение вместо x . Затем координата y находится с помощью подключив x к функции.
Пример: y = 0,55 x ² 13,2 x + 97
Координата x
координата y равна 0,55(12) ² 13,2(12) + 97 = 17,8
o       ( х z ₂ ):
Координата x вершины будет x — значение посередине между двумя нулями. (если нули настоящие. В противном случае вы можете переписать в одной из других форм и следовать ее методам.
)
Затем координату y можно найти, подставив x в формулу.
Пример: y = 3( х + 13,4)( х + 17,4). Нули х = -17,4 и х = -13,4. x = -15,4 находится на полпути между этими два значения. это х -координата вершины.
Затем, и = 3(-15,4 + 13,4)(-15,4 + 17,4) =
3(-2)(2) = -12. Вершина (-15.4, -12).
o       Вы также можете проверить , используя [2 ^nd ] [TRACE] Функция минимума или максимума на вашем графическом калькуляторе TI.
Если парабола Открывается вбок:
x = a(y k) ² + h Примечание y в квадрате.
Как найти вершину:
o       Если формула написана в завершение квадратная форма, x = a( y k) ² + h:
вершина прямая (h, k) .

Пример: x = 0,25( y 4) ² + 10. Вершиной является точка (10, 4)
Пример: х = -( х + 2) ² 12 Вершина – точка (-12, -2)
или Если формула в виде полинома, x = a y ² + b y + c:
Координата y вершины . Координата x затем найти, подставив это значение вместо y .
Пример: y = 0.25y ² 2y + 14
y -координата
Координата x 0,25(4) ² 2(4) + 14 = 10
Вершина (10, 4).
o       Если формула имеет нулевую форму, x = a( y z ₁ )( y z ₂ ):
y -координата вершины будет значение y посередине между z
1 и z ₂ . (Если нули вещественные. В противном случае, вы можете переписать в одной из других форм и следовать ее методам.)
x -координата может быть найдена путем подстановки y в формула.
Пример: x = -( г — 8)( г + 6). Значения, при которых график попадает на ось Y y = 8 и y = -6. г = 1 находится посередине между этими двумя значениями. Это координата вершины y .
Затем x = -( 1 — 8)(1 + 6) = 49
Вершина есть (49, 1).

Как найти оси Symmetry:
OSESIS OR SYMMETRY:
OSEIS OR SYMMETRY OR SYMMETRY OR SYMMETRY OR SYMMETRY OR SYMMETRY OR SYMMETRY OR SYMMETRY OR SYMMETRY OR SYMMETRY OR SYMMETRY OR SYMMETRY. горизонтальная линия, проходящая через вершину. парабола симметрична относительно этой прямой.

Пример: y = 3( х +13,4)( х + 17,4) имеет вершину (-15,4, -12), а осью симметрии является линия x = -15,4
Пример: y = 0,55( x 12) ² + 17,8 имеет вершина (12, 17. 8) и ось симметрии x = 12.
Пример: х = -( y 8)( y + 6) имеет вершина (49, 1) и ось симметрии
y = 1
Пример: x = 0,25( y 4) ² + 10 has vertex (10, 4) and the axis of symmetry is
y = 4.

How to find Фокус:
o       Расстояние вершины от фокуса
равно . а это старший коэффициент вершины. старший коэффициент — это значение, умноженное на x ² или y ² термин в формуле.
Пример : y = 0,55( х 12) ² + 17,8. Расстояние вершины от фокуса равно 1/(4(0,55)) = 1/(2,2) = 5/11. Фокус — это точка прямо над вершиной на расстоянии 5/11. Эта точка будет (12, 17,8 + 5/11) = (12, ).
Пример: x = 0,25( y 4) ² + 10. Расстояние вершины от фокуса равно 1/(4(0,25)) = 1/(1) = 1. Тогда в фокусе находится точка прямо справа от вершины на расстоянии 1. Эта точка будет (11, 4) .

Пример: x = -( y 8)( y + 6) = -y ² + 2y + 48. Расстояние вершины из фокуса составляет 1/(4(-1)) = — . В этом случае фокус находится в точке непосредственно слева от вершины в расстояние . Эта точка будет (48.75, 1) .

Как найти директрису: (директриса находится вне параболы)
o       директриса на том же расстоянии от вершины, как фокус. Это расстояние снова равно 1/(4a).
Пример : y = 0,55( x 12) ² + 17,8. Расстояние вершины от фокуса равно 1/(4(0,55)) = 1/(2,2) = 5/11. Тогда директриса горизонтальная линия прямо под вершиной на расстоянии 5/11. Эта линия будет быть у = 17,8 5/11 г = .
Пример: x = 0,25( y 4) ² + 10. Расстояние вершины от директрисы равно 1/(4(0,25)) = 1/(1) = 1. Направляющая тогда линия слева от вершины на расстоянии 1. Эта линия является вертикальная линия x = 9

Как найти нули:
o       Если формула в нулевой форме, y = а( х z ₁ )( х z ₂ ):
Нули прямые, z ₁ и г ₂ .
Пример: y = 3( х + 13,4)( х + 17,4). Нули 13,4 и 17,4.
o       Если , то формула дополняет форму квадрата: y = a(x h) ² + к:
Вы можете решить уравнение 0 = a(x h) ² + к. (Мы будем делать примеры в классе)
o      Если формула в стандартной форме, y = ax ² + bx + c:
Вы можете использовать Квадратная формула . Кстати, квадратичная формула — это процесс завершения квадрата, а затем решения для нулей.

о Вы также можете используйте опции [2 ^nd ] [TRACE] Zeros или Intersect на вашем калькуляторе как мы обсуждали в классе.
Как найти точку пересечения с осью Y:
o       Подставьте 0 вместо x в формулу и понять, что такое и .
Пример: y = 0,55( х 12) ² + 17,8. ۠ y = 0,55(0 12) ² + 17,8 y = 0,55(-12) ² + 17,8 97
(0, 97) — точка пересечения y .
о Если парабола открывается вбок , то график имеет два y-перехвата, найденных так же, как мы только что нашли нули.
Пример: x = -( y 8)( и + 6). и -перехваты находятся на виду. Это (0, 8) и (0, -6).
Пример: x = 2 года ² + 7,5 года 12,5. Y-перехваты находятся с помощью квадратичная формула.
. Y-перехваты равны (0, 1,25) и (0, -5).
Другое Обзор Информация

Коэффициент х ² term — это значение, умноженное на x ² . Это значение a , в
y = a x ² + bx + c. Информативно о форма и направление параболы .
Если a — это отрицательное число , тогда открывается парабола вниз и имеет
максимальный пик в вершине. Если а положительный , то парабола открывается вверх и
имеет точку минимальной долины в точке вершина.

Коэффициент у ² term — это значение, умноженное на y ² . Это значение и , в
х = а у ² +by + c. Информативно о форма и направление параболы .
Если , то является отрицательным число, то парабола открывается влево .Если положительное , то
парабола открывается вправо .

Если величина или абсолютное значение a на меньше 1 , парабола на шире чем общий y = x ² . Если модуль или абсолютное значение a на больше чем 1 , то парабола на уже и круче , чем общая y = х ² .
Пример. у =0,25(х — 12) ² +5 = 0,25(х — 12)(х — 12) + 5 = 0,25 (х ² — 24х + 144) + 5 = 0,25х ² — 6х + 36 + 5 = 0,25х ² -24x + 41
То есть y = 0,25(x — 12) ² + 5 эквивалентно y = 0,25x ² — 6x + 41
График y = 0,25x ² — 6x + 41 шире и менее крутой чем график y = x ² . (Может быть полезно подумать, что в беря 25% чего-то, вы умножаете на 0,25 и получаете только часть первоначальная сумма. …набирается медленнее) Эта парабола направлена вверх и имеет точку минимума. Эта минимальная точка является вершиной. (12, 5)

Пример. Примечание : у = -4(х + 7) ² — 2 = -4(х + 7)( х + 7) — 2 = -4(х ² + 14х + 49) — 2 =
= -4х ² — 56х — 196 — 2 = -4x ² -56x -198

График y = -4(x + 7) ² — 2 уже и круче графика y = х ² (Это может помочь подумать о том, как умножение на 4 дает большее значение …. поднимается быстрее, чем умножение на 1.) Он открывается вниз и имеет максимальную вершину в вершине (-7, -2).

Вот график из трех параболы. Два из вышеперечисленных упомянутые графики. Попробуйте определить, что есть что.

Параболы имеют эксцентриситет всегда равный 1.

00002
1. Дано y = x ² , найти вершину, фокус, направляющая, ноль и ось симметрии. Нарисуйте график.

2. По x = y ² найти вершину, фокус, директриса, y-перехват и ось симметрия. Нарисуйте график. Переписать как верхняя функция и нижняя функция, чтобы построить график на вашем графике калькулятор.

3. Дано x = -0,2(y 9) ² + 3, найти вершина, фокус, директриса, y-перехваты, x-пересечение и ось симметрии. Нарисуйте график.

4. Дано y = (x + 3,5) ² — 8, найти вершину, фокус, директриса, нули, y-перехват и ось симметрии. Нарисуйте график. Перепишите как верхнюю функцию и нижнюю функцию, чтобы построить график на ваш графический калькулятор.

5. Дано y = -x ² + 6.25, найти вершину, фокус, директриса, нули, y-перехват и ось симметрии. Нарисуйте график.

Ответ:_________________________________________________________
Y = — (x 0) ² + 6,25 вершина: (0, 6. 25) открывается вниз
a = -1 , 1/(4a ) = -1/4 фокус равен (0, 0) направляющая равна y = 6,5

нули появляются там, где y = 0 0 = -x ² + 6,25 6,25 = х ² x =

Y -Intercept -это точка, где x = 0. y = -0 ² + 6,25, (0, 6,25)

AXIS at Symtetry of Symtetry of Symtetry of Symtetry of Symtetry: Symtetry of Symtetr. x = 0 или ось y

_______________________________________________________________________
6. Дан x = 2(y + 104) 2
05 + 14 найти вершину, фокус, директрису, x-пересечение и ось симметрии. Нарисуйте график. Перепишите как верхнюю функцию и нижнюю функцию, чтобы график на вашем графическом калькуляторе.

Ответ:_____________________________________________________________

Вершина = (14, -10) открывается вправо a = 2 1/(4a) = 1/8

Фокус (14,125, -10) направляющая: x = 13,875 оси симметрии: y = -10

Примечание.
No related posts.