3.1 Некоторые U-образные графики | G’Day Math
Руководство для учителей PDF
РАЗДАТОЧНЫЕ МАТЕРИАЛЫ ДЛЯ СТУДЕНТОВ
Dexter_Course on Quadratics
Один из первых — обычно первый — непрямолинейный график, который встречается в школе, — это график квадратного уравнения . Сначала нарисуйте график, связанный с квадратным уравнением, чтобы увидеть красивую симметричную U-образную кривую.
Для ясности, график уравнения 92\) всегда вертикально?
(Все решения практических вопросов приведены в конце РУКОВОДСТВА ДЛЯ УЧИТЕЛЯ по этому опыту.)
это технически неправильно. Давайте просто поймем, что я имею в виду форму графика квадратного уравнения.
Эти U-образные графики полны сюрпризов. Вот один.
92\) (ну, на самом деле, поверните его) против часовой стрелки вокруг начала координат всего на \(0,01\) градусов.
Пересекает ли ось \(y\) этот наклонный график при каком-то большом ненулевом значении? Опять же, решения всех этих практических задач приведены в РУКОВОДСТВЕ ДЛЯ УЧИТЕЛЯ. Но позвольте мне помочь вам с этим вопросом прямо сейчас, так как на него кажется чрезвычайно сложным ответить.
Математики тоже люди, и их тоже пугают вопросы и математические задачи. Но одна из техник, которую они часто используют, когда сталкиваются с вопросом, на который не знают, как ответить, — это изменение вопроса!
Что самое страшное в этом вопросе? Он наклоняет U-образный график. Как на самом деле это сделать? лично не знаю! Итак, давайте вместо этого наклоним что-нибудь другое. Что, если мы сохраним график прежним и вместо этого наклоним вертикальную ось на \(0,01\) градусов по часовой стрелке? Пересекает ли эта наклонная линия U-образный график?
О! Подожди! Это эквивалентно ответу на исходную задачу?
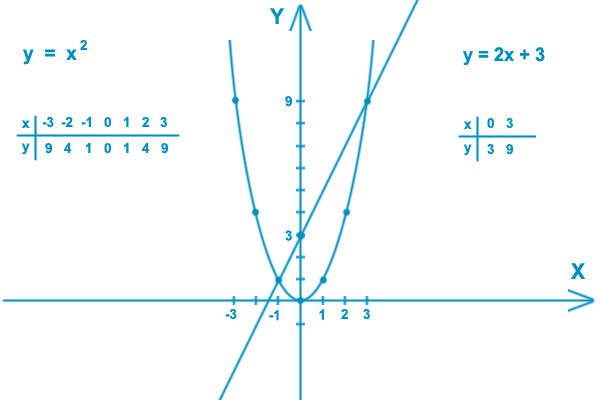
Вот самый большой сюрприз этих U-образных графиков.
Многие люди, кажется, пропускают этот шок, когда впервые изучают квадратные уравнения. 92\) представляет собой симметричную U-образную кривую. График \(y=2x\), с другой стороны, не является! Если хотите, это прямая линия, проходящая через начало координат с антисимметрией — график данных поднимается вправо, а уменьшается влево.
Теперь странный вопрос: какая картина получится, если «сложить» эти два графика?
Что мы могли этим сказать?
Давайте посмотрим на каждое значение \(x\) и добавим соответствующие значения \(y\). Например: 92\), а линейное выражение \(y=bx+c\) обязательно даст выражение, график которого представляет собой тот же симметричный U-образный график, возможно, немного сглаженный или закругленный, а может быть, сдвинутый в новое положение на плоскости .
Это просто поразительно!
Эта U-образная форма удивительно надежна, и невозможно не восхищаться ее прочностью.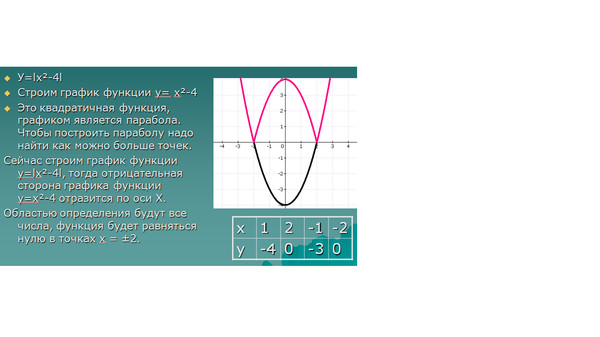
Конечно, можно объяснить, почему это графическое явление имеет место, анализируя алгебру квадратных уравнений. Но, надеюсь, вы были в равной степени потрясены этим явлением, когда впервые начали учиться строить квадратичные графики.
Комментарий: Если вы ищете обзор квадратичных уравнений, их алгебры и их графиков, полный сюрпризов и потрясений, см. www.gdaymath.com/courses.
Теперь о проблеме, которую мы рассмотрим в этих заметках.
Насколько вездесущи эти U-образные кривые из квадратичных уравнений?
Являются ли U-образные кривые, которые мы видим во всевозможных контекстах, в основном одной и той же U-образной формой (может быть, как я уже сказал, просто немного крутой или сплющенной и перемещенной или даже перевернутой)? Являются ли эти кривые настолько устойчивыми, чтобы быть универсальными по своей природе?
Например, школьная физика говорит нам, что траектория брошенного предмета следует дуге квадратичного графа.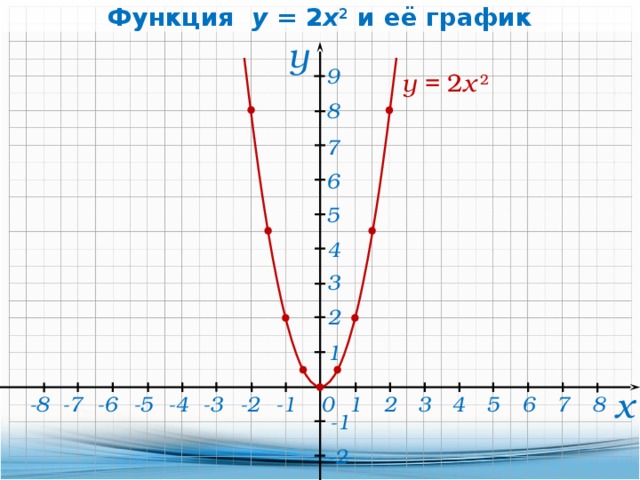
Это правда? Откуда нам знать?
Известный итальянский математик и физик Галилео Галилей (1564-1642) задавался вопросом о форме цепи, висящей между двумя полюсами. (Мы видим эту форму в висящих линиях электропередач, в форме веревок, которые окружают скульптуры в художественных музеях, и так далее.) Это та же квадратичная U-образная форма? Откуда мы могли знать?
Древнегреческие ученые использовали геометрию для описания всевозможных специальных кривых. Они назвали одну из своих кривых параболой , и она тоже имеет U-образную форму.
Алгебру не изобрели еще 800 лет или около того, поэтому эти ученые не задавались вопросом: Задается ли эта кривая квадратным уравнением? Но мы можем! Итак, это? Откуда мы могли знать?
Знаменитая арка ворот Сент-Луиса в штате Миссури, США, имеет форму квадратичной кривой?
Является ли график уравнения, в котором написано мое прозвище, ДЖИМ, квадратичным? Эта кривая проходит через точки
\(x=1\), \(y=10\) и 1 st буква моего имени есть 10 th буква алфавита J;
\(x=2\), \(y=9\) и 2 й буква моего имени есть 9 й буква алфавита, I;
\(x=3\), \(y=13\) и 3 rd буква моего имени есть 13 th буква алфавита, М.
Давайте ответим на все эти и другие вопросы! Нас ждет крутое приключение!
Присоединяйтесь к обсуждению в Facebook и Twitter и поделитесь этой страницей, используя кнопки ниже.
7.4 Преобразование и графическое отображение квадратичных чисел и радикалов — Алгебра среднего уровня
Цели обучения
- Использование преобразования, сжатия, расширения и отражения для преобразования функций и их графиков
- Выразите график преобразованной функции через исходную родительскую функцию
До сих пор мы работали с основными линейными, квадратичными, радикальными, экспоненциальными и логарифмическими функциями, но эти функции часто появляются в разных формах. В этом разделе представлен упрощенный визуальный пример нескольких способов преобразования функций: перевод, сжатие, расширение и отражение.
Перевод
На приведенном ниже графике показан пример «функции» \(H(x)\), которая рисует маленький красный домик в начале координат.
У дома есть точка рядом с трубой с координатой \((1,1)\). Если мы вычтем \(4\) из каждого выхода функции, мы получим \(H(x)-4\), что соответствует маленькому синему домику, сдвинутому вниз. Поскольку выходные данные функции соответствуют значениям по оси Y, мы можем сдвинуть функцию вверх, добавив или вниз, вычитая из всей функции.
Ось x соответствует входу функции, поэтому, если мы хотим сдвинуть дом вправо или влево, нам нужно будет изменить то, что находится внутри скобок функции (функция аргумент ) . Горизонтальные сдвиги часто менее интуитивны, чем вертикальные сдвиги. Чтобы заставить дом сдвинуться на 3 единицы вправо, нам нужно вычесть 3 из входных данных. Почему? Если мы хотим, чтобы наша опорная точка рядом с дымоходом располагалась в \(x=4\), то нам нужно, чтобы вход \(x=4\) в нашей преобразованной функции обрабатывался так, как если бы мы положили \(x= 1\) в исходную функцию. Это достигается путем создания аргумента функции \((x-3)\).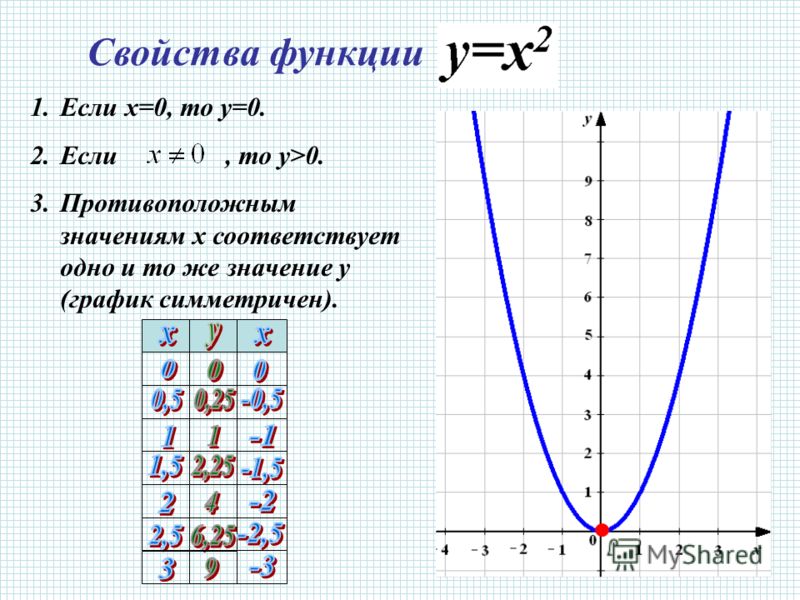
Когда наше значение x равно \(4\), то аргумент нашей преобразованной функции равен \((4-3)\), и функция отвечает так же, как исходная функция, когда аргумент был \(1\).
Горизонтальные сдвиги кажутся обратными, но это только потому, что мы влияем на ввод, а не на вывод функции. Мы сдвигаем функцию вправо, вычитая из аргумента, и сдвигаем влево, добавляя к аргументу.
Расширение, сжатие и отражение
Мы также можем растягивать или сжимать наш дом путем умножения. Как и в случае перевода, изменения в направлении Y производятся путем изменения вывода, который является результатом всей функции. Изменения в направлении x производятся путем изменения входных данных, которые являются аргументами функции. Как и в случае перевода, изменения в направлении x будут казаться обратными.
На приведенном ниже графике показан пример расширения и укорочения дома: \(\frac{1}{2}H(\frac{1}{3}x)\). Функция преобразуется путем умножения всего вывода на \(\frac{1}{2}\). Это делает новый дом только вдвое ниже оригинала.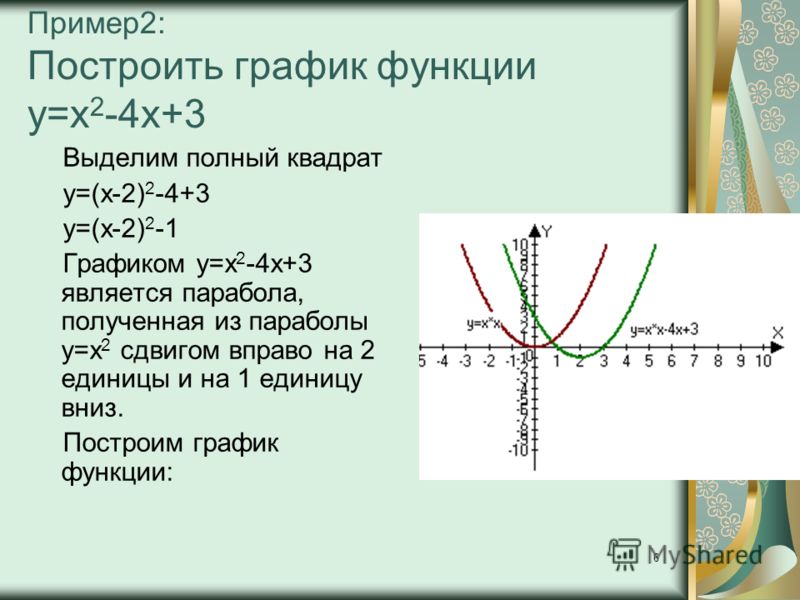
Аргумент функции умножается на \(\frac{1}{3}\), делая дом в три раза шире. Если мы поместим нашу контрольную точку в \(x=3\) в нашу преобразованную функцию, мы хотим, чтобы она реагировала так, как если бы мы поместили \(x=1\) в нашу исходную функцию, создав угол крыши у дымохода. . Когда \(x=3\), аргумент нашей функции равен \(\left(\frac{1}{3}\cdot3\right)\), что равнозначно подстановке \(1\) в исходную функцию.
Другой дом был отражен по вертикали и сжат по горизонтали: \(-3H(2x)\). Отражения возникают, когда мы умножаем на отрицательные числа. Замена \(H(x)\) на \(-3H(x)\) делает дом в три раза выше и перевернутым. Наша контрольная точка перемещается из исходного положения \(y=1\) на конечную высоту \(y=-3\). Мы делаем дом вдвое шире, увеличивая аргумент в два раза. Несмотря на то, что \(x=\frac{1}{2}\) в нашей контрольной точке, аргумент функции равен \(\left(2\cdot\frac{1}{2}\right)\), а функция реагирует так, как если бы это было \(H(1)\), что является местоположением ссылки в исходном доме.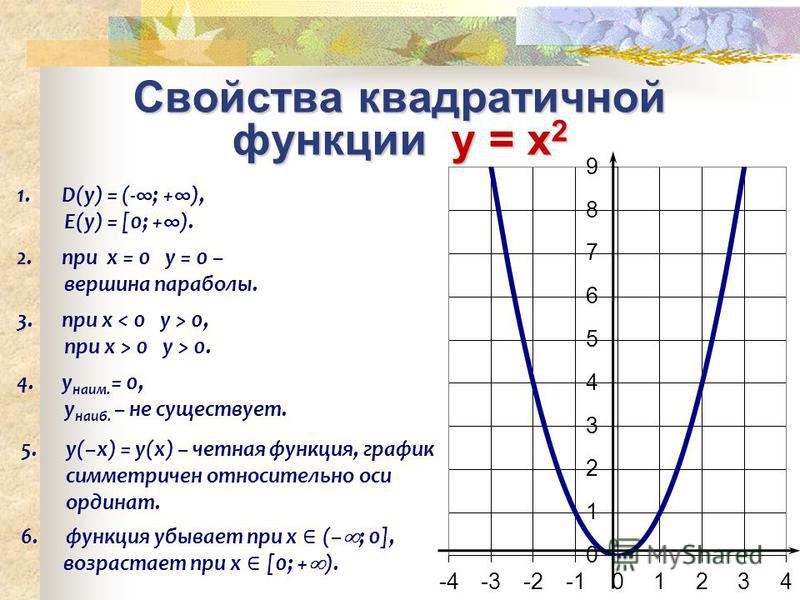
Наш последний пример на рисунке выше объединяет несколько преобразований: \(-1\cdot H(x+4)-1\). Дом был инвертирован путем умножения на -1, сдвинут влево путем прибавления к аргументу и сдвинут вниз путем вычитания из функции. Когда мы подставляем \(x=-3\) в качестве нашей контрольной точки, аргумент функции становится \(\left(-3+4\right)\), и функция создает угол у дымохода, как и требовалось. Обратите внимание, что порядок операций подразумевает, что значения по оси Y умножаются на \(-1\) до того, как они будут сдвинуты вниз на 1. Наша контрольная точка начинается на высоте \(1\) и заканчивается на высота \(-2\), потому что \(-1\cdot1-1\) равно \(-2\).
Преобразования функции главного квадратного корня
В последнем разделе показано, как «функция», рисующая домик, может быть преобразована путем перемещения, сжатия, расширения и отражения. Те же концепции применяются к традиционным функциям, таким как \(f(x)=\sqrt{x}\). На рисунке ниже эталонная кривая показана серым цветом.
Начните с таблицы значений. Тогда подумайте о таблице как об упорядоченных парах.
| х | ж ( х ) |
|---|---|
| \(−2\) | \(4\) |
| \(−1\) | \(1\) |
| \(0\) | \(0\) |
| \(1\) | \(1\) |
| \(2\) | \(4\) |
Постройте точки \((-2,4), (-1,1), (0,0), (1,1), (2,4)\)
Так как точки не на линии, вы не можете использовать линейку.
Обратите внимание, что форма напоминает букву V с закругленным низом. Это называется парабола. Половина параболы является зеркальным отражением другой половины. Линия, идущая по середине, называется линией симметрии или линией отражения , и в данном случае эта линия является осью y . Самая нижняя точка на этом графе называется вершиной .
В следующем видео показан пример построения квадратичной функции с использованием таблицы значений. 92\), поэтому \(a=1\), \(b=0\) и \(c=0\).
Изменение \(a\) масштабирует параболу по вертикали, в результате чего она становится шире или уже. Когда \(a\) положителен, график открывается вверх, а когда \(a\) отрицателен, график открывается вниз.
- Парабола направлена вверх, если \(а\) > 0, и вниз, если \(а\) < 0.
- \(a\) изменяет ширину параболы.
Парабола сужается, если \(\left|a\right|\gt 1\), и шире, если \(\left|a\right| \lt 1\). - Вершина зависит от значений \(a\), \(b\) и \(c\). Вершина расположена в точке \((h,\;k)\), где \(h=-\frac{b}{2a}\) и \(k=f(h)\).
- Каждая парабола пересекает ось y в точке \(f(0)\), которая является координатой \((0,\;c)\).
Парабола сужается, если \(\left|a\right|\gt 1\), и шире, если \(\left|a\right| \lt 1\).В следующем примере мы покажем, как вы можете использовать свойства параболы, чтобы помочь вам построить график, не вычисляя исчерпывающую таблицу значений.
В следующем видео показан еще один пример построения квадратичной функции с использованием вершины.
Учитывая то, что мы узнали о квадратичных функциях, мы можем построить уравнение квадратичной функции, если нам задано положение вершины и еще одной точки на кривой.
Резюме
Создание графика функции — это один из способов понять взаимосвязь между входными и выходными данными этой функции. Создать график можно, выбрав значения для x , найдя соответствующие значения y и нанеся их на график.