Y x6 график: График y = f(x) = x/6 (х делить на 6) постройте график функции и изобразите его. Исследуйте данную функцию. [Есть ответ!]

Лучший ответ по мнению автора

04. 12.18 Лучший ответ по мнению автора Ответ понравился автору вопроса

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Коля, Дима и Саша собрали. ..

за 3 корочки хлеба и 2 кружки молока надо заплатить 20 монет. Сколько стоит 1 корочка хлеба, если она дешевле 1 кружки молока на 5 монет

Решено

Сколькими способами можно разместить числа 1, 2, 3, 4, 5, 6, 7, 8 и 9 в девяти клетках фигуры, изображенной на рисунке, так, чтобы сумма чисел в…

Используя в каждом случае 4 раза цифру 7 , знаки арифметических действий и , если надо , скобки , составь 5 выражений со значениями 5,6,7,8,9, например 7-(7+7):7=5

Решено

Найти расстояние от начала координат до плоскости, проходящей через три заданные точки: А(1;2;-1), В(3;0;1), С(-1;1;3)

Пользуйтесь нашим приложением

ЕГЭ по информатике 2022 — Задание 15 (Простым языком)

Натуральные числа — это целые, положительные числа. Например: 1, 2, 3, 4, и т. д.

Важно: Если было строгое неравенство, то оно станет нестрогим, и наоборот, если было неравенство нестрогим, то оно станет строгим.

Получилось выражение (X ≥ 7) ∧ (X

Обратимся к самому начальному логическому условию. Там два выражения соединятся логическим сложением. Значит, мы должны объединить те случаи, когда у нас первое выражение становится истинным (X=1, X=2), и те случаи, когда второе выражение становится истинным (X = 7, X = 8, X = 9).

Получается всего 5 натуральных чисел удовлетворяют изначальному логическому условию.

Для какого наибольшего целого неотрицательного числа A выражение

тождественно истинно, т.е. принимает значение 1 при любых целых положительных x и y ?

Первый способ (с помощью питона).

for A in range(0, 300):
    k=0
    for x in range(1, 301):
        for y in range(1, 301):
            if (x >= A) or (y >= A) or (x * y 

В первом цикле перебираем значения для A. Здесь мы пытаемся подобрать ответ в диапазоне от 0 до 300. Этот диапазон меньше, чем в прошлой задаче. Потому что здесь три вложенных цикла, и если перебирать числа от 0 до 1000, то программа может работать очень долго. При необходимости можно указать другой диапазон.

Для каждого A устанавливаем счётчик k в ноль.

Затем перебираем все числа в диапазоне от 1 до 300 (включительно) для переменных x и y, тем самым имитируем фразу «для любых x и y».

Если логическое выражение сработает при каждом значении x и y, то считается, что значение A нам подходит, и в счётчике по окончанию вложенных циклов будет значение 90000 (300 * 300 = 90000).

Наибольшее число, которое напечатает программа равно 15.

Второй способ (с помощью рассуждений).

Здесь есть три выражения в скобках, которые соединены логическим сложением. При логическом сложении достаточно хотя бы одного выражения, где будет истина, чтобы всё общее выражение было истинно.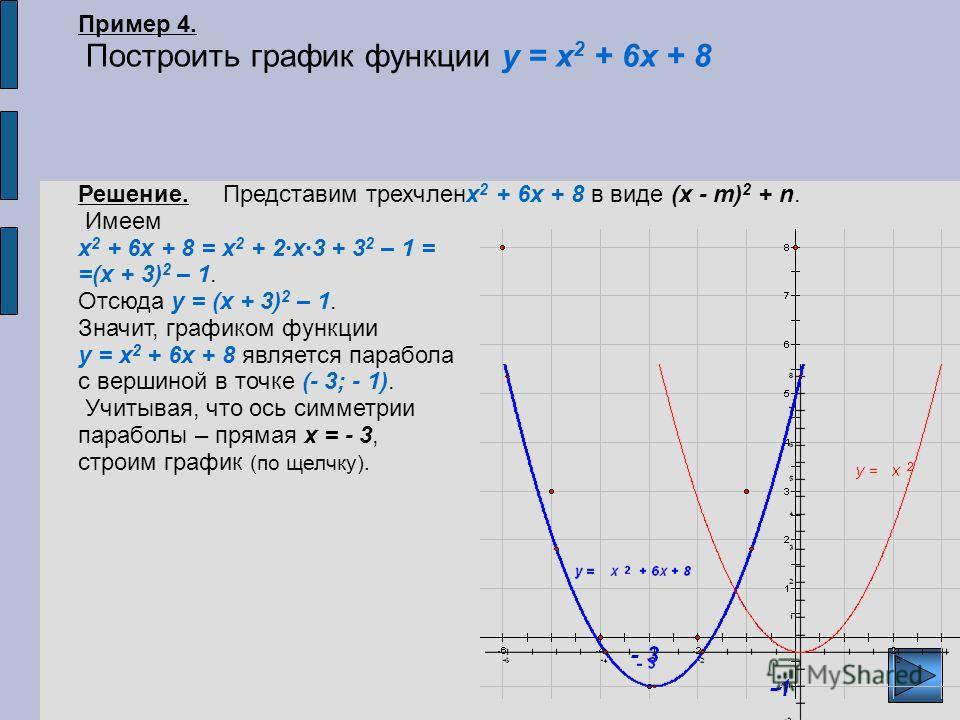

Если мы сделаем A слишком большим, к примеру A = 250, то найдутся такие x = 16, y = 16, при которых все три условия в скобках не будут выполняться, и, значит, всё общее выражение будет ложным.

Следовательно, нам нужно выбрать таким A, чтобы не было возможности подобрать x, y, при которых все три выражения ложны.

Сделаем так: пока x и y меньше A, должно «работать» третье выражение в скобках. Как только x или y сравняются с A — начинают «работать» первое или второе выражение.

До какого же максимального значения могут дойти x и y, чтобы перемножение этих двух чисел было меньше или равно 205 (x * y
15 * 15 = 225
14 * 14 = 196

Получается, пока числа x и y меньше 15, «выручает» третье выражение (x * y ≤ 205), как только станут x ≥ 15 и y ≥ 15, будут «работать» первое и второе выражение.

Отсюда получаем, что максимальное число A = 15

Задача (Функция ДЕЛ)

Обозначим через ДЕЛ(n, m)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?

Решение:

Первый способ (с помощью питона).

def D(n, m):
    if n%m==0:
        return True
    else:
        return False

for A in range(1, 1000):
    k=0
    for x in range(1, 1001):
        if D(x, A) or (not(D(x, 6)) or not(D(x, 9))):
            k=k+1
    if k==1000:
        print(A)

Здесь мы формируем функцию ДЕЛ (функцию D). Если n делится на m, то функция возвращает Истину, в противном случае функция возвращает Ложь.

Далее решаем примерно так же, как и в прошлых задачах: для каждого числа A перебираем все значения x. Следование расписываем по формуле A ⟶ B = ¬A ∨ B.

Наибольшее число здесь получается равно 18.

Второй способ (с помощью рассуждений).

Рассмотрим случай, когда в левой части логического выражения будет 1, а в правой 0. В остальных случаях беспокоится не за что, потому что вся формула будет выдавать истину.

Посмотрим, когда в правой части получается ноль. Функция ДЕЛ(x, 6) должна выдавать истину. Т.е. x должен делится на 6. А функция ¬ДЕЛ(x, 9) должна выдавать ноль. Т.е. без отрицания ДЕЛ(x, 9) должна выдавать истину. Значит, x так же делится на 9.

Чтобы выполнялся случай, когда в правой части получается ноль, икс должен быть равен x = 3*3*2*n (n ∈ N). Т.е. получается, что икс должен быть кратен 18.

Т.е. получается, что когда x делится на 18, в правой части логического выражения будет получатся ноль. Чтобы спасти ситуацию, мы должны в левой части логического выражения не получать 1.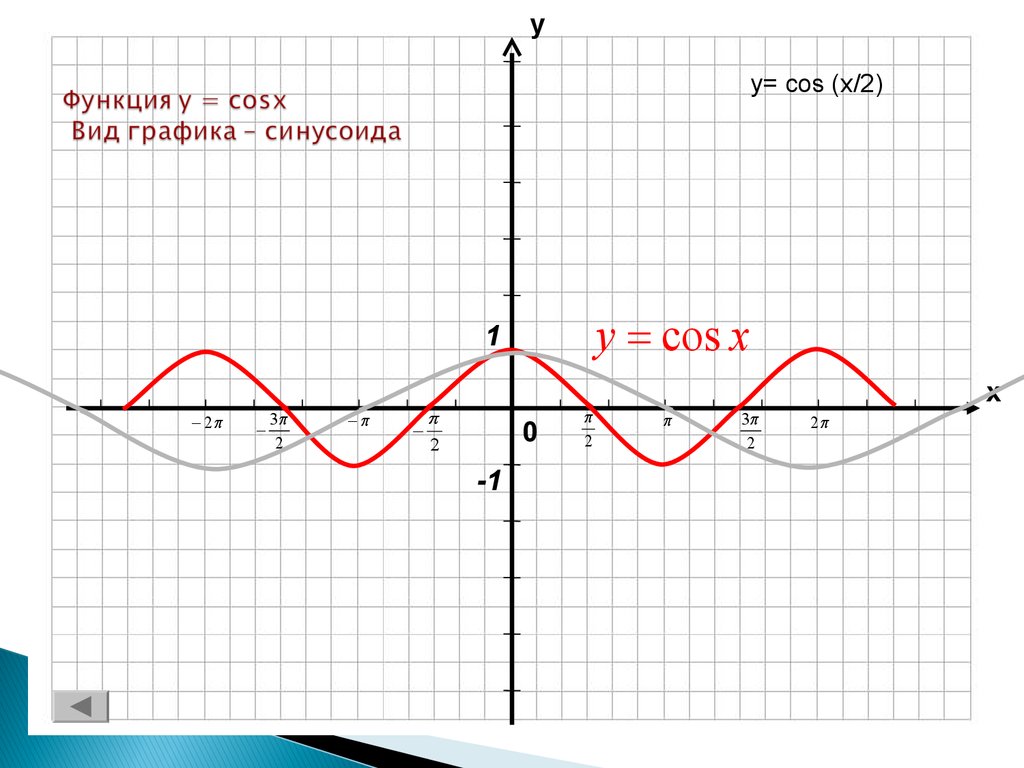 Следовательно, ¬ДЕЛ(x, А) должно выдавать ноль. Значит, ДЕЛ(x, А) должно выдавать 1. Таким образом, приходим к выводу, что A должно равняться 18.

Если получится опасная ситуация, когда x кратен 18, то она будет нейтрализована, ведь в левой части будет получатся ноль.

Ещё один важный тип задач 15 задания ЕГЭ по информатике 2022

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 1110₂ & 0101₂ = 4

Для какого наименьшего неотрицательного целого числа A формула

тождественно истинна (то есть принимает значение 1 при любом неотрицательном целом значении переменной x)?

Первый способ (с помощью питона).

for A in range(0, 1000):
    k=0
    for x in range(0, 1000):
        if x&51==0 or (x&A!=0 or x&25!=0):
            k=k+1

    if k==1000:
        print(A)

Здесь следование преобразовываем по формуле: A ⟶ B = ¬A ∨ B. Так же и A, и x неотрицательные числа. Поэтому мы перебираем их диапазон, начиная с нуля. Из-за этого в цикле, который перебирает переменную x, мы устанавливаем верхнюю границы равной 1000, а не 1001. Тогда тоже будет 1000 повторений в этом цикле.

Наименьшее число равно 34.

Второй способ (с помощью рассуждений).

Переведём числа 51 и 25 в двоичную систему.

Формула будет тождественно ложна, когда

Этого допустить нельзя!

При каком x получается в левой выражении формулы истина ? Если у икса в двоичном представлении в тех разрядах, где у числа 51 стоят 1, будет хотя бы в одном месте 1.

Рассмотрим правое выражение формулы. Ноль получается в единственном случае:

Рассмотрим выражение x&25 ≠ 0. Чтобы в этом логическом выражении получился ноль, нужно x&25 = 0.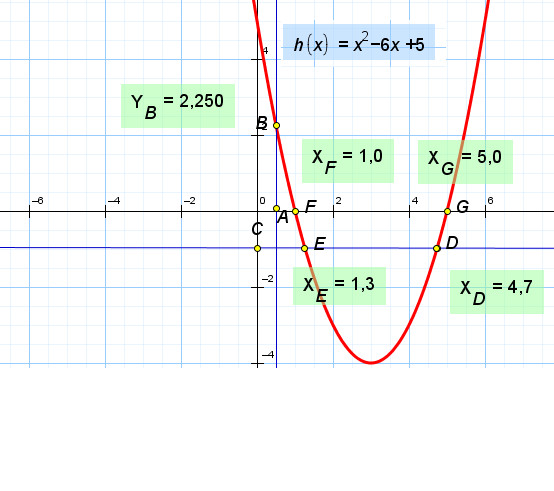 Посмотрим на двоичное представление числа 25. В тех разрядах, где стоят единицы, у икс должны быть нули (для x&25 = 0).

Сформулируем окончательное условие для x, при котором возникает опасность превращение общей формулы в ложь.

Нам нужно «поломать эту песенку» с помощью x&A = 0. Т.е. нельзя допускать, чтобы это выражение было истинно.

Получается, что A = 100010₂. Это наименьшее из возможных число, при котором мы точно себя обезопасим от того, что вся формула будет ложна.

A = 100010₂ в десятичной системе будет 34.

Ещё один тип задач 15 задания ЕГЭ по информатике

На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула (¬(x ∈ P) → (x ∈ Q)) → (x ∈ A ) верна при любых значениях x.

Первый способ (с помощью питона).

def F(a, b, x):
    if a 

Получается ответ 14. Более подробно, как решать задачи на ОТРЕЗКИ из 15 задания ЕГЭ по информатике на Python, можете посмотреть в этой статье.

Второй способ (с помощью рассуждений).

Если будут такие варианты:

То нам беспокоится не о чём. Потому что формула всегда будет истинна! (см. таблицу истинности для следования →)

Нас же будет интересовать этот случай.

При таком раскладе вся формула будет ложна! Нам нужно этого не допустить при любом значении x!

Единица получается в первом подвыражении в трёх случаях:

Выражение ¬(x ∈ P) получается ложно, когда (x ∈ P) будет истинно! Получается при x ∈ [5, 13] выражение ¬(x ∈ P) — ложно!

Выражение (x ∈ Q) ложно, когда x ∉ [8, 19]

Какой же минимальной длины должен быть отрезок A, чтобы этот случай не проходил при любом x ? При этом случае отрезок A должен быть равен [5, 8).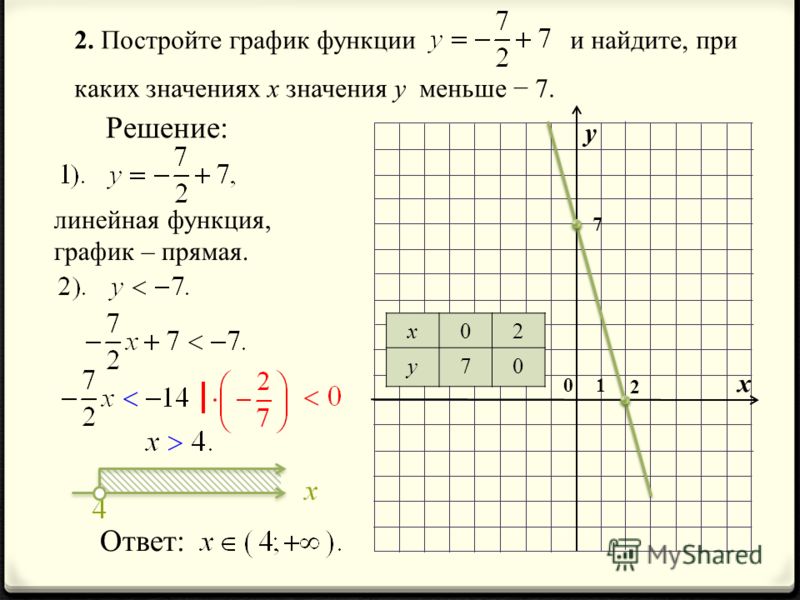 Тогда левое выражение пусть и может стать единицей при x ∈ [5, 8), но выражение (x ∈ A) будет также равно 1 при x ∈ [5, 8)! И схема 1 → 0 не пройдёт. Будет 1 → 1.

Для 1 случая A=[5, 8).

При каких x выражение ¬(x ∈ P) обращается в ноль, мы уже рассматривали: x ∈ [5, 13].

Второе выражение «выдаёт» 1 при x ∈ [8, 19].

Получается, что при при x ∈ [8; 13] первое выражение в скобках в главной формуле будет тождественно истинно!

С помощью отрезка A нужно это нейтрализовать путём превращения второго выражения в скобках в главной формуле в 1, пока x ∈ [8; 13]. Значит, для этого случая A = [8; 13]

В выражении ¬(x ∈ P) единица получается, когда в выражении (x ∈ P) получается ноль. Тогда x ∉ [5, 13]!

Чтобы во втором выражении (x ∈ Q) была единица, нужно, чтобы x ∈ [8, 19].

Получается, что 3 случай выполняется, если x ∈ (13, 19].

С помощью отрезка A нужно этому противодействовать! Нужно чтобы выражение (x ∈ A) было всегда 1 при x ∈ (13, 19]. Тогда A должно быть (13, 19].

Следовательно, для третьего случая A=(13, 19].

Нам нельзя допустить ни одного случая! Поэтому, объединив все случаи, получаем, что A=[5, 19].

Длина отрезка равна 14.

Ещё одна задача про числовую прямую из банка тренировочных заданий ЕГЭ по информатике 2021.

На числовой прямой даны отрезки P=[5, 13] и Q=[8, 19]. Укажите наименьшую возможную длину такого отрезка A, что формула ((x ∈ P) ∧ ¬(x ∈ A)) → ((x ∈ Q) ∧ ¬(x ∈ A)) верна при любых значениях x.

Первый способ (с помощью питона).

def F(a, b, x):
    if a 

Второй способ (с помощью рассуждений).

Формула может быть ложна, когда

Во всех остальных случаях, формула всегда верна.

Чтобы выражение ((x ∈ P) ∧ ¬(x ∈ A)) было тождественно 1, выражение (x ∈ P) обязательно должно быть тождественно 1. А, значит, x ∈ [5, 13] — это опасная зона, при которой появляется возможность обратить всю формулу в ноль!

Мы можем сразу пресечь эту опасность с помощью отрезка A. Выбрать такой отрезок, чтобы он всегда «выдавал» ложь при x ∈ [5, 13]. Для этого достаточно выбрать A=[5, 13]! Но вдруг его можно сделать ещё более маленьким за счёт правой части формулы ?

Предположим, что отрезок A сделали ещё меньшим. Тогда при каком-то x (x ∈ [5, 13]) выражение ¬(x ∈ A) будет «выдавать» 1! Причём такое же выражение стоит и в правой части формулы! Там тоже будет 1 для выражения ¬(x ∈ A).

Нас же в этом случае должно выручить выражение (x ∈ Q). Если оно «выдаст» 1 в этот «сложный» момент, то мы спасены! Ведь тогда получается, что правая часть всей формулы будет «выдавать» не 0, а 1. Посмотрим при каких x из отрезка [5, 13] приходит это спасение.

Видим, что в интервале x ∈ [8, 13] нас спасает выражение (x ∈ Q).

Значит, отрезок A можно сократить до A=[5, 8).

Длина отрезка будет равна 3!

Задача (Неравенство, две переменные, закрепление)

Для какого наибольшего целого неотрицательного числа A выражение

тождественно ложно, т.е. принимает значение 0 при любых целых положительных x и y ?

Первый способ (с помощью питона).

for A in range(0, 300):
    k=0
    for x in range(1, 301):
        for y in range(1, 301):
            if not( (x  603) ):
                k=k+1
    if k==90000:
        print(A)

Т.к. выражение должно быть ЛОЖНО, то обернём логическое выражение в функцию not(). Видим, что программа не сильно отличается от прошлой задачи. Данный шаблон подходит для большинства задач подобного типа.

Наибольшее число получается равно 25.

Второй способ (с помощью рассуждений).

В этой задаче нужно, чтобы общее выражение было ложно!

Если мы поставим отрицание над всем выражением, то можно искать такое максимальное A, при котором всё выражение тождественно истинно, а не ложно!

Здесь применили формулу де Моргана! Т.е. каждое подвыражение получило отрицание + соединительная логическая операция (логическое умножение) сменилась на противоположную операцию (логическое сложение).

Внесём отрицание в скобки. Получается:

Получили ситуацию, как в прошлой задаче! Напомню, что теперь нужно, чтобы общее выражение было истинно.

Найдём максимальное число, до которого могут «подняться» x и y, чтобы ещё работало третье выражение!

Обратите внимание, что x и y — симметричны. Значит, что верхняя планка для x и y будет одно и тоже число.

Поэтому вспоминаем таблицу квадратов.

Получается, что максимальное число до которого могут «дойти» x и y, чтобы «работало» третье выражение, равно 24.

Тогда, начиная с 25 для x и y, должны работать первое и второе выражение.

Получается, что максимальное число для A равно 25.

Ещё одна задачка подобного типа из тренировочных упражнений 15 задания ЕГЭ по информатике.

Для какого наименьшего целого числа A формула

for A in range(-300, 300):
    k=0
    for x in range(1, 301):
        for y in range(1, 301):
            if (3*x + y 

for A in range(0, 300):
    k=0
    for x in range(1, 301):
        for y in range(1, 301):
            if (x > A) or (y > x) or (2 * y + x 

def D(n, m):
    if n%m==0:
        return True
    else:
        return False

for A in range(1, 1000):
    k=0
    for x in range(1, 1001):
        if D(120, A) and (not(D(x, 70) and D(x, 30)) or D(x, A)):
            k=k+1
    if k==1000:
        print(A)

for A in range(1, 1000):
    k=0
    for x in range(1, 1001):
        if (x&49==0) or ((x&33!=0) or (x&A!=0)):
            k=k+1

    if k==1000:
        print(A)

def F(a, b, x):
    if a 

For the linear function f, f(6) = 4, and the graph of y = f (x)-Turito

Question

The correct answer is:

ПОДСКАЗКА:-  найдите уравнение линейной функции f(x), используя форму точки пересечения наклона, и наклон известен, найдите точку пересечения y, подставив (6,4){т.

е. f(6) =4] в уравнение .
Объяснение :
Шаг 1: найдите уравнение в форме пересечения наклона. Пусть отрезок y равен c и (дано)
Уравнение y = f(x) = mx + c
y = f(x) =  + c
Шаг 2: подставьте x = 6 и f(6) = 4
f(6) =  + c =4
3+c=4
∴c= 1
Подставим c= 1 в уравнение f(x)
Теперь f(x) = +1

Связанные вопросы для изучения

Общие

Математика-

Анри покупает 2 коробки синих ручек и несколько коробок черных ручек. В каждой коробке 10 ручек, и Генри покупает всего 50 ручек. Уравнение 10(x + 2) = 50 представляет эту ситуацию. Что из следующего является лучшей интерпретацией выражения x + 2 в этом контексте?

1. Количество синих ручек, которые покупает Анри
2. Количество коробок ручек, которые покупает Анри
3. Количество коробок синих ручек, которые покупает Анри
4. Количество коробок черных ручек, которые покупает Генри

Генри покупает 2 коробки синих ручек и несколько коробок черных ручек.

В каждой коробке 10 ручек, и Генри покупает всего 50 ручек. Уравнение 10(x + 2) = 50 представляет эту ситуацию. Что из следующего является лучшей интерпретацией выражения x + 2 в этом контексте?

/ask-a-tutor/sessions

Maths-General

1. Количество синих ручек, которые покупает Генри
2. Количество коробок ручек, которые покупает Генри
3. Количество коробок синих ручек, которые покупает Генри
4. Количество коробок черных ручек, которые покупает Анри

Общие

Математика-


В приведенной таблице представлены 100 предметов по типам и категориям. Элемент одного типа будет выбран случайным образом. Какова вероятность того, что выбранный товар будет в категории 3?

В приведенной таблице представлены 100 позиций по типам и категориям. Элемент одного типа будет выбран случайным образом. Какова вероятность того, что выбранный товар будет в категории 3?

/Ask-Ator /Sessions

Генерал математики

General

MATHS-

. футбольная команда забивает голы, равные среднему количеству голов за 29игры?


Исходя из приведенного выше графика, в скольких играх футбольная команда забила голы, равные среднему количеству голов в 29 играх?

/ask-a-tutor/sessions

Общая математика

Общая

Математика-

график отображается как константа или коэффициент в уравнении?

1. y-координата вершины
2. Точка пересечения с х
3. Точка пересечения с Y
4. Точка пересечения с линией симметрии по оси

Если y = 3x

² + 6x + 2 отображается в плоскости xy, какая из следующих характеристик графика отображается как константа или коэффициент в уравнении?

/ask-a-tutor/sessions

Maths-General

1. y-координата вершины
2. x-точка (точки)
3. y-точка пересечения
4. x-точка пересечения линии симметрии

Общий

Математика-

h(x) = −16x

² + 100x + 10
Приведенная выше квадратичная функция моделирует высоту снаряда над землей h в футах через x секунд после его запуска вертикально. Если y = h(x) отображается в плоскости xy, что из следующего представляет реальный смысл положительной точки пересечения x на графике?
1. Начальная высота снаряда
2. Максимальная высота снаряда
3. Время, когда снаряд достигает максимальной высоты
4. Время, когда снаряд достигает земли.

h(x) = −16x

² + 100x + 10
Приведенная выше квадратичная функция моделирует высоту снаряда над землей h в футах через x секунд после его вертикального запуска. Если y = h(x) отображается в плоскости xy, что из следующего представляет реальный смысл положительной точки пересечения x на графике?

/спросить репетитора/сеансы

Maths-General

1. Начальная высота снаряда
2. Максимальная высота снаряда
3. Время достижения снарядом максимальной высоты
4. Момент удара снаряда о землю.

General

Maths-

Ближе к концу американского кабельного новостного шоу ведущий предложил зрителям принять участие в опросе на веб-сайте шоу, в котором задавался вопрос: «Поддерживаете ли вы новую федеральную политику, обсуждавшуюся во время шоу?» В конце шоу ведущий сообщил, что 28% ответили «Да», а 70% ответили «Нет».

Что из следующего лучше всего объясняет, почему результаты вряд ли отражают настроения населения Соединенных Штатов?
1. Сумма процентов не равна 100%, поэтому любые выводы из опроса недействительны.
2. Принявшие участие в опросе не были случайной выборкой населения США.
3. Не было 50% ответов «Да» и 50% ответов «Нет».
4. Шоу не дало зрителям достаточно времени, чтобы ответить на опрос.

Ближе к концу американского кабельного новостного шоу ведущий предложил зрителям принять участие в опросе на веб-сайте шоу, в котором задавался вопрос: «Поддерживаете ли вы новую федеральную политику, обсуждавшуюся во время шоу?» В конце шоу ведущий сообщил, что 28% ответили «Да», а 70% ответили «Нет». Что из следующего лучше всего объясняет, почему результаты вряд ли отражают настроения населения Соединенных Штатов?

/ask-a-tutor/sessions

Maths-General

1. Проценты не составляют в сумме 100%, поэтому любые возможные выводы из опроса недействительны.
2. Принявшие участие в опросе не были случайной выборкой населения США.
3. Не было 50% ответов «Да» и 50% ответов «Нет».
4. Шоу не дало зрителям достаточно времени, чтобы ответить на опрос.

Общий

Математика-


Приведенные уравнения представляют собой две разные модели, которые можно использовать для определения стоимости конкретной машины в долларах через t лет после ее покупки. Какое из следующих утверждений правильно сравнивает значения E и V для 0 < t < 9 ?
1. E всегда меньше V.
2. E всегда больше V.
3. E изначально больше V, но со временем становится меньше V.
4. E изначально меньше V, но со временем становится больше V.

Приведенные уравнения представляют собой две разные модели, которые можно использовать для определения стоимости конкретной машины в долларах через t лет после ее покупки. Какое из следующих утверждений правильно сравнивает значения E и V для 0 < t < 9 ?

/ask-a-tutor/sessions

Maths-General

1. E всегда меньше V.
2. E всегда больше V.
3. E изначально больше V, но со временем становится меньше V.
4. E изначально меньше, чем V, но со временем становится больше, чем V.

Общий

Математика-

Сообщалось о весе в фунтах для 15 лошадей в конюшне, а также были найдены среднее значение, медиана, диапазон и стандартное отклонение для данных. Было обнаружено, что лошадь с самым низким зарегистрированным весом на самом деле весит на 10 фунтов меньше, чем заявленный вес. Какое значение останется неизменным, если четыре значения сообщаются с использованием скорректированного веса?

1. Среднее
2. Медиана
3. Диапазон
4. Стандартное отклонение

Были зарегистрированы веса в фунтах для 15 лошадей в конюшне, а также были найдены среднее значение, медиана, диапазон и стандартное отклонение для данных. Было обнаружено, что лошадь с самым низким зарегистрированным весом на самом деле весит на 10 фунтов меньше, чем заявленный вес.

Какое значение останется неизменным, если четыре значения сообщаются с использованием скорректированного веса?

/спросить-репетитора/сеансы

Maths-General

1. Среднее
2. Медиана
3. Диапазон
4. Стандартное отклонение

Общий

Математика-

График экспоненциальной функции h в плоскости xy, где y = h(x), имеет точку пересечения y с d, где d — положительная константа. Что из следующего может определить функцию h ?

1. h(x) = −3(d) ^x
2. h(x) = 3(x)d
3. h(x) = d(-x) ³
4. h(x) = d(b) ^x

График показательной функции h в плоскости xy, где y = h(x), имеет точку пересечения y с d, где d — положительная константа. Что из следующего может определить функцию h ?

/спроси у репетитора/сеансы

Общая математика

1. h(x) = −3(d) ^x
2. h(x) = 3(x)d
3. h(x) = d(-x) ³
4. h(x) = d(b) ^x

Общее

Математика-

Скорость 60 метров в секунду эквивалентна z метрам в минуту.

Каково значение z ?
1. 1
2. 600
3. 1200
4. 3600

Скорость 60 метров в секунду эквивалентна z метрам в минуту. Каково значение z ?

/ask-a-tutor/sessions

Maths-General

1. 1
2. 600
3. 1,200
4. 3,600

General

Maths-


The graph of the linear function f is shown. Какое уравнение определяет f ?

Показан график линейной функции f. Какое уравнение определяет f ?

/спросить репетитора/сеансы

Общая математика

Общие

Математика-

В плоскости xy, какова точка пересечения по оси y линии с уравнением 4 + y = -2x?

1. (4,0)
2. (2,0)
3. (0,2)
4. (0,4)

В плоскости xy какова точка пересечения по оси y линии с уравнением y = -2x + 4?

/спросить репетитора/занятия

Общая математика

1. (4,0)
2. (2,0)
3. (0,2)
4. (0,4)

Общие

Математика-

(x + 1) = 2 (x + 1)


Какое значение x удовлетворяет данному уравнению?
1. -1
2. 0
4. 1

(x + 1) = 2 (x + 1)


Какое значение x удовлетворяет данному уравнению?

/спросить репетитора/сеансы

Математика-Общая

1. -1
2. 0
4. 1
Общая

Математика07

Общая стоимость приготовления одной порции супа составляет .



No related posts.